Chapter 6
Achieving the Optimum in Spite of Constraints
In This Chapter
![]() Breaking down the effect of a change in prices into income and substitution effects
Breaking down the effect of a change in prices into income and substitution effects
![]() How consumers’ preferences are revealed
How consumers’ preferences are revealed
![]() Comparing income and substitution effects
Comparing income and substitution effects
The single most important part of microeconomics is the constrained optimization model, which is based on the idea that people act to achieve the best they can, given some kind of constraint that limits their choice. This way of looking at people’s decisions runs through most of the microeconomic syllabus, finding its way into all sorts of things from consumer choice to environmental or health economics. Yet its roots lie in the way economists look at individual decision-making.
To microeconomists, people optimize. When prices change, people respond to the information and react. Suppose you have $1 in your pocket to spend on a treat. You have two types of available treats, chocolate bars and cookies, and you start by getting your best mix of the two: that’s two of each to begin with. Now imagine that the price of cookies goes up. What do you do? Well, if you’re behaving as microeconomists suggest, you switch some of your consumption from cookies to chocolate bars so that you can keep your level of utility as high as possible.
Putting the constrained optimization model into place means dealing with the effect of prices on utility. Chapters 2 and 4 lay the foundations on consumer preferences and utility functions, and Chapter 5 deals with the budget constraint. This chapter starts from the optimum consumption bundle or point in Chapter 5, where the indifference curve is exactly tangent to the budget constraint, and shows you what happens when something changes.
We hope that, given your time constraints, this chapter helps maximize your utility.
Investigating the Equilibrium: Coping with Price and Income Changes
When investigating the effect of a price change, a good place to start is by thinking about what the change will do to the behavior of a representative consumer. Indifference curves (see Chapters 2, 4, and 5) excel in this situation!
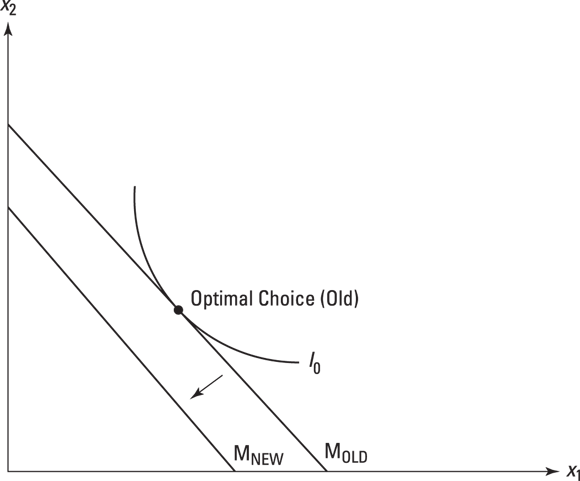
Start at a given equilibrium to get a sense of what is happening before you make changes. In this case, the plot in Figure 6-1 is an equilibrium with well-behaved indifference curves and a standard budget constraint, and at the consumer optimum, the price ratio equals the marginal rate of substitution between goods x1 and x2.
© John Wiley & Sons, Inc.
Figure 6-1: A parallel shift in the budget constraint simulates a change in income.
Now, imagine some situation that affects your income calamitously (such as losing your job, getting a new job that doesn’t pay as much, or a national economic disaster like that affecting Greece). The details don’t matter; the important thing is that it reduces your income.
Starting at the equilibrium, you can draw in a new budget constraint, one that’s parallel to the original one, but to the left of it. Of course, this means that the original equilibrium level of utility is now unattainable, and so you, as the representative consumer, react by reducing your consumption of goods x1 and x2 (see Figure 6-1). The parallel shift makes the old optimal choice unavailable, given the new constraint MNEW.
Dealing with Price Changes for One Good
This section explores what happens when a relative price changes. In reality, this tends to happen when people talk about price rises. Only very rarely do all prices change at the same rate, but in those rare cases the budget line merely shifts in and out in parallel with the original. More often, the price of one good changes while others don’t, or changes at a different rate than other goods. We take you through this scenario so that you can see its importance.
- The budget line, whose slope is the ratio of the two goods’ prices, changes.
- The equilibrium condition requires that the marginal rate of substitution (MRS) is equal to the ratio of the two prices. So, the slope of whatever indifference curve the consumer is now on after the price change must be different from the original (the point where the ratio of prices and MRS are the same).
Don’t worry if all this seems a little complicated. In this section, we break it down into simpler pieces in order to understand the behavior of the consumer.
Pivoting the budget line
In the optimization model, you take account of situations where one price changes by pivoting the budget line.
The budget line shows the maximum you can buy at the current prices. For example, you have $100, and a tennis racket costs $40, but a tennis lesson costs $20 per hour. You could buy one racket and have three lessons for the maximum, or two rackets (one for you and one for a tennis partner) and one lesson. Or you could buy five lessons and hope your old racket holds out. All these options are possible. But if the tennis lessons go up to $25, your options for substitution change. Now the maximum number of lessons you can buy while keeping your old racket falls to four.
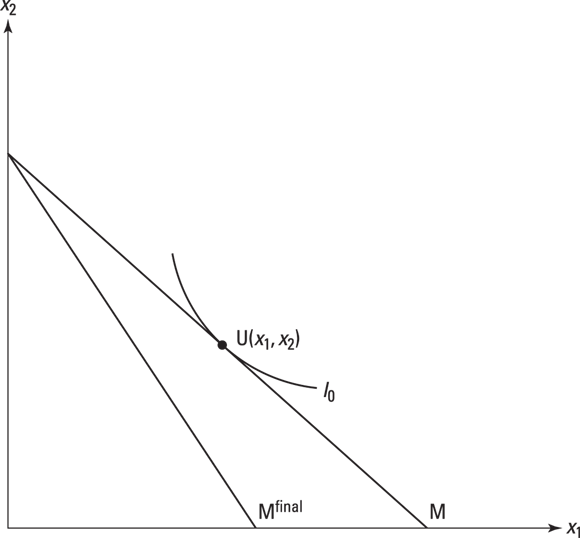
Figure 6-2 shows the old equilibrium (with indifference curve I0 tangent to the budget constraint, M). To this, we add the initial price change, which is illustrated by pivoting the budget line (as discussed in Chapter 5), so that the good whose price changes (x1) becomes more expensive, drawing in the line along the x axis (representing the ability a consumer has to purchase x1). This is the shape of the final budget line, and the slope of this line is the same as the MRS on whichever indifference curve the consumer ends up on. We label this Mfinal in Figure 6-2. In the figure, x1 and x2 = amounts of goods 1 and 2; M = budget constraint; U = utility at optimal bundle of goods, now unavailable; and I0 = the indifference curve at the old optimum.
© John Wiley & Sons, Inc.
Figure 6-2: Pivoting the budget constraint to simulate a relative price change.
Therefore, to simulate a rise in the price of good x1, you draw in the budget line so that maximum allocation to x1 is reduced from x1old to x1new. The optimal point on the old constraint is no longer available.
- Substitution effect occurs when a rise in the price of a good relative to other goods leads to a substitution away from the more expensive good and towards the less expensive ones.
- Income effect reflects the fact that when prices rise, people have less income or less purchasing power to spend overall.
The next stage of working through the change in the price of one good is to work out the two effects in two steps so that you can see clearly how they operate, as the following two sections demonstrate.
Seeing substitution in practice
Economists are interested in how people make decisions when they want to consume up to their budget constraint, but a price hike means that their previous level of preferred consumption is no longer attainable. Consider this example: A representative consumer (call her Kirsty) likes to meet up with her friends each week to watch movies and eat noodles. Suppose she has a total budget of $60 for her entertainment activities. If a movie costs $10, and a bowl of hot noodles costs $5, we will suppose that Kirsty maximizes her utility — remember, she’ll spend right up to the budget constraint if she can — when she goes to see a movie four times a week and has a bowl of noodles each time. Now suppose that — horrors! — the movie price goes up to $15: the movie becomes more expensive, relative to noodles. As a result, Kirsty can’t afford her optimal bundle. Now she will want to cut back on going to the cinema and instead consume more noodles. For example, suppose Kirsty re-optimizes by going two times to the cinema and eating noodles six times a week. Economists are interested in knowing how much of the change in her consumption bundle — two fewer movies and two more bowls of noodles — was due to movies becoming more expensive relative to noodles and how much was due to the reduced purchasing power of her weekly budget?
Of course, economists would like to set up the problem so that it’s as general as possible and doesn’t rely on in-depth knowledge about a particular person and a particular good. Kirsty makes these choices automatically, and economists want to set things up in a way that makes consumer behavior understandable and to some degree predictable.
Start with Figure 6-2 and draw a new shadow budget line parallel to the final budget line but tangent to I0 (though not at the original point of tangency — the slope of the new shadow budget line is different, which means that the optimal point where MRS on I0 is equal to the slope of the new shadow budget line will be different). We do so in Figure 6-3.

© John Wiley & Sons, Inc.
Figure 6-3: Unpacking the substitution effect.
The shadow budget line (MSHADOW) shows how the effect of the change in the price of x1 induces substitution, even in the absence of reduced purchasing power. In the figure, x1 and x2 = quantities of goods 1 and 2; M = budget constraint; I0 = indifference curve is tangent to original budget line.
Adding in the income effect
Here’s an example of the income effect, where someone’s original best bundle becomes unaffordable and the person consumes less in total. Ian, a representative consumer, would like to spend his weekly disposable income on shoot-em-up video games and pizza. He has $50 to spend. Initially a game costs $30 and a pizza $5, so he buys one game and has pizza four times a week. But — disaster — the price of video games goes up to $35. His initial consumption bundle is no longer possible, and he now gets only three pizzas a week because he doesn’t want to substitute away his game. There is no substitution effect, but still his total consumption must fall, from one game and four pizzas to one game and three pizzas. This is the income effect coming into play.
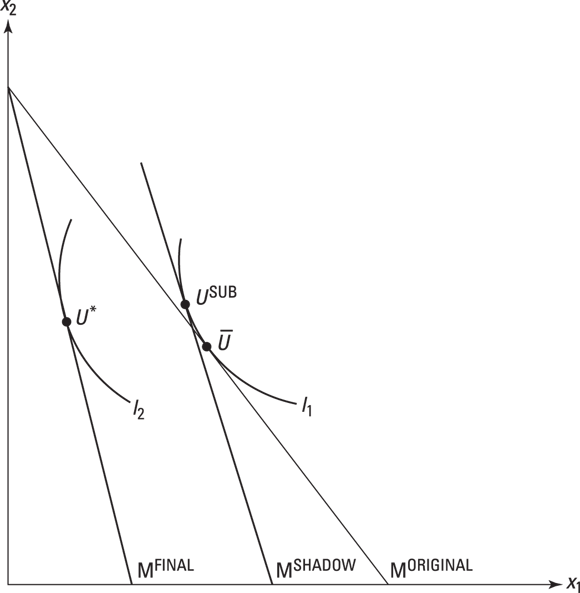
Again, economists want to generalize away from specific numbers and form a more general picture of the income effect. Follow along now as we show you the general model that economists use. The income effect occurs because the price change (and the corresponding shift in the budget constraint) means that the level of utility associated with I0 is no longer available. Thus, the economically rational consumer optimizes by shifting down to a new indifference curve denoted by I1 in Figure 6-4. As we discuss in the preceding section, MSHADOW covers the relative price changes, and so the move from MSHADOW to MFINAL just deals with the fact that the purchasing power of income has gone down.
© John Wiley & Sons, Inc.
Figure 6-4: Shifting back the shadow curve to investigate the substitution effect gives a new optimum U*.
Different strokes: Different goods have different income and substitution effects
The relative size and, in some cases, direction of the income and substitution effects depend on the type of good you’re examining. For instance, if (from the consumer’s point of view) a good has many close substitutes, the substitution effect is likely to be large (infinitely so in the case of perfect substitutes), and the income effect negligible. But if the good has no close substitutes and the consumer continues to buy roughly the same quantity at the higher price, the income effect is likely to be much larger compared to the substitute effect.
- Income elasticity: Measures the responsiveness of purchasing to a change in income. Normal goods are those that have income elasticities (see Chapter 9 for details) around 1, meaning that if income rises by 10%, consumption of those goods also rises by around 10%. But some goods (such as luxuries) respond more dramatically or elastically to income changes, whereas some respond less elastically and in some cases even negatively. A good is considered inferior if consumption of it falls as you become richer. Whether a good has an income elasticity of greater or less than one or is negative depends on consumer tastes.
- Existence and closeness of substitutes: When the two goods are perfectly interchangeable from a taste perspective, the indifference curve is a straight line and so a rise in the price of one substitute results in substitution away to the cheaper option. (Given the same units of measurement, the slope of the indifference curve is 1, so unless the prices are equal, the consumer gets to the highest indifference by buying the cheaper good. When the prices are same, the indifference and the budget line coincide.)
- Ability of a consumer to switch: An implicit assumption here is that switching from one option to another is free and costless, which isn’t always true — as you know if, say, you’ve tried to switch operating systems on your computer or your cell phone plan. Economists dealing with markets in information technology have to adapt models to add in switching costs, which are derived from, among other things, the cost of learning to use a technology or of giving up a network of users.
Discerning a Consumer’s Revealed Preference
Given the preceding section, you can say a few more things about the relationship between preferences and the budget constraint. One is about the principle of revealed preference. Utility isn’t measured, but things about utility can be found out by observing consumer choices and inferring from their choices the impact of price changes on their utility or welfare.
This somewhat back-to-front way of looking at things makes sense when you realize that economists know nothing about the consumer until he participates in a situation where inferences can be made regarding his behavior. For example, suppose the government levies a tax on a good. From the consumer’s perspective, it is as though the price of the good has increased and the consumer will be made worse off and hence will not be happy about the tax. The government may try and compensate the consumer by transferring a rebate to him that’s equivalent to the tax revenue collected. However, the principle of revealed preference tells us that the consumer will still be worse off under the tax and rebate scheme.
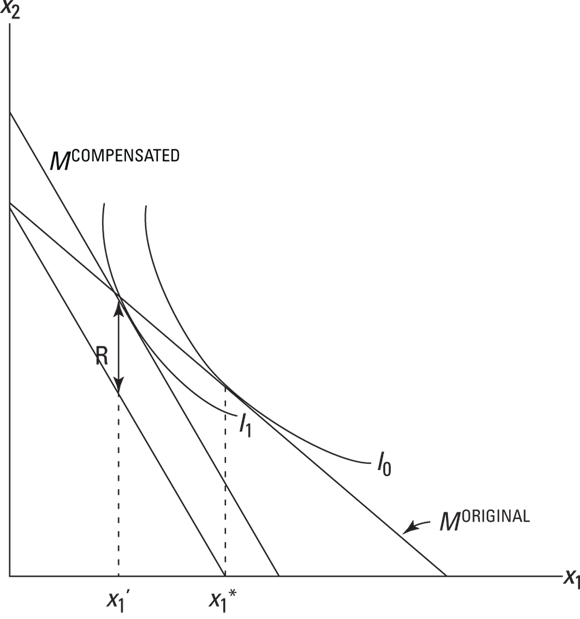
This is shown in Figure 6-5. When the consumer faces prices p1 and p2 and has an income M, the consumer optimizes by choosing the bundle (x1*,x2*). Now the government imposes a tax on good 1 so that the price becomes p1'= p1 +t. At the same time, the government offers the consumer a rebate R equal to the tax revenue it collects from the consumer. With this budget constraint, the consumer chooses the bundle (x1',x2') and we have that (p1 +t) x1'+ p2 x2' = M + tx1' where the rebate R is equal to the tax revenue tx1' collected. Simplifying this expression, you can see that it is equivalent to p1x1'+ p2 x2' = M. In other words, the bundle (x1',x2') lies on the original budget constraint but the consumer did not choose it. The consumer preferred (x1*,x2*). This tells us by revealed preferences that the consumer is on a higher indifference curve or level of utility with (x1*,x2*). The imposition of an income compensated tax still made the consumer worse off.
© John Wiley & Sons, Inc.
Figure 6-5: Revealed preference and income compensated tax.
Decomposing Income and Substitution Effects
The income and substitution effects of a change in prices occur simultaneously when someone makes a choice. When introducing these two effects in the earlier section “Pivoting the budget line,” however, we break them down so that the changes occur sequentially — pivoting the budget constraint indicated the substitution effect, and shifting it indicated the income effect.
Another way to gain insight into these two effects and their magnitude is to pivot the budget equation after a price change so that the consumer could afford the pre price change bundle. This approach uses a construction that is called the Slutsky equation, after the microeconomist Eugen Slutsky.
Remember that when a price changes, it causes two effects on the consumer:
- A substitution effect emerges when the budget line pivots, showing how much the change in consumption of one good changes relative to the other good.
- An income effect emerges when the budget line gets shifted to take into account a change in the total amount of money a consumer possesses.
Unpacking the effect of a price change in a model with two goods
In this walk-through, we consider a decrease in relative price that allows a representative consumer to afford more of the two goods. In Figure 6-6, the consumer substitutes towards the cheaper good: x1 OLD = old level of consumption of good 1; x2 OLD = old level of consumption of good 2; x1 NEW = post change consumption of good 1; x2 NEW = post change consumption of good 2 I0 = original indifference curve; I1 = new indifference curve; Mold = old budget constraint; Mnew = new budget constraint.
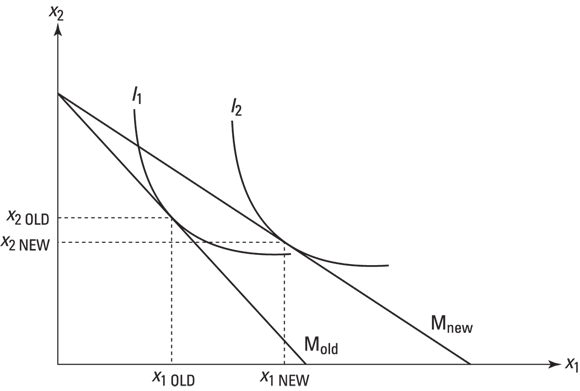
© John Wiley & Sons, Inc.
Figure 6-6: A change in consumption when a price falls.
Here’s the equation of a budget line (from Chapter 5):
![]()
![]()
For consistency, the equations show M as the original sum of money, M' as the changed sum, and p1 as the original price of good x1 and p1' as the changed price.
Now subtract the first equation from the second, and here’s what you get:
![]()
Use the shorthand of Δ to indicate a change so that M' – M = ΔM and p1' – p1 = Δp1, and substitute into the equation so that ΔM = x1Δp1.
Getting what you prefer
From the preceding section, you have a (slightly abstract) equation for determining what happens to income (M) and price (p1) when a representative consumer wants to keep the quantity of x1 he’s consuming at the same level.
Here’s an example to show how a consumer substitutes to keep utility at an optimum level: Carol has a bit of a coffee habit. Every week she allocates $10 of her disposable income to getting coffees at work. Each coffee — her choice is a vanilla latte — costs $2 (and she consumes up to her budget line, a maximum of $10, and has five coffees a week). Now suppose her coffee rises to $2.20, (from bad weather affecting coffee growers in Columbia) and she wants to keep her consumption at five delicious vanilla lattes a week. What must happen to her income to do so?
Developing the substitution effect in numbers
The model in the preceding section demonstrates the changes in M that will allow Carol to keep her original consumption level the same after the change in price. But when the budget line pivots, the bundle that was optimal usually is no longer optimal, because the relative prices of the two goods have changed, making one relatively dearer than before. Thus, the consumer is most likely to optimize by substituting towards the relatively cheaper option.
Meeting the useful demand function
![]()
Discerning the change in demand
The purpose of the exercise is to evaluate x1 (the old optimum) and x1' the new optimum when p1 and M change. The old level of demand is in the above equation and the new one is:
![]()
![]()
From this equation, you can see that when you know the change in demand and the level of money required to keep x1 the same, you can work out the substitution effect (see the next section).
Calculating the substitution effect from a demand function
Here we make an assumption about the shape of a particular demand function and take a look at the substitution effect. Adam needs to use his car for transport and buys gasoline in gallons from the local garage. His demand is described by the following function:
![]()
His allocatable income, M, is $240, and we assume that gas costs $3 a gallon. Prices for benchmark crude oil have plummeted and — somewhat implausibly — all that is being passed on to consumers, meaning Adam now pays $2 a gallon. As his microeconomist friend, you’re fascinated by this change in his fortunes, and you want to calculate how large the substitution effect is as Adam changes consumption in response to price (as his demand function tells you he will).
You know from his choices which of two feasible bundles Adam would prefer, because that was revealed when he chose. But to make a calculation, or prediction, you need an idea of the general relationship between the price of gasoline and the quantity demanded, derived by knowing how much gets bought at any particular price.
You’re in a quandary: You really want to show how much of the change in quantity consumed depends on substitution and how much on change in income, but you can’t know that until you know the relationship between price and total change in demand. As described in the earlier section “Discerning a Consumer’s Revealed Preference,” microeconomists never know what preferences exist until they’re revealed by a consumer making a choice. You can’t know until you’ve worked out that general relationship, but underlying that relationship are the substitution and income effects. As a result, you have to start by gaining intuition about how Adam may behave and then building up a consistent picture of the relationship between price and quantity.
Therefore, learning consumer theory is a little circular and requires you to work backwards in order to move forward. In this example, Adam’s demand function (see the preceding equation) relates quantity consumed (x1) to the price of good 1(p1) and the amount of income he had M ($240). So you can start performing your clever calculations given this simple relationship to work with.
-
Take Adam’s demand function and evaluate x1 for M and p1.
You know Adam’s original demand, and so you calculate x1 for the demand function. Plugging in 240 for M and 3 for p1 you get 28 gallons of fuel bought per week.
-
Find the value of M' that keeps x1 the same when p1 changes.
You apply the formula ΔM = x1Δp1. You know that x1 equals 28 and that Δp1 = (2 – 3) = –1, and so M must change by –$28. That means the new value of M' must be 240 – 28, which equals (ta-da!) $212.
-
Plug M' and p1' back into the demand function to evaluate new demand.
Going back to the original equation for Adam’s demand for gas, you put in the new numbers for M ($212) and p1 and now calculate: X1 = 20 + 212 / (10x 2) = 30.6 gallons.
-
Apply the formula for the substitution effect.
You use the equation

and plug in 30.6 for x1 (p1', M') — the new compensated demand from step 3 — and 28 for x1 (p1, M) – the original demand. Therefore, the substitution effect is responsible for 2.6 gallons of extra fuel being purchased per week.
If you simply plug in a value for p1' in the original demand function, you get an answer for the total change in demand (which you can verify by plugging in the numbers and see that it comes to 4 gallons). But this way, you identify that of the 4-gallon increase in demand, the substitution effect is responsible for 2.6 gallons, or 65% of the total change in demand.
Adding up the income effect
The other effect of a change in price is to change the purchasing power of the consumer. If the price of a good changes, it’s tantamount to arguing that a consumer’s income has also changed, because the new budget line either restricts the level of demand (when the price of a good goes up) or allows consumption of goods that were previously unavailable (when the price of a good goes down).
In the preceding section, you model the change in purchasing power by shifting the budget line out. But you can also use some clever adaptations to that process to make a calculation of the income effect on Adam’s demand — and of course adapt them to other demand situations.
To express the income effect mathematically, write the following:
![]()
Now plug in Adam’s numbers from the preceding section. For the expression x1 (p1', M) calculate his demand using the changed price of 2, but the uncompensated level of income, 240. You get this:
![]()
Evaluate demand given the compensated income from step 2 in the preceding section:
![]()
Apply the formula for the income effect, taking the second answer from the first, to get an answer of 1.4 gallons of gas.
The sum of the two effects comes to the total change in demand, and so although his demand changes by 4 gallons overall, the income effect is responsible for 1.4 gallons and the substitution effect for 2.6 gallons.
Putting the two effects together using the Slutsky equation
Put simply, the Slutsky equation says that the total change in demand is composed of an income and a substitution effect and that the two effects together must equal the total change in demand:
![]()
This equation is useful for describing how changes in demand are indicative of different types of good. Indifference curves are always downward sloping, and so the substitution effect must always turn out to be negative. But the income effect may not be, depending on how consumption of a good changes with income. A normal good has a negative income effect, and so if the price goes down and hence purchasing power or income goes up, then demand goes up. The reverse holds when price goes up and purchasing power or income falls, because then so does demand.
But not all goods are “normal.” Some are inferior in an economic sense. We don’t mean that they’re of poor quality but that they have a negative income profile — as income goes up, a person consumes less of them. Instant noodles, for instance, aren’t generally held to be a product that people consume unless they’re constrained in terms of money; as you get richer, you consume less of them. In this case, the substitution effect is negative, but the income effect is also negative. For the opposite situation, see the nearby sidebar “Giffen goods.”

 Suppose instead that just one price changes (remember, you can treat x1 and x2 as though x1 is the good you’re interested in and x2 represents all other goods). This is an interesting situation, because the effect on your purchasing opportunities isn’t due to an overall fall in income, but to the relative price effect whereby x1 is now more expensive relative to the price of all other goods available. This situation is where indifference curves fully unpack their awesome power — check out the next section.
Suppose instead that just one price changes (remember, you can treat x1 and x2 as though x1 is the good you’re interested in and x2 represents all other goods). This is an interesting situation, because the effect on your purchasing opportunities isn’t due to an overall fall in income, but to the relative price effect whereby x1 is now more expensive relative to the price of all other goods available. This situation is where indifference curves fully unpack their awesome power — check out the next section. When the price of one good changes:
When the price of one good changes: To put revealed preference as simply as possible, if a consumer chooses a bundle of goods — call it A — over another bundle — B — given that both B and A are affordable, you can say that the consumer prefers A to B. In other words, the act of choosing the bundle A reveals that the consumer preference is for bundle A over bundle B.
To put revealed preference as simply as possible, if a consumer chooses a bundle of goods — call it A — over another bundle — B — given that both B and A are affordable, you can say that the consumer prefers A to B. In other words, the act of choosing the bundle A reveals that the consumer preference is for bundle A over bundle B. You calculate the substitution effect by stripping out the effect of income (in other words, step 2): finding the level of income that compensates for the change in price is key. If you don’t find the compensated demand, you’re looking at total change in demand and not the size of the substitution effect.
You calculate the substitution effect by stripping out the effect of income (in other words, step 2): finding the level of income that compensates for the change in price is key. If you don’t find the compensated demand, you’re looking at total change in demand and not the size of the substitution effect.