Chapter 9

Related Techniques

Learning objectives

After studying this chapter, you should be able to:

1 Understand the basic approaches to scenario analysis and stress testing and the pros and cons of these two approaches

2 Outline the benefits of operational risk models and the differences between top-down and bottom-up approaches

3 Explain the more common top-down models such as stock factor, income-based, expense-based, operating leverage, and risk profiling models

4 Explain the more common bottom-up models such as asset and liability management, market factor, causal, and operational variance models.

Introduction

The previous chapters outlined the process of operational risk management, from the early stages of identifying and categorising risk, through the process of developing an operational risk management framework, measuring risk, limiting it, and reporting it. Here we delve deeper into the process of analysing risk, outlining in deeper fashion a series of tools and operational risk models.

Scenario analysis is particularly useful to understand the impact of operational and business events by creating scenarios and taking them to their conclusions. Effective scenario analysis considers the likely, the probable, and the improbable. Because it is very subjective, scenario analysis is also very flexible, and there is its strength.

Stress testing is another useful tool to consider the impact of events. In typical stress testing, key risk factors like price, volume, resources, and quality levels are tested to levels well beyond normal operating ranges. Like scenario analysis, stress testing has its limitations, not the least of which is its deceptive simplicity. The choices that operational risk managers make in deciding what factors to test and how far to test them are often subjective and the process can become useless if the criteria to select them is not strict.

This chapter also examines operational risk models that can be used as part of an advanced measurement approach (AMA) to operational risk. There are two fundamental approaches to modeling risk: top-down and bottom up. The top-down approach does not attempt to identify causes or losses. Bottom-up approaches, on the other hand, require strong databases with plenty of data on risk factors and events. The more common top-down approaches include stock factor models, income-based models, expense-based models, operating leverage models, and risk profiling models. Common bottom-up approaches include asset and liability management models, market factor models, causal models, and operational variance models. Choosing the right risk model is not a question of one or another; rather, it is best to think of risk models as complementary. Each addresses one aspect of operational risk. Several together can paint a comprehensive picture.

Scenario Analysis

Scenario analysis is a qualitative tool to better understand the impact of major operational and business events, and thereby develop contingency plans in response. It is top-down, strategic, and externally focused. It creates a number of scenarios—essentially stories describing a particular combination of events in an envisioned future. By definition, these events are abnormal, infrequent, potentially catastrophic, and therefore often without extensive statistically relevant data.

Some scenarios describe external shocks such as massive credit and market losses. Others focus on internal operations such as a key systems failure, major regulatory changes, loss of key people, or class action suits. It is useful to consider major debacles that have happened to other firms, and to develop appropriate preventive measures and contingency plans. Indeed, scenario analysis should consider even the improbable, as for example:

• A new settlement system implemented at the bank cannot be reconciled with the original system. As a result, payments cannot be made and trades cannot be booked.
• A large corporate client sues the investment bank because the IPO prospectus the bank prepared did not disclose all the necessary risks associated with a particular transaction.
• A major political event occurs in a country where the bank has large investments.
• A firm’s leading five credit exposures are hit by market movements of 15%.
• An employee embezzles funds for a year before being caught.
• Sluggish economic conditions reduce lending volumes to half of expectations.
• A retail staff strike.
• A disgruntled employee sabotages the computer systems, undermining the bank’s reputation.
• Government increases the corporate tax rate by 20%.
• A major political group makes unfounded attacks on the firm.
• There is inadequate due diligence of the firm’s public issue prospectus.
• Non-reconciliation between general ledger and back-office systems leads to incorrect published results.

Because compiling statistics on unexpected events is difficult, scenario analysis is most appropriate to apply to important infrequent occurrences and catastrophic losses typically driven by external events. The flexibility of scenario analysis derives from its subjectivity. Scenarios chosen for consideration are often based on either the analyst’s idiosyncratic historical experiences or his or her subjective assessment of the risk factors affecting the bank’s environment. The analysis is also subjective because it lacks an explicit model of the firm’s asset-sensitivities to guide the financial impact of different scenarios. Moreover, scenario analysis tells us nothing about the actual risks because we do not know how likely a particular scenario could be.

Nonetheless, scenario analysis is useful because it helps managers to question their assumptions, distinguish the firm’s sensitivities to catastrophic loss, and develop contingency plans. In any case, for most users of scenario analysis, the aim is prescription, not prediction. Managers use the scenarios to learn how to cope with uncertain future occurrences. Scenario analysis helps to rethink the assumptions behind prevalent business practices and to suggest other approaches in the future. Scenario analysis also is useful in times of extreme uncertainty and ambiguity in a business because it is evolving rapidly or is complex with many different interrelated causal forces.

Stress Testing

In a stress test, key risk factors such as price, volume, supplier price, resource availability, and quality level are “stressed” or given values beyond their normal operating ranges. The aim is to discover the impact on the bank if the selected risk factors hit abnormal levels. The test may also uncover deficiencies in processes and systems that may cause unexpected problems and point the way in redesigning systems internally or updating embedded controls.

Like scenario analysis, a stress test estimates the impact of an event and not its frequency and, therefore, captures only a single dimension of the risk. A stress test also usually ignores the relationship between different stress factors, although this could be captured by correlations (if data were available) or more likely through informal scenario analysis.

Despite these simplifications, stress testing can be a powerful diagnostic tool for operational risk management. We can stress information and communication systems using mock data to discover their deficiencies. For example, the Y2K computer problem in a settlement system can be studied by feeding a day’s worth of mock transactions dated after the year 2000 (after of course taking the system offline). We might estimate the impact of a tenfold increase in volume or estimate the downstream implication of a jump in the number of processing errors.

Limitations

Like scenario analysis, a stress test has its strengths. It is easy to set up—one only needs to give extreme inputs and analyse the results. It exposes hidden problems so they can be dealt with early. It reveals the inherent structural limitations of a given system—operating parameters can be set more realistically or the system can be redesigned. It also can be used by audit and internal control to evaluate existing controls.

However, the very simplicity of stress testing can be deceptive. The choice of factors to stress, systems to focus on, and linkages between risk factors and impacts can all be subjective and uncertain. It can quickly become an ad hoc process if strict criteria are not determined for selecting the systems and variables to stress. The wide range of potential stress that can be tested makes the technique potentially time-consuming and a source of data overload. It can be disruptive if real-time systems need to be stressed. A stress test is usually simplistic and does not consider the effects of combinations and relationships between variables (or they are assumed as constant).

Extreme Events

Stress tests, which stretch standard limits of known values to levels that are beyond the regularly tolerable, can be particularly useful to measure the ability of a bank to deal with extreme events or “acts of God” such as natural disasters that occur not at the hands of mankind but from nature. Most natural disasters happen because of abnormal weather, shifting of the Earth’s layers, or other occurrences over which humans have no control. What we can control, however, is the severity of the consequences of the natural disaster. This is true also of man-made accidents and intentional acts that cause disasters, such as terrorist attacks.

Disasters may seem disparate—a spewing volcano in Iceland seems quite different to a tsunami in Southeast Asia, and a terrorist attack in Tokyo, Japan, seems quite unlike a lethal gas leak in Bhopal, India. Yet in each catastrophe there is a pattern that is common to all. Each ingredient in this “recipe” can be thought of as an underlying risk factor that, when present either alone or in combination with other risk factors, chips away at a wall of safety that we try to build into our lives. Once that wall is weakened, a situation may unravel to tragic proportions.

We can discern ten basic risk factors related to man-made accidents, natural disasters, and intentional acts, and the catastrophic losses they can cause to banks and other organisations:

• Design and construction flaws. Major facilities, such as power plants, skyscrapers, refineries, and ships, are built according to detailed blueprints or design specifications. These are based on engineering analyses that focus on designing the structure to withstand the forces that will be imposed on it, such as load, wind, vibration, puncture, or blast. If a flaw in the design process is not discovered in time, the structure may fail when it is hit by natural forces. This can lead to a partial or complete collapse of the facility. Even when the design specification is valid, problems can arise if the materials used in the building components are faulty or the components are not assembled properly. In either event, the integrity of the structure is weakened, making it prone to failure.
• Deferred maintenance. Discovery of a mechanical problem often sparks an internal debate on whether the operation should be shut down and the glitch fixed immediately, or whether it should be kept running and the problem repaired at a more convenient time. Human nature tends to put off a problem, especially if the system is not actually malfunctioning. But deferring maintenance often leads to the breakdown of a key system component, resulting in a serious accident. Moreover, in cultures where maintenance problems are customarily deferred, the situation is ripe for the collapse of multiple components, thereby exacerbating and intensifying the consequences of an ensuing accident.
• Economic pressures. Limited funding is another common risk factor, whether in building a bridge, transporting cargo, or constructing a building. Resources therefore must be invested wisely—budgets that are too tight or spending that is badly controlled can encourage cutting of corners. This can result in shoddy workmanship, buying inferior-quality materials, or doing away with back-up operating and safety equipment. Budget constraints alone may not be the root cause of a disastrous event, but they are often the catalyst for human error that initiates the disastrous event.
• Schedule constraints. Economic pressures and schedule constraints often go hand in hand as risk factors. When a project or operation falls behind schedule, the pressure to claw back the time lost may result in ignoring important details. This could mean either eliminating certain critical steps entirely, or completing them in a cursory manner or out of sequence. Like economic pressure, schedule constraints can act as a catalyst for committing errors in judgment that can lead to catastrophe.
• Inadequate training. The complexity of modern technology and the highly integrated nature of various systems require several important functions to be performed by highly trained individuals. The trouble is that some organisations view training as a burden because it can be costly and takes employees away from actual production. This short-sightedness can lead to inadequately trained individuals being placed in positions of responsibility. Problems can also arise when personnel shortages force individuals to cover for others in key functions for which they are inadequately trained. Moreover, retraining is needed at regular intervals because most people tend to forget what was originally taught and because processes change over time and require new learning.
• Neglecting procedures. It is the duty of supervisors to ensure that each employee follows standard procedures. Yet procedural errors are at the root of many disasters. One reason is that engaging in a repetitive activity can lead to complacency, and to drifting away from following a strict protocol. An individual may neglect certain steps or may invent other ways to accomplish the task, without thinking of the ramifications on safety. Neglect of procedures can create a hazardous situation, which can be exacerbated by co-workers performing functions on the assumption that those procedures have been followed.
• Lack of planning and preparedness. Proper planning and preparedness are a pro active way to improve understanding of, and response to, a potential disaster. Depending on the nature of the threat, the focus can be on prevention, mitigation of consequences, or both. Planning and preparedness include the gathering of knowledge (intelligence), assessment of the likelihood and consequence of various disaster scenarios, evaluation of alternative risk-reduction strategies, and execution of exercises to determine state of readiness and the effectiveness of ongoing efforts.

• Communication failures. This can occur at various stages of a disaster, altering an outcome in different ways. One common form is among members of the same organisation, when critical information is not shared. For example, one group decides to shut down a key protection system for maintenance, but neglects to alert another group, which at the time is executing a dangerous experiment. Poor communication among different organisations can also cause problems. For example, two agencies engage in a response effort but each is unaware of what the other is doing. Finally, insufficient or inaccurate communication to the public can put lives at risk because people are neither properly informed of the dangers nor advised on protective measures.
• Arrogance. This human trait is a risk factor that can complicate an otherwise safe operation. Arrogance usually manifests itself in the person in charge who wants to succeed for individual gain with little heed for the safety of others. It is also seen in an experienced person who is overconfident of his or her ability to deal with a problem. Either form of arrogance may have serious repercussions. Institutions can also be arrogant. An organisation can have a culture that disregards others, is overconfident of its ability to solve problems, or is disdainful of beliefs and opinions that question desired objectives.
• Political agendas. Hard-nosed political agendas leave little room for dialogue and compromise, and disgruntled parties often resort to extreme measures in response. Historically, political agendas have been intimately linked to the majority of terrorist acts, which are reactions to what the aggressors perceive to be oppressive government policies. This risk factor is also seen in countries whose governments, in their bids to become economically competitive, are ready to relax safety rules to attract business, or whose desire for an elevated status in global politics puts its citizens at greater risk.

A reading of the ten basic risk factors listed above shows that human involvement is present in each of them. In other words, humans contribute to the cause and impact of every disaster. However, we also have an opportunity to control these risk factors better and achieve a better outcome. Towards this end, the first step would be a careful review of disasters. The sequence of events that caused the calamity should be reviewed to analyse what went wrong. Useful lessons on how to better control these risk factors can then be extracted. These can be coupled with a review of actions taken after each disaster in order to evaluate their effectiveness. All these initiatives can help to decrease the risk of a repeat of the disaster, and increase our ability to withstand its impact if it does recur.

Operational Risk Models

Typical approaches to calculate the operational risk capital charge are not always entirely accurate. Broad-strokes approaches to measuring risk such as the basic indicator approach (BIA) tend to overestimate or underestimate the capital charge. Institutions that use an advanced measurement approach (AMA), on the other hand, have a greater chance of coming up with accurate capital charges, but they need to examine bigger volumes of internal and external data.

There are many operational risk models that banks can use to develop their AMA framework. Broadly speaking, operational risk models follow two fundamentally different approaches: the top-down approach and the bottom-up approach. Top-down approaches quantify operational risk without attempting to identify the events or causes of losses. They use aggregate targets, such as net income or net asset value, to analyse the operational risk factors and loss events that generate fluctuations in a target. The principal advantage of top-down approaches is that little effort is required to collect data and evaluate operational risk.

Bottom-up approaches require robust databases. They quantify operational risk on the micro-level, disaggregating measures of company performance into many sub-measurements and evaluating the impact of various factors and events on these sub-measurements. The results are integrated to produce aggregate effects on performance, which are incorporated into the overall charge calculation. The advantage of bottom-up approaches over top-down approaches lies in their ability to explain the mechanism of how and why operational risk is formed within an organisation.

Note that operational risk models are used not only for capital allocation reasons (e.g., to help estimate the operational risk capital charge). They can be, and are, also utilised towards achievement of wider objectives such as internal control, capital management, efficiency, and growth. Given their different uses, the various risk modelling techniques should be regarded as complementary. No single risk model can provide a comprehensive solution to the operational risks (and other risks) facing an organisation.

Top-Down Risk Models

The simplicity of top-down risk models and the low level of resources required are advantages in situations where cost is an issue or the use of a more accurate bottom-up model does not have the support of various stakeholders.

But a top-down model has limitations. An operations manager may not see it as very relevant because the source of the operational loss is not made explicit and therefore is not actionable. Top-down models that estimate operational risk as a residual are always backward-looking; it is difficult to extrapolate the results to the next period. However, if internal factors are used to explain operational risks, as in expense models, then a top-down model can be used proactively to project the operational risk over the next period.

Stock Factor Model

If a company is a listed entity, its current market value can be used as a performance target. The stock factor model is similar to that for estimating a stock’s beta; it requires an estimate of the sensitivity of the stock’s rate of return to different factor returns.

For example, we can use a simple linear regression to explain stock returns:

where

rt = the rate of return on the firm’s equity

ΔPti/Pti = the ith factor return, and

the estimates of bi give the sensitivity of changes in the factor.

Knowing the risk factors driving the security price indicates the likely impact of market movements on net earnings, and any inconsistency with this assumption is presumed to be the result of operational risk. The latter therefore can be estimated by the level of total variance not explained by the model, as shown in Exhibit 9.1.

EXHIBIT 9.1 Stock return models

Christopher Marshall, Measuring and Managing Operational Risks in Financial Institutions (Singapore: John Wiley & Sons (Asia) Pte Ltd, 2001), 101.

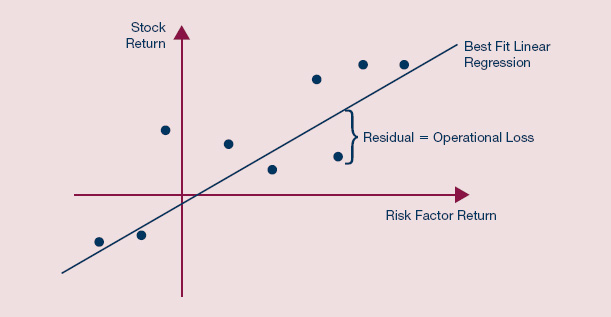
Like other such models, the stock-based approach can be executed fast and cheaply. Moreover, the process is transparent and needs few assumptions about accounting conventions. The stock-factor model is particularly useful for conglomerates with several publicly traded business units.

Income-Based Model

Consider this scenario: management has a short-term focus, a need for immediate income statement protection, and access to data on the bank’s historical earnings. In this instance, an income-based model to measure operational risk is both inexpensive and effective. Income-based models of operational risk, sometimes referred to as EaR (for earnings at risk), analyse historical income or losses in terms of specific underlying risk factors. These latter risk factors are external to the bank and include historical market, industry, and credit factors.

Like the stock factor model, the income-based model assesses operational risk as a quantitative residual after external factors have been removed from the historical earning fluctuations. More accurate (and more complex) income-based models can be developed by integrating separate factor models for revenues (prices and volumes) and external factor-related costs. The historical residual between the predicted pre-tax income and actual income is assumed to be the operational risk.

There are constraints to the income-based model. Creating a hierarchy of factor models requires substantial data and extensive modelling skills. One difficulty with this model is the difficulty of getting several years of relevant historical data. Monthly earnings or loss information are typically used in the analysis. The volatility of annualised earnings or losses is inferred by assuming that earnings or losses follow a Wiener process.1

Provided historical data is available, an income-based model can be built quickly. It can easily be used for capital allocation because it incorporates diversification across business areas. However, by focusing on net income, it ignores operational factors and events that affect long-term assets and liabilities on the balance sheet. As such, an operations manager may not consider the model to be very relevant since it is not explicit about the source of the operational loss.

Expense-Based Model

The expense-based model associates operational risk with fluctuations in historical expenses. This approach involves gathering historical expense data, adjusting the data to reflect structural changes in the organisation, and then estimating unexpected losses as the volatility of the adjusted expenses. Expense volatility refers to the operational errors, fines, and losses that a business may incur during its operations. These are generally posted to the profit-and-loss (P&L) accounts in the general ledger.

Expenses can be scaled according to a constant basis (e.g., assets, volumes, staff levels) to incorporate the impact of any organisation-wide event that significantly changes the level of expenses (for example, a merger or acquisition, or major change in staffing and systems). A more formal method would be to use time-series models that strip out the effect of the event on the expenses.

The main advantages of the expense-based model are its simplicity and low cost. But a focus on expenses captures only part of the risk—non-expense risks such as reputational risk and opportunity costs are ignored. Such an approach also penalises risk management and the development of expensive controls. No does it encourage behaviours to manage risk more effectively. Moreover, the expense-based model is not appropriate for capital allocation.

Operating Leverage Model

A rise in variable costs (such as most operating expenses) tends to synchronise with a rise in revenue, and therefore variable costs do not contribute much towards net income volatility. However, when there is a less-than-perfect match between revenue fluctuations and expense fluctuations, the bank faces what is known as operating leverage risk. The level of income volatility depends on the size of the asset base (fixed costs) relative to operating expense (variable costs).

In an operating leverage model, the proxies for operating leverage are usually simple functions of the fixed assets and the operating expenses. For example, one bank may estimates its operating leverage risk to be 10% multiplied by the fixed asset size plus 25% multiplied by three months of operating expenses. Another bank calculates its operating leverage risk as 2½ times the monthly fixed expenses for each line of business.

Operating leverage risk is an important component of operational risk, but it does not include many other aspects of operational risk such as the risk that losses will be sustained due to failure of internal controls, information systems, or human factors.

Risk Profiling Model

These models focus on monitoring a handful of risk indicators that are regarded as reflective of the health of a process or system health. The risk factors are not linked to any target variable. Typical indicators include trade volume, mishandling errors or losses, the number of exception reports or “no deals” outstanding, staff turnover rate, and percentage of staff vacancies.

Other measurements include:

• Number of incident reports;
• Number of repeat violations;
• Amount of overtime worked in a business area;
• Ratio of contractors to staff;
• Supervisory ratio;
• Pass–fail rate in staff licensing exam;
• Downtime;
• Number of limit violations;
• Number of temporary procedures;
• Number of process “fails”;
• Number of personnel errors;
• Average years of staff experience;
• Backlog levels;
• Backlog of change requests.

Profiling models are useful in analysing the evolution of operational risks over time, an exercise that helps focus the attention of operations managers on problems before they turn serious. These risk models are especially effective when used with a structured hierarchy of indicators such as Balanced Scorecard or with statistical quality control tools like control charts.

However, the lack of a linkage between the risk indicators and target variables may make managers focus too much on the symptoms, rather than the causes, of operational problems.

Bottom-up Risk Models

These models begin with the basic elements of operations, such as assets and liabilities or processes and resources, and in a bottom-up fashion, describe how potential changes to these elements could affect targets such as mark-to-market asset values and net income. These potential changes are modelled as either risk factors or specific loss events.

Designing a quantitative bottom-up model involves five steps:

• Identify target variable. Typically this will be P&L, costs, or net asset value.
• Identify a critical set of processes and resources (in the case of operational risk analysis) or a key set of assets and liabilities (in the case of purely financial risk analysis). Model developers should recall the Pareto principle (also known as the 80:20 rule) that most of the risks are found in a small number of assets and liabilities or processes and resources.
• Map these processes and resources to a combination of risk factors and loss events for which historical data has been compiled (that are believed to be relevant for the future) or which is seen as a strong candidate to be a future scenario.
• Simulate the potential changes in risk factors and events over the time horizon, taking into account any dependencies (usually correlations) between risk factors and events. This can be done analytically, assuming particular parametric distributions for factors and events, or by using Monte Carlo simulation methods.
• Infer from the mapping and the simulated change the effect on the relevant target variables such as interest margin, net income, or net asset value.

The bottom-up model has a wider target audience than the top-down model. It includes middle managers, operational managers, internal planning, and resource allocation, rather than just high-level strategic planning or capital allocation. Bottom-up models can be integrated with other models used for operational management. They require detailed data about specific losses that can affect the assets and liabilities in a company. Without this data, subjective assessments must be used, which limits the validity of the approach.

Asset and Liability Management Model

Traditional asset and liability management (ALM) looks at projected future earnings in a number of financial (usually interest-rate) scenarios. ALM approaches range from simple interest-rate gaps in different time periods, through more sophisticated duration and convexity models, to complex Monte Carlo simulations of the balance sheet. In all these cases, ALM aggregates the interest-rate sensitivities of specific assets and liabilities to infer net profits (in particular, the interest margin component) in a wide range of interest-rate scenarios.

In operational risk management, ALM approaches are most appropriate for those assets that are not marked-to-market, that is, booked at historical cost. One difficulty of the ALM model is the long-time horizon typically used (usually when the transactions mature). To simulate or develop market-rate scenarios over such long time periods is difficult. An ALM model used for balance-sheet simulation is also very sensitive to the precise accounting principles used.

Market Factor Model

For marketable assets (e.g. trading portfolios) affected largely by continuous market risk factors, parametric models based on an assumed factor distribution can be used. J.P. Morgan’s RiskMetrics model of VaR is an example of this market factor approach.

The model requires data about the distributions of factor returns for a short time horizon (usually days), the mapping between assets and risk factors, and the initial value of the asset. In the case of RiskMetrics, the factors are assumed to be normally distributed, which allows complete specification of the distributions in terms of the factors’ means (assumed zero) and the co-variance matrix. Most factor models also assume a linear mapping; this is usually a reasonable assumption except, for example, in the case of options portfolios, which are non-linear positions.

Given the return distribution (and thereby the distribution of potential asset values), the portfolio VaR is taken as just a percentile. If the assumption of normality is not made, factor models resort to simulation approaches to infer the effect of factor changes on asset values.

The market factor model has the benefit of being relatively transparent and forward-looking, and of avoiding the idiosyncrasies of accounting amortisation and depreciation schedules. On the other hand, market prices are very volatile and the resultant fluctuations in asset values can be hard to intuitively understand. Banks often find that market factor models make sense for the shorter term, while ALM measures are more operationally useful for the long term.

Actuarial Loss Model

Actuarial risk models have long been used by insurance companies to assess the effect of policy changes, marketing practices, and concentration changes on the payout of insurance claims and receipt of premiums. They can be adapted for use in operational risk management.

For example, an actuarial loss model is used to estimate the random incidence of claims when an insured party suffers damages that are partially covered by an insurance contract. Each event may cause a payment to be made to the policy holder as a result. In operational risk management, the model may be used to estimate the random occurrence of loss events and the impact of those events on the bank.

Insurance actuaries have no shortage of data to fit their models, which is not always the case with operations managers in financial institutions. However, insurance companies have less short-term control over their insurance payouts than do operational managers over their operations. Provided the required data is available, the actuarial loss model can be useful for operational risk management, particularly for the purposes of efficiency, internal control, and capital management.

Causal Model

A causal model combines data on historical losses with subjective causal relations to produce estimates of conditional probabilities of one loss event, given that another has already occurred. This is most useful for small but complex and risky systems that can be broken down into a number of simpler sub-systems. Causal models focus on helping users understand how failures propagate in the system as a whole and identify causes, rather than symptoms, that require dynamic attention as the system begins to fail.

While suitable for operations managers, causal modelling is complex—almost impossible—to execute on a large scale and less relevant for aggregate resource allocation. Formal causal models (such as fault trees, event trees, and event simulation) generally demand a great deal of data about the sources of systems failures. More informal causal models (such as belief networks, affinity and interrelationship diagramming, wishbone diagrams, and root-cause analysis) are inherently much less demanding, but also less precise and operationally useful.

Operational Variance

Management accountants have long used standard costs as the pre-determined cost of an activity based on current and projected costs. These standard costs are set at the beginning of the period and used to benchmark subsequent activities. One measure of operational risk, therefore, is the difference between the actual and the standard costs, which is known as the accounting or operational variance.

Sometimes this difference is standardised by dividing it by the standard cost. Variance analyses help control costs and highlight problem areas by focusing management attention on exceptional variances. Furthermore, variances can be separated into volume and unit cost components, allowing accountants to distinguish between the effects of changes in volume and in the unit cost per transaction.

Selecting a Risk Model

Which risk model should a bank use? The answer will depend on the size, structure, range of services, complexity, and other circumstances of the bank. What should be remembered is that the various models to estimate operational risk are not mutually exclusive. In many cases, they can be integrated, with use and focus varying with operational objectives.

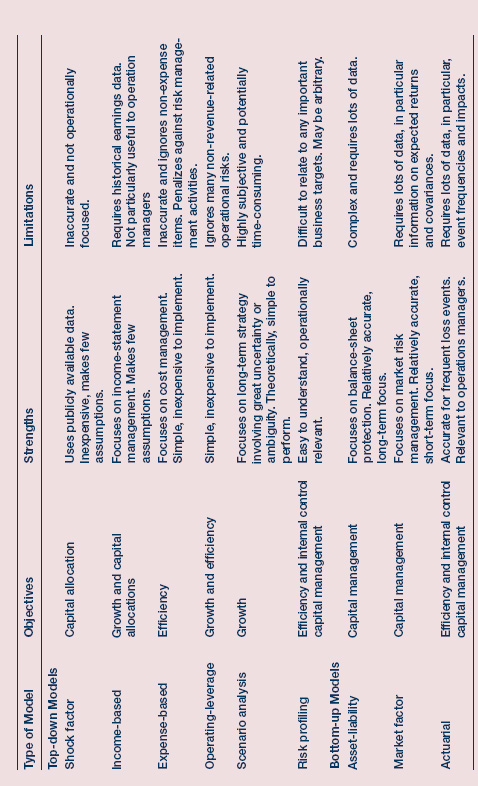
As mentioned earlier, the different risk models should be seen as complementary to, rather than substitutes for, one another. They address various aspects of operational risk, as the comparison of the various risk models in Exhibit 9.2 shows.

EXHIBIT 9.2 Comparison of different risk models

Christopher Marshall, Measuring and Managing Operational Risks in Financial Institutions (Singapore: John Wiley & Sons (Asia) Pte Ltd, 2001), 117-118.

Causal vs Statistical Models

Banks typically use hybrid models rather than just a single model to infer value at risk (VaR) and set the amount of capital they should set aside. The combination of models helps them take into account historical events, based on internal and external loss data, and the potential for events to happen in the future. The combination of methods helps make the operational risk management framework that much stronger. Although it is tempting to favor one approach over another, to prefer causal models over statistical ones, the reality is that both have their strengths and weaknesses.

A causal approach goes to the root causes of a particular risk and seeks to define where the loss might come from. A causal model seeks to assign a probability of a particular event happening while also assigning, when possible, a share of the responsibility for a particular loss event to each cause. For instance, a low frequency but large loss event such as a massive internal fraud might be caused by a combination of internal fraud, weak controls, inappropriate escalation triggers, and so forth. A causal model helps banks develop a probability-weighted average of what caused a particular event. Causal models, as discussed above, are bottom-up approaches to identifying exposures and analysing loss events.

Statistical models, on the other hand, are top-down approaches. An example of a statistical model is the basic indicator approach. For example, a bank earns USD1 billion in the past three years. Of that, 15% would be the operational risk capital. The question that top down approaches seek to answer is how to allocate that capital. While bottom up approaches start with the loss, top-down approaches start with the probability of loss and seek to address it before it happens. Statistical models use historical data to allocate loss capital to different units so that they are better protected.

Summary

• Scenario analysis is a qualitative tool to understand the impact of major operational and business events and develop plans to respond to them. Some scenarios describe external shocks while others focus on key systems. They are useful in that they can be used to determine the impact of risks for which there is little data.
• Stress testing gives values beyond normal operating ranges to a series of key risk factors such as price, volume, or availability of resources. Although it can sometimes be overly simplified, it is also a powerful diagnostic tool for operational risk management. But stress tests have their limits, not the least of which are the subjectivity of their nature and the fact that they are often simplistic.
• Stress tests are particularly useful to rate a bank’s ability to deal with extreme events or “acts of God,” highlighting a number of risk factors that can lead to potentially catastrophic losses. These risk factors include design and construction flaws, deferred maintenance, economic pressures, schedule constraints, neglecting procedures, lack of planning and preparedness, communication failures, arrogance, and political agendas.
• Operational risk models can be used not only to help calculate the operational risk capital charge but also towards achievement of wider objectives such as internal control, capital management, efficiency, and growth. Risk models are either top-down or bottom-up.
• Examples of top-down models include stock factor models, income-based models and expense-based models. These models are typically simple and may require a low level of resource but are limited by perceptions and are always backward-looking.
• Bottom-up risk models include asset and liability management models, market factor models and actuarial loss models. There are five basic steps to designing a quantitative bottom-up model: indentifying a target variable, identifying critical processes or resources, mapping processes and resources to a set of risk factors and loss events, simulating potential changes in risk factors and events, and inferring the changes to the target variables.
• The various risk models are not mutually exclusive. In many cases, they can be integrated, with use and focus varying with operational objectives. Choosing the right risk model depends on the size, structure, range of services, and complexity of a bank.

Key Terms

Study Guide

Further Reading

Allen, Linda, Boudoukh Jacob and Saunders Anthon. Understanding Market, Credit, and Operational Risk: The Value at Risk Approach. Oxford: Blackwell Publishing, 2004.

Bank for International Settlements. International Convergence of Capital Measurement and Capital Standards. Web. 23 July 2010. <http://www.bis.org/publ/bcbs128.pdf?noframes=1>

Chernobai, Anna S.; Rachev, Svetlozar T.; Fabozzi, Frank J., Operational Risk: A Guide to Basel II Capital Requirements, Models, and Analysis. Singapore: John Wiley & Sons (Asia) Pte Ltd, 2007. Print.

Hong Kong Monetary Authority. “CA-G-1: Overview of Capital Adequacy Regime for Locally Incorporated Authorized Institutions” in Supervisory Policy Manual. Web. 23 July 2010. <http://www.info.gov.hk/hkma/eng/bank/spma/attach/CA-G-1.pdf>

Marshall, Christopher. Measuring and Managing Operational Risks in Financial Institutions. Singapore: John Wiley & Sons (Asia) Pte Ltd, 2001. Print.

Taylor III, Bernard W.; and Russell, Roberta S. Operations Management. Singapore: John Wiley & Sons (Asia) Pte Ltd, 2009. Print.

1 Also known as Brownian motion, a Wiener process refers to changes in value over small time periods. It is a type of Markovian stochastic process, meaning that it is random and assumes that the future value of the price of an asset depends only on the current value, discounting all other factors.