Beware of Assumptions

Many of these problems are difficult because they lead you to assume something incorrect. The false assumption then leads to the wrong answer.

You might conclude that the best approach is to avoid making any assumptions. Unfortunately, that’s not practical—just understanding a problem is difficult without making a whole series of assumptions.

For example, suppose you are given the task of finding an arrangement that maximizes the number of oranges you can fit in the bottom of a square box. You would probably automatically assume that the oranges are small spherical fruit, that they are all about the same size, that “in the bottom” means in contact with the bottom surface of the box, and that the oranges must remain intact (you can’t puree them and pour them in). Calling these statements assumptions may seem ridiculous—they are all rather obvious and are all correct. The point is that assumptions are inherent in all communication or thought; you can’t begin to work on a problem without assumptions.

Carrying this example further, you might assume you could model this problem in two dimensions using circles in a square, and that the solution would involve some sort of orderly, repeating pattern. Based on these assumptions and the knowledge that a honeycomb-like hexagonal array provides the tightest pack of circles covering a plane, you might conclude that the best solution is to place the oranges in a regular hexagonal array. Depending on the relative sizes of the oranges and the box, however, this conclusion would be incorrect.

Although you can’t eliminate assumptions, it can be useful to try to identify and analyze them. As you identify your assumptions, categorize them as almost certainly correct, probably correct, or possibly incorrect. Starting with the assumption you feel is least likely to be correct, try reworking the problem without each assumption. These puzzles are rarely trick questions, so your definitional assumptions are usually correct.

In the preceding example, for instance, it would be reasonable to classify the assumptions that “oranges are spherical fruit” and that “they must remain intact and in contact with the bottom of the box” as almost certainly correct.

But how would you categorize the assumption that you can reduce this puzzle to a two-dimensional problem of circles in a square? If you think about it, you can see that the oranges make contact with each other in a single plane and that in this plane you’re essentially dealing with circles inside a square. This isn’t exactly a proof, but it’s solid enough to decide that this assumption is probably correct.

On the other hand, you’ll find you have more trouble supporting the assumption that the oranges should be in an orderly repeating pattern. It seems reasonable, and it is true for an infinite plane, but it’s not clear that the similarities between a plane and the box bottom are sufficient for this assumption to be true. In general, beware of any assumption that you “feel” is true but can’t quite explain—this is often the incorrect assumption. You would therefore conclude that the assumption that the oranges must form an ordered array is possibly incorrect.

This assumption is incorrect. In many cases the best packing involves putting most of the oranges in an ordered array and the remaining few in unordered positions.

Analyzing your assumptions is a particularly good strategy when you think you’ve found the only logically possible solution but you’re told it’s incorrect. It’s often the case that your logic was good but based on a flawed assumption.

Don’t Be Intimidated

Some problems are intimidating because they are so complex or difficult that you can’t see a path to the solution. You may not even know where to start. Don’t let this lock you up. You don’t have to devise a plan to get all the way to the solution before you start—things will come to you as you work on the problem:

• Break a problem into parts. If you can identify a subproblem, try solving that, even if you’re not sure it’s critical to solving the main problem.
• Try a simplified problem. Try solving a simplified version of the problem; you may gain insights that are useful in solving the full problem.
• Try specific examples. If the problem involves some sort of process, try working through a few specific examples. You may notice a pattern you can generalize to other cases.

Above all, keep talking, keep thinking, and keep working. The pieces of the puzzle are much more likely to fall into place when your mind is in motion than when you sit at the starting line praying for a revelation.

Even if you don’t make much progress, it looks much better to the interviewer when you actively attack a problem than when you sit back stumped, looking clueless and overwhelmed. You came to the interview to demonstrate that you will be a valuable employee. Analyzing the problems and patiently trying a variety of approaches shows this almost as well as solving problems.

Beware of Simple Problems

Other problems are tricky for the opposite reason: they are so simple or restricted that it seems that there’s no way to solve the problems within the given constraints. In these circumstances, brainstorming can be useful. Try to enumerate all the possible allowed actions within the constraints of the problem, even those that seem counterproductive. If the problem involves physical objects, consider every object, the properties of every object, what you might do to or with each object, and how the objects might interact.

When you’re stuck on a problem like this, there may be something allowed by the problem that you’re missing. If you make a list of everything allowed by the constraints of the problem, it will include the key to the solution that hasn’t occurred to you. It’s often easier to enumerate all the possibilities than it is to specifically come up with the one thing you haven’t thought of.

When you do this enumeration, don’t do it silently; think aloud or write it down. This shows the interviewer what you’re doing and helps you be more methodical and thorough.

Estimation Problems

There’s one more type of problem worth discussing. This is the estimation problem, where you’re asked to use a rational process to estimate the size of some figure you don’t know. These problems are relatively rare in interviews for pure development positions, but they may be more common in interviews for jobs that include a significant management or business aspect. One example is, “How many piano tuners are there in the United States?” It has been so widely reported that this problem was once commonly posed by Microsoft that it seems almost certain to be apocryphal; nevertheless, it is a good example.

These problems are usually not difficult compared with the more common brainteasers. You’re not expected to know the actual statistic or fact. Instead, you are expected to do a rough order of magnitude calculation based on facts you do know. Because everything is an estimate anyway, try to adjust or round your figures so that any large numbers you use are powers (or at least multiples) of ten—this can significantly simplify your arithmetic.

BRAINTEASER PROBLEMS

Brainteasers draw from a much broader and more diverse body of knowledge than programming and technical problems, so a comprehensive review is even less possible here. Because any brainteaser you encounter in an interview is likely to be unfamiliar, the problems that follow prepare you by providing opportunities to practice all of the techniques we’ve described so you can tackle anything that comes your way.

Count Open Lockers

This problem is designed to seem overwhelming. You don’t have time to draw a diagram of 100 lockers and count 100 passes through them. Even if you did, solving the problem that way won’t illustrate any skill or intuition, so there must be some trick that you can use to determine how many doors will be open. You just need to figure out what that trick is.

It’s unlikely that you can intuit the solution to this problem by just staring at it. What can you do? Although it’s not practical to solve the entire problem by brute force, solving a few lockers in this manner is reasonable. Perhaps you will notice some patterns you can apply to the larger problem.

Start by choosing an arbitrary locker, 12, and determining whether it will end open or closed. On which passes will you toggle locker 12? Two times are obvious: on the first pass, when you toggle every locker, and on the twelfth pass, when you start with locker 12. You don’t need to consider any pass after 12 because those will all start farther down the hall than locker 12. This leaves passes 2 through 11. You can count these out: 2, 4, 6, 8, 10, 12 (you toggle on pass 2); 3, 6, 9, 12 (on 3); 4, 8, 12 (on 4); 5, 10, 15 (not on 5); 6, 12 (on 6); 7, 14 (not on 7), and so on. Somewhere in this process, you probably notice that you toggle locker 12 only when the number of the pass you’re on is a factor of 12. This is because when counting by n, you hit 12 only when some integer number of n’s add to 12, which is another way of saying that n is a factor of 12. The solution seems to have something to do with factors. Though it seems simple in retrospect, this probably wasn’t obvious before you worked out an example.

The factors of 12 are 1, 2, 3, 4, 6, and 12. Correspondingly, the operations on the locker door are open, close, open, close, open, close. So locker 12 will end closed.

If factors are involved, perhaps it would be instructive to investigate a prime locker, because primes are numbers with unique factor properties. You might select 17 as a representative prime. The factors are 1 and 17, so the operations are open, close. It ends closed just like 12. Apparently primes are not necessarily different from nonprimes for the purposes of this problem.

What generalizations can you make about whether a locker ends open or closed? All lockers start closed and alternate between being open and closed. So lockers are closed after the second, fourth, sixth, and so on, times they are toggled—in other words, if a locker is toggled an even number of times, it ends closed; otherwise, it ends open. You know that a locker is toggled once for every factor of the locker number, so you can say that a locker ends open only if it has an odd number of factors.

The task has now been reduced to finding how many numbers between 1 and 100 have an odd number of factors. The two you’ve examined (and most others, if you try a few more examples) have even numbers of factors.

Why is that? If a number i is a factor of n, what does that mean? It means that i times some other number j is equal to n. Of course, because multiplication is commutative (i · j = j · i), that means that j is a factor of n, too, so the number of factors is usually even because factors tend to come in pairs. If you can find the numbers that have unpaired factors, you will know which lockers will be open. Multiplication is a binary operation, so two numbers will always be involved, but what if they are both the same number (that is, i = j)? In that case, a single number would effectively form both halves of the pair, and there would be an odd number of factors. When this is the case, i · i = n. Therefore, n must be a perfect square. Try a perfect square to check this solution. For example, for 16, the factors are 1, 2, 4, 8, 16; operations are open, close, open, close, open—as expected, it ends open.

Based on this reasoning, you can conclude that only lockers with numbers that are perfect squares end up open. The perfect squares between 1 and 100 (inclusive) are 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100. So 10 lockers would remain open.

Similarly, for the general case of k lockers, the number of open lockers is the number of perfect squares between 1 and k, inclusive. How can you best count these? The perfect squares themselves are inconvenient to count because they’re unevenly spaced. However, the square roots of the perfect squares greater than zero are the positive integers. These are easy to count: the last number in the list of consecutive positive integers gives the number of items in the list. For example, the square roots of 1, 4, 9, 16, and 25 are 1, 2, 3, 4, and 5; the last number in the list of square roots is the square root of the largest perfect square and is equal to the number of perfect squares. You need to find the square root of the largest perfect square less than or equal to k.

This task is trivial when k is a perfect square, but most of the time it won’t be. In these cases, the square root of k will be a noninteger. If you round this square root down to the nearest integer, its square is the largest perfect square less than k—just what you were looking for. The operation of rounding to the largest integer less than or equal to a given number is often called floor. Thus, in the general case of k lockers, there will be floor(sqrt(k)) lockers remaining open.

The key to solving this problem is trying strategies to solve parts of the problem even when it isn’t clear how these parts contribute to the overall solution. Although some attempts, such as the investigation of prime numbered lockers, may not be fruitful, others are likely to lead to greater insight about how to attack the problem, such as the strategy of calculating the result for a single locker. Even in the worst case, where none of the things you try lead you closer to the final solution, you show the interviewer that you aren’t intimidated by difficult problems with no clear solution and that you are willing to keep trying different approaches until you find one that works.

Three Switches

The crux of this problem quickly becomes obvious: only two possible positions exist for each switch (on or off) but there are three lights to identify. You can easily identify one light, by setting one switch differently than the other two, but this leaves you no way to distinguish the two left in the same position.

When confronted with a seemingly impossible task, you should go back to basics. The two key objects in this problem seem to be the switches and the lights. What do you know about switches and light bulbs? Switches make or break an electrical connection: when a switch is on, current flows through it. An incandescent light bulb consists of a resistive filament inside an evacuated glass bulb. When current flows through the filament, it consumes power, producing light and heat.

How can these properties help you solve the problem? Which of them can you detect or measure? The properties of a switch don’t seem too useful. It’s much easier to look at the switch to see whether it’s off or on than to measure current. The light bulbs sound a little more promising. You can detect light by looking at the bulbs, and you can detect heat by touching them. Whether there is light coming from a bulb is determined entirely by its switch—when the switch is on, there is light; when it’s off, there isn’t. What about heat? It takes some time for a light to heat up after it’s been switched on, and some time for it to cool after it’s switched off, so you could use heat to determine whether a bulb had been on, even if it were off when you walked into the room.

You can determine which switch goes with each bulb by turning the first switch on and the second and third off. After 10 minutes, turn the first switch off, leave the second off, and turn the third on. When you go into the room, the hot dark bulb corresponds to the first switch, the cold dark bulb to the second, and the lit bulb to the third.

Although there’s nothing truly outlandish about this question—it’s not just a stupid play on words, for instance—it is arguably a trick question. The solution involves coming up with something somewhat outside the definition of the problem. Some interviewers believe that questions like this help them identify people who can think outside the box and develop nontraditional, innovative solutions to difficult problems. In the authors’ opinion, these problems are cheap shots that don’t prove much of anything. Nevertheless, these problems do occasionally appear in interviews, and it’s best to be prepared for them.

Bridge Crossing

Because there is only one flashlight, each trip to the far side of the bridge (except the last trip) must be followed by a trip coming back. Each of these trips consists of either one or two travelers crossing the bridge. To get a net movement of travelers to the far side of the bridge, you probably want to have two travelers on each outbound trip and one on each inbound trip. This strategy gives you a total of five trips: three outbound and two inbound. Your task is to assign travelers to the trips so that you minimize the total time for the five trips. For clarity, you can refer to each traveler by the number of minutes it takes to cross the bridge.

Number 1 can cross the bridge at least twice as fast as any of the other travelers, so you can minimize the time of the return trips by always having 1 bring the flashlight back. This suggests a strategy whereby 1 escorts each of the other travelers across the bridge one by one.

One possible arrangement of trips using this strategy is illustrated in Figure 16-1. The order in which 1 escorts the other travelers doesn’t change the total time: the three outbound trips have times of 2, 5, and 10 minutes, and the two inbound trips are 1 minute each, for a total of 19 minutes.

This solution is logical, obvious, and doesn’t take long to discover. In short, it can’t possibly be the best solution to an interview problem. Your interviewer would tell you that you can do better than 19 minutes, but even without that hint you should guess you arrived at the preceding solution too easily.

This puts you in an uncomfortable, but unfortunately not unusual, position. You know your answer is wrong, yet based on the assumptions you made, it’s the only reasonable answer. It’s easy to get frustrated at this point. You may wonder if this is a trick question: perhaps you’re supposed to throw the flashlight back or have the second pair use a lantern. Such tricks are almost never the right answer, and they are not necessary here. A more efficient arrangement of trips exists. Because the only solution that seems logical is wrong, you must have made a false assumption.

Consider your assumptions, checking each one to see if it might be false. First among your assumptions was that outbound and inbound trips must alternate. This seems correct—there’s no way to have an outbound trip followed by another outbound trip because the flashlight would be on the wrong side of the bridge.

Next, you assumed that there would be two travelers on each outbound trip and one on each return trip. This seems logical, but it’s harder to prove. Putting two travelers on an inbound trip seems terribly counterproductive; after all, you’re trying to get them to the far side of the bridge. An outbound trip with only one traveler is potentially more worthwhile, but coupled with the requisite return trip all it actually accomplishes is exchanging the positions of two travelers. Exchanging two travelers might be useful, but it probably wastes too much time to be worth it. Because this possibility doesn’t look promising, try looking for a false assumption elsewhere and reconsider this one if necessary.

You also assumed that 1 should always bring the flashlight back. What basis do you have for this assumption? It minimizes the time for the return trips, but the goal is to minimize total time, not return trip time. Perhaps the best overall solution does not involve minimized return trip times. The assumption that 1 should always return the flashlight seems hard to support, so it probably merits further examination.

If you’re not going to have 1 make all the return trips, how will you arrange the trips? You might try a process of elimination. You obviously can’t have 10 make a return trip because then 10 would have at least three trips, which would take 30 minutes. Even without getting the remaining travelers across, this is already worse than your previous solution. Similarly, if 5 makes a return trip, then you have two trips that are at least 5 minutes, plus one that takes 10 minutes (when 10 crosses). Just those three trips total 20 minutes, so you won’t find a better solution by having 5 make a return trip.

You might also try analyzing some of the individual trips from your previous solution. Because 1 escorted everyone else, there was a trip with 1 and 10. In a sense, when you send 1 with 10, 1’s speed is wasted on that trip because the crossing still takes 10 minutes. Looking at that from a different perspective, any trip that includes 10 always takes 10 minutes, no matter which other traveler goes along. Therefore, if you’re going to have to spend 10 minutes on a trip, you might as well take advantage of it and get another slow traveler across. This reasoning indicates that 10 should cross with 5, rather than with 1.

Using this strategy, you might begin by sending 10 and 5 across. However, one of them has to bring the flashlight back, which you already know isn’t the right solution. You’ll want to already have someone faster than 5 waiting on the far side. Try starting by sending 1 and 2 across. Then have 1 bring the flashlight back. Now that there’s someone reasonably fast (2) on the far side, you can send 5 and 10 across together. Then 2 returns the flashlight. Finally, 1 and 2 cross the bridge again. This scheme is illustrated in Figure 16-2.

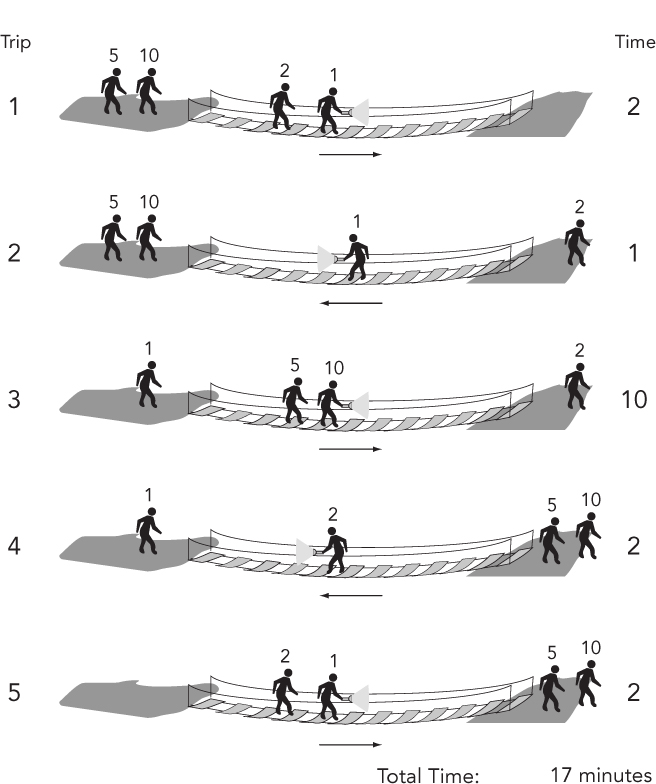
The times for the respective trips under this strategy are 2, 1, 10, 2, and 2, for a total of 17 minutes. Identifying the false assumption improved your solution by 2 minutes.

This problem is a slightly unusual example of a class of problems involving optimizing the process of moving a group of items a few at a time from one place to another. More commonly, the goal is to minimize the total number of trips, and restrictions often exist on which items can be left together. This particular problem is difficult because it suggests a false assumption (that 1 should escort each of the other travelers) that seems so obvious you may not even realize you’re making an assumption.

Heavy Marble

The first step to solve this problem is to realize that you can put more than one marble in each pan of the scale. If you have equal numbers of marbles in each pan, the heavy marble must be in the group on the heavy side of the scale. This saves you from having to weigh each marble individually, and it enables you to eliminate many marbles in a single weighing.

When you realize this, you are likely to devise a binary search-based strategy to find the heavy marble. In this method, you begin by putting half the marbles on each side of the scale. Then you eliminate the marbles from the light side of the scale and divide the marbles from the heavy side of the scale between the two pans. As shown in Figure 16-3, you continue this process until each pan holds only one marble, at which point the heavy marble is the only marble on the heavy side of the scale. Using this process you can always identify the heavy marble in three weighings.

This may seem to be the correct answer. The solution wasn’t completely obvious, and it’s an improvement over weighing the marbles one by one. But if you think that this seems too easy, you’re right. The method described so far is a good start, but it’s not the best you can do.

How can you find the heavy marble in fewer than three weighings? Obviously, you must eliminate more than half the marbles at each weighing, but how can you do that?

Try looking at this problem from an information flow perspective. Information about the marbles comes from the scale, and you use this information to identify the heavy marble. The more information you derive from each weighing, the more efficient your search for the marble can be. Think about how you get information from the scale: you place marbles on it and then look at the result. What are all the possible results? The left pan side could be heavier, the right side could be heavier, or both sides could weigh exactly the same. So there are three possible results, but so far you’ve been using only two of them. In effect, you’re only using two-thirds of the information that each weighing provides. Perhaps if you alter your method so that you use all the information from each weighing you can find the heavy marble in fewer weighings.

Using the binary search strategy, the heavy marble is always in one of the two pans, so there is always a heavy side of the scale. In other words, you can’t take advantage of all the information the scale can provide if the heavy marble is always on the scale. What if you divided the marbles into three equal-sized groups, and weighed two of the groups on the scale? Just as before, if either side of the scale is heavier, you know that the heavy marble is in the group on that side. But now it’s also possible that the two groups of marbles on the scale weigh the same—in this case, the heavy marble must be in the third group that’s not on the scale. Because you divided the marbles into three groups, keeping just the group with the heavy marble eliminates two-thirds of the marbles instead of half of them. This seems promising.

There’s still a minor wrinkle to work out before you can apply this process to the problem. Eight isn’t evenly divisible by 3, so you can’t divide the eight marbles into three equal groups. Why do you need the same number of marbles in each group? You need the same number of marbles so that when you put the groups on the scale the result doesn’t have anything to do with differing numbers of marbles on each side. Really, you need only two of the groups to be the same size. You still want all three groups to be approximately the same size so you can eliminate approximately two-thirds of the marbles after each weighing no matter which pile has the heavy marble.

Now you can apply the three-group technique to the problem you were given. Begin by dividing the marbles into two groups of three, which you put on the scale, and one group of two, which you leave off. If the two sides weigh the same, the heavy marble is in the group of two, and you can find it with one more weighing, for a total of two weighings. On the other hand, if either side of the scale is heavier, the heavy marble must be in that group of three. You can eliminate all the other marbles, and place one marble from this group on either side of the scale, leaving the third marble aside. If one side is heavier, it contains the heavy marble; if neither side is heavier, the heavy marble is the one you didn’t place on the scale. This is also a total of two weighings, so you can always find the heavy marble in a group of eight using two weighings. Figure 16-4 shows an example of this process.

This is the part where the interviewer determines whether you hit on the preceding solution by luck or because you really understand it. Think about what happens after each weighing. You eliminate two-thirds of the marbles and keep one-third. After each weighing you have one-third as many marbles as you did before. When you get down to one marble, you’ve found the heavy marble.

Based on this reasoning, you can reformulate the question as, “How many times do you have to divide the number of marbles by 3 before you end up with 1?” If you start with three marbles, you divide by 3 once to get 1, so it takes one weighing. If you start with nine marbles, you divide by 3 twice, so it takes two weighings. Similarly, 27 marbles require three weighings. What mathematical operation can you use to represent this “How many times do you divide by 3 to get to 1” process?

Because multiplication and division are inverse operations, the number of times you must divide the number of marbles by 3 before you end up with 1 is the same as the number of times you have to multiply by 3 (starting at 1) before you get to the number of marbles. Repeated multiplication is expressed using exponents. If you want to express multiplying by 3 twice, you can write 3², which is equal to 9. When you multiply twice by 3, you get 9—it takes two weighings to find the heavy marble among nine marbles. In more general terms, it takes i weighings to find the heavy marble from among n marbles, where 3i = n. You know the value of n and want to calculate i, so you need to solve this for i. You can solve for i using logarithms, the inverse operation of exponentiation. If you take log₃ of both sides of the preceding equation, you get i = log₃ n.

This works fine as long as n is a power of 3. However, if n isn’t a power of 3, this equation calculates a noninteger value for i, which doesn’t make much sense, given that it’s extremely difficult to perform a fractional weighing. For example, if n = 8, as in the previous part of the problem, log₃ 8 is some number between 1 and 2 (1.893. . . to be a little more precise). From your previous experience, you know it actually takes two weighings when you have eight marbles. This seems to indicate that if you calculate a fractional number of weighings, you should round it up to the nearest integer.

Does this make sense? Try applying it to n = 10 to see whether you can justify always rounding up. log₃ 9 is 2, so log₃ 10 will be a little more than two, or three if you round up to the nearest integer. Is that the correct number of weighings for 10 marbles? For 10 marbles, you would start out with two groups of 3 and one group of 4. If the heavy marble were in either of the groups of 3, you could find it with just one more weighing, but if it turns out to be in the group of 4, you might need as many as two more weighings for a total of 3, just as you calculated. In this case the fractional weighing seems to represent a weighing that you might need to make under some circumstances (if the heavy marble happens to be in the larger group) but not others. Because you’re trying to calculate the number of weighings needed to guarantee you can find the heavy marble, you must count that fractional weighing as a full weighing even though you won’t always perform it, so it makes sense to always round up to the nearest integer. In programming, the function that rounds up to the nearest integer is often called ceiling, so you might express the minimum number of weighings needed to guarantee you find the heavy marble among n marbles as ceiling(log₃(n)).

This is another example of a problem designed such that the wrong solution occurs first to most intelligent, logically thinking people. Most people find it quite difficult to come up with the idea to use three groups, but relatively easy to solve the problem after that leap. It’s not an accident that this problem begins by asking you to solve the case of eight marbles. As a power of 2, it works cleanly for the incorrect solution, but because it’s not a power (or multiple, for that matter) of 3, it’s a little messy for the correct solution. People generally get the correct answer more quickly when asked to solve the problem for nine marbles. Watch out for details like this that may steer your thinking in a particular (and often incorrect) direction.

This problem is a relatively easy example of a whole class of tricky problems involving weighing items with a two-pan scale. For more practice with these, you can work out the solution to the preceding problem for a group of marbles in which one marble has a different weight, but you don’t know whether it’s heavier or lighter.

Number of American Gas Stations

Clearly this is an estimation problem. Although it would probably be faster and more accurate to search for the figure on the Internet, you won’t get credit for that.

As with any estimation problem, the key is connecting the unknown quantity you’re trying to estimate to quantities that you know or can make a reasonable guess at. Often you can establish these connections by considering the interactions between the things you quantify. In this case, cars are filled with gas at gas stations, so it seems reasonable that the number of gas stations in a nation would be related to the number of vehicles. You probably don’t have any better idea of how many vehicles there are in the US than you do the number of gas stations, but vehicles have to be driven by people, so you can connect the number of vehicles to the population.

You might know that the population of the United States is a little over 300 million. (If not, you could estimate this, too. For instance: over a billion people live in China, and about 10 million people live in New York City. The US is much smaller than China, but must be much bigger than New York City, so a good order of magnitude estimate of the population of the United States is 100 million.) Try taking the population as a starting point.

Not everyone has a car, so suppose there are 150 million cars on the road. But there are also commercial vehicles to consider, say one commercial vehicle for every passenger car, for a total of 300 million vehicles. You can determine the number of gas stations from this figure by estimating how many vehicles a gas station can serve.

You can base the estimation of the number of vehicles served by a gas station on your own experiences. In our experience, it takes about 6 minutes to fill up a car. We go to the gas station about once a week, and there are usually two other cars there. Assuming this is average for Americans, each gas station services about 30 cars an hour. Suppose a gas station were open 12 hours a day, 7 days a week: that would be 84 hours a week. Eighty four is a difficult number for mental arithmetic, and in reality, a gas station is probably open more than 12 hours a day, so estimate that the average gas station is open 100 hours a week. That means it services 3,000 cars a week.

If every vehicle goes to the gas station about once a week and each station sees 3,000 vehicles a week, there must be approximately 100,000 gas stations in the United States. Figures estimated like this are not precise, but they are typically within an order of magnitude—that is, in this case we can be fairly confident that there are more than 10,000 gas stations and fewer than 1,000,000. In fact, in 2015 the United States Census Bureau put out a press release stating that there were about 112,000 gas stations in the United States.

It’s much more important that you can form a reasonable framework for the estimation and rapidly work through the calculations than that you accurately estimate the statistic.

For more practice, try estimating the number of kindergarten teachers in your state, the circumference of the earth, and the weight of a ferryboat.

SUMMARY

You may encounter a brainteaser or two during the interview process, even if they’re not directly related to your programming skills. Some interviewers use these kinds of problems to try to see your thought processes at work and determine how well you can think outside the box.

Brainteasers come in many different forms, but the obvious answer is almost invariably wrong. Start by verifying your assumptions to make sure you’re solving the right problem. Don’t be intimidated by the problem—break it into pieces, simplify the problem, and solve specific cases to find the general solution. Beware of simple problems because they’re trickier than they seem. If you don’t have all the facts you need, make reasonable estimates based on prior knowledge and experience.

Always think out loud and explain to the interviewer what you’re doing and the reasoning behind your decisions. Focus on the problem and keep working; it’s your thought processes that count the most here, not the answer.