Boat and Pier

You should begin this problem by drawing a diagram, both to ensure you understand the scenario and to get you started on the solution. The edge of the pier, the water, and the rope form the sides of a right triangle, as shown in Figure 17-1. To facilitate further discussion, these segments are labeled A, B, and C, respectively.

Here you have something familiar but with an unusual twist. You’ve probably worked with right triangles ad nauseam in your math classes, but those were static shapes. This triangle is collapsing. Be wary of this difference. Although it seems minor, it may be enough to make the wrong answer seem intuitively correct.

Given your experience with right triangles, you may decide to attack this problem mathematically. You need to determine whether side B or side C gets shorter more quickly as the boat moves. Put another way, for a given change in the length of B, what is the change in the length of C?

How might you calculate this? A derivative gives you the ratio of rates of change between two variables. If you calculated the derivative of C with respect to B and it was greater than 1, you would know that the rope was moving faster; conversely, if it was less than 1, the boat must have moved faster.

This is a good point at which to stop and consider where you’ve been and where you’re going. You can set up an equation relating B and C using the Pythagorean theorem. It looks as if this method will eventually lead you to the correct answer. If you’re good at math and comfortable with calculus, this may even be the best way to proceed. The apparent need for calculus, however, should serve as a warning that you may be missing an easier way to solve the problem.

Try returning to the original diagram and taking a more graphical approach. What other diagrams might you draw? Because you don’t know the boat’s initial distance from the pier or how high the pier is, all diagrams of the boat in motion are effectively equivalent. What about when the boat stops under the pier, as shown in Figure 17-2? That would be different; you no longer have a triangle because the rope hangs down the side of the pier.

How far does the boat travel, and how much rope is hauled in between the times shown in the two figures? Because you aren’t given any numbers, call the initial lengths of sides A, B, and C lowercase a, b, and c, respectively. When the boat is under the pier, side B has a length of 0, so the boat has moved through a distance of b. The rope, on the other hand, started with a length of c. In the second diagram, a length of rope equal to a is still out of the boat, so the total amount hauled in is c – a.

Because these distances were covered in the same time, the greater distance must have been covered at a higher speed. Which is greater: c – a or b? Recall from geometry that the sum of the lengths of two sides of a triangle must always be greater than the length of the third. For example, a + b > c. (If you think about this, it makes intuitive sense. Suppose one side were longer than the other two put together. There would be no way to arrange the sides so that they meet at three vertices because the shorter two sides are too short to span the distance from one end of the long side to the other.) Subtracting a from both sides gives b > c – a. The boat traveled a greater distance, so it was moving faster across the water than the speed of the rope through your hands.

For the mathematically curious, pick up the calculus where you left it, to show that you can determine the solution using that method. From the Pythagorean theorem, c² = a² + b². Use this to calculate the derivative of c with respect to b:

b is positive, so when a = 0, the final expression is equal to 1. When a is greater than 0, as in this problem, the denominator is greater than the numerator, and the expression is less than 1. (In case you’ve been out of a math class for too long, the numerator is the expression above the fraction bar, and the denominator is the expression below it.) This means that for a given infinitesimal change in b, there is a smaller change in c, so the boat is moving faster.

This problem belongs to a curious class of puzzles that seem to be more difficult when you know more mathematics, which are particularly devilish in interviews. Because you expect difficult questions and you may be a little nervous, you’re less likely to stop and ask yourself whether there’s an easier way.

One of the nastiest examples of this type of problem involves two locomotives, heading toward each other, each with a speed of 10 mph. When the locomotives are exactly 30 miles apart, a bird sitting on the front of one locomotive flies off at 60 mph toward the other locomotive. When it reaches the other locomotive, it immediately turns around and flies back to the first. The bird continues like this until, sadly, it is smashed between the two locomotives as they collide.

When asked how far the bird traveled, many calculus students spend hours trying to set up and sum impossibly difficult infinite series. Other students who have never heard of an infinite series might instead determine that it took the locomotives 1.5 hours to close the 30-mile gap, and that in that time a bird traveling 60 mph would have traveled 90 miles.

Counting Cubes

For this problem, it may help to picture a Rubik’s Cube, as shown in Figure 17-3.

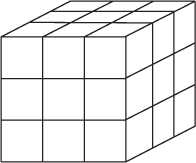
This is a spatial visualization problem. Different people find different techniques useful in visualization, so this discussion presents a variety of approaches. The hope is that you can find at least one of them useful. You can try to draw a diagram, but because the problem is in three dimensions, you may find your diagram more confusing than helpful.

One way you might try to solve this problem is by counting the cubes on each face of the array. A cube has six faces. Each face of the cubic array has nine cubes (3 × 3), so you might conclude that 6 × 9 = 54 cubes are on the surface. But you have only 3 × 3 × 3 = 27 cubes total, so it’s obviously not possible for twice that many to be on the surface. The fallacy in this method is that some cubes are on more than one face—for example, the corner cubes are on three faces. Rather than try to make complicated adjustments for cubes that are on more than one face, you should look for an easier solution.

A better way to attack this problem is to count the cubes in layers. The array is three cubes high, so you have three layers. All the cubes on the top layer are on the surface (nine cubes). All the cubes of the middle layer except for the center cube are on the surface (eight cubes). Finally, all the cubes on the bottom layer are on the surface (nine cubes). This gives a total of 9 + 8 + 9 = 26 cubes on the surface.

The preceding method works, but perhaps a better way to find the solution is to count the cubes that are not on the surface and then subtract this number from the total number of cubes. Vivid, specific objects are often easier to visualize than vague concepts—you may want to imagine the cubes on the surface to be transparent red and the nonsurface cubes to be bright blue. Hopefully, you can visualize only one bright blue cube surrounded by a shell of red cubes. Because this is the only cube that isn’t on the surface, there must be 27 – 1 = 26 cubes on the surface.

As the number of cubes increases, the accounting necessary for the layer approach becomes more complicated, so try to solve this by visualizing and counting the cubes that are not on the surface.

The nonsurface cubes form a smaller cubic array within the larger array. How many cubes are in this smaller array? Your initial impulse may be that there are four cubes in the array; if so, consider whether it’s possible to arrange four cubes into a cubic array. (It isn’t.) The correct answer is that the nonsurface cubes form a 2 × 2 × 2 array of eight cubes. You have a total of 4 × 4 × 4 = 64 cubes, so 64 – 8 = 56 cubes are on the surface.

Now that you can’t explicitly count the cubes, the problem starts to get a little more interesting. You know that you have n³ cubes total. If you can calculate the number of cubes that aren’t on the surface, you can also calculate the number of cubes that are on the surface. Try to visualize the situation, mentally coloring the surface cubes red and the interior cubes blue. What does it look like? You should see a cubic array of blue cubes surrounded by a one-cube-thick shell of red cubes. If you can determine the size of the smaller array, you can calculate the number of cubes it contains. Because the smaller array fits entirely within the larger one, it must be fewer than n cubes across, but how many fewer?

Visualize a single line of cubes running all the way through the array. The line would be n cubes long. Because the shell of red surface cubes is one cube thick, both the first and last cubes would be red, and all the other cubes would be blue. This means there would be n – 2 blue cubes in the row, so the array of interior cubes is n – 2 cubes across. It’s a cubic array, so its height and depth are the same as its width. Therefore, you can calculate that (n – 2)³ cubes are not on the surface. Subtracting this from the total number of cubes gives you n³ – (n – 2)³ cubes on the surface. Test this formula using the cases you’ve already worked out by hand: 3³ – (3 – 2)³ = 26; 4³ – (4 – 2)³ = 56. It looks as if you have the answer for this part, but you’re not done yet.

The real fun starts here. This began as a visualization problem, but taking it to four dimensions makes it difficult for most people to visualize. Visualization can still be helpful, though. You might find the following device useful.

People often represent time as a fourth dimension. The easiest way to visualize time in a concrete fashion is to imagine a strip of film from an analog movie. Each frame in the filmstrip represents a different time, or a different location along the fourth dimension. To fully represent four dimensions, you must imagine that each frame consists of a full three-dimensional space, not two-dimensional pictures as in an actual filmstrip. If you can visualize this, you can visualize four dimensions.

Because a hypercube measures the same distance in each direction, the filmstrip representing the hypercubic array in this problem is n frames long. In each of the frames, you see an n × n × n array of cubes, just as in the previous part of the problem. (The cubes in each frame are actually hypercubes because their existence in the frame gives them a duration of one frame, or a width of one unit in the time [fourth] dimension. However, it may be easier to think of them as normal 3-D cubes when trying to visualize a single frame.) This means you have n × n³ = n⁴ hypercubes in total. For color, the arrays you see in the middle frames of the filmstrip look just like the array from the previous part of the problem—a red shell surrounding a blue core.

All the cubes in the first and last frames are on the surface in the fourth dimension because they are at the ends of the filmstrip. All the cubes in these frames are red. In other words, n – 2 frames have blue cubes, and each of these frames looks like the array from the previous part of the problem.

Multiplying the number of frames with blue cubes by the number of blue cubes in each frame gives (n – 2)(n – 2)³ = (n – 2)⁴, the total number of blue hypercubes. Subtracting from the previous result yields n⁴ – (n – 2)⁴ hypercubes on the surface of the hypercubic array.

You’re almost there. At this point you may find it helpful to extend the device you’ve been using for visualization into many dimensions, or you may find it easier to dispense with visualization and solve the problem using patterns and mathematics. The following discussion examines both methods.

Visualizing a filmstrip gave you four dimensions, but there’s no reason to limit yourself to a single filmstrip. If you imagine lining up n filmstrips side by side, you have five dimensions: three in each frame, one given by the frame number, and one more given by the filmstrip that holds the frame. Each of these filmstrips would look just like the filmstrip from the four-dimensional case, except for the rightmost and leftmost filmstrips. These two filmstrips would be surface filmstrips in the fifth dimension, so all the cubes in each of their frames would be red. You can further extend this to six dimensions by imagining a stack of multiple layers of filmstrips.

Beyond six dimensions, it again becomes difficult to visualize the situation (you might think of different tables, each holding stacks of layers of filmstrips), but the device has served its purpose in illustrating that dimensions are an arbitrary construction—there is nothing special about objects with more than three dimensions.

Each dimension you add gives you n copies of what you were visualizing before. Of these, two of the copies are always entirely on the surface, leaving n – 2 copies that have blue interior cubes. This means that with each additional dimension, the total number of hypercubes increases by a factor of n and the number of nonsurface hypercubes increases by a factor of n – 2. You have one of each of these factors for each dimension, giving you a final result of nⁱ – (n – 2)ⁱ hypercubes on the surface of the array.

Alternatively, you might take a pattern-based approach and note that you raised both parts of the expression to the power of 3 in the three-dimensional case and to the power of 4 in the four-dimensional case. From this you might deduce that the exponent represents the number of dimensions in the problem. You might check this by trying the one- and two-dimensional cases (a line and a square), where you would find that your proposed solution appears to work. Thinking about it mathematically, when you have n hypercubes in each of i directions, it seems reasonable that you would have a total of nⁱ hypercubes; for the same reason, raising (n – 2) to the ith power also seems to make sense. This isn’t a proof, but it should be enough to make you confident that nⁱ – (n – 2)ⁱ is the right answer.

It’s interesting to look at the progression of the parts of this problem. The first part of the problem is quite easy. Taken by itself, the last part of the problem would seem almost impossible. Each part of the problem is only a little more difficult than the preceding, and each part helps you gain new insight, so by the time you reach the final part, it doesn’t seem so insurmountable. It’s good to remember this technique. Solving simpler, easier, more specific cases can give you insight into the solution of a more difficult, general problem, even if you aren’t led through the process explicitly as you were here.

The Fox and the Duck

The most obvious strategy for the duck is to swim directly away from where the fox is standing. The duck must swim a distance of r to the edge of the pond. The fox, meanwhile, has to run around half the circumference of the pond, a distance of πr. Because the fox moves four times faster than the duck, and πr < 4r, it’s apparent that any duck pursuing this strategy would soon be fox food.

Think about what this result tells you. Does it prove that the duck can’t escape? No, it just shows that the duck can’t escape using this strategy. If there weren’t anything else to this problem, it would be a trivial geometry exercise—not worth asking in an interview—so this result suggests the duck can escape, you just don’t know how.

Instead of focusing on the duck, try thinking about the fox’s strategy. The fox will run around the perimeter of the pond to stay as close to the duck as possible. Because the shortest distance from any point inside the circle to the edge lies along a radius, the fox will try to stay on the same radius as the duck.

How can the duck make life most difficult for the fox? If the duck swims back and forth along a radius, the fox can just sit on that radius. The duck could try swimming back and forth across the center point of the pond, which would keep the fox running as the duck’s radius repeatedly switched from one side of the pond to the other. However, consider that each time the duck crosses the center point, it returns to the problem’s initial configuration: the duck is in the center and the fox is at the edge. The duck won’t make much progress that way.

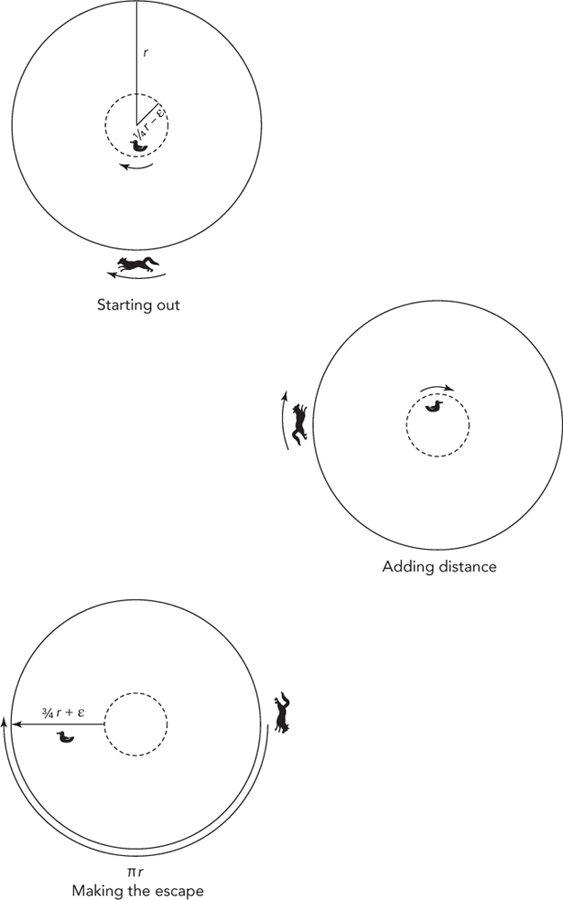
Another possibility would involve the duck swimming in a circle concentric with the pond, so the fox would have to keep running around the pond to stay on the duck’s radius. When the duck is near the edge of the pond, the fox has no trouble staying on the same radius as the duck because they are covering approximately equal distances and the fox is four times faster. However, as the duck moves closer to the center of the pond, the circumference of its circle becomes smaller and smaller. At a distance of ¼ r from the center of the pond, the duck’s circle is exactly four times smaller than the circumference of the pond, so the fox can just barely stay on the same radius as the duck. At any distance less than ¼ r from the center, the fox must cover more than four times the distance that the duck does to move between two radii. That means that as the duck circles, the fox starts to lag behind.

This strategy seems to give the duck a way to put some distance between it and the fox. If the duck swims long enough, eventually the fox will lag so far behind that the radius the duck is on will be 180 degrees from the fox; in other words, the point on the shore closest to the duck will be farthest from the fox. Perhaps this head start would be enough that the duck could make a radial beeline for the shore and get there ahead of the fox.

How can the head start be maximized? When the duck’s circle has a radius of ¼ r the fox just keeps pace with it, so at a radius of ¼ r minus some infinitesimal amount ε, the duck would just barely pull ahead. Eventually, when it got 180 degrees ahead of the fox, it would be ¾ r + ε from the nearest point on the shore. The fox, however, would be half the circumference of the pond from that point: πr. In this case, the fox would have to cover more than four times the distance that the duck does (¾r· 4 < πr), so the duck could make it to land and fly away, as shown in Figure 17-4.

You might want to try to work out the solution to a similar problem: this time, the fox chases a rabbit. They are inside a circular pen from which they cannot escape. If the rabbit can run at the same speed as the fox, is it possible for the fox to catch the rabbit?

Burning Fuses

One of the difficult parts of this problem is keeping firmly in mind that the length of a piece of fuse has nothing to do with the time it takes to burn. Although this is stated explicitly in the problem, constant rates and relationships between time and distance are so familiar that it can be easy to fall into the trap of trying to somehow measure a physical length of fuse. Because the burn rate is unknown and variable, the only useful measure is time. Mindful of this, you can begin to solve the problem.

The materials and actions available to you are fairly circumscribed in this problem. In such a case, it can be useful to begin by considering all possible actions and then identify which of these possible actions might be useful.

You can light the fuses at two locations: at an end or somewhere that is not an end (in the middle). If you light one of the fuses at an end, it will burn through in 60 minutes. That’s longer than the total length of time you need to measure, so it probably isn’t directly useful. If you light a fuse in the middle, you end up with two flames, each burning toward a different end of the fuse. If you were extremely lucky, you might light the exact center (in burn time; it might not be the physical center) of the fuse, in which case both flames would extinguish simultaneously after 30 minutes. It’s much more likely that you would miss the center of the fuse, giving you one flame that went out sometime before 30 minutes and a second that continued burning for some time after. This doesn’t seem like a reliable way to make a measurement.

When you lit the fuse in the middle, you got a different burn time than when you lit the end. Why is this? Lighting the middle of the fuse created two flames, so you were burning in two places at once. How else might you use two flames? You’ve seen that lighting the middle of the fuse is problematic because you don’t actually know where (in time) you’re lighting. That leaves the ends of the fuse. If you light both ends of the fuse, the flames will burn toward each other until they meet and extinguish each other after exactly 30 minutes. This could be useful.

So far, you can measure exactly 30 minutes using one fuse. If you could figure out how to measure 15 minutes with the other fuse, you could add the two times to solve the problem. What would you need to measure 15 minutes? Either a 15-minute length of fuse burning at one end, or a 30-minute length of fuse burning at both ends, would do the trick. Because you’re starting with a 60-minute length of fuse, this means you need to remove either 45 or 30 minutes from the fuse. Again, you must do this by burning because cutting the fuse would involve making a physical (distance) measurement, which would be meaningless. Forty-five minutes could be removed by burning from both ends for 22.5 minutes or one end for 45 minutes. Measuring 22.5 minutes seems an even harder problem than the one you were given; if you knew how to measure 45 minutes you’d have solved the problem, so this possibility doesn’t look particularly fruitful.

The other option is removing 30 minutes of the fuse, which you could do by burning from both ends for 15 minutes or one end for 30 minutes. The need to measure 15 minutes returns you to the task at hand, but you do know how to measure 30 minutes: exactly 30 minutes elapse from lighting both ends of the first fuse until the flames go out. If you light one end of the second fuse at the same moment you light both ends of the first, you’ll be left with 30 minutes of fuse on the second fuse when the first fuse is gone. You can light the other end (the one that isn’t already burning) of this second fuse as soon as the first goes out. The two flames burning on the 30-minute length of fuse extinguish each other after exactly 15 minutes, giving you a total of 30 + 15 = 45 minutes.

Escaping the Train

At first, this seems like a classic algebraic word problem, straight out of your high school homework. When you begin to set up your x’s and y’s, however, you realize you’re missing a lot of the information you would expect to have in a standard algebra rate problem. Specifically, although you know the boys’ speeds, you don’t have any information about distances or times. Perhaps this is more challenging than it first appeared.

A good way to start is by drawing a diagram using the information you have. Call the boys Abner and Brent (A and B to their friends). At the moment the problem begins, when the boys have just noticed the train, the train is an unknown distance from the tunnel, heading toward them. A and B are both in the same place, one-third of the tunnel length from the entrance closest to the train. A is running toward the train and B away from it, as shown in Figure 17-5.

The only additional information you have is that both boys just barely escape. Try drawing diagrams of the moments of their escapes. A is running toward the train and has only one-third of the tunnel to cover, so he’ll escape before B. Because he reaches the end of the tunnel at the last possible instant, he and the train must be at the end of the tunnel at the same time. Where would B be at this time? A and B run at the same speed; A moves one-third of the length of the tunnel before escaping, so B must also have run one-third of the length of the tunnel. That would put him one-third of the way from the end of the tunnel he’s headed for, as shown in Figure 17-6.

Now diagram B’s escape. The train has come all the way through the tunnel, and both it and B are right at the end of the tunnel. (A is somewhere outside the other end of the tunnel, counting his blessings.) Figure 17-7 shows this situation.

None of these diagrams seem particularly illuminating on their own. Because you need to determine the speed of the train, you should look at how it moves—how its position changes between your three diagrams. Between the first and second diagrams, A and B each run one-third of the length of the tunnel, while the train moves an unknown distance. No help there. Between the second and third diagrams, B again runs one-third the tunnel length, while the train runs through the whole tunnel. Therefore, the train covers three times more distance than B in the same amount of time. This means the train must be three times as fast as B. B travels 10 miles per hour, so the train moves at 30 miles per hour.

SUMMARY

Many brainteasers are graphical in nature and serve to test your spatial thinking. You need to apply the general brainteaser guidelines from the previous chapter to these kinds of questions, but often the correct answer is evident only when you visualize the problem. Don’t underestimate the power of diagrams!