3
Fuzzy Logic
Key Concepts
Abduction, Induction and Analogy, Addition, Chain rule, Consistency, Contradiction, Existential quantifier, First order predicate logic (FOPL), Fuzzy if-then, Fuzzy if-then-else, Fuzzy logic operations, Fuzzy proposition, Fuzzy quantifier, Fuzzy reasoning, Fuzzy rules, Fuzzy truth value, Generalized modus ponens, Generalized modus tolens, Interpretation, Linguistic variable, Logical equivalence, Modus Ponens, Modus Tollens/Indirect Reasoning/Law of Contraposition, Non-deductive rules of inference, Propositional logic, Resolution, Rules of inference, Simplification, Tautology, Universal quantifier, Universal specialization, Validity of argument, Well-formed formulae (wwf)
Chapter Outline
Various features of the fuzzy set theory are discussed in Chapter 2. This chapter presents the fundamentals of fuzzy logic. It starts with a review of the classical crisp logic and then presents fuzzy logic as an extension, or generalization of crisp logic. Logic is the study of the structure and principles of reasoning and sound argument. The universe of discourse of logic is the set of all statements, or, propositions. A statement, or proposition, is a sentence that has a truth value, either True or False, in crisp logic. Logic is not concerned about the content or meaning of a statement, but only with their possible truth values. Symbolic logic is logic using symbols that represent actual statements. Crisp logic asserts that a statement can be either true or false. It does not accept a third possibility. However, in real life we come across situations where such sharp distinction between truth and falsehood do not exist. On the contrary, there are infinite shades of truths between black and white absolute truth and absolute falsehood. Fuzzy logic accepts this state of affair and builds a system of reasoning on the basis of the possibility of infinite number of truth values. Over the last few decades fuzzy logic has been successfully applied to solve numerous practical problems of engineering, science and business.
3.1 CRISP LOGIC: A REVIEW
Classical logic is based on the Aristotlian ‘Law of excluded middle’ which states that a statement is either true or false and nothing else. In contrast, fuzzy logic accepts to the point of view that there are infinitely many shades of truth (or falsehood) between absolutely false and absolutely true. The logical system that allows only two truth-values is called crisp logic. This section presents a review of the essential features of crisp logic. We start with propositional logic, followed by the more powerful system called the predicate logic. A brief discussion on rules of inferences is provided at the end of this section.
3.1.1 Propositional Logic
Propositional logic is concerned about the properties and laws governing the universe of propositions. A proposition is a statement that is either true or false and nothing else. A few propositions are cited below.
- This rose is red.
- Mona Lisa was painted by Leonardo de Vinci.
- Tiger is a domestic animal.
- The smallest prime number is 5.
- Every action has an equal and opposite reaction.
As far as logic is concerned it does not matter whether a proposition is empirically true or false, or not known at all whether true or false. This is an empirical problem and logic is not concerned about it. The only matter of logical concern is that the statement has a definite truth-value, known or unknown. Here are a few sentences that are not valid propositions.
|
1. Is this a red rose? |
(Interrogation) |
|
2. What a great artist was Leonardo de Vinci! |
(Exclamation) |
|
3. The blue ideas are sleeping furiously. |
(Meaningless) |
In symbolic logic, propositions are expressed with symbols or symbolic expressions that are combinations of symbols.
Propositional calculus deals with the symbolic expressions of propositional logic and their manipulation. The valid symbolic expressions of propositional logic are known as well-formed formulae (wff). These wffs are composed of
- The logical constants ‘True’ (represented by T or 1) and ‘False’ (F or 0)
- Propositions (usually symbolically represented by a, b, p, q etc.)
- Parenthesis (, and)
- Logical operators or connectives, e.g.,
|
AND |
(Conjunction, denoted as ^ or ‘.’) |
|
OR |
(Disjunction, denoted as ∨ or ‘+’) |
|
NOT |
(Negation, denoted as ¬ or ‘′’) |
|
Implication |
(Conditional, If ... Then ..., denoted as →) |
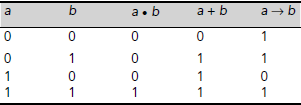
The behaviour of logical operators are described with the help of truth tables. The truth tables for the logical operators NOT, AND, OR are shown in Table 3.1 and Table 3.2.
Table 3.1. Truth table for logical NOT operation
a |
a′ |
|---|---|
0 |
1 |
1 |
0 |
Table 3.2. Truth table for logical AND, OR, IMPLICATION
Definition 3.1 (Propositional logic well-formed-formula) A propositional logic well-formed formula (wff) is recursively defined as follows.
- The logical constants T and F are wffs.
- A propositional symbol (e.g. a, b, p, q etc.) is a wff.
- Given two wffs W1 and W2, the following are also wffs
• (W1) . (W2)
(Conjunction of two wffs is a wff)
• (W1) + (W2)
(Disjunction of two wffs is a wff)
• (¬W1)
(Negation of a wffs is a wff)
• (W1) → (W2)
(Implication of two wffs is a wff)
• (W1) ↔ (W2)
(Equivalence of two wffs is a wff)
- Nothing else is a propositional logic well-formed formula (wff).
The symbol ↔ stands for logical equivalence (implies and implied by, or bicondition) and is defined as (a → b) • (b → a). The truth table for ↔ is shown in Table 3.3. In practice, while writing a wff, the number of parentheses is usually minimized by obeying a set of precedence rules among the operators.
Table 3.3. Truth table of logical equivalence
a |
b |
a ↔ b |
|---|---|---|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Example 3.1 (Propositional logic well-formed-formulae)
Some valid and invalid propositional logic wffs are given below in Table 3.4. For the sake of simplicity the parentheses are used sparingly. Moreover the conjunction operation is not explicitly used where its existence is obvious from the context.
Table 3.4. Examples of valid and invalid wffs
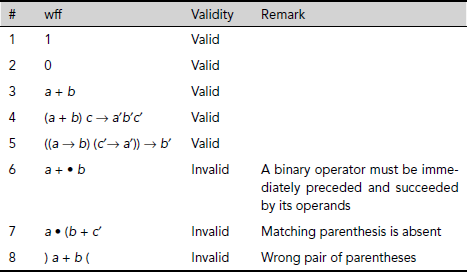
Table 3.5. Properties of propositional logic wffs
# |
Relation |
Remarks |
|---|---|---|
1
|
(A • B) • C ≡ A • (B • C) |
Associativity |
(A + B) + C ≡ A + (B + C) |
| |
2
|
A • B ≡ B • A |
Commutativity |
A + B ≡ B + A |
| |
3
|
A • (B + C) ≡ (A • B) + (A • C) |
Distributivity |
A + (B • C) ≡ (A + B) • (A + C) |
| |
4
|
(A • B)′ ≡ A′ + B′ |
De Morgan’s law |
(A + B)′ ≡ A′• B′ |
| |
5 |
A → B ≡ B′→ A′ |
Contrapositive law |
6 |
A + A′ ≡ 1 |
Law of excluded middle |
7 |
A • A′ ≡ 0 |
Law of Contradiction |
8
|
A + A ≡ A |
Idempotency |
A • A ≡ A |
| |
9
|
A • (A + B) ≡ A |
Absorption |
A + (A • B) ≡ A |
|
Properties of Propositional Logic wffs Propositional logic statements in the form of wffs obey certain properties. Some of these are listed in Table 3.5.
Definition 3.2 (Interpretation of a logical expression) Let e (x1, x2, ..., xn) be a logical expression involving n propositions x1, x2, ..., xn. An interpretation of the expression e (x1, x2, ..., xn) is a combination of truth values for the constituent individual propositions x1, x2, ..., xn.
Obviously, an expression e (x1, x2, ..., xn) involving n propositions have exactly 2n interpretations. For example, if e (a, b, c)) = a + b + a • b′ be the logical expression then a = 1, b = 0, c = 0 is one of its interpretations. For this interpretation the expression attains the truth value e (a, b, c) = a + b + a • b′ = 1.
Definition 3.3 (Logical equivalence of two wffs) Two wffs are said to be equivalent if they attain the same truth value for all possible interpretations.
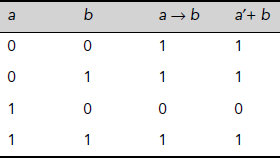
The logical equivalence of two expressions can be easily checked with the help of their truth tables. For example Table 3.6 shows that the expression a → b is equivalent to a′ + b.
Table 3.6. Equivalence of a → b and a′ + b
Definition 3.4 (Tautology) A tautology is a proposition which is true for all possible interpretations.
Definition 3.5 (Contradiction) A contradiction is a proposition which is false for all possible interpretations.
Definition 3.6 (Consistency) A collection of statements is said to be consistent if they can all be true simultaneously.
Example 3.2 (Tautology, Contradiction, Consistency)
The most obvious examples of a tautology and a contradiction are a′ + a and a′ • a respectively. A few more tautologies and contradictions are cited below in Table 3.7. Table 3.8 presents a number of consistent and a few inconsistent pairs of propositional logic expressions. Verification of the tautologies, contradictions, consistencies and inconsistencies using the truth table method is left as an exercise.
Table 3.7. Tautologies and contradictions
# |
wff |
Category |
|---|---|---|
1 |
1 |
Tautology |
2 |
ab + a′ + b′ |
Tautology |
a + b + a′b′ |
Tautology | |
4 |
a′b′ + a′b + ab′ + ab |
Tautology |
5 |
(1 + a) (1 + b) |
Tautology |
6 |
0 |
Contradiction |
7 |
a′b′ (a + b) |
Contradiction |
8 |
(a + b) (a′ + b) (a + b′) (a′ + b′) |
Contradiction |
9 |
a′b (a + b′) |
Contradiction |
Table 3.8. Consistent and inconsistent expressions
# |
wff pairs |
Remark |
|---|---|---|
1 |
{a, b} |
Consistent. Both are true when a = 1, b = 1 |
2 |
{a′, b′} |
Consistent. Both are true when a = 0, b = 0 |
3 |
{a′ + b, a + b′} |
Consistent. Both are true when a = 1, b = 1 |
4 |
{a + b′c′, ab + b} |
Consistent. Both are true when a = 1, b = 1, c = 0 |
5 |
{a, a′} |
Inconsistent. Complimentary wffs. |
6 |
{a + b, a′b′} |
Inconsistent. Complimentary wffs. |
7 |
{(a + b) c, a′b′ + c′} |
Inconsistent. Complimentary wffs. |
Definition 3.7 (Validity of an argument) An argument is said to be valid if the conclusion is true whenever the premises are true.
Example 3.3 (Validity of an argument)
As an example, let us consider the following argument: If Basant Kumar plays the role of the hero’s, then the film will be a hit if Basanti Devi is the heroine. If Basant Kumar plays the hero’s role, then Basanti Devi will be the heroine. Therefore, if Basant Kumar plays the hero’s role, the film will be a hit. Is the argument valid? This can be easily answered by constructing the corresponding truth table and checking if the conclusion is True whenever the premises are True. Let us denote
Statement ‘Basant Kumar plays the hero’s part’ as a
Statement ‘The film will be a hit’ as b
Statement ‘Basanti Devi is the heroine’ as c
Then the argument is symbolically presented as
Premise No. 1. |
|
a → (c → b) |
Premise No. 2. |
|
a → c |
Conclusion. |
Therefore, |
a → b |
The corresponding truth table is shown in Table 3.9. The two premises of the argument, a → (c → b) and a → c, are arranged in Columns 5 and 6, respectively. The conclusion a → b is shown in Column 7. In Rows 1, 2, 3, 4 and 8, both the premises are true. The corresponding truth-values of the conclusion, noted in Column 7 are also true. Hence the argument is valid
Table 3.9. Consistency checking

3.1.2 Predicate Logic
The propositional logic described above suffers from certain limitations. These limitations motivated the logicians to extend it to a more powerful formalism called the Predicate Logic. It provides mechanisms to capture the inner structure of propositions such as the subject–predicate relation, or quantifiers like ‘for all’ or ‘there exists’. Natural language statements can be expressed as predicate logic wffs, so that they could be processed by automated tools of intelligent systems according to the rules of sound reasoning. This subsection provides a discussion on the basic features of First Order Predicate Logic (FOPL). We start with an exposure to the limitations of propositional logic. The features of FOPL are presented subsequently.
Limitations of propositional logic Let us consider the argument: If monkeys have hair on their bodies then they are mammals. Monkeys have hairs on their bodies. Therefore, monkeys are mammals. This argument can be symbolically presented as
Premise No. 1. |
|
p → q |
Premise No. 2. |
|
p |
Conclusion. |
Therefore, |
q |
where p denotes the proposition Monkeys have hairs on their bodies and q denotes the proposition Monkeys are mammals. Validity of this argument can be easily verified using the truth table method. This is shown in Table 3.10, which shows that the conclusion q is true whenever both the premises are true (Row 4).
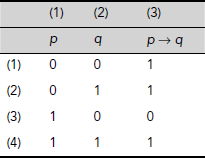
Now, consider another argument leading to the same conclusion as before: All animals having hairs on their bodies are mammals. Monkeys have hairs on their bodies. Therefore monkeys are mammals. This argument has the form
Premise No. 1. |
a | |
Premise No. 2. |
|
b |
Conclusion. |
Therefore, |
c |
where a denotes the statement All animals having hairs on their bodies are mammals, b denotes the statement Monkeys have hairs on their bodies and c denotes the statement Monkeys are mammals. This is not a valid argument because given the two propositions a and b as premises we cannot conclude a third proposition c that is independent of the premises. Applying the truth table method we obtain the combinations of truth values of a, b and c as shown in Table 3.11.
Table 3.11
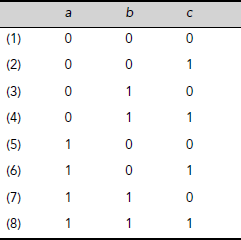
The 7th row of the table shows that the conclusion c is false even though both the premises a, b are true. We know that an argument is valid if and only if the conclusion is true whenever the premises are true. Therefore, according to the formalism of propositional calculus, the second argument is invalid. However, intuitively we feel that the second argument is as valid as the first argument.
The weakness of propositional logic is, it is inadequate to express the inner meaning of a statement like ‘All animals having hairs on their bodies are mammals’. A more powerful logical system is required to overcome this limitation. Predicate logic offers the solution. In predicate logic, the aforementioned argument will be represented as:
Premise No. 1. |
For all x, if x is a hairy animal, then x is a mammal. |
Premise No. 2. |
Monkey is a hairy animal. |
Conclusion. |
Therefore, Monkey is a mammal. |
Using predicate logic expressions, the argument looks like
|
(∀x) H (x) → M (x) |
|
H (Monkey) |
∴ |
M (Monkey) |
where, the symbols have the following meanings
|
∀ x |
: for all x |
|
H (x) |
: x is a hairy animal. |
|
M (x) |
: x is a mammal. |
|
H (Monkey) |
: Monkey is a hairy animal. |
|
M (Monkey) |
: Monkey is a mammal. |
H and M are two predicate symbols used in this argument. The validity of such argument will be proved later in this subsection.
Table 3.12. Constituents of predicate logic wffs
# |
Element type |
Symbols commonly used |
|---|---|---|
1 |
Non-predicate constants |
a, b, c, … |
2 |
Variables |
x, y, z, … |
3 |
Predicate constants |
P, Q, R, … |
4 |
Function Constants |
f, g, h, … |
5 |
Universal quantifier |
∀ (for all) |
6 |
Existential quantifier |
∃ (there exists) |
7 |
Logical connectives |
¬,′ (NOT), • (AND), + (OR), → (implication), ↔ (equivalence) |
8 |
Parentheses |
(,) |
Syntax As in propositional logic, statements of predicate logic are also expressed as well-formed formulae (wffs). However, predicate logic wffs are extensions of propositional logic wffs. The structural elements of these wffs are listed in Table 3.12. These elements are briefly described below.
Non-predicate constants Non-predicate constants are symbolic or numeric non-predicate values that do not change over time. Examples of non-predicate constants are Socrates, X-123, 007, -63, India etc.
Variables Variables are symbolic expressions that can assume different non-predicate values over a certain domain. For example, if x is a variable denoting the name of a month, then x may assume any value from January to December.
Predicate constants Predicate constants are symbols that denote the predicate part of a proposition. They are relations or mappings from the elements of a certain domain D to a truth value. For example, let MAN be a predicate constant and MAN (x) means ‘x is a man’. Then MAN (John) is true as John is a man but MAN (Mary) is false because Mary is not a man. Similarly, if SON is a predicate constant such that SON (x, y) means x is the son of y, then SON (John, Smith) is True if John is the son of Smith, otherwise it returns false. The argument(s) of a predicate constant are non-predicate constants, variables, or functions.
Function constant A predicate logic function is syntactically similar to a predicate constant except that instead of a truth value, it may return a value from any domain. As an instance of a function, consider age (person) which returns the age of a person. If we substitute Sam for the variable person whose age is 30 years, then age (Sam) would return 30. Similarly, owner (phone-number) might be a function that returns the name of the owner of a given phone-number.
Quantifiers There are two quantifiers, the universal quantifier (denoted by ∀ and pronounced as for all) and the existential quantifier (denoted by ∃ and pronounced as there exists). The universal quantifier ∀ is employed when a statement applies to all members of a domain. For example, the statement ‘All integers are real numbers’ is universally quantified. On the other hand, the existential quantifier is used when a statement holds good for at least one element of the concerned domain. Consider, for example, the statement, There is an employee who is a doctorate. It does not state that all employees are doctorates (though that possibility is not negated by the given statement) but it ensures that there are some, at least one, employee who is a doctorate.
Logical connectives The five logical connectives frequently used in predicate logic wffs are ¬, or (NOT), • (AND), + (OR), → (implication), ↔ (equivalence). They have the same semantics as in propositional logic.
Parentheses Parentheses are used as delimiters. Braces and square brackets are also used as delimiters for the sake of better readability.
Apart from the elements mentioned above, there are a few terms used frequently in first order predicate logic. These are defined below.
Definition 3.8 (Term) In predicate logic, a term is a non-predicate constant symbol, or a variable symbol, or a function symbol.
Examples of terms are A, min, f (a, b) etc.
Definition 3.9 (Atom) A predicate expression, consisting of a predicate symbol followed by the list of parameters within a pair of parentheses, is said to be an atom, or atomic formula.
Examples of atoms are MAN (x), LESS-THAN (x, y) etc.
Definition 3.10 (Literal) A literal is either an atom, or the negation of an atom.
So if MAN (x) is an atom, both MAN (x) and MAN (x)′ are literals.
Example 3.4 (wff expression for a predicate logic proposition)
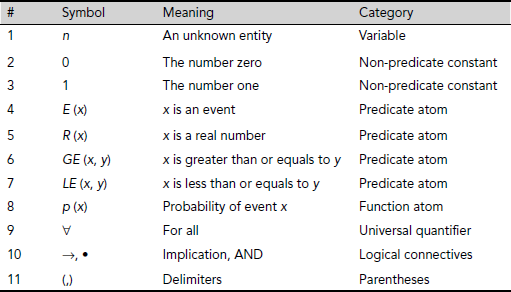
Let us consider the proposition The probability of any event is a real number between 0 and 1, both inclusive. Logically, this is equivalent to the statement: For all n, if n is an event then probability of n is a real number, and probability of n is greater than or equal to 0, and probability of n is less than or equal to 1. The wff for the statement is
The symbols used in this wff have meanings and categories as listed in Table 3.13.
Table 3.13
It must be understood that a predicate and a function, though syntactically similar, are actually different. When evaluated a predicate term returns a truth value, true or false, whereas a function term may return any value from the related domain. In the present example, given real numbers x and y, GE (x, y) is either true, or false. However, given an event x, p (x) is a real number within the range [0, 1].
The predicate logic discussed here is of first order in the sense that only constants over predicates and functions are allowed and no variables over predicates or functions are allowed. The first order predicate logic wffs are recursively defined as follows.
Definition 3.11 (First order predicate logic well-formed formula) The first order predicate logic well formed formula can be recursively defined as follows:
- If P is a predicate constant with k arguments and α1, …, αk are terms, i.e., variables, constants, or functions, then P (α1, …, αk) is a wff.
- If W is a wff then (¬W) is a wff.
- If W1 and W2 are wffs, then the following are wffs.
- (W1 • W2)
- (W1 + W2)
- (W1 → W2)
- (W1 ↔ W2)
- If W (x) is a wff containing a free variable x (x is free if it is not already quantified by either ∀, or ∃ in W (x)) then (∀x) W (x) and (∃x) W (x) are also wffs.
- Only those which are obtained using the rules 1 to 4 cited above are wffs.
It is obvious from the recursive definition given above that all FOPL wffs are composed of atomic formulae with appropriate logical connectives, quantifiers and the parentheses. A few valid propositions and corresponding FOPL wffs are given below.
|
Proposition |
FOPL wff |
|---|---|---|
(i) |
The earth is a planet. |
PLANET (earth) |
(ii) |
The sky is blue and forst is green |
BLUE (sky) • GREEN (forest) |
(iii) |
If x is greater than y and y is greater than z then x is greater than z. |
(∀ x, y, z) [GE (x, y) • GE (y, z)] → GE (x, z) |
(iv) |
For every x there is a y such that y = x2. |
(∀x) (∃y) EQ (y, square-of (x)) |
(v) |
Every man has a father and a mother. |
(∀x) MAN (x) → [(∃y, z) FATHER |
(vi) |
If x is irrational then x is not an integer. |
(∀x) IRRATIONAL (x) → ¬ INTEGER (x) |
However, the following expressions are not valid FOPL wffs due to the reasons specified on the right.
|
PLANET (Sun′) |
A constant term cannot be negated. |
|
(∀P) (∃Q) P(x) → ¬ Q(x) |
Predicate cannot be quantified. |
|
LESS-THAN (NEG (x), POS (y)) |
A predicate cannot be an argument of a function. |
|
score-of (Sam) |
A function is not a wff. |
Semantics of FOPL wffs The semantics of FOPL is an extension of the semantics of propositional logic. The logical connectives ′, •, +, →, ↔ have the same truth tables in both systems. However, unlike propositional logic, an FOPL wff is always understood in the context of some domain, or universe of discourse. For example, let Family = {Sam, Mita, Bilu, Milu} be a domain. We may define predicates like HUSBAND (x), WIFE (y), CHILD (x), MARRIED-TO (x, y) etc. and functions like son-of (x), or spouse-of (y) etc. on this domain. It is tacitly assumed that all variables and constants take values from the corresponding domain.
An interpretation is a set of values assigned to various terms and atomic formulae of an FOPL wff. An atomic formula, which is nothing but a predicate expression, evaluates to a truth value. Since a wff is composed of literals, i.e., atomic formulae in negated or non-negated forms, the truth value of a wff should be computable with the help of the truth table method. Just as in propositional logic, if two wffs evaluate to the same truth value under any interpretation, they are said to be equivalent. Moreover, a predicate that has no variables is called a ground atom. For example, MAN (Socrates) is a ground atom, but (∀x) MAN (x) → MORTAL (x) is not a ground atom.
Table 3.14. ODD (x) and EVEN (x) OVER ∪ = {0, 1}
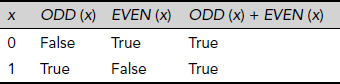
Table 3.15. SUM (x, y)
x |
y |
Sum (x, y) |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Evaluation of a wff containing variable arguments needs special attention. This is because the wff (∀x) P [x], where P [x] is a wff containing the free variable x, is true if and only if P [x] is true for all values of x within its domain. Therefore, to determine whether the statement (∀ x) P [x] is true or false one must evaluate P [x] for every possible value of x within its domain. On the other hand, (∃ x) P [x] is true if and only if there exists at least one value of x for which P [x] is true. Moreover, to determine the truth of the statement (∃x) P [x] one has to go on evaluating P [x] for various possible values of x until either P [x] is true for same x or all possible values of x have been tried. Evaluation of an FOPL wff containing quantified variables is illustrated in Example 3.5.
Example 3.5 (Interpretation of Predicate Logic wff)
Let U = {0, 1} be the universe of discourse. There are two predicates ODD (x) and EVEN (x) and a function sum (x, y) that returns addition modulo two of its arguments x and y, i.e., sum (x, y) = (x + y) % 2. The values of the predicates and the functions for various combinations of their arguments are given in Table 3.14 and Table 3.15.
Now consider the statements
- (∀x) ODD (x) + EVEN (x)
- (∀x) ODD (x) → (∃y) EVEN (sum (x, y))
The first statement can be evaluated by checking whether ODD (x) + EVEN (x) is true for all possible values of x. Table 3.14 shows that the statement ODD (x) + EVEN (x) is true for all possible values of x in its domain, i.e., for both x = 0, and x = 1. Hence statement (∀x) ODD (x) + EVEN (x) is true. The truth table for the second statement is shown in Table 3.16.
There is only one odd value of x, 1, and so ODD (x) is True for x = 1. Now, to evaluate the expression (∀x) ODD (x) → (∃y) EVEN (sum (x, y)) is true, we have to set x = 1 and then look for a value of y such that sum (x, y) is even, or 0. Table 3.16 shows that there does exist a y that satisfies the condition stated above. We see that for x = 1, and y = 1, ODD (x) is True and EVEN (sum (x, y)) is also true so that ODD (x) → (∃y) EVEN (sum (x, y)) is true which in turn makes the given wff true.

In contrast, consider the statement (∀x) (∀y) ODD (sum (x, y)) → ODD (y). This is not true because at x = 1 and y = 0 we find that ODD (sum (x, y)) is true but ODD (y) is false
Properties of FOPL well-formed formulae As in propositional logic, the concepts of validity, consistency, satisfiability, logical consequence etc. applies to FOPL too.
An FOPL wff is valid if it is true for every interpretation. A wff is inconsistent (or unsatisfiable) if it is false for every interpretation. An invalid wff is one that is not valid. In other words, if a wff evaluates to False for some interpretation then it is invalid. Similarly, a consistent (or satisfiable) wff is one that is not inconsistent, and hence, is True for some interpretation. Moreover, a wff W is a logical consequence of certain wffs, say W1, W2, …, Wk, if and only if whenever W1, …, Wk are true for some interpretation, W is also true for the same interpretation.
Table 3.17. Some important FOPL identities
# |
Identity |
|
|---|---|---|
1.
|
P • Q ≡ Q • P |
Commutative law |
P + Q ≡ Q + P |
| |
2.
|
P • (Q • R) ≡ (P • Q) • R |
Associative law |
P + (Q + R) ≡ (P + Q) + R |
| |
3.
|
P + (Q • R) ≡ (P + Q) • (P + Q) |
Distributive law |
P • (Q + R) ≡ (P • Q) +(P • R) |
| |
4.
|
¬(P + Q) ≡ (¬P) • (¬Q) |
De Morgan’s law |
¬(P • Q) ≡ (¬P) + (¬Q) |
| |
5.
|
¬((∀x) P [x]) ≡ (∃x) (¬P [x]) |
|
¬((∃x) P [x]) ≡ (∀x) (¬P [x]) |
| |
6.
|
(∀x) P [x] • (∀y) Q [y] ≡ (∀z) (P [z] • Q [z]) |
|
(∃x) P [x] + (∃y) Q [y] ≡ (∃z) (P [z] + Q [z]) |
|
The concepts of free and bound variables in FOPL wffs are important. A variable that exists within the scope of a quantifier is called a bound variable. For example, in the formula (∀x) (∃y) P (x) → Q (y), both x and y are bound variables. However, in (∀x) P (x, y) → (∃z) Q (x, z) x and z are bound variables but y is free. It should be noted that an FOPL wff can be evaluated only when all variables in it are bound. Such wffs are also referred to as sentences.
Two FOPL wffs are said to be equivalent if for all interpretations, both of them evaluate to the same truth value. Table 3.17 presents some important logical identities involving FOPL wffs. Here P and Q are arbitrary wffs and P[x] represents a wff P that involves the variable x.
The identities in Row 6 should be considered carefully. First of all, we must appreciate that all variables are essentially ‘dummy’ variables in the sense that any symbol can be used for them, so long as they do not ‘collide’ with one another. For example, (∀x) P [x] is equivalent to (∀y) P [y]. Similarly, (∀x) P [x] • (∀y) Q [y] is equivalent to (∀x) P [x] • (∀x) Q [x] because in the later expression the scope of the first x is P [x], while the scope of the latter x is Q [x]. So, though the same symbol x is used in both cases actually they represent two unrelated variables.
Now let us consider the equivalence (∀x) P [x] • (∀y) Q [y] ≡ (∀z) (P [z] • Q [z]). As a supporting example, let P [x] means ‘x is a rational number’, and Q [y] means ‘y is a real number’. Obviously, for the aforementioned identity hold good the variables x, y and z must belong to the same universe of discourse. Let us suppose that the universe here is the set of all integers. Now the left hand side and the right hand side of the identity (∀x) P [x] • (∀y) Q [y] ≡ (∀z) (P [z] • Q [z]) can be stated as :
L.H.S.: |
(∀x) P [x] • (∀y) Q [y] |
All integers are rational numbers and all integers are real numbers. |
R.H.S.: |
(∀z) (P [z] • Q [z]) |
All integers are rational numbers as well as real numbers. |
Both the statements are true. However, if we replace conjunction with disjunction, the identity no longer holds good.
To convince ourselves about the non-equivalence of the L.H.S and the R.H.S, let us suppose P [x] represents the statement ‘x is an even number’ and Q [y] represents ‘y is an odd number’. Then the statements on the L.H.S. and R.H.S. correspond to
L.H.S.: |
(∀x) P [x] + (∀y) Q [y] |
All integers are odd or all integers are even. |
R.H.S.: |
(∀z) (P [z] + Q [z]) |
All integers are either odd, or even. |
Here the second statement is true but the first is not. Hence they are not equivalent.
To appreciate the equivalence (∃x) P [x] + (∃y) Q [y] ≡ (∃z) (P [z] + Q [z]) and the non-equivalence (∃x) P [x] • (∃y) Q [y] ≠ (∃z) (P [z] • Q [z]) we may consider the propositions P [x] = ‘x is alive’ and Q [x] = ‘x is dead’ with the assumption that nothing can be simultaneously alive and dead. Here the universe of discourse may be the set of all human beings, dead or alive.
3.1.3 Rules of Inference
Rules of inference are rules with which new propositions are obtained from a set of given statements. There are two kinds of rules of inference, deductive and non-deductive. Some important deductive rules of inference are Modus Ponens, Universal Specialization, Chain Rule, Resolution, Modus Tollens (also called Indirect Reasoning, or Law of Contraposition), Simplification, Addition, etc. Examples of non-deductive rules of inference are Abduction, Induction, and Analogy. These are briefly described in this Subsection.
Deductive rules of inference An inference rule consists of two parts, the premise(s) and the conclusion. For instance, Modus Ponens has two premises, P → Q, and P. And the conclusion is Q.
-
Modus Ponens
Premise No. 1.
P → Q
Premise No. 2.
P
Conclusion
Therefore, Q
Example 3.6 (Modus Ponens)
Premise No. 1.
If the car is expensive then it is comfortable.
Premise No. 2.
The car is expensive.
Conclusion
Therefore, the car is comfortable.
The other inference rules are described below with illustrative examples.
-
Universal Specialization
Premise No. 1.
(∀x) W [x]
Conclusion.
Therefore, W [A]
A is a constant belonging to the universe of discourse.
Example 3.7 (Universal Specialization)
Premise No. 1.
All natural numbers are integers.
Conclusion.
Therefore, 3 is an integer.
-
Chain Rule
Premise No. 1.
P → Q
Premise No. 2.
Q → R
Conclusion.
Therefore, P → R
Example 3.8 (Chain Rule)
Premise No. 1.
If the day is sunny then there will be a large crowd.
Premise No. 2.
If there is a large crowd then the sell is high.
Conclusion.
Therefore, If the day is sunny then the sell is high.
-
Simplification
Premise No. 1.
P • Q
Conclusion.
Therefore, P (or Q).
Premise No. 1.
The sky is blue and 2 is a prime number.
Conclusion.
Therefore, The sky is blue. (or, 2 is a prime number)
-
Resolution
Premise No. 1.
P1 + … + Pm
Premise No. 2.
¬P1 + Q2 + … + Qn
Conclusion.
Therefore, P2 + … + Pm + Q2 + … + Qn
Example 3.10 (Resolution)
Premise No. 1.
It is a rainy day, or I have a raincoat.
Premise No. 2.
It is not a rainy day, or dog is a faithful animal.
Conclusion.
Therefore, I have a raincoat, or dog is a faithful animal.
-
Modus Tollens
Premise No. 1.
P → Q
Premise No. 2.
¬Q
Conclusion.
Therefore, ¬P
Example 3.11 (Modus Tollens)
Premise No. 1.
If the shirt is cheap then there is life on Mars.
Premise No. 2.
There is no life on Mars.
Conclusion.
Therefore, The shirt is not cheap.
-
Addition
Premise No. 1.
P
Conclusion.
Therefore, P + Q
Example 3.12 (Addition)
Premise No. 1.
The Earth is round.
Conclusion.
Therefore, Earth is round, or Man is mortal.
Non-deductive Rules of Inference Non-deductive inference rules are important because they represent the common sense reasoning process that we employ in everyday life to tackle practical problems. These rules are followed to arrive at a conclusion or take a decision which is most likely to be valid or correct though not guaranteed to be so. The three non-deductive inference rules Abduction, Induction and Analogy are briefly explained below.
Abduction Let ![]() be the expression for a possible cause and effect relationship between the statements P and Q where P is the cause and Q is its possible effect. In abduction, given
be the expression for a possible cause and effect relationship between the statements P and Q where P is the cause and Q is its possible effect. In abduction, given ![]() and Q, we can conclude P. Hence
and Q, we can conclude P. Hence
-
Abduction
Premise No. 1.
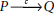
Premise No. 2.
Q
Conclusion.
Therefore, P
Example 3.13 (Abduction)
Premise No. 1.
If you work hard then you will be successful.
Premise No. 2.
You are successful.
Conclusion.
Therefore, You have worked hard.
Induction In practical life, if we find a statement to be true for a number of cases, we tend to assume that it is true in general. This is expressed by the inductive rule of inference.
-
Induction
Premise No. 1.
P [A1]
Premise No. 2.
P [A2]
:
:
:
:
Premise No. k.
P [Ak]
Conclusion.
Therefore, (∀x) P [x]
Example 3.14 (Induction)
Premise No. 1.
Mr Ghosh is a businessman and he is rich.
Premise No. 2.
Mr Rao is a businessman and he is rich.
Premise No. 3.
Mr Smith is a businessman and he is rich.
Premise No. 4.
Mr Ansari is a businessman and he is rich.
Premise No. 5.
Mr Fujiwara is a businessman and he is rich.
Conclusion.
Therefore, all businessmen are rich.
Analogy Our everyday experience tells us that if a situation, or object, or entity is similar to another situation, or object, or entity in some aspect, then they are likely to be similar in other aspects too. If we represent the fact that P is related to Q as
 , and P is similar to P1 as P ≈ P1, then, the analogical rule of inference can be stated as
, and P is similar to P1 as P ≈ P1, then, the analogical rule of inference can be stated as -
Analogy
Premise No. 1.

Premise No. 2.
P ≈ P1
Premise No. 3.
Q ≈ Q1
Conclusion.
Therefore,
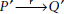
Example 3.15 (Analogy)
Premise No. 1.
Gentle people are generally soft spoken.
Premise No. 2.
Gorillas are much like people.
Premise No. 3.
Soft spoken creatures seem to be humble.
Conclusion.
Therefore, Gentle gorillas are generally humble.
3.2 FUZZY LOGIC BASICS
The propositional logic and the predicate logic discussed so far are crisp. These are two-valued logic because they are based on the law of excluded middle according to which a statement can be either true or false, and nothing else. Fuzzy logic extends crisp logic by accepting the possibility of the infinite shades truths between absolute falsehood and absolute truth. This section presents the fundamental concepts of fuzzy logic.
Table 3.18. Fuzzy truth values
Linguistic |
Numeric (tentative) |
|---|---|
Absolutely False |
0.00 |
Partly False |
0.25 |
Neither False nor True |
0.50 |
Both False and True |
0.50 |
Partly True |
0.75 |
Absolutely True |
1.00 |
3.2.1 Fuzzy Truth Values
In classical (or crisp) logic there are only two possible truth values, true and false, numerically expressed as 1 and 0 respectively. Unlike crisp truth values, there are various fuzzy truth values including the crisp truth values. Certain common linguistic fuzzy truth values and their tentative numeric values are shown in Table 3.18. The numeric truth values indicated above are not absolute. They may vary depending on requirement of context and interpretation. There may be other linguistic truth values such as more-or-less false, very true, almost true etc.
Fuzzy propositions A proposition that can have a fuzzy truth value is known as a fuzzy proposition. Let p be a fuzzy proposition. Then the truth value of p is denoted by τ(p) where 0 ≤ τ(p) ≤ 1. A few examples of fuzzy propositions are cited in Table 3.19 along with their possible fuzzy truth values – both linguistic and numeric.
Table 3.19. Fuzzy proposition and their possible truth values
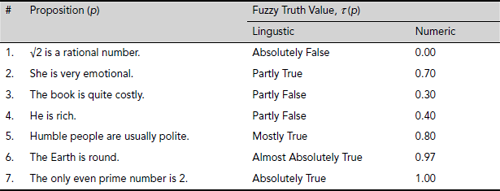
Obviously, the numeric truth values against their linguistic counterparts are tentative. They may vary depending on requirement of context and interpretation.
Fuzzy logic operations Various operations of crisp logic, e.g., disjunction (+), conjunction (•), negation (′), implication (→) etc., have their fuzzy counterparts. The basic fuzzy operations are given in Table 3.20.
Table 3.20. Fuzzy logic operations
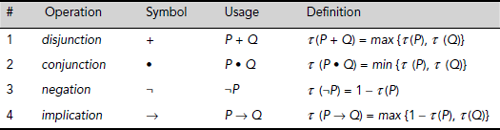
There are various interpretations of fuzzy implication such as
τ(P → Q) = 1 if τ(P) ≤ τ(Q),
= 0, otherwise
τ(P → Q) = 1 if τ(P) ≤ τ(Q),
= τ(Q), otherwise
τ(P → Q) = min {1, τ(Q) / τ(P)}
τ(P → Q) = min {1, [τ(Q) (1 – τ(P)] / [τ(P) (1 − τ(Q)]}
τ(P → Q) = min {1, 1 − τ(P) + τ(Q)}
τ(P → Q) = max {min (τ(P), τ(Q)), 1 − τ(P)}
The last one was proposed by Zadeh. Depending on the context and application, user has to identify and select the appropriate interpretation of fuzzy implication.
Example 3.16 (Fuzzy logic operations)
Let us consider the following two fuzzy propositions along with their fuzzy truth values
Various fuzzy operations on these fuzzy operations are shown below.
Fuzzy AND. |
τ (p • q) = min {τ(p), τ(q)} = min {0.7, 0.4} = 0.4 |
Fuzzy OR. |
τ (p + q) = max {τ(p), τ(q)} = max {0.7, 0.4} = 0.7 |
Fuzzy NOT. |
τ (p′) = 1 − τ(p) = 1 – 0.7 = 0.3, |
|
τ (q′) = 1 − τ(q) = 1 – 0.4 = 0.6 |
Fuzzy implication |
τ(p → q) = max {1 − τ(p), τ(q)} = max {1-0.7, 0.4} = 0.4 |
3.3 FUZZY TRUTH IN TERMS OF FUZZY SETS
Fuzzy logic can be related to fuzzy sets by equating fuzzy truth values to the degrees membership to fuzzy sets. Let F be a fuzzy set over the universe U and x ∈ U. Then what is the truth value of the statement p = ‘x is a member of F’? Obviously, it should be nothing but the extent to which x is a member of F. Hence τ(p) = μF(x). This association between fuzzy set membership and fuzzy logic truth value is illustrated in Example 3.17.
Example 3.17 (Fuzzy truth values in terms of fuzzy membership)
Let a = warm-colour, and b = cool-colour be fuzzy sets on the universe of colour = {violet, mauve, magenta, blue, green, brown, yellow, orange, pink}.
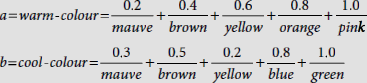
Then the truth values of the fuzzy proposition p = ‘yellow is a warm-colour’, and q = ‘blue is a cool-colour’ would be
Let a and b be two fuzzy sets on the universe U and p = ‘x is a member of a,’q = ‘x is a member of b’ are two fuzzy propositions. Then τ(p + q) = max {τ(p), τ(q)} = max {μA(x), μB(x)} = μA∪B(x). Similarly τ(p • q) = μA∩B(x), and τ(p′) = μA′(x). Therefore fuzzy logic and fuzzy set theory are isomorphic systems.
Fuzzy truth and linguistic variables An atomic fuzzy proposition has the form ‘x is P’ where P is a predicate and a linguistic fuzzy value of a linguistic variable, say L. Moreover, L must be measurable and must have a crisp value corresponding for x. How to find the truth value of a fuzzy proposition s = ‘x is P’? The truth value of s, τ(s), can be obtained in the following way
- Evaluate L for x. This is possible because L is measurable.
- Find the membership of L(x) in P, i.e., find μP(L (x)).
- τ(s) = μP(L (x)).
Hence, s is true to the extent L (x) is a member of P. This is illustrated in Example 3.18.
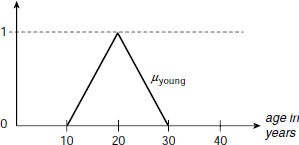
Fig. 3.1. Membership profile of young
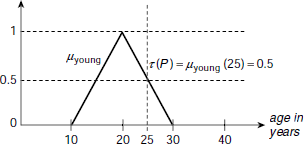
Fig. 3.2. Finding fuzzy truth value from degree of membership
Example 3.18 (Fuzzy truth-value in terms of fuzzy membership)
Consider the fuzzy proposition p = ‘Anita is young’. Here the predicate young is a linguistic value of the linguistic variable age. Other possible linguistic values of age are very young, middle-aged, aged, old, very old, and so on. Each of these linguistic values corresponds to a fuzzy set on the universe of age. Let the membership profile of young be as shown in Fig. 3.1. As age is a measurable quantity it is possible to find the value of age of Anita. If Anita’s age is 25 years then we have age (Anita) = 25. From the membership profile of young we see that μyoung(age (Anita)) = μyoung(25) = 0.5 (Fig. 3.2). Hence the fuzzy truth value of the proposition p = ‘Anita is young’ is τ (p) = 0.5.
3.4 FUZZY RULES
Fuzzy rules are of special interest because they constitute an integral part of the so called fuzzy inference systems, or fuzzy inference mechanisms. The core of fuzzy inference system is the fuzzy rule base, which consists of a set of fuzzy rules. In real life, the concept of fuzzy inference system is used to construct fuzzy controllers. These topics are discussed in greater details in the next chapter.
3.4.1 Fuzzy If-Then
An elementary fuzzy rule R is a statement of the form
where p and q are atomic fuzzy propositions known as the antecedent and the consequent respectively. They have the form of an atomic propositions ‘x is A’.
We have seen that the truth value of a fuzzy statement p = ‘x is A’ is given by the membership value of the fuzzy set A. Moreover, A is the predicate of the statement p = ‘x is A’ so that using the formalism of predicate logic p is denoted as A (x). Therefore the fuzzy rule
is symbolically expressed as
Hence, the fuzzy rule If ‘x is A’ Then ‘y is B’ can be expressed as a fuzzy relation between A and B where
There are various interpretations of fuzzy rule. Among these, interpretations proposed by Mamdani and Zadeh are the most popular. These are
- Mamdani’s interpretation of fuzzy rule:
R (x, y) = τ [A (x) → B (y)]= min [τ (A (x)), τ (B (y))] = min [µ A (x), µ B (y)] (3.5)
- Zadeh’s interpretation of fuzzy rule:
R (x, y) = τ [A (x) → B (y)]= max [min {µ A (x), µ B (y)}, 1 − µ A (x)] (3.6)
Assuming U and V to be the universes for the fuzzy sets A and B respectively, Zadeh’s interpretation of fuzzy rule is equivalent to the relation
where V is used as a fuzzy set in which all the members have membership value 1.
Example 3.19 (Zadeh’s interpretation of fuzzy rules)
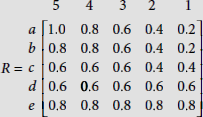
Let R : If ‘job is risky’ Then ‘compensation is high’ be a fuzzy rule. There are four jobs job1, job2, job3 and job4, constituting the universe job = {job1, job2, job3, job4}. Also, there are four categories of compensation c1, c2, c3, and c4 in ascending order. Hence the universe for compensations is compensation = {c1, c2, c3, c4}. The fuzzy sets risky-job and high-compensation are defined on the universes job and compensation respectively as given below.
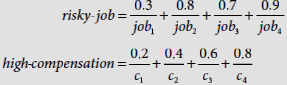
Using Zadeh’s interpretation, the truth value of rule R is expressed by the relation
Now,

Hence the matrix R obtained above embodies the information in the fuzzy implication IF job is risky THEN compensation is high on the basis of the fuzzy concepts risky-job and high-compensation as defined above.
3.4.2 Fuzzy If-Then-Else
A fuzzy If-Then-Else rule R has the form
where A is a fuzzy set on some universe U and B and C are fuzzy sets on the universe V. The truth value of R, in terms of the membership values of the fuzzy sets is given by
This is nothing but the fuzzy relation
Example 3.20 illustrates the fuzzy If-Then-Else rule.
Example 3.20 (Fuzzy If-Then-Else rule)
The fuzzy If-Then-Else rule under consideration is R : If ‘distance is long’ Then ‘drive at high speed’ Else ‘drive at moderate speed’. To match with the form given in Expression 3.8, this rule can be restated as R : If ‘distance is long’ Then ‘speed is high’ Else ‘speed is moderate’. The relevant sets (crisp and fuzzy) are, distance = {100, 500, 1000, 5000} is the universe of the fuzzy set long-distance, speed = {30, 50, 70, 90, 120} is the universe of the fuzzy sets high-speed as well as moderate-speed, and

Applying Expression 3.10 we get
The relation matrix R is computed as follows.

So far we have discussed the simplest kind of fuzzy rules. They can be generalized to accommodate several fuzzy propositions into the antecedent part. The Generalized Fuzzy Rule is expressed as
Fuzzy rules are the foundation of reasoning in fuzzy logic. Fuzzy reasoning is discussed in the next Section.
3.5 FUZZY REASONING
Reasoning is the process of finding new propositions from old propositions. It is accomplished by applying the rules of inference on propositions already known to be true. In subsection 3.1.3, the rules of inference of crisp logic, e.g., modus ponens, universal specialization, chain rule, resolution etc. have been discussed. Fuzzy reasoning refers to reasoning involving fuzzy propositions, applying fuzzy rules of inference, producing new fuzzy propositions. The fundamentals of fuzzy reasoning are presented in the subsequent parts of this section.
3.5.1 Fuzzy Quantifiers
Recall that predicate logic had two quantifiers, the universal quantifier ∀, and the existential quantifier ∃. Fuzzy propositions too may contain quantifiers and these quantifiers are usually referred to as fuzzy quantifiers. There are two kinds of fuzzy quantifiers, absolute and relative. A fuzzy quantifier that refers to some specific value is known as absolute fuzzy quantifier. A relative fuzzy quantifier, however, do not refer to any specific value. A few instances of both types of fuzzy quantifiers are cited below.
Fuzzy Quantifiers
Absolute |
Relative |
|---|---|
Nearly 100 |
Almost |
Far below 0 |
Most |
Much greater than 50 |
About |
Somewhere around 300 |
Few |
Round about 1000 |
Nearly |
3.5.2 Generalized Modus Ponens
As the name suggests, generalized modus ponens is the generalization of crisp modus ponens but differs in two aspects. First, it applies to statements that are fuzzy, and second, the conclusion need not be exactly the same as the consequent. A typical fuzzy reasoning employing generalized modus ponens may look like
Premise No. 1. |
If this car is expensive Then it is comfortable. |
Premise No. 2. |
This car is more or less expensive. |
Conclusion. |
Therefore, This car is more or less comfortable. |
Therefore, the generalized modus ponens rule of inference may be presented as follows :
Generalized Modus Ponens |
|
Premise No. 1. |
If ‘x is A’ Then ‘y is B’. |
Premise No. 2. |
x is A1. |
Conclusion. |
Therefore, y is B1. |
where A, A1, B, B1 are fuzzy statements and A1 and B1 are modified versions of A and B respectively.
The generalized modus ponens described above is also known as fuzzy inference. Zadeh interpreted fuzzy inference in terms of max-min composition of relations on fuzzy sets. Let A and A1 be fuzzy sets on the universe U, and B, B1 are fuzzy sets on the universe V. Then the truth value of the conclusion ‘y is B1’ in terms of membership functions of the related fuzzy sets is obtained as
where R represents the relation corresponding to the rule ‘If ‘x is A’ Then ‘y is B’. The formula stated above actually computes the fuzzy set B1 as the max-min composition of A and R.
Example 3.21 (Fuzzy reasoning with the help of generalized modus ponens)
Let us reconsider the implication ‘If service is good Then customer is satisfied’. The associated universes of discourse are
Both the sequences a, b, c, d, e and 1, 2, 3, 4, 5 are in ascending order. The fuzzy sets good-service and satisfied are given below.
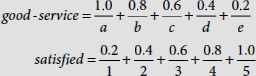
The information contained in the implication stated above is expressed by the relation
The relation R is found to be
Let us now consider very-good-service, a modified version of good-service as given below.
The reasoning process may now be expressed as
Premise No. 1. |
If service is good Then customer is satisfied. |
Premise No. 2. |
Service is very good. |
Conclusion. |
Therefore, Customer is very satisfied. |
The fuzzy information content of the conclusion is obtained by applying generalized modus ponens in the form of the relation
Computation of the individual elements of the fuzzy set very-satisfied is illustrated subsequently.
Similarly,
Hence the conclusion ‘Customer is very-satisfied’ is defined by the fuzzy set
3.5.3 Generalized Modus Tollens
As in case of generalized modus ponens, generalized modus tollens is the generalization of crisp modus tollens. A typical fuzzy reasoning employing generalized modus tollens has the form
Premise No. 1. |
If this car is expensive Then it is comfortable. |
Premise No. 2. |
This car is more or less comfortable. |
Conclusion. |
Therefore, This car is more or less expensive. |
Hence, the generalized modus tollens rule of inference may be presented as follows :
Generalized Modus Tollens |
|
Premise No. 1. |
If ‘x is A’ Then ‘y is B’. |
Premise No. 2. |
x is B1. |
Conclusion. |
Therefore, y is A1. |
where A, A1, B, B1 are fuzzy statements and A1 and B1 are modified versions of A and B respectively. The formula to compute the fuzzy set A1 as the max-min composition of B1 and R.
This can be computed by applying the formula
where R represents the relation corresponding to the rule ‘If ‘x is A’ Then ‘y is B’.
Example 3.22 (Fuzzy reasoning with the help of Generalized Modus Tollens)
Premise No. 1. |
If a man is honest Then he is happy. |
Premise No. 2. |
This man is most probably happy. |
Conclusion. |
Therefore, This man is most probably honest. |
CHAPTER SUMMARY
The main points of the foregoing discussion are given below.
- In classical, or crisp, logic a proposition is either true or false. It does not allow more than these two truth values. Fuzzy logic accepts infinite number of truth values between false and true. Numerically a fuzzy truth value is any real number between 0 and 1, both inclusive.
- In propositional logic an interpretation of a logical expression is a combination of truth values for the constituent individual propositions.
- Symbolic expressions of propositional logic and predicate logic are known as well-formed formulae (wffs). Two wffs are said to be logically equivalent if they attain the same truth value for all possible interpretations. A proposition which is true for all possible interpretations is said to be a tautology. A contradiction is a proposition which is false for all possible interpretations. A number of statements is said to be consistent if they can all be true simultaneously. An argument is said to be valid if the conclusion is true whenever the premises are true.
- Predicate logic is an extension of propositional logic. It captures the inner structure of a statement by introducing symbolic representation of the predicate part of a statement, and also by including the two quantifiers, viz., the universal quantifier (∀), and the existential quantifier (∃) into its formalism.
- Unlike propositional logic, a predicate logic statement is always interpreted in the context of some domain called the universe of discourse.
- An FOPL wff is valid if it is true for every interpretation. It is inconsistent (or unsatisfiable) if it is false for every interpretation. An FOPL wff W is a logical consequence of certain wffs, say W1, W2, ..., Wk, if and only if whenever W1, ..., Wk are true for some interpretation, W is also true for the same interpretation.
- An FOPL wff of the form (∀x) P[x] is true if and only if it is true for all values of x within its domain. And the wff (∃x) P[x] is true if and only if there exists at least one value of x for which P[x] is true.
- Rules of Inference are rules with which new propositions are obtained from a set of given statements. There are two kinds of rules of inference, deductive and non-deductive. Some important deductive rules of inference are Modus Ponens, Universal Specialization, Chain Rule, Resolution, Modus Tollens (also called Indirect Reasoning, or Law of Contraposition), Simplification, Addition, etc. The most useful non-deductive rules of inference are Abduction, Induction, and Analogy.
- An atomic fuzzy proposition has the form ‘x is P’ where P is a predicate that corresponds to a fuzzy set. The truth value of the fuzzy statement ‘x is P’ is evaluated in terms of the membership function of the fuzzy set for the predicate P.
- A fuzzy rule has the form If ‘x is A’ Then ‘y is B’. It can be interpreted as a fuzzy relation. According to Zadeh’s interpretation, a fuzzy rule may be expressed as the relation
R = (A×B)∪(A′×V)
where V is the universe of B and is used here as a fuzzy set in which all the members have membership value 1. - Two widely used fuzzy inference rules are the generalized modus ponens (GMP) and the generalized modus tollens (GMT). These two rules of inference are stated below.
Generalized Modus Ponens (GMP)
Premise No. 1.
If ‘x is A’ Then ‘y is B’.
Premise No. 2.
x is A1.
Conclusion.
Therefore, y is B1.
Generalized Modus Tollens (GMT)
Premise No. 1.
If ‘x is A’ Then ‘y is B’.
Premise No. 2.
x is B1.
Conclusion.
Therefore, y is A1.
A, A1, B, B1 are fuzzy statements. A1 and B1 are modified versions of A and B respectively. The reasoning process using GMP is also referred to as fuzzy inference.
- In fuzzy inference, the truth value of the conclusion ‘y is B1’ in terms of membership functions of the related fuzzy sets is obtained as
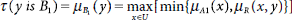
This corresponds to the max-min composition of A and R.
B1 = A1°RHere R denotes the relation corresponding to the rule If ‘x is A’ Then ‘y is B’.
- In case of GMT, the fuzzy set A1 is computed as the max-min composition of B1 and R.
A1 = B1°R
Or,

As usual, R denotes the relation corresponding to the rule If ‘x is A’ Then ‘y is B’.
SOLVED PROBLEMS
Problem 3.1. Determine whether the following propositional logic formulae are tautologies.
- (a→b) → ((a→b′) → a′)
- (a→b) → ((a + c) → (b + c))
Solution 3.1.
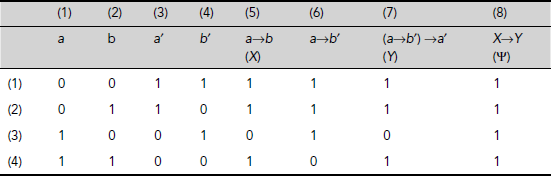
- The truth table for Ψ = (a→b) → ((a→b′)→a′) = X→Y where X = a→b, and Y = (a→b)→a′ is shown in Table 3.21. Column 8 of Table 3.21 tabulates the truth values of Ψ = (a→b) → ((a→b′)→a′) = X→Y corresponding to different combinations of truth values of a, b, and c. As all entries of column 8, which represents the given expression, are true, the expression is a tautology.
Table 3.21. Truth Table for Ψ = (a→b) → ((a→b′)→a′)
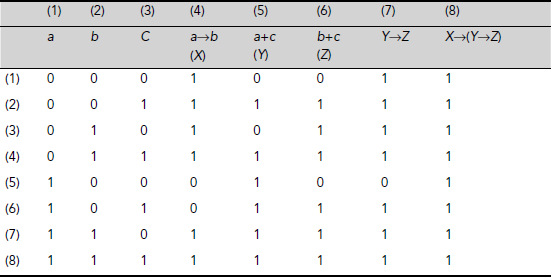
- Let X = (a→b), Y = (a + c), Z = (b + c). Then the expression Ψ = (a→b) → ((a + c) → (b + c)) is represented as X→(Y→Z). The corresponding truth table is shown in Table 3.22. Column 8 of Table 3.22, which tabulates the truth values of the given expression under different interpretations, contains true value in all its entries. Therefore, the given expression is a tautology.
Table 3.22. Truth Table for Ψ = (a→b) → ((a + c) → (b + c))
Problem 3.2. Find out whether the following formulae are equivalent.
- a → (b + c) and a′ + b + c
- a + (b′→ c) and a + (b→c)′
- (a→ b) → c and a → (b→c)
Solution 3.2
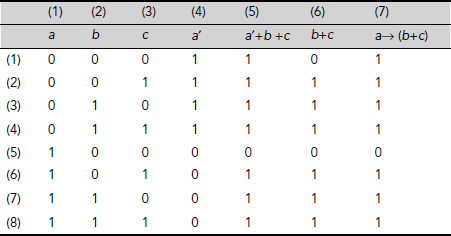
- The Truth Table for a → (b + c) and a′ + b + c is shown in Table 3.23. Column 5 and Column 7, representing the formulae a+ b + c and a → (b + c) respectively, are identical. Therefore they attain the same truth value for all possible interpretations. Hence, these two expressions are equivalent.
Table 3.23. Truth Tables for a → (b + c) and a′ + b + c
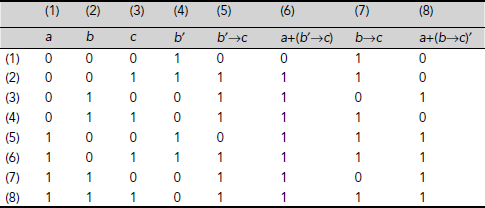
- The truth table for a + (b′→c) and a + (b→c)′ is shown in Table 3.24. Column 6 and column 8 of Table 3.24 represent the formulae a + (b′→c) and a + (b→c)′ respectively. The truth values in the entries of row 2 and row 4 for these columns are complementary. Hence, these two expressions are not equivalent.
Table 3.24. Truth Tables for a + (b′→c) and a + (b→c)′
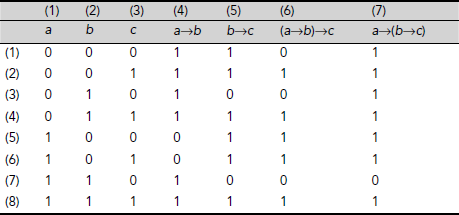
- Table 3.25 shows the truth table for (a→b)→c and a→(b→c). Column 6 and column 7 of Table 3.25 represent the formulae (a→b)→c and a→(b→c), respectively. The truth values in the entries of row 1 and row 3 for these columns are complementary. Hence, these two expressions are not equivalent.
Table 3.25. Truth Tables for (a→b)→c and a→(b →c)
Problem 3.3. Determine whether the following argument is valid or not. ‘If today is a holiday and the weather is sunny then we shall go for shopping. Today is a holiday. Today’s weather is sunny. Therefore we shall go for shopping.’
Table 3.26
Solution 3.3. Let us denote ‘Today is a holiday’ as a, ‘The weather is sunny’ as b, and ‘We shall go for shopping’ as c. Then the argument can be represented by the following sequence of expressions.
|
Proposition |
Expression |
|---|---|---|
Premise No. 1. |
If today is a holiday and the weather is sunny Then we shall go for shopping. |
(aΛb) → c |
Premise No. 2. |
Today is a holiday. |
a |
Premise No. 3. |
Today’s weather is sunny. |
b |
Conclusion. |
Therefore, we shall go for shopping |
∴c |
Table 3.26 presents the various combinations of truth values for these expressions. An argument is said to be valid if the conclusion is true whenever the premises are true. It may be noted that the only case where all the premises, i.e., (a•b)→c, a, and b, are simultaneously true corresponds to Row 8 of the table. And the conclusion c is also true for this row. Therefore the given argument is valid.
Problem 3.4. Determine whether the following sets of formulae are consistent or not.
(i) {a + b, b•c, (a + b)→(b•c)}
(ii) {a→c′, (a→b)′, a→(c′→b)}
Solution. 3.4 A set of propositions is consistent if they all can be true simultaneously. Table 3.27 shows the truth table for the set of propositional formulae {a + b, b•c, (a + b)→(b•c)}. The truth values of a + b, b•c, and (a + b)→(b•c) for various interpretations are noted in columns 4, 5, and 6 respectively. A careful scrutiny of the table reveals that there are truth value combinations for a, b, and c which renders all three propositions true (Rows 4 and 8). Hence the propositions are consistent.
Table 3.27. Truth Table for a + b, b•c, and (a + b)→(b•c)
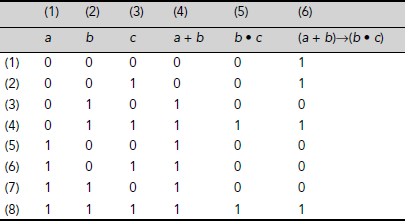
Table 3.28. Truth Table for a→c′, (a→b)′, a →(c′→b)
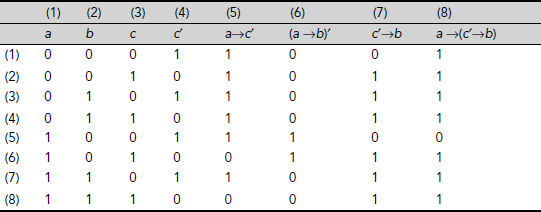
(iii) Table 3.28 presents the Truth Tables for the propositional formulae a→c′, (a→b)′, a→(c′→b). The truth values of a→c′, (a→b)′, a→(c′→b) for various interpretations are noted in Columns 5, 6, and 8 respectively. It is seen that these formulae are never true simultaneously. Since a set of propositions is consistent only when they all can be true simultaneously, the given formulae are not consistent.
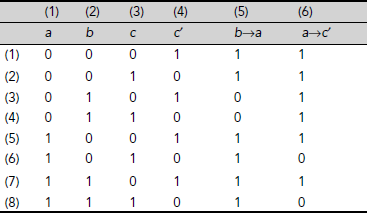
Problem 3.5. Consider the following statements: ‘I may fall sick if I smoke. I am not happy if I fall sick. I smoke. I am happy’. Are they consistent?
Solution 3.5. Let denote the statement ‘I may fall sick’ by a, ‘I smoke’ by b, and ‘I am happy’ by c. Then, the given statements are represented by a sequence of Propositional Logic formulae as shown below:
# |
Proposition |
Formula |
|---|---|---|
1. |
I may fall sick if I smoke. |
b→a |
2. |
I am not happy if I fall sick. |
a→c′ |
3. |
I smoke. |
b |
4. |
I am happy. |
c |
From the Truth Table shown in Table 3.29 it is evident that these formulae are never simultaneously true.
Hence the statements are not consistent.
Table 3.29. Truth table for b→a and a→c′
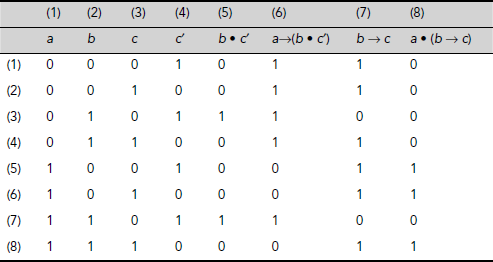
Problem 3.6. Determine whether the following argument is valid or not.
|
Proposition |
Premise No. 1. |
a→(b•c′ ) |
Premise No. 2. |
a•(b→c) |
Conclusion. |
∴a |
Solution 3.6. Table 3.30 shows the truth tables for the propositions of the given argument. An argument is valid if the conclusion is true whenever the premises are true. However, there is no interpretation for which both the premises (Column 6 and Column 8) are true simultaneously. Therefore the condition for validity of an argument is not violated in this case. Hence the argument is valid.
Table 3.30. Truth table for a→(b • c′) and a • (b → c)
Problem 3.7. Illustrate the following inference rules with an example for each: Modus Ponens, Universal Specialization, Chain Rule, Resolution, Modus Tollens, Simplification, Addition, Abduction, Induction, and Analogy.
Solution 3.7. The illustrative examples are cited below.
- Modus Ponens
Premise No. 1.
If Anand is good Then Anand is popular.
Premise No. 2.
Anand is good.
Conclusion.
Therefore, Anand is popular.
- Universal Specialization
Premise No. 1.
All men are mortal.
Conclusion.
Therefore, Anand is mortal.
- Chain Rule
Premise No. 1.
If x is a natural number Then x is an integer.
Premise No. 2.
If x is an integer Then x is a real number.
Conclusion.
Therefore, If x is a natural number Then x is a real number.
- Resolution
Premise No. 1.
Man is rational or God is divine.
Premise No. 2.
Man is not rational or The universe is expanding.
Conclusion.
Therefore, Gods is divine or The universe is expanding.
- Modus tollens
Premise No. 1.
If man is rational Then man is good.
Premise No. 2.
Man is not good.
Conclusion.
Therefore, Man is not rational.
- Simplification
Premise No. 1.
Anand is a man and Anand plays chess.
Conclusion.
Therefore, Anand is a man (or Anand plays chess)
- Addition
Premise No. 1.
Anand is a man.
Conclusion.
Therefore, Anand is a man or 2 is a prime number.
- Abduction
Premise No. 1.
If it rains Then the grass is wet.
Premise No. 2.
The grass is wet.
Conclusion.
Therefore, it has rained.
- Induction
Premise No. 1.
The prime number 29 is odd.
Premise No. 2.
The prime number 53 is odd.
Premise No. 3.
The prime number 41 is odd.
Premise No. 4.
The prime number 211 is odd.
Conclusion.
Therefore, All prime numbers are odd.
- Analogy Consider the fact that man can stand on two legs and therefore, they can use their two free hands for various purposes which the four legged animals generally cannot. Now, gorillas also occasionally stand on two legs. Hence, by virtue of the analogical reasoning we may conclude that gorillas can also employ their hands to perform various activities similar to human beings.
Problem 3.8. Apply the resolution rule of inference to prove statement 4 from statements 1, 2, and 3 as given below.
-
1.
p → q
2.
r → s
3.
p + r
4.
∴q + s
-
1.
p → q
2.
r → s
3.
q′ + s′
4.
∴ p′ + r′
Solution 3.8 The proofs are given below, with brief explanation of each step on the right.
-
1. p′ + q
[ 1, since p → q ≡ p′ + q]
2. r′ + s
[2, since r → s ≡ r′ + s]
3. p + r
[3]
4. q + r
[1 and 3, Resolution]
5. q + s
[2 and 4, Resolution]
-
1. p′ + q
[ 1, since p → q ≡ p′ + q]
2. r′ + s
[2, since r → s ≡ r′ + s]
3. q′ + s′
[3]
4. p′ + s′
[1 and 3, Resolution]
5. p′ + r′
[2 and 4, Resolution]
Problem 3.9 Prove that any statement can be derived from a contradiction.
Solution 3.9. Given, a + a′ as the premise, we have to derive b, where b is an arbitrary statement. The proof is given below.
1. |
a + a′ |
[1] |
2. |
a |
[1, Simplification] |
3. |
a′ |
[1, Simplification] |
4. |
a′ + b |
[3, Addition] |
5. |
b |
[2 and 4, Resolution] |
Problem 3.10. Given p → q, prove that p → (p • q). This is called Absoption.
Solution 3.10. The proof is given below.
1. |
p′ + q |
[1, since p → q ≡ p′ + q] |
2. |
True • (p′ + q) |
[1, since X = True • X] |
3. |
(p′ + p) • (p′ + q) |
[2, since T = p′ + p] |
4. |
p′ + (p•q) |
[3, Distributive law] |
5. |
p→(p•q) |
[4, since a → b ≡ a′ + b] |
Problem 3.11. Prove the validity of the following argument.
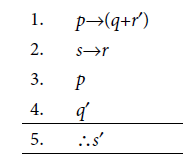
Solution 3.11. Validity of the argument is given below.
1. |
p→(q + r′) |
[1] |
2. |
s→r |
[2] |
3. |
p |
[3] |
4. |
q′ |
[4] |
5. |
q + r′ |
[1 and 3, Modus Ponens] |
6. |
r→q |
[5, since r→q ≡ r′ + q] |
7. |
s→q |
[2 and 6, Chain Rule] |
8. |
s′ |
[4 and 7, Modus Tollens] |
Problem 3.12. Consider the fuzzy rule R : If service is good Then customer is satisfied. Related universes are service-rating = {a, b, c, d, e}, and satisfaction-grade = {1, 2, 3, 4, 5} where the service-ratings a, b, c, d, e are in descending order and the satisfaction-grades 1, 2, 3, 4, 5 are in the ascending order. The fuzzy sets good-service and satisfied are defined as follows:
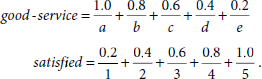
Find the relation matrix for this rule according to Jadeh’s interpretation.
Solution 3.12. According to Zadeh’s interpretation, the rule R is expressed by the relation
The computation of the relation R representing the information contained in the fuzzy rule stated above is given below.
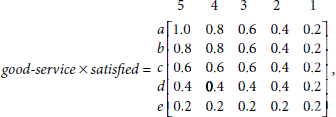
Problem 3.13. Recall the rule If job is risky Then compensation is high’ discussed in Example 3.19. The related fuzzy sets are
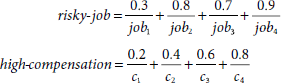
on the universes job = {job1, job2, job3, job4} and compensation = {c1, c2, c3, c4}. Now, let the premise be ‘job is risky1’ where the predicate risky1 is represented by the fuzzy set
Employing Generalized Modus Ponens, we reach the conclusion ‘compensation is high1’. Compute high1-compensation.
Solution 3.13. The rule R : If job is risky Then ‘compensation is high’ is represented by the fuzzy relation
Which, on necessary calculations, is expressed by the fuzzy relation
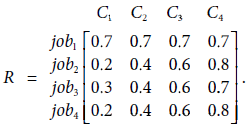
Now, the fuzzy set high1-compensation = risky1-job°R is obtained as

Hence,
Problem 3.14. Let U = V = {0, 1, 2, 3, 4} be the universe of discourse on which the fuzzy set ![]() is defined. Again, let R be the fuzzy relation ‘more or less the same’ which is defined by the relation matrix shown below.
is defined. Again, let R be the fuzzy relation ‘more or less the same’ which is defined by the relation matrix shown below.

If the premise and the rule are stated as
then apply a suitable fuzzy rule of inference to obtain the conclusion and express it suitably as a relation.
Solution 3.14. The conclusion C is given by the fuzzy set obtained by the max-min composition of the fuzzy set small and the relation R, i.e., C = small °R. Therefore,
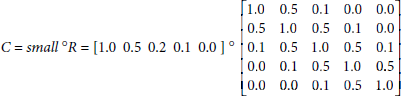
According to the definition of max-min composition
Therefore,
µC(0) = max [min{µsmall(0), µR(0,0)}, min{µsmall(1), µR(1,0)}, min{µsmall(2), µR(2,0)}, min{µsmall(3), µR(3,0)}, min{µsmall(4), µR(4,0)}]
= max [min{1, 1}, min{.5, .5}, min{.2, .1}, min{.1, 0}, min{0, 0}]
= max [1, .5, .1, 0, 0]
= 1.
µC(1) = max [min{1, .5}, min{.5, 1}, min{.2, .5}, min{.1, .1}, min {0, 0}]
= max [.5, .5, .2, .1, 0]
= .5.
µC(2) = max [min{1, .1}, min{.5, .5}, min{.2, 1}, min{.1, .5}, min {0, .1}]
= max [.1, .5, .2, .1, 0]
= .5
µC(3) = max [min{1, 0}, min{.5, .1}, min{.2, .5}, min{.1, 1}, min {0, .5}]
= max [0, .1, .2, .1, 0]
= .2.
µC(4) = max [min{1, 0}, min{.5, 0}, min{.2, .1}, min{.1, .5}, min {0, 1}]
= max [0, 0, .1, .1, 0]
= .1.
Therefore, the conclusion is ![]() . This can be fairly interpreted as ‘more or less small’. Hence the conclusion can be stated as ‘y is more or less small’.
. This can be fairly interpreted as ‘more or less small’. Hence the conclusion can be stated as ‘y is more or less small’.
TEST YOUR KNOWLEDGE
3.1 Which of the following is a logical constant?
- True
- False
- Both (a) and (b)
- None of the above
3.2 Which of the following sets of logical operations is not functionally complete?
- {•, ′}
- {+, ′}
- {→, ′}
- None of the above
3.3 Which of the following expressions is not equivalent to the others?
- p → q
- p′ → q′
- q′ → p′
- None of the above
3.4 Which of the following is a tautology?
- p → q
- p + q
- p • p′
- True
3.5 Which of the following is a contradiction?
- p → p′
- p′ → p
- p • (p → p′)
- p • (p′ → p)
3.6 Given a set of propositional logic expressions, if there is an interpretation for which the expressions are all False, then the set of expressions
- Must be consistent
- Must be inconsistent
- Can be consistent or inconsistent
- Can neither be consistent nor inconsistent
3. 7 Consider the following argument.
Premise No. 1. |
The universe is expanding. |
Premise No. 2. |
The universe is not expanding. |
Conclusion. |
Therefore, this is a red rose. |
The argument is
- Valid
- Invalid
- Both (a) and (b)
- Neither (a) nor (b)
3. 8 Which of the following equivalences is incorrect?
- a • (a + b) ≡ a
- a → b ≡ b′ → a′
- a + (b • c) ≡ (a + b) • (a+ c)
- None of the above
3.9 What is the truth-value of the statement “2 + 3 = 7 or 7 is a prime number”?
- False
- True
- Both (a) and (b)
- Neither (a) nor (b)
3.10 Which of the following is true for the proposition p • (p′ + q)?
- It’s a tautology
- It’s a contradiction
- Both (a) and (b)
- Neither (a) nor (b)
3.11 Which of the following logic systems support universal and existential quantification of variables?
- Propositional Logic
- Predicate Logic
- Both (a) and (b)
- None of the above
3.12 Which of the following is not an atomic formula of First Order Predicate Logic?
- P(A)
- [(∀x) P (x)]′
- [(∀x) (∃y)P(x)∧Q(y)]′
- None of the above
3.13 First Order Predicate Logic is called ‘first order’ because
- It does not allow predicate variables
- It does not allow function variables
- Both (a) and (b)
- None of the above
3.14 Which of the following is a ground atom?
- P (f(A, B))
- P(x)
- P(x, y)
- None of the above
3.15 Which of the following wffs contain a free variable?
- (∀x)P[x]
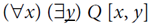
- (∃y)R [A, y]
- None of the above
3.16 Which of the following identities is not valid?
- (∀x) P[x] + (∀y) Q[y] = (∀z)(P[z] + Q[z])
- (∃x) P[x] • (∃y) Q[y] = (∃z) (P[z] • Q[z])
- Both (a) and (b)
- None of the above
3.17 Which of the following identities is valid?
- ¬(∀x)P[x] = (∃x)(¬P[x])
- ¬(∃x)P[x] = (∀x)(¬P[x])
- Both (a) and (b)
- None of the above
3.18 Which of the following is true with respect to the expression (∀x)P[x]•(∃y)(P[y])?
- Variable x is inside the scope of variable y
- Variable y is inside the scope of variable x
- None of the variables x and y is inside the scope of the other
- None of the above
3.19 Which of the following wffs is equivalent to (∀x)P[x] • (∃y)(Q[y])?
- (∃x)P[x] • (∀y)(Q[y])
- (∀y)P[y] • (∃x)(Q[x])
- (∃y)P[y] • (∀x)(Q[x])
- None of the above
3.20 Which of the following identities is valid?
- (∀x) P[x] • (∀y) Q[y] = (∀z) (P[z] • Q[z])
- (∃x) P[x] + (∃y) Q[y] = (∃z) (P[z] + Q[z])
- Both (a) and (b)
- None of the above
3.21 Which of the following inference rules does not follow deductive logic?
- Modus Ponens
- Abduction
- Modus Tollens
- Simplification.
3.22 Which of the following inference rules follow deductive logic?
- Analogy
- Induction
- Abduction
- None of the above
3.23 Applying the Resolution rule of inference on the clauses p and p′, we get -
- False
- True
- p
- p′
3.24 I meet three Englishmen consecutively, each of whom have blue eyes. I conclude that all Englishmen have blue eyes. Which rule of inference I apply?
- Abduction
- Induction
- Analogy
- None of the above
3.25 A pair of simultaneous equations under two variables x, y can be solved through the method of elimination. When I am asked to solve three simultaneous equations under three variables x, y, z, I assume that the same method applies here too. What rule of inference I am employing here?
- Abduction
- Induction
- Analogy
- None of the above
3.26 If one is bitten by a honeybee on his nose, his nose swells up. You see a person with swollen nose and conclude that he must have been bitten by some honeybee. What rule of inference you are following while making this conclusion?
- Abduction
- Induction
- Analogy
- None of the above
3.27 Which of the following rules of inference cannot be obtained using resolution?
- Modus Ponens
- Modus Tollens
- Chain Rule
- Universal specialization
3.28 Which of the following rules of inference relates to our commonsense reasoning?
- Analogy
- Abduction
- Both (a) and (b)
- Neither (a) nor (b)
3.29 In order to apply the resolution rules of inference, the prepositions must be in the form of
- Well formed formulae
- Clauses
- Conjunctive normal form
- Disjunctive normal form
3.30 Which of the following is not a fuzzy linguistic truth value?
- True
- Almost true
- Very much true
- None of the above
3.31 Which of the following can be regarded as a fuzzy linguistic truth value?
- Nearly false
- Absolutely false
- Both (a) and (b)
- None of the above
3.32 If τ (a) and τ (b) be the fuzzy truth values of propositions a and b, then which of the following is not an interpretation of τ(a→b)?
- max {(1 − τ(a)), τ(b)}
- min {1, 1 − τ(a) + τ(b)}
- max {min (τ(a), τ(b)), 1 − τ(a)}
- None of the above
3.33 Let R be the fuzzy rule If ‘x is A’ Then ‘y is B’, where A, B are fuzzy predicates corresponding to the fuzzy sets A, B defined on the universes U and V respectively. Then which of the following is Zadeh’s interpretation?
- R = A × B
- R = (A × B)∪(A′× V)
- R = (A′ × B)
- None of the above
3.34 Let R be the fuzzy rule If ‘x is A’ Then ‘y is B’ Else ‘y is C’. Then
- R = (A×B)∪(A′× C)
- R = (A′× B)∪(A × C)
- R = (A × B)∪(A × C)
- None of the above
3.35 Which of the following represents the most generalized form of a fuzzy rule?
- If ‘x1 is A1’ •...• ‘xk is Ak’ Then ‘y is B’
- If ‘x is A’ Then ‘y1 is B1’ • ... • ‘yk is Bk’
- If ‘x1 is A1’ • ...• ‘xk is Ak’ Then ‘y1 is B1’ • ...• ‘yk is Bk’
- None of the above
3.36 Which of the following is involved in a reasoning process using Generalized Modus Ponens?
- Fuzzy propositions
- A set of clauses
- Universal quantifier
- None of the above
3.37 Let R : If ‘x is A’ Then ‘y is B’ be a fuzzy rule. In a fuzzy reasoning process employing Generalized Modus Ponens, A1, a modified version of A, is used as the premise. Moreover, let B1 be the conclusion where B1 is probably a modified version of B. If B1 = A1 op R, then according to Zadeh’s interpretation, op is :
- Fuzzy Cartesian product
- Max-min composition
- Fuzzy implication
- None of the above
3.38 Which of the following is known as Fuzzy Inference?
- Generalized Modus Ponens
- Generalized Modus Tollens
- Both (a) and (b)
- None of the above
3.39 Which of the following is an ‘absolute’ fuzzy quantifier?
- Most
- nearly 1000
- Few
- None of the above
3.40 Which of the following cannot be a linguistic variable?
- Age
- Speed
- Price
- None of the above
Answers
3.1 (c) |
3.2 (d) |
3.3 (b) |
3.4 (d) |
3.5 (c) |
3.6 (c) |
3.7 (a) |
3.8 (d) |
3.9 (b) |
3.10 (d) |
3.11 (b) |
3.12 (c) |
3.13 (a) |
3.14 (a) |
3.15 (d) |
3.16 (c) |
3.17 (c) |
3.18 (c) |
3.19 (b) |
3.20 (c) |
3.21 (b) |
3.22 (d) |
3.23 (a) |
3.24 (b) |
3.25 (c) |
3.26 (a) |
3.27 (d) |
3.28 (c) |
3.29 (b) |
3.30 (d) |
3.31 (c) |
3.32 (d) |
3.33 (b) |
3.34 (a) |
3.35 (c) |
3.36 (a) |
3.37 (b) |
3.38 (a) |
3.39 (b) |
3.40 (d) |
EXERCISES
3.1 Show that the set of logical operators {→, ′} is functionally complete.
3.2 Prove that the proposition a + (a • b)′ is a tautology.
3.3 Determine the validity of the argument given below.
Premise No. 1. |
a → b′ |
Premise No. 2. |
c → b |
Premise No. 3. |
c |
Conclusion. |
∴ a′ |
3.4 Determine the validity of the argument given below.
Premise No. 1. |
If Hari works hard Then he will be successful. |
Premise No. 2. |
If Hari is not sick Then he works hard. |
Premise No. 3. |
Hari is not successful. |
Conclusion. |
Therefore, Hari is sick. |
3.5 Find whether the following propositions are consistent.
- If rose is red Then ice is white.
- If ice is not white Then the earth is a tetrahedron.
- Rose is not red And ice is not white.
3.6 Show that Modus Ponens, Modus Tollens, and Chain rules are special cases of Resolution.
3.7 Derive the conclusion p′ from the premises p → q, p → r, and q′ + r′ using the resolution rule of inference. Also, derive the conclusion p → r from the premises p → (q → r) and q using the resolution rule of inference.
3.8 Let us consider the universe of discourse U = {John, Jane, Smith, Monica} of four persons. Jane is married to John, and Monica is married to Smith. Three predicates, MLE (x), FML (y), MRD (x, y) are defined on U meaning ‘x is a male’, ‘y is a female’, and ‘x and y are married’ respectively. They have the following combinations truth values.
x |
MLE (x) |
|---|---|
John |
True |
Jane |
False |
Smith |
True |
Monica |
False |
x |
FML (x) |
|---|---|
John |
False |
Jane |
True |
Smith |
False |
Monica |
True |
x |
y |
MRD (x, y) |
|---|---|---|
John |
John |
False |
John |
Jane |
True |
John |
Smith |
False |
John |
Monica |
False |
Jane |
John |
True |
Jane |
Jane |
False |
Jane |
Smith |
False |
Jane |
Monica |
False |
Smith |
John |
False |
Smith |
Jane |
False |
Smith |
Smith |
False |
Smith |
Monica |
True |
Monica |
John |
False |
Monica |
Jane |
False |
Monica |
Smith |
True |
Monica |
Monica |
False |
In this context determine if the following statements are true.
- (∀x)(∀y) MRD(x, y) → MRD(y, x)
- (∀x)(∀y) MRD(x, y) → {MLE(x) • FML(y)}
- (∀x) MLE (x) → (∃y){FML(y) • MRD(x, y)}
3.9 Given the statements ‘All men are mortal’ and ‘Anand is a man prove that Anand is mortal’. Indicate the rules of inference you apply at each step of the proof.
3.10 Consider the fuzzy rule R : If the car is expensive Then it is comfortable. The related universes are cars = {a, b, c, d}, and comfort-levels = {1, 2, 3, 4, 5}. The fuzzy sets expensive-cars and comfortable are defined on the universes cars and comfort-levels respectively. These sets are as given below.
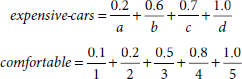
Express the rule R : ‘If the car is expensive Then it is comfortable’ as a fuzzy relation using Zadeh’s interpretation.
3.11 Let U = V = {0, 1, 2, 3, 4} be two universes. The fuzzy set ![]() is defined on U. Moreover, R is the relation ‘much less than’, symbolized as ‘<<’ and is defined by the relation matrix
is defined on U. Moreover, R is the relation ‘much less than’, symbolized as ‘<<’ and is defined by the relation matrix

Now given the propositions ‘x is small’ and ‘x << y’ find the conclusion. How can you describe the conclusion in language?
3.12 Let ![]() be fuzzy sets defined on the universes U = V = {0, 1, 2, 3, 4}. If R : If ‘x is low’ Then ‘y is high’ be the fuzzy If-Then rule and the premise is ‘x is very low’, then what is the conclusion? The fuzzy predicate ‘very low’ is to be interpreted as the set
be fuzzy sets defined on the universes U = V = {0, 1, 2, 3, 4}. If R : If ‘x is low’ Then ‘y is high’ be the fuzzy If-Then rule and the premise is ‘x is very low’, then what is the conclusion? The fuzzy predicate ‘very low’ is to be interpreted as the set
BIBLIOGRAPHY AND HISTORICAL NOTES
Numerous papers, books etc. have been published on fuzzy logic since its inception by A. Zadeh. A list of selected articles and books are cited below.
Hájek, P. (1995). Fuzzy Logic and Arithmetical Hierarchy. Fuzzy Sets and Systems, Vol. 3, No. 8, pp. 359–363.
Hájek, P. (1998). Metamathematics of Fuzzy Logic. Kluwer.
Klir, G. and Folger, T. (1987). Fuzzy Sets, Uncertainty, and Information. Englewood Cliffs, NJ: Prentice Hall.
Kosko, B. (1993). Fuzzy Thinking: The New Science of Fuzzy Logic. New York: Hyperion.
Kosko, B. and Isaka, S. (1993). Fuzzy Logic. Scientific American, Vol. 269, No. 1, pp. 76–81.
McNeill, D. and Freiberger, P. (1992). Fuzzy Logic: The Discovery of a Revolutionary Computer Technology. Simon and Schuster.
McNeill F. M. and Thro, E. (1994). Fuzzy Logic: A Practical Approach. Academic Press.
Novák, V., Perfilieva, I., and Močkoř, J. (1999). Mathematical Principles of Fuzzy Logic. Kluwer Academic.
Zadeh, Lotfi A. (1974). Fuzzy logic and its application to approximate reasoning. Information Processing, Proc. IFIP Congr., pp. 591–594.
Zadeh., Lotfi A. (2002). From Computing with Numbers to Computing with Words — From Manipulation of Measurements to Manipulation of Perceptions. International Journal of Applied Mathematics and Computer Science, Vol. 12, No. 3, pp. 307–324.


