3
Concurrent Objects
The behavior of concurrent objects is best described through their safety and liveness properties, often referred to as correctness and progress. In this chapter we examine various ways of specifying correctness and progress.
While all notions of correctness for concurrent objects are based on some notion of equivalence with sequential behavior, different notions are appropriate for different systems. We examine three correctness conditions. Quiescent consistency is appropriate for applications that require high performance at the cost of placing relatively weak constraints on object behavior. Sequential consistency is a stronger condition, often useful for describing low-level systems such as hardware memory interfaces. Linearizability, even stronger, is useful for describing higher-level systems composed from linearizable components.
Along a different dimension, different method implementations provide different progress guarantees. Some are blocking, where the delay of any one thread can delay others, and some are nonblocking, where the delay of a thread cannot delay the others.
3.1 Concurrency and Correctness
What does it mean for a concurrent object to be correct? Fig. 3.1 shows a simple lock-based concurrent FIFO queue. The enq() and deq() methods synchronize by a mutual exclusion lock of the kind studied in Chapter 2. It is easy to see that this implementation is a correct concurrent FIFO queue. Because each method accesses and updates fields while holding an exclusive lock, the method calls take effect sequentially.

Figure 3.1 A lock-based FIFO queue. The queue’s items are kept in an array Items, where head is the index of the next item to dequeue, and tail is the index of the first open array slot (modulo the capacity). The lock field is a lock that ensures that methods are mutually exclusive. Initially head and tail are zero, and the queue is empty. If enq() finds the queue is full, i.e., head and tail differ by the queue size, then it throws an exception. Otherwise, there is room, so enq() stores the item at array entry tail, and then increments tail. The deq() method works in a symmetric way.
This idea is illustrated in Fig. 3.2, which shows an execution in which A enqueues a, B enqueues b, and C dequeues twice, first throwing EmptyException, and second returning b. Overlapping intervals indicate concurrent method calls. All three method calls overlap in time. In this figure, as in others, time moves from left to right, and dark lines indicate intervals. The intervals for a single thread are displayed along a single horizontal line. When convenient, the thread name appears on the left. A bar represents an interval with a fixed start and stop time. A bar with dotted lines on the right represents an interval with a fixed start-time and an unknown stop-time. The label "![]() " means that a thread enqueues item x at object q, while "
" means that a thread enqueues item x at object q, while "![]() " means that the thread dequeues item x from object q.
" means that the thread dequeues item x from object q.
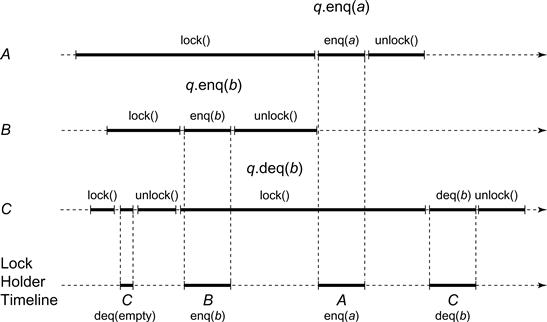
Figure 3.2 Locking queue execution. Here, ![]() acquires the lock, observes the queue to be empty, releases the lock, and throws an exception.
acquires the lock, observes the queue to be empty, releases the lock, and throws an exception. ![]() acquires the lock, inserts b, and releases the lock.
acquires the lock, inserts b, and releases the lock. ![]() acquires the lock, inserts a, and releases the lock.
acquires the lock, inserts a, and releases the lock. ![]() re-acquires the lock, dequeues b, releases the lock, and returns.
re-acquires the lock, dequeues b, releases the lock, and returns.
The timeline shows which thread holds the lock. Here, C acquires the lock, observes the queue to be empty, releases the lock, and throws an exception. It does not modify the queue. B acquires the lock, inserts b, and releases the lock. A acquires the lock, inserts a, and releases the lock. C reacquires the lock, dequeues b, releases the lock, and returns. Each of these calls takes effect sequentially, and we can easily verify that dequeuing b before a is consistent with our understanding of sequential FIFO queue behavior.
Let us consider, however, the alternative concurrent queue implementation in Fig. 3.3. (This queue is correct only if it is shared by a single enqueuer and a single dequeuer.) It has almost the same internal representation as the lock-based queue of Fig. 3.1. The only difference is the absence of a lock. We claim this is a correct implementation of a single-enqueuer/single-dequeuer FIFO queue, although it is no longer easy to explain why. It may not even be clear what it means for a queue to be FIFO when enqueues and dequeues are concurrent.

Figure 3.3 A single-enqueuer/single-dequeuer FIFO queue. The structure is identical to that of the lock-based FIFO queue, except that there is no need for the lock to coordinate access.
Unfortunately, it follows from Amdahl’s Law (Chapter 1) that concurrent objects whose methods hold exclusive locks, and therefore effectively execute one after the other, are less desirable than ones with finer-grained locking or no locks at all. We therefore need a way to specify the behavior of concurrent objects, and to reason about their implementations, without relying on method-level locking. Nevertheless, the lock-based queue example illustrates a useful principle: it is easier to reason about concurrent objects if we can somehow map their concurrent executions to sequential ones, and limit our reasoning to these sequential executions. This principle is the key to the correctness properties introduced in this chapter.
3.2 Sequential Objects
An object in languages such as Java and C++ is a container for data. Each object provides a set of methods which are the only way to manipulate that object. Each object has a class, which defines the object’s methods and how they behave. An object has a well-defined state (for example, the FIFO queue’s current sequence of items). There are many ways to describe how an object’s methods behave, ranging from formal specifications to plain English. The application program interface (API) documentation that we use every day lies somewhere in between.
The API documentation typically says something like the following: if the object is in such-and-such a state before you call the method, then the object will be in some other state when the method returns, and the call will return a particular value, or throw a particular exception. This kind of description divides naturally into a precondition (describing the object’s state before invoking the method) and a postcondition, describing, once the method returns, the object’s state and return value. A change to an object’s state is sometimes called a side effect. For example, consider how one might specify a first-in-first-out (FIFO) queue class. The class provides two methods: enq() and deq(). The queue state is just a sequence of items, possibly empty. If the queue state is a sequence q (precondition), then a call to z leaves the queue in state ![]() , where "·" denotes concatenation. If the queue object is nonempty (precondition), say
, where "·" denotes concatenation. If the queue object is nonempty (precondition), say ![]() , then the deq() method removes and returns the sequence’s first element (postcondition), leaving the queue in state q (side effect). If, instead, the queue object is empty (precondition), the method throws Empty Exception and leaves the queue state unchanged (postcondition).
, then the deq() method removes and returns the sequence’s first element (postcondition), leaving the queue in state q (side effect). If, instead, the queue object is empty (precondition), the method throws Empty Exception and leaves the queue state unchanged (postcondition).
This style of documentation, called a sequential specification, is so familiar that it is easy to overlook how elegant and powerful it is. The length of the object’s documentation is linear in the number of methods, because each method can be described in isolation. There are a vast number of potential interactions among methods, and all such interactions are characterized succinctly by the methods' side effects on the object state. The object’s documentation describes the object state before and after each call, and we can safely ignore any intermediate states that the object may assume while the method call is in progress.
Defining objects in terms of preconditions and postconditions makes perfect sense in a sequential model of computation where a single thread manipulates a collection of objects. Unfortunately, for objects shared by multiple threads, this successful and familiar style of documentation falls apart. If an object’s methods can be invoked by concurrent threads, then the method calls can overlap in time, and it no longer makes sense to talk about their order. What does it mean, in a multithreaded program, if x and y are enqueued on a FIFO queue during overlapping intervals? Which will be dequeued first? Can we continue to describe methods in isolation, via preconditions and postconditions, or must we provide explicit descriptions of every possible interaction among every possible collection of concurrent method calls?
Even the notion of an object’s state becomes confusing. In single-threaded programs, an object must assume a meaningful state only between method calls.1 For concurrent objects, however, overlapping method calls may be in progress at every instant, so the object may never be between method calls. Any method call must be prepared to encounter an object state that reflects the incomplete effects of other concurrent method calls, a problem that simply does not arise in single-threaded programs.
3.3 Quiescent Consistency
One way to develop an intuition about how concurrent objects should behave is to review examples of concurrent computations involving simple objects, and to decide, in each case, whether the behavior agrees with our intuition about how a concurrent object should behave.
Method calls take time. A method call is the interval that starts with an invocation event and ends with a response event. Method calls by concurrent threads may overlap, while method calls by a single thread are always sequential (non-overlapping, one-after-the-other). We say a method call is pending if its call event has occurred, but not its response event.
For historical reasons, the object version of a read–write memory location is called a register (see Chapter 4). In Fig. 3.4, two threads concurrently write −3 and 7 to a shared register r (as before, "![]() " means that a thread reads value x from register object r, and similarly for "
" means that a thread reads value x from register object r, and similarly for "![]() .”). Later, one thread reads r and returns the value −7. This behavior is clearly not acceptable. We expect to find either 7 or −3 in the register, not a mixture of both. This example suggests the following principle:
.”). Later, one thread reads r and returns the value −7. This behavior is clearly not acceptable. We expect to find either 7 or −3 in the register, not a mixture of both. This example suggests the following principle:
Principle 3.3.1
Method calls should appear to happen in a one-at-a-time, sequential order.
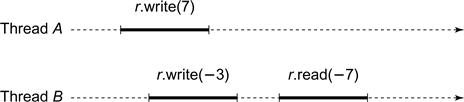
Figure 3.4 Why each method call should appear to take effect instantaneously. Two threads concurrently write −3 and 7 to a shared register r. Later, one thread reads r and returns the value −7. We expect to find either 7 or −3 in the register, not a mixture of both.
By itself, this principle is usually too weak to be useful. For example, it permits reads always to return the object’s initial state, even in sequential executions.
Here is a slightly stronger condition. An object is quiescent if it has no pending method calls.
Principle 3.3.2
Method calls separated by a period of quiescence should appear to take effect in their real-time order.
For example, suppose A and B concurrently enqueue x and y in a FIFO queue. The queue becomes quiescent, and then C enqueues z. We may not be able to predict the relative order of x and y in the queue, but we know they are ahead of z.
Together, Principles 3.3.1 and 3.3.2 define a correctness property called quiescent consistency. Informally, it says that any time an object becomes quiescent, then the execution so far is equivalent to some sequential execution of the completed calls.
As an example of a quiescently consistent object, consider the shared counter from Chapter 1. A quiescently-consistent shared counter would return numbers, not necessarily in the order of the getAndIncrement() requests, but always without duplicating or omitting a number. The execution of a quiescently consistent object is somewhat like a musical-chairs game: at any point, the music might stop, that is, the state could become quiescent. At that point, each pending method call must return an index so that all the indexes together meet the specification of a sequential counter, implying no duplicated or omitted numbers. In other words, a quiescently consistent counter is an index distribution mechanism, useful as a “loop counter” in programs that do not care about the order in which indexes are issued.
3.3.1 Remarks
How much does quiescent consistency limit concurrency? Specifically, under what circumstances does quiescent consistency require one method call to block waiting for another to complete? Surprisingly, the answer is (essentially), never. A method is total if it is defined for every object state; otherwise it is partial. For example, let us consider the following alternative specification for an unbounded sequential FIFO queue. One can always enqueue another item, but one can dequeue only from a nonempty queue. In the sequential specification of a FIFO queue, enq() is total, since its effects are defined in every queue state, but deq() is partial, since its effects are defined only for nonempty queues.
In any concurrent execution, for any pending invocation of a total method, there exists a quiescently consistent response. This observation does not mean that it is easy (or even always possible) to figure out what that response is, but only that the correctness condition itself does not stand in the way. We say that quiescent consistency is a nonblocking correctness condition. We make this notion more clear in Section 3.6.
A correctness property ![]() is compositional if, whenever each object in the system satisfies
is compositional if, whenever each object in the system satisfies ![]() , the system as a whole satisfies
, the system as a whole satisfies ![]() . Compositionality is important in large systems. Any sufficiently complex system must be designed and implemented in a modular fashion. Components are designed, implemented, and proved correct independently. Each component makes a clear distinction between its implementation, which is hidden, and its interface, which precisely characterizes the guarantees it makes to the other components. For example, if a concurrent object’s interface states that it is a sequentially consistent FIFO queue, then users of the queue need to know nothing about how the queue is implemented. The result of composing individually correct components that rely only on one anothers' interfaces should itself be a correct system. Can we, in fact, compose a collection of independently implemented quiescently consistent objects to construct a quiescently consistent system? The answer is, yes: quiescent consistency is compositional, so quiescently consistent objects can be composed to construct more complex quiescently consistent objects.
. Compositionality is important in large systems. Any sufficiently complex system must be designed and implemented in a modular fashion. Components are designed, implemented, and proved correct independently. Each component makes a clear distinction between its implementation, which is hidden, and its interface, which precisely characterizes the guarantees it makes to the other components. For example, if a concurrent object’s interface states that it is a sequentially consistent FIFO queue, then users of the queue need to know nothing about how the queue is implemented. The result of composing individually correct components that rely only on one anothers' interfaces should itself be a correct system. Can we, in fact, compose a collection of independently implemented quiescently consistent objects to construct a quiescently consistent system? The answer is, yes: quiescent consistency is compositional, so quiescently consistent objects can be composed to construct more complex quiescently consistent objects.
3.4 Sequential Consistency
In Fig. 3.5, a single thread writes 7 and then −3 to a shared register r. Later, it reads r and returns 7. For some applications, this behavior might not be acceptable because the value the thread read is not the last value it wrote. The order in which a single thread issues method calls is called its program order. (Method calls by different threads are unrelated by program order.)
![]()
Figure 3.5 Why method calls should appear to take effect in program order. This behavior is not acceptable because the value the thread read is not the last value it wrote.
In this example, we were surprised that operation calls did not take effect in program order. This example suggests an alternative principle:
Principle 3.4.1
Method calls should appear to take effect in program order.
This principle ensures that purely sequential computations behave the way we would expect.
Together, Principles 3.3.1 and 3.4.1 define a correctness property called sequential consistency, which is widely used in the literature on multiprocessor synchronization.
Sequential consistency requires that method calls act as if they occurred in a sequential order consistent with program order. That is, in any concurrent execution, there is a way to order the method calls sequentially so that they (1) are consistent with program order, and (2) meet the object’s sequential specification. There may be more than one order satisfying this condition. In Fig. 3.6, thread A enqueues x while B enqueues y, and then A dequeues y while B dequeues x. There are two possible sequential orders that can explain these results: (1) A enqueues x, B enqueues y, B dequeues x, then A dequeues y, or (2) B enqueues y, A enqueues x, A dequeues y, then B dequeues x. Both these orders are consistent with the method calls' program order, and either one is enough to show the execution is sequentially consistent.
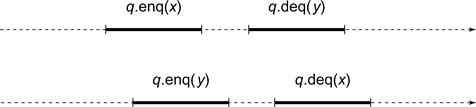
Figure 3.6 There are two possible sequential orders that can justify this execution. Both orders are consistent with the method calls’ program order, and either one is enough to show the execution is sequentially consistent.
3.4.1 Remarks
It is worth noting that sequential consistency and quiescent consistency are incomparable: there exist sequentially consistent executions that are not quiescently consistent, and vice versa. Quiescent consistency does not necessarily preserve program order, and sequential consistency is unaffected by quiescent periods.
In most modern multiprocessor architectures, memory reads and writes are not sequentially consistent: they can be typically reordered in complex ways. Most of the time no one can tell, because the vast majority of reads–writes are not used for synchronization. In those specific cases where programmers need sequential consistency, they must ask for it explicitly. The architectures provide special instructions (usually called memory barriers or fences ) that instruct the processor to propagate updates to and from memory as needed, to ensure that reads and writes interact correctly. In the end, the architectures do implement sequential consistency, but only on demand. We discuss further issues related to sequential consistency and the Java programming language in detail in Section 3.8.
In Fig. 3.7, thread A enqueues x, and later B enqueues y, and finally A dequeues y. This execution may violate our intuitive notion of how a FIFO queue should behave: the call enqueuing x finishes before the call dequeuing y starts, so although y is enqueued after x, it is dequeued before. Nevertheless, this execution is sequentially consistent. Even though the call that enqueues x happens before the call that enqueues y, these calls are unrelated by program order, so sequential consistency is free to reorder them.
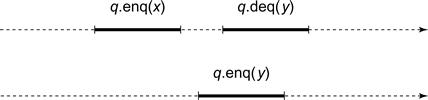
Figure 3.7 Sequential consistency versus real-time order. Thread A enqueues x, and later thread B enqueues y, and finally A dequeues y. This execution may violate our intuitive notion of how a FIFO queue should behave because the method call enqueuing x finishes before the method call dequeuing y starts, so although y is enqueued after x, it is dequeued before. Nevertheless, this execution is sequentially consistent.
One could argue whether it is acceptable to reorder method calls whose intervals do not overlap, even if they occur in different threads. For example, we might be unhappy if we deposit our paycheck on Monday, but the bank bounces our rent check the following Friday because it reordered our deposit after your withdrawal.
Sequential consistency, like quiescent consistency, is nonblocking: any pending call to a total method can always be completed.
Is sequential consistency compositional? That is, is the result of composing multiple sequentially consistent objects itself sequentially consistent? Here, unfortunately, the answer is no. In Fig. 3.8, two threads, A and B, call enqueue and dequeue methods for two queue objects, p and q. It is not hard to see that p and q are each sequentially consistent: the sequence of method calls for p is the same as in the sequentially consistent execution shown in Fig. 3.7, and the behavior of q is symmetric. Nevertheless, the execution as a whole is not sequentially consistent.
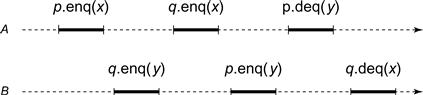
Figure 3.8 Sequential consistency is not compositional. Two threads, ![]() and
and ![]() , call enqueue and dequeue methods on two queue objects, p and q. It is not hard to see that p and q are each sequentially consistent, yet the execution as a whole is not sequentially consistent.
, call enqueue and dequeue methods on two queue objects, p and q. It is not hard to see that p and q are each sequentially consistent, yet the execution as a whole is not sequentially consistent.
Let us check that there is no correct sequential execution in which these method calls can be ordered in a way consistent with their program order. Let us assume, by way of contradiction, that these method calls can be reordered to form a correct FIFO queue execution, where the order of the method calls is consistent with the program order. We use the following shorthand: ![]() means that any sequential execution must order A ’s enqueue of x at p before B ’s dequeue of x at p, and so on. Because p is FIFO and A dequeues y from p, y must have been enqueued before x:
means that any sequential execution must order A ’s enqueue of x at p before B ’s dequeue of x at p, and so on. Because p is FIFO and A dequeues y from p, y must have been enqueued before x:
![]()
Likewise,
![]()
But program order implies that
![]()
Together, these orderings form a cycle.
3.5 Linearizability
We have seen that the principal drawback of sequential consistency is that it is not compositional: the result of composing sequentially consistent components is not itself necessarily sequentially consistent. We propose the following way out of this dilemma. Let us replace the requirement that method calls appear to happen in program order with the following stronger restriction:
Principle 3.5.1
Each method call should appear to take effect instantaneously at some moment between its invocation and response.
This principle states that the real-time behavior of method calls must be preserved. We call this correctness property linearizability. Every linearizable execution is sequentially consistent, but not vice versa.
3.5.1 Linearization Points
The usual way to show that a concurrent object implementation is linearizable is to identify for each method a linearization point where the method takes effect. For lock-based implementations, each method’s critical section can serve as its linearization point. For implementations that do not use locking, the linearization point is typically a single step where the effects of the method call become visible to other method calls.
For example, let us recall the single-enqueuer/single-dequeuer queue of Fig. 3.3. This implementation has no critical sections, and yet we can identify its linearization points. Here, the linearization points depend on the execution. If it returns an item, the deq() method has a linearization point when the head field is updated (Line ). If the queue is empty, the deq() method has a linearization point when it throws EmptyException (Line ). The enq() method is similar.
3.5.2 Remarks
Sequential consistency is a good way to describe standalone systems, such as hardware memories, where composition is not an issue. Linearizability, by contrast, is a good way to describe components of large systems, where components must be implemented and verified independently. Moreover, the techniques we use to implement concurrent objects, are all linearizable. Because we are interested in systems that preserve program order and compose, most (but not all) data structures considered in this book are linearizable.
How much does linearizability limit concurrency? Linearizability, like sequential consistency, is nonblocking. Moreover, like quiescent consistency, but unlike sequential consistency, linearizability is compositional; the result of composing linearizable objects is linearizable.
3.6 Formal Definitions
We now consider more precise definitions. Here, we focus on the formal properties of linearizability, since it is the property most often used in this book. We leave it as an exercise to provide the same kinds of definitions for quiescent consistency and sequential consistency.
Informally, we know that a concurrent object is linearizable if each method call appears to take effect instantaneously at some moment between that method’s invocation and return events. This statement is probably enough for most informal reasoning, but a more precise formulation is needed to take care of some tricky cases (such as method calls that have not returned), and for more rigorous styles of argument.
An execution of a concurrent system is modeled by a history, a finite sequence of method invocation and response events. A subhistory of a history H is a subsequence of the events of H. We write a method invocation as ![]() , where x is an object, m a method name, a* a sequence of arguments, and A a thread. We write a method response as
, where x is an object, m a method name, a* a sequence of arguments, and A a thread. We write a method response as ![]() where t is either Ok or an exception name, and r* is a sequence of result values. Sometimes we refer to an event labeled with thread A as a step of A.
where t is either Ok or an exception name, and r* is a sequence of result values. Sometimes we refer to an event labeled with thread A as a step of A.
A response matches an invocation if they have the same object and thread. We have been using the term “method call” informally, but here is a more formal definition: a method call in a history H is a pair consisting of an invocation and the next matching response in H. We need to distinguish calls that have returned from those that have not: An invocation is pending in H if no matching response follows the invocation. An extension of H is a history constructed by appending responses to zero or more pending invocations of H. Sometimes, we ignore all pending invocations: ![]() is the subsequence of H consisting of all matching invocations and responses.
is the subsequence of H consisting of all matching invocations and responses.
In some histories, method calls do not overlap: A history H is sequential if the first event of H is an invocation, and each invocation, except possibly the last, is immediately followed by a matching response.
Sometimes we focus on a single thread or object: a thread subhistory, ![]() (“H at A”), of a history H is the subsequence of all events in H whose thread names are A. An object subhistory
(“H at A”), of a history H is the subsequence of all events in H whose thread names are A. An object subhistory![]() is similarly defined for an object x. In the end, all that matters is how each thread views what happened: two histories H and H′ are equivalent if for every thread A,
is similarly defined for an object x. In the end, all that matters is how each thread views what happened: two histories H and H′ are equivalent if for every thread A, ![]() . Finally, we need to rule out histories that make no sense: A history H is well formed if each thread subhistory is sequential. All histories we consider here are well-formed. Notice that thread subhistories of a well-formed history are always sequential, but object subhistories need not be.
. Finally, we need to rule out histories that make no sense: A history H is well formed if each thread subhistory is sequential. All histories we consider here are well-formed. Notice that thread subhistories of a well-formed history are always sequential, but object subhistories need not be.
How can we tell whether an object is really a FIFO queue? We simply assume that we have some effective way of recognizing whether any sequential object history is or is not a legal history for that object’s class. A sequential specification for an object is just a set of sequential histories for the object. A sequential history H is legal if each object subhistory is legal for that object.
Recall from Chapter 2 that a partial order→ on a set X is a relation that is irreflexive and transitive. That is, it is never true that ![]() , and whenever
, and whenever ![]() and
and ![]() , then
, then ![]() . Note that it is possible that there are distinct x and y such that neither
. Note that it is possible that there are distinct x and y such that neither ![]() nor
nor ![]() . A total order< on X is a partial order such that for all distinct x and y in X, either
. A total order< on X is a partial order such that for all distinct x and y in X, either ![]() or
or ![]() .
.
Any partial order can be extended to a total order:
Fact 6.3.1. If → is a partial order on X, then there exists a total order "<" on X such that if ![]() , then
, then ![]() .
.
We say that a method call ![]() precedes a method call
precedes a method call ![]() in history H if
in history H if ![]() finished before
finished before ![]() started: that is,
started: that is, ![]() 's response event occurs before
's response event occurs before ![]() 's invocation event. This notion is important enough to introduce some shorthand notation. Given a history H containing method calls
's invocation event. This notion is important enough to introduce some shorthand notation. Given a history H containing method calls ![]() and
and ![]() , we say that
, we say that ![]() if
if ![]() precedes
precedes ![]() in H. We leave it as an exercise to show that
in H. We leave it as an exercise to show that ![]() is a partial order. Notice that if H is sequential, then
is a partial order. Notice that if H is sequential, then ![]() is a total order. Given a history H and an object x, such that
is a total order. Given a history H and an object x, such that ![]() contains method calls
contains method calls ![]() and
and ![]() , we say that
, we say that ![]() if
if ![]() precedes
precedes ![]() in
in ![]() .
.
3.6.1 Linearizability
The basic idea behind linearizability is that every concurrent history is equivalent, in the following sense, to some sequential history. The basic rule is that if one method call precedes another, then the earlier call must have taken effect before the later call. By contrast, if two method calls overlap, then their order is ambiguous, and we are free to order them in any convenient way.
More formally,
Definition 6.3.1
A history H is linearizable if it has an extension H′ and there is a legal sequential history S such that
We refer to S as a linearization of H. (H may have multiple linearizations.)
Informally, extending H to H′ captures the idea that some pending invocations may have taken effect, even though their responses have not yet been returned to the caller. Fig. 3.9 illustrates the notion: we must complete the pending enq(x) method call to justify the deq() call that returns x. The second condition says that if one method call precedes another in the original history, then that ordering must be preserved in the linearization.
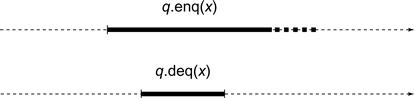
Figure 3.9 The pending enq(x) method call must take effect early to justify the deq() call that returns x.
3.6.2 Compositional Linearizability
Linearizability is compositional:
Theorem 3.6.1
H is linearizable if, and only if, for each object x, ![]() is linearizable.
is linearizable.
Proof:
The “only if” part is left as an exercise.
For each object x, pick a linearization of ![]() . Let
. Let ![]() be the set of responses appended to
be the set of responses appended to ![]() to construct that linearization, and let
to construct that linearization, and let ![]() be the corresponding linearization order. Let H′ be the history constructed by appending to H each response in
be the corresponding linearization order. Let H′ be the history constructed by appending to H each response in ![]() .
.
We argue by induction on the number of method calls in H′. For the base case, if H′ contains only one method call, we are done. Otherwise, assume the claim for every H containing fewer than ![]() method calls. For each object x, consider the last method call in
method calls. For each object x, consider the last method call in ![]() . One of these calls m must be maximal with respect to
. One of these calls m must be maximal with respect to ![]() : that is, there is no m′ such that
: that is, there is no m′ such that ![]() . Let G′ be the history defined by removing m from H′. Because m is maximal, H′ is equivalent to
. Let G′ be the history defined by removing m from H′. Because m is maximal, H′ is equivalent to ![]() . By the induction hypothesis, G′ is linearizable to a sequential history S′, and both H′ and H are linearizable to
. By the induction hypothesis, G′ is linearizable to a sequential history S′, and both H′ and H are linearizable to ![]() .
.
Compositionality is important because it allows concurrent systems to be designed and constructed in a modular fashion; linearizable objects can be implemented, verified, and executed independently. A concurrent system based on a noncompositional correctness property must either rely on a centralized scheduler for all objects, or else satisfy additional constraints placed on objects to ensure that they follow compatible scheduling protocols.
3.6.3 The Nonblocking Property
Linearizability is a nonblocking property: a pending invocation of a total method is never required to wait for another pending invocation to complete.
Theorem 3.6.2
Let inv(m) be an invocation of a total method. If ![]() is a pending invocation in a linearizable history H, then there exists a response
is a pending invocation in a linearizable history H, then there exists a response ![]() such that
such that ![]() is linearizable.
is linearizable.
Proof:
Let S be any linearization of H. If S includes a response ![]() to
to ![]() , we are done, since S is also a linearization of
, we are done, since S is also a linearization of ![]() . Otherwise,
. Otherwise, ![]() does not appear in S either, since linearizations, by definition, include no pending invocations. Because the method is total, there exists a response
does not appear in S either, since linearizations, by definition, include no pending invocations. Because the method is total, there exists a response ![]() such that
such that
![]()
is legal. S′, however, is a linearization of ![]() , and hence is also a linearization of H.
, and hence is also a linearization of H.
This theorem implies that linearizability by itself never forces a thread with a pending invocation of a total method to block. Of course, blocking (or even deadlock) may occur as artifacts of particular implementations of linearizability, but it is not inherent to the correctness property itself. This theorem suggests that linearizability is an appropriate correctness condition for systems where concurrency and real-time response are important.
The nonblocking property does not rule out blocking in situations where it is explicitly intended. For example, it may be sensible for a thread attempting to dequeue from an empty queue to block, waiting until another thread enqueues an item. A queue specification would capture this intention by making the deq() method’s specification partial, leaving its effect undefined when applied to an empty queue. The most natural concurrent interpretation of a partial sequential specification is simply to wait until the object reaches a state in which the method is defined.
3.7 Progress Conditions
Linearizability’s nonblocking property states that any pending invocation has a correct response, but does not talk about how to compute such a response. For example, let us consider the scenario for the lock-based queue shown in Fig. 3.1. Suppose the queue is initially empty. A halts half-way through enqueuing x, and B then invokes deq(). The nonblocking property guarantees that B ’s call to deq() has a response: it could either throw an exception or return x. In this implementation, however, B is unable to acquire the lock, and will be delayed as long as A is delayed.
Such an implementation is called blocking, because an unexpected delay by one thread can prevent others from making progress. Unexpected thread delays are common in multiprocessors. A cache miss might delay a processor for a hundred cycles, a page fault for a few million cycles, preemption by the operating system for hundreds of millions of cycles. These delays depend on the specifics of the machine and the operating system.
A method is wait-free if it guarantees that every call finishes its execution in a finite number of steps. It is bounded wait-free if there is a bound on the number of steps a method call can take. This bound may depend on the number of threads. For example, the Bakery algorithm’s doorway section studied in Chapter 2 is bounded wait-free, where the bound is the number of threads. A wait-free method whose performance does not depend on the number of active threads is called population-oblivious. We say that an object is wait-free if its methods are wait-free, and in an object oriented language, we say that a class is wait-free if all instances of its objects are wait-free. Being wait-free is an example of a nonblocking progress condition, meaning that an arbitrary and unexpected delay by one thread (say, the one holding a lock) does not necessarily prevent the others from making progress.
The queue shown in Fig. 3.3 is wait-free. For example, in the scenario where A halts half-way through enqueuing x, and B then invokes deq(), then B will either throw EmptyException (if A halted before storing the item in the array) or it will return x (if A halted afterward). The lock-based queue is not nonblocking because B will take an unbounded number of steps unsuccessfully trying to acquire the lock.
The wait-free property is attractive because it guarantees that every thread that takes steps makes progress. However, wait-free algorithms can be inefficient, and sometimes we are willing to settle for a weaker nonblocking property.
A method is lock-free if it guarantees that infinitely often some method call finishes in a finite number of steps. Clearly, any wait-free method implementation is also lock-free, but not vice versa. Lock-free algorithms admit the possibility that some threads could starve. As a practical matter, there are many situations in which starvation, while possible, is extremely unlikely, so a fast lock-free algorithm may be more attractive than a slower wait-free algorithm.
3.7.1 Dependent Progress Conditions
The wait-free and lock-free nonblocking progress conditions guarantee that the computation as a whole makes progress, independently of how the system schedules threads.
In Chapter 2 we encountered two progress conditions for blocking implementations: the deadlock-free and starvation-free properties. These properties are dependent progress conditions: progress occurs only if the underlying platform (i.e., the operating system) provides certain guarantees. In principle, the deadlock-free and starvation-free properties are useful when the operating system guarantees that every thread eventually leaves every critical section. In practice, these properties are useful when the operating system guarantees that every thread eventually leaves every critical section in a timely manner.
Classes whose methods rely on lock-based synchronization can guarantee, at best, dependent progress properties. Does this observation mean that lock-based algorithms should be avoided? Not necessarily. If preemption in the middle of a critical section is sufficiently rare, then dependent blocking progress conditions are effectively indistinguishable from their nonblocking counterparts. If preemption is common enough to cause concern, or if the cost of preemption-based delay is sufficiently high, then it is sensible to consider nonblocking progress conditions.
There is also a dependent nonblocking progress condition: the obstruction-free property. We say that a method call executes in isolation if no other threads take steps.
Definition 3.7.1
A method is obstruction-free if, from any point after which it executes in isolation, it finishes in a finite number of steps.
Like the other nonblocking progress conditions, the obstruction-free condition ensures that not all threads can be blocked by a sudden delay of one or more other threads. A lock-free algorithm is obstruction-free, but not vice versa.
The obstruction-free algorithm rules out the use of locks but does not guarantee progress when multiple threads execute concurrently. It seems to defy the fair approach of most operating system schedulers by guaranteeing progress only when one thread is unfairly scheduled ahead of the others.
In practice, however, there is no problem. The obstruction-free condition does not require pausing all threads, only those threads that conflict, meaning that they call the same shared object’s methods. The simplest way to exploit an obstruction-free algorithm is to introduce a back-off mechanism: a thread that detects a conflict pauses to give an earlier thread time to finish. Choosing when to back off, and for how long, is a complicated subject discussed in detail in Chapter 7.
Picking a progress condition for a concurrent object implementation depends on both the needs of the application and the characteristics of the underlying platform. The absolute wait-free and lock-free progress properties have good theoretical properties, they work on just about any platform, and they provide real-time guarantees useful to applications such as music, electronic games, and other interactive applications. The dependent obstruction-free, deadlock-free, and starvation-free properties rely on guarantees provided by the underlying platform. Given those guarantees, however, the dependent properties often admit simpler and more efficient implementations.
3.8 The Java Memory Model
The Java programming language does not guarantee linearizability, or even sequential consistency, when reading or writing fields of shared objects. Why not? The principal reason is that strict adherence to sequential consistency would outlaw widely used compiler optimizations, such as register allocation, common subexpression elimination, and redundant read elimination, all of which work by reordering memory reads–writes. In a single-threaded computation, such reorderings are invisible to the optimized program, but in a multithreaded computation, one thread can spy on another and observe out-of-order executions.
The Java memory model satisfies the Fundamental Property of relaxed memory models: if a program’s sequentially consistent executions follow certain rules, then every execution of that program in the relaxed model will still be sequentially consistent. In this section, we describe rules that guarantee that the Java programs are sequentially consistent. We will not try to cover the complete set of rules, which is rather large and complex. Instead, we focus on a set of straightforward rules that should be enough for most purposes.
Fig. 3.10 shows double-checked locking, a once-common programming idiom that falls victim to Java’s lack of sequential consistency. Here, the Singleton class manages a single instance of a Singleton object, accessible through the getInstance() method. This method creates the instance the first time it is called. This method must be synchronized to ensure that only one instance is created, even if several threads observe instance to be Null. Once the instance has been created, however, no further synchronization should be necessary. As an optimization, the code in Fig. 3.10 enters the synchronized block only when it observes an instance to be Null. Once it has entered, it double-checks that instance is still null before creating the instance.

Figure 3.10 Double-checked locking.
This pattern, once common, is incorrect. At Line, the constructor call appears to take place before the instance field is assigned, but the Java memory model allows these steps to occur out of order, effectively making a partially initialized Singleton object visible to other programs.
In the Java memory model, objects reside in a shared memory and each thread has a private working memory that contains cached copies of fields it has read or written. In the absence of explicit synchronization (explained later), a thread that writes to a field might not propagate that update to memory right away, and a thread that reads a field might not update its working memory if the field’s copy in memory changes value. Naturally, a Java virtual machine is free to keep such cached copies consistent, and in practice they often do, but they are not required to do so. At this point, we can guarantee only that a thread’s own reads–writes appear to that thread to happen in order, and that any field value read by a thread was written to that field (i.e., values do not appear out of thin air).
Certain statements are synchronization events. Usually, the term “synchronization” implies some form of atomicity or mutual exclusion. In Java, however, it also implies reconciling a thread’s working memory with the shared memory. Some synchronization events cause a thread to write cached changes back to shared memory, making those changes visible to other threads. Other synchronization events cause the thread to invalidate its cached values, forcing it to reread field values from memory, making other threads' changes visible. Synchronization events are linearizable: they are totally ordered, and all threads agree on that ordering. We now look at different kinds of synchronization events.
3.8.1 Locks and Synchronized Blocks
A thread can achieve mutual exclusion either by entering a Synchronized block or method, which acquires an implicit lock, or by acquiring an explicit lock (such as the ReentrantLock from the java.util.concurrent.locks package). Both approaches have the same implications for memory behavior.
If all accesses to a particular field are protected by the same lock, then reads–writes to that field are linearizable. Specifically, when a thread releases a lock, modified fields in working memory are written back to shared memory, performing modifications while holding the lock accessible to other threads. When a thread acquires the lock, it invalidates its working memory to ensure fields are reread from shared memory. Together, these conditions ensure that reads–writes to the fields of any object protected by a single lock are linearizable.
3.8.2 Volatile Fields
Volatile fields are linearizable. Reading a volatile field is like acquiring a lock: the working memory is invalidated and the volatile field’s current value is reread from memory. Writing a volatile field is like releasing a lock: the volatile field is immediately written back to memory.
Although reading and writing a volatile field has the same effect on memory consistency as acquiring and releasing a lock, multiple reads–writes are not atomic. For example, if x is a volatile variable, the expression x++ will not necessarily increment x if concurrent threads can modify x. Some form of mutual exclusion is needed as well. One common usage pattern for volatile variables occurs when a field is read by multiple threads, but only written by one.
The java.util.concurrent.locks package includes classes that provide linearizable memory such as AtomicReference<T> or AtomicInteger. The compareAndSet and set() methods act like volatile writes, and get() acts like a volatile read.
3.8.3 Final Fields
Recall that a field declared to be final cannot be modified once it has been initialized. An object’s final fields are initialized in its constructor. If the constructor follows certain simple rules, described in the following paragraphs, then the correct value of any final fields will be visible to other threads without synchronization. For example, in the code shown in Fig. 3.11, a thread that calls reader() is guaranteed to see x equal to 3, because the x field is final. There is no guarantee that y will be equal to 4, because y is not final.

Figure 3.11 Constructor with final field.
If a constructor is synchronized incorrectly, however, then final fields may be observed to change value. The rule is simple: the this reference must not be released from the constructor before the constructor returns.
Fig. 3.12 shows an example of an incorrect constructor in an event-driven system. Here, an EventListener class registers itself with an EventSource class, making a reference to the listener object accessible to other threads. This code may appear safe, since registration is the last step in the constructor, but it is incorrect, because if another thread calls the event listener’s onEvent() method before the constructor finishes, then the OnEvent() method is not guaranteed to see a correct value for x.

Figure 3.12 Incorrect EventListener class.
In summary, reads–writes to fields are linearizable if either the field is volatile, or the field is protected by a unique lock which is acquired by all readers and writers.
3.9 Remarks
What progress condition is right for one’s application? Obviously, it depends on the needs of the application and the nature of the system it is intended to run on. However, this is actually a “trick question” since different methods, even ones applied to the same object, can have different progress conditions. A frequently called time-critical method such as a table lookup in a firewall program, should be wait-free, while an infrequent call to update a table entry can be implemented using mutual exclusion. As we will see, it is quite natural to write applications whose methods differ in their progress guarantees.
Which correctness condition is right for one’s application? Well, it depends on the needs of the application. A lightly loaded printer server that uses a queue to hold, say print jobs, might be satisfied with a quiescently-consistent queue, since the order in which documents are printed is of little importance. A banking server should execute customer requests in program order (transfer $100 from savings to checking, write a check for $50), so it should use a sequentially consistent queue. A stock-trading server is required to be fair, so orders from different customers must be executed in the order they arrive, so it would require a linearizable queue.
The following joke circulated in Italy in the 1920s. According to Mussolini, the ideal citizen is intelligent, honest, and Fascist. Unfortunately, no one is perfect, which explains why everyone you meet is either intelligent and Fascist but not honest, honest and Fascist but not intelligent, or honest and intelligent but not Fascist.
As programmers, it would be ideal to have linearizable hardware, linearizable data structures, and good performance. Unfortunately, technology is imperfect, and for the time being, hardware that performs well is not even sequentially consistent. As the joke goes, that leaves open the possibility that data structures might still be linearizable while performing well. Nevertheless, there are many challenges to make this vision work, and the remainder of this book is a road map showing how to attain this goal.
3.10 Chapter Notes
The notion of quiescent consistency was introduced implicitly by James Aspnes, Maurice Herlihy, and Nir Shavit [16] and more explicitly by Nir Shavit and Asaph Zemach [143]. Leslie Lamport [90] introduced the notion of sequential consistency, while Christos Papadimitriou [123] formulated the canonical formal characterization of serializability. William Weihl [149] was the first to point out the importance of compositionality (which he called locality ). Maurice Herlihy and Jeannette Wing [69] introduced the notion of linearizability in 1990. Leslie Lamport [93, 94] introduced the notion of an atomic register in 1986.
To the best of our knowledge, the notion of wait-freedom first appeared implicitly in Leslie Lamport’s Bakery algorithm [88]. Lock-freedom has had several historical meanings and only in recent years has it converged to its current definition. Obstruction-freedom was introduced by Maurice Herlihy, Victor Luchangco, and Mark Moir [61]. The notion of dependent progress was introduced by Maurice Herlihy and Nir Shavit [63].
Programming languages such as C or C++ were not defined with concurrency in mind, so they do not define a memory model. The actual behavior of a concurrent C or C++ program is the result of a complex combination of the underlying hardware, the compiler, and concurrency library. See Hans Boehm [21] for a more detailed discussion of these issues. The Java memory model proposed here is the second memory model proposed for Java. Jeremy Manson, Bill Pugh, and Sarita Adve [111] give a more complete description of the current Java memory.
The 2-thread queue is considered folklore, yet as far as we are aware, it first appeared in print in a paper by Leslie Lamport [91].
Exercise 21. Explain why quiescent consistency is compositional.
Exercise 22. Consider a memory object that encompasses two register components. We know that if both registers are quiescently consistent, then so is the memory. Does the converse hold? If the memory is quiescently consistent, are the individual registers quiescently consistent? Outline a proof, or give a counterexample.
Exercise 23. Give an example of an execution that is quiescently consistent but not sequentially consistent, and another that is sequentially consistent but not quiescently consistent.
Exercise 24. For each of the histories shown in Figs. 3.13 and 3.14, are they quiescently consistent? Sequentially consistent? Linearizable? Justify your answer.

Figure 3.13 First history for Exercise 24.
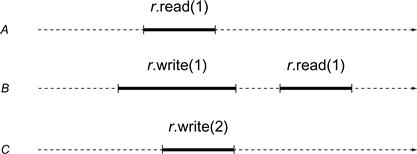
Figure 3.14 Second history for Exercise 24.
Exercise 25. If we drop condition L2 from the linearizability definition, is the resulting property the same as sequential consistency? Explain.
Exercise 26. Prove the “only if” part of Theorem 3.6.1
Exercise 27. The AtomicInteger class (in the java.util.concurrent.atomic package) is a container for an integer value. One of its methods is
boolean compareAndSet(int expect, int update).
This method compares the object’s current value to pre+expect+. If the values are equal, then it atomically replaces the object’s value with pre+update+ and returns true. Otherwise, it leaves the object’s value unchanged, and returns false. This class also provides
int get()
which returns the object’s actual value.
Consider the FIFO queue implementation shown in Fig. 3.15. It stores its items in an array items, which, for simplicity, we will assume has unbounded size. It has two AtomicInteger: fields: Head is the index of the next slot from which to remove an item, and Tail is the index of the next slot in which to place an item. Give an example showing that this implementation is not linearizable.

Figure 3.15 IQueue implementation.
Exercise 28. Consider the class shown in Fig. 3.16. According to what you have been told about the Java memory model, will the reader method ever divide by zero?

Figure 3.16 Volatile field example from Exercise 28.
Exercise 29. Is the following property equivalent to saying that object x is wait-free?
For every infinite history H of x, every thread that takes an infinite number of steps in H completes an infinite number of method calls.
Exercise 30. Is the following property equivalent to saying that object x is lock-free?
For every infinite history H of x, an infinite number of method calls are completed.
Exercise 31. Consider the following rather unusual implementation of a method m. In every history, the ![]() time a thread calls m, the call returns after
time a thread calls m, the call returns after ![]() steps. Is this method wait-free, bounded wait-free, or neither?
steps. Is this method wait-free, bounded wait-free, or neither?
Exercise 32. This exercise examines a queue implementation (Fig. 3.17) whose enq() method does not have a linearization point.

Figure 3.17 Herlihy/Wing queue.
The queue stores its items in an Items array, which for simplicity we will assume is unbounded. The tail field is an AtomicInteger, initially zero. The enq() method reserves a slot by incrementing Tail, and then stores the item at that location. Note that these two steps are not atomic: there is an interval after tail has been incremented but before the item has been stored in the array.
The deq() method reads the value of Tail, and then traverses the array in ascending order from slot zero to the tail. For each slot, it swaps null with the current contents, returning the first non-null item it finds. If all slots are null, the procedure is restarted.
Give an example execution showing that the linearization point for enq() cannot occur at Line.
Hint: give an execution where two enq() calls are not linearized in the order they execute Line.
Give another example execution showing that the linearization point for enq() cannot occur at Line 16.
Since these are the only two memory accesses in enq(), we must conclude that enq() has no single linearization point. Does this mean enq() is not linearizable?
Exercise 33. Prove that sequential consistency is nonblocking.
1 There is an exception: care must be taken if one method partially changes an object’s state and then calls another method of that same object.
