15.5.1 Declarations of Data Structures Assumed in All Programs

Let us start by declaring the variables and data structures needed. These declarations, in turn, refer to other declarations, such as page headers, log records, buffer control blocks, and so on, which have been discussed earlier. Here is the list of basic variables and control blocks needed.

The parameters used to invoke the B-tree routines, and the result variables returned, are described by the following declarations:

Access to the nodes in a B-tree is assumed to be implemented in two subroutines; these are not spelled out in C because they do not contain any aspects that are interesting from a transaction processing perspective. The first one, pagesearch(), gets as parameters a pointer to a page in buffer and a requested key value. It returns the index of an entry in the page according to the following convention: if the page is an index node, the index denotes the entry that contains the proper pointer to the next-lower layer in the traversal sequence. If it is a leaf page, the index denotes the entry that either contains the specified value (if it is present), or the entry that would have to receive that value in case of an insert. The prototype declare is given here:

The second routine, getvalue, serves two purposes: first, it simply returns the key value from a leaf page, given its index. Second, it finds the maximum key value currently stored in a node and returns both that value and its index in the page.

In what follows, these routines are used without further explanation. Exception handling is omitted. Since the results they produce are fairly obvious, the discussion of B-tree implementation should be understandable without any additional functional details.

15.5.2 Implementation of the readkey Operation on a B-Tree

The readkey() function has to go through some logic having to do with the file descriptor, cursor management, and so on; these details are omitted here. For simplicity, it is assumed that the root page number of the tree and its height have already been determined from the file descriptor. With this, an internal routine, readbt(), is invoked. This routine will also be used by the insert function to determine the insert position. It returns the pointer to the buffer access control block of the page with the entry—that page is fixed and protected by a semaphore. It also returns the index of the entry with the key value or the index of the entry after which the search key value would have to be inserted; this parameter is passed via the index entry of the buffer access control block in the parameter list.

The return code of readbt() is FALSE if no match was found, TRUE if a match was found. For simplicity, it is assumed that the tree implements a unique index; there is no checking if more than one entry matches the search argument. We also ignore the special case of a single-page tree, where leaf and root coincide.

Since a full B-tree implementation with all provisions for synchronization, recovery, and so forth, is a fairly complex piece of code, the following explanation is based on pseudo-code rather than C-code, used in the previous chapters. The pseudo-code is close to C, though, whenever the use of an interesting data structure or interface is discussed. Otherwise, the statements are high-level references to explanations that are given in Section 15.4. Code that is at the C level is printed in the same font as the other C code in this book; for the pseudo-code, the text font is used.

The pseudo-code implementing the traversal of a B-tree in order to determine the page and index position of an existing key value, or the insert position of a new key value, follows the next paragraph. Except for getvalue(), the routine invokes a number of lower-level services: bufferfix(), bufferunfix(), and pagesearch().

Since the pagesearch() routine has not been spelled out completely, we must explain the meaning of the index in the leaf page that is returned in its buffer access control block. If the requested key value is found, it is the index of the entry containing that value. If searchkey is not found, the index points to the entry with the next-higher key value. We must also consider the situation in which searchkey is larger than any key value in the tree; in that case, there is no next page to crab to. This is taken care of by some reserved value representing “infinity,” that is, a value larger than any legal value of the index attribute domain. This value can also be used for next-key locking. Again, this technique is assumed without further explanation. The problems that can arise when crabbing along the leaf level are discussed in Subsection 15.4.4.3.

15.5.3 Key-Range Locking in a B-Tree

The readbt() routine is not all that is required to implement the readkey() access, although it does most of the work. The rest has to do with error handling, which is omitted here, and locking, which needs some explanation. According to the protocol explained in this chapter (see Table 15.12), the retrieved key value has to be locked in S mode in case the value was found. Otherwise, the enclosing key range must be locked by locking the next-lower value to avoid phantoms. To do this, we assume another ancillary routine that makes lock names from key values in accord with the declares in Chapters 7 and 8. The function prototype looks like this:

The preceding calls demonstrate the mainline logic used to access a B-tree and to synchronize these accesses using the next-key locking protocol introduced in Subsection 15.4.4. Of course, subsequent lock requests on the tuple pointed to by the B-tree must also be issued, but since these issues have nothing to do with B-tree management, they are ignored here.

The use of the timeout parameter in the invocation of the lock manager needs some explanation. As discussed earlier, one should not wait for a (potentially long) lock while holding a page semaphore. With the interfaces to the lock manager introduced in Chapter 8, there is no clean way to avoid this. We need bounce mode locks to achieve the desired effect: a lock request is issued, and it returns immediately with an indication if the object is already locked by another transaction. Issuing the lock request with a timeout interval of zero gives bounce mode locking, and that is why this trick is used here. If the transaction accessing the B-tree actually has to wait for the lock, it first gives up the semaphore, then requests the lock again (this time with a reasonable timeout), and, of course, has to verify that the leaf page has not changed while the transaction was waiting for the lock. This verification is done by comparing the leaf page’s LSN with the LSN of the same page after it has reacquired the semaphore. If the LSN has changed, the page must be reanalyzed. It can be the case that the desired entry is still in the page—the intermediate update has affected another entry. If this is so, processing proceeds normally. Otherwise, the client has to give up and retry the retrieval operation by going through readbt again.

Note that in case the lock is successfully acquired, the translation still holds a semaphore on the leaf page. The actual code hiding behind the phrase “prepare the results” must make sure that the lock gets released properly and the page is unfixed. If the key value was not found, the implementation may also decide to release the read lock on the next key, depending on what kind of read operation the transaction is executing. It was shown in Section 15.4 that there are situations where it is safe to proceed in that fashion.

15.5.4 Implementation of the Insert Operation for a B-Tree: The Simple Case

The routine that inserts a new tuple (or a reference to the tuple) into a B-tree structure first calls readbt to get the leaf page required and the index position in the page where the new tuple has to go (see Subsection 15.5.3). The readbt() routine ensures that there is an exclusive semaphore on the leaf node page and returns the path from the root to the leaf in the structure searchpath, which is passed via the variable pathptr in the parameter list. The function prototype declaration of this routine looks like the following:

For the reasons mentioned previously, all aspects related to handling the actual tuple are ignored here, because they are largely independent of the properties of the B-tree access path structure.

We present the implementation of the inserto routine as a sequence of code blocks. The explanation of the implementation issues starts with the simplest case, which is the insertion of the new entry somewhere in a leaf page; that is, special cases such as the new entry being the highest value in a leaf are ignored. Given this standard path through the insert logic, we will then consider some more complicated situations, such as page splits. Again, all the following considerations are based on the assumption that the B-tree implements a unique index and that the tuples are stored somewhere else; that is, the tree only contains TID references to the tuples. The logic for the simple case looks like this:

Let us now consider the case of an insert that requires a leaf to be split. To keep the discussion simple, the code is restricted to a leaf split only. This is justified by the fact that splitting an intermediate node requires the same essential steps as splitting a leaf node—with the exception of the root.

15.5.5 Implementing B-Tree Insert: The Split Case

The first thing that needs to be done is to protect all the nodes that will be affected by the split with exclusive semaphores. When it is discovered that a page must be split, only the leaf to be split has such a semaphore. This must be released, because the search path is revisited top-down based on the entries in searchpath, and we want to avoid deadlocks among transactions requesting semaphores. Once the nodes to be updated are covered by semaphores, the actual split can be performed and, finally, the semaphores can be released. The pseudo-code portion for the leaf node split implementing the techniques described in Subsection 15.4.1 is presented on the next page (the previous declares are assumed without repeating them).

This piece of code needs some additional comments. First, the idea of releasing the exclusive semaphores on those interior nodes that are not affected by the split rests on a critical asumption: one must be able to tell whether or not the discriminating key being propagated from the lower layer fits into the node before one actually knows which discriminating key that is. If all keys have fixed length (which, for simplicity, was assumed here), this is trivial.

If their keys have variable length (and if key compression is used), then it is not possible, in general. If it is not possible to safely decide whether or not an interior node has to be split, then either the entire search path (including the root) must be protected by an exclusive semaphore, or semaphores must be acquired bottom-up during the split processing, which requires means to detect deadlocks involving both locks and semaphores.

Second, it must be noted that there is a subtle problem with the ancillary routine getfreepage that returns the PAGEID of an empty page in the file holding the B-tree. Free page administration is typically done by the tuple-oriented file system, which probably is a different resource manager than the B-tree manager. Consequently, it does its own logging. If it does log the allocation operation in the conventional manner, then there is a problem if the transaction in which the split occurs is later rolled back. The B-tree manager logically undoes the insert but does not revert the split; the file manager, however, would do its part of the rollback, which implies claiming the empty page again. On the other hand, if the file manager does no logging and the transaction crashes early, empty storage might be lost. Therefore, a cooperation between the two components is needed; this cooperation can be defined in different ways. One possibilty is to give the authority for free page management to the B-tree manager; this means that from the file system’s perspective, the B-tree manager claims all the space right away and keeps track of which pages are used and which are not. Then, there is no problem in recovering allocation operations according to the scheme introduced here. Another possibility is to enclose the allocation operation (done by the file system) and the log write for the allocation (done by the B-tree manager) into one common, nested top-level transaction. Then, two things can happen: either the page is allocated and the B-tree manager’s log record for it is written, which means it can explicitly return that page if the closing parenthesis is missing after a crash; or the nested top-level transaction fails, in which case normal UNDO will take care of recovery.

The point about the code here has to do with splitting higher-level nodes. In our example, the operation “modify parent” is assumed to affect only one node. In general, however, it would have to call the split routine recursively, until the level recorded in split_up_to is reached. For each split operation on the way, the same logic is applied. A new opening parenthesis is written to the log, identifying the page to be split; all the log records pertaining to that split are recorded the same way; and so on. In effect, the log will contain nested parentheses, and the insert is complete only if the outer closing parenthesis is found.

15.5.6 Summary

The implementation section has presented (pseudo-) code pieces to illustrate the application of the guiding principles for implementing transactional resource managers: the use of semaphores and logging to perform consistent, isolated, and atomic page changes; the combination of low-level locks (semaphores) and key-range locks to achieve high concurrency on a popular data structure such as a B-tree; the combination of physical REDO and logical UNDO to reduce lock holding times.

15.6.1 Extendible Hashing

Extendible hashing provides exactly the same functionality as the static hash algorithms described in Section 15.3, with one exception: the number of hash-table buckets can grow and shrink with usage. Essentially, it can start out as an empty file with no pages, grow to whatever is needed, and shrink. The pages need not be allocated in contiguous order; rather, they can be requested and released one by one, just as for B-trees. The performance of extendible hashing for single-tuple access via the primary key is not as good as static hashing, but it is still better than B-trees.

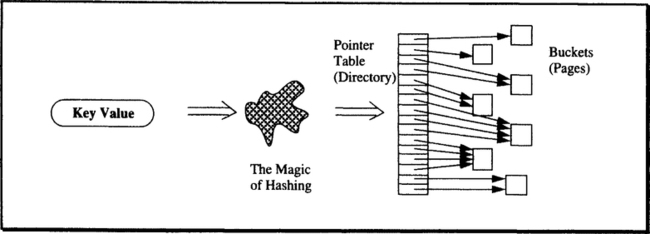
The basic idea is simple. Since pages can be allocated and deallocated as needed, the hashing function cannot produce page numbers (or an offset thereof). There has to be an intermediate data structure for translating the hash results into page addresses, and the question is how to make this auxiliary structure as compact and efficient as possible.

A very simple data structure, well-suited for random access, is the array. Static hashing, in fact, uses an array of buckets. Extendible hashing, for the sake of flexibility, employs one level of indirection and instead hashes into an array of pointers to buckets.¹⁵ This array is called directory. Of course, the array has to be contiguously allocated in memory, but since the array is much smaller than the file itself (≈ 0.1%), it is less of a problem to make a generous allocation in the beginning. The basic mapping scheme is shown in Figure 15.14. This illustration explains why pages need not be allocated in a row and why allocation can change over time. However, it says little about how dynamic growing and shrinking is actually handled. To present this in more detail, some preparation is needed.

The bit string produced by the hash function is called S in the following. The directory grows and shrinks as the file does, but its number of entries is always a power of two. The directory is always kept large enough to hold pointers to all the pages needed for storing the tuples in the file. At any point in time, each entry in the directory contains a valid pointer to an allocated page. Assume the directory has 2^d entries. Then, for a given key value, d bits are taken out of S from a defined position. The resulting d-bit pattern is then interpreted as a positive integer, that is, as the index to the directory table. The pointer in that entry points to the page holding the tuple. There is no overflow handling comparable to the methods for static hashing. Extendibility takes care of that, as we will soon see.

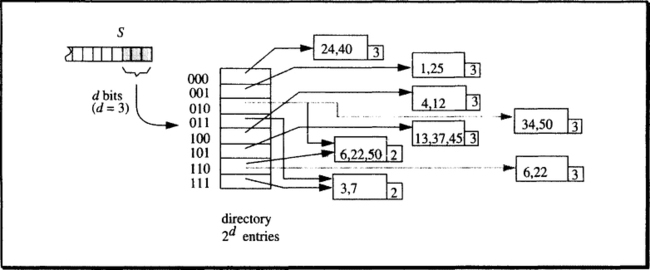
Based on these definitions, let us now explain the key steps of extendible hashing by means of an example. For simplicity, the hashing function is cut short: the binary representation of the numerical key value is used as the bit string S. The example starts at a moment when the directory has 2³ = 8 entries (see Figure 15.15).

The convention adopted for addressing the directory of 2^d entries is the following: given the bit pattern S, take the d rightmost bits interpreted as a binary integer and examine the corresponding directory entry. This is why the directory always contains 2^d entries, with integer d. Since by definition each entry contains a valid pointer, each hashed key will be routed to a bucket page where either the corresponding tuple is found or the decision can be made that the value does not exist. Figure 15.15 contains the example for key value 37. Now try the same thing with 41. Its binary representation is 101001₂; thus the three low-value binary digits to consider are 001, which leads to entry 1, pointing to a bucket with key values 1 and 25. Therefore, no tuple with key value 41 is stored in the file.

Looking at Figure 15.15 a bit closer reveals some more detail. There is a number associated with each bucket, and there are some buckets with two pointers going to them. With a larger directory, there could be more pointers to the same bucket, but the number of pointers directed at any bucket will always be a power of two; the reasons for that will soon become obvious. The number going with each bucket is called local depth (as opposed to d, the global depth). Let b_j denote the local depth of an arbitrary bucket j, and let #pj be the number of pointers directed at j from the directory (1 ≤ #pj ≤ d). Then the following invariance holds: b_j = d – #pj + 1.

A more intuitive interpretation is the following: the local depth says how many bits of S are actually needed to decide that the key value must be in that bucket. Because d is its maximum value, the local depth can never be larger than the global depth. But it may well be lower, which is the case for all buckets to which more than one pointer is directed. Consider, for example, the entries with indexes 2 and 6. Their binary representations are 010₂ and 110₂, respectively. The bucket both entries point to contains 50, which is characterized by 010; as well as 22, the last bits of which are 110. Effectively, then, this bucket holds all keys with 10 as the last 2 bits; whether the next bit is 0 or 1 is irrelevant. This is what “local depth = 2” refers to.

How does update work with extendible hashing? The normal case is straightforward. Assume a new tuple with key value 24 is to be stored. Its three relevant bits are 000. First, a normal retrieval is done. The bucket pointed to by entry 0 only contains key value 40; thus, 24 is not a duplicate. Since there is enough space in the bucket, the tuple with key value 24 is stored, and the insert operation is completed.

The next case is demonstrated by assuming that a tuple with key value 34 is inserted. Its three index bits are 010; that is, it is directed to a bucket with local depth = 2. Because this bucket cannot accommodate another tuple, a file extension must be performed—remember that there are no overflow buckets. Since the local depth of the affected page is smaller than the global depth, this amounts to a simple bucket split, as it is illustrated in Figure 15.16.

What is key here is that two pointers are pointing to the overflowing bucket (or 2ⁿ, in general). Since this routes too many tuples to the bucket, another bucket is installed, and the tuples are distributed over these two buckets. To distinguish between the two buckets after the split, one more bit from S is considered; note that the local depth of the overflowing bucket is smaller than the global one. As a result, the local depth of each of the buckets resulting from the split is one higher than the local depth of the bucket before the split. Accordingly, the criterion for deciding which tuple goes to which bucket is different from the one used in B-tree splits. Consider Figure 15.16: the two buckets resulting from the split will have one pointer each (shown as shaded arrows), corresponding to the directory entries 010₂ and 110₂, respectively. Therefore, the tuples must be assigned to the buckets by the following rule: let b₁ and b₂ be the buckets resulting from a split and i₁ and i₂ be the indices of the directory entries holding the pointers to b₁ and b₂. Then all tuples from the old bucket (including the new one that caused the split) whose index bits are equal to i₁ are assigned to b₁. The index bits of the others will necessarily be equal to i₂; they therefore go to b₂.

The locking and logging issues are straightforward for the operations described so far. Locks are acquired for the tuples, and the required access paths are protected by semaphores. For recovery purposes, the same physiological logging design is used as was described for B-trees. So the insert (or delete operation is logged in the beginning, and all the subsequent page maintenance operations are logged physically for REDO (note that the directory is mapped onto pages, too).

In case of a bucket split as illustrated in Figure 15.16, there is a potential for semaphore deadlock. Assume transaction T₁ comes via directory entry 010₂ to the page before the split, protecting its path with exclusive semaphores. Transaction T₂ comes via entry 110₂, trying to insert into the same page. Now T₂ waits for a semaphore on the page, whereas T₁ waits for a semaphore on directory entry 110₂ to perform the split. In order to avoid such deadlocks, there must be additional rules about when a transaction must not wait for a semaphore. We will not discuss that issue here.

This gives an idea of how the file can grow, given a directory with 2^d entries. But now assume a tuple with key value 61 is to be inserted. Its index bits are 101, the corresponding bucket has local depth = 3, and it is full. Another bit cannot be appended to the left to distinguish two buckets after a split, because the directory itself is addressed by only three bits. Before the bucket can be split, therefore, a larger directory must be built. Its number of entries must be a power of two, so its current size is simply doubled. This implies that the global depth d is increased by 1 (the next bit from S left of the ones currently used is included). As a consequence, all buckets have a local depth smaller than the (new) global one and, therefore, the split algorithm can be applied.

This whole procedure is illustrated in Figure 15.17; its left-hand side is a cleaned-up version of Figure 15.16.

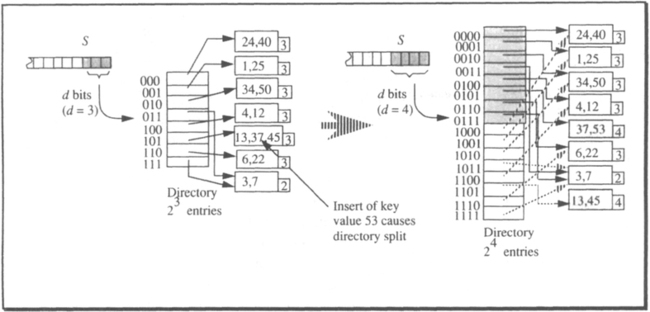
The question of how to double the directory and what to put into the new entries is simple. Since the bits from S are included with increasing exponents, an entry with the old number xyz will now turn into two entries with number Oxyz and lxyz. Of course, all key values that up to now had index bits xyz will remain unchanged; that is, for locating them, the string xyz is sufficient. Therefore, both new entries will contain the same pointer, the one that was stored in entry xyz in the old directory. Since this consideration applies to all entries, doubling the directory means the following: a copy of the old directory is placed directly behind its highest entry. The resulting table with twice the number of entries is the new directory.¹⁶ Note that when doubling the directory, the whole directory must be locked exclusively until the operation is completed. This is not comparable to the situation of a root split in a B-tree. Whereas even in a large B-tree at most five to six pages are modified during an insert causing a root split, doubling the directory of an extendible hashing file with 10⁶ pages means that some 6 MB must be copied explicitly—potentially causing substantial I/O along the way.

In Figure 15.17, the old directory portion is shaded; the new one is not. The copied pointers are indicated by shaded arrows. The figure also contains the result of the bucket split that originally triggered the directory split. The resulting buckets are represented by shaded boxes; of course, after the bucket split is completed, both buckets have the new global depth as their local depth.

The performance of the extendible hashing scheme is fairly easy to estimate. For simplicity, let us concentrate on retrieval operations. The additional cost for inserts only depends on the frequency of splits, which in turn is influenced by how much the file grows compared to the original space allocation. Because the frequency of directory splits decreases exponentially as the file grows, this should not be a cost factor.

There are always two steps for retrieving a tuple (not counting the hash function): first, access the directory to find the bucket pointer; then read the bucket page. As long as the directory completely fits into main memory (into the buffer), each retrieval is one page access—the minimum cost. Assuming 4 bytes per entry and 4 KB pages, then with a 1 MB buffer space for the directory, a 1 GB extendible hash file can be maintained, allowing for one-access associative retrieval.

This sounds pretty attractive, but there are some hidden problems that will surface as soon as a real implementation is considered. We will list just a few of them. The estimate yielding the 1 GB file is based on the assumption that each pointer in the directory goes to a different bucket. Of course, this is only the case if the index bits of the key values in the file are uniformly distributed. If the hash function does not produce a uniformly distributed bit pattern, those parts of the directory corresponding to the more frequent bit patterns will experience a higher frequency of splits. This, in turn, means the directory will be larger than it had to be to address the given number of buckets. And note that the directory doubles each time one bucket is about to exceed the global depth. It does not help if the local depth of the others is way below that value. In other words, for hash value distributions with a noticeable bias, there will quickly be a directory that is relatively large compared to the number of buckets it manages. Once the bucket entries can no longer be kept in buffer, additional page accesses are required for reading the needed portion of the directory. In the worst case, each tuple access requires two page accesses. This is worse than static hashing, and it is not much better than B-tree performance (if at all), considering that the top two levels of a B-tree can be kept in buffer. The question, then, of whether the additional flexibility provided by extendible hashing is worth the effort from a performance perspective critically depends on the quality of the hash function.

Another problem is shrinking an extendible hash file. If a bucket becomes empty, its pointer can be redirected, but deciding whether or not the directory can be cut in half requires additional bookkeeping. It should also be clear that each structural change of the directory is a complex operation, rendering the file inaccessible for quite some time.

And, finally, there is the question of how to map the directory onto disk. A small directory fitting into main memory is not a problem, but what about large ones that have to be paged just like any other data structure? The speed of the algorithm is due to the fact that, based on the index bits, the bucket pointer can be located at almost no cost. If this is to translate to a disk-based directory, then the directory must at any point in time be stored in consecutive pages. If one does not want to allocate space for the largest directory possible, what happens at a directory split?

15.6.2 The Grid File

The grid access method addresses a functional limitation inherent in all the techniques described so far: symmetric access via multiple attributes. Consider the B-tree algorithm and assume that a relation is to be associatively accessed using the values of two attributes, A and B. The queries can be of any of the following types: (p₁(A,B)), (p₁(A) con p₂(B)), (p₁(A)), (p₂(B)). Here pi denotes predicates defined over the respective attributes, and con is a logical connector, such as and, or, exor.

There are two possibilities for supporting such B-trees queries:

Detailed analysis reveals that neither variant works for all query types. The first one has the problem of employing two access paths. This is substantially more expensive than using just one adequate access path; the necessity of maintaining partial result lists and storing them for final processing further adds to the complexity of this solution. But even if all this were acceptable, it is clear that a query with a simple predicate like (A > B) cannot be supported by having two separate B-trees.

Creating a B-tree over the concatenation of both attributes reduces the cost for query processing in some cases, but there are also query types that do not benefit from such an access path. The predicate (A > B), and all variations thereof, is one example. But there are even more trivial cases. Assume the B-tree has been created for A || B; this tree can then be used for answering the query (A < const), but it is useless for (B < const).

Maintaining separate trees for all types of attribute combinations in all permutations solves some of the retrieval problems, but it adds unacceptable costs to the update operations. Considering the arguments already given, it is obvious that for n attributes, virtually all n! attribute concatenations would have to be turned into a B-tree in order to get symmetric behavior with respect to range queries on arbitrary subsets; this is certainly not a reasonable scheme.

What is needed, then, is an access path to allow efficient associative access in an unbiased fashion, based on n attributes with queries of the types shown for the special case of two attributes. For simplicity, all the following presentations are also restricted to two attributes, but a generalization to n attributes is not difficult.

The grid file is one of the most thoroughly investigated access methods for symmetric multi-attribute access in large files. The best way to introduce the basic idea is to use the metaphor of a point set in a plane. Each attribute is an axis in a euclidian space. The tuples have well-defined values in the search attributes A and B; thus, each tuple corresponds to the point in the plane having the tuple’s attribute values as its coordinates. This is illustrated in Figure 15.18.

There are two evident reasons why such a “tuple space” cannot be used directly for storing the tuples: first, it has at least two dimensions, whereas the page address space is one-dimensional; second, the n-dimensional tuple space has clusters as well as unused regions, whereas the utilization of the storage space should be uniformly high. But as Figure 15.18 suggests, the arrangement of the points in the plane (sticking to the two-dimensional example) contains enough information to decide for which regions (subspaces) storage space must be allocated, where the density of tuples is high, where no tuples are, and so on.

Given the point set shown at the left-hand side of Figure 15.19, and given pages which can hold up to three tuples, we can replace the plane with a two-dimensional array of pointers, as shown on the right-hand side. Each of the four cells contains exactly one pointer to a page where the actual tuples are stored; the shaded points in the cells merely indicate which of the tuples of the point set on the left are in the pages to which the pointers refer.

The key point of the grid file concept is the following: as Figure 15.18 shows, the subspaces called cells are not of equal size in terms of the attribute dimensions, although each of them contains one page pointer. The criterion for determining the cell sizes is the number of points in the cell. In other words, the limits between neighboring cells along each dimension are adjusted such that biases in the value distribution are compensated. In value ranges with high tuple frequencies, the sides of the cells are smaller; ranges with fewer tuples allow for larger cells.

Since the value space is divided by parallel planes to the axes, the dividing points for each dimension can be stored separately in an array called scale. Each scale corresponds to one attribute dimension, and it contains the values of that attribute where a dividing plane cuts through the value space, thus creating the cells. It is assumed that each scale array contains the dividing points in ascending order; that is, the larger the index, the larger the attribute value. The data structures required for the two-dimensional case can be declared as follows:

Note that these declarations serve only the purpose of illustrating the functional principles of the grid file. In a real implementation, scales would probably not be defined as a two-dimensional array, because the number of cell boundaries along the different attribute-dimensions may vary widely. The array of page pointers cells cannot be kept in main memory for large files. Consequently, there must be some way of mapping the array onto pages; this is discussed later in this subsection. (See also the remarks on maintaining the directory for extendible hashing in Subsection 15.6.1.) By the way, the cell array is often referred to as the directory of a grid file.

Given these data structures, it is easy to explain how retrieval works with a grid file. Let us start with an exact-match query, which is also referred to as point search when talking about multi-attribute search structures. A point query has a search predicate of the type (A = c₁ and B = c₂). In terms of the point set metaphor, this means that the tuple corresponding to the point in the plane with the coordinates (c₁,c₂) has to be retrieved. The basic steps are illustrated in the piece of code that follows (note that all concurrency control on the scales, index arrays, and cells is omitted).

Thanks to the simplifications explained previously, the code skeleton for retrieval is surprisingly small. It stops in a situation comparable to the moment when the right leaf node in a B-tree is located: the page accessed through bufferfix is the one where the tuple with the specified search must be stored, if it exists. Locating the actual tuple requires a subsequent search in the page.

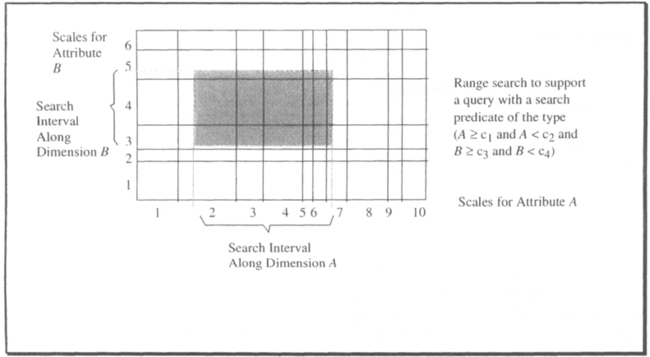
The generalization from point search to interval search along arbitrary dimensions is obvious. Search intervals are defined by specifying the coordinate ranges along each dimension, rather than single coordinate values. Accordingly, for each dimension, a cell index range, rather than a single index, is determined from scales. And finally, cells is accessed with all possible combinations of the cell indexes within the relevant ranges. This yields a set of page numbers completely covering the subspace defined by the range query. It is illustrated in Figure 15.19. The indexes of the two scale vectors are explicitly shown in the figure, for ease of reference.

Given the specified search ranges, the scale for attribute-dimension A says that cells must be accessed with the first index varying between 2 and 7; the scale for B prescribes an index range between 3 and 5. Therefore, the access to all tuples potentially falling into the search rectangle requires the following actions:

Because the whole business of updating a grid file—especially inserting new tuples—is fairly complex, we will only explain the principles involved. The key issues are that grid files are dynamic (pages are allocated and freed as needed) and that the subdivison of the scales into value ranges for determining the cell boundaries has to be dynamic. In other words, there is no prearranged cell structure (this would make things very easy); rather, the boundaries of the cells are adjusted according to the value distributions of the tuples in the file. As an example, assume more tuples are inserted into the scenario of Figure 15.18. These tuples are given names, for ease of reference. Figure 15.20 illustrates the aspects of updating a grid file.

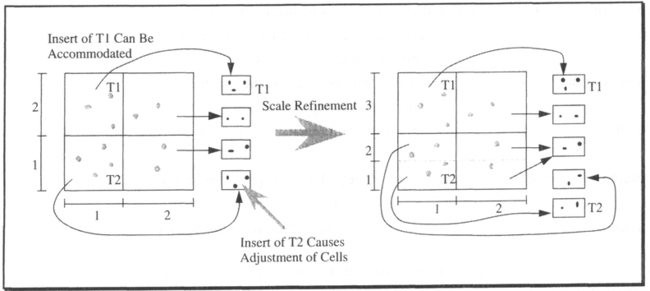
As always, insertion begins with a retrieval operation (a point search for a grid file) to locate the page where the tuple to be inserted has to go. If the page can accommodate the tuple, the tuple is stored there, and no other data structures are affected. In the example, this is the case for tuple t1. If, however, the page is full, its contents have to be distributed across two pages, and the addressing scheme has to be adjusted accordingly. This is similar to how extendible hashing works.

The directory of a grid file has a page pointer for each subspace, the limits of which are determined by the scales. If a page has to be split, two pointers are needed; that is, the subspace entry in the directory must also be split. As Figure 15.20 shows, the critical subspace with cell indexes (1,1) is split along the vertical dimension (shaded line). As a consequence, all cell entries with indexes (*,1) turn into two entries with indexes (*,1) and (*,2). Except for the split cell, all other cell contents are simply copied; this is also shown in the illustration.

Along the dimension that was chosen for the split, all index values above the point of split for existing cells must be increased by one. This requires special techniques for efficiently maintaining the multidimensional directory, discussion of which is beyond the scope of this short introduction.

If a page becomes empty, its pointer in the directory can be redirected to a neighboring page. Neighborhood is defined along any of the dimensions. If an entire subspace along one dimension becomes empty, no entries for it are needed in the directory, and the scale for that dimension can be reduced accordingly. This is the inverse of the process shown previously.

There are a number of difficult problems associated with an efficient implementation of the grid file scheme for a general-purpose transaction system. Splitting is much more complex than shown in our example. The first question concerns which dimension to split along in case of a page overflow. There are different options, depending on how much information about the state of neighboring cells is included. The really tricky issue, however, is how to maintain the (large) directory on disk efficiently. As was demonstrated, the directory is a dynamic, n-dimensional array, and each split operation means that (n – l)-dimensional subarrays are inserted at the split position. Such an operation should not imply a total reorganization of the whole directory. Furthermore, it would be desirable to store the pages associated with neighboring subspaces within a narrow address range. Such a clustering should be maintained under update.

And then, of course, there is the problem of synchronization on a grid file. Which locking protocols are needed for the scales, the directories, and so forth? Is the value locking technique used for B-trees applicable?

Assuming that all these problems can be solved, grid files yield a constant cost of two page accesses for a single-point retrieval. This assumes that the scales can be kept in buffer which is reasonable because they normally comprise just a few KB. Then, one access is required to find the directory page for the subspace in which the point lies, and one access goes to the data page. The performance characteristics and the functional principle are very similar to the extendible hashing scheme. One difference is that extendible hashing is one-dimensional, whereas the grid file supports multidimensional access. Another difference is that extendible hashing relies on a hashing function (hence the name) to produce uniform access frequencies to all directory entries; the grid file employs the scales for the same purpose. And the last, but important, difference is that the directory of an extendible hashing file is much simpler to maintain (and therefore to implement) than the multidimensional directory of the grid file.

15.6.3 Holey Brick B-Trees

Holey brick B-trees (hB-trees) address the same problem as grid files: symmetric multi-attribute search on large files. Just like grid files, they support both exact-match queries and range searches along arbitrary subsets of the attributes on which the search structure is defined. But whereas grid files rely on a multidimensional array that actually resembles the structure of the search space, hB-trees (as their name suggests) are much more akin to B-trees as they have been described in this chapter. It makes an interesting exercise to compare these two radically different approaches to the same problem. But let us first illustrate the basic idea behind hB-trees.¹⁷

The name holey brick B-trees intuitively conveys its idea. Each node in the tree corresponds to a rectangular k-dimensional subspace of the total search space (assuming the search structure has been defined on k attributes of the file). These subspaces are referred to as bricks. In contrast to similar search structures, where this correspondence is strict, a node in an hB-tree generally describes a brick from which smaller bricks may have been removed. This means that the bricks into which the search space is decomposed can have “holes”—hence the name of the access path structure. Like a B-tree, an hB-tree grows from the leaves to the root. The leaves contain the data, whereas the higher levels consist of index nodes.

When speaking of hB-trees, we have to distinguish carefully between two types of tree structures. One is the overall structure of the hB-tree; that is, the way its index and data nodes are tied together. This is taken from the K-D-B-tree (K-D stands for k-dimensional), a B-tree generalization for k attributes. This method was introduced by Robinson [1984], and its principle will become clear during the following description. The second type of tree structure is the k-d-tree [Bentley 1975], which is used to internally organize the entries of the index nodes in an hB-tree. Let us first sketch the ideas behind a k-d-tree.

A k-d-tree is a binary tree that structures the search via k different attributes. Its principle is illustrated in Figure 15.21. A node in a k-d-tree represents an attribute value. If the search key value is less than the node value, search proceeds to the left, otherwise it proceeds to the right.¹⁸ So far, this is exactly how a binary tree works.

However, in a conventional binary tree, each node represents a value of the same attribute; in a k-d-tree, on the other hand, subsequent nodes along a search path can represent values of different attributes. The simplest rule to cope with this is to use the k attributes in a fixed order. Therefore, if the tree is defined on k = 3 attributes (a, b and c), then the root node contains a value of a, its two successors contain values of b, their successors contain c values, then comes a again, and so forth. This is simple but potentially inefficient, because at a certain level it forces the use of an attribute even if the subspace considered at that level need not be partitioned along that dimension. For example, in Figure 15.21, subspaces C and D are defined by values of b only; attribute a is not relevant for them. Thus, a more sophisticated scheme for the k-d-tree permits using along any search path, that attribute for the next node that yields the most efficient partitioning of the remaining subspace. As Figure 15.21 shows, this may result in the same attribute being used repeatedly. Since with that convention, a node’s distance from the root allows no conclusion as to which attribute the node represents, another scheme is sometimes used: each node except for the value must also carry an identifier of the attribute to which it belongs. In what follows, that second scheme is assumed.

As shown in Figure 15.22, the representation of holey bricks by generalizing the k-d-tree technique is straightforward. The conventional search structure is based on the assumption that each node defines a partitioning of the subspace it represents along one dimension, and all dependent nodes further subdivide that partition; here, however, multiple nodes can point to the same partition. When you look at Figure 15.22, the consequences become obvious: in a conventional k-d-tree, the left pointer of the node representing a1 would have to point to a separate subspace, thus partitioning the right-hand region of the search space. However, since this portion of the region, together with the left-hand part of the search space, establishes the subspace B, from which the hole A has been removed, the pointer refers to B, too.

So much for the introduction of the data structures used in the index nodes of an hB-tree. Let us now consider overall organization of an hB-tree. This is where the need for holey bricks comes in. As mentioned, the structure of an hB-tree is similar to a K-D-B-tree. K-D-B-trees are much like B-trees in that they are balanced, the data is in the leaves only, and so on. But while each index node in a B-tree describes the partitioning of a region of a one-dimensional search space into disjoint intervals, an index node in a K-D-B-tree describes the partitioning of a region of a k-dimensional search space into k-dimensional subspaces. For each subspace, a lower-level index node is pointed to, describing the partitioning of that subspace into even finer granules, down to the leaf level.

Up to this point, we have described exactly what the hB-tree does. The difference lies in the techniques used to maintain the tree structure during update. When an index node has to be split in a K-D-B-tree, one attribute (dimension) is picked, along which the subspace represented by that node is divided into two. In other words, the old subspace is completely partitioned along a (k – 1)-dimensional hyperplane. There are two problems with this approach:

The hB-tree uses a different split strategy. It allows a node to be split along more than one dimension in order to avoid both of the problems just mentioned. As a consequence, however, one must be able to cope with holes in the subspaces represented by the index nodes. Since the representation of holey bricks is based on multiple nodes pointing to the same successor (see Figure 15.22), this may result in one index node having more than one parent. Strictly speaking, then, we would have to talk about “hB-DAGs,” but since we will not go into any detail with respect to mutiple parents, the notion of trees is used throughout this section.

To understand the following description of the operations on hB-trees, we have to appreciate the global layout of this search structure, which is depicted in Figure 15.23. The leaves of the k-d-trees in the index nodes point to lower-level nodes in the tree. More than one pointer can reference the same successor node, and these multiple references of the same lower-level node can come from different higher-level index nodes. In each k-d-tree, holes that have been extracted from the region described by the node are tagged (* in the figure). The data nodes also contain k-d-trees to guide the local search, but here the leaves are the actual tuples (or pointers to the tuples, for that matter). Note that in the general case, a leaf of a data node k-d-tree can represent many tuples, namely all those falling into the subspace denoted by that node in the k-d-tree.

Searching in an hB-tree is straightforward. Let us briefly consider the two types of access operations supported by such a search structure.

Update operations follow the same general logic as B-trees; this is explained by considering the insert of a new tuple. First, an exact-match query is performed to determine the insert location. If the tuple fits into the data page, the insert is complete; no structural modifications are necessary.

The specific properties of an hB-tree become relevant when a node split is necessary. For brevity, we do not discuss all the variants and special situations that have to be considered. Rather, we focus on some typical scenarios to demonstrate the principles of splitting nodes that contain k-d-trees describing holey bricks.

At the core of the split algorithm lies the observation that it is always possible to achieve a worst-case split ratio of 1:2, no matter what the value of k, provided the split can involve more than one attribute.¹⁹ When a page needs to be split, therefore, one first checks to see if a split at the current root of the node’s k-d-tree would partition the entries in the page in a ratio of 1:2 or better. If that is the case, the node is split at the root. The left subtree forms one new node, the right sub-tree the other one. If the old node (before the split) represented a complete brick (no holes in it), then there was just one reference to it from an index node. In that case, the old root node must be propagated up to the index node to augment its k-d-tree. If, however, the old node already had holes, then the split may not require any key values to be propagated up the hierarchy; only the adjustment of some pointers is necessary (have them point to the right sub-tree in the new page, rather than in the old one).

If the root node does not achieve the 1:2 split ratio, there must be one sub-tree accounting for more than two-thirds of the entries in the node. Going down this sub-tree produces the first of two possible outcomes (the second will be considered shortly).

Split at lower sub-tree. In the large sub-tree, a node is found, one of whose sub-trees accounts for less than two-thirds and more than one-third of the entries. Then the k-d-tree, and thereby the hB-tree node, is split at this point. This is illustrated in Figure 15.24.

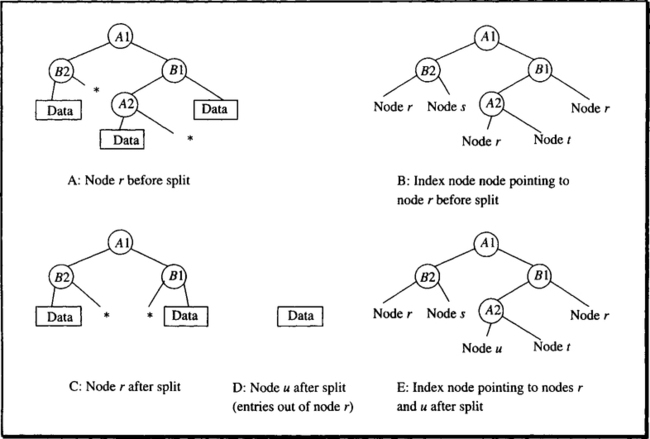
The node to be split (node r) represents a holey brick. Splitting at the node for attribute b1 gives the required split ratio, so the left sub-tree of that node is removed. Since it contains only one portion of data, the new node (node u) can, for the moment, do without any local k-d-tree. The removal of the sub-tree is marked in node u by the tag representing a hole in the appropriate branch. In other words, the split has caused the brick described by node r to get a new (bigger) hole. The example also illustrates that in cases where the discriminating attribute’s values are already present at higher levels, a split may result in mere pointer adjustments in the index.

Note also that the local k-d-trees resulting from the split are generally reduced to the minimum number of nodes required to represent the remaining region in space. This may also result in the removal of hole references (see node u).

Split at leaf. If no sub-tree with the required property is found, then one of the leaves must account for more than two-thirds of the entries; this can only occur in data nodes. In that case, the data in that leaf must be redistributed. According to the split ratio property mentioned earlier, it is always possible to determine a hole lying at a corner of that subspace, such that the ratio of entries in the hole and in the remaining brick is 1:2 or better. The attribute values defining that corner must be propagated up to the index level. An example in two dimensions is shown in Figure 15.25.

The tree structure of the data node and its index node is assumed to be the same as in the previous example. However, we now consider the case in which no sub-tree accounts for a number of entries that lie between one-third and two-thirds of the entries in the page. Assume the data portion in the high-value branch of b1 has more than two-thirds of the entries. This brick must be partitioned, and, as we have seen, there is always a corner hole to remove from the brick such that both the removed part and the remaining part of the node to be split hold between one-third and two-thirds of the entries. Figure 15.25 shows the result of the split, assuming that the removed part was actually sliced off the large subspace along dimension a at point a3. As in the previous scenario, the removed data portion goes to a new page (node u); being the only portion in that node, it needs no k-d-tree for the moment. The new node in the k-d-tree of node r is propagated up to the index node.

As an aside, assuming a1 < a2 < a3 and b1 < b2, we find that the holey brick described by node r now has become holey to the degree that it is noncontiguous. In other words, the holes separate the remaining parts of the subspace that actually contain data maintained in that node.

To keep this discussion short, we do not elaborate on exactly how nodes resulting from a split are propagated up to the index nodes; what happens in case of multiple parents; and so forth. The material presented so far should be sufficient to convey the idea.

The hB-tree structure is interesting for a number of reasons. First, it is a generalization of the well-established B-tree access path, and some of its organizational principles can be applied without any changes. It guarantees a fixed minimum node utilization, even with the worst-case data distribution. This is its major difference from the grid file, for example, which works well only if the data points are evenly distributed in the search space, and which can deteriorate badly if that is not the case. A consequence of the one-third minimum node occupancy is a limit on the height of the hB-tree. For a given file, the hB-tree should come out only slightly higher than a B-tree. This is partly due to the lower (minimum) node utilization and partly due to the fact that the number of entries per node is lower for an hB-tree in the first place, because information about k attributes (rather than one attribute) has to be maintained. Analytic models show that an hB-tree with just one dimension has a performance comparable to that of a B-tree.

A consideration of synchronization and recovery techniques for hB-trees is beyond the scope of this discussion. Even these brief explanations, however, should convey the fact that this is an altogether different story.