Chapter 5. Projection Views
Updating projections?
Just follow directions!
—
Now I want to consider what’s involved in updating projection views (i.e., “updating through” a projection operation). Note: I claimed in the previous chapter that restriction and union views are two sides of the same coin, so to speak; well, a similar remark applies to projection and join views, as we’ll see in this chapter and the next three.
Let me give you some idea as to how the chapter is structured. The discussion overall centers round a set of examples—three of them, to be exact. The first two both have to do primarily with situations in which we have full information equivalence; the third shows what happens if we don’t (i.e., if certain information is hidden). In all three cases, I’ll appeal to The Principle of Interchangeability and begin by considering what happens if all of the relvars concerned are base ones; then I’ll go on to see how the situation changes if some of them are in fact views.
Example 1: A Nonloss Decomposition
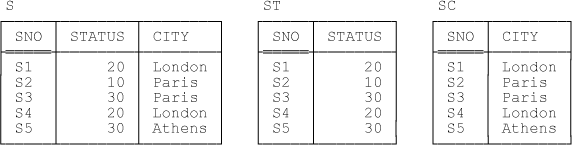
Let’s agree for simplicity to drop attribute SNAME from the suppliers relvar, so that throughout this chapter the name “S” refers to the following reduced form of that relvar:
S { SNO , STATUS , CITY } KEY { SNO }(As you can see, I haven’t just dropped attribute SNAME, I’ve also abbreviated the relvar definition considerably. In particular, I’ve omitted the attribute type specifications, again in the interest of simplicity.)
Now let relvars ST and SC be defined as projections of this relvar. To be specific, let ST be the projection on SNO and STATUS and let SC be the projection on SNO and CITY:
ST { SNO , STATUS } KEY { SNO }
SC { SNO , CITY } KEY { SNO }Observe that these two projections taken together correspond to what in normalization terms we’d call a nonloss decomposition of relvar S—at all times, (a) the current values of relvars ST and SC are equal to the pertinent projections of the current value of relvar S and (b) the current value of relvar S is equal to the join of the current values of relvars ST and SC. As a direct consequence, the two designs, S by itself and the combination of ST and SC, are information equivalent.[68] Note that {SNO} is a key for each of the three relvars, as already indicated. Sample values are shown in Figure 5-1.
Here now are the predicates for ST and SC:
| ST: Supplier SNO is under contract and has status STATUS. |
| SC: Supplier SNO is under contract and is located in city CITY. |
Aside: In accordance with the discussions in Chapter 2, it might be more accurate to say the predicate for relvar ST is “Supplier SNO is under contract and has status STATUS and is located somewhere” (and similarly for relvar SC). In this chapter, however, I prefer to give predicates, most of the time, in slightly simplified or truncated form. The issue isn’t crucial for present purposes. End of aside.
As indicated in the introduction to the chapter, I’ll begin by considering what happens if all three relvars are base ones, living alongside one another as it were. Of course, if they are indeed all base relvars, we’re looking at a database that involves some redundancy once again, and so we’re going to want to control that redundancy accordingly. Here then are the integrity constraints that capture that redundancy (observe that they’re all EQDs—equality dependencies—and together they spell out the specifics of the redundancy and guarantee the information equivalence referred to above):
CONSTRAINT ... ST = S { SNO , STATUS } ;
CONSTRAINT ... SC = S { SNO , CITY } ;
CONSTRAINT ... S = JOIN { ST , SC } ;Note: In connection with the third constraint here (which is, of course, implied by the other two together with the fact that {SNO} is a key for S), I remind you from Chapter 4 that Tutorial D—at least, the version of Tutorial D I’m using in this book—supports both dyadic (infix) and n-adic (prefix) versions of certain relational operators, including join in particular. Thus, for example, the join of ST and SC can be expressed as either ST JOIN SC or (as above) JOIN {ST,SC}. As noted in that previous chapter, I’ll use both styles in this book, whichever best suits my purpose at the time.
The following constraint is also implied by the first two above:
CONSTRAINT ... IDENTICAL { S { SNO } , ST { SNO } , SC { SNO } } ;
And here I should explain that the Tutorial D expression IDENTICAL {r1,…,rn} returns TRUE if and only if the argument relations r1, …, rn are all equal (IDENTICAL can be thought of as a kind of “n-adic equals” operator). Thus, this particular constraint is really the logical AND of three separate equality dependencies:
S { SNO } = ST { SNO } AND
ST { SNO } = SC { SNO } AND
SC { SNO } = S { SNO }What compensatory actions apply? Well, these ones are fairly obvious:
ON DELETEdFROM S : DELETEd{ SNO , STATUS } FROM ST , DELETEd{ SNO , CITY } FROM SC ; ON INSERTiINTO S : INSERTi{ SNO , STATUS } INTO ST , INSERTi{ SNO , CITY } INTO SC ;
These rules take care of updates on S. What about updates on ST and SC? Let’s think about DELETE operations first. Now, the following “double DELETE” certainly seems reasonable:[69]
DELETE ( S1 , 20 ) FROM ST , DELETE ( S1 , London ) FROM SC ;
The effect is to delete the specified tuples from ST and SC and—assuming, not unreasonably, that appropriate cascade delete rules are in effect—also the tuple (S1,20,London) from relvar S. But what about this “single DELETE”?—
DELETE ( S1 , 20 ) FROM ST ;
Now, what can’t be allowed to happen here is for the tuple (S1,20) to be deleted from relvar ST, exactly as requested, while everything else remains unchanged (because such an outcome would clearly violate certain of the constraints specified earlier). So one possibility would be simply to reject the specified DELETE on a Golden Rule violation. On the grounds that it’s surely desirable in general for user requests to succeed if they sensibly can, however, it seems preferable to accept the DELETE and let it cascade appropriately.[70] In other words, I propose the following as an appropriate rule for deletes on ST:
ON DELETEdFROM ST : DELETE ( S MATCHINGd) FROM S ;
Note that cascading a delete on the projection relvar ST to relvar S will cause the rule previously defined for deletes on S to come into play; the net effect will thus be that the original DELETE cascades to the other projection relvar SC as well.
Naturally we need a similar rule for SC:
ON DELETEdFROM SC : DELETE ( S MATCHINGd) FROM S ;
Aside: Of course, if you don’t agree with my position that it’s better for single DELETEs like those above to succeed by having them cascade as indicated—i.e., if you’d rather have such DELETEs simply fail—then I presume you should be able to achieve the effect you want by means of the DBMS’s authorization subsystem. End of aside.
Now what about INSERT operations on those projection relvars? Well, the following “double INSERT” does seem reasonable:
INSERT ( S9 , 20 ) INTO ST , INSERT ( S9 , London ) INTO SC ;
The effect is to insert the specified tuples into ST and SC and—again assuming, not unreasonably, that an appropriate cascade rule is in effect (see below)—also the tuple (S9,20,London) into relvar S. But what about this “single INSERT”?—
INSERT ( S9 , 20 ) INTO ST ;
Now, what can’t be allowed to happen here is for the tuple (S9,20) to be inserted into relvar ST, exactly as requested, while everything else remains unchanged, because such an outcome would clearly violate certain of the constraints specified earlier. What’s more, no cascading makes sense here (contrast the situation with DELETE operations as discussed above)—we can’t make the insertion of tuple (S9,20) into relvar ST cascade to insert some tuple (S9,20,c) into relvar S, precisely because the user who requested the original INSERT hasn’t provided us with that value c that we need to “complete the tuple,” as it were.[71] (By the same token, no cascading of the original INSERT to relvar SC makes sense, either.) So the original INSERT has to fail on a Golden Rule violation, and the only insert rule that seems to make any sense is as follows:
ON INSERTitINTO ST , INSERTicINTO SC : INSERT (itJOINic) INTO S ;
Note in connection with this rule that if the projections of it and ic on SNO aren’t equal, the INSERT overall will fail on, again, a violation of The Golden Rule. As a consequence, the fact that INSERT operations must (among other things) be “double INSERTs” if they’re to succeed is automatically taken care of.
In the interest of clarity, let me now restate the foregoing rule in the following expanded but logically equivalent form (note in particular the introduced names t1 and t2):
ON INSERTitINTO ST , INSERTicINTO SC : WITH (t1:=itJOIN SC ,t2:=icJOIN ST ) : INSERTt1INTO S , INSERTt2INTO S ;
Note carefully here that (as explained in Chapter 4) the original INSERTs into ST and SC are done before the specified compensatory actions—the two INSERTs into S—come into play. Thus, the symbols “ST” and “SC” in those compensatory actions (in the expressions ic JOIN ST and it JOIN SC, respectively) refer to the values of those relvars after the original INSERTs into those relvars have been done.
Aside: As you can see, line 3 of the expanded rule—INSERT t1 INTO S, INSERT t2 INTO S—effectively specifies a double INSERT in which the target in each of the two individual INSERTs is the same (it’s relvar S in both cases). In other words, we have here an example—the first we’ve seen—of a multiple assignment in which two or more of the individual assignments specify the same target variable. What happens in such a situation, loosely speaking, is that the individual assignments are executed in sequence as written (see Appendix A for further explanation). In the particular case at hand, however, we could simplify matters, at least conceptually, by combining the two individual INSERTs into one, thus:
INSERT UNION { t1 , t2 } INTO S ;Note, however, that (again in the particular case at hand) if t1 ≠ t2 we have a Golden Rule violation on our hands anyway. End of aside.
For convenience, let me now summarize the rules as defined so far for INSERTs and DELETEs on ST and SC as a single combined rule (again I use introduced names for clarity):
ON DELETEdtFROM ST , DELETEdcFROM SC , INSERTitINTO ST , INSERTicINTO SC : WITH (t1:=itJOIN SC ,t2:=icJOIN ST ,t3:= S MATCHINGdt,t4:= S MATCHINGdc) : INSERTt1INTO S , INSERTt2INTO S , DELETEt3FROM S , DELETEt4FROM S ;
Let me also restate the rules for INSERTs and DELETEs on S as a single combined rule:
ON DELETEdFROM S , INSERTiINTO S : DELETEd{ SNO , STATUS } FROM ST , DELETEd{ SNO , CITY } FROM SC , INSERTi{ SNO , STATUS } INTO ST , INSERTi{ SNO , CITY } INTO SC ;
Aside: Again we have a situation—actually it arises in connection with both of the foregoing combined rules—in which two or more of the individual assignments within some multiple assignment specify the same target variable. But it’s easy to see that the sequence in which those individual assignments are executed makes no difference to the overall outcome anyway, in these particular cases. Again, see Appendix A for further explanation. End of aside.
Now let’s think about explicit UPDATE operations. First, I’ll leave it as an exercise to show that explicit UPDATEs on relvar S all work as you would intuitively expect. (To convince yourself of this fact, you might like to consider the following examples:
UPDATE S WHERE SNO = 'S1' : { CITY := 'Paris' } ;
UPDATE S WHERE SNO = 'S1' : { SNO := 'S9' } ;Note in particular that the second of these examples is a “key UPDATE.”)
But what about UPDATEs on ST and SC? By way of example, consider the following UPDATE request on ST:
UPDATE ST WHERE SNO = 'S1' : { STATUS := 10 } ;Given our usual sample values, what happens here is as follows:
First, the requested update is done—i.e., the tuple (S1,20) is deleted from relvar ST and the tuple (S1,10) is inserted into relvar ST.
Second, the compensatory actions are performed—i.e., the tuple (S1,20,London) is deleted from relvar S, thanks to the cascade delete rule from ST to S, and the tuple (S1,10,London) is inserted into relvar S, thanks to the cascade insert rule from ST to S. Note: Observe that dc and ic are both empty in this example. As a consequence, the symbol “SC” in the expression it JOIN SC, in the rule for INSERTs on ST and SC, effectively denotes the value of relvar SC as it was before any updating is done, and that expression therefore yields the desired S tuple (S1,10,London).
So this UPDATE works just fine. But what about the following “key UPDATE”?—
UPDATE ST WHERE SNO = 'S1' : { SNO := 'S9' } ;Well, it’s easy to see here that this UPDATE unfortunately fails (to be specific, it fails on a Golden Rule violation). As in the case of the suppliers and shipments example in the previous chapter, in fact, it seems to me that here there’s no alternative to writing out the necessary multiple assignment explicitly, thus:
UPDATE ST WHERE SNO = 'S1' : { SNO := 'S9' } ,
UPDATE SC WHERE SNO = 'S1' : { SNO := 'S9' } ;This “double UPDATE” succeeds, as you can easily confirm.
So: Despite this latter minor annoyance, it’s still the case that (a) the two designs, S by itself and the combination of ST and SC, are information equivalent, and hence that (b) for every update on one, there’s a logically equivalent update on the other that has the same overall effect. So far, so good.
Example 1 Continued: The Projection Relvars
Let’s continue to assume that relvars S, ST, and SC are all base relvars (still no views yet). Now consider a user who sees just the projection relvars ST and SC. That user:
Knows the corresponding predicates:
ST: Supplier SNO is under contract and has status STATUS.
SC: Supplier SNO is under contract and is located in city CITY.
Is aware of all pertinent type information,[72] is aware of the fact that {SNO} is a key for each of these relvars, and is aware of the following constraint:
CONSTRAINT ... ST { SNO } = SC { SNO } ;(This is the only constraint from the previous section that makes no mention of relvar S.)
Is aware of the following compensatory actions:
ON DELETE
dtFROM ST , DELETEdcFROM SC , INSERTitINTO ST , INSERTicINTO SC : WITH (t1:=itJOIN SC ,t2:=icJOIN ST ,t3:= SC MATCHINGdt,t4:= ST MATCHINGdc) : INSERTt1{ SNO , STATUS } INTO ST , INSERTt2{ SNO , CITY } INTO SC , DELETEt3FROM SC , DELETEt4FROM ST ;(This rule might look a little complicated, but it’s basically just an edited version of the rule for DELETEs and INSERTs on ST and SC from the previous section, revised primarily to replace references to S by references to ST and/or SC, as appropriate.)
Given all of the above, I’ll leave it as an exercise to show that, from this user’s perspective, all updates on ST and/or SC work exactly as described in the previous section.
Information Hiding
Now what about a user who sees only (say) relvar ST? Well, such a user knows the predicate (see above) and knows also that {SNO} is a key for that relvar, but of course isn’t aware of any constraints that mention either SC or S. Perhaps more to the point, that user isn’t aware of any compensatory actions, either. Clearly, then, that user can’t be allowed to insert tuples into relvar ST, nor to update supplier numbers within that relvar, because such operations have the potential to violate constraints of which this user is, and must be, unaware. (Note too that updating ST to change a supplier’s status implicitly requires relvar SC to exist, even if that relvar is hidden from the user. Thus, if ST is defined and SC is not—in particular, if ST is defined without SC purely for security reasons—then such updates will have to be prohibited also.)
Example 1 Continued: Views
In Chapter 4, I showed it made essentially no difference if some or all of the relvars under discussion were views instead of base relvars, just so long as information equivalence was preserved. And as I’m sure you’ve been expecting, the message here is the same, viz.: Everything I’ve said in this chapter so far applies pretty much unchanged if some or all of the relvars concerned are views. To be specific, suppose now that S is a base relvar and ST and SC are views. Then:
The constraints specified by the various CONSTRAINT statements in the section before last will all be enforced automatically, precisely because ST and SC are views of S.
The compensatory actions from S to ST and SC will also happen automatically, again because ST and SC are views of S; that is, updates to S will automatically be reflected appropriately in ST or SC or both.
The compensatory actions from ST and SC to S—these are the ones that are generally thought of as the view updating rules as such—will also happen automatically, again precisely because ST and SC are views of S. That is, updates to ST or SC are “really” updates to the underlying relvar S, and so will automatically be visible in S, as well as in ST or SC or both.
A user who sees only views ST and SC can behave in all respects exactly as if those views were base relvars—in fact, exactly as described in the previous section for the case in which they actually were base relvars. To spell out the details, that user knows that (a) DELETEs on either relvar cascade to the other; (b) INSERTs and key UPDATEs must be “double updates”; (c) other UPDATEs behave normally; and (d) explicit assignments must be logically equivalent to some sensible combination of the foregoing.
By contrast, a user who sees, say, only view ST will clearly be limited in the operations he or she is allowed to perform—again just like a user who sees only base relvar ST, when all three relvars are base ones (again as described in the previous section). To be specific, such a user won’t be allowed to insert tuples into that relvar or to update supplier numbers within that relvar (and possibly not to change STATUS values, either).
Example 2: Another Nonloss Decomposition
Now I want to consider a revised version—in a way, a generalized version—of Example 1. Again I’ll start with relvar S. This time, however, I’ll add a constraint to the effect that the functional dependency (FD)
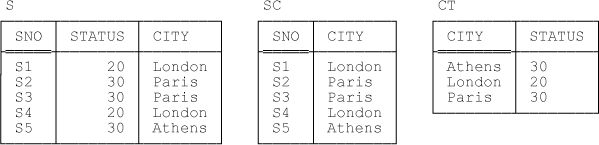
{ CITY } → { STATUS }holds in that relvar; in other words, whenever two suppliers have the same city, they also have the same status.[73] (In order to bring our usual sample values into line with this new constraint, let’s temporarily change the status of supplier S2 from 10 to 30.) Now suppose we define two projection relvars—SC, the projection of S on SNO and CITY (as in Example 1), and CT, the projection of S on CITY and STATUS:
SC { SNO , CITY } KEY { SNO }
CT { CITY , STATUS } KEY { CITY }Observe that, as with Example 1, these two projections taken together correspond to a nonloss decomposition of relvar S—at all times, (a) the values of SC and CT are equal to the pertinent projections of the value of S and (b) the value of S is equal to the value of the expression SC JOIN CT. Thus, the two designs, S by itself and the combination of SC and CT, are information equivalent.[74] The sole keys for these relvars are {SNO} for SC and {CITY} for CT. Sample values are shown in Figure 5-2.
Here now are the predicates for SC and CT:
| SC: Supplier SNO is under contract and is located in city CITY. |
| CT: City CITY has status STATUS.[75] |
As usual, first let’s see what happens if all three relvars are base ones. The following constraints clearly hold:
CONSTRAINT ... SC = S { SNO , CITY } ;
CONSTRAINT ... CT = S { CITY , STATUS } ;
CONSTRAINT ... S = JOIN { SC , CT } ;
CONSTRAINT ... IDENTICAL { S { SNO } , SC { SNO } } ;
CONSTRAINT ... IDENTICAL { S { CITY } , SC { CITY } , CT { CITY } } ;As for updates, INSERTs and DELETEs on S certainly cascade to SC appropriately:
ON INSERTiINTO S : INSERTi{ SNO , CITY } INTO SC ; ON DELETEdFROM S : DELETEd{ SNO , CITY } FROM SC ;
But what about cascades to CT? Well, INSERTs are straightforward:
ON INSERTiINTO S : INSERTi{ CITY , STATUS } INTO CT ;
(I remind you once again that an attempt to insert a tuple that already exists is effectively a “no op.”) However, DELETEs are a little more complicated:
ON DELETEdFROM S : DELETE ( ( CT MATCHINGd) NOT MATCHING S ) FROM CT ;
Explanation: Let r denote the relation represented by the subexpression CT MATCHING d. Then, assuming sample values as given in Figure 5-2:
Suppose we delete (S5,30,Athens) from S; S now contains just the tuples for S1, S2, S3, and S4. Then (a) r contains just the single tuple (30,Athens); (b) the expression r NOT MATCHING S thus reduces to just r (since the only tuple that included (30,Athens) as a subtuple has just been deleted from S); hence, (c) the tuple (30,Athens) is deleted from CT.
Aside: Note that to say that, e.g., (30,Athens) is a subtuple of the tuple (S5,30,Athens) is to say the former is a projection of the latter. More generally, if t is a supplier tuple, then the projection t{SNO,CITY} of t on attributes SNO and CITY is that subtuple of t that contains just the SNO and CITY components from t. In other words, we can (and Tutorial D does) conveniently define a version of—i.e., we can “overload”—the well known relational projection operator to apply to tuples as well as to relations. Refer to SQL and Relational Theory for further discussion. End of aside.
By contrast, suppose we delete (S1,20,London) from S; S now contains just the tuples for S2, S3, S4, and S5. Then (a) r contains just the single tuple (20,London); (b) the expression r NOT MATCHING S thus evaluates to an empty relation (since S still has a tuple—viz., that for supplier S4—that includes (20,London) as a subtuple); hence, (c) nothing is deleted from CT (in particular, the tuple (20,London) is not deleted), and CT thus remains unchanged.
Also, I observe without detailed discussion that given the foregoing compensatory actions, explicit UPDATEs on S all work exactly as expected, as you might like to confirm for yourself. Note in particular that updates that attempt to infringe the FD {CITY} → {STATUS} will fail on a Golden Rule violation.
Now what about updates on SC and CT? Well, again let’s consider some examples (all based, of course, on the sample values in Figure 5-2). First relvar SC:
Suppose we delete (S1,London) from SC; then it seems reasonable (a) to delete (S1,20,London) from S and (b) to do nothing to CT (since there’s another supplier, S4, with status 20 and city London). By contrast, suppose we delete (S5,Athens) from SC; then it seems reasonable (a) to delete (S5,30,Athens) from S and (b) to delete (30,Athens) from CT as well. Note: When I say these actions seem reasonable, what I mean, of course, is that they achieve the desired effect, and they do so without either violating The Golden Rule or requiring the user to write an explicit multiple assignment.
Suppose we insert (S9,London) into SC. This update succeeds (it has the effect of inserting (S9,20,London) into S). By contrast, suppose we try to insert (S9,Rome) into SC; this update fails, because there’s no tuple with city Rome in CT.[76]
Suppose we try to insert (Rome,20) into CT. Assuming no “simultaneous” update has been requested on SC (and hence, effectively, on S—see 4. below), the result can only be a Golden Rule violation, and the attempt must therefore fail.
Suppose we try to insert (London,40) into CT. This attempt also fails on a Golden Rule violation (a key constraint violation, in fact).
Suppose we delete (London,20) from CT. Then it seems reasonable (a) to delete (S1,20,London) and (S4,20,London) from S and (b) to delete (S1,London) and (S4,London) from SC.[77]
Suppose we insert (S9,Rome) into SC and (Rome,20) into CT, “simultaneously.” This update succeeds (it has the effect of inserting (S9,20,Rome) into S).
Considerations such as the foregoing suggest the following rules:
ON DELETE
dcFROM SC , DELETEdtFROM CT : DELETE ( S MATCHINGdc) FROM S , DELETE ( S MATCHINGdt) FROM S ; ON INSERTicINTO SC , INSERTitINTO CT : INSERT (icJOIN CT ) INTO S ;
Note: This latter rule could in fact be simplified to the following without loss (why, exactly?):
ON INSERTiINTO SC : INSERT (iJOIN CT ) INTO S ;
Given these rules, the foregoing INSERT and DELETE examples all work as described, and as intuitively expected. Also, I observe without detailed discussion that explicit UPDATEs work as expected as well (exercise for the reader). As with Example 1, therefore, the situation is that (a) the two designs, S by itself and the combination of SC and CT, are information equivalent, and hence that (b) for every update on one, there’s a logically equivalent update on the other that has the same overall effect.
Aside: Now I can take care of a small piece of unfinished business from earlier chapters, having to do with view LS (“London suppliers”). In those chapters, I said that in practice we would probably drop attribute CITY from that relvar. In fact, we can and probably should decompose that relvar into its projections (a) SNT, on SNO, SNAME, and STATUS, and (b) C, on CITY. (Of course, this latter projection has just one tuple, containing the single value London.) As explained in Database Design and Relational Theory, the FD {} → {CITY} holds in relvar LS;[78] thus, Heath’s Theorem, mentioned in a footnote earlier in this chapter, guarantees that the decomposition is nonloss. So relvar SNT can be updated in accordance with these rules:
ON INSERTiINTO SNT : INSERT (iJOIN C ) INTO LS ; ON DELETEdFROM SNT : DELETE (dMATCHING C ) FROM LS ;(assuming, of course, that relvar LS is updatable in turn). Note: I’ll leave consideration of updates on relvar C here as an exercise for you. End of aside.
Now, for completeness I do plan to round out my discussion of Example 2, as I did with Example 1, by (a) considering relvars SC and CT independently of relvar S; (b) considering what happens if the user sees just one of those two relvars (i.e., if part of the total picture is hidden); and (c) considering what happens if SC and CT are actually views. However, I think it’s only fair to say up front that there aren’t going to be any surprises in those discussions; indeed, I think it would be surprising if there were any surprises. In fact, let me draw your attention to a more important point: namely that, as you might have already realized, the update rules I’ve given for Example 2 are essentially identical to their counterparts for Example 1—or, to state the matter a little more precisely, the rules for Example 1 are a degenerate special case of those for Example 2. What’s more, this state of affairs is only to be expected, given that the situation illustrated by Example 1 is a degenerate special case of that illustrated by Example 2. (Recall that Example 1 also involved a nonloss decomposition of relvar S, albeit into different projections.)
The Projection Relvars
So let’s continue to assume that relvars S, SC, and CT are all base relvars (still no views yet). Now consider a user who sees just the projection relvars SC and CT (and I observe again that the design consisting of those two relvars together is information equivalent to the design consisting of relvar S by itself). That user:
Knows the corresponding predicates:
SC: Supplier SNO is under contract and is located in city CITY.
CT: City CITY has status STATUS.
Is aware that {SNO} is a key for SC, {CITY} is a key for CT, and is aware also of the following constraint:
CONSTRAINT ... IDENTICAL { SC { CITY } , CT { CITY } } ;Is aware of the following compensatory actions:
ON DELETE
dcFROM SC , DELETEdtFROM CT : DELETE ( SC MATCHINGdt) FROM SC , DELETE ( CT MATCHINGdc) NOT MATCHING SC ) FROM CT ;
Given all of the above, I’ll leave it as an exercise to show that from this user’s perspective, all updates on SC and/or CT work as intuitively expected.
Information Hiding
What about a user who sees only (say) relvar SC? Well, such a user knows the predicate (see above) and knows also that {SNO} is a key for that relvar, but of course isn’t aware of any constraints that mention either CT or S. Perhaps more to the point, that user isn’t aware of any compensatory actions, either. As a consequence, that user can’t be allowed to perform either INSERTs or UPDATEs if the CITY values in the new or updated tuples don’t already exist in the relvar. As for a user who sees only relvar CT, that user can’t be allowed to do INSERTs, nor UPDATEs on CITY values. And yet again the reason for these limitations is, of course, that the user is seeing only part of the picture (information equivalence no longer applies).
Views
Finally, everything I’ve said in this chapter so far applies effectively unchanged if some or all of the relvars concerned are views. To be specific, suppose now that S is a base relvar and SC and CT are views. Then:
The constraints specified by the various CONSTRAINT statements given earlier in the section will all be enforced automatically, precisely because SC and CT are views of S.
The compensatory actions from S to SC and CT will also happen automatically, again because SC and CT are views of S; that is, updates to S will automatically be reflected appropriately in SC or CT or both.
The compensatory actions from SC and CT to S—these are the ones that are generally thought of as the view updating rules as such—will also happen automatically, again precisely because SC and CT are views of S. That is, updates to SC or CT are “really” updates to the underlying relvar S, and so will automatically be visible in S, as well as in SC or CT or both.
A user who sees only views SC and CT can behave in all respects exactly as if those views were base relvars—in fact, exactly as described above for the case in which they actually were base relvars.
By contrast, a user who sees, say, only view SC will clearly be limited in the operations he or she is allowed to perform—just like a user who sees only base relvar SC, when all three relvars are base ones (again as described above).
Example 3: A Lossy Decomposition
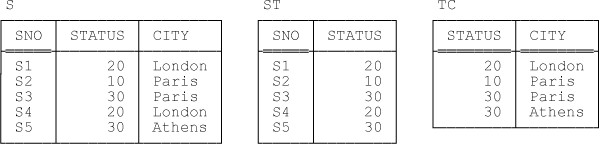
Now I want to change the example one final time (this is the last example I’ll be discussing in this chapter). As usual I’ll start with relvar S, but now I’ll assume (in contrast to Example 2) that the functional dependency {CITY} → {STATUS} does not hold. Now let’s define two projection relvars—ST, the projection on SNO and STATUS, and TC, the projection on STATUS and CITY:
ST { SNO , STATUS } KEY { SNO }
TC { STATUS , CITY } KEY { STATUS , CITY }Note: Relvar ST is exactly as it was in Example 1. Relvar TC, by contrast, though it has the same heading as relvar CT in Example 2, has different semantics (as is reflected by the fact that it has a different key); for that reason, I’ve given it a different name in order—I hope—to reduce confusion. Sample values are shown in Figure 5-3. Observe that I’ve changed the status of supplier S2 back to 10, since the FD {CITY} → {STATUS} no longer holds.
As indicated, the sole keys for these relvars are {SNO} for ST and {STATUS,CITY} (the entire heading) for TC. Note that, in contrast to Examples 1 and 2, relvars ST and TC together correspond to a lossy, not a nonloss, decomposition of relvar S. In other words, S isn’t equal to the join of ST and TC,[79] and the two designs—S by itself and the combination of ST and TC—are thus not information equivalent (to be specific, information regarding which suppliers are in which cities is lost in the latter design).
Be that as it may, let’s begin as usual by assuming that all three relvars are base ones. Here then are the predicates for ST and TC:
| ST: Supplier SNO is under contract and has status STATUS. |
| TC: Some supplier is under contract and has status STATUS and is located in city CITY. |
Aside: Here, mainly just to stress the fact that the decomposition of relvar S of which relvar TC is a part is lossy, I depart from my usual practice in this chapter and give the predicate for that relvar in quantified form (“Some supplier …”). End of aside.
The following constraints clearly hold:
CONSTRAINT ... ST = S { SNO , STATUS } ;
CONSTRAINT ... TC = S { STATUS , CITY } ;
CONSTRAINT ... S { SNO } = ST { SNO } ;
CONSTRAINT ... ST { STATUS } = TC { STATUS } ;Next, an analysis essentially similar to the one we went through for Example 2—I’ll leave the details to you—shows that the rules for updates on S are as follows:
ON INSERTiINTO S : INSERTi{ SNO , STATUS } INTO ST , INSERTi{ STATUS , CITY } INTO TC ; ON DELETEdFROM S : DELETEd{ SNO , STATUS } FROM ST , DELETE ( ( TC MATCHINGd) NOT MATCHING S ) FROM TC ;
But what about updates on ST and TC? Well, again let’s consider some examples:
Suppose we delete (S1,20) from ST; then it seems reasonable (a) to delete (S1,20,London) from S and (b) to do nothing to TC (since there’s another supplier, S4, with status 20 and city London). By contrast, suppose we delete (S2,10) from ST; then it seems reasonable (a) to delete (S2,10,Paris) from S and (b) to delete (10,Paris) from TC as well.
Suppose we try to insert (S9,20) into ST. Given our usual sample values, this update succeeds (it has the effect of inserting (S9,20,London) into S). By contrast, suppose we try to insert (S9,30) into ST; then this update fails on a key constraint violation on relvar S (because it attempts to insert two distinct tuples for supplier S9 into that relvar). Likewise, if we try to insert (S9,40) into ST, the update fails, this time because there’s no tuple with status 40 in TC.
Suppose we try to delete some existing tuple from, or insert some new tuple into, TC. Assuming no “simultaneous” update has been requested on ST (and hence, effectively, on S—see 4. below), the result can only be a Golden Rule violation, and the attempt must therefore fail.
Suppose we insert (S9,40) into ST and (40,Rome) into TC, “simultaneously.” That update succeeds (it has the effect of inserting (S9,40,Rome) into S). Likewise, suppose we delete (S2,10) from ST and (10,Paris) from TC “simultaneously.” Again this update succeeds (it has the effect of deleting (S2,10,Paris) from S); however, it seems to reasonable in this case to say the DELETE on TC should happen anyway, regardless of whether we request it explicitly (see 1. above).
Considerations such as the foregoing suggest the following rules:
ON DELETEdFROM ST : DELETE ( S MATCHINGd) FROM S ; ON INSERTiINTO ST : INSERT (iJOIN TC ) INTO S ;
Given these rules, the foregoing INSERT and DELETE examples all work as described. Explicit UPDATE operations are another matter, however. In fact, it seems that most such operations, on either ST or TC, will either fail or have undesirable side effects. By way of example, you might like to consider what happens if we try to update ST, changing the status for supplier S2 to (a) 40, (b) 20, (c) 30, or changing the supplier number for supplier S1 to S9. (Analogs of all of these updates can certainly be done on relvar S, of course.) And the reason for this state of affairs is, of course, that the two designs—S by itself and the combination of ST and TC—aren’t information equivalent; to be specific (and to repeat), the fact that a given supplier is in a given city can be represented in the former design but not, in general, in the latter. Thus, while such explicit UPDATE operations can certainly be requested, they probably shouldn’t be.
Now, once again I’ll complete my investigation into the example overall by (a) considering the projection relvars independently of relvar S, (b) considering what happens if the user sees just one of those projection relvars, and (c) considering what happens if those relvars are views—but again I don’t think you’ll find any surprises in those discussions. What you might find a little surprising, however, is that the update rules I’ve given for the example overall are extremely similar, if not quite identical, to the rules I gave earlier for Examples 1 and 2. (To repeat, they’re similar, but—speaking very loosely—updates are more likely to fail in the case of Example 3 than they are in the case of Examples 1 and 2.) It seems to me, therefore, that examples like the ones discussed in this chapter should suffice as a basis on which to define a set of rules for updating projections in general.
The Projection Relvars
Consider a user who sees just the projection relvars ST and TC. That user:
Knows the corresponding predicates:
ST: Supplier SNO is under contract and has status STATUS.
TC: Some supplier is under contract and has status STATUS and is located in city CITY.
Is aware that {SNO} is a key for relvar ST and that TC is “all key,” and is aware also of the following constraint:
CONSTRAINT ... ST { STATUS } = TC { STATUS } ;Is aware that updates on TC always fail (absent an appropriate “simultaneous” update on relvar ST) and that DELETEs on ST are subject to the following rule:
ON DELETEdFROM ST : DELETE ( ( TC MATCHINGd) NOT MATCHING ST ) FROM TC ;
Note that there’s no rule for INSERTs on ST. In fact, such operations will fail unless both of the following are true: (a) the SNO value in each new tuple doesn’t currently occur in ST, and (b) the STATUS value in each new tuple does currently occur in TC, but only once. As for explicit UPDATEs, the remarks in the second to last paragraph in the previous subsection apply.
Information Hiding
Of course, Example 3 already involves information hiding, since we don’t have information equivalence in the first place. But we can hide even more (as it were) by presenting a user with just one of the two projection relvars, either ST or TC, in isolation. What operations can the user perform in such a situation? Well, in the case of ST, DELETEs make sense, but nothing else does; in the case of TC, no updates make sense at all.
Views
Finally, everything I’ve said in this section so far applies essentially unchanged if some or all of the relvars concerned are views. To be specific, suppose now that S is a base relvar and ST and TC are views. Then:
The constraints specified by the various CONSTRAINT statements given earlier in this section will all be enforced automatically, precisely because ST and TC are views of S.
The compensatory actions from S to ST and TC will happen automatically, precisely because ST and TC are views of S; that is, updates to S will automatically be reflected appropriately in ST or TC or both.
The compensatory actions from ST and TC to S—these are the ones that are generally thought of as the view updating rules as such—will also happen automatically, again precisely because ST and TC are views of S.[80] That is, updates to ST and/or TC are “really” updates to the underlying relvar S, and so are automatically visible in S, as well as in ST or TC or both.
A user who sees only views ST and TC can behave exactly as if those views were base relvars (to the extent described previously, that is, no more and no less, for the case in which they actually were base relvars).
Note: There’s a point here you might find a trifle odd, however, regarding explicit UPDATE operations in particular. I’ve said that attempts to change a supplier’s status in relvar ST will either fail or have undesirable side effects (in general), and hence that such operations probably shouldn’t be requested in the first place. Under the conventional approach to view updating, however (such as it is), such operations don’t seem to be problematic at all; that is, they seem to work as intuitively expected. But that’s because the conventional approach tacitly assumes information equivalence. That is, in the case at hand, the conventional approach effectively assumes we’re dealing with a design consisting of relvars ST and SC (as in Example 1, earlier in the chapter), not a design consisting of relvars ST and TC as in the present discussion. In Example 1, as you’ll recall, attempts to change a supplier’s status in relvar ST worked just fine.
By contrast, a user who sees just view ST or just view TC will clearly be limited in the operations he or she is allowed to perform—again exactly as previously described in the present section.
Concluding Remarks
There are two final remarks I want to make. First, I haven’t said quite all I want to say about updating projection views as such—I’ll come back to the topic briefly in Chapter 7, in the section Projection Views Revisited Second, I’d like to clarify something I ought perhaps to have clarified much earlier … In Chapter 1, I claimed that all views are updatable; in this chapter, by contrast, I’ve said that certain updates on certain views don’t work after all. As an extreme case in point, view TC—defined as the projection of relvar S on STATUS and CITY, in the case where the functional dependency {CITY} → {STATUS} doesn’t hold—can’t sensibly be updated at all. So am I talking out of both sides of my mouth here? What exactly is going on?
Well, I did also say in Chapter 1 that I would elaborate later on “this very strong claim” (the claim, that is, that all views are updatable). The point is this: It’s not that certain views are intrinsically nonupdatable. Rather, it’s that certain updates on certain views fail because, if they—the updates, that is—were accepted, they would cause some integrity constraint to be violated (and no compensatory actions are in place to prevent such violations from occurring.) Note that this state of affairs exactly parallels the situation with base relvars: Certain updates on certain base relvars fail too, not because the relvar in question is intrinsically nonupdatable, but because some integrity constraint would otherwise be violated. Inserting a tuple for a nonexistent supplier into the shipments relvar SP is a case in point.
[68] The general statement is this: Consider two databases, DB1 and DB2, such that DB1 contains only a single relvar R and DB2 contains only projections of R. Then, in order for DB1 and DB2 to be information equivalent, it’s necessary and sufficient that (a) the projections in DB2 be, precisely, the projections obtained by decomposing R in accordance with some join dependency (JD) that holds in R and (b) each relvar in DB2 is constrained to be equal at all times to the pertinent projection of the current value of R. See Database Design and Relational Theory for more background on such matters.
[69] This example is the first we’ve seen to illustrate a kind of pseudocode syntax I’ll be making frequent use of from this point forward. I hope it’s self-explanatory. Just to spell the details out, however, the expression (S1,20) in the example ought strictly to be the relation selector invocation RELATION {TUPLE {SNO ‘S1’, STATUS 20}}, and the expression (S1,London) ought strictly to be the relation selector invocation RELATION {TUPLE {SNO ‘S1’, CITY ‘London’}}.
[70] It’s relevant to mention that such a cascade would certainly occur in today’s DBMSs if ST and SC were in fact views of relvar S instead of separate base relvars.
[71] If anyone dares mention “nulls” at this point, I’m afraid I’ll have to ask them to go and wash their mouth out with soap.
[72] I won’t bother to keep saying this—you can just take it as true, wherever applicable, for all subsequent examples in the book.
[73] FDs are discussed in depth in Database Design and Relational Theory. Here I just note that if K is a key for relvar R, then the FD K → X holds in R for all subsets X of the heading of R, and Example 1 thus implicitly involved certain FDs already.
[74] I said earlier that database DB1 (containing only a single relvar R) and database DB2 (containing only projections of R) are information equivalent only if the projections in DB2 are obtained by decomposing R in accordance with some JD that holds in R—but the example under discussion (Example 2) involves FDs, not JDs. However, there’s a theorem (Heath’s Theorem) to the effect that if the union of A, B, and C is equal to the heading of R and the FD A → B holds in R, then a JD with components AB (= the union of A and B) and AC (= the union of A and C) also holds in R.
[75] Cities thus become “entities in their own right” in this design.
[76] You might feel that INSERTs on SC thus succeed or fail unpredictably depending on the current state of the database and should therefore be rejected out of hand. But when they do fail, at least they do so because they violate some constraint of which the user is explicitly aware. In fact, such failures aren’t really different in kind from failures arising from, e.g., conventional key constraint violations (which also occur, when they do, on account of the current state of the database).
[77] If you feel a trifle uncomfortable with the idea that deletes on CT cascade to S, recall that cities are now “entities in their own right.” You might also care to reflect on the notion that deletes on S cascade to SP (the cases are essentially similar).
[78] Implying, incidentally, that LS isn’t even in second normal form (2NF).
[79] That’s because ST and TC aren’t obtained from S in accordance with any JD that holds in S. Once again, see Database Design and Relational Theory for further explanation.
[80] Actually there aren’t any compensatory actions for relvar TC, but of course that fact doesn’t invalidate the general point being made here.