Chapter 8. Join Views III: One to Many Joins
What Codd hath joined
Update such without blunder
—
Chapters Chapter 6 and Chapter 7 discussed one to one and many to many joins, respectively; this chapter is concerned with the sole remaining case, one to many joins. But of course you know by now where our investigations are going to take us—we’re going to wind up with the same general rules as we did in the previous two chapters:
ON INSERT INTOV: INSERTA(sub)tuples if they don't already exist, INSERTB(sub)tuples if they don't already exist ON DELETE FROMV: DELETEA(sub)tuples if they don't exist elsewhere, DELETEB(sub)tuples if they don't exist elsewhere
Example 1: Information Equivalence
Once again I’ll start with our usual suppliers-and-parts database, but I want to focus in this chapter on relvars S and SP and ignore relvar P (I’ll also continue to ignore attribute SNAME and, for simplicity, attribute STATUS as well). So we have two base relvars looking like this:
S { SNO , CITY } KEY { SNO }
SP { SNO , PNO , QTY } KEY { SNO , PNO }Moreover, suppose for the sake of this first example that every supplier has to supply at least one part. In other words, suppose there’s a constraint in effect (actually an equality dependency once again) that looks like this:
CONSTRAINT ... S { SNO } = SP { SNO } ;In order to conform to this requirement, let’s also agree for the sake of the example to drop the tuple for supplier S5 from our usual suppliers relation.
Now let’s define the join of relvars S and SP as a view SSP:
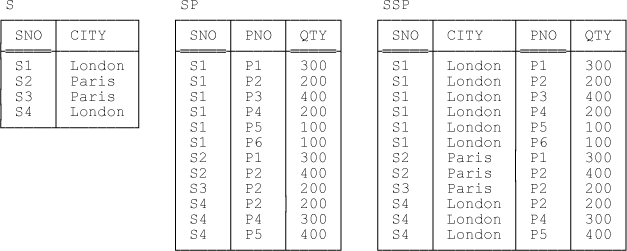
SSP { SNO , CITY , PNO , QTY } KEY { SNO , PNO }Observe that the join here is indeed one to many, in the sense that every tuple in S joins to many tuples in SP (at least one) and every tuple in SP joins to exactly one tuple in S. The two designs—that consisting of just relvar SSP and that consisting of the combination of relvars S and SP—are clearly information equivalent. Sample values are shown in Figure 8-1.
Here now are the predicates:
| S: Supplier SNO has city CITY. |
| SP: Supplier SNO supplies part PNO in quantity QTY. |
| SSP: Supplier SNO has city CITY and supplies part PNO in quantity QTY. |
As usual, I’ll begin by considering what happens if all three relvars are base ones. If they are, what constraints hold? Well, first of all, relvars S, SP, and SSP have {SNO}, {SNO,PNO}, and {SNO,PNO} again, respectively, as their sole key (as already indicated). Second, we also clearly have:
CONSTRAINT ... SSP = S JOIN SP ;
CONSTRAINT ... S = SSP { SNO , CITY } ;
CONSTRAINT ... SP = SSP { SNO , PNO , QTY } ;These constraints are all equality dependencies (EQDs), and together they guarantee the information equivalence referred to above. In fact, we can regard the combination of S and SP as a nonloss decomposition of SSP, because the following functional dependency (FD)—
{ SNO } → { CITY }—holds in that latter relvar (i.e., SSP).[97] It follows that the example overall is essentially similar to Example 2 in Chapter 5. For that reason, I won’t go through a detailed analysis in order to come up with the pertinent compensatory actions. Instead, I’ll simply present them here as a fait accompli, as it were:
ON INSERTisINTO S , INSERTispINTO SP : INSERT (isJOIN SP ) INTO SSP , INSERT ( S JOINisp) INTO SSP ; ON DELETEdsFROM S , DELETEdspFROM SP : DELETE ( SSP MATCHINGds) FROM SSP , DELETE ( SSP MATCHINGdsp) FROM SSP ; ON INSERTiINTO SSP : INSERTi{ SNO , PNO , QTY } INTO SP , INSERTi{ SNO , CITY } INTO S ; ON DELETEdFROM SSP : DELETE ( SP MATCHINGd) FROM SP , DELETE ( ( S MATCHINGd) NOT MATCHING SSP ) FROM S ;
Let’s consider some examples, using the sample values from Figure 8-1. Note: Given that our ultimate objective is to study the case in which relvars S and SP are base ones and relvar SSP is a view, I’ll concentrate first on updates on relvar SSP specifically.
Suppose we delete the tuple (S1,London,P1,300) from relvar SSP. The effect will be to delete the tuple (S1,P1,300) from relvar SP and (because relvar SSP still has some tuples for supplier S1 remaining after the original delete) to leave relvar S unchanged.
Suppose we delete the tuple (S3,Paris,P2,400) from relvar SSP. The effect will be to delete the tuple (S3,P2,400) from relvar SP and (because relvar SSP has no tuples for supplier S3 remaining after the original delete) also to delete the tuple (S3,Paris) from relvar S. Note: I remind you that we’re assuming for the sake of the example that every supplier does supply at least one part.
Suppose we insert the tuple (S2,Paris,P3,500) into relvar SSP. The effect will be to insert the tuple (S2,P3,500) into relvar SP and to leave relvar S unchanged.
Suppose we insert the tuple (S5,Athens,P3,500) into relvar SSP. The effect will be to insert the tuple (S5,P3,500) into relvar SP and also to insert the tuple (S5,Athens) into relvar S.
Without going into details, I claim also that explicit UPDATEs on SSP (a) to change the supplier number, part number, or quantity for some shipment, or (b) to change the city for some supplier, or even (c) to change the supplier number for some supplier, all work as intuitively expected.
Turning now to updates on relvars S and SP:
Suppose we delete the tuple (S1,P1,300) from relvar SP. The effect will be to delete the tuple (S1,London,P1,300) from relvar SSP and (because relvar SSP still has some tuples for supplier S1 remaining after the original delete) to leave relvar S unchanged.
Suppose we delete all tuples for supplier S1 from relvar SP. The effect will be to delete all tuples for supplier S1 from relvar SSP and also to delete the tuple (S1,20) from relvar S.
Suppose we insert the tuple (S2,P3,500) into relvar SP. The effect will be to insert the tuple (S2,Paris,P3,500) into relvar SSP.
Suppose we attempt to insert the tuple (S5,P3,500) into relvar SP. Absent an appropriate simultaneous insert into relvar S, this insert will fail.
Suppose we attempt to insert the tuple (S5,Athens) into relvar S. Absent an appropriate simultaneous insert into relvar SP, this insert will fail.
Suppose we delete the tuple (S1,20) from relvar S. The effect will be to delete all tuples for supplier S1 from relvar SSP. Of course, the rule governing deletes on SSP will now come into play, which will (not unreasonably) have the effect of deleting all tuples for supplier S1 from relvar SP as well.
As for explicit UPDATEs, I’ll leave it as an exercise to show that (a) as certain discussions in Chapter 4 should have led us to expect, if we want to change the supplier number of some supplier, then there’s no real alternative to writing out the necessary double UPDATE explicitly, as in this example—
UPDATE S WHERE SNO = 'S1' : { SNO := 'S9' } ,
UPDATE SP WHERE SNO = 'S1' : { SNO := 'S9' } ;—but (b) other explicit UPDATEs all work satisfactorily.
Finally, let me state for the record that the foregoing rules, as they apply to updates on relvar SSP in particular, are essentially identical to the rules I gave for updating joins in Chapters Chapter 6 and Chapter 7. For that reason, I won’t bother to go into details on what happens if (a) the user sees just that relvar SSP or (b) that relvar SSP is a view and S and SP are base relvars. Suffice it to say that, once again, everything works satisfactorily.
Example 2: Information Hiding
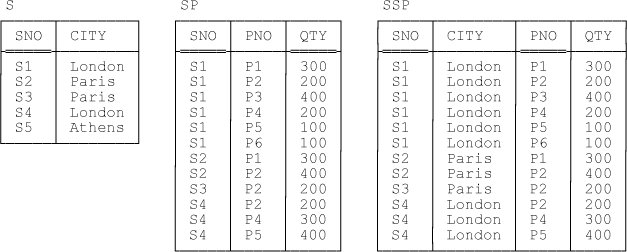
Now let me revise the foregoing example and suppose that—as in our original suppliers-and-parts database, in fact—it’s not the case that every supplier has to supply at least one part. Then information equivalence is lost; to be specific, the design consisting of relvars S and SP in combination is capable of representing suppliers (such as supplier S5 in our usual set of sample values for the suppliers-and-parts database) who currently supply no parts at all, while the design consisting of just the join SSP obviously can’t represent such information. (Equivalently, it’s no longer guaranteed that relvar S is equal to the projection of SSP, the join of S and SP, on SNO and CITY. On the other hand, it’s at least still true that relvar SP is equal to the projection of that join on SNO, PNO, and QTY.)
Be that as it may, the following constraints among others apply to this revised form of the database:
The usual key constraints all hold—{SNO} is a key for S and {SNO,PNO} is a key for each of SP and SSP.
At any given time, the current value of SSP is equal to the join of the current values of S and SP.
The FD {SNO} → {CITY} holds in SSP (also in S, of course).
A concrete example of a database value satisfying the foregoing conditions can be obtained by extending Figure 8-1 to reinstate the usual tuple for supplier S5 (see Figure 8-2 overleaf, and observe in particular that the relations shown as the current values of relvar SP and SSP in that figure are the same as they were in Figure 8-1).
A remark on terminology: The title of this chapter implies, or at least strongly suggests, that S JOIN SP is still a one to many join, but it needs to be clearly understood that “many” here includes the zero case. The truth is, the term “one to many” is often used somewhat loosely to include both (a) what might be called the strict case, as in Example 1 in the previous section, and (b) cases like the one currently under discussion, in which it’s possible for one participant to have an element with no counterpart in the other. Here’s a lightly edited quote from The Relational Database Dictionary, Extended Edition (Apress, 2008):
A one to many correspondence is, strictly, a rule pairing two sets s1 and s2 (not necessarily distinct) such that each element of s1 corresponds to at least one element of s2 and each element of s2 corresponds to exactly one element of s1. However, the term is often used somewhat loosely to mean a pairing such that (a) each element of s1 corresponds to any number of elements of s2 (possibly none at all) and each element of s2 corresponds to exactly one element of s1, or (b) each element of s1 corresponds to at least one element of s2 and each element of s2 corresponds to at most one element of s1, or (c) each element of s1 corresponds to any number of elements of s2 (possibly none at all) and each element of s2 corresponds to at most one element of s1. The term is probably best avoided unless the intended meaning is clear.
The final sentence here notwithstanding, I will in fact be using the term occasionally in the rest of this chapter, but I think my intended meaning will always be clear from the context. End of remark.
To say it again, the join SSP of S and SP loses information, inasmuch as it’s no longer guaranteed that relvar S in particular is equal to the projection of that join on the corresponding attributes. More precisely, any information that can be represented by relvar SSP alone can certainly be represented by the combination of relvars S and P, but the converse is false. (An example of a query on the latter that has no exact counterpart on the former is “Get supplier numbers for suppliers who currently supply no parts.”) As a consequence, it’s obvious that there are going to be certain updates that can be done on S in particular that have no counterpart on SSP. An example is “Insert a tuple into S for supplier S9,” without simultaneously inserting at least one tuple for that same supplier S9 into SP.
I don’t propose to investigate this example in any further detail here. Instead, I’m simply going to appeal, as I did in Chapter 7, to the analysis of Example 2 in Chapter 6; to be more specific, I’m going to claim that the detailed analysis of that example in Chapter 6 applies to the present example also, mutatis mutandis. In other words, it’s my opinion that the rules discussed earlier in the present chapter for updating a strict one to many join view can be taken, if desired, to apply to the present case as well. To paraphrase a remark from the discussions in Chapter 6, if we can agree on this position, then we’ll have agreed on a universal set of rules for updating one to many join views that do at least always work and do guarantee that joins are strictly one to many when they’re supposed to be—not to mention the point that the rules in question in fact work for all join views, regardless of whether the join in question is one to one, one to many, or many to many. What’s more, if those rules do sometimes give rise to consequences that are considered unpalatable for some reason, then there are always certain pragmatic fixes, such as using the DBMS’s authorization subsystem to prohibit certain updates, that can be adopted to avoid those consequences.
Concluding Remarks
This brings us to the end of these three chapters on updating joins. In closing, however, there are a few additional remarks I’d like to make (they’re all somewhat tangential to our main topic, however, and you can ignore them if you want). The first concerns foreign keys. As you might have noticed, I made no explicit mention of foreign keys as such in any of these three chapters (nor in Chapter 5 either, on projections, come to that). In fact this omission was deliberate on my part. The point is, there seems to be a vague notion in the database community at large that updating joins has something to do with whether the join in a question is defined on the basis of some foreign key and its corresponding target key, and I wanted to get away from that notion if I could. That said, it’s certainly true that several of my examples were indeed “foreign key joins” (if I might be permitted to use such a term)—but not all of them were; in particular, the ones in Chapter 7 weren’t.
That said, I’d still like to say something about foreign keys in Tutorial D specifically. The following example, repeated from Chapter 2, illustrates the kind of syntax normally used to declare foreign keys:
VAR SP BASE RELATION
{ SNO CHAR , PNO CHAR , QTY INTEGER }
KEY { SNO , PNO }
FOREIGN KEY { SNO } REFERENCES S
FOREIGN KEY { PNO } REFERENCES P ;However, I also said in Chapter 2 that FOREIGN KEY specifications like the ones shown here are essentially just shorthand for constraints that can also be expressed, possibly more longwindedly, using explicit CONSTRAINT syntax. More specifically, I showed in Chapter 3 how the fact that, e.g., {SNO} in relvar SP is a foreign key referencing the key {SNO} in relvar S could be expressed in relational calculus as a multivariable constraint, like this:
FORALLx∈ SP ( UNIQUEy∈ S (x.SNO =y.SNO ) )
(I remind you that the UNIQUE quantifier can be read as “there exists exactly one … such that.”) So you might be wondering what the Tutorial D “longhand” equivalent of this relational calculus expression would look like.
Well, we could certainly write the following in Tutorial D:
CONSTRAINT ... IS_EMPTY ( SP NOT MATCHING S ) ;
But this statement doesn’t quite do the job (at least, not by itself). What it says is that every shipment has at least one corresponding supplier. What we want to say, however, is that each shipment has exactly one corresponding supplier.[98] Well, we can do that too by making use of another convenient shorthand called image relations (see SQL and Relational Theory for further discussion of this construct). To be specific, we can write:
CONSTRAINT ... IS_EMPTY ( SP WHERE COUNT ( !!S ) ≠ 1 ) ;
Explanation: For a given SP tuple, the expression !!S—pronounced “bang bang S” or “double bang S”—denotes the set of S tuples with the same supplier number as that SP tuple. Thus, the constraint overall requires every SP tuple to be such that the count of corresponding S tuples is exactly one.
Still on the subject of Tutorial D syntax, you might also be wondering how functional dependencies (FDs) can be formulated in Tutorial D. (You might have noticed that I didn’t give any such formulations in connection with the examples in which I was making use of such FDs.) In fact there are several ways to do it, of which the most elegant is probably the one illustrated here:
CONSTRAINT ... SSP { SNO , CITY } KEY { SNO } ;You can read this CONSTRAINT statement as saying “If we were to define a relvar consisting of the projection of SSP on SNO and CITY, then that relvar would have {SNO} as a key”—which effectively does what we want, since it states implicitly that the FD
{ SNO } → { CITY }holds in relvar SSP.[99] (Recall from a footnote in Chapter 5 that if K is a key for relvar R, then the FD K → X holds in R for all subsets X of the heading of R.)
Aside: Please take note of the idea, illustrated by the foregoing example, that we should be able to declare keys in connection with relational expressions of arbitrary complexity. I’ll be appealing to it again in later chapters. End of aside.
Finally, you might be wondering whether we need any special syntax for declaring join dependencies (JDs) or multivalued dependencies (MVDs). In fact I don’t think we do. For example, with reference to the first example from Chapter 7, specifying the following constraint—
CONSTRAINT ... SCP = JOIN { SCP { SNO , CITY } , SCP { PNO , CITY } } ;—is precisely equivalent to stating that the following JD holds in relvar SCP:
{ { SNO , CITY } , { PNO , CITY } }
It’s also precisely equivalent to stating that a certain pair of MVDs hold in relvar SCP. The situation is different with FDs; to say some relvar is equal to the join of certain of its projections is not equivalent to saying some FD holds, and that’s why FDs in general need to be separately specified.
[97] I’m appealing here to Heath’s Theorem, which was mentioned a couple of times in Chapter 5. For further explanation, see Database Design and Relational Theory.
[98] Actually the statement does do the job in a sense, thanks to the fact that there’s an additional constraint in effect that requires supplier numbers in S to be unique. But having to deduce that some constraint—a rather important constraint at that—holds implicitly from the fact that two other constraints have been declared explicitly does seem, from the user’s point of view at least. a trifle unfriendly.
[99] Well, actually it states implicitly that the FD {SNO} → {CITY} holds in the projection of that relvar SSP on SNO and CITY. But it’s easy to prove that a given FD holds in a given projection of a given relvar R if and only if it holds in that given relvar R itself.