Chapter 9. Intersection Views
Updating intersections
Can sometimes need corrections
—
In this chapter and the next two, I turn my attention to intersection, union, and difference views. Of course, I’ve already said something in Chapter 6 about intersection views in particular (the subject of the present chapter)—recall that intersection is a special case of one to one join—but there’s quite a lot more to be said on the subject.
First I need to say something about the structure of the chapter. Let DB1 and DB2 be a set of base relvars and a set of views, respectively. Now, in the last few chapters, on restriction, projection, and join views, I proceeded in general terms as follows: First, I considered a particular DB1; then I considered a particular DB2 that was information equivalent to that DB1; finally, I considered another DB2 that wasn’t information equivalent to that DB1 but involved some information hiding instead. But that approach doesn’t work very well for intersection views.[100] The reason is this: Suppose DB1 consists of base relvars A and B (only) and DB2 consists of view V only, defined as the intersection of A and B (i.e., V = A INTERSECT B). Then DB2 will be information equivalent to DB1 only if A = B—in which case (as I hinted in a footnote near the end of Chapter 6) there’s not much point in defining view V in the first place.
So there’s not much point in considering the case in which A and B are equal. What’s more, there’s also not much point in considering the case in which they’re totally disjoint, in the sense that no tuple ever appears in both. For if they’re disjoint in this sense, then the intersection view V will always be empty; deletes on V will thus always be “no ops” and inserts on V will always fail (unless they’re “no ops” as well). So the interesting case—the one I do want to examine—is the one in which A and B aren’t equal but do at least overlap, in the sense that it’s possible for the very same tuple to appear in both. Thus, I’ll consider two principal examples, one in which the overlap is explicit (and I’ll explain what I mean by that term), and one in which it’s merely implicit. Also, I won’t bother to examine in either case the situation in which all relvars concerned are base ones; instead, I’ll start with two given relvars A and B and immediately define their intersection A INTERSECT B as a view per se, and see what happens.
Example 1: Explicit Overlap
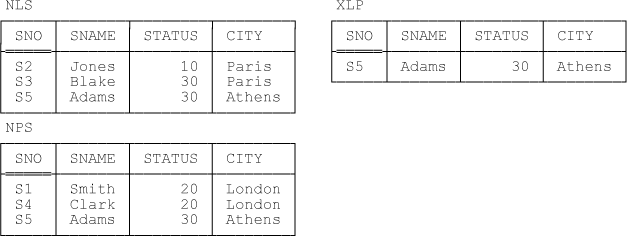
My first example is based on one previously examined in the section Overlapping Restrictions in Chapter 4, on restriction views. It involves two relvars, NLS (“non London suppliers”) and NPS (“non Paris suppliers”), that look like this:
NLS { SNO , SNAME , STATUS , CITY } KEY { SNO }
NPS { SNO , SNAME , STATUS , CITY } KEY { SNO }Of course, given our usual suppliers-and-parts database, these relvars are probably views—views of relvar S, to be specific—but you can think of them as base relvars if you like. More to the point, observe that these relvars certainly do overlap; to be specific, tuples for suppliers who are in neither London nor Paris will appear in both. (Indeed, such tuples must appear in both, thanks to the corresponding predicates—see below—and The Closed World Assumption.)[101] And now perhaps you can see why I say the overlap is explicit in this example: The condition a tuple has to satisfy in order to appear in both relvars (a) can be checked by examining values explicitly appearing in the tuple in question, and (b) is in fact explicitly reflected in the corresponding constraints (which I’ll be examining in a few moments). Note: Formally, in fact, the condition in question is a simple restriction condition (see Appendix B for a definition of this concept).
Here now are the relvar predicates:
| NLS: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY isn’t London). |
| NPS: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY isn’t Paris). |
Now let’s define the intersection of relvars NLS and NPS as a view XLP:
XLP { SNO , SNAME , STATUS , CITY } KEY { SNO }The predicate for this relvar is:
| XLP: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY is neither London nor Paris). |
Sample values are shown in Figure 9-1.
What constraints hold in this example? Well, first, each of the three relvars has {SNO} as its sole key, as already indicated. Second, {SNO} in XLP is a foreign key, referencing both NLS and NPS. Third, we also clearly have:
CONSTRAINT ... XLP = NLS INTERSECT NPS ;
CONSTRAINT ... IS_EMPTY ( NLS WHERE CITY = 'London' ) ;
CONSTRAINT ... IS_EMPTY ( NPS WHERE CITY = 'Paris' ) ;
CONSTRAINT ... ( NLS WHERE CITY ≠ 'Paris' ) =
( NPS WHERE CITY ≠ 'London' ) ;Note the last of these in particular, which implies among other things that certain updates on each of NLS and NPS must cascade appropriately to the other:
ON INSERTiINTO NLS : INSERT (iWHERE CITY ≠ 'Paris' ) INTO NPS ; ON INSERTiINTO NPS : INSERT (iWHERE CITY ≠ 'London' ) INTO NLS ; ON DELETEdFROM NLS : DELETE (dWHERE CITY ≠ 'Paris' ) FROM NPS ; ON DELETEdFROM NPS : DELETE (dWHERE CITY ≠ 'London' ) FROM NLS ;
Points arising:
First of all, note that the rules just shown make no mention of relvar XLP—in fact, they would be needed even if relvar XLP didn’t exist.
In the delete rules, the restriction conditions CITY ≠ ‘Paris’ and CITY ≠ ‘London’ could be dropped (or, more precisely, replaced by just TRUE) without significant loss. I’ve included them for reasons of explicitness, also for symmetry with the insert rules.
As was previously mentioned in Chapter 4, the last of the foregoing constraints—the one that implies the need for the cascade rules—also implies that relvars NLS and NPS together violate The Principle of Orthogonal Design. However, the fact that they do so is unimportant for present purposes.
Finally, we need a constraint to the effect that if some supplier is represented in both NLS and NPS, then the two tuples representing that supplier are in fact one and the same. The following constraint, which states that {SNO} is a key for the union of those two relvars, does the trick:
CONSTRAINT ... UNION { NLS , NPS } KEY { SNO } ;Of course, this constraint will be enforced automatically if relvars NLS and NPS are in fact views of the suppliers relvar S.
Back to the rules as such. What about cascades from NLS and NPS to the intersection relvar XLP? In fact these rules are straightforward:
ON INSERTiINTO NLS : INSERT (iWHERE CITY ≠ 'Paris' ) INTO XLP ; ON INSERTiINTO NPS : INSERT (iWHERE CITY ≠ 'London' ) INTO XLP ; ON DELETEdFROM NLS : DELETE (dWHERE CITY ≠ 'Paris' ) FROM XLP ; ON DELETEdFROM NPS : DELETE (dWHERE CITY ≠ 'London' ) FROM XLP ;
(Again the restriction conditions could be dropped from the delete rules without loss.)
Finally, here are the rules for updates on the intersection relvar as such:
ON INSERTiINTO XLP : INSERT (iWHERE CITY ≠ 'London' ) INTO NLS , INSERT (iWHERE CITY ≠ 'Paris' ) INTO NPS ; ON DELETEdFROM XLP : DELETE (dWHERE CITY ≠ 'London' ) FROM NLS , DELETE (dWHERE CITY ≠ 'Paris' ) FROM NPS ;
Points arising:
Let’s focus on the delete rule for a moment. As far as relvar XLP is concerned, it would of course be sufficient to cascade to just one of the relvars NLS and NPS. But cascading to either will cause an additional cascade to the other one anyway; and since there’s no good reason to favor one over the other, at least in concrete syntax (assuming, of course, that both relvars are visible)—it’s a difference that makes no difference, so to speak—I’ve specified cascades to both, for reasons of symmetry and explicitness.
As a matter of fact, a similar remark applies to the insert rule also (in general, inserting into an intersection needs to cascade to both of the relvars involved; in the case at hand, however, cascading to either will cause an additional cascade to the other one anyway).
Once again, the restriction conditions could be dropped without loss, this time from both the insert rule and the delete rule (why, exactly, in each case?).
Of course, as explained in the introduction to this chapter, we’re talking about an intersection example, and thus we’re dealing with a situation in which information equivalence is lost more or less by definition. To spell the point out, any information that can be represented by relvar XLP alone can certainly be represented by relvars NLS and NPS taken in combination, but the converse is false. (Here’s an example of a query on the latter that has no exact counterpart on the former: “Get suppliers in London.”) As a consequence, it should be obvious that there’ll be certain updates that can be done on NLS and/or NPS that have no exact counterpart on XLP. An example of such an update is “Insert a tuple for supplier S9 into NPS without simultaneously inserting that same tuple into NLS” (i.e., update the database to say there’s a “new” supplier S9 who is located in London). However, despite all of the foregoing—despite the lack of information equivalence in particular—it is at least true that updates on the intersection view XLP always work satisfactorily. And the reason for this satisfactory state of affairs is precisely that the overlap in this example is explicit.
Now let’s briefly consider a user who sees just relvar XLP (an information hiding situation). Such a user:
Will know the relvar predicate;
Will know that supplier numbers are unique and CITY values are never London or Paris;
Won’t be aware of any compensatory actions.
Such a user can’t be allowed to insert tuples into the relvar, nor to update supplier numbers within the relvar, because such operations have the potential to violate constraints of which the user is unaware.
Finally, let me point out that if NLS and NPS are indeed themselves views (i.e., views of relvar S), then XLP could alternatively have been defined directly as a restriction of S, thus:
S WHERE CITY ≠ 'London' AND CITY ≠ 'Paris'
Let’s call this restriction XLP’. Clearly, then, updates on XLP’ should have the same effect as updates on XLP—and so they do. To be specific:
INSERT: Tuples to be inserted into either XLP or XLP’ must have CITY value neither London nor Paris and so must be inserted into the other as well.
DELETE: Tuples to be deleted from either XLP or XLP’ certainly do have CITY value neither London nor Paris and so must be deleted from the other as well.
Note: I’ll have quite a bit more to say about the general question of updates on relvars—more specifically, views—with different but equivalent definitions in Chapter 14.
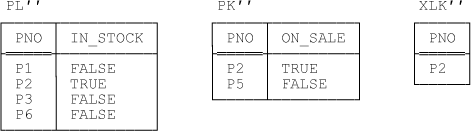
Example 2: Implicit Overlap
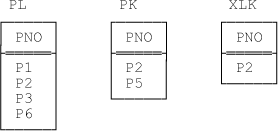
For our second example, let’s switch from suppliers to parts, just for a change. Suppose that, at any given time, some parts are on sale, some parts are in stock, and some are both. Suppose further that we represent this situation by means of two relvars, each with just a single attribute PNO—one relvar (PL) giving part numbers for parts on sale, the other (PK) giving part numbers for parts in stock. Of course, the intersection of these two relvars—call it XLK—gives part numbers for parts that are both on sale and in stock. The point is, however, we can’t tell just by looking at a given tuple in the original parts relvar P whether that part ought to be represented in PL, PK, both, or neither; in other words, the overlap here is implicit, not explicit.[102] Thus, the predicates are very simple:
| PL: Part PNO is on sale. |
| PK: Part PNO is in stock. |
| XLK: Part PNO is on sale and in stock. |
Sample values are shown in Figure 9-2. Note that (with reference to our usual set of PNO values) I’m assuming for the sake of the example that part P4 is neither on sale nor in stock.
As for constraints, {PNO} is obviously the sole key for each of these three relvars, and of course XLK is equal to the intersection of the other two:
CONSTRAINT ... XLK = PL INTERSECT PK ;
Updates on PL and/or PK are noncontroversial:
ON INSERTiINTO PL : INSERT (iINTERSECT PK ) INTO XLK ; ON INSERTiINTO PK : INSERT (iINTERSECT PL ) INTO XLK ; ON DELETEdFROM PL : DELETEdFROM XLK ; ON DELETEdFROM PK : DELETEdFROM XLK ;
Now what about updates on XLK? Well, the insert rule is obvious:
ON INSERTiINTO XLK : INSERTiINTO PL , INSERTiINTO PK ;
As for the delete rule, clearly it would be sufficient for deletes on XLK to cascade to just one of PL and PK (it must cascade to at least one, of course). However, there’s no good reason for choosing either of these possibilities over the other; in fact, what we have here once again is the ambiguity (?) issue that I discussed in detail in Chapter 6—at least, it’s a special case of that issue—and the discussions in that chapter apply here also, mutatis mutandis.[103] I therefore propose the following as an appropriate delete rule (and observe that, not incidentally, it has the same general form as its counterpart in Example 1 in the previous section):
ON DELETEdFROM XLK : DELETEdFROM PL , DELETEdFROM PK ;
Of course, once again we’re dealing with a situation in which information equivalence is lost. To spell the point out, any information that can be represented by relvar XLK alone can certainly be represented by relvars PL and PK taken in combination, but the converse is false. (Here’s an example of a query on the latter that has no exact counterpart on the former: “Get part numbers for parts that are on sale and not in stock.”) As a consequence, it should be obvious that there’ll be certain updates that can be done on PL and/or PK that have no exact counterpart on XLK. An example of such an update is “Insert a new tuple into PL without simultaneously inserting that same tuple into PK” (i.e., update the database to say some part is on sale but, if it wasn’t previously in stock, still isn’t).
I’ll leave it as an exercise to determine the implications of all of the foregoing for a user who sees just relvar XLK. However, let me now point out that, sadly, there’s another issue here (I touched on this issue in Chapter 6, but I didn’t elaborate on it in that chapter). Suppose we start off with just relvars PL and PK, without the intersection view, and suppose too that part P2 is represented in both relvars. Then the following update is clearly legitimate:
DELETE ( P2 ) FROM PL ;
Observe in particular that there’s no question of this delete cascading to relvar PK. But now suppose we introduce the intersection view XLK. Given the rules defined above, then, this delete will now cascade to relvar PK!—and it’ll do so, moreover, even if view XLK isn’t visible to the user issuing the delete on relvar PL. Or to put the point another way: Introducing that view apparently requires the simultaneous introduction of a cascade delete rule from PL to PK and vice versa.[104]
Such a state of affairs doesn’t seem very desirable, to say the least. Can we do anything about it? Well, one possible (though annoying) pragmatic fix, in the particular case at hand, is to execute an appropriate insert immediately after the delete, thus:
DELETE ( P2 ) FROM PL ; INSERT ( P2 ) INTO PK ;
To my mind, however, the solution to be discussed in the subsection immediately following is greatly to be preferred.
A Better Design
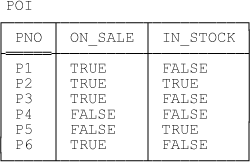
Suppose we replace relvars PL and PK in their entirety by a single relvar—let’s call it POI—with attributes PNO, ON_SALE, and IN_STOCK, where attributes ON_SALE and IN_STOCK are of type BOOLEAN (and have the obvious interpretations) and {PNO} is the sole key. A possible value for such a relvar is shown in Figure 9-3 (note the tuple for part P4 in particular).
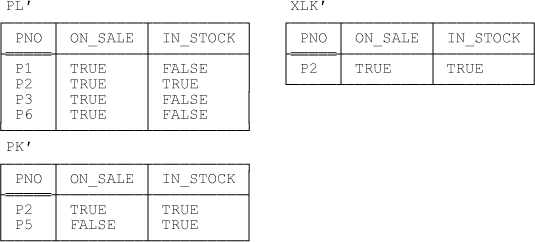
Now we define restriction views PL’ and PK’ of relvar POI as indicated by the following constraints (I use the primed names PL’ and PK’ in order to avoid confusion with relvars PL and PK as previously defined, but of course they—i.e., relvars PL’ and PK’—serve essentially the same purpose as those earlier relvars did):[105]
CONSTRAINT ... PL' = POI WHERE ON_SALE ; CONSTRAINT ... PK' = POI WHERE IN_STOCK ;
And now we can define XLK’ as the intersection of PL’ and PK’, and we have:
CONSTRAINT ... XLK' = PL' INTERSECT PK' ;
(Of course, we could also define XLK’ as a direct restriction of POI, thus: POI WHERE ON_SALE AND IN_STOCK. But let’s ignore this possibility until further notice.) See Figure 9-4 for some sample values, corresponding of course to the sample value of relvar POI as shown in Figure 9-3.
The predicates (deliberately spelled out in somewhat excruciating detail) are as follows:
| PL’: Part PNO is on sale if and only if ON_SALE is TRUE and in stock if and only if IN_STOCK is TRUE (and ON_SALE is TRUE). |
| PK’: Part PNO is on sale if and only if ON_SALE is TRUE and in stock if and only if IN_STOCK is TRUE (and IN_STOCK is TRUE). |
| XLK’: Part PNO is on sale if and only if ON_SALE is TRUE and in stock if and only if IN_STOCK is TRUE (and ON_SALE is TRUE and IN_STOCK is TRUE). |
As for constraints, note first that each of the three relvars has {PNO} as sole key, and {PNO} in XLK’ is a foreign key, referencing both PL’ and PK’. The following constraints also obviously hold:
CONSTRAINT ... IS_EMPTY ( PL' WHERE NOT ( ON_SALE ) ) ; CONSTRAINT ... IS_EMPTY ( PK' WHERE NOT ( IN_STOCK ) ) ; CONSTRAINT ... IS_EMPTY ( XLK' WHERE NOT ( ON_SALE AND IN_STOCK ) ) ;
We also need a constraint to the effect that if some part is represented in both PL’; and PK’, then the two tuples representing that part are in fact one and the same:
CONSTRAINT ... UNION { PL' , PK' } KEY { PNO } ;Of course, this constraint will automatically be enforced if relvars PL’ and PK’ are indeed, as stated, views of POI.
Aside: By the way, we also have the following:
CONSTRAINT ... ( PL' WHERE IN_STOCK ) = ( PK' WHERE ON_SALE ) ;As a consequence (of the fact that this constraint holds, that is), relvars PL’ and PK’, like relvars NLS and NPS in the previous section, clearly violate The Principle of Orthogonal Design. In other words, I seem to be contravening one of my own design recommendations in this example! To be specific, in Database Design and Relational Theory, I suggested rather strongly that orthogonality should never be violated. But of course the violation here won’t hurt, because the redundancy it causes will certainly be controlled. End of aside.
Be that as it may, what happens to the update rules? Well, first we have to consider how updates on relvar POI itself affect relvars PL’ and PK’:
ON INSERTiINTO POI : INSERT (iWHERE ON_SALE ) INTO PL' , INSERT (iWHERE IN_STOCK ) INTO PK' ; ON DELETEdFROM POI : DELETE (dWHERE ON SALE ) FROM PL' , DELETE (dWHERE IN_STOCK ) FROM PK' ;
Next we have to consider how updates on relvars PL’ and PK’ affect relvar POI:
ON INSERTiINTO PL' : INSERTiINTO POI ; ON INSERTiINTO PK' : INSERTiINTO POI ; ON DELETEdFROM PL' : DELETEdFROM POI ; ON DELETEdFROM PK' : DELETEdFROM POI ;
Note that the foregoing rules taken together imply that (a) inserting a tuple of the form (p,TRUE,TRUE) into either of PL’ and PK’ will effectively cascade to the other; likewise, (b) deleting a tuple of the form (p,TRUE,TRUE) from either of PL’ and PK’ will effectively cascade to the other. In fact, of course, such cascades would be logically necessary even if relvar POI—and in particular the rules that cascade inserts to, and deletes from, that relvar to relvars PL’ and PK’—didn’t exist.
Now we can bring relvar XLK’ into the picture (to be specific, now we can consider how updates on relvars PL’ and PK’ affect relvar XLK’ and vice versa):
ON INSERTiINTO PL' : INSERT (iWHERE IN_STOCK ) INTO XLK' ; ON INSERTiINTO PK' : INSERT (iWHERE ON_SALE ) INTO XLK' ; ON DELETEdFROM PL' : DELETE (dWHERE IN_STOCK ) FROM XLK' ; ON DELETEdFROM PK' : DELETE (dWHERE ON_SALE ) FROM XLK' ; ON INSERTiINTO XLK' : INSERTiINTO PL' , INSERTiINTO PK' ; ON DELETEdFROM XLK' : DELETEdFROM PL' , DELETEdFROM PK' ;
And these rules are all, as I hope you’ll agree, completely noncontroversial[106] (though I think it’s instructive to compare them with the rules I gave in connection with the previous version of the example). In effect, what I’ve done is redesign the database in such a way that information that was previously represented only implicitly, by the relvar names PL and PK, is now represented explicitly by values of the attributes ON_SALE and IN_STOCK instead. And the effect of that redesign is to convert the previous version of the example—which suffered from update behavior that was at least arguably unacceptable—into a version that behaves just like Example 1 as discussed earlier in the chapter. And, of course, this latter example didn’t suffer from the ambiguities and consequent update problems that arose with the previous version of the example currently under discussion.
Aside: It’s tempting to suggest there might be a general design principle here: Whenever two relvars have the same heading but different semantics, (a) introduce an attribute or attributes whose values serve to represent that difference and then (b) consider replacing those relvars by a single relvar. Or: Whenever some relvar B is such that its value is always a subset of the value of some other relvar A, but B can’t be defined as a restriction as such of A, then introduce an attribute or attributes into both A and B whose values can be used to turn B into a restriction as such after all. Further consideration of such matters is beyond the scope of this book, however. End of aside.
I’ll leave it as an exercise to determine the implications of all of the foregoing for a user who sees just relvar XLK’. As for defining XLK’ directly as a restriction of POI, I’ll leave it as another exercise to show that the behavior of such a restriction with respect to updates would be essentially identical to that of the intersection version as described above.
Another Possible Design
Now, it might have occurred to you that, given that attribute ON_SALE necessarily has the value TRUE in every tuple of PL’ and attribute IN_STOCK necessarily has the value TRUE in every tuple of PK’, we could redefine those relvars—more specifically, those views—in such a way as to drop those attributes, as indicated by the following constraints:
CONSTRAINT ... PL'' = ( POI WHERE ON_SALE ) { PNO , IN_STOCK } ;
CONSTRAINT ... PK'' = ( POI WHERE IN_STOCK ) { PNO , ON_SALE } ;(I’ve used double primes to distinguish these versions of the relvars from previous versions.) Here are the predicates:
| PL’’: Part PNO is on sale and, if and only if IN_STOCK is TRUE, also in stock. |
| PK’’: Part PNO is in stock and, if and only if ON_SALE is TRUE, also on sale. |
And now we could (re)define relvar XLK’—or XLK’’, rather—as the intersection of the projections of PL’’ and PK’’ on PNO:
CONSTRAINT ... XLK'' = PL'' { PNO } INTERSECT PK'' { PNO } ;The predicate is as for our original relvar XLK:
| XLK’’: Part PNO is on sale and in stock. |
For some sample values for this redesigned database, see Figure 9-5. You might find it instructive to compare this figure with Figure 9-2.
Now let’s focus for a moment on relvar PL’’. That relvar is, of course, a projection relvar; to be specific, it’s a projection of (a certain restriction of) relvar POI. As explained in Chapter 5, therefore, there’s a loss of information equivalence here, as a consequence of which that relvar PL’’ supports deletes but not inserts.[107] The pertinent delete rule is:
ON DELETEdFROM PL'' : DELETE ( POI MATCHINGd) FROM POI ;
Analogously, we also have:
ON DELETEdFROM PK'' : DELETE ( POI MATCHINGd) FROM POI ;
And the rule for deletes on XLK’’ is as follows (note, however, that there can’t be any insert rule):
ON DELETEdFROM XLK'' : DELETEdFROM PL'' , DELETEdFROM PK'' ;
In other words, while deletes on XLK’’ work satisfactorily (or so it might be argued, at any rate), inserts on XLK’’ can’t be done at all. Overall, therefore, I think this “double prime” design is a nonstarter, at least if it’s supposed to be capable of supporting update operations properly.
Concluding Remarks
Now, you might have found this chapter rather confusing—especially with respect to Example 2 in the previous section, where I kept changing the rules of the game, so to speak. So let me abstract from the discussions in that section and summarize the update rules for the case where there’s an intersection involved. Let V be defined as A INTERSECT B. Further, assume for simplicity that tuples to be inserted into A and B are required to satisfy boolean expressions ax and bx, respectively, where ax and bx denote restriction conditions on the pertinent relvars (default simply TRUE). Then we have:
ON INSERTiINTOA: INSERT (iWHEREbx) INTOV; ON INSERTiINTOB: INSERT (iWHEREax) INTOV; ON DELETEdFROMA: DELETE (dWHEREbx) FROMV; ON DELETEdFROMB: DELETE (dWHEREax) FROMV; ON INSERTiINTOV: INSERTiINTOA, INSERTiINTOB; ON DELETEdFROMV: DELETEdFROMA, DELETEdFROMB;
Note: I’ll leave it as another exercise to show that the specific rules given in connection with the examples earlier in the chapter are all special cases—sometimes slightly “optimized” special cases—of the foregoing general rules.
We also saw that the rule for deleting through an intersection can sometimes lead to results that might be unacceptable, or at least undesirable, in practice. In particular, this criticism—which arises, as I pointed out in Chapter 6, because the rule effectively means treating logical OR as logical AND, or possibly the other way around—applied to the first version of the “parts on sale” vs. “parts in stock” example. But let’s think about that example a moment longer … The real problem with that example was that, given a particular tuple to be deleted from the intersection XLK, the DBMS was unable to tell whether that tuple still logically belonged in relvar PL or relvar PK or neither. In effect, the pertinent restriction condition for each of PL and PK in that example was simply TRUE (contrast the situation with Example 1, the NLS vs. NPS example, as discussed earlier in the chapter). And my proposed solution to this problem was, in effect, to redesign the database in such a way that the DBMS could tell which relvar(s) a given tuple logically belonged in after all—a solution that (I venture to suggest) will often work in practice, and indeed is likely to offer benefits in other areas as well, in addition to view updating as such.
One last point on the foregoing: Clearly, what we have in this example is a situation in which information is hidden once again. But the information hiding we’re talking about here is different in kind from what we’ve seen earlier in this book. In earlier examples, information was hidden from some user, because (as I put it in earlier chapters) the user in question was seeing only part of the total picture—e.g., consider the example in Chapter 1, where the user saw the restriction LS (“London suppliers”) and not the restriction NLS (“non London suppliers”). But in the present situation we’re talking about information that’s hidden not from the user, but from the DBMS. To be specific, what’s being hidden in the case at hand is the criterion for deciding whether a given tuple logically belongs in PL or PK or neither. And as already indicated, my solution to this problem is to change the design in such a way as to make that information available to the DBMS after all.
[100] It also doesn’t work very well (for different reasons) for union or difference views, the topics of the next two chapters.
[101] To spell the point out, we have here (as we did in Chapter 4) a situation in which the predicates violate the discipline, suggested in a footnote in Chapter 2, to the effect that the predicates for relvars R1 and R2 should preferably be such as to preclude the possibility that the same tuple might satisfy both.
[102] Observe that relvars PL and PK resemble relvars NLS and NPS from the previous section in that they violate the suggested discipline that (in general) the pertinent predicates, q.v., should be such as to preclude the possibility that the same tuple might satisfy both. On the other hand, they differ from NLS and NPS in that they do not violate The Principle of Orthogonal Design. That’s because there’s no constraint in effect—nor can there be—to say that if a certain tuple appears in one of those relvars, it must appear in the other.
[103] I remind you that David McGoveran has a proposal for resolving the ambiguity, which I’ll be discussing in Chapter 15. Do note carefully, however, that the ambiguity problem didn’t arise with Example 1, where the overlap was explicit.
[104] A related issue is the following. Under the stated rules for updates on XLK, deleting a tuple from XLK and then inserting it again will preserve the status quo, but inserting a tuple into XLK and then deleting it again might not. The reason is that inserting a tuple into XLK might actually cause a tuple to be inserted into just one of PL and PK, whereas deleting a tuple from XLK will always cause a tuple to be deleted from both. Of course, the status quo with respect to relvar XLK as such is always preserved.
[105] Here’s a question for you: Is the design consisting of relvars PL’ and PK’ information equivalent to the one consisting of relvars PL and PK?
[106] In the case of the delete rule, it would of course be sufficient to cascade to just one of the relvars PL’ and PK’, but deleting from either will cascade to the other one anyway.
[107] Inserting the tuple (p,k) into PL’’, if it were allowed, would have to cause insertion of the tuple (p,TRUE,k) into POI. The trouble is, we know this, but the DBMS doesn’t. Note: Actually, the example is essentially identical, or at least isomorphic, to one discussed in earlier chapters—viz., the one in which we considered dropping the CITY attribute from relvar LS (“London suppliers”). Refer to Chapter 5 for further discussion.