I claimed in Chapter 2 that the generic relational assignment—

R := rx

(where R is a relvar reference, or in other words a relvar name, syntactically speaking, and rx is a relational expression)—is logically equivalent to an assignment of the form:^[157]

R := r - d ∪ i

Well, actually, in Chapter 2 I used the keywords MINUS and UNION in place of the set difference symbol “–” and the set union symbol “∪”, respectively. In this appendix I find it more convenient to use the symbols. Other symbols I’ll be using include “∩” (set intersection), “⊆” (set inclusion) and “Ø” (the empty set). What’s more, in all of these contexts I ought really to be talking in terms of relations rather than general sets, but I propose to overlook this point of detail in what follows. Note: In Chapter 2 I also enclosed the subexpression r – d (or r MINUS d, rather) in parentheses; in fact, however, no parentheses are needed, as we’ll soon see.

Be that as it may, let me now explain my notation in detail and elaborate on a few important points:

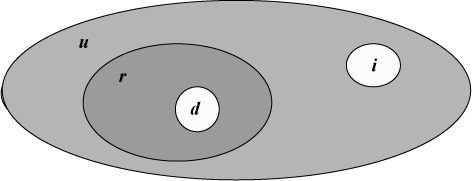
These points can be illustrated by means of a Venn diagram (see Figure A-1, a repeat of Figure 2-2 from Chapter 2). Explanation: In that diagram, r, d, and i are as above, and u is the universal relation of the pertinent type (i.e., the relation whose body consists of all tuples with the same heading as R—including, of course, those tuples that currently appear in R). Note that the difference u – r is the (absolute) complement of r, i.e., the relation whose body consists of all tuples with the same heading as R that don’t currently appear in R.

Figure A-1. The delete set d and the insert set i

Note: Of course, the delete set d might be empty, in which case the original assignment is effectively an INSERT operation. Or the insert set i might be empty, in which case it’s effectively a DELETE operation. Or they might both be empty, in which case the assignment overall degenerates to a “no op.”

I now show that, given the assignment R := r – d ∪ i (where r, d, and i are as defined above), the delete set d and the insert set i are unique. Suppose, contrariwise, that for some d1 ≠ d2 and/or some i1 ≠ i2, where in accordance with the conditions spelled out above d1 – r = d2 – r = r ∩ i1 = r ∩ i2 = d1 ∩ i1 = d2 ∩ i2 = Ø. Then:

r - d1 ∪ i1 = r - d2 ∪ i2

It follows from the foregoing that if x is the relation to be assigned to R, then x can be expressed as either r - d ∪ i or r ∪ i - d (i.e., it makes no difference whether we “do the delete first” or “do the insert first”). It further follows that, given r and x, we have:

d = r - x
i = x - r

Now, to repeat a point I made earlier, an INSERT is basically an assignment for which d is empty, and a DELETE is basically an assignment for which i is empty. But now I’d like to say something about UPDATE specifically (by which I mean, of course, explicit UPDATE operations). Clearly, d and i must both be nonempty (in general) for such an operation. In fact, let’s consider the generic form of such an operation:

UPDATE R WHERE bx : { A := ax }

Here R is a relvar reference; bx is a boolean expression (default simply TRUE); A is some attribute of relvar R; and ax is an expression denoting a value a of the same type as A. (For simplicity I limit my attention to the case of an UPDATE involving just the single “attribute assignment” A := ax. The discussion that follows can obviously be generalized to the case of an UPDATE involving two or more such assignments.)

Given this UPDATE, then it should be clear that the delete set d is defined as follows (I remind you that the symbol means “is defined as”):

d  { t : t ∈ R AND bx ( t ) AND t.A ≠ ax }

Explanation: What this definition means is that d consists of just those tuples t such that, first, t appears in R; second, bx evaluates to TRUE for t; and third, the A value within t isn’t equal to a already.

The insert set i is then defined in terms of d, thus:

i  { t' : EXISTS
 t ∈ d (
 t' = EXTEND t : {
 A := ax } ) }

Explanation: As elsewhere in this book, the keyword EXISTS denotes the existential quantifier (it can be read as “there exists”). Thus, what the definition means is that i consists of just those tuples t’ such that there exists a tuple t in d equal to that tuple t’, except that the A value in that tuple t has been replaced in that tuple t’ by the value a. Note: I’m making use here of the “what if” version of EXTEND (see either Chapter 2 or Appendix B). Perhaps more to the point, I’m appealing also to the fact that—as mentioned in passing at various points earlier in this book—we can readily define analogs of several of the conventional relational operators, including EXTEND in particular, that apply to individual tuples instead of entire relations. See SQL and Relational Theory for further discussion of this point.

It follows from all of the above that explicit UPDATE operations do indeed correspond to a relational assignment for which d and i are (in general) both nonempty. However, it’s worth pointing out that the converse is not true; that is, not all relational assignments for which d and i are both nonempty correspond to some explicit UPDATE operation. In fact, this is easy to see, for the following reason if no other:

The last issue I want to discuss in this appendix is the question of multiple assignment with repeated targets. Here again is what I had to say on the semantics of multiple assignment in Chapter 2:

However, I did also note that the foregoing explanation required some slight refinement in the case where two or more of the individual assignments specify the same target variable. Now I’d like to explain that refinement, briefly.

First of all, consider the following simple example:

DELETE ( S WHERE SNO = 'S1' ) FROM S ,
DELETE ( S WHERE SNO = 'S2' ) FROM S ;

Here’s the corresponding expanded form:

S := S MINUS ( S WHERE SNO = 'S1' ) ,
S := S MINUS ( S WHERE SNO = 'S2' ) ;

Clearly, then, if both source expressions are evaluated before either of the individual assignments is executed, then one of these two assignments has no effect!—in other words, one of the DELETEs is “lost.” (And to make matters worse, which of the two is lost is apparently not even defined.)

Because of situations like the foregoing, the definition of multiple assignment is extended to say, in effect, that if two or more of the individual assignments in that multiple assignment specify the same target variable, then those particular individual assignments are executed in sequence as written. A little more precisely, we can say of the foregoing double assignment that it’s logically equivalent to the following single assignment:

S := WITH ( S := S MINUS ( S WHERE SNO = 'S1' ) ) :
                                   S MINUS ( S WHERE SNO = 'S2' ) ;

This assignment in turn is equivalent to the following:

WITH ( DELETE ( S WHERE SNO = 'S1' ) FROM S ) :
       DELETE ( S WHERE SNO = 'S2' ) FROM S ;

Note: Of course, the particular double assignment we’re considering here is logically equivalent to the following single assignment:

S := ( S MINUS ( S WHERE SNO = 'S1' ) ) MINUS ( S WHERE SNO = 'S2' ) ;

More generally, it’s intuitively obvious that a multiple assignment in which all of the individual assignments specify the same target relvar R is logically equivalent to some single assignment to that same relvar R. Why? Because any assignment, multiple or otherwise, to relvar R effectively assigns some “new” value R - d ∪ i to R, for some d and some i.

Of course, the foregoing observation, while obviously correct, is of no help in computing the actual values of d and i in the general case. But the following remarks might help a little in this regard. Consider the following double assignment (and note carefully that the relvar reference R in the expression on the right side of the second assignment denotes the value of relvar R after the first assignment has been executed):

R := R - d1 ∪ i1 , R := R - d2 ∪ i2 ;

Now, the following pairs of sets aren’t necessarily disjoint, in general: d1 and d2; i1 and i2; d1 and i2; d2 and i1. However, it’s fairly easy to see (exercise for the reader!) that the foregoing double assignment is logically equivalent to a single assignment of the form—

R := r - d ∪ i ;

—where:

Note that d and i here are certainly disjoint; however, it’s not the case, in general, that d is included in r or that i and r are disjoint. Now define:

Then the original double assignment is logically equivalent to the following single assignment—

R := r - d' ∪ i' ;

—where d’ - r = r ∩ i’ = d’ ∩ i’ = Ø.

Note finally that it follows by induction from all of the above that a multiple assignment of the form

R := rx1 , R := rx2 , ... , R := rxn

for arbitrary n > 0 can always be reduced to a single assignment of the form

R := r - d ∪ i

where r is the initial value of R and d – r = r ∩ i = d ∩ i = Ø.