Chapter 7. Join Views II: Many to Many Joins
Recent researches at Harvard
And further researches at Yale
Show that joins can all be updated
By removing the spikes from their tail
—
Now I want to examine the question of many to many joins (I’m deliberately leaving the one to many case till last). As in Chapter 6, I think it might help to state right at the outset where our investigations are going to take us. As you might intuitively expect, the many to many case is going to turn out to involve certain complications, complications that didn’t arise in the one to one case; nevertheless, I claim we’re still going to wind up with essentially the same rules as before. That is, given a view V defined as A JOIN B—where the join is now a many to many join specifically—the rules are still going to look like this (in outline):
ON INSERT INTOV: INSERTA(sub)tuples if they don't already exist, INSERTB(sub)tuples if they don't already exist ON DELETE FROMV: DELETEA(sub)tuples if they don't exist elsewhere, DELETEB(sub)tuples if they don't exist elsewhere
Example 1: Information Equivalence
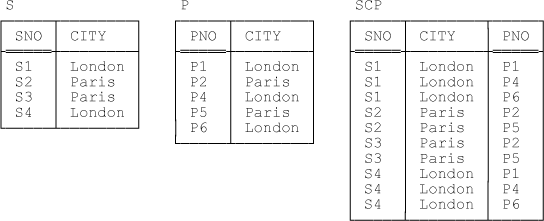
Consider a simplified version of our usual suppliers and parts relvars in which suppliers have no attributes except SNO and CITY and parts have no attributes except PNO and CITY, thus:
S { SNO , CITY } KEY { SNO }
P { PNO , CITY } KEY { PNO }Suppose also for the sake of the example that every supplier city is required to be a part city and vice versa—in other words, there’s a constraint in effect (actually an equality dependency once again) that looks like this:
CONSTRAINT ... S { CITY } = P { CITY } ;In order to conform to this new requirement, let’s agree until further notice to drop the tuple for supplier S5 (city Athens) from our usual suppliers relation and the tuple for part P3 (city Oslo) from our usual parts relation.
Now let’s define the join of relvars S and P as a view SCP:
SCP { SNO , CITY , PNO } KEY { SNO , PNO }Observe that the join here is indeed many to many, in the sense that (in general) every tuple in S joins to many tuples in P and vice versa. Nevertheless, we do have information equivalence, precisely because every tuple in either relvar does join to at least one tuple in the other. Sample values are shown in Figure 7-1.
Here now are the predicates:[93]
| S: Supplier SNO has city CITY. |
| P: Part PNO has city CITY. |
| SCP: Supplier SNO and part PNO both have city CITY. |
As usual, I’ll begin by considering what happens if all three relvars are base ones. If they are, what constraints hold? Well, first, the three relvars have {SNO}, {PNO}, and {SNO,PNO}, respectively, as their sole key (as already indicated). Second, we also clearly have:
CONSTRAINT ... SCP = S JOIN P ;
CONSTRAINT ... S = SCP { SNO , CITY } ;
CONSTRAINT ... P = SCP { PNO , CITY } ;These constraints are, of course, all equality dependencies (EQDs), and together they ensure that the two designs—that consisting of just relvar SCP and that consisting of the combination of relvars S and P—are information equivalent, as previously claimed.
The following constraints—also EQDs—hold as well (actually they’re just logical consequences of the three just stated):
CONSTRAINT ... IDENTICAL { S { CITY } , P { CITY } , SCP { CITY } } ;
CONSTRAINT ... SCP = JOIN { SCP { SNO , CITY } , SCP { PNO , CITY } } ;I want to elaborate somewhat on this last constraint, however. The fact that it holds means relvar SCP isn’t in fourth normal form (4NF), because the constraint in question is equivalent to the following join dependency (JD):
{ { SNO , CITY } , { PNO , CITY } }
And this JD in turn is equivalent to the following pair of multivalued dependencies (MVDs):
{ CITY } →→ { SNO }
{ CITY } →→ { PNO }Or writing them as a “one liner”:
{ CITY } →→ { SNO } | { PNO }These MVDs are neither trivial nor implied by the sole key {SNO,PNO} of SCP, and SCP is thus not in 4NF.[94] Note: Informally, what these MVDs mean is this: If tuples (c, s, p) and (c, s’;, p’) appear in the relvar, then tuples (c, s, p’) and (c, s’, p) must appear as well (where c is a city, s and s’ are supplier numbers, and p and p’ are part numbers). By way of illustration of this point (with reference to Figure 7-1), take c as Paris, s and s’ as S2 and S3, respectively, and p and p’ as P2 and P5, respectively.
Of course, the fact that the foregoing MVDs hold in relvar SCP isn’t a fluke—it will always be the case with a many to many join that MVDs like those just shown hold. And the reason I mention all this is that relvars in which such MVDs hold (i.e., relvars not in 4NF) are of course subject to redundancy, and it’s generally true that relvars that are subject to redundancy can be awkward to update—as we’ll see later, in the case at hand.
While I’m on the subject of dependencies, let me also point out that the following functional dependencies (FDs) hold in relvar SCP as well:[95]
{ SNO } → { CITY }
{ PNO } → { CITY }These FDs are inherited from relvars S and P, respectively (where they certainly hold, because the determinant—the set of attributes on the left side—is a key in each case).
Compensatory Actions
Consider the following INSERT on relvar S:
INSERT ( S9 , London ) INTO S ;
Given the sample values in Figure 7-1, this insert can and will succeed, just so long as it has the additional effect of inserting the following tuples into relvar SCP:
( S9 , London , P1 ) ( S9 , London , P4 ) ( S9 , London , P6 )
By contrast, consider this INSERT:
INSERT ( S9 , Madrid ) INTO S ;
Given the sample values in Figure 7-1, this insert must fail, because there aren’t any parts in Madrid (and there’s no possible compensatory action that makes sense here, either). On the other hand, the following double INSERT can and will succeed—
INSERT ( S9 , Madrid ) INTO S , INSERT ( P8 , Madrid ) INTO P ;
—so long as it has the additional effect of inserting the following tuple into relvar SCP:
( S9 , Madrid , P8 )
From these examples and others like them, I hope it’s clear that the following is an appropriate rule for inserts on S and/or P:
ON INSERTisINTO S , INSERTipINTO P : INSERT ( P JOINis) INTO SCP , INSERT ( S JOINip) INTO SCP ;
Turning now to deletes: Suppose just for the moment that we reinstate the tuples for supplier S5 and part P3, where the city for S5 is Athens as usual, but we make the city for P3 Athens as well instead of Oslo. Thus, relvar SCP additionally contains the tuple (S5,Athens,P3)—but note that this tuple is the only one for Athens in that relvar. Now the following double DELETE clearly makes sense:
DELETE ( S5 , Athens ) FROM S , DELETE ( P3 , Athens ) FROM P ;
The effect is to delete the specified tuples from S and P and—assuming an appropriate cascade delete rule is in effect—also the tuple (S5,Athens,P3) from relvar SCP. But what about this single DELETE?—
DELETE ( S5 , Athens ) FROM S ;
Now, what can’t be allowed to happen here is for the tuple (S5,Athens) to be deleted from relvar S, exactly as requested, while everything else remains unchanged. So one possibility would be simply to reject the specified DELETE on a violation of The Golden Rule. On the grounds once again that it’s surely desirable in general for user requests to succeed if they sensibly can, however, it seems preferable to accept the DELETE and let it cascade appropriately. In other words, I propose the following as a suitable rule for deletes on relvars S and/or P:
ON DELETEdsFROM S , DELETEdpFROM P : DELETE ( SCP JOINds) FROM SCP , DELETE ( SCP JOINdp) FROM SCP ;
Given the foregoing insert and delete rules, I’ll leave it as an exercise to show that explicit UPDATEs on S and/or P all work as expected, too.
I turn now to updates on the join SCP. The insert rule is fairly obvious:
ON INSERTiINTO SCP : INSERTi{ SNO , CITY } INTO S , INSERTi{ PNO , CITY } INTO P ;
Note: I say this rule is obvious, but its consequences might not be, at least not immediately. Let’s look at a couple of examples, using the sample values from Figure 7-1:
Suppose we insert (S9,London,P1) into SCP. This insert will cause (S9,London) to be inserted into S but will have no effect on P (because (P1,London) already appears in P). But inserting (S9,London) into S will cause the insert rule for S to come into play, and the net effect will be that (S9,London,P4) and (S9,London,P6) will be inserted into SCP in addition to the originally requested tuple (S9,London,P1).
Suppose we insert (S7,Paris,P7) into SCP. The net effect will be to insert (S7,Paris) into S, (P7,Paris) into P, and all of the following tuples into SCP:
( S7 , Paris , P7 ) ( S7 , Paris , P2 ) ( S2 , Paris , P7 ) ( S7 , Paris , P5 ) ( S3 , Paris , P7 )
And now let me point out, just in case you haven’t realized it already, that the foregoing insert rule is essentially the same as its counterpart as described in Chapter 6 for the one to one case (though of course there was no question in this latter case of the original INSERT cascading to cause additional tuples to be inserted into the join).
Now, given that the foregoing insert rule can be characterized, loosely, as “Insert S subtuples unless they already exist and insert P subtuples unless they already exist,” intuition and symmetry both suggest the corresponding delete rule should be “Delete S subtuples unless they exist elsewhere and delete P subtuples unless they exist elsewhere.” Formally:
ON DELETEdFROM SCP : DELETE ( ( S MATCHINGd) NOT MATCHING SCP ) FROM S , DELETE ( ( P MATCHINGd) NOT MATCHING SCP ) FROM P ;
Again let’s consider some examples, using the sample values from Figure 7-1:
Suppose we delete all tuples from SCP where the city is Paris. This delete will cascade to delete the tuples for suppliers S2 and S3 from relvar S and the tuples for parts P2 and P5 from relvar P.
Suppose we delete all tuples for supplier S1 from SCP. This delete will cascade to delete the tuple for supplier S1 from relvar S but will have no effect on relvar P, because SCP still contains some tuples where the city is London—to be specific, the tuples (S4,London,P1), (S4,London,P4), and (S4,London,P6).
Suppose we attempt to delete just the tuple (S1,London,P1) from SCP. This attempt must fail; since SCP contains other tuples for both supplier S1 and part P1, the attempted delete has no effect on relvars S and P, and so if it were allowed to succeed we would have a Golden Rule violation on our hands (to be specific, SCP would no longer be equal to the join of S and P).
Now, if you compare the foregoing delete rule with its counterpart as described in Chapter 6 for the one to one case (repeated here for convenience)—
ON DELETEdFROM S : DELETEd{ SNO , STATUS } FROM ST , DELETEd{ SNO , CITY } FROM SC ;
—you might think the two are rather different. But they’re not. To see why not, suppose just for the moment that no city has more than one supplier or more than one part (and so the many to many join reduces to a one to one join). Then, using s, c, and p to denote a supplier number, a city, and a part number, respectively, no (s, c) subtuple appears in SPC more than once and no (p, c) subtuple appears in SCP more than once either, and so (S MATCHING d) NOT MATCHING SCP and (P MATCHING d) NOT MATCHING SCP reduce to just S MATCHING d and P MATCHING d, respectively. Furthermore, S MATCHING d and P MATCHING d in turn are equivalent to just d{SNO,CITY} and d{PNO,CITY}, respectively. Thus, the delete rule in the one to one case can be regarded as a reduced or degenerate form of the delete rule in the many to many case.
Finally, I’ll leave it as an exercise to show that, given the foregoing insert and delete rules, explicit UPDATEs all work as intuitively expected.
View Updating
Now suppose SCP is in fact a view, the join of S and P. Then:
Most, though not quite all, of the constraints spelled out near the beginning of this section will be enforced automatically. In particular, of course, the constraint to the effect that the projections S{CITY} and P{CITY} are supposed to be equal won’t automatically be enforced.
The compensatory actions from S and P to SCP will happen automatically, precisely because SCP is a view; that is, updates on S and/or P will automatically be reflected appropriately in SCP.
The compensatory actions from SCP to S and SP—these are the view updating rules as such—will also happen automatically, again precisely because SCP is a view. That is, updates on SCP are “really” updates on the underlying relvars S and/or P, and so are automatically visible in SCP, as well as in S or P or both.
What about a user who sees only the join view SCP? Well, that view will behave in all respects exactly as if it were a base relvar (though it’s only fair to point out that the behavior in question isn’t entirely straightforward, as I’ll explain in a moment). Such a user will be aware that {SNO,PNO} is a key and aware also that the following FDs and MVDs hold:
{ SNO } → { CITY }
{ PNO } → { CITY }
{ CITY } →→ { SNO } | { PNO }With regard to these MVDs, let me remind you that together they’re equivalent to the following constraint:
CONSTRAINT ... SCP = JOIN { SCP { SNO , CITY } , SCP { PNO , CITY } } ;The user will also be aware of the pertinent predicate:
| SCP: Supplier SNO and part PNO both have city CITY. |
Now, I said earlier that SCP isn’t in 4NF, and I suggested that it might therefore be awkward to update (and let me stress that this remark applies regardless of whether SCP is a base relvar or a view). Now I can be more specific. First, updates in general must (of course) abide by those MVDs. Second, INSERTs in particular are subject to the following rule:[96]
ON INSERTiINTO SCP : INSERT ( SCP JOINi{ SNO , CITY } ) INTO SCP , INSERT ( SCP JOINi{ PNO , CITY } ) INTO SCP ;
Note: This rule might look a little complicated, but it’s basically just a combination of the earlier rules for INSERTs on S, P, and SCP, revised to eliminate references to S and P as such. Observe the implication that such a rule ought to, and does, apply even in the case where SCP is a base relvar and relvars S and P don’t exist (or are hidden). Indeed, we could have arrived at this rule by considering just relvar SCP in isolation. Also, it’s worth noting that the rule in question is an example—the first we’ve seen in this book so far—of a rule that has the effect of causing certain updates to cascade to the target relvar itself.
Projection Views Revisited
I’ve discussed the case in which S and P are base relvars and SCP is a view. To complete my examination of Example 1, I ought really to discuss the inverse situation also, in which SCP is a base relvar and S and P are views of that relvar. Of course, S and P would then be projection views specifically, and such a discussion thus logically belongs in Chapter 5. Rightly or wrongly, however, I felt Chapter 5 was complicated enough already, and so I decided to defer that discussion to the present chapter.
Actually I don’t think there’s all that much to be said. Recall from Chapter 5 that if DB1 contains just a single relvar R and DB2 contains just projections of R, then DB1 and DB2 are information equivalent only if those projections are obtained by decomposing R in accordance with some join dependency (JD) that holds in R. Well, the following JD does hold in SCP:
{ { SNO , CITY } , { PNO , CITY } }
As a direct consequence, SCP can be nonloss decomposed into its projections on {SNO,CITY} and {PNO,CITY}—in other words, into relvars S and P—and those relvars are necessarily updatable (just so long as SCP itself is updatable in the first place, which of course it is). The various compensatory actions are as previously discussed:
ON INSERTiINTO SCP : INSERTi{ SNO , CITY } INTO S , INSERTi{ PNO , CITY } INTO P ; ON DELETEdFROM SCP : DELETE ( ( S MATCHINGd) NOT MATCHING SCP ) FROM S , DELETE ( ( P MATCHINGd) NOT MATCHING SCP ) FROM P ; ON INSERTisINTO S , INSERTipINTO P : INSERT ( P JOINis) INTO SCP , INSERT ( S JOINip) INTO SCP ; ON DELETEdsFROM S , DELETEdpFROM P : DELETE ( SCP JOINds) FROM SCP , DELETE ( SCP JOINdp) FROM SCP ;
Let me now add that (of course) the relationship between views S and P is many to many. And although I didn’t discuss this specific example in Chapter 5, I did in fact discuss another example in that chapter involving projection views in a many to many relationship—namely, Example 3, which involved views ST (the projection of S on SNO and STATUS) and TC (the projection of S on STATUS and CITY). To spell the point out, the relationship in that example was indeed many to many, because the same STATUS value could be associated with many suppliers and many cities (STATUS value 30 is a case in point, given our usual sample values). However, that example involved a lossy decomposition, not a nonloss one. As a consequence, updates on the projection relvars didn’t always work terribly well.
Example 2: Information Hiding
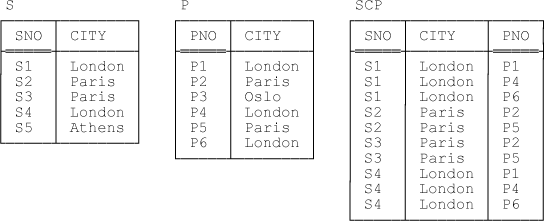
Let’s get back to the case in which S and P are both base relvars. Suppose now that (as in our original suppliers-and-parts database, in fact) a city can be represented in base relvar S and not base relvar P or the other way around; in other words, some cities have suppliers but no parts or vice versa). Then the join SCP of S and P loses information, inasmuch as it’s no longer guaranteed that S and P are equal to the projections of that join on the corresponding attributes. In fact, of the constraints mentioned in the section before last, the only ones that still apply are the following (and this time I’ll give them in prose form instead of formal syntax):
The usual key constraints all hold—{SNO} is a key for S, {PNO} is a key for P, and {SNO,PNO} is a key for SCP.
At any given time, the current value of SCP is equal to the join of the current values of S and P.
The FDs {SNO} → {CITY} and {PNO} → {CITY} and the MVDs {CITY} →→ {SNO} and {CITY} →→ {PNO} hold in SCP.
(Certain inclusion dependencies hold too, but as with the second example in Chapter 6, I won’t bother to spell out the details here.)
A concrete example of a database value satisfying the foregoing conditions can be obtained by extending Figure 7-1 to reinstate the usual tuples for supplier S5 and part P3 (see Figure 7-2, and observe in particular that the relation shown as the current value of relvar SCP in that figure is the same as it was in Figure 7-1).
A remark on terminology: The title of this chapter implies, or at least strongly suggests, that S JOIN P is still a many to many join, but it must be understood that “many” here includes the zero case. The truth is, the term “many to many” is often used somewhat loosely to include both (a) what might be called the strict case, as in Example 1 as discussed earlier, and (b) cases like the one currently under discussion, in which it’s possible for one participant to have an element with no counterpart in the other. Here’s a lightly edited quote from The Relational Database Dictionary, Extended Edition (Apress, 2008):
A many to many correspondence is, strictly, a rule pairing two sets s1 and s2 (not necessarily distinct) such that each element of s1 corresponds to at least one element of s2 and each element of s2 corresponds to at least one element of s1. However, the term is often used somewhat loosely to mean a pairing such that (a) each element of s1 corresponds to any number of elements of s2 (possibly none at all) and each element of s2 corresponds to at least one element of s1, or (b) each element of s1 corresponds to at least one element of s2 and each element of s2 corresponds to any number of elements of s1 (possibly none at all), or (c) each element of s1 corresponds to any number of elements of s2 (possibly none at all) and each element of s2 corresponds to any number of elements of s1 (possibly none at all). The term is probably best avoided unless the intended meaning is clear.
The final sentence here notwithstanding, I will in fact be using the term occasionally in the little that’s still to come of this chapter, but I think my intended meaning will always be clear from the context. End of remark.
Following on from the foregoing, let me now point out that, precisely because (as I’ve said) it loses information, the design consisting of relvar SCP alone is no longer information equivalent to the one consisting of relvars S and P taken together. (An example of a query on the latter that has no exact counterpart on the former is “Get supplier numbers for suppliers in a city in which there’s no part.”). More precisely, any information that can be represented by relvar SCP alone can certainly be represented by relvars S and P together, but the converse is false. As a consequence, it’s obvious that there are going to be certain updates that can be done on S and/or P that have no exact counterpart on SCP. An example is “Insert a tuple into S for a supplier with city Madrid,” without simultaneously inserting a tuple for that same city into P.
I don’t propose to investigate this example in any further detail here. Instead, I’m simply going to appeal to the analysis of Example 2 in Chapter 6; to be more specific, I’m going to claim that the detailed analysis of that example in that previous chapter applies to the present example also, mutatis mutandis. In other words, it’s my opinion that the rules developed earlier in the present chapter for updating a strict many to many join view can be taken, if desired, to apply to the present case as well. To paraphrase a remark from the discussions in Chapter 6, if we can agree on this position, then at least we’ll have agreed on a universal set of rules for updating many to many join views that do always work and do guarantee that joins are strictly many to many when they’re supposed to be—not to mention the point that the rules in question in fact work for all join views, regardless of whether the join in question is one to one, one to many, or many to many. What’s more, if those rules do sometimes give rise to consequences that are considered unpalatable for some reason, then there are always certain pragmatic fixes, such as using the DBMS’s authorization subsystem to prohibit certain updates, that can be adopted to avoid those consequences.
Concluding Remarks
There’s one more point I want to make in connection with many to many joins. It has to do with the fact that—as is of course well known—cartesian product is a special case of many to many join. It follows that the rules for updating through a many to many join apply to cartesian product in particular (more precisely, they reduce to the rules for updating through a cartesian product, in the case where the join itself reduces to a cartesian product). To spell those rules out, let V be defined as A TIMES B and let HA and HB be the attributes of A and B, respectively, and let HA and HB have no attribute names in common. Then we have:
ON INSERTiINTOV: INSERTi{HA} INTOA, INSERTi{HB} INTOB; ON DELETEdFROMV: DELETE ( (AMATCHINGd) NOT MATCHINGV) FROMA, DELETE ( (BMATCHINGd) NOT MATCHINGV) FROMB; ON INSERTiaINTOA, INSERTibINTOB: INSERT (BTIMESia) INTOV, INSERT (ATIMESib) INTOV; ON DELETEdaFROMA, DELETEdbFROMB: DELETE (VMATCHINGda) FROMV, DELETE (VMATCHINGdb) FROMV;
[93] I’ve simplified these predicates slightly (a) to drop “is under contract” (for suppliers) and “is used in the enterprise” (for parts), and (b) to say that suppliers and parts both “have” a city (instead of saying suppliers are “located in,” and parts are “stored in,” a city). These changes are purely cosmetic, of course; I make the first merely for simplicity and the second in order to stress the parallel nature of the roles being played by suppliers and parts in this example.
[94] An MVD is trivial if and only if either (a) the determinant (the set of attributes on the left side) includes the dependant (the set of attributes on the right side) or (b) the union of the determinant and the dependant is equal to the entire heading; a nontrivial MVD is implied by a key if and only if the determinant is a superkey. Refer to Database Design and Relational Theory if you need further explanation of these matters.
[95] As a consequence, SCP isn’t even in second normal form (2NF), let alone fourth. But it’s the violation of 4NF as such that leads to the relvar’s characteristic behavior as a many to many join.
[96] Observe that I don’t give an analogous delete rule. In fact, DELETEs on SCP will always fail unless they request, explicitly or implicitly, deletion of all tuples for some particular supplier(s) and/or deletion of all tuples for some particular part(s). E.g., given the sample values shown in Figure 7-1, a request to delete just the tuple (S1,London,P1) will fail, while a request to delete all tuples for city Paris will succeed (as we saw earlier in both cases).