Chapter 12. Group and Ungroup Views
Updating groups
Don’t need no loops
—
I turn now to the question of updating through the relational grouping and ungrouping operators (GROUP and UNGROUP, in Tutorial D). Since you might not be familiar with those operators, I’ll begin with a brief tutorial.
The Group and Ungroup Operators
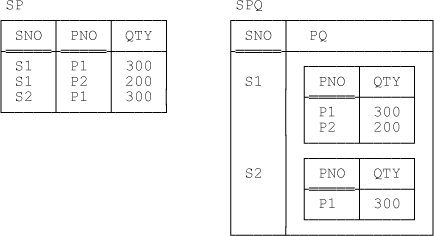
Consider the relations shown in Figure 12-1, which we can take to be the current values of two relvars called SP and SPQ, respectively. Of course, relvar SP is just the shipments relvar from our usual suppliers-and-parts database.
Now, I hope it’s at least intuitively obvious that we have information equivalence here once again[119] (certainly the relations shown in the figure both represent the exact same information).
Now, with regard to those two relations, the one on the left of the figure is just a reduced version of our usual sample value for relvar SP, while the one on the right is what we get if we evaluate the following expression on that sample SP value:
SP GROUP ( { PNO , QTY } AS PQ )
Aside: In fact the GROUP invocation just shown is logically equivalent to a certain EXTEND invocation—to be specific, the invocation EXTEND SP{SNO}:{PQ := s!!SP}, where !!SP denotes a certain image relation[120]—and there are reasons to prefer this EXTEND formulation over its GROUP equivalent. Detailed discussion of such matters is beyond the scope of this book, however. Refer to SQL and Relational Theory for further explanation. End of aside.
Now, given that the relation on the right of the figure is supposed to be the current value of a relvar called SPQ, if we evaluate the following expression on that current value—
SPQ UNGROUP ( PQ )
—then we get back to the relation on the left. Terminology: The relation on the right of the figure is a grouped version of the one on the left (grouped on PNO and QTY, to be precise), and the relation on the left is an ungrouped version of the one on the right (ungrouped on PQ, to be precise once again). Attribute PQ is a relation valued attribute (RVA for short).[121]
Let me get back for a moment to that relvar SPQ. Here’s a Tutorial D definition for that relvar:
VAR SPQ BASE RELATION
{ SNO CHAR , PQ RELATION { PNO CHAR , QTY INTEGER } }
KEY { SNO } ;Observe in particular that attribute PQ is of a certain relation type, since as I’ve said that attribute is relation valued. Note: As usual, the relvar is subject to a variety of constraints, of course; I’ve specified just one here—viz., the constraint that {SNO} is the sole key for the relvar—but I don’t want to get sidetracked into discussing any others at this juncture.
Now let me define the GROUP and UNGROUP operators more formally. In order to do so, however, it’s convenient first to introduce two auxiliary operators called WRAP and UNWRAP. Basically, WRAP wraps up specified attributes of a given relation into a single attribute that’s tuple valued, and UNWRAP does the opposite. For example, if the relation on the left of Figure 12-1 is the current value of relvar SP, the expression
SP WRAP ( { PNO , QTY } AS PQ )
yields this relation:
+---------------------+ | SNO | PQ | +-----+---------------| | | +-----------+ | | S1 | | PNO | QTY | | | | +-----+-----| | | | | P1 | 300 | | | | +-----------+ | | | +-----------+ | | S1 | | PNO | QTY | | | | +-----+-----| | | | | P2 | 200 | | | | +-----------+ | | | +-----------+ | | S2 | | PNO | QTY | | | | +-----+-----| | | | | P1 | 300 | | | | +-----------+ | +---------------------+
Note that the PQ values in this relation are tuples, not relations—PQ here is a tuple valued attribute, not a relation valued attribute. Note also that (a) attribute PQ is double underlined (if this relation is understood as the current value of some relvar, then the sole key for that relvar is the entire heading); (b) attribute PNO in the three PQ values is not double underlined, because (to say it again) those PQ values are tuples, not relations, and keys apply to relations, not tuples.
As for UNWRAP, let’s call the result of the foregoing WRAP operation spw. Then the expression
spw UNWRAP ( PQ )returns the shipments relation we started with (the one with three tuples shown on the left of Figure 12-1).
Here now are definitions of GROUP and UNGROUP. Note: I give these definitions here mainly for purposes of reference. Like many formal definitions, they might be a little difficult to understand, at least on a first reading. So I think it’s important to say up front that it’s not crucial to understand them 100 percent at this stage.
Definition: Let the heading of relation r be partitioned into subsets X = {X1,X2,…,Xm} and Y = {Y1,Y2…,Yn}; also, let YR be an attribute name not appearing in X. Then the expression r GROUP ({Y1,Y2,…,Yn} AS YR) returns a relation s. The heading of s is {X1,X2,…,Xm,YR}, where YR is of type RELATION {Y1,Y2,…,Yn}. The body of s is defined as follows. Let z be the result of r WRAP ({Y1,Y2,…,Yn} AS YT). For each distinct X value x in z, let yr be the relation whose tuples are all and only those YT values from tuples in z in which the X value is x; let t be a tuple of type TUPLE {X,YR} with X value x and YR value yr; then, and only then, t is a tuple of s.
Definition: Let relation s have an attribute YR of type RELATION {Y1,Y2,…,Yn}, and let X = {X1,X2,…,Xm} be all of the attributes of s other than YR; also, let no Xi have the same name as any Yj (0 = ≤i ≤ m, 0 ≤ j ≤ n). Then the expression s UNGROUP (YR) returns a relation r. The heading of r is {X1,X2,…,Xm,Y1,Y2,…,Yn}. The body of r is defined as follows. Let z be a relation with heading {X1,X2,…,Xm,YT}, where YT is of type TUPLE {Y1,Y2,…,Yn}, and body defined thus: For each tuple of s, z contains a set of tuples of type {X,YT}, one (t, say) for each tuple in the YR value in that s tuple; each such tuple t contains an X value equal to the X value from the s tuple in question and a YT value equal to some tuple from the YR value in the s tuple in question. Let z contain no other tuples. Then r is the result of z UNWRAP (YT).
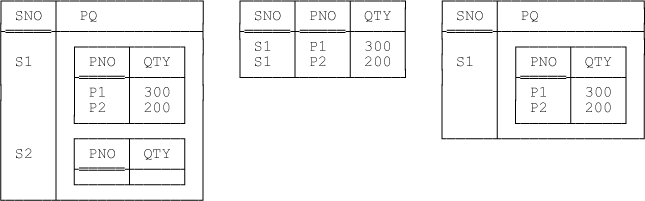
Note: Given a relation r and some grouping of r, there’s always an inverse ungrouping that yields r again; however, the converse isn’t necessarily so. The following example illustrates this point. Consider the relation—call it spq—shown on the left in Figure 12-2; note in particular that the PQ value for supplier S2 in spq is an empty relation. The expression spq UNGROUP (PQ) yields the relation—call it sp—shown in the middle of the figure. And the expression sp GROUP ({PNO,QTY} AS PQ) then yields the relation shown on the right, which is obviously not equal to the original relation spq.[122]
A Group / Ungroup Example
In order to investigate the question of updating grouped and ungrouped relvars, let’s start with the shipments relvar SP, and let’s group that relvar on PNO and QTY to define another relvar SPQ in which the grouped attribute is named PQ (basically as in the previous section). Also, to be definite, let’s assume until further notice that relvars SP and SPQ are both base ones—no views yet. The predicates are as follows:
| SP: Supplier SNO supplies part PNO in quantity QTY. |
| SPQ: Supplier SNO supplies part p in quantity q, if and only if the set of pairs PQ contains a pair (PNO,QTY) in which PNO is equal to p and QTY is equal to q.[123] |
As for constraints, {SNO,PNO} is the sole key for SP and {SNO} is the sole key for SPQ. Also, we obviously have:
CONSTRAINT ... SPQ = SP GROUP ( { PNO , QTY } AS PQ ) ;
CONSTRAINT ... SP = SPQ UNGROUP ( PQ ) ;Note: We do have reversibility here, because SPQ is defined in terms of SP instead of the other way around, implying among other things that no tuple in SPQ ever has an empty relation as its PQ value.
Now, it’s also the case that no tuple in SPQ is ever such that two distinct tuples in the PQ value within that SPQ tuple have the same PNO value. In fact this constraint is a logical consequence of the fact that {SNO,PNO} is a key for SP, together with the fact that the grouping is done (in part) on attribute PNO—but we could state it explicitly if we wanted to:
CONSTRAINT ... ( SPQ UNGROUP ( PQ ) ) KEY { SNO , PNO } ;Finally, we obviously have
CONSTRAINT ... SPQ { SNO } = SP { SNO } ;(though this constraint too is in fact a logical consequence of the way SPQ is defined).
Now let’s think about updates on relvar SP and the corresponding compensatory actions on relvar SPQ. For definiteness, let the current values of SP and SPQ be as shown in Figure 12-1. Suppose, then, that we insert the shipment tuple (S3,P2,200) into SP. (The point about this first example is that relvar SP doesn’t currently contain any tuples for supplier S3, and therefore relvar SPQ doesn’t do so either.) Clearly, then, all we need to do to relvar SPQ in this case is just insert the following tuple:
+---------------------+ | SNO | PQ | +-----+---------------| | | +-----------+ | | S3 | | PNO | QTY | | | | +-----+-----| | | | | P2 | 200 | | | | +-----------+ | +---------------------+
By contrast, suppose we insert the shipment tuple (S1,P3,400) into SP. (The point about this second example is that relvar SP does currently contain some tuples for supplier S1, and therefore relvar SPQ does so too; in fact, of course, it contains exactly one such tuple.) Clearly, then, what we need to do to relvar SPQ in this case is replace the existing tuple for supplier S1 by the following one:
+---------------------+ | SNO | PQ | +-----+---------------| | | +-----------+ | | S1 | | PNO | QTY | | | | +-----+-----| | | | | P1 | 300 | | | | | P2 | 200 | | | | | P3 | 400 | | | | +-----------+ | +---------------------+
Considerations such as the foregoing lead to the following rule for inserts on SP:
ON INSERTiINTO SP : DELETE ( SPQ MATCHINGi) FROM SPQ , INSERT ( ( SP MATCHINGi{ SNO } ) GROUP ( { PNO , QTY } AS PQ ) ) INTO SPQ ;
Note: I’m relying here on the fact that—thanks to the way multiple assignment is defined when two or more of the individual assignments involve the same target (see Appendix A)—the delete on SPQ will be done before the insert on that same relvar. However, we can avoid any such reliance by reformulating the rule as follows:
ON INSERTiINTO SP : WITH (t1:= SPQ MATCHINGi,t2:= SP MATCHINGi{ SNO } ,t3:=t2GROUP ( { PNO , QTY } AS PQ ) ) : DELETEt1FROM SPQ , INSERTt3INTO SPQ ;
Now, one interesting thing about this example is that the corresponding delete rule is very similar to the insert rule as just defined. To be more specific, if a tuple is deleted from SP, the sole SPQ tuple for the pertinent supplier needs to be deleted too; then the remaining SP tuples (if any) for that supplier can be used to compute a new tuple to be inserted into SPQ. So here’s the rule:
ON DELETEdFROM SP : WITH (t1:= SPQ MATCHINGd,t2:= SP MATCHINGd{ SNO } ,t3:=t2GROUP ( { PNO , QTY } AS PQ ) ) : DELETEt1FROM SPQ , INSERTt3INTO SPQ ;
What about updates on SPQ? Well, deletes are easy:
ON DELETEdFROM SPQ : DELETE ( SP MATCHINGd) FROM SP ;
In fact I think inserts are easy too. By way of example, assume again that the current values of relvars SP and SPQ are the relations shown in Figure 12-1. Now consider what happens if we try to insert the following tuple into relvar SPQ:
+---------------------+ | SNO | PQ | +-----+---------------| | | +-----------+ | | S4 | | PNO | QTY | | | | +-----+-----| | | | | P2 | 200 | | | | | P4 | 300 | | | | | P5 | 400 | | | | +-----------+ | +---------------------+
Well, I think it’s clear that what we need to do here is insert the following three tuples into relvar SP:
+-----------------+ +-----------------+ +-----------------+ | SNO | PNO | QTY | | SNO | PNO | QTY | | SNO | PNO | QTY | +-----+-----+-----| +-----+-----+-----| +-----+-----+-----| | S4 | P2 | 200 | | S4 | P4 | 300 | | S4 | P5 | 400 | +-----------------+ +-----------------+ +-----------------+
So here’s the insert rule:
ON INSERTiINTO SPQ : INSERT (iUNGROUP ( PQ ) ) INTO SP ;
By the way, consider what happens according to this rule if we try to insert an SPQ tuple with an empty relation as its PQ value—the following tuple, say:
+---------------------+ | SNO | PQ | +-----+---------------| | | +-----------+ | | S4 | | PNO | QTY | | | | +-----+-----| | | | +-----------+ | +---------------------+
Well, i here is the relation containing just the foregoing tuple, and the expression i UNGROUP (PQ) thus evaluates to an empty relation. Thus, nothing is inserted into relvar SP. So the operation overall fails on a Golden Rule violation—to be specific, it violates the constraint to the effect that SPQ{SNO} = SP{SNO}.
Recall now that, so far, I’ve been assuming SP and SPQ are both base relvars. But I think you can see that if SPQ is in fact a (grouped) view of SP, it really makes no difference—all of the update rules as previously discussed apply unchanged. And the same is true if, conversely, SP is an (ungrouped) view of SPQ; what’s more, it remains true even if it can’t be guaranteed that no tuple in SPQ ever has an empty relation as its PQ value, despite the fact that information equivalence is clearly lost in this case (because the constraint SPQ = SP GROUP ({ PNO,QTY} AS PQ) no longer holds).
A Summarize Example
The Tutorial D SUMMARIZE operator comes in two forms. I defer discussion of the more general form to the next chapter (Chapter 13); however, it’s convenient to discuss the simpler form here. (The reason it’s convenient is that the simpler version, although it’s actually a special case of the more general version, can be thought of as a variation on the GROUP operator as discussed in the previous two sections.) Here’s an example. Once again, let the current value of relvar SP be the relation shown on the left in Figure 12-1. Then the following expression—
SUMMARIZE SP BY { SNO } : { TQY := SUM ( QTY ) } ;—yields the relation shown here:
+-----------+ | SNO | TQY | +-----+-----| | S1 | 500 | | S2 | 300 | +-----------+
You can think of this result being produced as follows (see later for a formal definition): First, the expression SP GROUP ({PNO,QTY} AS PQ) is evaluated, to produce an intermediate result spq, say; then, in each tuple in spq, the PQ value—which is a relation, of course—is replaced by a TQY value, that TQY value being obtained by computing the “summary” SUM(QTY) on that PQ relation.
Aside: In fact the foregoing SUMMARIZE invocation is logically equivalent to a certain EXTEND invocation—to be specific, the invocation EXTEND SP{SNO}:{TQY := SUM(!!SP,QTY)}, where !!SP denotes a certain image relation—and there are reasons to prefer this EXTEND formulation over its SUMMARIZE equivalent. Again, however, detailed discussion of such matters is beyond the scope of this book. Refer to SQL and Relational Theory for further explanation. End of aside.
Here now is another example (“for each supplier, compute the sum of distinct shipment quantities”):
SUMMARIZE SP { SNO , QTY } BY { SNO } : { TQY := SUM ( QTY ) }This expression denotes a summarization of a certain projection of SP—the projection on SNO and QTY, to be specific—and that projection contains, for each supplier number, just the pertinent distinct shipment quantities, as required.[124] Note: Given the sample value of SP in Figure 12-1, the expression overall happens to yield the same result as the previous example does, but it won’t do so in general, of course.
Here now is a definition of this form of SUMMARIZE:[125]
Definition: Let relation r have attributes called A1, A2,…, An (and possibly others) and no attribute called B. Then the expression SUMMARIZE r BY {A1,A2,…,An} : {B := summary} returns a relation with heading {A1,A2,…,An,B} and body the set of all tuples t such that t is equal to the projection of some tuple of r on A1, A2,…, An, extended with a value b for B. That value b is computed by evaluating summary over all tuples of r that have the same value for attributes A1, A2,…, An as t does.
Aside: I assume for the purposes of this book that the notion of “evaluating a summary” can be defined precisely.[126] I certainly don’t want to attempt such a definition here—there are certain complexities involved, complexities that (perhaps fortunately) have no bearing on the main subject of this book. So I’ll just assume you have an adequate intuitive understanding of what’s involved and leave it at that. I’ll assume also that you’re familiar with the kinds of summaries that can typically be requested—counts, sums, averages, and so forth. End of aside.
So now let’s assume SP is a base relvar, and let’s define a view STQ as indicated by the following constraint:
CONSTRAINT ... STQ = SUMMARIZE SP BY { SNO } : { TQY := SUM ( QTY ) } ;The predicates are as follows:
| SP: Supplier SNO supplies part PNO in quantity QTY. |
| STQ: Supplier SNO supplies parts in total quantity TQY. |
Note: Actually, the predicate for STQ is inadequate as it stands—it could do with a tiny refinement. I’ll come back to this point in the next chapter, but you might like to see if you can figure out for yourself just what it is I’m getting at here.
Of course, there’s no information equivalence in this example. That’s why defining STQ as a view of SP makes sense, but defining SP as a view of STQ certainly doesn’t—in fact, it can’t be done.
As for constraints, {SNO,PNO} is the sole key for SP and {SNO} is the sole key for STQ. Also, we obviously have the following—
CONSTRAINT ... STQ { SNO } = SP { SNO } ;—though this constraint is in fact a logical consequence of the way STQ is defined.
Now let’s think about updates on relvar SP and the corresponding compensatory actions. For definiteness, let the current values of relvars SP and STQ be as shown in Figure 12-3.
Suppose we insert the shipment tuple (S3,P2,200) into SP. Clearly, then, all we need to do to relvar STQ in this case is insert the tuple (S3,200). By contrast, suppose we insert the shipment tuple (S1,P3,400) into SP; now what we need to do is replace the existing tuple for supplier S1 in relvar STQ by this one: (S1,900). So the rule for inserts on SP looks like this:
ON INSERTiINTO SP : WITH (t1:= STQ MATCHINGi,t2:= SP MATCHINGi{ SNO } ,t3:= SUMMARIZEt2BY { SNO } : { TQY := SUM ( QTY ) } ) : DELETEt1FROM STQ , INSERTt3INTO STQ ;
As you can see, therefore, the foregoing is very similar to its counterpart in the GROUP/UNGROUP example from the previous section. And it should be clear that an analogous remark applies to the delete rule as well. To be specific, if a tuple is deleted from SP, the sole STQ tuple for the pertinent supplier needs to be deleted too; then the remaining SP tuples (if any) for that supplier can be used to compute a new tuple to be inserted into STQ. So here’s the rule:
ON DELETEdFROM SP : WITH (t1:= STQ MATCHINGd,t2:= SP MATCHINGd{ SNO } ,t3:= SUMMARIZEt2BY { SNO } : { TQY := SUM ( QTY ) } ) : DELETEt1FROM STQ , INSERTt3INTO STQ ;
What about updates on STQ? Well, once again deletes are easy:
ON DELETEdFROM STQ : DELETE ( SP MATCHINGd) FROM SP ;
However, inserts make no sense, in general; for example, what could it possibly mean to insert the tuple (S5,600) into STQ? So there’s no rule for inserts on STQ.[127] Of course, the fact that there’s no rule doesn’t mean we can’t do inserts (indeed, the update rules for SP explicitly call for such actions)—it only means that such operations are likely to fail on a Golden Rule violation, except possibly if they’re part of some multiple assignment (as indeed they are, in the case of the rules for updates on SP).
[119] But see the footnote at the very end of this section.
[122] But do you think those two relations are information equivalent? (You might want to revisit this question after reading Chapter 14.)
[123] As you can see, the RVA makes the predicate for relvar SPQ a little tricky. This state of affairs gives some indication as to why RVAs are usually—though not invariably—contraindicated, at least in base relvars. Detailed consideration of this point would take us much too far afield here, however; see Database Design and Relational Theory for further discussion.
[124] As this example should be sufficient to suggest, Tutorial D has no need for—nor does it support anything analogous to—SQL’s ad hoc trick of allowing summaries to include the keyword DISTINCT.
[125] Observe that this definition makes use of the tuple version of projection, also a tuple version of the relational EXTEND operator. See SQL and Relational Theory for further discussion.
[126] In the example, evaluating the summary SUM(QTY) actually requires invoking the SUM aggregate operator on the QTY attribute of what I earlier referred to as “the PQ relation.” For further explanation, see SQL and Relational Theory.
[127] Actually it might sometimes be possible to perform inserts on a view such as STQ after all; for example, there might be just one summand. Alternatively, some constraint might hold that has the effect of making the view “insertable into”; an example might be a constraint to the effect that the summands must all be equal. (Thanks to David McGoveran for these observations.)