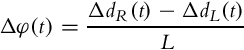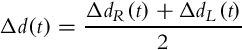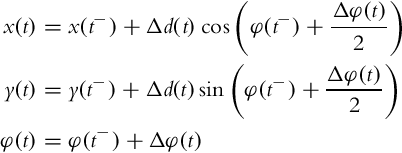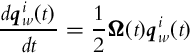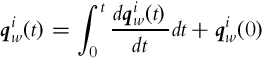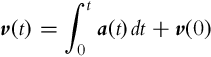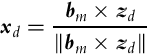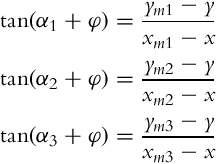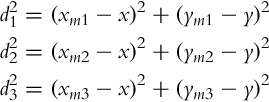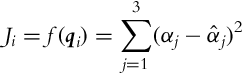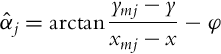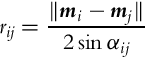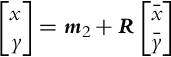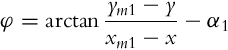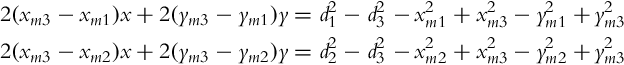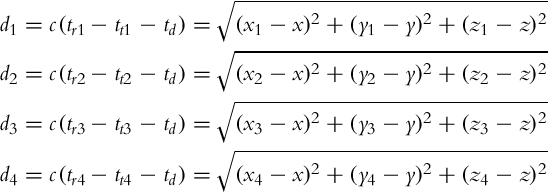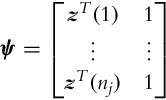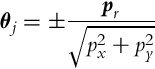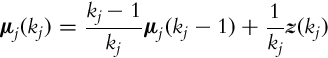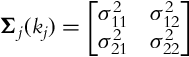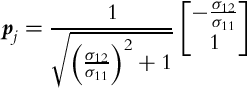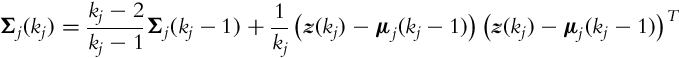5.3 Pose Measurement Methods

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

5.3 Pose Measurement Methods

In the following the main methodologies are introduced showing how sensors are used to estimate robot pose in the environment. Those approaches can measure relative pose advancement according to previously determined pose or absolute pose according to some reference-based coordinate system.

5.3.1 Dead Reckoning

Dead reckoning (also called deduced reckoning) approaches estimate the robot’s (equipped with relative sensors) current pose from the known previous pose and relative measured displacements from the previous pose. Those displacements or motion increments (distance and orientation) are calculated from measured speeds over the elapsed time and heading. Common to those approaches is the use of path integration to estimate the current pose; therefore, the accumulation of different errors (error of integration method, measurement error, bias, noise, etc.) typically appears.

The two basic approaches used in mobile robotics are odometry and inertial navigation.

Odometry

Odometry is used to estimate the robot pose by integration of motion increments that can be measured or gathered from applied motion commands. Relative motion increments are in mobile robotics usually obtained from axis sensors (e.g., incremental encoder) that are attached to the robot’s wheels. Using an internal kinematic model (see Eq. 2.1 for differential drive) these wheel rotation measurements are related to the position and the orientation changes of the mobile robot. The position and orientation changes given in the known time period between successive measurements can also be expressed by robot velocities. In some cases wheel angular velocities can be measured directly or inferred from known velocity commands (supposing that implemented speed controllers are accurate).

Let us assume there is a robot with differential drive and incremental encoder sensors mounted on the wheels. The measurements give relative rotation change of the left and right wheel, namely Δα_L(t) and Δα_R(t), from the previous orientation at time t⁻ = t −Δt. Supposing that there is pure rolling of the wheels the traveled distances are

$\begin{array}{l} Δ d_{L} (t) = Δ α_{L} (t) R, Δ d_{R} (t) = Δ α_{R} (t) R \end{array}$ $\begin{array}{l} Δ d_{L} (t) = Δ α_{L} (t) R, Δ d_{R} (t) = Δ α_{R} (t) R \end{array}$

where R is the wheel’s radius. Using the internal kinematic model (2.1) orientation displacement and traveled distance (position displacements) are

$\begin{array}{l} Δ φ (t) = \frac{Δ d_{R} (t) - Δ d_{L} (t)}{L} \end{array}$ $\begin{array}{l} Δ φ (t) = \frac{Δ d_{R} (t) - Δ d_{L} (t)}{L} \end{array}$

si154_e

and

$\begin{array}{l} Δ d (t) = \frac{Δ d_{R} (t) + Δ d_{L} (t)}{2} \end{array}$ $\begin{array}{l} Δ d (t) = \frac{Δ d_{R} (t) + Δ d_{L} (t)}{2} \end{array}$

si155_e

where L is the distance between the wheels.

The robot pose estimate is obtained by integration of the external kinematic model (2.2) from measured robot velocities or as a summation of calculated robot position and orientation displacements. Applying trapezoidal numerical integration the estimated robot pose is

$\begin{array}{l} \begin{matrix} x (t) & = x (t^{-}) + Δ d (t) cos (φ (t^{-}) + \frac{Δ φ (t)}{2}) \\ y (t) & = y (t^{-}) + Δ d (t) sin (φ (t^{-}) + \frac{Δ φ (t)}{2}) \\ φ (t) & = φ (t^{-}) + Δ φ (t) \end{matrix} \end{array}$ $\begin{array}{l} \begin{matrix} x (t) & = x (t^{-}) + Δ d (t) cos (φ (t^{-}) + \frac{Δ φ (t)}{2}) \\ y (t) & = y (t^{-}) + Δ d (t) sin (φ (t^{-}) + \frac{Δ φ (t)}{2}) \\ φ (t) & = φ (t^{-}) + Δ φ (t) \end{matrix} \end{array}$

si156_e (5.59)

However, due to the integral nature of odometry, cumulative error occurs. The main source of the error consists of the systematic and nondeterministic error sources. The former includes errors due to approximate kinematic models (e.g., wrong radius of the wheel), error due to accuracy of applied integration method, and measurement error (unknown bias), and the latter includes slippage of the wheels, noise, and the like. Therefore, independent use of odometry is applicable only for short-term pose estimation at a known initial pose. More commonly, odometry is used in combination with pose measurements from absolute sensors where odometry is used for prediction and filtration of absolute pose measurements to obtain better pose estimates.

In wheeled mobile systems sensors used in odometry usually are axis sensors (e.g., incremental optical or magnetic encoders, potentiometers) that are attached to the wheels’ axes and measure rotation angle or velocity.

Inertial Navigation

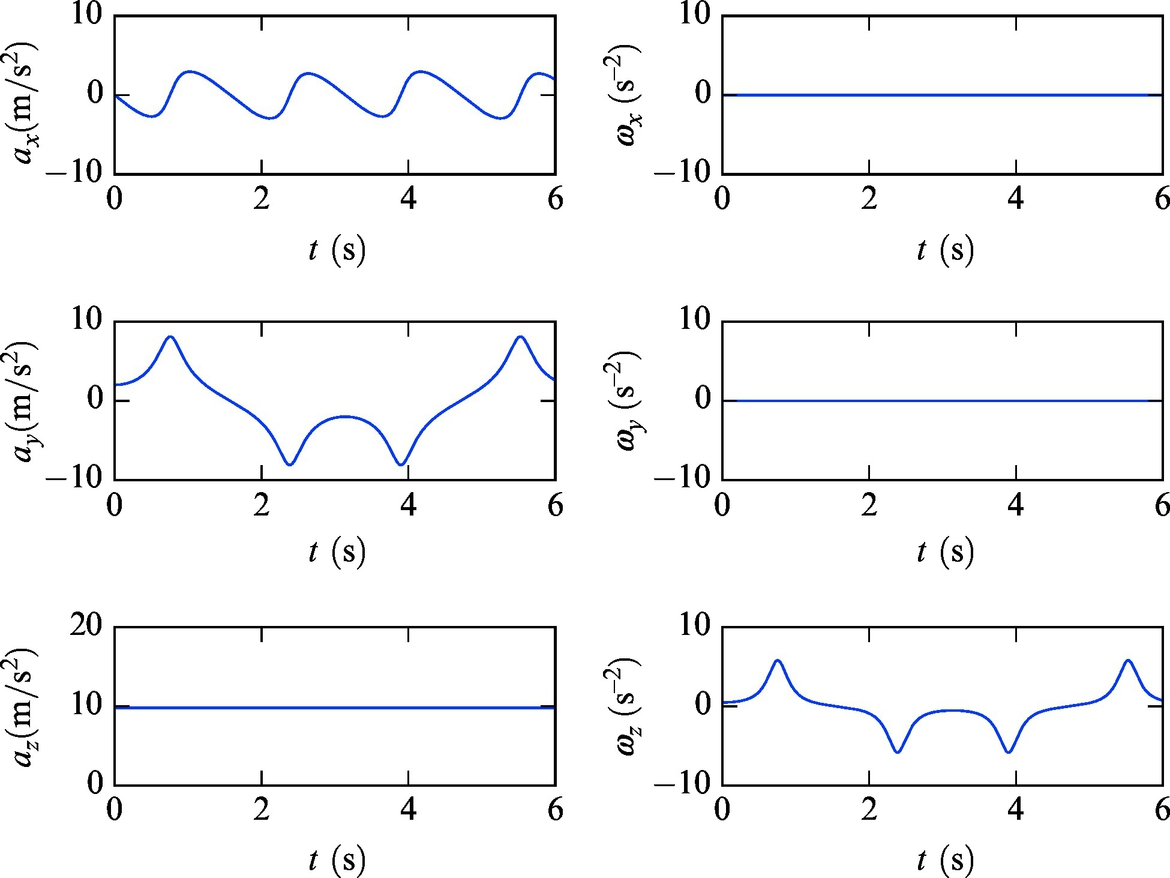
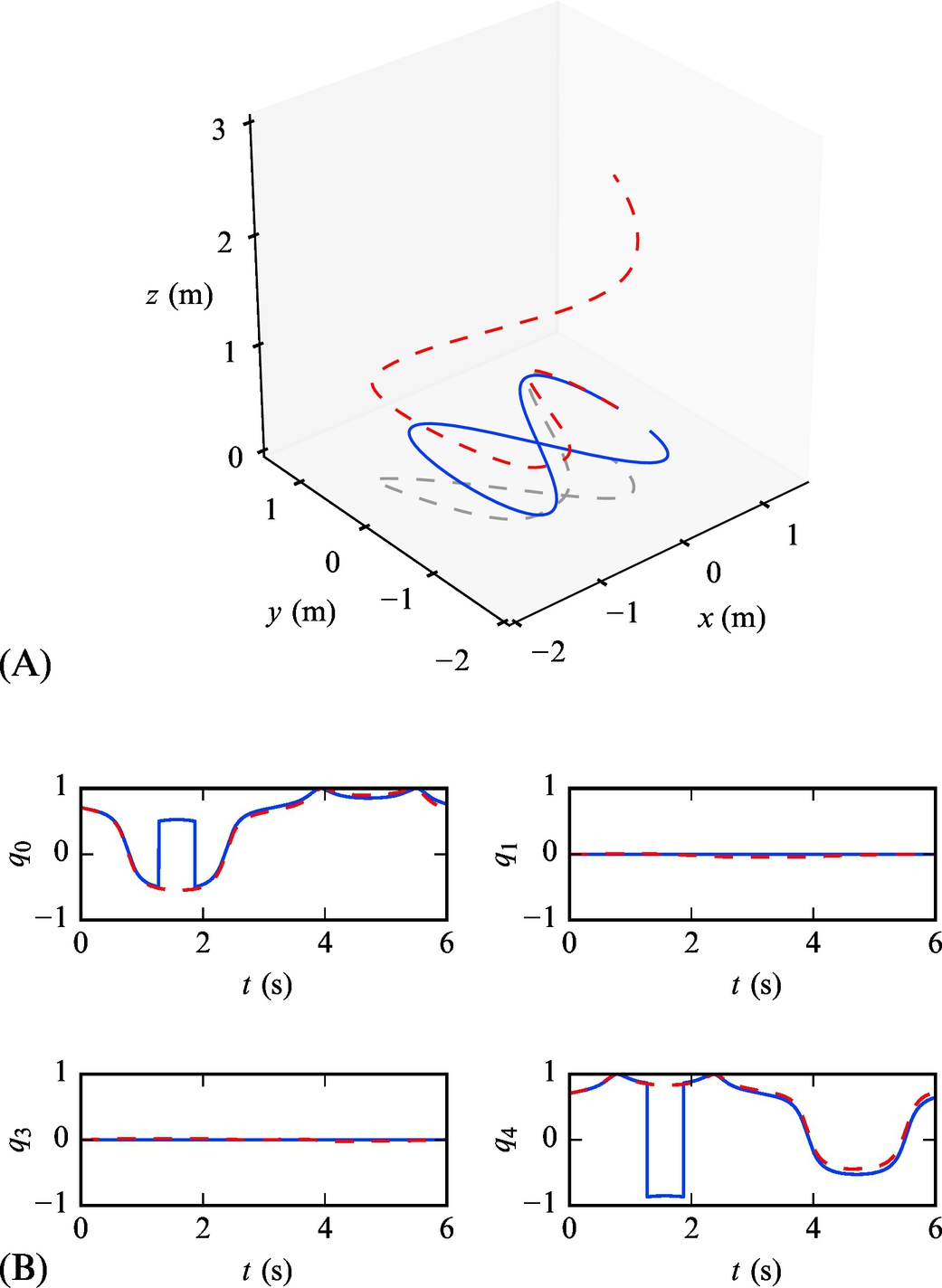
An inertial navigation system (INS) is a self-contained technique to estimate vehicle position, orientation, and velocity by means of dead reckoning. INS includes motion sensors (accelerometers) and rotation sensors (gyroscopes) where position and orientation of the vehicle is estimated relatively to a known initial starting pose.

Output of accelerometer and gyroscope measurements are 3D vectors of accelerations and angular velocities in space. To estimate robot position and orientation double integration of acceleration measurement and single integration of angular velocity is required. Use of integration is the main cause for pose error of INSs because of accumulation of constant (systematic) errors (sensor drift, bad sensor calibration, etc.). Constant measurement error causes quadratic growth of the position estimate error with time while the error of orientation estimate grows linearly with time. Additionally the error of position estimate in INS is dependent on the error of orientation estimate because the accelerometer measures total acceleration including gravitation. Vehicle (INS unit) acceleration is obtained from acceleration measurement by subtracting gravity acceleration, which requires the accurate knowledge of the vehicle orientation. Any error in orientation therefore causes incorrect virtual acceleration due to inexact gravity canceling. This is especially problematic because vehicle accelerations are usually much smaller than gravity. A small signal-to-noise ratio (SNR) at lower accelerations causes additional troubles. These effects are clearly seen from the acceleration sensor model consisting of translational vehicle acceleration a, gravity g = [0, 0, 0.981]^T, and radial acceleration,

$\begin{array}{l} a_{m} = {R_{i}^{w}}^{T} (a + R_{e}^{w} g + ω \times v) + a_{bias} + a_{noise} \end{array}$ $\begin{array}{l} a_{m} = {R_{i}^{w}}^{T} (a + R_{e}^{w} g + ω \times v) + a_{bias} + a_{noise} \end{array}$

(5.60)

where a_m is the acceleration measurement from a sensor in its local coordinates, $R_{e}^{w}$ $R_{e}^{w}$ is the rotation matrix between Earth’s coordinates and world coordinates where pose tracking is performed, $R_{i}^{w}$ $R_{i}^{w}$ is the rotation matrix from the local INS coordinates to the world coordinates, ω is angular velocity in world coordinates, v is translational velocity, a_bias is acceleration bias, and a_noise is noise.

To estimate orientation a gyroscope measurement is used. The model of a gyroscope sensor is

$\begin{array}{l} ω_{m} = ω_{i} + ω_{bias} + ω_{noise} \end{array}$ $\begin{array}{l} ω_{m} = ω_{i} + ω_{bias} + ω_{noise} \end{array}$

(5.61)

where ω_m is a vector of measured angular rates, ω_i is a true vector of angular rates of the body in local coordinates, ω_bias is sensor bias, and ω_noise is sensor noise.

To estimate INS unit orientation the unit angular rate estimates are obtained from Eq. (5.61) as follows: ω_i =ω_m −ω_bias. The biased part is usually estimated online by means of some estimator (e.g., Kalman filter). Exceptionally, for shorter estimation periods, the bias can be supposed constant if quality gyroscope is used and initial calibration (estimation of ω_bias) is made. Note, however, that bias is changing with time. Therefore, the latter approach is sufficient for short-term use only. The simplest calibration may be obtained by averaging the gyroscope measurement (for N measurements) while holding the INS unit in a constant position ( $ω_{bias} = \frac{1}{N} \sum_{i = 1}^{N} ω_{m}$ $ω_{bias} = \frac{1}{N} \sum_{i = 1}^{N} ω_{m}$ , when ω_i = 0).

A relative estimate of INS unit orientation according to initial orientation is then obtained using rotational kinematics for quaternions (5.39) as follows:

$\begin{array}{l} \frac{d q_{w}^{i} (t)}{d t} & = \frac{1}{2} Ω (t) q_{w}^{i} (t) \end{array}$ $\begin{array}{l} \frac{d q_{w}^{i} (t)}{d t} & = \frac{1}{2} Ω (t) q_{w}^{i} (t) \end{array}$

si162_e (5.62)

$\begin{array}{l} q_{w}^{i} (t) & = \int_{0}^{t} \frac{d q_{w}^{i} (t)}{d t} d t + q_{w}^{i} (0) \end{array}$ $\begin{array}{l} q_{w}^{i} (t) & = \int_{0}^{t} \frac{d q_{w}^{i} (t)}{d t} d t + q_{w}^{i} (0) \end{array}$

si163_e (5.63)

where $q_{w}^{i} (t)$ $q_{w}^{i} (t)$ is the quaternion that describes the rotation from world (w) coordinates to INS unit coordinates (i), $q_{w}^{i} (0)$ $q_{w}^{i} (0)$ is the initial orientation,

$\begin{array}{l} Ω (t) = [\begin{array}{l} 0 & - ω_{x} & - ω_{y} & - ω_{z} \\ ω_{x} & 0 & ω_{z} & - ω_{y} \\ ω_{y} & - ω_{z} & 0 & ω_{x} \\ ω_{z} & ω_{y} & - ω_{x} & 0 \end{array}] \end{array}$ $\begin{array}{l} Ω (t) = [\begin{array}{l} 0 & - ω_{x} & - ω_{y} & - ω_{z} \\ ω_{x} & 0 & ω_{z} & - ω_{y} \\ ω_{y} & - ω_{z} & 0 & ω_{x} \\ ω_{z} & ω_{y} & - ω_{x} & 0 \end{array}] \end{array}$

si166_e

and ω_i(t) = [ω_x, ω_y, ω_z]^T. To obtain the DCM $R_{w}^{i} = {R_{i}^{w}}^{T}$ $R_{w}^{i} = {R_{i}^{w}}^{T}$ use relation (5.18). In implementation of Eq. (5.63) a numerical integration (5.36) can be used.

To estimate INS unit position a translational acceleration in world coordinates is computed from Eq. (5.60):

$\begin{array}{l} a = R_{i}^{w} (a_{m} - a_{bias}) - R_{e}^{w} g - ω \times v \end{array}$ $\begin{array}{l} a = R_{i}^{w} (a_{m} - a_{bias}) - R_{e}^{w} g - ω \times v \end{array}$

(5.64)

where the angular velocity vector in world coordinates is $ω = R_{i}^{w} ω_{i}$ $ω = R_{i}^{w} ω_{i}$ and the bias term a_bias needs to be estimated online by means of some estimator (e.g., Kalman filter). Also, a proper acceleration sensor calibration is required. The velocity estimate v(t) and position x(t) are obtained by integration:

$\begin{array}{l} v (t) & = \int_{0}^{t} a (t) d t + v (0) \end{array}$ $\begin{array}{l} v (t) & = \int_{0}^{t} a (t) d t + v (0) \end{array}$

si170_e (5.65)

$\begin{array}{l} x (t) & = \int_{0}^{t} v (t) d t + x (0) \end{array}$ $\begin{array}{l} x (t) & = \int_{0}^{t} v (t) d t + x (0) \end{array}$

si171_e (5.66)

Example 5.8

Simulate measured acceleration and angular rates for a differential robot with an INS unit that drives on the curve $x (t) = cos (t)$ $x (t) = cos (t)$ , $y (t) = sin (2 t)$ $y (t) = sin (2 t)$ , and z(t) = 0 (all defined in world coordinates). The time of simulation is 6 s and the sampling time is 1 ms. The INS unit is oriented so that its x-axis is tangent to trajectory, the y-axis is perpendicular to the x-axis, and the z-axis is aligned with the z-axis of the world coordinates.

From the measurements, estimate, the INS unit position and orientation in world coordinates. Additionally, consider sensor bias and noise and observe how this influences the estimated INS pose.

Solution

The INS unit angular rates in the simulation are obtained considering relation (5.46) to obtain the matrix of angular rates $Ω^{'} = \frac{d R}{d t} Ω^{'} R^{T}$ $Ω^{'} = \frac{d R}{d t} Ω^{'} R^{T}$ . The simulated accelerometer and gyroscope measurements are modeled using Eqs. (5.60), (5.61) and are shown in Fig. 5.7.

f05-07-9780128042045 — Fig. 5.7 Simulated acceleration (left column) and angular rate (right column) measurements of INS unit.

The estimated position and orientation of INS in an ideal case with no noise and bias are shown in Fig. 5.8.

f05-08-9780128042045 — Fig. 5.8 Estimated position (A) and orientation (B) of INS unit from accelerometer and gyroscope measurements in an ideal situation (no noise and no bias). A smaller position error can be observed at the end of the simulation due to numeric integration.

The estimated pose in the case of noisy measurements and included bias are shown in Fig. 5.9, where fast growth of the position error can be observed.

f05-09-9780128042045 — Fig. 5.9 Estimated position (A) and orientation (B) of the INS unit from the accelerometer and gyroscope measurements with included sensor noise and bias. Because bias is not compensated, a huge error in the position estimate and a smaller error in orientation appears.

A script to simulate the INS unit and estimate its pose is given in Listing 5.5 (functions rotX, rotY, and rotZ are Matlab implementations of Eqs. 5.3, 5.4, 5.5, respectively).

Listing 5.5

Simulation of the INS unit

1 biasA = [ 1 ; 1; 1]*0.02; biasW = [ 1 ; 1; 1]*0.04; % Sensor bias

2 SigmaA = 0 . 1 ; SigmaW = 0.05; % Sensor noise

4 nSteps = 6000; dT = 0.001; t = 0; % Time samples , step s i z e

6 for k = 1: nSteps

7 % INS motion simulation: get true robot pose , acceleration and rotation

8 x = [cos( t ) ; sin(2* t ) ; 0 ] ; % Position

9 v = [− sin ( t ) ; 2*cos(2* t ) ; 0 ] ; % Velocity

10 a = [− cos ( t );−4* sin (2* t ) ; 0 ] ; % Acceleration

12 f i = [ 0 ; 0; atan2(v (2) , v (1) ) ] ; % Euler angles (from world to INS)

13 dfi = [ 0 ; 0; (v (1) *a (2) − v (2) * a (1) ) /( v (1)ˆ2 + v (2) ˆ2) ] ; % Derivative

14 Rx = rotX ( f i (1) ) ; Ry = rotY ( f i (2) ) ; Rz = rotZ ( f i (3) ) ;

15 dRx = [0 , 0 , 0; 0,− sin( f i (1) ) , cos( f i (1) ) ; 0,− cos( f i (1) ),− sin ( f i (1) ) ] ;

16 dRy = [− sin ( f i (2) ) , 0,− cos( f i (2) ) ; 0 , 0 , 0; cos( f i (2) ) , 0,− sin( f i (2) ) ] ;

17 dRz = [− sin ( f i (3) ) , cos( f i (3) ) , 0;− cos ( f i (3) ),− sin ( f i (3) ) , 0; 0 , 0 , 0 ] ;

18 R = Rx*Ry*Rz ;

19 dR = dRx*Ry*Rz* dfi (1) + Rx*dRy*Rz* dfi (2) + Rx*Ry*dRz* dfi (3) ;

20 q = dcm2quat(R) . ’ ; % Quaterion from world to INS

22 % Gyro measurements

23 Omega = dR* R. ’ ; % Skew− symmetric form of the angular rate vector wb

24 wb = −[ Omega (3 ,2) ; Omega (1 ,3) ; − Omega (1 ,2) ] ; % Angular rates of the INS

26 % Accelerometer measurements

27 agDyn = a ; % Dynamic acceleration in world coordinates

28 agGrav = [ 0 ; 0; 9 . 8 1 ] ; % Gravitation

29 Rearth = eye(3) ; % Assume world and Earth frames are the same

30 wg = R. ’*wb; % True angular rates in world frame

31 wgSkew = [0 − wg (3) wg (2) ; wg (3) 0 − wg (1) ; − wg (2) wg (1) 0 ] ;

32 vg = v ; % Velocity in world frame

34 % Measured angular rates and accelerations

35 wbMea = wb + biasW + randn(3 ,1) *SigmaW;

36 abMea = R*(agDyn + Rearth*agGrav + wgSkew*vg) + biasA + randn(3 ,1) *SigmaA ;

38 % I n e r t i a l navigation

39 if k ==1 % I n i t i a l i z a t i o n

40 qEst = q ; xEst = x ; vEst = v ; % Init true i n i t i a l values

41 else % Update

42 % Gyro

43 wx = wbMea(1) ; wy = wbMea(2) ; wz = wbMea(3) ;

44 OMEGA = [ 0 − wx − wy − wz ; …

45 wx 0 wz − wy ; …

46 wy − wz 0 wx ; …

47 wz wy − wx 0 ] ;

48 dQest = 0.5* OMEGA *qEst ;

49 qEst = qEst + dQest*dT; % Quaterninon integration

50 qEst = qEst/norm( qEst ) ; % Quaternion normalization

51 % Acceleration

52 agGrav = [ 0; 0; 9 . 8 1 ] ; % Gravity

53 R_ = quat2dcm( qEst . ’ ) ; % Ratation from world to INS

54 Rearth = eye(3) ; % Earth frame i s the same as world frame

55 wg_ = R_. ’ * [wx; wy; wz ] ; % Angular rates in world frame

56 wgSkew_ = [0 − wg_ (3) wg_ (2) ; wg_(3) 0 − wg_ (1) ; − wg_ (2) wg_ (1) 0 ] ;

57 Aest = R_. ’*abMea − Rearth * agGrav − wgSkew_ * vEst ; % Estimated a

58 vEst = vEst + Aest*dT; % Estimated velocity

59 xEst = xEst + vEst*dT; % Estimated position

60 end

61 t = t + dT;

62 end

5.3.2 Heading Measurement

Heading measurement systems provide information about the vehicle orientation (or attitude) in space, the direction the vehicle is pointing. Several sensors can be used to estimate heading information such as a magnetometer, gyroscope, and accelerometer. Their information is integrated in sensor systems to estimate heading information (e.g., attitude, compass, or inclinometer).

The magnetometer and accelerometer provide absolute measurements of 3D direction vectors of Earth’s magnetic field (strength and direction) and Earth’s gravity direction vector (if the sensor unit is not accelerating), respectively. To lower heading estimation noise and improve accuracy also the relative measurements from the gyroscope are included in estimation filters.

To estimate orientation of the sensor unit according to some reference frame (e.g., Earth’s fixed coordinates) at least two directional vectors are required. To illustrate the idea the first sensor can be a magnetometer whose measurement model reads

$\begin{array}{l} b_{m} = R_{w}^{i} R_{e}^{w} b_{true} + b_{bias} + b_{noise} \end{array}$ $\begin{array}{l} b_{m} = R_{w}^{i} R_{e}^{w} b_{true} + b_{bias} + b_{noise} \end{array}$

(5.67)

where b_m is the measured magnetic field in sensor coordinates, b_true is Earth’s magnetic field in Earth coordinates for some place on Earth, and rotation matrices are defined as in Eq. (5.60). b_true can be approximated as constant for some small area on Earth (e.g., 10 × 10 km²). The second sensor is the accelerometer with a model given in Eq. (5.60), whose measurement in the case of nonaccelerating motion points in the direction of gravity and the defined z-axis of Earth’s fixed coordinates.

Orientation of the sensor unit according to Earth’s fixed coordinates is described by the DCM $R_{e}^{i} = {R_{i}^{w}}^{T} R_{e}^{w}$ $R_{e}^{i} = {R_{i}^{w}}^{T} R_{e}^{w}$ . This can be obtained by creating a matrix of the Earth’s coordinate axis vectors expressed in the local coordinates as follows. In static case accelerometer measures the direction vector from Earth’s center to the INS position. This direction therefore defines the z-axis of Earth coordinates and is expressed in a local (sensor) frame as follows:

$\begin{array}{l} z_{d} = \frac{a_{m}}{∥ a_{m} ∥} \end{array}$ $\begin{array}{l} z_{d} = \frac{a_{m}}{∥ a_{m} ∥} \end{array}$

si177_e

The direction of Earth axis x expressed in local coordinates is defined by the component of the magnetometer vector that is perpendicular to z_d:

$\begin{array}{l} x_{d} = \frac{b_{m} \times z_{d}}{∥ b_{m} \times z_{d} ∥} \end{array}$ $\begin{array}{l} x_{d} = \frac{b_{m} \times z_{d}}{∥ b_{m} \times z_{d} ∥} \end{array}$

si178_e

where × denotes the cross product. Direction to the north defines Earth’s y-axis expressed in local coordinates:

$\begin{array}{l} y_{d} = z_{d} \times x_{d} \end{array}$ $\begin{array}{l} y_{d} = z_{d} \times x_{d} \end{array}$

The obtained rotation matrix is

$\begin{array}{l} R_{e}^{i} = [x_{d}, y_{d}, z_{d}] \end{array}$ $\begin{array}{l} R_{e}^{i} = [x_{d}, y_{d}, z_{d}] \end{array}$

(5.68)

from where the DCM between the world and Earth coordinates is $R_{w}^{i} = {R_{i}^{w}}^{T} = {(R_{e}^{i} {R_{e}^{w}}^{T})}^{T}$ $R_{w}^{i} = {R_{i}^{w}}^{T} = {(R_{e}^{i} {R_{e}^{w}}^{T})}^{T}$ . This orientation can also be described by quaternions using relations (5.19)–(5.22) or by Euler angles using relation (5.6).

Accurate orientation estimation of the vehicle is important also when performing odometry or inertial navigation to lower orientation error and consequentially the error in position estimates. Therefore, absolute heading measurements are often combined with dead reckoning as a correction measurement in the correction step of estimators (e.g., Kalman filter).

5.3.3 Active Markers and Global Position Measurement

Localization in the environment is possible also by observing markers located at known positions in the environment. These markers can be natural if they are already part of the environment (e.g., lights on the ceiling, Wi-Fi transmitters, etc.) or they can be artificial if they are placed in the environment for the purpose of localization (e.g., radiofrequency transmitters, ultrasonic or infrared transmitters (beacons), wires buried in the ground for robotic lawn mowers, GNSS satellites, etc.).

The main advantages of using active markers are simplicity, robustness, and fast localization. However, their operational cost, maintenance, and setup cost are relatively high.

To estimate the position or pose of the system usually the triangulation or trilateration approach is applied. Trilateration uses measured distances from more transmitters to estimate the position of the receiver (mounted on the vehicle). A very well-known trilateration approach is global positioning using a global navigation satellite system (GNSS) where active markers are GNSS satellites at known locations in space. Triangulation uses measured angles to three or more markers (e.g., light source) on known locations.

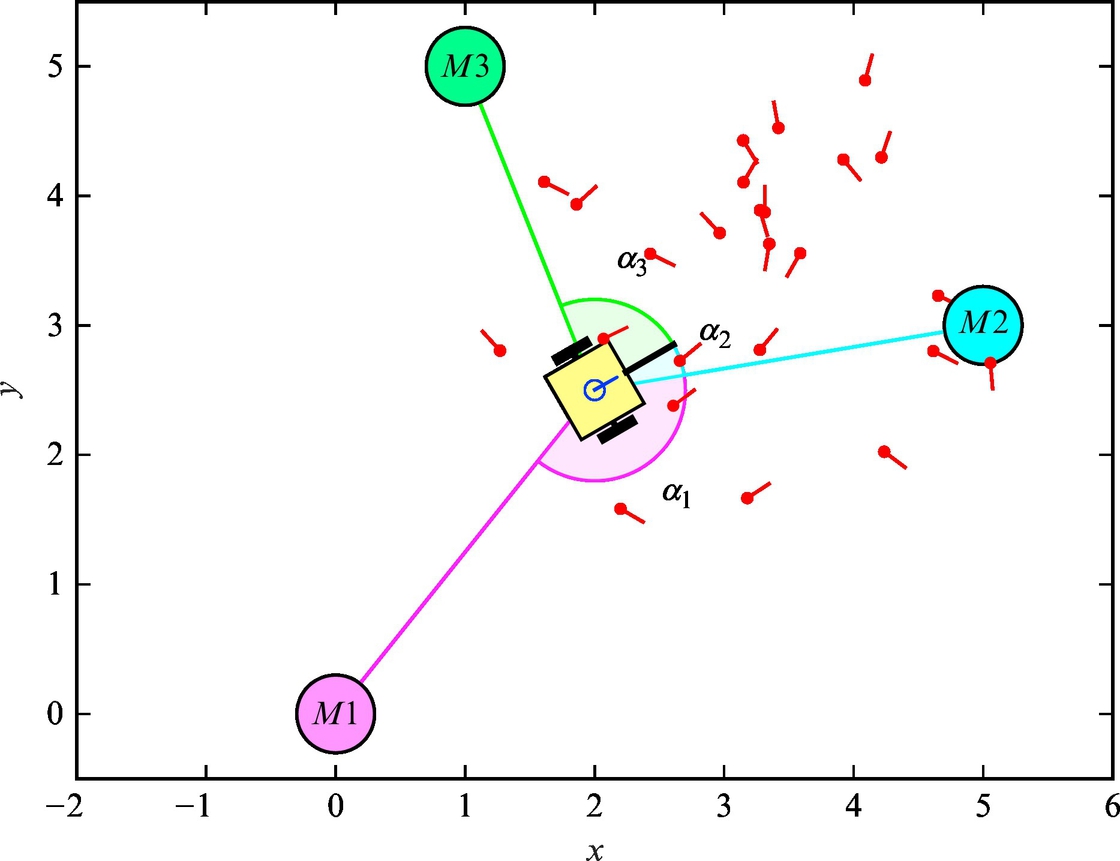
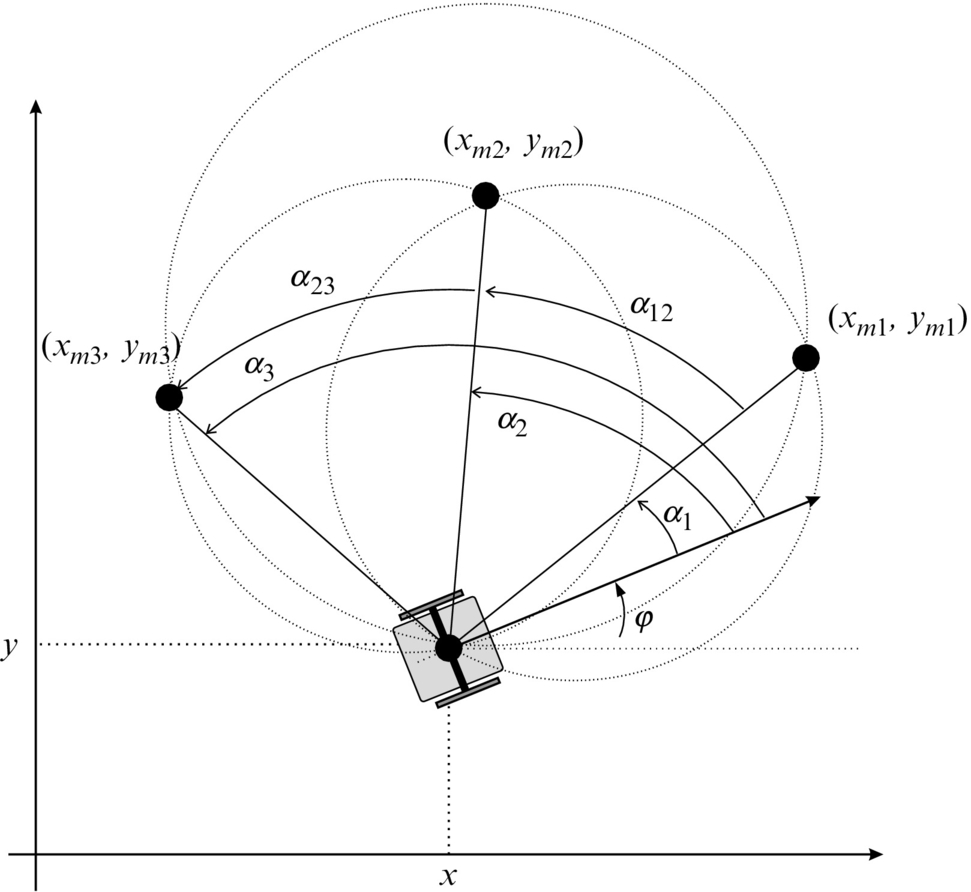
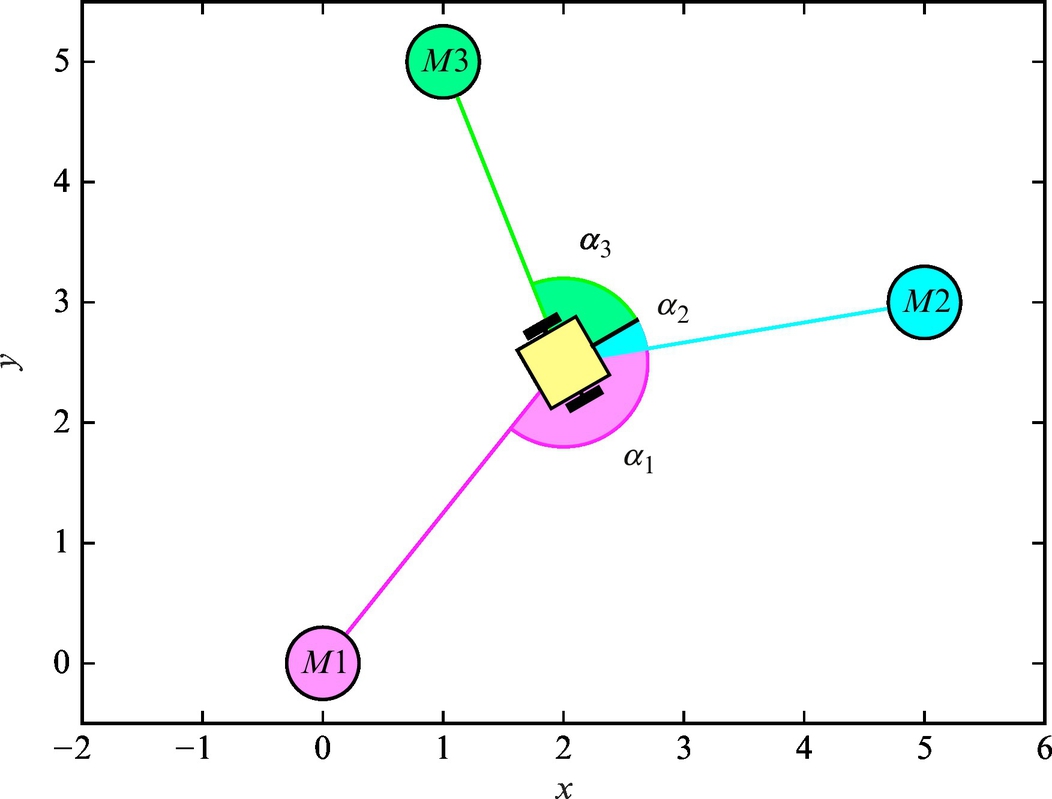
The basic idea of triangulation is illustrated in Fig. 5.10, where the robot measures relative angles α_i to the active markers. Suppose there are three markers as in Fig. 5.10, the current robot pose q = [x, y, φ]^T and measured angles α_j (j = 1, 2, 3) are related by the following relations:

$\begin{array}{l} \begin{matrix} tan (α_{1} + φ) & = \frac{y_{m 1} - y}{x_{m 1} - x} \\ tan (α_{2} + φ) & = \frac{y_{m 2} - y}{x_{m 2} - x} \\ tan (α_{3} + φ) & = \frac{y_{m 3} - y}{x_{m 3} - x} \end{matrix} \end{array}$ $\begin{array}{l} \begin{matrix} tan (α_{1} + φ) & = \frac{y_{m 1} - y}{x_{m 1} - x} \\ tan (α_{2} + φ) & = \frac{y_{m 2} - y}{x_{m 2} - x} \\ tan (α_{3} + φ) & = \frac{y_{m 3} - y}{x_{m 3} - x} \end{matrix} \end{array}$

si182_e (5.69)

To obtain the triangulation problem solution relations in Eq. (5.69) need to be solved for q = [x, y, φ]^T.

f05-10-9780128042045 — Fig. 5.10 Robot localization using triangulation where relative angles α_i to the markers are measured.

The basic idea of trilateration is illustrated in Fig. 5.14, where the current robot position, measured distances to markers, and their positions are related by the following set of equations:

$\begin{array}{l} \begin{matrix} d_{1}^{2} & = {(x_{m 1} - x)}^{2} + {(y_{m 1} - y)}^{2} \\ d_{2}^{2} & = {(x_{m 2} - x)}^{2} + {(y_{m 2} - y)}^{2} \\ d_{3}^{2} & = {(x_{m 3} - x)}^{2} + {(y_{m 3} - y)}^{2} \end{matrix} \end{array}$ $\begin{array}{l} \begin{matrix} d_{1}^{2} & = {(x_{m 1} - x)}^{2} + {(y_{m 1} - y)}^{2} \\ d_{2}^{2} & = {(x_{m 2} - x)}^{2} + {(y_{m 2} - y)}^{2} \\ d_{3}^{2} & = {(x_{m 3} - x)}^{2} + {(y_{m 3} - y)}^{2} \end{matrix} \end{array}$

si183_e (5.70)

In the following some examples of trilateration and triangulation are illustrated.

Example 5.9

The robot is equipped with sensor which can measure direction to the active markers. There are three active markers placed at known locations m₁ = [x_m1, y_m1]^T = [0, 0]^T, m₂ = [x_m2, y_m2]^T = [5, 3]^T, and m₃ = [x_m3, y_m3]^T = [1, 5]^T. At a current robot pose q = [x, y, φ]^T measured directions are given as a relative angles α₁ = −2.7691, α₂ = −0.3585, and α₃ = 1.4277.

What is the current robot pose q?

There are many possible solutions to solve this triangulation problem, and here two possibilities are shown. In the first part of the solution, particle swarm optimization (PSO) is applied. Some more details about PSO can be found in Section 3.3.9. In the second part of the solution a popular geometric algorithm based on the intersection of circular arcs is used.

Solution A

The current robot pose q = [x, y, φ]^T and measured angles α_j (j = 1, 2, 3) are related by the relations in Eq. (5.69). The task of the PSO algorithm is to find unknowns (x, y, and φ) so that the relations in Eq. (5.69) are valid. Each particle position presents one candidate solution (q_i) and during optimizations a swarm of particles updates toward more optimal solutions. The criteria for optimality of the ith particle solution is given as follows:

$\begin{array}{l} J_{i} = f (q_{i}) = \sum_{j = 1}^{3} {(α_{j} - {\hat{α}}_{j})}^{2} \end{array}$ $\begin{array}{l} J_{i} = f (q_{i}) = \sum_{j = 1}^{3} {(α_{j} - {\hat{α}}_{j})}^{2} \end{array}$

si184_e

where ${\hat{α}}_{j}$ ${\hat{α}}_{j}$ is the simulated measurement of the ith particle that is obtained from Eq. (5.69):

$\begin{array}{l} {\hat{α}}_{j} = arctan \frac{y_{m j} - y}{x_{m j} - x} - φ \end{array}$ $\begin{array}{l} {\hat{α}}_{j} = arctan \frac{y_{m j} - y}{x_{m j} - x} - φ \end{array}$

si186_e

Note that the $arctan$ $arctan$ function must return a correct angle in range (−π, π] (in Matlab function atan2 should be used).

The correct solution is q = [2, 2.5, π/6]^T, and the solution script is given in Listing 5.6 and the resulting situation is shown in Fig. 5.11.

f05-11-9780128042045 — Fig. 5.11 Solution of triangulation problem from Example 5.9 obtained with particle swarm optimization (PSO). Initial poses of particles are shown with dot-line markers, and final particle poses are shown with circle-line markers.

Listing 5.6

Triangulation problem solved by PSO

1 m = [0 , 0; 5 , 3; 1 , 5 ] . ’ ; % Markers

2 r0 = [ 2 ; 2 . 5 ; pi / 6 ] ; % True robot pose (x, y and f i ) , unknown.

4 % Measured angles

5 alpha = wrapToPi(atan2( m( 2 , : )− r0 (2) , m ( 1 , : )− r0 (1) )− r0 (3) ) ;

7 % Method using PSO

8 i t e r a t i o n s = 50; % Number of i t e r a t i o n s

9 omega = 0 . 5 ; % Inertia

10 c1 = 0 . 5 ; % Correction factor

11 c2 = 0 . 5 ; % Global correction factor

12 N = 25; % Swarm s i z e

14 % I n i t i a l swarm position

15 swarm = zeros([3 ,N, 4 ] ) ;

16 swarm (1 ,: ,1) = 3 + randn(1 ,N) ; % Init of x

17 swarm (2 ,: ,1) = 3 + randn(1 ,N) ; % Init of y

18 swarm (3 ,: ,1) = 0 + randn(1 ,N) ; % Init of f i

19 swarm ( : , : , 2 ) = 0; % I n i t i a l velocity

20 swarm (1 ,: ,4) = 1000; % Best value so far

22 for i t e r = 1: i t e r a t i o n s % PSO i t e r a t i v e l y find best solution

23 % Evaluate p a r t i c l e s parameters

24 for i = 1:N

25 % Compute predicted angle measurments using i − th p a r t i c l e

26 pEst = swarm ( : , i ,1) ; % Estimated p a r t i c l e parameters (x, y, f i )

28 % Compare obtained predicted angles to the true angle measurments

29 alphaEst = wrapToPi(atan2( m( 2 , : )− pEst (2) , m ( 1 , : )− pEst (1) )− pEst (3) ) ;

31 % Compute cost function

32 cost = ( alphaEst− alpha ) *( alphaEst − alpha ) . ’ ;

33 if cost< swarm(1 , i ,4) % if new parameter i s better , update:

34 swarm ( : , i ,3) = swarm ( : , i ,1) ; % param values (x, y and f i )

35 swarm(1 , i ,4) = cost ; % and best c r i t e r i a value.

36 end

37 end

38 [˜ , gBest ] = min(swarm (1 ,: ,4) ) ; % Global best particle parameters

40 % Updating parameters by velocity vectors

41 swarm ( : , : , 2 ) = omega*swarm ( : , : , 2 ) + …

42 c1*rand(3 ,N) .*( swarm ( : , : , 3 )− swarm ( : , : , 1 ) ) + …

43 c2*rand(3 ,N) .*( repmat (swarm ( : , gBest ,3) , 1 , N) − swarm ( : , : , 1 ) ) ;

44 swarm ( : , : , 1 ) = swarm ( : , : , 1 ) + swarm ( : , : , 2 ) ;

45 end

47 r = swarm ( : , gBest ,1) % Solution , best pose estimate

Solution B

Among many analytical solutions for the triangulation problem, the most often used one computes the intersection of circular arcs. Here the basic idea is described and only the final analytical solution is used to compute robot pose. The complete derivation of the algorithm can be found in [3].

The algorithm is based on three circles where each circle is defined by three points: any pair of markers m_i, m_j, (i, j = 1, 2, 3, i≠j), and robot position x, y (see Fig. 5.12).

f05-12-9780128042045 — Fig. 5.12 Robot localization using the triangulation algorithm based on intersection of circles.

The robot position and the two markers are connected by two lines with the angle between the lines α_ij = α_j − α_i. The centers and radius of those three circles are

$\begin{array}{l} c_{i j} & = [\begin{array}{l} x_{c i j} \\ y_{c i j} \end{array}] = \frac{1}{2} (m_{i} + m_{j} + [\begin{array}{l} (y_{m i} - y_{m j} cot α_{i j}) \\ (x_{m j} - x_{m i} cot α_{i j}) \end{array}]) \end{array}$ $\begin{array}{l} c_{i j} & = [\begin{array}{l} x_{c i j} \\ y_{c i j} \end{array}] = \frac{1}{2} (m_{i} + m_{j} + [\begin{array}{l} (y_{m i} - y_{m j} cot α_{i j}) \\ (x_{m j} - x_{m i} cot α_{i j}) \end{array}]) \end{array}$

si188_e (5.71)

$\begin{array}{l} r_{i j} & = \frac{∥ m_{i} - m_{j} ∥}{2 sin α_{i j}} \end{array}$ $\begin{array}{l} r_{i j} & = \frac{∥ m_{i} - m_{j} ∥}{2 sin α_{i j}} \end{array}$

si189_e (5.72)

Because α₁₃ = α₁₂ + α₃₃ only two of those angles are independent and the two belonging circles (for α₁₂ and α₂₃) are

$\begin{array}{l} {(x - x_{12})}^{2} + {(y - y_{12})}^{2} & = r_{12}^{2} \end{array}$ $\begin{array}{l} {(x - x_{12})}^{2} + {(y - y_{12})}^{2} & = r_{12}^{2} \end{array}$

(5.73)

$\begin{array}{l} {(x - x_{23})}^{2} + {(y - y_{23})}^{2} & = r_{23}^{2} \end{array}$ $\begin{array}{l} {(x - x_{23})}^{2} + {(y - y_{23})}^{2} & = r_{23}^{2} \end{array}$

(5.74)

The intersection of both circles (Eq. 5.73) is the solution for the robot position. For more details on how to obtain the analytical solution see [3]. Here, only the final solution is stated. A new temporary coordinate frame is defined so that m₂ is in its origin and m₃ lies on its x-axis. With these temporary coordinates the solution is easier to find. The rotation matrix from reference to temporary coordinates reads

$\begin{array}{l} R = [\begin{array}{l} cos β & - sin β \\ sin β & cos β \end{array}] \end{array}$ $\begin{array}{l} R = [\begin{array}{l} cos β & - sin β \\ sin β & cos β \end{array}] \end{array}$

si192_e

where $β = tan \frac{y_{m 3} - y_{m 2}}{x_{m 3} - x_{m 2}}$ $β = tan \frac{y_{m 3} - y_{m 2}}{x_{m 3} - x_{m 2}}$ . Markers expressed in temporary coordinates ( ${\bar{m}}_{i} = {[{\bar{x}}_{m i}, {\bar{y}}_{m i}]}^{T}$ ${\bar{m}}_{i} = {[{\bar{x}}_{m i}, {\bar{y}}_{m i}]}^{T}$ ) are obtained by transformation ${\bar{m}}_{i} = R^{- 1} (m_{i} - m_{2})$ ${\bar{m}}_{i} = R^{- 1} (m_{i} - m_{2})$ . The intersection of the circles in temporal coordinates ( $\bar{x}$ $\bar{x}$ , $\bar{y}$ $\bar{y}$ ) reads

$\begin{array}{l} [\begin{array}{l} \bar{x} \\ \bar{y} \end{array}] = {\bar{x}}_{m 3} \frac{1 - η cot α_{12}}{1 - η^{2}} [\begin{array}{l} 1 \\ - η \end{array}] \end{array}$ $\begin{array}{l} [\begin{array}{l} \bar{x} \\ \bar{y} \end{array}] = {\bar{x}}_{m 3} \frac{1 - η cot α_{12}}{1 - η^{2}} [\begin{array}{l} 1 \\ - η \end{array}] \end{array}$

si198_e

where $η = \frac{{\bar{x}}_{m 3} - {\bar{x}}_{m 1} - {\bar{y}}_{m 1} cot α_{12}}{{\bar{x}}_{m 3} cot α_{23} - {\bar{y}}_{m 1} + {\bar{x}}_{m 1} cot α_{12}}$ $η = \frac{{\bar{x}}_{m 3} - {\bar{x}}_{m 1} - {\bar{y}}_{m 1} cot α_{12}}{{\bar{x}}_{m 3} cot α_{23} - {\bar{y}}_{m 1} + {\bar{x}}_{m 1} cot α_{12}}$ . The solution in the reference coordinates is

$\begin{array}{l} [\begin{array}{l} x \\ y \end{array}] = m_{2} + R [\begin{array}{l} \bar{x} \\ \bar{y} \end{array}] \end{array}$ $\begin{array}{l} [\begin{array}{l} x \\ y \end{array}] = m_{2} + R [\begin{array}{l} \bar{x} \\ \bar{y} \end{array}] \end{array}$

si200_e

and orientation of the robot is

$\begin{array}{l} φ = arctan \frac{y_{m 1} - y}{x_{m 1} - x} - α_{1} \end{array}$ $\begin{array}{l} φ = arctan \frac{y_{m 1} - y}{x_{m 1} - x} - α_{1} \end{array}$

si201_e

A complete algorithm to obtain the solution is given in Matlab Listing 5.7. The solution is shown graphically in Fig. 5.13.

Listing 5.7

Triangulation problem solved using geometric approach

1 m = [0 , 0; 5 , 3; 1 , 5 ] . ’ ; % Three markers

2 r0 = [ 2 ; 2 . 5 ; pi / 6 ] ; % True robot pose (x, y and f i ) , unknown.

4 % Measured angles

5 alpha = wrapToPi(atan2( m( 2 , : )− r0 (2) , m ( 1 , : )− r0 (1) )− r0 (3) ) ;

7 % Triangulation: compute robot pose from measured angles

8 f = atan2( m(2 ,3)− m (2 ,2) , m (1 ,3)− m (1 ,2) ) ;

9 S = [ cos( f ) − sin ( f ) ; sin( f ) cos( f ) ] ; % Rotation for corrdinate frame in m2

10 m_ = S . ’*(m − repmat ( m ( : , 2 ) ,1 ,3) ) ; % Transformed markers

12 cta = cot( alpha (2)− alpha (1) ) ;

13 ctb = cot( alpha (3)− alpha (2) ) ;

14 ni = ( m_(1 ,3)− m_ (1 ,1)− m_ (2 ,1) * cta ) /( m_ (1 ,3) *ctb − m_ (2 ,1) + m_ (1 ,1) * cta ) ;

15 p_ = m_(1 ,3) *(1− ni * ctb ) /(1+ ni ˆ2) * [ 1 ; − ni ] ;

17 % Solution

18 p = m( : , 2 ) + S*p_ % Position

19 f i = wrapToPi(atan2( m(2 ,1)− p (2) , m (1 ,1)− r0 (1) )− alpha (1) ) % Orientation

p =

2.0000

2.5000

f i =

0.5236

f05-13-9780128042045 — Fig. 5.13 Solution of the triangulation problem from Example 5.9 with a direct approach.

Example 5.10

The robot is equipped with a sensor that can measure the distance to the active markers. This can be done by measuring the traveling time of the signal from the marker (transmitter) to the robot with the receiver.

There are three active markers placed at known locations: m₁ = [x_m1, y_m1]^T = [0, 0]^T, m₂ = [x_m2, y_m2]^T = [5, 3]^T, and m₃ = [x_m3, y_m3]^T = [1, 5]^T.

At a current robot position r = [x, y]^T measured distances are d₁ = 3.2016 m, d₂ = 3.0414 m, and d₃ = 2.6926 m as illustrated in Fig. 5.14.

f05-14-9780128042045 — Fig. 5.14 Robot localization using trilateration where distances d_i to the markers are measured.

What is the current robot position r?

This can again be solved by some optimization algorithm similarly as in Example 5.9 with PSO or using some analytical solution.

Solution

The task of the trilateration algorithm is to find unknown position x, y so that the relations in Eq. (5.70) are valid. This can be done with PSO similarly as in Example 5.9, where the implementation needs to be modified to include relations (5.70) in computation of the criteria function.

The solution of Eq. (5.70) can also be done analytically. Many different algorithms can be implemented; here, a simple solution is given. Subtracting the third equation in Eq. (5.70) from the first and the second one results in

$\begin{array}{l} \begin{matrix} d_{1}^{2} - d_{3}^{2} & = {(x_{m 1} - x)}^{2} - {(x_{m 3} - x)}^{2} + {(y_{m 1} - y)}^{2} - {(y_{m 3} - y)}^{2} \\ d_{2}^{2} - d_{3}^{2} & = {(x_{m 2} - x)}^{2} - {(x_{m 3} - x)}^{2} + {(y_{m 2} - y)}^{2} - {(y_{m 3} - y)}^{2} \end{matrix} \end{array}$ $\begin{array}{l} \begin{matrix} d_{1}^{2} - d_{3}^{2} & = {(x_{m 1} - x)}^{2} - {(x_{m 3} - x)}^{2} + {(y_{m 1} - y)}^{2} - {(y_{m 3} - y)}^{2} \\ d_{2}^{2} - d_{3}^{2} & = {(x_{m 2} - x)}^{2} - {(x_{m 3} - x)}^{2} + {(y_{m 2} - y)}^{2} - {(y_{m 3} - y)}^{2} \end{matrix} \end{array}$

si202_e (5.75)

By rearranging

$\begin{array}{l} \begin{matrix} 2 (x_{m 3} - x_{m 1}) x + 2 (y_{m 3} - y_{m 1}) y & = d_{1}^{2} - d_{3}^{2} - x_{m 1}^{2} + x_{m 3}^{2} - y_{m 1}^{2} + y_{m 3}^{2} \\ 2 (x_{m 3} - x_{m 2}) x + 2 (y_{m 3} - y_{m 2}) y & = d_{2}^{2} - d_{3}^{2} - x_{m 2}^{2} + x_{m 3}^{2} - y_{m 2}^{2} + y_{m 3}^{2} \end{matrix} \end{array}$ $\begin{array}{l} \begin{matrix} 2 (x_{m 3} - x_{m 1}) x + 2 (y_{m 3} - y_{m 1}) y & = d_{1}^{2} - d_{3}^{2} - x_{m 1}^{2} + x_{m 3}^{2} - y_{m 1}^{2} + y_{m 3}^{2} \\ 2 (x_{m 3} - x_{m 2}) x + 2 (y_{m 3} - y_{m 2}) y & = d_{2}^{2} - d_{3}^{2} - x_{m 2}^{2} + x_{m 3}^{2} - y_{m 2}^{2} + y_{m 3}^{2} \end{matrix} \end{array}$

si203_e (5.76)

we obtain linear equations in terms of x and y, which can be written in matrix A r = b where

$\begin{array}{l} A = [\begin{array}{l} 2 (x_{m 3} - x_{m 1}) & 2 (y_{m 3} - y_{m 1}) \\ 2 (x_{m 3} - x_{m 2}) & 2 (y_{m 3} - y_{m 2}) \end{array}] \end{array}$ $\begin{array}{l} A = [\begin{array}{l} 2 (x_{m 3} - x_{m 1}) & 2 (y_{m 3} - y_{m 1}) \\ 2 (x_{m 3} - x_{m 2}) & 2 (y_{m 3} - y_{m 2}) \end{array}] \end{array}$

si204_e

and

$\begin{array}{l} b = [\begin{array}{l} d_{1}^{2} - d_{3}^{2} - x_{m 1}^{2} + x_{m 3}^{2} - y_{m 1}^{2} + y_{m 3}^{2} \\ d_{2}^{2} - d_{3}^{2} - x_{m 2}^{2} + x_{m 3}^{2} - y_{m 2}^{2} + y_{m 3}^{2} \end{array}] \end{array}$ $\begin{array}{l} b = [\begin{array}{l} d_{1}^{2} - d_{3}^{2} - x_{m 1}^{2} + x_{m 3}^{2} - y_{m 1}^{2} + y_{m 3}^{2} \\ d_{2}^{2} - d_{3}^{2} - x_{m 2}^{2} + x_{m 3}^{2} - y_{m 2}^{2} + y_{m 3}^{2} \end{array}] \end{array}$

si205_e

from where an unknown position is obtained:

$\begin{array}{l} r = A^{- 1} b \end{array}$ $\begin{array}{l} r = A^{- 1} b \end{array}$

(5.77)

The correct solution is r = [2, 2.5]^T, and Matlab script implementation is given in Listing 5.8.

Listing 5.8

Trilateration problem

1 m = [0 , 0; 5 , 3; 1 , 5 ] . ’ ; % Markers

2 r0 = [ 2 ; 2 . 5 ; pi / 6 ] ; % True robot position (x and y) , unknown.

4 % Measured distances to the markers

5 d = sqrt((m( 1 , : )− r0 (1) ) .ˆ2+( m ( 2 , : )− r0 (2) ) .ˆ2) ;

7 % Trilateration: find the robot position from measured distances

8 N = s i z e (m,2) ; A = zeros(N−1,2) ; b = zeros ( N−1,1) ;

9 for i = 1: N−1

10 A ( i , : ) = 2*[ m (1 , N )− m (1 , i ) , m (2 , N ) − m (2 , i ) ] ;

11 b ( i ) = d( i ) ˆ2− d ( N ) ˆ2− m (1 , i ) ˆ2 + m(1 ,N) ˆ2− m (2 , i ) ˆ2 + m(2 ,N) ˆ2;

12 end

14 r = A ∖b % Calculated position

r =

2.0000

2.5000

Example 5.11

In Example 5.10 measured distances were exact, which is an unrealistic assumption. Measurements are normally corrupted with noise and other disturbances; therefore, an overdetermined system with more than three markers is needed to minimize error in the position estimate. To illustrate this use n = 4 markers at locations m₁ = [x_m1, y_m1]^T = [0, 0]^T, m₂ = [x_m2, y_m2]^T = [5, 3]^T, m₃ = [x_m3, y_m3]^T = [1, 5]^T, and m₄ = [x_m4, y_m4]^T = [2, 4]^T. And measured distances corrupted with noise are d₁ = 3.2297 m, d₂ = 3.0697 m, d₃ = 2.7060 m, and d₄ = 1.4759 m. Estimate the current robot position r.

Solution

The solution that minimize mean-square error ∥A r −b∥ of an overdetermined system with n active markers is obtained as follows. Matrix A becomes

$\begin{array}{l} A = [\begin{array}{l} 2 (x_{m n} - x_{m 1}) & 2 (y_{m n} - y_{m 1}) \\ 2 (x_{m n} - x_{m 2}) & 2 (y_{m n} - y_{m 2}) \\ ⋮ & ⋮ \\ 2 (x_{m n} - x_{m n - 1}) & 2 (y_{m n} - y_{m n - 1}) \end{array}] \end{array}$ $\begin{array}{l} A = [\begin{array}{l} 2 (x_{m n} - x_{m 1}) & 2 (y_{m n} - y_{m 1}) \\ 2 (x_{m n} - x_{m 2}) & 2 (y_{m n} - y_{m 2}) \\ ⋮ & ⋮ \\ 2 (x_{m n} - x_{m n - 1}) & 2 (y_{m n} - y_{m n - 1}) \end{array}] \end{array}$

si207_e (5.78)

and

$\begin{array}{l} b = [\begin{array}{l} d_{1}^{2} - d_{n}^{2} - x_{m 1}^{2} + x_{m n}^{2} - y_{m 1}^{2} + y_{m n}^{2} \\ d_{2}^{2} - d_{n}^{2} - x_{m 2}^{2} + x_{m n}^{2} - y_{m 2}^{2} + y_{m n}^{2} \\ ⋮ \\ d_{n - 1}^{2} - d_{n}^{2} - x_{m n - 1}^{2} + x_{m n}^{2} - y_{m n - 1}^{2} + y_{m n}^{2} \end{array}] \end{array}$ $\begin{array}{l} b = [\begin{array}{l} d_{1}^{2} - d_{n}^{2} - x_{m 1}^{2} + x_{m n}^{2} - y_{m 1}^{2} + y_{m n}^{2} \\ d_{2}^{2} - d_{n}^{2} - x_{m 2}^{2} + x_{m n}^{2} - y_{m 2}^{2} + y_{m n}^{2} \\ ⋮ \\ d_{n - 1}^{2} - d_{n}^{2} - x_{m n - 1}^{2} + x_{m n}^{2} - y_{m n - 1}^{2} + y_{m n}^{2} \end{array}] \end{array}$

si208_e (5.79)

Finally using pseudo inverse the solution is obtained:

$\begin{array}{l} r = {(A^{T} A)}^{- 1} A^{T} b \end{array}$ $\begin{array}{l} r = {(A^{T} A)}^{- 1} A^{T} b \end{array}$

(5.80)

For given distances the solution is r = [1.9873, 2.5337]^T and the Matlab script implementation is given in Listing 5.9. The solution is also shown in Fig. 5.15.

f05-15-9780128042045 — Fig. 5.15 Solution of trilateration problem from Example 5.11.

Listing 5.9

Trilateration problem of an overdetermined system

1 m = [0 , 0; 5 , 3; 1 , 5; 2 , 4 ] . ’ ; % Markers

3 % Measured distances to the markers

4 d = [3.2297 , 3.0697 , 2.7060 , 1.4759];

6 % Trilateration: find the robot position from measured distances

7 N = s i z e (m,2) ; A = zeros(N−1,2) ; b = zeros ( N−1,1) ;

8 for i = 1: N−1

9 A ( i , : ) = 2*[ m (1 , N )− m (1 , i ) , m (2 , N ) − m (2 , i ) ] ;

10 b ( i ) = d( i ) ˆ2− d ( N ) ˆ2− m (1 , i ) ˆ2 + m(1 ,N) ˆ2− m (2 , i ) ˆ2 + m(2 ,N) ˆ2;

11 end

13 r = A ∖b % Calculated position

r =

1.9873

2.5337

Global Navigation Satellite System

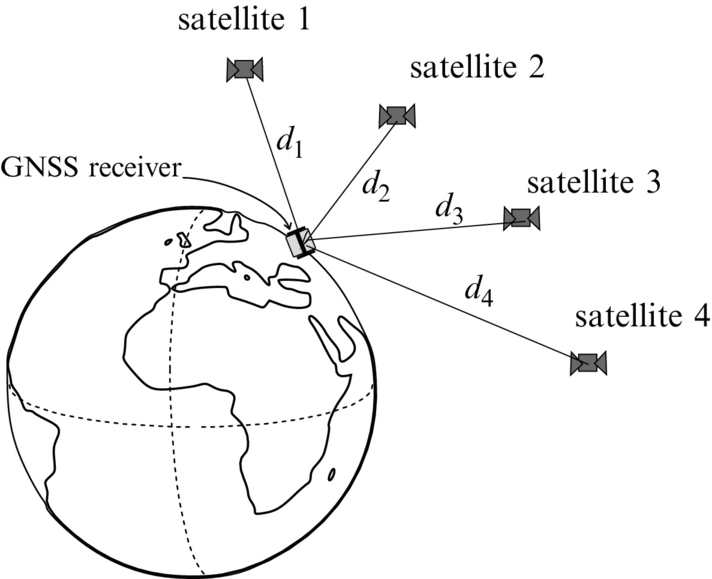
The most often used localization system using the trilateration principle is the Global Navigation Satellite System (GNSS). Satellites present active markers that transmit coded signals to the GNSS receiver station whose position needs to be estimated by trilateration. Satellites have very accurate atomic clocks and their positions are known (computed using Kepler elements and other TLE [two-line element set] parameters). There are several GNSS systems: Navstar GPS from ZDA, Glonass from Russia, and Galileo from Europe. The Navstar GPS system is designed to operate with at least 24 satellites that encircle Earth twice a day at a height of 20,200 km.

GNSS seems to be a very convenient sensor system for localization but it has some limitations that need to be considered when designing mobile systems. Its use is not possible where obstacles (e.g., trees, hills, buildings, indoors, etc.) can block the GNSS signal. Multiple signal reflections lead to multipath problems (wrong distance estimate). The expected accuracy of the system is approximately 5 m for single receiver system and approximately 1 cm for referenced systems (with additional receiver in reference station).

A simplified explanation of GNSS localization is as follows. GNSS receivers measure the traveling time of a GNSS signal from a certain satellite. Traveling time is the difference of the reception time t_r and transmission time t_t. Knowing that the signal travels at the speed of light c the distance between the receiver and satellite is computed. However, the receiver clock is not as accurate as the atomic clock on satellites. Therefore, some time bias or distance error appears, which is unknown but equal for all distances to satellites. The GNSS receiver therefore needs to estimate four parameters, namely its 3D position (x, y, and z) and time bias t_b.

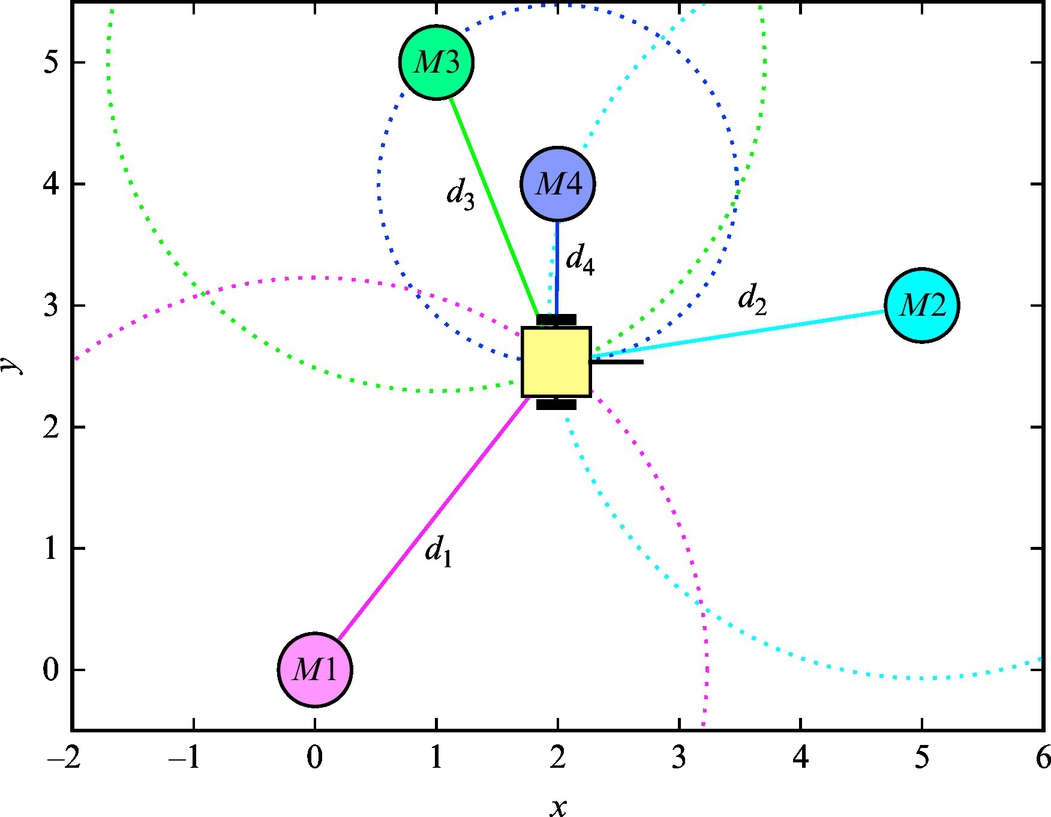
If around each received satellite a sphere with measured distance is drawn, the following can be concluded. The intersection of two spheres is a circle and the intersection of three spheres are two points where the receiver can be located. Therefore, we need at least four spheres to reliably estimate the position of the receiver. If the receiver is on the Earth’s surface then Earth can be considered as the fourth sphere to isolate a correct point obtained from the intersection of three satellite’ spheres. Ideally only three satellite receptions would be enough. But as already mentioned the receiver clock is inaccurate and this causes unknown time bias t_b. The intersection of the four spheres (three from satellites and the fourth from Earth) is therefore not a point but an area. To estimate t_b and lower localization error also the reception of the fourth satellite is required. Therefore, a minimum of four satellite receptions is required for GNSS localization as shown in Fig. 5.16. GNSS localization therefore is needed to solve the following set of equations:

$\begin{array}{l} \begin{matrix} d_{1} & = c (t_{r 1} - t_{t 1} - t_{d}) = \sqrt{{(x_{1} - x)}^{2} + {(y_{1} - y)}^{2} + {(z_{1} - z)}^{2}} \\ d_{2} & = c (t_{r 2} - t_{t 2} - t_{d}) = \sqrt{{(x_{2} - x)}^{2} + {(y_{2} - y)}^{2} + {(z_{2} - z)}^{2}} \\ d_{3} & = c (t_{r 3} - t_{t 3} - t_{d}) = \sqrt{{(x_{3} - x)}^{2} + {(y_{3} - y)}^{2} + {(z_{3} - z)}^{2}} \\ d_{4} & = c (t_{r 4} - t_{t 4} - t_{d}) = \sqrt{{(x_{4} - x)}^{2} + {(y_{4} - y)}^{2} + {(z_{4} - z)}^{2}} \end{matrix} \end{array}$ $\begin{array}{l} \begin{matrix} d_{1} & = c (t_{r 1} - t_{t 1} - t_{d}) = \sqrt{{(x_{1} - x)}^{2} + {(y_{1} - y)}^{2} + {(z_{1} - z)}^{2}} \\ d_{2} & = c (t_{r 2} - t_{t 2} - t_{d}) = \sqrt{{(x_{2} - x)}^{2} + {(y_{2} - y)}^{2} + {(z_{2} - z)}^{2}} \\ d_{3} & = c (t_{r 3} - t_{t 3} - t_{d}) = \sqrt{{(x_{3} - x)}^{2} + {(y_{3} - y)}^{2} + {(z_{3} - z)}^{2}} \\ d_{4} & = c (t_{r 4} - t_{t 4} - t_{d}) = \sqrt{{(x_{4} - x)}^{2} + {(y_{4} - y)}^{2} + {(z_{4} - z)}^{2}} \end{matrix} \end{array}$

si210_e (5.81)

where unknowns are the receiver position x, y, z and the receiver time drift t_d. For ith satellite the known values are position (x_i, y_i, z_i), reception time t_ri and transmission time t_ti, and speed of light c.

f05-16-9780128042045 — Fig. 5.16 GNSS localization requires reception of minimally four satellites to estimate the GNSS receiver position and the time drift.

5.3.4 Navigation Using Environmental Features

Features are a subset of patterns that can be robustly extracted from raw sensor measurements or other data. Some examples of features are lines, line segments, circles, blobs, edges, corners, and other patterns. Among other applications, features detected in the environment can be utilized for the purpose of mobile robot pose estimation (localization) and map building. For example, in the case of a 2D laser range scanner the obtained range (distance and angle) data can be processed to extract line segments (features). Line features in the local coordinate frame of the mobile robot can then be compared to the global map of the environment, which is also represented with a set of lines, in order to determine the mobile robot pose in the map. Nowadays, among the various sensors used in mobile robotics, the camera as a sensor is gaining more and more attention. Over the recent years many machine vision algorithms have been developed that enable detection of image features, which can also be used for measurement of a robot pose in the environment. Approaches that are based on features normally include the following steps: feature extraction, feature description, and feature matching. In the phase of feature extraction, raw data are processed in order to determine feature locations. The neighboring area around the detected feature location is normally used in order to describe the feature. Feature descriptors can then be used in order to find similar features in the process of feature matching.

Features are located at known locations. Therefore, their observation can improve knowledge about mobile robot location (lower location uncertainty). The list of features with their locations is called a map. This requires either an offline learning phase to construct a map of features or online localization and map building (simultaneous localization and mapping [SLAM]). The former approach is methodologically simpler but impractical in practice especially for larger environments. It requires the use of some reference localization system to map observed features, or this must be done manually. The latter approach builds a map simultaneously while localizing, and the main idea is to localize from observed features that are already in the map and storing newly observed features based on localized location. For reliable feature detection and robot localization usually as accurate as possible, dead reckoning is preferred. In case features are non or weakly separable (e.g., tree trunks in an orchard or detection of straight-line segments in buildings) the approximate information about the robot’s location is needed to identify the observed features.

An approximate location of the robot in current time is obtained from the location at a previous time and dead reckoning prediction of relative motion from a previous location to the current one.

Features are said to be natural if they are already part of the environment, and they are artificial if they are made especially for localization purposes. Examples of natural features in structured environments (typically indoor) are walls, floor pates, lights, corners, and similar features, while in the nonstructured environments (usually outdoor) examples of features are three trunks, road signs, etc. Artificial features are made solely for the purpose of localization to be easily and robustly recognized (color patches, bar codes, lines on the floor, etc.).

Usually obtaining features requires some processing over raw sensor data in order to obtain more compact, more informative, and abstract presentation of the current sensor view (line presentation vs set of points). In some cases also a raw sensor measurement (LRF scan or camera image) can be used for the localization process by correlating the sensor view with a stored map.

Very often can visual features be detected with some image sensors. One of the simplest and most used features are straight lines. They can be detected in the environment by a camera or a laser range scanner (LRF).

Straight-Line Features

The use of straight lines as features in localization is a very common choice as they are the simplest geometric features. Straight-line features can be used to describe indoor or outdoor environments (walls, flat objects, road lines, etc.). By comparing currently observed feature parameters and the parameters of a priori known environment map the robot pose can be estimated.

A very popular sensor for this purpose is the LRF, which measures the cloud of reflection points in the environment. From this measured cloud of points (usually 2D) straight-line parameters are estimated using one of several line-extraction algorithms. The line fitting process usually requires two steps: the first one is identification of clusters that can be presented by a line, and the second is estimation of line fitting parameters for each cluster using the least squares method or something similar. Usually these two steps are performed iteratively.

Split-and-Merge Algorithm

A very popular algorithm for LRF data is the split-and-merge algorithm [4, 5], which is simple for realization and has low computational complexity and good performance. Its main operation is as follows. The algorithm requires batched data that is iteratively split to clusters where each cluster is described by a linear prototype (straight line for 2D data). The algorithm can only be applied to sorted data where consecutive data samples belong to the same straight line (data from LRF are sorted).

Initially all data samples belong to one cluster whose linear prototype (straight-line) parameters are identified. The initial cluster is then split in two new clusters at the sample which has the highest distance from the initial prototype if this distance is higher than the threshold d_split. The choice of d_split depends on data noise and must be selected higher than the expected measurement error due to the noise (e.g., three standard deviations). When clustering is finished collinear clusters are merged. This step is optional and is usually not needed in sorted data streams.

For each cluster j (j = 1, …, m) the linear prototype is defined in normal form:

$\begin{array}{l} [z^{T} (k), 1] θ_{j} = 0 \end{array}$ $\begin{array}{l} [z^{T} (k), 1] θ_{j} = 0 \end{array}$

(5.82)

where z(k) = [x(k), y(k)]^T is the kth sample (k = 1, …, n and n is the number of all samples) which lies on the straight line defined by parameters θ. For cluster j, which contains samples k_j = 1, …, n_j the parameter vector θ_j can be estimated using singular value decomposition as follows. The regression matrix,

$\begin{array}{l} ψ = [\begin{array}{l} z^{T} (1) & 1 \\ ⋮ & ⋮ \\ z^{T} (n_{j}) & 1 \end{array}] \end{array}$ $\begin{array}{l} ψ = [\begin{array}{l} z^{T} (1) & 1 \\ ⋮ & ⋮ \\ z^{T} (n_{j}) & 1 \end{array}] \end{array}$

si212_e

defines a set of homogenous equations in matrix form ψ θ_j = 0, where the prototype parameters θ_j need to be estimated in the sense of a least-squares minimization. The solution presents the eigenvector (p_r = [p_x, p_y, p_p]^T) of the regression matrix ψ^Tψ belonging to the minimum eigenvalue (calculated using singular value decomposition). The normal-form parameters of the prototype are obtained by normalization of p_r:

$\begin{array}{l} θ_{j} = \pm \frac{p_{r}}{\sqrt{p_{x}^{2} + p_{y}^{2}}} \end{array}$ $\begin{array}{l} θ_{j} = \pm \frac{p_{r}}{\sqrt{p_{x}^{2} + p_{y}^{2}}} \end{array}$

si213_e

where the sign is selected opposite to the third parameter of p_r (p_p). For data sample z(k) that is not on the prototype j the orthogonal distance is calculated by

$\begin{array}{l} d_{j} (k) = |[z^{T} (k), 1] θ_{j}| \end{array}$ $\begin{array}{l} d_{j} (k) = |[z^{T} (k), 1] θ_{j}| \end{array}$

(5.83)

In the case of 2D data the linear prototype can alternatively be estimated simply by connecting the first and the last data sample in the cluster. This, however, is not optimal in a least squares sense but it lowers the computational complexity and ensures that the sample that defines the split does not appear at the first or the last data sample.

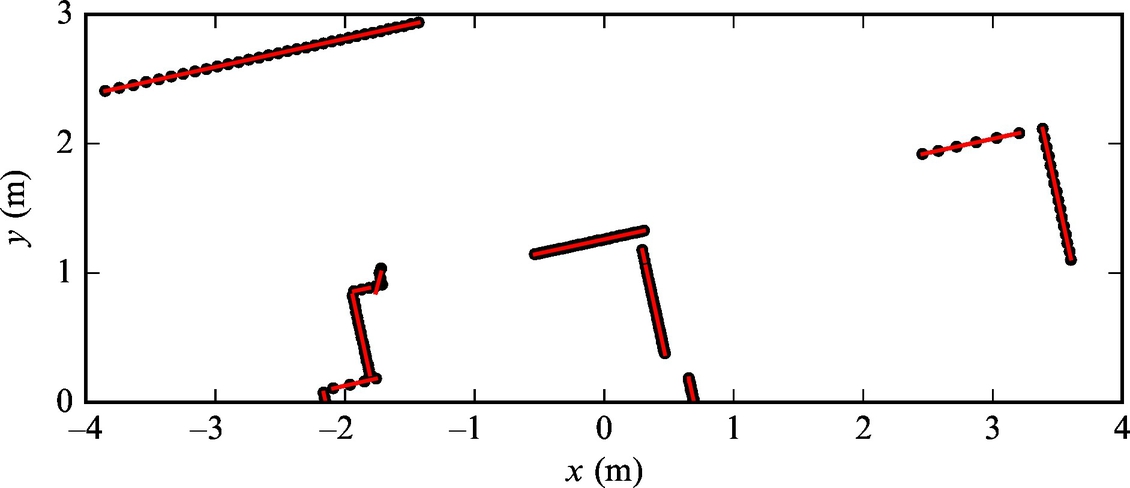
An example of fitting raw LRF data to straight lines is given in Example 5.12.

Example 5.12

For raw laser range scanner data consisting of 180 reflection points (see Fig. 5.17 and Listing 5.10) estimate straight-line clusters that best describe the scan. Clustering is done using distance threshold d_split = 0.06 m.

f05-17-9780128042045 — Fig. 5.17 Laser range scanner data and identified straight-line clusters using the split-and-merge algorithm.

Listing 5.10

Laser scan data

1 data = [−0 −2149 38 −2158 76 −2166 110 −2092 137 −1962 162 −1851 …

2 185 −1761 222 −1809 255 −1817 289 −1822 324 −1835 358 −1840 …

3 393 −1849 428 −1853 464 −1862 502 −1873 539 −1879 577 −1887 …

4 617 −1898 656 −1905 697 −1915 738 −1921 780 −1929 824 −1942 …

5 860 −1931 873 −1872 885 −1814 898 −1763 911 −1714 957 −1726 …

6 1001 −1734 1035 −1722 2407 −3852 2431 −3743 2452 −3635 2476 …

7 −3536 2497 −3437 2519 −3342 2539 −3250 2558 −3158 2576 −3070 …

8 2596 −2986 2614 −2903 2630 −2821 2649 −2744 2664 −2664 2683 …

9 −2591 2698 −2516 2715 −2445 2730 −2373 2742 −2301 2759 −2234 …

10 2774 −2167 2790 −2102 2802 −2036 2817 −1973 2831 −1910 2845 …

11 −1847 2857 −1785 2869 −1724 2885 −1666 2898 −1606 2908 −1546 …

12 2924 −1490 2936 −1432 1146 −535 1149 −512 1155 −490 1160 −469 …

13 1164 −447 1169 −425 1174 −404 1178 −383 1182 −361 1188 −341 …

14 1190 −319 1195 −298 1199 −277 1205 −256 1210 −235 1214 −214 …

15 1220 −193 1222 −172 1227 −151 1231 −129 1238 −108 1241 −87 …

16 1248 −65 1253 −44 1254 −22 1259 0 1265 22 1268 44 1277 67 …

17 1279 89 1287 113 1291 136 1295 159 1300 183 1306 207 1312 …

18 231 1315 256 1320 280 1328 307 1178 294 1133 304 1092 313 …

19 1050 321 1014 329 977 336 944 344 915 351 885 357 856 363 …

20 829 369 805 375 778 380 756 385 735 391 713 395 694 401 674 …

21 405 652 408 637 413 617 416 600 420 582 423 566 427 552 432 …

22 537 435 520 436 507 441 493 444 478 446 463 447 452 452 439 …

23 455 426 456 414 459 401 461 391 466 380 469 1920 2457 1944 …

24 2580 1976 2720 2011 2872 2044 3030 2081 3204 2115 3385 2042 …

25 3399 1971 3415 1903 3433 1832 3445 1764 3462 1694 3474 1629 …

26 3493 1561 3506 1495 3522 1428 3533 1362 3549 1297 3564 1231 …

27 3575 1167 3593 1102 3603 187 654 175 655 164 656 153 662 …

28 141 662 130 667 118 668 106 671 94 670 83 677 71 678 60 681 …

29 48 683 36 686 24 691 12 6 9 0 ] . ’ ;

30 x = data ( 2 : 2 : end) /1000;

31 y = data ( 1 : 2 : end−1) /1000;

Solution

A simple algorithm implementation presented here computes line parameters of each cluster in a least squares sense. If a cluster needs to be split and the splitting sample appears as the first or the last point of the cluster then cluster cannot be split. If so the straight-line parameters are computed again to fit only the first and the last sample and the split is made.

Implementation of line estimation is given in Listing 5.11 (laser scan data is defined in Listing 5.10). Estimated line segments are shown in Fig. 5.17.

Listing 5.11

Line estimation using split-and-merge algorithm

1 X = [ x , y ] ; % Laser scan data

2 [N, M] = s i z e (X) ;

4 % Init

5 C = 50; % Maximum number of c l u s t e r s

6 c l u s t e r s = 1; % Last active cluster

7 dMin = 0.06; % Threshold distance to s p l i t cluster

9 sizeOfCluster = zeros(C,1) ; % Number of points in c l u s t e r s

10 clusterBounds = zeros(C,2) ; % Indexes of boundary points in c l u s t e r s

11 clusterParams = zeros(C,M +1) ; % Cluster parameters

12 splitCluster = zeros(C,1) ; % Split flag

14 % At the begining add a l l points to a single cluster

15 sizeOfCluster ( clusters ,1) = N;

16 clusterBounds ( clusters , : )= [1 , N] ; % Points are ordered

17 splitCluster ( clusters ,1) = 1; % I n i t i a l cluster can be s p l i t

19 exit = f a l s e ;

20 while ˜ exit

21 exit = true ;

22 tmpLastCluster = c l u s t e r s ;

23 for i = 1: tmpLastCluster

24 if splitCluster ( i )

25 p0 = clusterBounds ( i ,1) ; % First point in the cluster

26 p1 = clusterBounds ( i ,2) ; % Last point in the cluster

28 % Estimation of cluster params in the least − square sense (LSQ )

29 Psi = [X(p0 : p1 , : ) , ones (p1 − p0 +1 ,1) ] ;

30 [˜ , ˜ , V] = svd( Psi ) ;

31 thetaEst = V( : , 3 ) ;

32 % Transform l i n e ax+ by+ c=0 to normal form

33 s = − sign ( thetaEst (3) ) ; if s==0, s = 1; end

34 mi = 1/sqrt( thetaEst (1)ˆ2+thetaEst (2) ˆ2)*s ;

35 Theta = thetaEst *mi ;

37 % Estimation of simple l i n e parameters (through the f i r s t and

38 % the l a s t point). These params are used when the s p l i t point

39 % i s at the cluster boundary.

40 if abs(X(p1 ,1)− X ( p0 , 1 ) ) <100* eps % Vertical l i n e

41 a = 1; b = 0; c = − X (1 ,1) ;

42 else

43 a = (X(p1 ,2)− X ( p0 , 2 ) ) /( X ( p1 , 1 ) − X ( p0 , 1 ) ) ;

44 b = −1;

45 c = − a * X ( p0 , 1 ) + X ( p0 , 2) ;

46 end

47 % Transform l i n e ax+ by+ c=0 to normal form

48 thetaEst = [ a ; b ; c ] ;

49 s = − sign ( thetaEst (3) ) ; if s==0, s = 1; end

50 mi = 1/sqrt( thetaEst (1)ˆ2+thetaEst (2) ˆ2)*s ;

51 Theta0 = thetaEst *mi ;

53 % Store LSQ params

54 clusterParams ( i , : ) = Theta . ’ ;

55 ind = p0 : p1 ;

56 XX = X( ind , : ) ;

58 % Calculate distance obtained from the f i r s t and the l a s t

59 % cluster sample (simple l i n e )

60 dik = [XX, ones ( s i z e (XX,1) ,1) ]* Theta0 ;

61 [ dd0 , i i i ] = max (abs( dik ) ) ; i i 0 = ind ( i i i ) ;

63 % Calculate distance from l i n e obtained in the LSQ sense

64 dik = [XX, ones ( s i z e (XX,1) ,1) ]* Theta ;

65 [ dd , i i i ] = max (abs( dik ) ) ; i i = ind ( i i i ) ;

67 % Cluster s p l i t t i n g

68 doSplit = 0;

69 if dd > dMin && ( ii− p0 ) >=2 && ( p1 − i i ) >=1 % Use LSQ l i n e

70 if clusters < C

71 iiFin = i i ; % Split location

72 doSplit = 1;

73 clusterParams ( i , : ) = Theta . ’ ;

74 end

75 elseif dd0 > dMin && ( ii0− p0 ) >=2 && ( p1 − i i 0 ) >=1 % Use simple l i n e

76 if clusters < C

77 iiFin = i i 0 ; % Split location

78 doSplit = 1;

79 clusterParams ( i , : ) = Theta0 . ’ ;

80 end

81 else

82 splitCluster ( i ) = 0;

83 end

86 if doSplit==1 && clusters < C

87 % Split the cluster to cluster A and B

88 c l u s t e r s = c l u s t e r s + 1; % New cluster

89 % First and l a s t point in cluster A

90 clusterBounds ( i ,1) ;

91 clusterBounds ( i ,2) = iiFin −1;

92 s p l i t C l u s t e r ( i ) = 1;

93 % First and l a s t point in cluster B

94 clusterBounds ( clusters ,1) = iiFin +1;

95 clusterBounds ( clusters ,2) = p1 ;

96 splitCluster ( c l u s t e r s ) = 1;

98 exit = f a l s e ;

99 end

100 end

101 end

102 end

Evolving Straight-Line Clustering

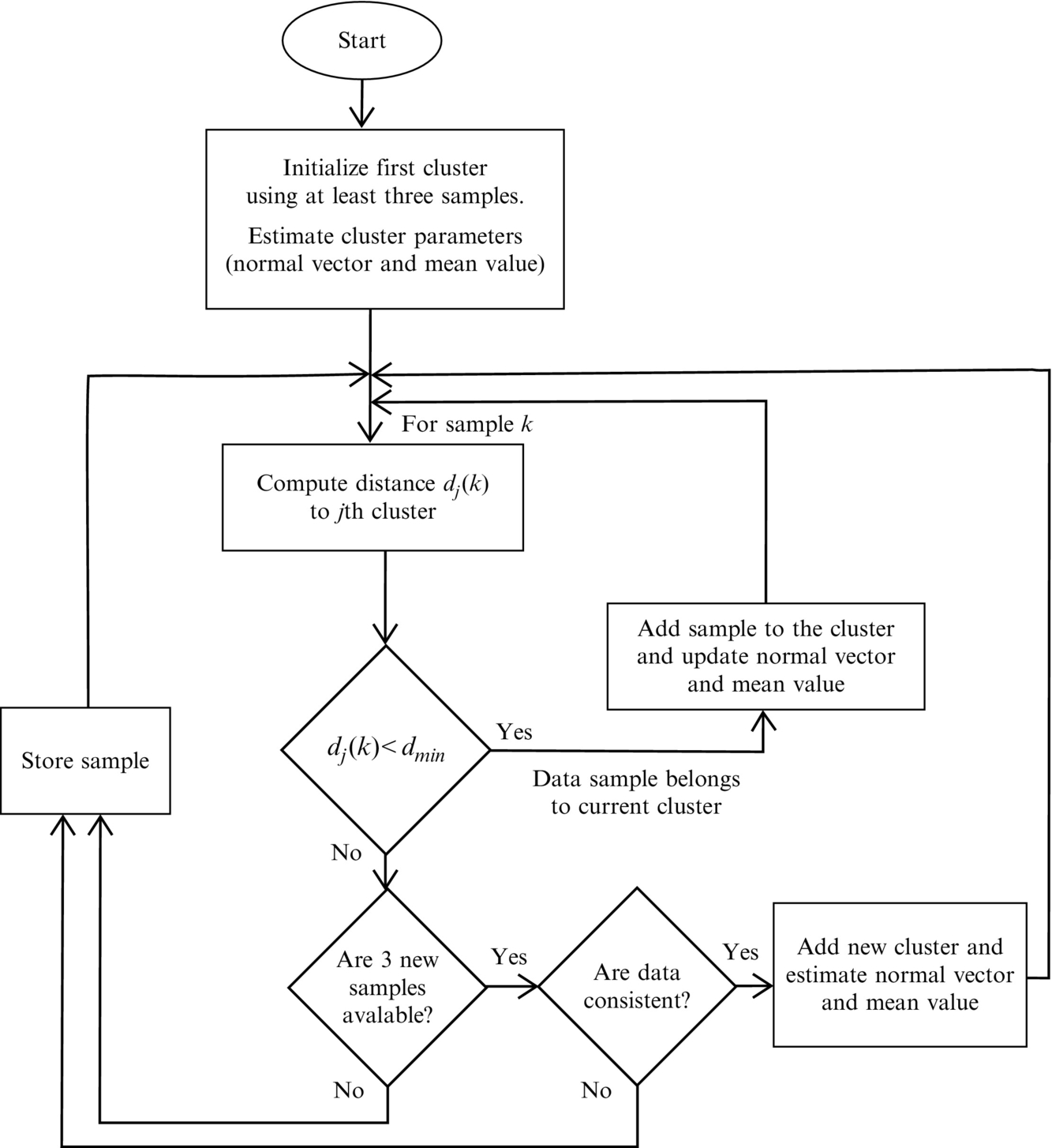
Similarly as in split-and-merge clustering, straight lines can also be estimated in the case of streamed data. Clustering is done online and is iteratively updated when new data arrives. An example of a simple and computationally efficient algorithm is the evolving principal component clustering [6]. A brief description of its main steps are as follows.

The jth prototype that models the data z(k_j) (k_j = 1, …, n_j) in the cluster j is as follows:

$\begin{array}{l} {(z (k_{j}) - μ_{j})}^{T} \cdot p_{j} = 0 \end{array}$ $\begin{array}{l} {(z (k_{j}) - μ_{j})}^{T} \cdot p_{j} = 0 \end{array}$

where μ_j(k_j) is the mean value of the data in cluster j that updates in each iteration (when new sample is available) by

$\begin{array}{l} μ_{j} (k_{j}) = \frac{k_{j} - 1}{k_{j}} μ_{j} (k_{j} - 1) + \frac{1}{k_{j}} z (k_{j}) \end{array}$ $\begin{array}{l} μ_{j} (k_{j}) = \frac{k_{j} - 1}{k_{j}} μ_{j} (k_{j} - 1) + \frac{1}{k_{j}} z (k_{j}) \end{array}$

si216_e (5.84)

and p_j is the normal vector of the jth prototype. It is computed from the jth cluster covariance matrix (for 2D data),

$\begin{array}{l} Σ_{j} (k_{j}) = [\begin{array}{l} σ_{11}^{2} & σ_{12}^{2} \\ σ_{21}^{2} & σ_{22}^{2} \end{array}] \end{array}$ $\begin{array}{l} Σ_{j} (k_{j}) = [\begin{array}{l} σ_{11}^{2} & σ_{12}^{2} \\ σ_{21}^{2} & σ_{22}^{2} \end{array}] \end{array}$

si217_e

as follows:

$\begin{array}{l} p_{j} = \frac{1}{\sqrt{{(\frac{σ_{12}}{σ_{11}})}^{2} + 1}} [\begin{array}{l} - \frac{σ_{12}}{σ_{11}} \\ 1 \end{array}] \end{array}$ $\begin{array}{l} p_{j} = \frac{1}{\sqrt{{(\frac{σ_{12}}{σ_{11}})}^{2} + 1}} [\begin{array}{l} - \frac{σ_{12}}{σ_{11}} \\ 1 \end{array}] \end{array}$

si218_e

The covariance matrix is updated iteratively using

$\begin{array}{l} Σ_{j} (k_{j}) = \frac{k_{j} - 2}{k_{j} - 1} Σ_{j} (k_{j} - 1) + \frac{1}{k_{j}} (z (k_{j}) - μ_{j} (k_{j} - 1)) {(z (k_{j}) - μ_{j} (k_{j} - 1))}^{T} \end{array}$ $\begin{array}{l} Σ_{j} (k_{j}) = \frac{k_{j} - 2}{k_{j} - 1} Σ_{j} (k_{j} - 1) + \frac{1}{k_{j}} (z (k_{j}) - μ_{j} (k_{j} - 1)) {(z (k_{j}) - μ_{j} (k_{j} - 1))}^{T} \end{array}$

si219_e (5.85)

The current sample, z(k), needs to be classified in one of the existing prototypes j (j ∈{1, …, m}). This is done by calculating the orthogonal distance d_j(k) from each jth prototype:

$\begin{array}{l} d_{j} (k) = | {(z (k) - μ_{j})}^{T} p_{j} | \end{array}$ $\begin{array}{l} d_{j} (k) = | {(z (k) - μ_{j})}^{T} p_{j} | \end{array}$

(5.86)

If d_j(k) = 0 the data sample lies on the linear prototype j. The sample belongs to the jth cluster if d_j(k) for the jth cluster is the smallest and less than the predefined threshold distance d_min (d_j(k) < d_min). In [6] robust clustering is proposed, where d_min is estimated online from the jth cluster data.

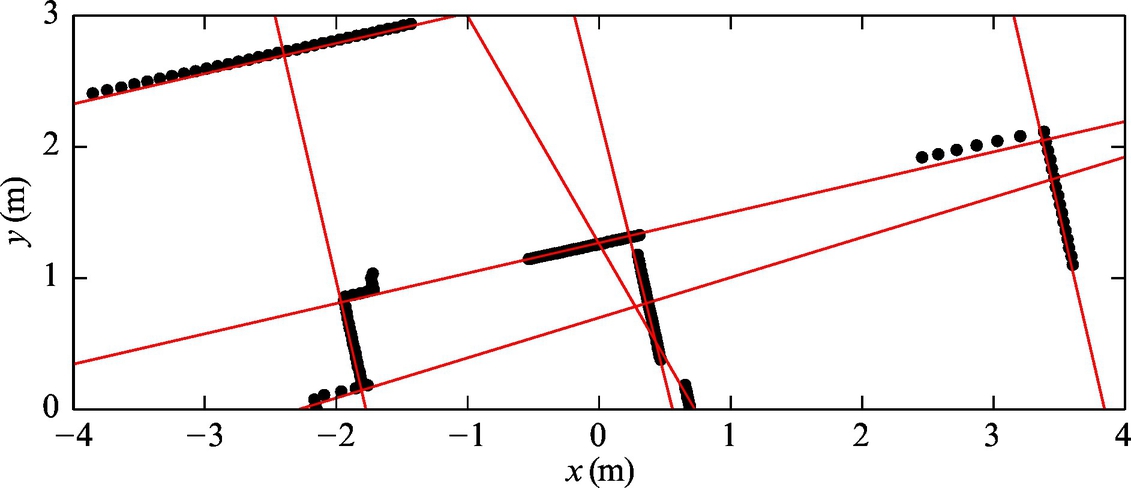
The basic idea of the clustering algorithm is illustrated in Fig. 5.18. It can be applied online to sorted data arriving from some stream or to a batched data sample (as split-and-merge). Classification results of Example 5.12 would, at a similar clustering quality as the split-and-merge algorithm, require less computational effort.

f05-18-9780128042045 — Fig. 5.18 Idea of evolving clustering for streamed data where clusters are defined by straight-line prototypes.

Example 5.13

For raw laser range scanner data consisting of 180 reflection points (see Fig. 5.17 and the beginning of the solution for points coordinates) estimate straight-line clusters that best describes the scan. Clustering is done using the evolving straight-line clustering algorithm.

Solution

The current sample belongs to jth cluster if its distance d_j(k) to the cluster’s line is smaller than the threshold d_min (d_j(k) < d_min). d_min can be a constant or as in this example estimated online. The threshold distance parameter d_min is computed from the estimated cluster distance variance σ_j(k_j) (distance variance of samples from the line). The variance recursive estimate reads $σ_{j} (k_{j}) = σ_{j} (k_{j} - 1) \frac{k_{j} - 2}{k_{j} - 1} + \frac{d_{j}^{2} (k)}{k_{j}}$ $σ_{j} (k_{j}) = σ_{j} (k_{j} - 1) \frac{k_{j} - 2}{k_{j} - 1} + \frac{d_{j}^{2} (k)}{k_{j}}$ and the threshold is $d_{\min} = κ_{\max} \sqrt{σ_{j}}$ $d_{\min} = κ_{\max} \sqrt{σ_{j}}$ , where κ_max = 7 is the tuning parameter.

Implementation of line estimation is given in Listing 5.12 (laser scan data is defined in Listing 5.10). Estimated line segments are shown in Fig. 5.19.

f05-19-9780128042045 — Fig. 5.19 Laser range scanner data and identified straight-line clusters using the evolving straight-line clustering algorithm.

Listing 5.12

Evolving straight-line clustering algorithm

1 X = [ x , y ] ; % Laser scan data

2 Kapa_Max=7;

4 [ n ,m] = s i z e (X) ; dimension = m;

5 % %%%%% i n i t

6 Nr_cloud_max = 20; Current_clust = 1;

8 Nr_points_in_cloud = zeros(Nr_cloud_max ,1) ; % vector specifying the number

9 % of data points in the cloud where rows correspond to d i f f e r e n t clouds

10 M_of_clouds = zeros(Nr_cloud_max , dimension ) ; % matrix − rows correspond to

11 % d i f f e r e n t clouds and columns to elements of the input vector

12 V_of_clouds = zeros(Nr_cloud_max , dimension ) ;

13 VarD_of_cloud = zeros(Nr_cloud_max ,1) ; % distance variance of points

14 % from cluster

15 M_dist = zeros(Nr_cloud_max ,1) ; % distances among points in cluster

16 Eig_of_clouds = zeros(Nr_cloud_max , dimension ) ;

17 EigLat_of_cloud = zeros(Nr_cloud_max , dimension ) ;

18 Points_in_buffer= zeros(6 , dimension ) ; % stores up to 6 samples

19 StartEndX_points_in_cloud = zeros(Nr_cloud_max ,2) ;

21 M_old=0;V_old=0;

23 % %%%%%%%%%%%% i n i t %%%%%%%%%%%%%%%%%

24 % f i r s t cluster receives 3 points (the points must be c o l l i n e a r )

25 Nr_points_in_cloud ( Current_clust ,1) =3;

26 Nr_points_in_buffer =0;

28 N =3;

29 XX = X(1:N, : ) ;

30 M = sum(XX)/ N;

31 Mold = M;

33 V=[0 , 0 ] ;

34 sumD=0;

35 for i =1: N

36 V = V +( XX( i , : )− M ) . * ( XX ( i , : )− M ) ; % variance of cluster points

37 end

38 V = V/(N−1) ;

39 Vold = V ;

41 % covariance matrix of samples

42 Vmat =( XX− repmat ( M , N , 1 ) ) ’ * ( XX − repmat ( M , N , 1 ) ) / ( N −1) ;

44 p = [ sqrt ( V (1 ,1) ) sqrt ( V(1 ,2) ) ] ;

45 signC= sign(X( 2 , : )− X ( 1 , : ) ) ;

46 p = p .* signC / sqrt(p*p ’ ) ; % 1. eigen vector , normalised

47 pL = [ p(1 ,2) , − p (1 ,1) ] ; % 2. eigen vector , normalised

49 % distance from l i n e

50 sumD=0;

51 for i =1: N

52 sumD = sumD + ( ((X( i , : ) − M ) * pL ’ ) /( pL * pL ’ ) ) ˆ2;

53 end

54 varD = sumD/(N−1) ;

55 varDold = varD ;

57 % mean distance between points

58 d1 = sqrt( (X( 1 , : )− X ( 2 , : ) ) *( X ( 1 , : )− X ( 2 , : ) ) ’ ) ;

59 d2 = sqrt( (X( 3 , : )− X ( 2 , : ) ) *( X ( 3 , : )− X ( 2 , : ) ) ’ ) ;

60 d_med_toc=(d1 + d2) /2;

62 % storing

63 M_of_clouds ( Current_clust , : )= M;

64 V_of_clouds ( Current_clust , : )= V;

65 Eig_of_clouds ( Current_clust , : )= p ;

66 EigLat_of_cloud ( Current_clust , : )= pL ;

67 VarD_of_cloud ( Current_clust ,1) = varD ;

69 M_dist ( Current_clust ,1) = d_med_toc ;

70 StartEndX_points_in_cloud ( Current_clust ,1) =1;

71 StartEndX_points_in_cloud ( Current_clust ,2) =3;

74 for k=4:n % loop through a l l samples

75 % compute distance to current sample

76 pL =EigLat_of_cloud ( Current_clust , : ) ;

77 M =M_of_clouds ( Current_clust , : ) ;

78 V =V_of_clouds ( Current_clust , : ) ;

79 varD = VarD_of_cloud ( Current_clust ,1) ;

81 d = abs( (X(k , : ) − M ) * pL ’ ) ;

83 if ( Nr_points_in_cloud ( Current_clust )>1)

84 d_med_toc = sqrt((X(k , : ) − X ( k −1,:) ) *( X ( k , : ) − X ( k −1,:) ) ’) ;

85 end

87 % new point belongs to cluster i f i t s distance to cluster i s small

88 % enough and sample are close enough

89 if (d < Kapa_Max*sqrt(varD) & d_med_toc < 2*M_dist ( Current_clust ,1) )

90 StartEndX_points_in_cloud ( Current_clust ,2)= k ;

91 Nr_points_in_buffer =0;

92 j=Nr_points_in_cloud ( Current_clust ) +1; % increase cluster samples

93 M = Mold+( X(k , : )− Mold ) / j ; % recursive mean

94 V = Vold *( j −2) /( j −1) + j *( M − Mold ) . ˆ 2 ; % recursive variance

96 % covariance matrix of data

97 Vmat = Vmat*( j −2) /( j −1) + 1/ j *( X ( k , : ) − Mold ) ’*( X ( k , : ) − Mold ) ;

99 Mold = M;

100 Vold = V;

101

102 p = [sqrt(V(1 ,1) ) sqrt(V(1 ,2) ) ] ;

103 signC= sign(X(k , : )− X ( StartEndX_points_in_cloud ( Current_clust ,1) , : ) ) ;

104

105 p = p.* signC / sqrt(p*p ’ ) ; % 1. eigen vector , normalised

106 pL = [ p(1 ,2) , − p (1 ,1) ] ; % 2. eigen vector , normalised

107

108 % recursive distance variance

109 d = abs( (X(k , : ) − M ) * pL ’ ) ;

110 varD = varDold *( j −2) /( j −1) + d ˆ2/ j ;

111 varDold = varD ;

112

113 % storing

114 M_of_clouds ( Current_clust , : )= M;

115 V_of_clouds ( Current_clust , : )= V;

116 Eig_of_clouds ( Current_clust , : )= p ;

117 EigLat_of_cloud ( Current_clust , : )= pL ;

118 Nr_points_in_cloud ( Current_clust )=j ;

119 VarD_of_cloud ( Current_clust ,1) = varD ;

120

121 else % new point does not belong to cluster , make new cluster

122

123 Nr_points_in_buffer= Nr_points_in_buffer +1;

124 Points_in_buffer ( Nr_points_in_buffer , : )= X(k , : ) ;

125

126 % new cluster need to have 3 consistent samples

127 if ( Nr_points_in_buffer >=3)

128

129 XX =Points_in_buffer (1: Nr_points_in_buffer , : ) ;

130 M = sum( XX )/ Nr_points_in_buffer ;

131

132 d_min_toc=0;

133 V=[0 , 0 ] ;

134 for i =1: Nr_points_in_buffer

135 d_tmp=( XX( i , : )− M ) . * ( XX ( i , : ) − M ) ;

136 V = V + d_tmp ;

137 if (d_tmp > d_min_toc ) , d_min_toc = d_tmp ; end

138 end

139 V = V/( Nr_points_in_buffer −1) ;

140

141 Mold = M ;

142 Vold = V;

143

144 p = [sqrt(V(1 ,1) ) sqrt(V(1 ,2) ) ] ;

145 signC= sign(XX( Nr_points_in_buffer , : )− XX ( 1 , : ) ) ;

146 p = p.* signC / sqrt(p*p ’ ) ;

147 pL = [ p(1 ,2) , − p (1 ,1) ] ;

148

149 Vmat =( XX− repmat ( M , N , 1 ) ) ’ * ( XX − repmat ( M , N , 1 ) ) / ( N −1) ;

150

151 % test consistency of samples

152 sumD=0;

153 for i =1: N

154 d = abs((XX( i , : ) − M ) * pL ’ ) ;

155 sumD = sumD + dˆ2;

156 end

157 varD = sumD/(N −1) ;

158 varDold = varD ;

159

160 d1 = sqrt( (XX( 1 , : )− XX ( 2 , : ) ) *( XX ( 1 , : )− XX ( 2 , : ) ) ’ ) ;

161 d2 = sqrt( (XX( 3 , : )− XX ( 2 , : ) ) *( XX ( 3 , : )− XX ( 2 , : ) ) ’ ) ;

162

163 if ( d < Kapa_Max/2*sqrt(varD) & abs(d2− d1 ) < min ( d1 , d2 ) )

164 % samples are consistent and correctly spaced

165 Current_clust = Current_clust +1;

166 M_of_clouds ( Current_clust , : )= M;

167 V_of_clouds ( Current_clust , : )= V;

168 Eig_of_clouds ( Current_clust , : )= p ;

169 EigLat_of_cloud ( Current_clust , : )= pL ;

170 Nr_points_in_cloud ( Current_clust ) =2;

171 VarD_of_cloud ( Current_clust ,1) = varD ;

172

173 StartEndX_points_in_cloud ( Current_clust ,1)= k −2;

174 StartEndX_points_in_cloud ( Current_clust ,2)= k ;

175

176 d_med_toc=(d1 + d2) /2;

177 M_dist ( Current_clust ,1) = d_med_toc ;

178 end

179 Nr_points_in_buffer =0; % clear buffer

180

181 else % wait until buffer has 3 samples

182 %

183 end

184 end

185 end % end: loop through a l l samples

Hough Transform

The Hough transform [7] is a very powerful approach to estimating geometric primitives mostly used in image processing. The incoming data are transformed in the parameter space (e.g., straight-line parameters), and by locating the maxima the number and the parameters of the lines are obtained.

The algorithm requires quantization of parameter space. Fine quantization increases accuracy but requires quite some computational effort and storage. Several studies proposed methods to avoid quantization and increase accuracy of Hough transform, such as randomized Hough transform or adaptive implementations, as reported in [8, 9].

The Hough transform can reliably estimate the clusters in the presence of outliers. In its basic version the straight-line parameters α and d are defined by the linear prototype (5.82), where $θ_{j} = [cos α, sin α, - d]$ $θ_{j} = [cos α, sin α, - d]$ . The normal line parameters’ ranges − π < α ≤ π and d_min < d ≤ d_max are presented in the accumulator by quantization to N discrete values for α and M discrete values for d.

For each data sample x(k), y(k) and all possible values for $α (n) = - π + \frac{π n}{N}$ $α (n) = - π + \frac{π n}{N}$ where n ∈{1, …, N}) solutions for parameter d(n) are computed. Each pair α(n), d(n) presents a possible straight line containing sample x(k), y(k). A corresponding location in the accumulator is increased by 1 for each computed parameter. When all data samples are processed the cells of the accumulator with the highest values are identified straight-line clusters. Some a priori knowledge is therefore required to properly select quantization of the parameter space and the threshold value to locate the maximum in the accumulator.

Example 5.14

For raw laser range scanner data consisting of 180 reflection points (see Fig. 5.21 and the beginning of the solution for point coordinates) estimate straight-line clusters that best describe the scan. Clustering is done using the Hough transform where normal straight-line parameters α and d are quantized to 720 discrete values.

Solution

A possible solution in Matlab script is given in Listing 5.13 (laser scan data is defined in Listing 5.10) where the function houghpeaks is used to find maximums in the accumulator. The obtained accumulator is shown in Fig. 5.20 and identified clusters in Fig. 5.21.

f05-20-9780128042045 — Fig. 5.20 Accumulator of the Hough transform where the ranges of α ∈ (−π, π] and d ∈ [0, 4.5] are quantized to 360 discrete values.

f05-21-9780128042045 — Fig. 5.21 Laser range scanner data and identified straight-line clusters using Hough transform.

Listing 5.13

Straight-line clusters using Hough transform

1 [ x , y ] ; % Laser scan data

2 N = length(x) ;

4 dAlpha = pi/180; % Angle quant

5 nAlpha = round(2*pi/dAlpha) ;

6 nDist = nAlpha ; % Use the same quantisation for distance

7 lutDist = zeros(N, nAlpha) ; % Distance look − up table

8 for i = 1:N % For each point compute l i n e s for the range of alpha

9 for j = 1: nAlpha

10 alpha = ( j −1) * dAlpha − pi ;

11 % Distance to the cordinate frame origin

12 d = x( i )*cos( alpha )+ y( i )*sin( alpha ) ;

13 if d<0

14 if alpha> pi , alpha = alpha − pi ;

15 else alpha = alpha + pi; end

16 j j = round(( alpha+ pi)/dAlpha) ;

17 lutDist ( i , j j ) = − d ;

18 else

19 lutDist ( i , j ) = d ;

20 end

21 end

22 end

24 % Find range for distance parameter

25 minLutDist = min( lutDist ( : ) ) ;

26 maxLutDist = max ( lutDist ( : ) ) ;

27 dDist = ( maxLutDist− minLutDist ) / nDist ; % Distance quant

29 % Realize accumulator of parameter space

30 A = zeros( nDist , nAlpha) ;

31 for i = 1:N % Go through a l l the points

32 for j = 1: nAlpha

33 k = round(( lutDist ( i , j )− minLutDist ) / dDist) +1;

34 if k > nDist , k = nDist ; end

35 A(k , j ) = A(k , j ) +1;

36 end

37 end

38 H = A(2: nAlpha , : ) ; % Accumulators

40 % Locate maximums in the accumulator (the most probable l i n e s )

41 nLines = 7; % Requested number of top most probable l i n e s

42 peaks = houghpeaks (H, nLines , ’threshold ’ , 3 , ’NHoodSize ’ , [31 , 31]) ;

43 % Line parameters: distance from the origin and l i n e angle

44 distAlpha = [ peaks ( : , 1 ) . ’* dDist+ minLutDist ; peaks ( : , 2 ) . ’* dAlpha − pi ] ;

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 5.3 Pose Measurement Methods

Create new playlist

Sign In

Sign Up

5.3 Pose Measurement Methods

5.3.1 Dead Reckoning

Odometry

Inertial Navigation

5.3.2 Heading Measurement

5.3.3 Active Markers and Global Position Measurement

Global Navigation Satellite System

5.3.4 Navigation Using Environmental Features

Straight-Line Features

Split-and-Merge Algorithm

Evolving Straight-Line Clustering

Hough Transform

Table of Contents for
5.3 Pose Measurement Methods