Chapter 6
Asymmetric Public-Key Cryptosystems
Public-key cryptography became public soon after Whitefield Diffie and Martin Hellman (1976) proposed the innovative concept of an exponential key exchange scheme. Since 1976, numerous public-key algorithms have been proposed, but many of them have since been broken. Of the many algorithms that are still considered to be secure, most are impractical.
Only a few public-key algorithms are both secure and practical. Of these, only some are suitable for encryption. Others are only suitable for digital signatures. Among these numerous public-key cryptography algorithms, only four algorithms, RSA (1978), ElGamal (1985), Schnorr (1990), and ECC (1985), are considered to be suitable for both encryption and digital signatures. Another public-key algorithm that is designed to only be suitable for secure digital signatures is DSA (Digital Signature Algorithm; 1991). The designer should bear in mind that the security of any encryption scheme depends on the length of the key and the computational work involved in breaking a cipher.
6.1 Diffie–Hellman Exponential Key Exchange
In 1976, Diffie and Hellman proposed a scheme using the exponentiation modulo q (a prime) as a public key exchange algorithm. Exponential key exchange takes advantage of easy computation of exponentials in a finite field GF(q) with a prime q compared with the difficulty of computing logarithms over GF(q) with q elements ![]() . Let q be a prime number and
. Let q be a prime number and ![]() a primitive element of the prime number q. Then the powers of
a primitive element of the prime number q. Then the powers of ![]() generate all the distinct integers from 1 to
generate all the distinct integers from 1 to ![]() in some order. For any integer Y and a primitive element
in some order. For any integer Y and a primitive element ![]() of prime number q, a unique exponent X is found such that
of prime number q, a unique exponent X is found such that
![]()
Then X is referred to as the discrete logarithm of Y to the base ![]() over GF(q):
over GF(q):
![]()
Calculation of Y from X is comparatively easy, using repeated squaring, but computation of X from Y is typically far more difficult.
Suppose the user i chooses a random integer ![]() and the user j a random integer
and the user j a random integer ![]() . Then the user i picks a random number
. Then the user i picks a random number ![]() from the integer set
from the integer set ![]() . The user i keeps
. The user i keeps ![]() secret, but sends
secret, but sends
![]()
to the user j. Similarly, the user j chooses a random integer ![]() and sends
and sends
![]()
to the user i.
Both users i and j can now compute:
![]()
and use ![]() as their common key.
as their common key.
The user i computes ![]() by raising
by raising ![]() to the power
to the power ![]() :
:

and the user j computes ![]() in a similar fashion:
in a similar fashion:
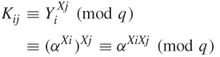
Thus, both users i and j have exchanged a secret key. Since ![]() and
and ![]() are private, the only available factors are the public values q,
are private, the only available factors are the public values q, ![]() ,
, ![]() , and
, and ![]() . Therefore, the opponent is forced to compute a discrete logarithm which is considered to be unrealistic, particularly for large primes. Figure 6.1 illustrates the Diffie–Hellman (D-H) key exchange scheme.
. Therefore, the opponent is forced to compute a discrete logarithm which is considered to be unrealistic, particularly for large primes. Figure 6.1 illustrates the Diffie–Hellman (D-H) key exchange scheme.
Figure 6.1 The Diffie–Hellman exponential key exchange scheme.

When utilizing finite field GF(q), where q is either a prime or ![]() , it is necessary to ensure the
, it is necessary to ensure the ![]() factor has a large prime, otherwise it is easy to find discrete logarithms in GF(q).
factor has a large prime, otherwise it is easy to find discrete logarithms in GF(q).
Table 6.1 Powers of primitive element ![]() (over
(over ![]() )
)


To initiate communication, the user i chooses ![]() randomly from the integer set
randomly from the integer set ![]() and keeps it secret. The user i sends
and keeps it secret. The user i sends

to the user j. Similarly, the user j chooses a random number ![]() and sends
and sends

to the user i.

and
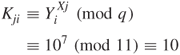
Thus, each user computes the common key.
Table 6.2 Field elements of GF(2![]() ) for
) for ![]()
| Power | Polynomial | Vector |
| 1 | 1 | 100 |
| 010 | ||
| 001 | ||
| 110 | ||
| 011 | ||
| 111 | ||
| 101 |
Suppose users i and j select ![]() and
and ![]() , respectively. Both
, respectively. Both ![]() and
and ![]() are kept secret, but
are kept secret, but
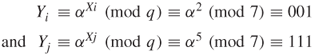
are placed in the public file. User i can communicate with user j by taking ![]() from the public file and computing their common key
from the public file and computing their common key ![]() as follows:
as follows:
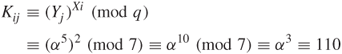
User j computes ![]() in a similer fashion:
in a similer fashion:
![]()
Thus two users i and j arrive at a key ![]() in common. These examples are extremely small in size and are intended only to illustrate the technique. So far, we have shown how to calculate the D-H key exchange, the security of which lies in the fact that it is very difficult to compute discrete logarithms for large primes.
in common. These examples are extremely small in size and are intended only to illustrate the technique. So far, we have shown how to calculate the D-H key exchange, the security of which lies in the fact that it is very difficult to compute discrete logarithms for large primes.
This pioneering work relating to the key-exchange algorithm introduced a new approach to cryptography that met the requirements for public-key systems. The first response to the challenge was the development of the RSA scheme which was the only widely accepted approach to the public key encryption. The RSA cryptosystem will be examined in the next section.
6.2 RSA Public-Key Cryptosystem
In 1976, Diffie and Hellman introduced the idea of the exponential key exchange. In 1977 Rivest, Schamir, and Adleman invented the RSA algorithm for encryption and digital signatures which was the first public-key cryptosystem. Soon after the publication of the RSA algorithm, Merkle and Hellman devised a public-key cryptosystem for encryption based on the knapsack algorithm. The RSA cryptosystem resembles the D-H key exchange system in using exponentiation in modula arithmetic for its encryption and decryption, except that RSA operates its arithmetic over the composite numbers. Even though the cryptanalysis was researched for many years for RSA's security, it is still popular and reliable. The security of RSA depends on the problem of factoring large numbers. It is proved that 110-digit numbers are being factored with the power of current factoring technology. To keep RSA's level of security, more than 150-digit values for n will be required. The speed of RSA does not beat DES, because DES is about 100 times faster than RSA in software.
6.2.1 RSA Encryption Algorithm
Given the public key e and the modulus n, the private key d for decryption has to be found by factoring n. Choose two large prime numbers, p and q, and compute the modulus n which is the product of the two primes:
![]()
Choose the encryption key e such that e and ![]() are coprime, that is, gcd
are coprime, that is, gcd ![]() , in which
, in which ![]() is called Euler's totient function.
is called Euler's totient function.
Using euclidean algorithm, the private key d for decryption can be computed by taking the multiplicative inverse of e such that

The decryption key d and the modulus n are also relatively prime. The numbers e and n are called the public keys, while the number d is called the private key.
To encrypt a message m, the ciphertext c corresponding to the message block can be found using the following encryption formula:
![]()
To decrypt the ciphertext c, c is raised to the power d in order to recover the message m as follows:
![]()
It is proved that
![]()
due to the fact that ![]() .
.
Because Euler's formula is ![]() , the message m is relatively prime to n such that gcd
, the message m is relatively prime to n such that gcd ![]() . Since
. Since ![]() for some integer
for some integer ![]() , it can be written
, it can be written ![]() , because
, because ![]() . Thus, the message m can be restored.
. Thus, the message m can be restored.
Figure 6.2 and Table 6.3 illustrate the RSA algorithm for encryption and decryption.
Figure 6.2 RSA public-key cryptosystem for encryption/decryption.
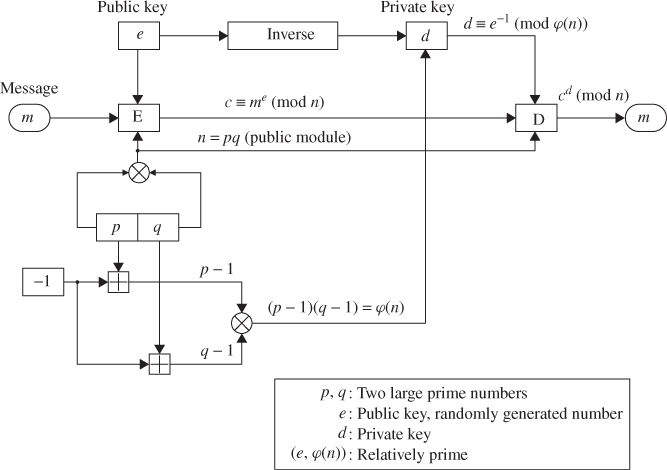
Table 6.3 RSA encryption algorithm
| Public key e: |
| Private key d: |
| Encryption: |
| Decryption: |
Using Table 6.3, the following examples are demonstrated.
![]()
If ![]() is chosen, then compute:
is chosen, then compute:
![]()
This decryption key d is calculated using the extended euclidean algorithm.
![]()
The public key (![]() ) is required for encryption of m. If
) is required for encryption of m. If ![]() , then the message m is encrypted as:
, then the message m is encrypted as:
![]()
To decipher, the private key d is needed to compute the message as follows:

![]()
Choose the encryption key ![]() randomly such that gcd
randomly such that gcd ![]() , that is, e and
, that is, e and ![]() are relatively prime. Using the extended euclidean algorithm (i.e., gcd
are relatively prime. Using the extended euclidean algorithm (i.e., gcd ![]() ), compute the decryption key d such that
), compute the decryption key d such that

To encrypt a message ![]() with
with ![]() , compute
, compute

To decrypt a message, perform the same exponentiation process using the decryption key ![]() such that
such that

Thus, the message is recovered.
Table 6.4 Two-digit numbers representing each character

![]()
Choose ![]() and
and ![]() . Then
. Then
![]()
Break the message m into blocks of four digits each:
![]()
Choose the encryption key ![]() . Then the decryption key d becomes
. Then the decryption key d becomes
![]()
The first block, ![]() , is encrypted by raising it to the power
, is encrypted by raising it to the power ![]() and dividing by
and dividing by ![]() and taking the remainder
and taking the remainder ![]() as the first block of ciphertext:
as the first block of ciphertext:

Thus, the whole ciphertext blocks ![]() ,
, ![]() , are computed as
, are computed as
![]()
To decrypt the first ciphertext ![]() , use the decryption key,
, use the decryption key, ![]() , and compute
, and compute

The recreated message of this example is computed as
![]()
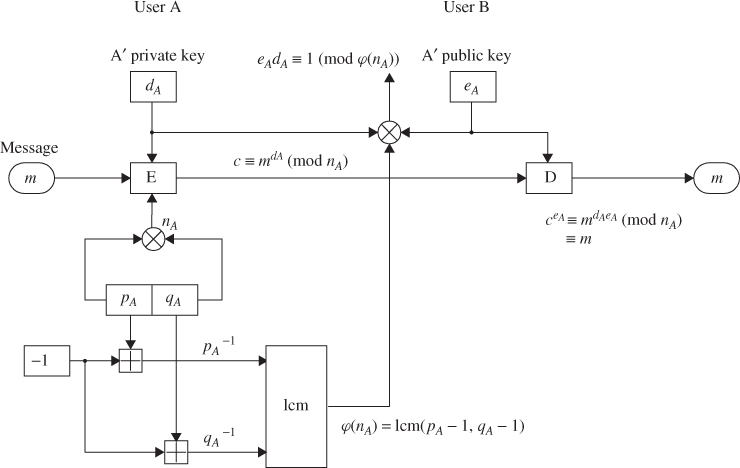
6.2.2 RSA Signature Scheme
The RSA public-key cryptosystem can be used for both encryption and signatures. Each user has three integers e, d, and ![]() with p and q large primes. For the key pair (
with p and q large primes. For the key pair (![]() ),
), ![]() must be satisfied. If sender A wants to send signed message c corresponding to message m to receiver B, A signs it using A's private key, computing
must be satisfied. If sender A wants to send signed message c corresponding to message m to receiver B, A signs it using A's private key, computing ![]() (mod
(mod ![]() ). First A computes
). First A computes
![]()
where 1 cm stands for the least common multiple. The sender A selects his own key pair (![]() ) such that
) such that
![]()
The modulus ![]() and the public key
and the public key ![]() are published., Figure 6.3 illustrates the RSA signature scheme.
are published., Figure 6.3 illustrates the RSA signature scheme.
Figure 6.3 The RSA signature scheme.
![]()
Select ![]() . Then
. Then ![]()

Suppose ![]() . Then the signed message is
. Then the signed message is
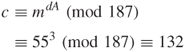
The message will be recreated as:

Thus, the message m is accepted as authentic.
Next, consider a case where the message is much longer. The larger m requires more computation in signing and verification steps. Therefore, it is better to compute the message digest using an appropriate hash function, for example, the SHA-1 (Secure Hash Algorithm). Signing the message digest rather than the message often improves the efficiency of the process because the message digest is usually much smaller than the message.
When the message is assumed to be ![]() , the message digest h of m is computed using the SHA-1 as follows:
, the message digest h of m is computed using the SHA-1 as follows:

The message digest h is then computed as
![]()
Signing h with A's private key ![]() produces
produces

Thus, the signature verification proceeds as follows:
![]()
which shows that verification is accomplished.
In hardware, RSA is about 1000 times slower than DES. RSA is also implemented in smartcards, but these implementations are slower. DES is about 100 times faster than RSA. However, RSA will never reach the speed of symmetric cipher algorithms.
It is known that the security of RSA depends on the problem of factoring large numbers. To find the private key from the public key e and the modulus n, one has to factor n. Currently, n must be larger than a 129 decimal digit modulus. Easy methods to break RSA have not yet been found. A brute-force attack is even less efficient than trying to factor n. RSA encryption and signature verification are faster if you use a low value for e, but can be insecure.
6.3 ElGamal's Public-Key Cryptosystem
ElGamal proposed a public-key cryptosystem in 1985. The ElGamal algorithm can be used for both encryption and digital signatures. The security of the ElGamal scheme relies on the difficulty of computing discrete logarithms over GF(p), where p is a large prime. Prime factorization and discrete logarithms are required to implement the RSA and the ElGamal cryptosystems.
In the RSA cryptosystems, each user has three integers e, d, and n, where ![]() with two large primes p and q, and
with two large primes p and q, and ![]() ,
, ![]() being Euler's totient function. User A has a public key consisting of the pair (
being Euler's totient function. User A has a public key consisting of the pair (![]() ) and a private key
) and a private key ![]() ; similarly,user B has (
; similarly,user B has (![]() ) and
) and ![]() . To encrypt the message m to
. To encrypt the message m to ![]() uses B's public key for computing the encrypted message (or ciphertext) such that
uses B's public key for computing the encrypted message (or ciphertext) such that ![]() . If A wants to send the signed message to
. If A wants to send the signed message to ![]() signs the message m using his own private key
signs the message m using his own private key ![]() such that
such that ![]() .
.
To describe the ElGamal system, choose a prime number p and two random numbers, g and x, such that both ![]() and
and ![]() , where x is a private key. The random number g is a primitive root modulo p. The public key is defined by y, g, and p. Then we compute
, where x is a private key. The random number g is a primitive root modulo p. The public key is defined by y, g, and p. Then we compute ![]() . To encrypt the message m,
. To encrypt the message m, ![]() , first pick a random number k such that gcd
, first pick a random number k such that gcd ![]() . The encrypted message (or ciphertext) can be expressed by the pair (
. The encrypted message (or ciphertext) can be expressed by the pair (![]() ) as follows:
) as follows:

To decrypt m, divide s by ![]() such that
such that ![]() . To sign a given message m, first choose a random number k such that gcd
. To sign a given message m, first choose a random number k such that gcd ![]() , and compute
, and compute ![]() using the extended euclidean algorithm to solve s. The basic technique for encryption and signature using the ElGamal algorithm as a two-key cryptosystem is described in the following section.
using the extended euclidean algorithm to solve s. The basic technique for encryption and signature using the ElGamal algorithm as a two-key cryptosystem is described in the following section.
6.3.1 ElGamal Encryption
To generate a key pair, first choose a prime p and two random numbers g and x such that ![]() and
and ![]() . Then compute
. Then compute
![]()
The public key is (![]() ) and the private key is
) and the private key is ![]() .
.
To encrypt the message ![]() , first choose a random number k such that gcd
, first choose a random number k such that gcd ![]() . The encrypted message (or ciphertext) is then the following pair (
. The encrypted message (or ciphertext) is then the following pair (![]() ):
):
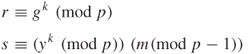
Note that the size of the ciphertext is double the size of the message. To decrypt the message, divide s by ![]() , as shown below:
, as shown below:
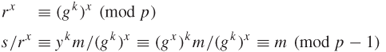
The ElGamal encryption scheme is plotted in Figure 6.4 and Table 6.5.
Figure 6.4 The ElGamal encryption scheme.

Table 6.5 The ElGamal encryption algorithm
| Public key: |
| p (a prime number) |
| |
| |
| |
| Private key: |
| |
| Enciphering: |
| k: a random number such that gcd |
| |
| |
| Deciphering: |
| |

Then compute:
![]()
The public key is ![]() , and
, and ![]() . The private key
. The private key ![]() is given above. To encrypt the message
is given above. To encrypt the message ![]() , first choose a random number
, first choose a random number ![]() such that gcd
such that gcd ![]() and then compute:
and then compute:

To decipher the message m, first compute:
![]()
and take the ratio:
![]()
It thus proves that the message m is completely restored using the ElGamal encryption algorithm (Table 6.5).
6.3.2 ElGamal Signatures
To sign a message m, first choose a random number k such that gcd ![]() (relatively prime). The public key is described by
(relatively prime). The public key is described by
![]()
where the private key is ![]() . Let m be a message to be signed,
. Let m be a message to be signed, ![]() . Choose first a random number k such that gcd
. Choose first a random number k such that gcd ![]() (relatively prime). Then compute
(relatively prime). Then compute
![]()
The signature for m is the pair ![]() ,
, ![]() ,
, ![]() .
.
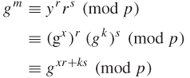
from which
![]()
Use the extended euclidean algorithm to solve s. The signature for m is the pair (![]() ). The random number s should be kept secret. To verify a signature, confirm that:
). The random number s should be kept secret. To verify a signature, confirm that:
![]()
Figure 6.5 illustrates the ElGamal signature scheme based on Table 6.6.
Figure 6.5 The ElGamal signature scheme.

Table 6.6 The ElGamal signature algorithm
| Public key: |
| p (a prime number) |
| |
| |
| Private key: |
| k: a random number |
| |
| s: compute from |
| Verifying: |
| Accept as valid if |
| |
![]()
The public key is ![]() ,
, ![]() , and
, and ![]() .
.

The signature is the pair of ![]() and
and ![]() .
.
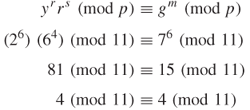
6.3.3 ElGamal Authentication Scheme
The ElGamal signature or authentication scheme looking at another angle is described in the following.
The sender chooses a finite field GF(p) where p is a prime. Let g be a primitive element of GF(p). First choose two random integers g and x such that ![]() and
and ![]() . A key x is kept secret by both the sender and the receiver. Let m denote a message which is relatively prime to p. Then compute:
. A key x is kept secret by both the sender and the receiver. Let m denote a message which is relatively prime to p. Then compute:
![]()
Let c denote a ciphertext such that gcd ![]() .
.
Using the extended euclidean algorithm, the following congruence is to solve for v:
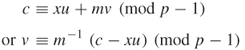
To authenticate the ciphertext c, the signed cryptogram (![]() ) is transmitted to the receiver. Upon receipt of (
) is transmitted to the receiver. Upon receipt of (![]() ), the receiver computes
), the receiver computes

Thus, the ciphertext c is accepted as authentic if ![]() (mod p). Once this ciphertext has been accepted, the message m is recovered by:
(mod p). Once this ciphertext has been accepted, the message m is recovered by:
![]()
The ElGamal authentication scheme is shown in Figure 6.6. The ElGamal authentication algorithm given in Table 6.7 is illustrated by the following example.
Figure 6.6 The ElGamal authentication scheme.

Table 6.7 The ElGamal authentication algorithm
| Sender |
| p (a prime integer) |
| |
| |
| |
| c (ciphertext) |
| |
| |
| Receiver |
| |
| Verifying: |
| Accept as valid if and only if |
| Decryption: |
| |
![]()
Next, compute ![]() by solving the following congruence:
by solving the following congruence:

where ![]() is assumed.
is assumed.

Thus, the cryptogram (7, 2, 9) is accepted, and ![]() is authentic. Finally, the message is restored in the following manner:
is authentic. Finally, the message is restored in the following manner:

The message ![]() has been completely recovered.
has been completely recovered.
6.4 Schnorr's Public-Key Cryptosystem
In 1990, Schnorr introduced his authentication and signature schemes based on discrete logarithms.
6.4.1 Schnorr's Authentication Algorithm
First choose two primes, p and q, such that q (![]() ) is a prime factor of
) is a prime factor of ![]() . To generate a public key, choose
. To generate a public key, choose ![]() such that
such that ![]() , that is,
, that is, ![]() . If h is relatively prime to p, by Fermat's theorem it can then be written as
. If h is relatively prime to p, by Fermat's theorem it can then be written as ![]() . As a result, we have
. As a result, we have ![]() . All these numbers, p, q, and a, can be freely published and shared with a group of users. To generate a key pair, choose a random number
. All these numbers, p, q, and a, can be freely published and shared with a group of users. To generate a key pair, choose a random number ![]() which is used as the private key. Next, compute
which is used as the private key. Next, compute ![]() which is the public key.
which is the public key.
Now, user A picks a random number ![]() and computes
and computes ![]() . User B picks a random number t and sends it to user A, where
. User B picks a random number t and sends it to user A, where ![]() ) indicates the security level. Schnorr recommends the value of
) indicates the security level. Schnorr recommends the value of ![]() for sufficient security. User A computes
for sufficient security. User A computes ![]() and sends it to user B. Thus, user B tests verification of authenticity such that
and sends it to user B. Thus, user B tests verification of authenticity such that ![]() . Figure 6.7 illustrates Schnorr's authentication scheme, and Table 6.8 shows the related algorithm.
. Figure 6.7 illustrates Schnorr's authentication scheme, and Table 6.8 shows the related algorithm.
Figure 6.7 Schnorr's authentication scheme.

Table 6.8 Schnorr's authentication algorithm
| Preprocessing: | |
| Choose two primes, p and q, such that q is a prime factor of |
|
| Choose a such that |
|
| Key generation: | |
| Choose a random number |
|
| Compute |
|
| User A | User B |
| Choose a random number |
|
| Compute |
Pick a random number t such that |
| Send t to user A | |
| Compute |
|
| Send y to user B |
Verify that |
![]()
The receiver sends ![]() to the sender and the sender computes:
to the sender and the sender computes:

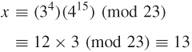
Since ![]() , the authentication is accepted.
, the authentication is accepted.
6.4.2 Schnorr's Signature Algorithm
For a digital signature, user A concatenates the message m and x and computes the hash code:
![]()
User A sends the signature (![]() ) to user B. User B computes
) to user B. User B computes ![]() (mod p) and confirms whether hashing the concatenation of m and z yields:
(mod p) and confirms whether hashing the concatenation of m and z yields:
![]()
If ![]() , then user B accepts the signature as valid.
, then user B accepts the signature as valid.
For the same level of security, Schnorr's signature algorithms are shorter than the RSA ones. Also, Schnorr's signatures are much shorter than ElGamal signatures. Figure 6.8 and Table 6.9 illustrate Schnorr's signature algorithm.
Figure 6.8 Schnorr's signature scheme.
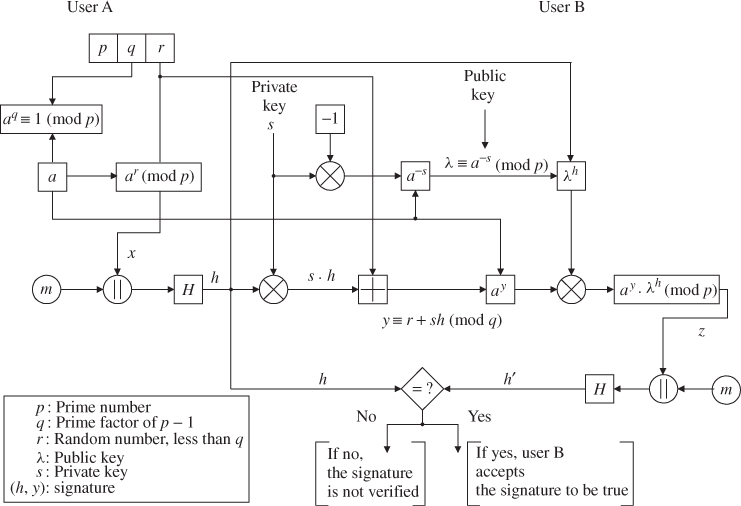
Table 6.9 Schnorr's signature algorithm
| Preprocessing stage and the two key pair are the same. | |
| User A | User B |
| Choose |
|
| Compute |
|
| Concatenate m and x, that is, |
|
| such that |
|
| Compute |
|
| Send the signature ( |
Compute |
| Concatenate m and z and hash: | |
| If the two hash values match ( |
|
| then user B accepts the | |
| signature as valid | |

![]()
Concatenate m and x and hash ![]() such that
such that
![]()
where the message ![]() is assumed. To produce the message digest
is assumed. To produce the message digest![]() , use the SHA which is closely modeled on MD4. Utilizing SHA for h yields a 160-bit message digest as the output, as follows:
, use the SHA which is closely modeled on MD4. Utilizing SHA for h yields a 160-bit message digest as the output, as follows:

User A computes ![]() (mod q):
(mod q):
![]()
Send signature ![]() to user B. User B first computes:
to user B. User B first computes:

Concatenate ![]() and z and hash it as follows:
and z and hash it as follows:

which is identical to h. Therefore, user B accepts the signature as valid because ![]() .
.

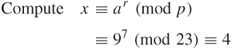
Using the MD5 algorithm, compute the message digest:

Using ![]() (mod q) becomes
(mod q) becomes ![]() (mod 11).
(mod 11).
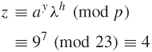
Applying MD5 to ![]() (
(![]() ) (mod 11), we have
) (mod 11), we have
![]()
Thus, user B confirms verification of ![]() .
.
6.5 Digital Signature Algorithm
In 1991, the National Institute of Standards and Technology (NIST) proposed the DSA for federal digital signature applications. The proposed new Digital Signature Standard (DSS) uses a public-key signature scheme to verify to a recipient the integrity of data received and the identity of the sender of the data.
DSA provides smartcard applications for digital signature. Key generation in DSA is faster than that in RSA. Signature generation has the same level of speed as RSA, but signature verification is much slower than RSA.
Many software companies, such as IBM, Microsoft, Novell, and Apple, that have already licensed the RSA algorithm protested against the DSS. Many companies wanted NIST to adopt ISO/IEC 9796 for use instead of RSA as the international digital signature standard.
The DSA is based on the difficulty of computing discrete logarithms, and originated from schemes presented by ElGamal and Schnorr. The public key consists of three parameters, ![]() , and g, and is common to a group of users. Choose q of a 160-bit prime number and select a prime number p with
, and g, and is common to a group of users. Choose q of a 160-bit prime number and select a prime number p with ![]() bits such that q is a prime factor of
bits such that q is a prime factor of ![]() . Next, choose
. Next, choose ![]() to be of the form
to be of the form ![]() such that
such that ![]() is an integer between 1 and
is an integer between 1 and ![]() .
.
With these three numbers, each user chooses a private key x in the range ![]() and the public key y is computed from x as
and the public key y is computed from x as ![]() (mod p). Recall that determining x is computationally impossible because the discrete logarithm of y to the base g (mod p) is difficult to calculate.
(mod p). Recall that determining x is computationally impossible because the discrete logarithm of y to the base g (mod p) is difficult to calculate.
To sign a message m, the sender computes two parameters, r and s, which are functions of (![]() , and x), the message digest
, and x), the message digest ![]() ), and a random number
), and a random number ![]() . At the receiver, verification is performed as shown in Table 6.10. The receiver generates a quantity v that is a function of parameters (
. At the receiver, verification is performed as shown in Table 6.10. The receiver generates a quantity v that is a function of parameters (![]() , and
, and ![]() ).
).
Table 6.10 DSA signatures
| Key pair generation: |
| p: a prime number between 512 and 1024 bits long |
| q: a prime factor of |
| ( |
| Signing process (sender): |
| ( |
| Verifying signature (receiver): |
| If |
When a one-way hash function H operates on a message m of any length, a fixed-length message digest (hash code) h can be produced such that ![]() . The message digest h to the DSA input computes the signature for the message m. Signing the message digest rather than the message itself often improves the efficiency of the signature process, because the message digest h is usually much smaller than the message m. The SHA is called secure because it is designed to be computationally impossible to recover a message corresponding to a given message digest. Any change to a message in transit will result in a different message digest,and the signature will fail to verify. The structure of the DSA algorithm is illustrated in Figure 6.9.
. The message digest h to the DSA input computes the signature for the message m. Signing the message digest rather than the message itself often improves the efficiency of the signature process, because the message digest h is usually much smaller than the message m. The SHA is called secure because it is designed to be computationally impossible to recover a message corresponding to a given message digest. Any change to a message in transit will result in a different message digest,and the signature will fail to verify. The structure of the DSA algorithm is illustrated in Figure 6.9.
Figure 6.9 DSA digital signature scheme.

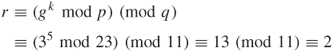
Assume that ![]() and compute:
and compute:
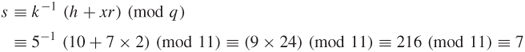
where the multiplicative inverse ![]() is:
is:
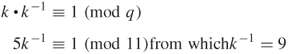
Receiver: (verifying)

Since ![]() , the signature is verified.
, the signature is verified.
6.6 The Elliptic Curve Cryptosystem (ECC)
The Elliptic Curve Cryptosystem (ECC) was introduced by Neal Koblitz and Victor Miller in 1985. The elliptic curve (EC) discrete logarithm problem appears to be substantially more difficult than the existing discrete logarithm problem. Considering they have equal levels of security, ECC uses smaller parameters than the conventional discrete logarithm systems.
In this section, we first present the concept of an EC and then discuss its applications to existing public-key algorithms. Finally, we will look at cryptographic algorithms with ECs over the prime or finite fields.
6.6.1 Elliptic Curves
ECs have been studied for many years. ECs over the prime field ![]() or the finite field GF(
or the finite field GF(![]() ) are particularly interesting because they provide a way of constructing cryptographic algorithms. ECs have the potential to provide faster public-key cryptosystem with smaller key sizes.
) are particularly interesting because they provide a way of constructing cryptographic algorithms. ECs have the potential to provide faster public-key cryptosystem with smaller key sizes.
Elliptic Curves over Prime Field Zp
Figure 6.10 shows the EC ![]() defined over
defined over ![]() where
where ![]() ,
, ![]() is called a prime field if and only if
is called a prime field if and only if ![]() is an odd prime. An EC can be made into an abelian group with all points on an EC, including the point at infinity
is an odd prime. An EC can be made into an abelian group with all points on an EC, including the point at infinity ![]() under the condition of
under the condition of ![]() (mod
(mod ![]() ).
).
Figure 6.10 An elliptic curve.

Computation over Prime Field Zp
If the points on an EC ![]() over
over ![]() are represented by
are represented by ![]() ,
, ![]() , and
, and ![]() , then two cases can be considered:
, then two cases can be considered:
 (addition of two points on EC).
(addition of two points on EC). (doubling of two points on EC).
(doubling of two points on EC).
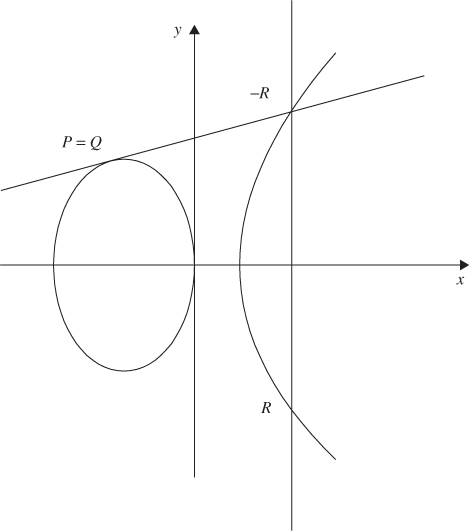
Consider the curve where ![]() as shown in Figure 6.10
as shown in Figure 6.10
![]()
First draw a linear curve ![]() (where
(where ![]() /
/![]() );
); ![]() ) passing through two points
) passing through two points ![]() and
and ![]() and find the intersection point
and find the intersection point ![]() . As shown in Figure 6.10, draw a straight line vertically (perpendicularly) across the
. As shown in Figure 6.10, draw a straight line vertically (perpendicularly) across the ![]() -axis so that it meets the third point
-axis so that it meets the third point ![]() , which is the sum of
, which is the sum of ![]() and
and ![]() .
.
EC: ![]() expresses
expresses
Consider a cubic equation with three roots:
From which
Comparing Equations 6.1 and 6.2 results in
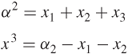
Using

If ![]() does have a constant value
does have a constant value ![]() , EC becomes
, EC becomes
![]()
or
![]()
Thus, ![]() will have two roots:
will have two roots:
Since the third point ![]() , it results in
, it results in
![]()
Finally, we have
![]()
This can be summed up as
Consider the case ![]() as shown in Figure 6.11
as shown in Figure 6.11
Figure 6.11 The doubling of an elliptic curve point.
![]() (doubling of two points on EC)
(doubling of two points on EC)
![]()
Differentiating with respect to ![]() yields
yields

Considering ![]() , we have
, we have ![]()
Since ![]() ,
,
Comparing Equation 6.6 with Equation 6.4 results in ![]() (by doubling)
(by doubling)
![]()
Since ![]()
![]()
Thus, the case of ![]() can be summed up as shown below:
can be summed up as shown below:

![]()



![]()
The square of the integers in ![]() for modulo 13 is computed as:
for modulo 13 is computed as:
![]()
Hence, the quadratic nonresidues modulo 13 are ![]() . Now you can see that the set
. Now you can see that the set ![]() is equally divided into quadratic residues and nonresidues. In general, there are precisely
is equally divided into quadratic residues and nonresidues. In general, there are precisely ![]() quadratic residues and
quadratic residues and ![]() quadratic nonresidues of p.
quadratic nonresidues of p.
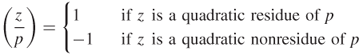
Table 6.11 Quadratic residues and points on EC ![]() over
over ![]()

Let EC be an elliptic curve over ![]() . Hasse states that the number of points on an EC, including the point at infinity O, is
. Hasse states that the number of points on an EC, including the point at infinity O, is ![]() where
where ![]() .
. ![]() is called the order of EC and t is called the trace of EC.
is called the order of EC and t is called the trace of EC.
![]()
Any point other than the point at infinity can be a generator G of EC. If we pick ![]() as the generator, the multiples of G can be computed as follows:
as the generator, the multiples of G can be computed as follows:
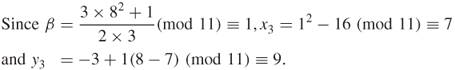
Hence, ![]() .
.
![]()
where ![]() and
and ![]() . The set of EC over GF(2
. The set of EC over GF(2![]() ) consists of all points
) consists of all points ![]() ,
, ![]() , that satisfy the above defining equation, together with the point at infinity O.
, that satisfy the above defining equation, together with the point at infinity O.
![]()
Table 6.12 Field elements of GF(2![]() ) using
) using ![]()
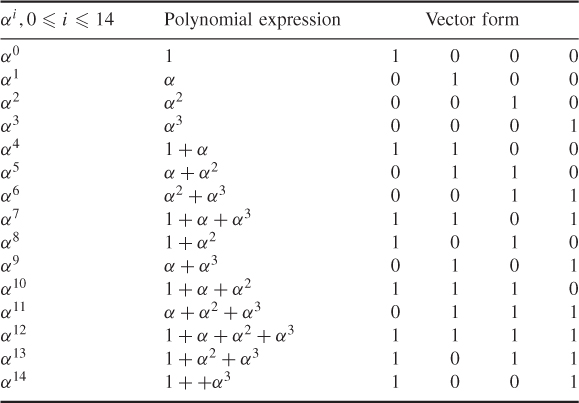
![]()
Check whether one element (![]() ) satisfies the EC equation over GF(2
) satisfies the EC equation over GF(2![]() ).
).
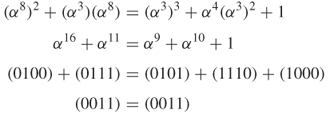
Thus, the points on the EC(GF(2![]() are O (point at infinity) and the following 15 elements:
are O (point at infinity) and the following 15 elements:


Hence, ![]()
6.6.2 Elliptic Curve Cryptosystem Applied to the ElGamal Algorithm
As an application problem to ECC, consider the ElGamal public-key cryptosystem based on the EC defined over the prime field ![]() . The ElGamal crypto-algorithm is based on the discrete logarithm problem. Referring to Table 6.5 for the ElGamal encryption algorithm, choose a prime p such that the discrete logarithm problem in
. The ElGamal crypto-algorithm is based on the discrete logarithm problem. Referring to Table 6.5 for the ElGamal encryption algorithm, choose a prime p such that the discrete logarithm problem in ![]() is intractable, and let
is intractable, and let ![]() be a primitive element of
be a primitive element of ![]() . The values of
. The values of ![]() , and y are public, and x is secret.
, and y are public, and x is secret.
![]()
Choose a random number k such that gcd![]() . Then the encryption process of the message
. Then the encryption process of the message ![]() , is accomplished by the following pair
, is accomplished by the following pair ![]() :
:

For ![]() , the decryption is defined as:
, the decryption is defined as:
![]()
Elliptic Curve Cryptosystem by the ElGamal Algorithm
| User A | User B | |
| Let X be the plaintext and k a random number. Choose X and k | Generate B's private key |
|
| Compute |
Receive |
|
| Send Y to user B | Decryption yields |
Many public-key algorithms, such as D-H, ElGamal, and Schnorr, can be implemented in ECs over finite fields.

B receives Y and decrypts it as follows:
![]()
Thus, the correct plaintext X is recovered by decryption.
6.6.3 Elliptic Curve Digital Signature Algorithm
In the author's recent book “Mobile Communications and Security,” John-Wiley (2009), Chapter 9 presents some cryptography algorithms for providing the data security in the air interface security layer. One of the topics is ECC. Some examples on Elliptic Curve Digital Signature Algorithm (ECDSA) over the finite binary extension field GF(2![]() ) is analyzed with the Weierstrass equations without derivation of addition and doubling formula. The purpose of this presentation is twofold: derivation of addition and doubling formula applicable to EC(GF(2
) is analyzed with the Weierstrass equations without derivation of addition and doubling formula. The purpose of this presentation is twofold: derivation of addition and doubling formula applicable to EC(GF(2![]() )) and pointing out some innovative derivation in an example.
)) and pointing out some innovative derivation in an example.
Analysis of the effect of different extension field of ECDSA is examined. Some practical examples of EC(GF(2![]() )) field are presented to illustrate performances based on changing some of the parameters. The results examine the relationship between analyses and predict any future performances of DSA.
)) field are presented to illustrate performances based on changing some of the parameters. The results examine the relationship between analyses and predict any future performances of DSA.
Definition
The Weierstrass equations are described by
![]()
where ![]() (2
(2![]() ) (from Rosen, K.H., Handbook of Elliptic and Hyperelliptic Curve Cryptography. Boca Raton, FL: Chapman & Hall/CRC).
) (from Rosen, K.H., Handbook of Elliptic and Hyperelliptic Curve Cryptography. Boca Raton, FL: Chapman & Hall/CRC).
Arithmetic of EC over GF( )
)
This section shows the basic arithmetic of EC over GF(![]() ), especially for
), especially for
![]()
where ![]() GF(
GF(![]() ).
).
Addition
The addition on an EC is defined as the point addition of the two given points ![]() (
(![]() ) and
) and ![]() (
(![]() ) on an EC to obtain another point
) on an EC to obtain another point ![]() (
(![]() ) on the same EC, which is expressed as
) on the same EC, which is expressed as
![]()
where ![]() .
.
![]() (
(![]() ) is defined as the additive inverse of the third crossing point on the EC by the line determined by
) is defined as the additive inverse of the third crossing point on the EC by the line determined by ![]() (
(![]() ) and
) and ![]() (
(![]() ); that is, the third crossing point is
); that is, the third crossing point is ![]() (
(![]() ). Now, we are going to find
). Now, we are going to find ![]() and
and ![]() from the definition.
from the definition.
Let, ![]() be the line determined by
be the line determined by ![]() and
and ![]() and we can get
and we can get ![]() by solving the following simultaneous equations with
by solving the following simultaneous equations with ![]() and
and ![]() .
.
6.7![]()
6.8![]()
where
![]()
Substituting ![]() in Equation 6.7 results in
in Equation 6.7 results in
6.10 ![]()
If ![]() ,
, ![]() , and
, and ![]() are the roots of the equation, then they should be expressed as
are the roots of the equation, then they should be expressed as
Comparing coefficients of like terms of Equations 6.7 and 6.9 yields
6.13 ![]()
6.14 ![]()
From Equation 6.10, we get ![]() as
as
6.15 ![]()
Next we are going to find ![]() . Since R(
. Since R(![]() ,
, ![]() ) and
) and ![]() (
(![]() ,
, ![]() ) are additive inverse, it should be
) are additive inverse, it should be ![]() (details may be required). Since
(details may be required). Since ![]() is on the straight line l, we get the following equations.
is on the straight line l, we get the following equations.
6.16 ![]()
6.17 ![]()
which results in
6.18 ![]()
In summary, the addition on the EC
![]()
is defined as
![]()
and the resulting point is calculated as
![]()
where

Verification of
![]()
Doubling
When ![]() , we cannot get
, we cannot get ![]() in Equation 6.5 because
in Equation 6.5 because ![]()
![]() . Therefore, we need another way to get
. Therefore, we need another way to get ![]() in Equation 6.6. Let us differentiate the Equation (6.3) with respect to
in Equation 6.6. Let us differentiate the Equation (6.3) with respect to ![]() and letting
and letting ![]() , then we get the following.
, then we get the following.

and

In short,
6.19 ![]()
By solving Equations 6.7 and 6.8 with ![]() , we get
, we get ![]() as
as

In short,
6.20 ![]()
Now, we are going to find ![]() . Again, from the straight line through
. Again, from the straight line through ![]() and
and ![]() , we get the following equations.
, we get the following equations.
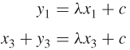
By substituting ![]() with
with ![]() , we get
, we get

Therefore,
6.21 ![]()
In summary, the doubling on the EC
![]()
is defined as
![]()
And the resulting point is calculated as

6.6.4 ECDSA Signature Computation
ECCs are viewed as EC analogs to the conventional discrete logarithm cryptosystems in which the subgroup of ![]() is replaced by the group of point on an EC over a finite field. In that sense, ECDSA is the EC analog of DSA. The ECDSA signature and verification algorithms are presented in this section. In addition, the ECDSA examples are presented to clarify the algorithms.
is replaced by the group of point on an EC over a finite field. In that sense, ECDSA is the EC analog of DSA. The ECDSA signature and verification algorithms are presented in this section. In addition, the ECDSA examples are presented to clarify the algorithms.
ECDSA Signature Scheme over GF(2 )
)
The domain parameters for ECDSA consist of a proper EC defined over an extension field of GF(![]() ) of characteristic 2. A set of EC domain parameters is composed of
) of characteristic 2. A set of EC domain parameters is composed of
![]()
where
![]()
Algorithm
Key Pair Generation
An ECDSA key pair is associated with a particular set of EC domain parameters ![]() that must be valid before key generation.
that must be valid before key generation.
User A selects a random integer ![]() for
for ![]() and computes
and computes ![]() , where Q is A's public key and
, where Q is A's public key and ![]() is A's private key.
is A's private key.
- Choose that
 .
. - Check whether a public key
 is properly represented by the elements of
is properly represented by the elements of  over (0,
over (0,  ) and m-bit string over GF(
) and m-bit string over GF( ) of
) of  .
. - Check that
 lies on the EC defined by
lies on the EC defined by  and
and  .
. - Check
 .
. - If any check fails, then
 is invalid; otherwise
is invalid; otherwise  is valid.
is valid.

To verify A's signature (![]() ) on
) on ![]() , the following computations are required:
, the following computations are required:

Since ![]() , the signature is accepted.
, the signature is accepted.

For example, when ![]() is converted into an integer, it would be 7, that is,
is converted into an integer, it would be 7, that is, ![]() .
.

User A's signature for the message is ![]() .
.
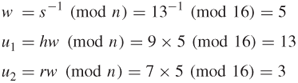
Finally, user B computes
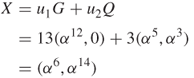
We can again convert ![]() into an integer
into an integer ![]() . Since
. Since ![]() , the ECDSA signature is accepted.
, the ECDSA signature is accepted.
