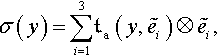Mechanics of Material Mutations
Paolo Maria Mariano DICeA, University of Florence, Florence, Italy
Abstract
Mutations in solids are defined here as dissipative reorganizations of the material texture at different spatial scales. We discuss possible views on the description of material mutations with special attention to the interpretations of the idea of multiple reference shapes for mutant bodies. In particular, we analyze the notion of relative power—it allows us to derive standard, microstructural, and configurational actions from a unique source—and the description of crack nucleation in simple and complex materials in terms of a variational selection in a family of bodies differing from one another by the defect pattern, a family parameterized by vector-valued measures. We also show that the balance equations can be derived by imposing structure invariance on the mechanical dissipation inequality.
1 A general view
1.1 A matter of terminology
The word “mutation” appearing in the title indicates the occurrence of changes in the material structure of a body, a reorganization of matter with dissipative nature. Implicit is the idea of considering mutations that have a nontrivial influence on the gross behavior of a body under external actions—the adjective “nontrivial” being significant from time to time. I use the word “mutation” here in this sense, relating it to dissipation, although not strictly to irreversible paths in state space1—mentioning dissipation appears necessary because even a standard elastic deformation implies a “reorganization” of the matter (think, for example, of deformation-induced anisotropies).
Mutation implies a relation with some reference configuration or state; in general, a mutation is with respect to a setting that we take as a paragon. Such a setting does not necessarily coincide only with the reference place of a continuum body. In fact, affirming that a mutation is macroscopic or microscopic implies the selection of spatial scales that we consider in representing the characteristic geometric features of a body morphology. Not all these features are entirely described by the assignment of a macroscopic reference place. To clarify this point, it can be useful to recall a few basic issues in continuum mechanics, i.e., the mechanics of tangible bodies, leaving aside corpuscular phenomena adequately treated by using concepts and methods pertaining to quantum theories, or considering just the effects of such phenomena emerging in the long-wavelength approximation.2
1.2 Material elements: monads or systems?
In the first pages of typical basic treatises in continuum mechanics, we read that a body is a set of not further specified material elements (let us say ordered sets of atoms and/or entangled molecules) that we represent just by mapping the body in the three-dimensional Euclidean point space. Then we consider how bodies deform during motions, imposing conditions that select among possible changes of place. Strain tensors indicate just how and how much lines, areas, and volumes are stretched, i.e., the way neighboring material elements move near to or away from each other. They do not provide information on how the matter at a point changes its geometry—if it does it—during a motion. In other words, we consider commonly the material element at a point as an indistinct piece of matter, a black box without further structure. We introduce information on the material texture at the level of constitutive relations—think, for example, of the material symmetries in the case of simple bodies. However, the parameters that the constitutive relations introduce refer to peculiar material features averaged over a piece of matter extended in space, what we call, in homogenization procedures, a representative volume element.3 In other words, in assigning constitutive relations we implicitly specify what we intend for the material element, and this is a matter of modeling in the specific case considered from time to time. This way we include a length scale in the continuum scheme, even when we do not declare it explicitly. This remark is rather clear already in linear elasticity. In fact, when in the linear setting we assign to a point a fourth-rank constitutive tensor, declaring some material symmetry (e.g., cubic), the symmetry at hand is associated with a subclass of rotations, and they are referred to the point considered. A point, however, does not rotate around itself. Hence, in speaking of material symmetries at a point, we are implicitly attributing to it the characteristic features of a piece of matter extended in space, with finite size. For example, in the case of cubic symmetry mentioned above, we imagine that a material point represents at least a cubic crystal, but we do not declare its size, which in this way is an implicit material length scale. We need not declare explicitly the size of the material element in traditional linear elasticity but, nevertheless, such a material length scale does exist. The events occurring above a length-scale considered in a specific continuum model, whatever is its origin, are described by relations among neighboring material elements. The ones below are collapsed at a point. Hence, in thinking of mutations, we can grossly distinguish between rearrangements of matter
• among material elements, and
• inside them.
When we restrict the description of the body morphology to the sole choice of the place occupied by the body (the standard approach), mutations inside material elements appear just in the selection of constitutive equations—material symmetry breaking in linear elasticity is an example—and possible flow rules. However, such mutations can generate interactions which can be hardly described by using only the standard representation of contact actions in terms of the Cauchy or Piola–Kirchhoff stresses. Some examples follow:
• Local couples orient the stick molecules that constitute liquid crystals in nematic order.
• In solid-to-solid phase transition (e.g., austenite to martensite), microactions occur between the different phases.
• Microactions of different types appear in ferroelectrics, produced by neighboring different polarizations and even inside a single crystal by the electric field generated by the local dipole.
• Another example is rather evident when we think of a material constituted by entangled polymers scattered in a soft melt. External actions may produce indirectly local polymer disentanglements or entanglements without altering the connection of the body. Moreover, in principle, every molecule might deform with respect to the surrounding matter, independently of what is placed around it, owing to mechanical, chemical, or electrical effects, the latter occurring when the polymer can suffer polarization. The common limit procedure defining the standard (canonical) traction at a point does not allow us to distinguish between the contributions of the matrix and the polymer. Considering explicitly the local stress fluctuations induced by the polymer would, however, require a refined description of the mechanics of the composite, which could be helpful in specific applications.
• Finally (but the list would not end here), we can think of the actions generated in quasicrystals by atomic flips.
However, beyond these examples, the issue is essentially connected with the standard definition of tractions. At a given point and with respect to an assigned (smooth) surface crossing that point, the traction is a force developing power when multiplied by the velocity of that point, i.e., the local rate at which material elements are crowded and/or sheared. And the velocity vector does not bring with it explicit information on what happens inside the material element at that point, even relatively to the events inside the surrounding elements. When physics suggests we account for the effects of microscopic events, we generally need a representation of the contact actions refined with respect to the standard one. In these cases, the quest does not reduce exclusively to the proposal of an appropriate constitutive relation (often obtained by data-fitting procedures) in the standard setting. We often have to start from the description of the morphology of a body, inserting fields that may bring at a continuum-level information on the microstructure. In this sense, we can call them descriptors of the material morphology (or inner degrees of freedom, even if to me the first expression could be clearer at times). This way, at the level of the geometric description of body morphology, we are considering every material element as a system that can have its own (internal) evolution with respect to the surrounding elements, rather than a monad, which is, in contrast, the view adopted in the traditional setting. I use here the word “monad” (coming from ancient Greek) to indicate an ultimate unit that cannot be divided further into pieces. Hence, I use system as opposite to monad, intending in short to indicate an articulate structure, a microworld from which we select the features that are of certain prominence, even essential (at least we believe that they are so), in the specific investigation that we are pursuing, and that define what we call microstructure.
1.3 Manifold of microstructural shapes
A long list of possible examples of material morphology descriptors emerges from the current literature: scalars, vectors, tensors of various ranks, combinations of them, etc. However, in checking the examples, we realize that for the construction of the basic structures of a mechanical models we do not need to specify the nature of the descriptor of the material morphology (descriptor, in short). What we need is
• the possibility of representing these descriptors in terms of components—a number list—and
• the differentiability of the map assigning the descriptor to each point in the reference place.
The former requirement is necessary in numerical computations. The prominence of the latter appears when we try to construct balance equations or to evaluate how much microstructural shapes4 vary from place to place. We do not need much more to construct the skeletal format of a model-building framework. We have just to require that the descriptors of the finer spatial scale material morphology are selected over a differentiable manifold5—this is a set admitting a covering of intersecting subsets which can be mapped by means of homeomorphisms into Euclidean spaces, all assumed here with a certain dimension; let us assume it is finite, for the sake of simplicity.6
The choice of assigning to every point of the place occupied by a body—say, B![]() , a fit region of the three-dimensional Euclidean point space—a descriptor of the material microstructure, selected in a manifold M
, a fit region of the three-dimensional Euclidean point space—a descriptor of the material microstructure, selected in a manifold M![]() , is a way to introduce a multiscale representation since v∈M
, is a way to introduce a multiscale representation since v∈M![]() brings at macroscopic scales information on the microscopic structure of the matter. Time variations of ν account for both reversible and irreversible changes in the material microstructure at the scale (or scales) the choice of ν is referred to. Moreover, when ν is considered a differentiable function of time, its time derivative ˙v
brings at macroscopic scales information on the microscopic structure of the matter. Time variations of ν account for both reversible and irreversible changes in the material microstructure at the scale (or scales) the choice of ν is referred to. Moreover, when ν is considered a differentiable function of time, its time derivative ˙v![]() enters the expression of the power of actions associated with microstructural changes. They can be classified essentially into two families: self-actions occurring inside what is considered the material element in the continuum modeling, and microstresses, which are contact actions between neighboring material elements, due to microstructural changes that differ with each other from place to place.
enters the expression of the power of actions associated with microstructural changes. They can be classified essentially into two families: self-actions occurring inside what is considered the material element in the continuum modeling, and microstresses, which are contact actions between neighboring material elements, due to microstructural changes that differ with each other from place to place.
1.4 Caution
The selection of a generic differentiable manifold as the ambient hosting the finer-scale geometry of the matter unifies the classes of available models. However, we could ask the reason for working with an abstract manifold when, in the end, we select it to be finite-dimensional, and we know that any finite-dimensional, differentiable manifold can be embedded in a linear space with appropriate dimension—this is the Whitney theorem (1936). Moreover, in the special case where M![]() is selected to be Riemannian,7 the Nash theorems (1954,1956) ensure that the embedding in a linear space can be even isometric. Hence, we could select a linear space from the beginning, instead of starting with M
is selected to be Riemannian,7 the Nash theorems (1954,1956) ensure that the embedding in a linear space can be even isometric. Hence, we could select a linear space from the beginning, instead of starting with M![]() , which is, in general, nonlinear for no special restrictions appear in its definition. The choice would surely simplify the developments: formally, the resulting mechanical structures would appear as the canonical ones plus analogous constructs linked with the microstructure description. Examples of schemes admitting naturally a linear space as a manifold of microstructural shapes are the ones describing the so-called micromorphic continua (an appropriate format for polymeric structures), nematic elastomers, and quasicrystals.
, which is, in general, nonlinear for no special restrictions appear in its definition. The choice would surely simplify the developments: formally, the resulting mechanical structures would appear as the canonical ones plus analogous constructs linked with the microstructure description. Examples of schemes admitting naturally a linear space as a manifold of microstructural shapes are the ones describing the so-called micromorphic continua (an appropriate format for polymeric structures), nematic elastomers, and quasicrystals.
A convenient choice like that, however, would erode the generality of the resulting mechanical structures. The reason is that both the Whitney theorem and the Nash theorems do not ensure at all uniqueness of the embedding in a linear space. In particular, the Nash theorems state that the regularity of the embedding determines the dimension of the target linear space. The recourse to an embedding would be necessary essentially when physics would suggest not precisely an element of a linear space as a descriptor of the material morphology. There are intermediate examples: when a body admits polarization under certain conditions, a three-dimensional vector naturally describes at a point the electric or magnetic dipole created there. However, in saturation conditions (the maximum admissible polarization for the material is reached), an instinctive choice for M![]() would be a sphere in R3
would be a sphere in R3![]() , i.e., a nonlinear manifold obtained by imposing a constraint into a linear space. For this reason, in developing formal mechanical structures, we could work in R3
, i.e., a nonlinear manifold obtained by imposing a constraint into a linear space. For this reason, in developing formal mechanical structures, we could work in R3![]() directly, taking care to add a constraint limiting the values of the polarization vector. This way we have the advantage of working at the beginning in a linear space, but meeting certain difficulties at a later stage. The alternative would be to consider the sphere just mentioned not as a portion of R3
directly, taking care to add a constraint limiting the values of the polarization vector. This way we have the advantage of working at the beginning in a linear space, but meeting certain difficulties at a later stage. The alternative would be to consider the sphere just mentioned not as a portion of R3![]() but as an independent manifold, accepting its intrinsic nonlinearity.
but as an independent manifold, accepting its intrinsic nonlinearity.
To maintain generality and with the aim of indicating tools that could be sufficiently flexible to be adapted to several situations, it could be preferable to consider M![]() as a nonlinear manifold from the beginning. The additional effort should also be to introduce the smallest possible number of assumptions on the geometric nature of M
as a nonlinear manifold from the beginning. The additional effort should also be to introduce the smallest possible number of assumptions on the geometric nature of M![]() . Every geometric property brings possible physical meaning, so not all properties are generically appropriate.
. Every geometric property brings possible physical meaning, so not all properties are generically appropriate.
The embedding of M![]() in a linear space appears expedient when we want to construct finite element schemes for numerical computations.
in a linear space appears expedient when we want to construct finite element schemes for numerical computations.
1.5 Refined descriptions of the material texture
The assignment of a single ν to a point x∈B![]() as a representative of the material microstructure implies one of the two following options:
as a representative of the material microstructure implies one of the two following options:
1. ν refers to a single microstructural individual—an example is when we consider the material element of a polymer-reinforced composite as a patch of matter containing a single macromolecule embedded in a matrix, and ν describes only the molecule.
2. We consider the material element as a container of a family of distinct microstructural entities. In this case, ν is a sort of average over the family in a sense that must be specified from time to time. Nematic liquid crystals are an example: ν represents at a point the prevalent orientation direction of a family of stick molecules with head-to-tail symmetry.
In both cases, implicit is an axiom of permanence of the material element typology, and such an element is considered as a system in energetic contact with the surrounding environment, but not exchanging mass with it (Capriz, 1989; Germain, 1973; Mariano, 2002; Mindlin, 1964).
Refined views are possible:
• A first attempt is to consider the material element as a container of several microstructural individuals, each one described by ν—an example is a system of linear polymeric chains, each one represented by an end-to-tail vector—and to introduce the number of microstructures at x characterized by ν, which we call microstructural numerosity (Brocato & Capriz, 2011; Mariano, 2005), or even the entire distribution function of microstructural elements (Svendsen, 2001). In this case it is possible to imagine the material element as a system open to the exchange of mass owing to the migration of microstructures. Fluids containing polymers are an example since the molecules are free to migrate in the surrounding liquid. Other special cases can be given. An evolution equation for the microstructural numerosity was derived in Mariano (2005). The result tells us that the migration of microstructures is due primarily to the competition of the microstructural actions between neighboring material elements. That evolution equation reduces to the Cahn–Hilliard equation when ν is a scalar indicating the volume or mass fraction of one phase in a two-phase material, and the free energy is double-walled.
• Another approach accounts for the local multiplicity of microstructural elements not in a statistical sense, as occurs in the use of distribution functions. When we imagine r microstructural elements at a place x (remember, the description is multiscale), each one described by ν, the map x↦v∈M![]() is r-valued over M
is r-valued over M![]() . Moreover, the multivalues of the microstructural descriptor must be determined up to permutations of the labels that we assign to the r microstructural elements in the family at x. In general, there is no reason to presume a priori a hierarchy between the elements of the microstructural family for they are identical with one another. This point of view, presented first in Focardi, Mariano, and Spadaro (2014), implies a number of analytical problems:
. Moreover, the multivalues of the microstructural descriptor must be determined up to permutations of the labels that we assign to the r microstructural elements in the family at x. In general, there is no reason to presume a priori a hierarchy between the elements of the microstructural family for they are identical with one another. This point of view, presented first in Focardi, Mariano, and Spadaro (2014), implies a number of analytical problems:
– Although we can give meaning to the notion of differentiability for a manifold-r-valued map, there is no representation such that each component mapping x ![]() να(x) is differentiable, taking into account the quotient with respect to the permutations.
να(x) is differentiable, taking into account the quotient with respect to the permutations.
– Even in the case in which M![]() is a smooth manifold, the set of r-valued maps over M
is a smooth manifold, the set of r-valued maps over M![]() defined above is not a smooth manifold anymore, and it has to be treated as a metric space only.
defined above is not a smooth manifold anymore, and it has to be treated as a metric space only.
– The appropriate interpretations in this setting, even extensions when this is the case, of concepts in calculus of variations, such as the notion of quasiconvexity, which can allow us to determine the existence of minimizers (ground states) for an energy depending on that type of maps and their gradients, besides the standard deformation, are necessary.
Answers to these problems are given in Focardi et al. (2014). A key ingredient for them is the completeness of M![]() . Affirming that M
. Affirming that M![]() is a complete manifold means that the notion of a geodetic curve is available for it and any pair of elements of M
is a complete manifold means that the notion of a geodetic curve is available for it and any pair of elements of M![]() can be connected by a geodetic path.
can be connected by a geodetic path.
1.6 Comparison between microstructural descriptor maps and displacements over M
An assumption of completeness for M![]() is also appropriate when we want to define distances between different global microstructural states with the aim of giving some sense to the following question: How far is a certain distribution of microstructures over the body from another one?
is also appropriate when we want to define distances between different global microstructural states with the aim of giving some sense to the following question: How far is a certain distribution of microstructures over the body from another one?
Since we consider here the entire map x↦v∈M![]() , not specific values of it, the distances in a space of maps that we can define are not all equivalent, for the space they belong to is infinite-dimensional. An example including two natural distances that give results with opposite physical meaning when they are used in the same concrete situation is described in de Fabritiis and Mariano (2005).
, not specific values of it, the distances in a space of maps that we can define are not all equivalent, for the space they belong to is infinite-dimensional. An example including two natural distances that give results with opposite physical meaning when they are used in the same concrete situation is described in de Fabritiis and Mariano (2005).
With the care suggested by these remarks, answering the previous question is another possible way of describing material mutations. This view is global, however, and the selection of a distance between maps is a structural ingredient of the specific model that we construct. Local microstructural mutations can, in turn, be described by the amount of sudden shifts of ν over M![]() , i.e., by nonsmooth variations of the map x
, i.e., by nonsmooth variations of the map x ![]() ν. Comparisons between different values of ν can be made by assigning a metric over M
ν. Comparisons between different values of ν can be made by assigning a metric over M![]() . When M
. When M![]() is complete, the amount of transformation from ν1 to ν2 can be defined as the length of the geodetic curve connecting them. It can be interpreted as
is complete, the amount of transformation from ν1 to ν2 can be defined as the length of the geodetic curve connecting them. It can be interpreted as
1. an amount of mutation when the transformation produces dissipation or
2. a sort of displacement length over M![]() .
.
1.7 Classification of microstructural defects
The choice of M![]() enters the stage when we want to describe microscopic material mutations: structural changes in the microstructure, the one below the spatial scale defining the material element even implicitly. However, the possibility of selecting M
enters the stage when we want to describe microscopic material mutations: structural changes in the microstructure, the one below the spatial scale defining the material element even implicitly. However, the possibility of selecting M![]() implies a certain microscopic order in the material, at least recurrence in the type of microscopic features that we represent through the elements of M
implies a certain microscopic order in the material, at least recurrence in the type of microscopic features that we represent through the elements of M![]() .
.
This way we can call a defect in the order represented by M![]() a p-dimensional subset of the reference place B
a p-dimensional subset of the reference place B![]() where the map x↦v=˜v(x)∈M
where the map x↦v=˜v(x)∈M![]() is not defined or takes as values the entire M
is not defined or takes as values the entire M![]() .
.
Such a defect is unstable when it is generated by a mutation which is compatible with a reversible path in the state space, meaning that the matter can readjust itself to cancel the defect during some physically admissible processes, by producing dissipation and without adding material (e.g., a glue). Otherwise, we call it stable. The classification of both classes can be made by exploring the topological properties of M![]() (Mermin, 1979), in particular its homological and/or cohomological structures.
(Mermin, 1979), in particular its homological and/or cohomological structures.
We can also describe at least some aspects of the alteration of the microstructural order by considering the geometry associated with the reference place B![]() of the body. An example is provided by the description of plastic changes in metals.
of the body. An example is provided by the description of plastic changes in metals.
Consider a crystalline material: an ordered set of atoms composing crystals possibly crowded in grains. In the continuum modeling, at every point of B![]() we imagine assigning at least a crystal. Hence, in the continuum approximation we can consider at every point the optical axes pertaining to the crystal placed there: three linearly independent vectors that determine point by point a metric tensor g, which we call commonly a material metric. The time evolution of g is a way to indicate that the crystalline texture changes (see details in Miehe, 1998), and we could consider the occurrence of defects indirectly by changing the material metric instead of describing directly the distortions that they produce (Yavari & Goriely, 2013). We shall mention other geometric options in the ensuing sections.
we imagine assigning at least a crystal. Hence, in the continuum approximation we can consider at every point the optical axes pertaining to the crystal placed there: three linearly independent vectors that determine point by point a metric tensor g, which we call commonly a material metric. The time evolution of g is a way to indicate that the crystalline texture changes (see details in Miehe, 1998), and we could consider the occurrence of defects indirectly by changing the material metric instead of describing directly the distortions that they produce (Yavari & Goriely, 2013). We shall mention other geometric options in the ensuing sections.
1.8 Macroscopic mutations
Material elements detach from one another: cracks may occur, voids can be nucleated, subsets of B![]() with nonvanishing volume may grow and have their own motion relative to the rest of the body, as, e.g., the phenomenology of biological tissues shows. All these examples are structural mutations appearing at the macroscopic scale. In the presence of them, the deformation map ˜u:B→˜E3
with nonvanishing volume may grow and have their own motion relative to the rest of the body, as, e.g., the phenomenology of biological tissues shows. All these examples are structural mutations appearing at the macroscopic scale. In the presence of them, the deformation map ˜u:B→˜E3![]() is no more one-to-one or loses regularity on some subset of B
is no more one-to-one or loses regularity on some subset of B![]() . And the one-to-one property is a basic assumption in the standard description of deformation processes.
. And the one-to-one property is a basic assumption in the standard description of deformation processes.
An instinctive way to account for these circumstances is to enlarge the functional space containing fields that can be solutions of the basic equations, with the awareness that the selection of a function space is a constitutive choice. In fact, to belong to a space, a map must satisfy a number of properties, and they are able to describe some physical phenomena, but not others.
Such an approach considers mutations in terms of loss of regularity in the maps satisfying appropriate boundary value problems. For example, let us imagine we have a certain energy depending on a material parameter and associated boundary conditions. We assume we are able to determine for a fixed value of the parameter the existence of minimizers of the energy, which will be maps depending on the parameter itself. If we allow the parameter to vary, it is possible that the family of minimizers will admit a limit into a space endowed with less regularity with respect to the initial choice for a fixed parameter. The behavior could be interpreted from a physical viewpoint as a phase transition. The approach can be successful in some cases and too restrictive in others.
Another point of view can be followed. In fact, when a macroscopic defect occurs—think of a crack, for example—the current location of a body (the region that it occupies in the Euclidean space) is no longer in one-to-one correspondence with the original reference shape B![]() , but rather, at a certain instant, with B
, but rather, at a certain instant, with B![]() minus a distinguished subset of B
minus a distinguished subset of B![]() , which is the “shadow”8 over B
, which is the “shadow”8 over B![]() of the defect (the picture is particularly appropriate for cracked bodies). In other words, a process involving nucleation and growth of macroscopic defects can be pictured by considering multiple reference shapes. They are distinguished from one another by the preimage of what we consider a defect.
of the defect (the picture is particularly appropriate for cracked bodies). In other words, a process involving nucleation and growth of macroscopic defects can be pictured by considering multiple reference shapes. They are distinguished from one another by the preimage of what we consider a defect.
1.9 Multiple reference shapes
The idea of multiple reference shapes is, in a sense, as old as the calculus of variations. It appears when we perform the so-called horizontal variations (details can be found in Giaquinta & Hildebrandt, 1996). A clear example emerges when we consider the energy of a simple elastic body undergoing large strains. It is
E(u,B):=∫Be(x,D(x))dx,
where e(x, Du(x)) is the energy density, and u is the deformation. Minimizers for such a functional are Sobolev maps (the first theorem on the existence of minimizers of the energy in nonlinear elasticity has been given in Ball (1976/77)), so they do not always admit tangential derivatives. For this reason, the variations of E(u,B)![]() can be calculated just by acting with smooth diffeomorphisms9 on (1) the actual shape of the body, namely, u(B)
can be calculated just by acting with smooth diffeomorphisms9 on (1) the actual shape of the body, namely, u(B)![]() , or (2) the reference shape B
, or (2) the reference shape B![]() . In the first case, we get the canonical balance of forces in terms of the Cauchy stress (although in a weak form in the absence of appropriate regularity of the fields involved). In the latter case—what we call horizontal variations—the result is the so-called balance of configurational actions, in a form free of dissipative structures such as driving forces (see Giaquinta, Modica, & Souček, 1989 for details and generalizations). The conceptual independence between the two balances has been known since the early days of the calculus of variations (see the remarks in Giaquinta & Hildebrandt, 1996, pp. 152–153). In the presence of appropriate regularity for the fields involved, a link between the two classes of equations can be established (see, e.g., Giaquinta & Hildebrandt, 1996; Maugin, 1995).
. In the first case, we get the canonical balance of forces in terms of the Cauchy stress (although in a weak form in the absence of appropriate regularity of the fields involved). In the latter case—what we call horizontal variations—the result is the so-called balance of configurational actions, in a form free of dissipative structures such as driving forces (see Giaquinta, Modica, & Souček, 1989 for details and generalizations). The conceptual independence between the two balances has been known since the early days of the calculus of variations (see the remarks in Giaquinta & Hildebrandt, 1996, pp. 152–153). In the presence of appropriate regularity for the fields involved, a link between the two classes of equations can be established (see, e.g., Giaquinta & Hildebrandt, 1996; Maugin, 1995).
In general, the Nöther theorem in classical field theories points out clearly the role of horizontal variations. However, what I have mentioned in previous lines deals with conservative behavior.
A basic question then arises: In which way could we transfer the idea implicit in the technique of horizontal variations in the dissipative setting pertaining to structural material mutations? In other words: What is the formal way to express the idea of having multiple reference configurations in a dissipative setting?
I list below three possibilities: they are possible views leading to answers. A preliminary remark seems, however, necessary. The horizontal variations mentioned above are determined by defining over B![]() a parameterized family of diffeomorphisms—they map B
a parameterized family of diffeomorphisms—they map B![]() onto other possible reference places—which are differentiable with respect to the parameter. When we identify the parameter with time, the derivative of these diffeomorphisms with respect to it determines a velocity field over B
onto other possible reference places—which are differentiable with respect to the parameter. When we identify the parameter with time, the derivative of these diffeomorphisms with respect to it determines a velocity field over B![]() . The way to consider it leads the possibilities already mentioned:
. The way to consider it leads the possibilities already mentioned:
• With the idea of accounting for dissipative effects, we can start directly from the assignment of a vector velocity field over B![]() that is not necessarily integrable in time, so a flow is not always associated with it. When integrability is to be ensured, such a vector field will coincide with the infinitesimal generator of the action of the group of diffeomorphisms over B
that is not necessarily integrable in time, so a flow is not always associated with it. When integrability is to be ensured, such a vector field will coincide with the infinitesimal generator of the action of the group of diffeomorphisms over B![]() , and we shall come back to the standard technique of the horizontal variations.10 Such a not-necessarily-time-integrable vector field can be interpreted as a sort of infinitesimal generator of the incoming mutations: the tendency of material elements to reorganize themselves with dissipation. Having in mind time-varying reference places, Gurtin (2000a) has adopted this view11 for writing the power developed during structural mutations by actions—called configurational to remind us of their nature, a term that can be attributed to Nabarro, as Ericksen (1998) pointed out—working on the reference place along the fictitious path described by the “shadow” of the defect evolution on B
, and we shall come back to the standard technique of the horizontal variations.10 Such a not-necessarily-time-integrable vector field can be interpreted as a sort of infinitesimal generator of the incoming mutations: the tendency of material elements to reorganize themselves with dissipation. Having in mind time-varying reference places, Gurtin (2000a) has adopted this view11 for writing the power developed during structural mutations by actions—called configurational to remind us of their nature, a term that can be attributed to Nabarro, as Ericksen (1998) pointed out—working on the reference place along the fictitious path described by the “shadow” of the defect evolution on B![]() . Along this path, configurational forces, couples, and stresses are postulated a priori and are identified later (at least some of them) in terms of energy and standard stresses, by using a procedure based on a requirement of invariance with respect to reparameterization of the boundary pertaining to the region in B
. Along this path, configurational forces, couples, and stresses are postulated a priori and are identified later (at least some of them) in terms of energy and standard stresses, by using a procedure based on a requirement of invariance with respect to reparameterization of the boundary pertaining to the region in B![]() occupied by what we are considering to be a defect (see details in Gurtin, 1995; see also Maugin, 1995 for other approaches). Alternatively, I use the velocity field previously mentioned to write what I call relative power (see Mariano, 2009 for its first definition in a nonconservative setting, with improvements in Mariano, 2012a), which is the power of canonical external actions on a generic part of the body augmented by what I call the power of disarrangements, which is a functional involving energy fluxes determined by the rearrangement of matter and configurational forces and couples due to breaking of material bonds and mutation-induced anisotropy. Canonical balances of standard and microstructural actions and the ones of configurational actions follow directly from a requirement of invariance of the relative power with respect to enlarged classes of isometric changes in observers. The advantage is that we do not need to connect some configurational actions (Eshelby stress, inertia, and volume terms) with energy and the canonical ones (bulk forces and stresses in the current place of the body, and self-actions and microstresses due to microstructural rearrangements) at a subsequent stage, as it is necessary to do in the procedure proposed in Gurtin (1995). Also, when we restrict the treatment to the conservative setting, the relative power reduces to an integral expression that emerges from the Nöther theorem in classical field theories—it is from there that I arrived at the idea of the relative power, interpreting a relation appearing when we include in nonlinear elasticity discontinuity surfaces endowed with their own surface energy, and we try to determine the relevant Nöther theorem (specific remarks and proofs are given in de Fabritiis & Mariano, 2005)—and the link with classical instances is established.
occupied by what we are considering to be a defect (see details in Gurtin, 1995; see also Maugin, 1995 for other approaches). Alternatively, I use the velocity field previously mentioned to write what I call relative power (see Mariano, 2009 for its first definition in a nonconservative setting, with improvements in Mariano, 2012a), which is the power of canonical external actions on a generic part of the body augmented by what I call the power of disarrangements, which is a functional involving energy fluxes determined by the rearrangement of matter and configurational forces and couples due to breaking of material bonds and mutation-induced anisotropy. Canonical balances of standard and microstructural actions and the ones of configurational actions follow directly from a requirement of invariance of the relative power with respect to enlarged classes of isometric changes in observers. The advantage is that we do not need to connect some configurational actions (Eshelby stress, inertia, and volume terms) with energy and the canonical ones (bulk forces and stresses in the current place of the body, and self-actions and microstresses due to microstructural rearrangements) at a subsequent stage, as it is necessary to do in the procedure proposed in Gurtin (1995). Also, when we restrict the treatment to the conservative setting, the relative power reduces to an integral expression that emerges from the Nöther theorem in classical field theories—it is from there that I arrived at the idea of the relative power, interpreting a relation appearing when we include in nonlinear elasticity discontinuity surfaces endowed with their own surface energy, and we try to determine the relevant Nöther theorem (specific remarks and proofs are given in de Fabritiis & Mariano, 2005)—and the link with classical instances is established.
• Instead of considering a vector (velocity) field over B![]() , and always with the idea of extending to the dissipative setting what is hidden in the technique of horizontal variations, or better, what is implied by the idea of multiple reference shapes, we could consider local maps defined over the tangent bundle of B
, and always with the idea of extending to the dissipative setting what is hidden in the technique of horizontal variations, or better, what is implied by the idea of multiple reference shapes, we could consider local maps defined over the tangent bundle of B![]() and pushing it forward onto the ambient physical space. We take into account the dissipative nature of material mutations, in the description of the body morphology, by affirming that these tangent maps are not compatible, i.e., their curl does not vanish. This is the case of the multiplicative decomposition of the deformation gradient into elastic and plastic components that we accept in traditional formulations of finite-strain plasticity (see the pioneering papers Kröner, 1960; Lee, 1969 and the book Simo & Hughes, 1998 for more recent advances). However, leaving as independent the tangent maps that act at distinct points, we are not always able to recognize different reference configurations—in plasticity we cannot individualize the so-called intermediate configuration, in fact, and we could also avoid imagining it. Such a view (it can be adopted even in conjunction with what is indicated in the previous item, as we shall see in the next sections) is not only pertinent to plasticity, with its peculiar features. The idea of different configurations reached by “virtual” tangent maps appears useful even in describing relaxation processes in materials, as suggested by Rajagopal and Srinivasa (2004a, 2004b). In both cases just mentioned, however, the use of tangent maps is a way to simulate at the macroscopic level irreversible rearrangements of matter at the microscopic scale, leaving invariant the geometric connection of the body. In other words, the approach does not include nucleation and subsequent growth of cracks.
and pushing it forward onto the ambient physical space. We take into account the dissipative nature of material mutations, in the description of the body morphology, by affirming that these tangent maps are not compatible, i.e., their curl does not vanish. This is the case of the multiplicative decomposition of the deformation gradient into elastic and plastic components that we accept in traditional formulations of finite-strain plasticity (see the pioneering papers Kröner, 1960; Lee, 1969 and the book Simo & Hughes, 1998 for more recent advances). However, leaving as independent the tangent maps that act at distinct points, we are not always able to recognize different reference configurations—in plasticity we cannot individualize the so-called intermediate configuration, in fact, and we could also avoid imagining it. Such a view (it can be adopted even in conjunction with what is indicated in the previous item, as we shall see in the next sections) is not only pertinent to plasticity, with its peculiar features. The idea of different configurations reached by “virtual” tangent maps appears useful even in describing relaxation processes in materials, as suggested by Rajagopal and Srinivasa (2004a, 2004b). In both cases just mentioned, however, the use of tangent maps is a way to simulate at the macroscopic level irreversible rearrangements of matter at the microscopic scale, leaving invariant the geometric connection of the body. In other words, the approach does not include nucleation and subsequent growth of cracks.
• To describe the occurrence of cracks or line or point defects in solids remaining otherwise elastic, a view in terms of multiple reference shapes is also appropriate. In particular, it seems necessary to consider the set of all possible reference shapes, all occupying the same gross place B![]() and differing from one another by the defect pattern. A variational principle selects both the appropriate reference shape and a standard deformation determining the current macroscopic shape of the body. To define such a principle, we need to parameterize the family of possible body gross shapes. For cracks and line defects, special measures help us: varifolds. For cracks, at every point they bring information on whether that point can be crossed by a crack and in what direction. These measures play an analogous role for line defects. They enter the energy that appears in the selecting variational principle and, by their nature, they introduce directly curvature terms—for elastic–brittle materials the resulting energy is a generalization of the Griffith's energy (that discussed in Griffith, 1920). Such an approach, introduced in Giaquinta, Mariano, Modica, and Mucci (2010) (see related explanations in Mariano, 2010), is then particularly appropriate in cases in which curvature-dependent physical effects contribute to the energy of cracks or line defects. And the relevant cases do not seem to be rare (see, e.g., Spatschek & Brener, 2001), or better, the appropriateness of the scheme depends on whether we model intermolecular bonds as springs or beams, nothing more, essentially.
and differing from one another by the defect pattern. A variational principle selects both the appropriate reference shape and a standard deformation determining the current macroscopic shape of the body. To define such a principle, we need to parameterize the family of possible body gross shapes. For cracks and line defects, special measures help us: varifolds. For cracks, at every point they bring information on whether that point can be crossed by a crack and in what direction. These measures play an analogous role for line defects. They enter the energy that appears in the selecting variational principle and, by their nature, they introduce directly curvature terms—for elastic–brittle materials the resulting energy is a generalization of the Griffith's energy (that discussed in Griffith, 1920). Such an approach, introduced in Giaquinta, Mariano, Modica, and Mucci (2010) (see related explanations in Mariano, 2010), is then particularly appropriate in cases in which curvature-dependent physical effects contribute to the energy of cracks or line defects. And the relevant cases do not seem to be rare (see, e.g., Spatschek & Brener, 2001), or better, the appropriateness of the scheme depends on whether we model intermolecular bonds as springs or beams, nothing more, essentially.
1.10 Micro-to-macro interactions
The choice of representing peculiar aspects of the microstructural shapes on a manifold M![]() and what we call macroscopic mutations on the reference place B
and what we call macroscopic mutations on the reference place B![]() , attributing also to its geometric structures (metric, torsion) the role of a witness of microscopic features, is a matter of modeling. And a mathematical model is just a representation of the phenomenological world, a linguistic structure on empirical data. It is addressed by data but, at the same time, overcomes them and may suggest, in turn, ways that we can follow in constructing experiments—in short, a model is not reality, rather it is an interpretative tale over it.
, attributing also to its geometric structures (metric, torsion) the role of a witness of microscopic features, is a matter of modeling. And a mathematical model is just a representation of the phenomenological world, a linguistic structure on empirical data. It is addressed by data but, at the same time, overcomes them and may suggest, in turn, ways that we can follow in constructing experiments—in short, a model is not reality, rather it is an interpretative tale over it.
There are nontrivial interactions between microscopic events and the occurrence of macroscopic defects in a material. Examples are manifold: a visible crack is nucleated by the coalescence of multiple ruptures of microscopic material bonds; a plastic flow (a mutation, which can be considered in a sense as a phase transition; Ortiz, 1999) is generated in a metal by the migration of dislocations grouping along intergranular boundaries. We could also think of epitaxial growth, above all when the deposition of particles is coupled with elasticity of the stepped surfaces (E & Yip, 2001; Xiang & E, 2004). Another example is growth and remodeling of biological tissues. It is almost superfluous to remind ourselves that cellular mutations and interactions are essential in that case. Humphrey (2003) has reviewed results in biomechanics and has indicated trends on the matter (see also Athesian & Humphrey, 2012; Nedjar, 2011). Non-trivial theoretical issues are involved already at the level of the geometric description of the relevant processes. To date, an essential foundational contribution to the growth and remodeling issues seems to me the one by Segev (1996). Remarkably, to avoid repeating standard topics in plasticity (which is a remodeling of matter) just with a different nomenclature, models of growth and remodeling (the processes together) should take into account the presence of nutrients: generically, a growing body is an open system.
Without going further into the specific issues and coming back to general themes, we remind ourselves that the representations of microscopic and macroscopic events should merge into one another. The interaction appears already in the definition of observers and their changes. In fact, although we can decide to describe events at various spatial scales in different spaces, they occur all together in the physical space. Hence, we must consider this obvious aspect in our modeling, with consequent nontrivial implications.12
1.11 A plan for the next sections
A treatise would be perhaps necessary to furnish appropriate details on all the themes sketched above. The space of a monograph would be useful not only for technical developments but also, and above all probably, for the discussion of the physical meaning of formal choices made along the path, and their consequences in terms of foundational aspects in continuum mechanics. This target is, of course, far from the limits imposed on these notes. Hence, in the next sections, I shall make choices, presenting just some details about questions that seem to me to be prominent in the description of material mutations. The list of references is neither complete nor unbiased. It suffers from the limits in my knowledge of the work produced and also from the consequence of personal choices and interpretations, which aim to be useful to the reader in underlining concepts that are sometimes not completely usual, which could, in principle, open questions and avenues for further developments.
1.12 Advantages
In constructing models of the mechanics of materials with nonstandard behavior, in particular in the presence of prominent microstructural events, we face two main problems: (1) the correct assessment of balance equations and (2) the assignment of appropriate constitutive relations.
In the latter case, we may resort to (1) experimental data, (2) requirements of objectivity or covariance under changes in observers (see the pertinent definitions in the next sections), (3) identification from discrete schemes, and (4) more general homogenization procedures.
As regards balance equations, I am always suspicious when proposals in nonstandard circumstances emerge just by analogy with what is commonly accepted in different well-known domains. The reason for my suspiciousness is that analogy is a sort of hope to hit the mark in the fog. Although such behavior could be convenient for production, it is not obvious that it always brings us to results illuminating the real physical mechanisms. In contrast, the search by first principles may lead us to a reasonably safe derivation of balance equations.
We meet a number of possibilities, and we have to select among them with care. In fact, when we accept the principle of virtual power (or work) as a starting point, we are just prescribing a priori the weak form of balance equations and we have introduced all the ingredients pertaining to them. In the case of simple bodies, we cannot do drastically more, in a sense. However, when we involve the description of intricate microstructural events in our models, we can start from principles involving fewer ingredients than those appearing eventually in the pointwise balances. I shall come back in detail to this issue in the next sections.
Here, I just summarize some aspects of what is included in the rest of the paper that are to me advantages with respect to what is presented in different literature.
The reader will find
• a way to derive for several microstructured materials balance equations of standard (canonical), microstructural, and configurational actions from a unique source, by using a requirement of invariance from changes in observers determined by isometric variations of frames in space;
• the deduction of a version of the action–reaction principle and the Cauchy stress theorem for microstructural contact actions;
• an extension to a nonconservative setting of the Marsden–Hughes theorem—such a generalization allows us to derive the Cauchy stress theorem, balances of standard and configurational actions, constitutive restrictions, and the structure of the dissipation from the requirement of covariance (the meaning will be clear in the next sections) of the second law of thermodynamics, written in an appropriate way (the result is presented just with reference to standard finite-strain hardening plasticity, but further generalizations of it can be rather easily obtained); and
• a description of crack nucleation and/or growth in terms of a variational principle selecting among all possible cracked or intact versions of the body considered. The principle includes a generalization of the Griffith's energy to a structure, including curvature effects. The procedure can be adopted also for the nucleation and/or growth of linear defects.
Comparisons with alternative proposals and reasons for considering as advantages the items above are scattered throughout the text.
With these notes I would like to push the reader to think of what we exactly do when we construct mathematical models of mechanical phenomena.
1.13 Readership
The remark above opens the question of the readership. In starting the present notes, I assumed vaguely to be writing for a reader rather familiar with basic structures of traditional continuum mechanics in the large-strain regime. After I had written the first draft and discussed it with some colleagues, we agreed that the result could not be intended for absolute beginners in continuum mechanics, but each of us had a different opinion about the meaning of not being a beginner. We were also conscious that the style becomes substance eventually.
To me, the appropriate reader of these notes is a person who is culturally curious, not a prejudiced rival of formal general structures. I think of a person with the patience to arrive at the end, a person who could think that there could be some aspects deserving further deeper reading when thoughts decant and our natural precomprehension—exerted unconsciously every time we start reading a text—becomes softer, the inapt writer notwithstanding.
2 Material morphologies and deformations
2.1 Gross shapes and macroscopic strain measures
A canonical assumption is that a set that a body may occupy in the three-dimensional Euclidean point space E3![]() , a place that we can take as a reference, is a connected, regularly open region B
, a place that we can take as a reference, is a connected, regularly open region B![]() , endowed with metric13 g and provided with a surface-like boundary, oriented by the normal n everywhere but with a finite number of corners and edges. Less canonical is the choice of an isomorphic copy of E3
, endowed with metric13 g and provided with a surface-like boundary, oriented by the normal n everywhere but with a finite number of corners and edges. Less canonical is the choice of an isomorphic copy of E3![]() —write ˜E3
—write ˜E3![]() for it—that we use as the ambient physical space where we describe all gross places that we consider deformed with respect to B
for it—that we use as the ambient physical space where we describe all gross places that we consider deformed with respect to B![]() . When we assign an orientation to E3
. When we assign an orientation to E3![]() , we must presume (physical reasons will emerge below) that ˜E3
, we must presume (physical reasons will emerge below) that ˜E3![]() is oriented in the same way, and the isomorphism is then an isometry, the identification eventually.14 Below, ˜g
is oriented in the same way, and the isomorphism is then an isometry, the identification eventually.14 Below, ˜g![]() will indicate a metric in ˜E3
will indicate a metric in ˜E3![]() . There is no reason forcing us to assume a priori that g and ˜g
. There is no reason forcing us to assume a priori that g and ˜g![]() are the same.
are the same.
Actual macroscopic places for the body are reached from B![]() by means of deformations: they are differentiable, orientation-preserving maps assigning to every point x in B
by means of deformations: they are differentiable, orientation-preserving maps assigning to every point x in B![]() its current place y in ˜E3
its current place y in ˜E3![]() , namely,
, namely,
x↦y:=u(x)∈˜E3.
We shall indicate by Ba![]() the image of B
the image of B![]() under u, namely, Ba:=u(B)
under u, namely, Ba:=u(B)![]() , the index a meaning actual.
, the index a meaning actual.
As usual, we write F for the spatial derivative Du (x) evaluated at x∈B![]() . We call it the deformation gradient according to tradition. Du (x) and the gradient ∇u (x) satisfy the relation ∇u (x) = Du (x)g−1. In other words, F is 1-contravariant, 1-covariant, while ∇u (x) is contravariant in both components. This difference is usually not emphasized in standard continuum mechanics because we use implicitly the identification of R3
. We call it the deformation gradient according to tradition. Du (x) and the gradient ∇u (x) satisfy the relation ∇u (x) = Du (x)g−1. In other words, F is 1-contravariant, 1-covariant, while ∇u (x) is contravariant in both components. This difference is usually not emphasized in standard continuum mechanics because we use implicitly the identification of R3![]() with its dual R3*
with its dual R3*![]() . Hence, we do not distinguish between contravariant and covariant components, the former belonging to the vector space R3
. Hence, we do not distinguish between contravariant and covariant components, the former belonging to the vector space R3![]() , the latter to its dual. Here, in contrast, I stress the difference because in the following developments we shall meet an abstract manifold—what I have already mentioned, calling it a manifold of microstructural shapes—with finite dimension and for it the natural simplifications in R3
, the latter to its dual. Here, in contrast, I stress the difference because in the following developments we shall meet an abstract manifold—what I have already mentioned, calling it a manifold of microstructural shapes—with finite dimension and for it the natural simplifications in R3![]() are, in general, not available, unless we embed the manifold in a linear space, a circumstance that I try to avoid for reasons already explained. As a consequence, to maintain a parallelism in the treatment, I distinguish explicitly between contravariant and covariant components even in cases, like the one of F, where it may not be strictly necessary. This way the advantage is a rather clear construction of mathematical structures, paying for formal clearness, which helps us in connecting mathematical representations and physical meaning, with the need of being mindful of the geometric nature of some objects. Of course, the reader could have a different opinion.
are, in general, not available, unless we embed the manifold in a linear space, a circumstance that I try to avoid for reasons already explained. As a consequence, to maintain a parallelism in the treatment, I distinguish explicitly between contravariant and covariant components even in cases, like the one of F, where it may not be strictly necessary. This way the advantage is a rather clear construction of mathematical structures, paying for formal clearness, which helps us in connecting mathematical representations and physical meaning, with the need of being mindful of the geometric nature of some objects. Of course, the reader could have a different opinion.
At x∈B![]() , consider the three linearly independent vectors {e1, e2, e3}. They are a basis in the tangent space15 TxB
, consider the three linearly independent vectors {e1, e2, e3}. They are a basis in the tangent space15 TxB![]() . Correspondingly, there is another basis, indicated by {e1, e2, e3}, in the dual space to TxB
. Correspondingly, there is another basis, indicated by {e1, e2, e3}, in the dual space to TxB![]() , namely, the cotangent space TxB*
, namely, the cotangent space TxB*![]() . Moreover, we take another three linearly independent vectors at y = u(x), say, {˜e1,˜e2,˜e3}
. Moreover, we take another three linearly independent vectors at y = u(x), say, {˜e1,˜e2,˜e3}![]() . They constitute a basis in the tangent space TyBa
. They constitute a basis in the tangent space TyBa![]() . With respect to {e1, e2, e3} and {˜e1,˜e2,˜e3}
. With respect to {e1, e2, e3} and {˜e1,˜e2,˜e3}![]() , and by adopting here once and for all summation over repeated indexes, we have F=FiAeA⊗˜ei=∂ui(x)∂xAeA⊗˜ei
, and by adopting here once and for all summation over repeated indexes, we have F=FiAeA⊗˜ei=∂ui(x)∂xAeA⊗˜ei![]() . Lowercase indexes refer to coordinates on Ba
. Lowercase indexes refer to coordinates on Ba![]() , while uppercase indexes label coordinates over B
, while uppercase indexes label coordinates over B![]() .
.
By remembering the relation between F and ∇u, written previously, in components, we then have (∇ui (x))B = FiAgAB. By definition, F is a linear operator mapping the tangent space to B![]() at x, namely, TxB
at x, namely, TxB![]() , to TyBa
, to TyBa![]() , so we write shortly F∈Hom(TxB,TyBa)
, so we write shortly F∈Hom(TxB,TyBa)![]() .16 Different is the behavior of ∇u(x), which maps covectors over B
.16 Different is the behavior of ∇u(x), which maps covectors over B![]() , namely, elements of TxB*
, namely, elements of TxB*![]() , onto vectors over the actual shape Ba
, onto vectors over the actual shape Ba![]() . The standard identification of F with ∇u(x) is motivated by the common choice of an orthogonal metric in B
. The standard identification of F with ∇u(x) is motivated by the common choice of an orthogonal metric in B![]() , the second-rank covariant identity I = δABeA⊗eB, with δAB the Kronecker delta.
, the second-rank covariant identity I = δABeA⊗eB, with δAB the Kronecker delta.
Two linear operators are naturally associated with F: the formal adjoint F*, which maps elements of the cotangent space T*yBa![]() to elements of T*xB
to elements of T*xB![]() , and the transpose FT, a linear map from TyBa
, and the transpose FT, a linear map from TyBa![]() to TxB
to TxB![]() . An operational definition of them requires (1) the use of the scalar product in R3
. An operational definition of them requires (1) the use of the scalar product in R3![]() , namely, 〈·,·〉R3
, namely, 〈·,·〉R3![]() , and the analogous product in its isomorphic copy17 ˆR3
, and the analogous product in its isomorphic copy17 ˆR3![]() , namely, 〈·,·〉˜R3
, namely, 〈·,·〉˜R3![]() , and (2) the duality pairing between a linear space and its dual. For such a pairing I shall use a dot in the rest of this paper.18 Specifically, given a generic element v of a linear space Lin, formally v ∈ Lin, and another element b ∈ Lin*—b is a linear function over Lin—we shall indicate by b · v the value b(v). In particular, for v1,v2∈R3
, and (2) the duality pairing between a linear space and its dual. For such a pairing I shall use a dot in the rest of this paper.18 Specifically, given a generic element v of a linear space Lin, formally v ∈ Lin, and another element b ∈ Lin*—b is a linear function over Lin—we shall indicate by b · v the value b(v). In particular, for v1,v2∈R3![]() , we have, by definition, 〈v1, v2〉 = gv1 · v2, with gv1∈R3*
, we have, by definition, 〈v1, v2〉 = gv1 · v2, with gv1∈R3*![]() . Hence, FT is defined as the unique linear operator such that, for every pair v∈R3
. Hence, FT is defined as the unique linear operator such that, for every pair v∈R3![]() and ˉv∈˜R3
and ˉv∈˜R3![]() , 〈Fv,ˉv〉˜R3=〈v,FTˉv〉R3
, 〈Fv,ˉv〉˜R3=〈v,FTˉv〉R3![]() , while F* is such that, for every pair v∈R3
, while F* is such that, for every pair v∈R3![]() and b∈˜R3*
and b∈˜R3*![]() , b · Fv = F*b · v.
, b · Fv = F*b · v.
Proof. By direct calculation, we get 〈Fv,ˉv〉˜R3=Fv·˜gˉv=v·F*˜gˉv=〈v,g−1F*˜gˉv〉R3![]() .
.
On the other hand, by definition 〈Fv,ˉv〉˜R3=〈v,FTˉv〉R3![]() . By comparing the two expressions, we get the result.
. By comparing the two expressions, we get the result.
The orientation-preserving condition for the deformation map u is formally written as det F > 0.19 It ensures the existence of two other linear operators: the inverse F−1 of F, namely, F−1∈Hom(TyBa,TxB)![]() , and its formal adjoint F−*∈Hom(T*xB,TyBa)
, and its formal adjoint F−*∈Hom(T*xB,TyBa)![]() .
.
To measure strain, we compare lengths, angles, surfaces, and volumes in the reference place with the ones in the actual configuration. We must select an ambient for the comparison of related quantities, once they are measured in the same frame to make significant the operation. The procedure is well known. When we select, for example, the reference place B![]() as an ambient for the comparison and pull back in it objects pertaining to the actual place, we find primarily two versions of the strain tensor: The one that we immediately meet by direct calculation is given by E:=12(C−g)
as an ambient for the comparison and pull back in it objects pertaining to the actual place, we find primarily two versions of the strain tensor: The one that we immediately meet by direct calculation is given by E:=12(C−g)![]() , where the second-rank tensor C=F*˜gF
, where the second-rank tensor C=F*˜gF![]() , with components CAB=FiA˜gijFjB
, with components CAB=FiA˜gijFjB![]() , is the fully covariant version of the right Cauchy–Green tensor, the pullback of the spatial metric ˜g
, is the fully covariant version of the right Cauchy–Green tensor, the pullback of the spatial metric ˜g![]() in the reference place, so E is a difference between two metric tensors. The second version of the strain tensor is ˜E:=12(˜C−˜I)
in the reference place, so E is a difference between two metric tensors. The second version of the strain tensor is ˜E:=12(˜C−˜I)![]() , where ˜C
, where ˜C![]() is the 1-contravariant, 1-covariant version of the right Cauchy–Green tensor, namely, ˜C:=g−1C
is the 1-contravariant, 1-covariant version of the right Cauchy–Green tensor, namely, ˜C:=g−1C![]() , with components ˜CAB=gACCCB
, with components ˜CAB=gACCCB![]() , and ˜I:=g−1g=δABeB⊗eA
, and ˜I:=g−1g=δABeB⊗eA![]() . ˜E
. ˜E![]() has the meaning of a relative difference between metric tensors, the emphasized adjective being justified by the premultiplication of E by the inverse, namely, g−1 of the metric in the reference place.
has the meaning of a relative difference between metric tensors, the emphasized adjective being justified by the premultiplication of E by the inverse, namely, g−1 of the metric in the reference place.
2.2 Maps describing the inner morphology
As anticipated above, information on the structure of matter at finer spatial scales can be attributed in beginning the construction of a mechanical model by assigning to every point x∈B![]() a variable—say, ν—that describes the microstructure. In general, to construct basic structures of a mechanical model it suffices to affirm that ν is an element of a differentiable manifold20 M
a variable—say, ν—that describes the microstructure. In general, to construct basic structures of a mechanical model it suffices to affirm that ν is an element of a differentiable manifold20 M![]() . Hence, we have a map
. Hence, we have a map
x↦ν:=˜ν(x)∈M.
The following assumptions apply:
1. M![]() is finite-dimensional and such that every cover of it, made of open sets,21 contains a subcover such that every point of M
is finite-dimensional and such that every cover of it, made of open sets,21 contains a subcover such that every point of M![]() has a neighborhood that meets only a finite number of the elements of the subcover.22
has a neighborhood that meets only a finite number of the elements of the subcover.22
2. In principle, M![]() is not embedded in any linear space. In special cases, however, physics may suggest we select M
is not embedded in any linear space. In special cases, however, physics may suggest we select M![]() as a linear space per se (e.g., when ν is a generic second-rank tensor or a stretchable vector, etc.).
as a linear space per se (e.g., when ν is a generic second-rank tensor or a stretchable vector, etc.).
3. The map ˜ν![]() is differentiable.23
is differentiable.23
The notions of tangent and cotangent spaces to M![]() at ν, indicated, respectively, by TνM
at ν, indicated, respectively, by TνM![]() and T*νM
and T*νM![]() , are available.24 We do not introduce further geometric structures over M
, are available.24 We do not introduce further geometric structures over M![]() , as anticipated in the first section, maintaining M
, as anticipated in the first section, maintaining M![]() as abstract as possible in order to construct a framework sufficiently flexible to cover the special cases that we know and to constitute a tool for stipulating further models of specific material classes.
as abstract as possible in order to construct a framework sufficiently flexible to cover the special cases that we know and to constitute a tool for stipulating further models of specific material classes.
The spatial derivative of the map ˜ν![]() is indicated by N, namely, N:=D˜ν(x)
is indicated by N, namely, N:=D˜ν(x)![]() . It is a linear operator from the tangent space to B
. It is a linear operator from the tangent space to B![]() at x onto TνM
at x onto TνM![]() . In short, we write N∈Hom(TxB,T˜ν(x)M)
. In short, we write N∈Hom(TxB,T˜ν(x)M)![]() .
.
When we assign a unique M![]() to the whole body, we are presuming in a sense that the typology of microstructures is uniform, or better, that we choose to describe microstructural features of the same type at every point. We are tacitly adopting the already mentioned axiom of permanence of the material element for we presume implicitly that the microstructure is always adequately represented by ν∈M
to the whole body, we are presuming in a sense that the typology of microstructures is uniform, or better, that we choose to describe microstructural features of the same type at every point. We are tacitly adopting the already mentioned axiom of permanence of the material element for we presume implicitly that the microstructure is always adequately represented by ν∈M![]() during motions. Of course, the choice limits the description of some classes of possible material mutations.
during motions. Of course, the choice limits the description of some classes of possible material mutations.
2.3 Additional remarks on strain measures
We have constructed so far an enriched description of the body morphology, and a question is whether the traditional deformation measures, i.e., E or the right Cauchy–Green tensor C or their Eulerian counterparts (not rendered explicit here but a matter in standard textbooks), are sufficient to evaluate completely the strain. An example motivating the question can be found in the special case of micromorphic media (Mindlin, 1964). For them, ν is a second-rank symmetric tensor and represents a microscopic strain: every material element is considered as a cell able to deform independently of its neighbors.25 Hence, it is possible to think of a relative strain (Mindlin, 1964): it is the macroscopic strain deprived of the microscopic part, a type of strain measure, indeed. Another example is in the theory of the Cosserat brothers (1909); there M![]() coincides with the special orthogonal group26 SO(3) or, alternatively, with the unit sphere S2; in other words, the material element is considered as a small rigid body27 able to rotate independently of the neighboring elements.
coincides with the special orthogonal group26 SO(3) or, alternatively, with the unit sphere S2; in other words, the material element is considered as a small rigid body27 able to rotate independently of the neighboring elements.
To answer the previous question on the extension of strain measures, the key point is the specific nature of ν. In fact, when ν represents an independent microstrain or a rotation, or else a microdisplacement, it is possible to define strain measures involving ν and/or its spatial derivative N. In contrast, when ν describes something like the volume fraction of a phase or the spontaneous polarization in ferroelectrics, the common strain tensor in Lagrangian or Eulerian representation is sufficient to measure strain.
In general, what I can say is that we could imagine defining a second-rank symmetric tensor—let us say G—depending on F, the spatial metric ˜g![]() , ν, and N, which is a metric on B
, ν, and N, which is a metric on B![]() and reduces to the right Cauchy–Green tensor C when ν does not describe a deformation-type property. This way, we could have a generalized deformation tensor ˆE
and reduces to the right Cauchy–Green tensor C when ν does not describe a deformation-type property. This way, we could have a generalized deformation tensor ˆE![]() , defined by ˆE:=12(G−g)
, defined by ˆE:=12(G−g)![]() .
.
Another question is the possible comparison between microstructural states. The paragon between ν and ν1, values at x of two different maps, say, ˜ν![]() and ˜ν1
and ˜ν1![]() , is not the sole point. We could require a comparison between the two derivatives at x, namely, N:=D˜ν(x)
, is not the sole point. We could require a comparison between the two derivatives at x, namely, N:=D˜ν(x)![]() and N1:=D˜ν1(x)
and N1:=D˜ν1(x)![]() , or even the two maps ˜ν
, or even the two maps ˜ν![]() and ˜ν1
and ˜ν1![]() . To this aim, we need to define additional geometric structures over M
. To this aim, we need to define additional geometric structures over M![]() and/or to impose the condition that M
and/or to impose the condition that M![]() is a complete manifold, as already mentioned in the introduction. Further details are given in de Fabritiis and Mariano (2005).
is a complete manifold, as already mentioned in the introduction. Further details are given in de Fabritiis and Mariano (2005).
2.4 Motions
In the standard format of continuum mechanics, motions are time-parameterized families of deformations, namely, (x,t)↦y:=u(x,t)∈˜E3![]() , with t the time running in some interval of the real line. We assume that u is at least twice piecewise differentiable with respect to time, and we write ˙y
, with t the time running in some interval of the real line. We assume that u is at least twice piecewise differentiable with respect to time, and we write ˙y![]() for the velocity dudt(x,t)
for the velocity dudt(x,t)![]() , considered as a field over B
, considered as a field over B![]() , taking values in TyBa
, taking values in TyBa![]() , and v:=˜v(y,t)
, and v:=˜v(y,t)![]() for the same velocity viewed now as the value in TyBa
for the same velocity viewed now as the value in TyBa![]() of a field over the actual place Ba:=u(B,t)
of a field over the actual place Ba:=u(B,t)![]() —the latter is the Euclidean representation of the velocity, while the former is the Lagrangian one. The second derivative of u with respect to time, evaluated at x and t, and indicated by ¨y
—the latter is the Euclidean representation of the velocity, while the former is the Lagrangian one. The second derivative of u with respect to time, evaluated at x and t, and indicated by ¨y![]() , defines the acceleration in the Lagrangian description. Its Eulerian version a(y, t) is given by a:=∂v∂t+(Dyv)v
, defines the acceleration in the Lagrangian description. Its Eulerian version a(y, t) is given by a:=∂v∂t+(Dyv)v![]() , where Dy is the derivative with respect to y.
, where Dy is the derivative with respect to y.
The scheme presented so far, however, includes the description of the geometry of the texture of the finer-scale material. Hence, we have to intend motions as pairs of time-parameterized families of deformations and descriptors of the material morphology at microscales in space. In addition to u(x, t), we consider maps (x,t)↦ν:=˜ν(x,t)∈TνM![]() and indicate by ˙ν
and indicate by ˙ν![]() the rate of change of the finer-scale morphology in the Lagrangian representation, namely, ˙v:=d˜νdt(x,t)
the rate of change of the finer-scale morphology in the Lagrangian representation, namely, ˙v:=d˜νdt(x,t)![]() .
.
We can also have an Eulerian view on the rate of microstructural shapes by defining a map ˜νa:=u−1∘˜ν![]() , the Eulerian version of ˜ν
, the Eulerian version of ˜ν![]() , and a field (y,t)↦υ:=˜υ(y,t)∈T˜νa(y,t)M
, and a field (y,t)↦υ:=˜υ(y,t)∈T˜νa(y,t)M![]() . While ˙y=v
. While ˙y=v![]() , we do not get the identity between ˙ν
, we do not get the identity between ˙ν![]() and its Eulerian version.
and its Eulerian version.
2.5 Further geometric notes
In principle, the reader can jump this section during a first reading, coming back to it just before beginning the last section. Consider a vector a∈R3![]() at x∈B
at x∈B![]() . Its image under the deformation u is ˜a=Fa
. Its image under the deformation u is ˜a=Fa![]() , with F given by Du(x). I am repeating here what is written above just to remind ourselves that F governs how line elements change from the reference to the current shape of the body—they are stretched and rotated. The way in which oriented areas change is described by the Nanson formula: in it the key role is played by the cofactor cof F. Finally, the determinant det F is the factor linking a volume in B
, with F given by Du(x). I am repeating here what is written above just to remind ourselves that F governs how line elements change from the reference to the current shape of the body—they are stretched and rotated. The way in which oriented areas change is described by the Nanson formula: in it the key role is played by the cofactor cof F. Finally, the determinant det F is the factor linking a volume in B![]() with its counterpart in the actual shape Ba
with its counterpart in the actual shape Ba![]() . These three aspects of the way in which a body deforms can be collected in a unique geometric entity, a three-vector indicated by M (F). It is a third-rank, skew-symmetric tensor, with all contravariant components. It is defined by using the wedge product ∧.28
. These three aspects of the way in which a body deforms can be collected in a unique geometric entity, a three-vector indicated by M (F). It is a third-rank, skew-symmetric tensor, with all contravariant components. It is defined by using the wedge product ∧.28
To construct M (F), select linearly independent vectors a1, a2, and a3 at a point x in B![]() and consider maps of the type
and consider maps of the type
a1∧a2∧a3↦Fa1∧a2∧a3,a1∧a2∧a3↦Fa1∧Fa2∧a3,a1∧a2∧a3↦Fa1∧Fa2∧Fa3,
obtained by pushing forward by means of F one or more vectors from E3![]() to ˜E3
to ˜E3![]() . The values of these three maps are all third-rank, skew-symmetric contravariant tensors. We then define M (F) as the third-rank, skew-symmetric contravariant tensor given by
. The values of these three maps are all third-rank, skew-symmetric contravariant tensors. We then define M (F) as the third-rank, skew-symmetric contravariant tensor given by
M(F):=a1∧a2∧a3+Fa1∧a2∧a3+a1∧Fa2∧a3+a1∧a2∧Fa3+Fa1∧Fa2∧a3+Fa1∧a2∧Fa3+a1∧Fa2∧Fa3+Fa1∧Fa2∧Fa3=(a1,Fa1)∧(a2,Fa2)∧(a3,Fa3).
Its components are the number 1, and all the entries of F (in the terms where F acts on just one vector), cof F (where F is applied to two vectors), and det F (the last term).
In deriving the standard strain measures, we have in mind that F := Du (x), while we can construct M (F) even in the case of incompatible strain, i.e., when the map x ![]() F (x) is such that curlF ≠ 0, then F ≠ Du (x). M (F) belongs to Λ3(R3טR3)
F (x) is such that curlF ≠ 0, then F ≠ Du (x). M (F) belongs to Λ3(R3טR3)![]() (see the previous footnote) but not all elements of Λ3(R3טR3)
(see the previous footnote) but not all elements of Λ3(R3טR3)![]() are of the type M (F). In other words, not all three vectors are generated by only one linear operator, as M (F) is by construction. Two constants, say, ζ and a
are of the type M (F). In other words, not all three vectors are generated by only one linear operator, as M (F) is by construction. Two constants, say, ζ and a![]() , and two independent linear operators, e.g., H and A, determine, in fact, a generic element M of Λ3(R3טR3)
, and two independent linear operators, e.g., H and A, determine, in fact, a generic element M of Λ3(R3טR3)![]() . With respect to the bases in R3
. With respect to the bases in R3![]() and ˜R3
and ˜R3![]() indicated above, namely, (e1, e2, e3) and (˜e1,˜e2,˜e3)
indicated above, namely, (e1, e2, e3) and (˜e1,˜e2,˜e3)![]() , every three-vector M∈Λ3(R3טR3)
, every three-vector M∈Λ3(R3טR3)![]() has the form
has the form
M=ζe1∧e2∧e3+3∑i,J(−1)J−1HiJeˉJ∧˜ei+3∑i,J(−1)i−1AiJeJ∧˜eˉi+a˜e1∧˜e2∧˜e3,
where ˉJ![]() is the complementary multi-index to J with respect to (1,2,3), and ˉι
is the complementary multi-index to J with respect to (1,2,3), and ˉι![]() has an analogous relation with i (e.g., if J = 1, then ˉJ=(2,3)
has an analogous relation with i (e.g., if J = 1, then ˉJ=(2,3)![]() and eˉJ=e2∧e3
and eˉJ=e2∧e3![]() , and the same holds for the index i and its pertinent ˉι
, and the same holds for the index i and its pertinent ˉι![]() ).29 For the sake of conciseness, we shall write M=(ζ,H,A,a)
).29 For the sake of conciseness, we shall write M=(ζ,H,A,a)![]() . In the previous definition of M, we used the algebraic signs to allow easily the identification of the coefficients in the special case M = M (F).
. In the previous definition of M, we used the algebraic signs to allow easily the identification of the coefficients in the special case M = M (F).
M coincides with M (F) when ζ = 1, H = Fg−1, A=˜gcofF![]() when cof F is defined by (det F) (F−1)* or A = cof Fg−1 when we consider cof F as given by (det F) (F−1)T, and a=detF
when cof F is defined by (det F) (F−1)* or A = cof Fg−1 when we consider cof F as given by (det F) (F−1)T, and a=detF![]() . In short, we can write M (F) for the list (F, cof F, det F) so that, when M = M (F), we have M (F) = (1, M (F)). Remember that a special case of M (F) is when M = M (Du).
. In short, we can write M (F) for the list (F, cof F, det F) so that, when M = M (F), we have M (F) = (1, M (F)). Remember that a special case of M (F) is when M = M (Du).
The role of M (F) clearly appears when we analyze the existence of ground states in nonlinear elasticity of simple bodies (Giaquinta et al., 1989), even including a detailed description of the microstructure (Mariano & Modica, 2009),30 as we do here, and in describing the occurrence of cracks through the measures called varifolds (Giaquinta, Mariano, Modica, & Mucci, 2010), as I shall sketch below.
3 Observers
In traditional continuum mechanics, an observer is a frame in the ambient space and a timescale. Changes in observers are largely used to restrict possible constitutive choices by imposing requirements of objectivity or covariance. Specifically, scalars, vectors, and tensors are objective when they are altered in accord with their tensor nature under isometric changes in observers in space—in the classical approach the timescale is assumed to be invariant or to undergo an affine change, so the attention is primarily focused on space.
For example, the energy density should be invariant if we presume that it is objective—in this case physics does not suggest alternatives, and the consequence in the nonlinear mechanics of simple elastic bodies undergoing large strains is the incompatibility of the objectivity of the energy with its possible convexity with respect to F (Coleman & Noll, 1959).
Another role played by the changes in observers appears when we realize that the inner power of actions vanishes when it is evaluated on rigid-body motions. A consequence is the invariance of the external power of actions under changes in observers (frames) governed by time-parameterized families of isometries in space (rigid-body motions). Such a remark, due to Gabrio Piola, has been adopted in a reverse way, roughly speaking, by Noll (1963, 1973), who has used in the standard setting of continuum mechanics (the one of Cauchy bodies31) the invariance of the sole external power of actions as a first principle from which we can derive standard integral balances of actions, the existence of the stress, and finally, pointwise balance equations under appropriate regularity of the fields involved.
Because of its crucial (in the sense just specified) significance, the notion of an observer has to be discussed in the enlarged setting that we are treating here.
In the standard framework, the ambient space and the timescale are the sole geometric environments where we represent motion and body morphology. Hence, I find it reasonable to suggest for the enlarged setting discussed here a definition that accounts strictly for the essence of the standard approach.
In the present framework, beyond the ambient space ˜E3![]() , and the timescale (an interval of the real line), the complete list would include the space E3
, and the timescale (an interval of the real line), the complete list would include the space E3![]() where we place the reference shape, and the manifold M
where we place the reference shape, and the manifold M![]() of microstructural shapes. In defining changes in observers, alternatives are possible. The main list follows.
of microstructural shapes. In defining changes in observers, alternatives are possible. The main list follows.
3.1 Isometry-based changes in observers
The classes of changes in observers listed below are synchronous. Including affine changes in time would not alter the results. Moreover, more intricate changes in time would lead us toward the relativistic setting, which is not considered here.
3.1.1 Class 1: leaving invariant the reference space
Two observers O![]() and O′
and O′![]() differ in the representation of the ambient space ˜E3
differ in the representation of the ambient space ˜E3![]() by time-parameterized families of isometries (rigid-body motions). Smooth maps t↦a(t)∈R3
by time-parameterized families of isometries (rigid-body motions). Smooth maps t↦a(t)∈R3![]() and t
and t ![]() Q (t) ∈ SO (3), with t∈R
Q (t) ∈ SO (3), with t∈R![]() the time, describe the isometries just mentioned. If ˙y
the time, describe the isometries just mentioned. If ˙y![]() and ˙y′
and ˙y′![]() are the velocities evaluated at x and t by O
are the velocities evaluated at x and t by O![]() and O′
and O′![]() , respectively, the pullback of ˙y′
, respectively, the pullback of ˙y′![]() into the frame defining O
into the frame defining O![]() , namely, ˙y*:=QT˙y′
, namely, ˙y*:=QT˙y′![]() , is given by
, is given by
˙y*=˙y+c(t)+q(t)×(y−y0),
where y0 is an arbitrary point in space, c:=QT˙a∈R3![]() , and q is the axial vector of the skew-symmetric tensor QT˙Q
, and q is the axial vector of the skew-symmetric tensor QT˙Q![]() . The relation is standard. Since Lagrangian and Eulerian representations of the velocity coincide, i.e., ˙y(x,t)=v(y,t)
. The relation is standard. Since Lagrangian and Eulerian representations of the velocity coincide, i.e., ˙y(x,t)=v(y,t)![]() , with v the velocity intended as a field over Ba
, with v the velocity intended as a field over Ba![]() at the instant t, the Eulerian counterpart of Eq. (1.1) is given by
at the instant t, the Eulerian counterpart of Eq. (1.1) is given by
v*=v+c(t)+q(t)×(y−y0).
The problem is now to understand how we have to interpret changes in observers on the manifold of microstructural shapes M![]() .
.
Picturing the morphology of bodies in the product space ˜E3×M![]() is just a model. There are interactions between macroscopic deformation and microstructural events. In contrast, in the scheme sketched above, gross deformation and microstructural changes are described in different spaces. Also, what we define formally to be an observer is a picture of our physical observation of phenomena. In the laboratory, when we change frame (and it is in the physical space), in principle we may perceive a different picture of microstructural events, according to the change, so in the continuum model we must take into account that microstructures are in fact in the physical space and that their representation over M
is just a model. There are interactions between macroscopic deformation and microstructural events. In contrast, in the scheme sketched above, gross deformation and microstructural changes are described in different spaces. Also, what we define formally to be an observer is a picture of our physical observation of phenomena. In the laboratory, when we change frame (and it is in the physical space), in principle we may perceive a different picture of microstructural events, according to the change, so in the continuum model we must take into account that microstructures are in fact in the physical space and that their representation over M![]() is just a convenient tool that allows us to transfer at a macroscopic level information on microscopic events. We have to consider then a possible link between changes in observers in the ambient space E3
is just a convenient tool that allows us to transfer at a macroscopic level information on microscopic events. We have to consider then a possible link between changes in observers in the ambient space E3![]() and the ones over M
and the ones over M![]() .
.
Before specifying the link, we have to define the manner in which we can change the atlas over M![]() . To this aim we use smooth diffeomorphisms of M
. To this aim we use smooth diffeomorphisms of M![]() onto itself. They constitute a group, indicated by Diff(M,M)
onto itself. They constitute a group, indicated by Diff(M,M)![]() . It is not precisely necessary to consider changes on M
. It is not precisely necessary to consider changes on M![]() determined by any arbitrary element of Diff(M,M)
determined by any arbitrary element of Diff(M,M)![]() . More specifically, we can affirm that we alter M
. More specifically, we can affirm that we alter M![]() by a Lie group32 G which can coincide either with Diff(M,M)
by a Lie group32 G which can coincide either with Diff(M,M)![]() or with a subgroup of it and is such that its action over M
or with a subgroup of it and is such that its action over M![]() is nonsingular. g
is nonsingular. g![]() is a common notation for its Lie algebra: the tangent space to the identity of G.
is a common notation for its Lie algebra: the tangent space to the identity of G.
Consider a one-parameter smooth curve R+∋s↦gs∈G![]() over G. The tangent vector to the curve at s = 0, where it crosses the identity, namely, ξ:=dgsds|s=0
over G. The tangent vector to the curve at s = 0, where it crosses the identity, namely, ξ:=dgsds|s=0![]() belongs to g
belongs to g![]() . Its action over ν∈M
. Its action over ν∈M![]() is denoted by ξM(ν)
is denoted by ξM(ν)![]() . In particular, we indicate by νg the value g
. In particular, we indicate by νg the value g ![]() ν = g (ν). From a given ν∈M
ν = g (ν). From a given ν∈M![]() , the curve s
, the curve s ![]() gs generates an orbit s↦νgs
gs generates an orbit s↦νgs![]() over M
over M![]() itself, so we get ξM(ν)=ddsνgs|s=0
itself, so we get ξM(ν)=ddsνgs|s=0![]() . Essentially, we can consider a field x↦υ(x):=ξM(ν(x))
. Essentially, we can consider a field x↦υ(x):=ξM(ν(x))![]() assigning to every x in B
assigning to every x in B![]() an element of the tangent space of M
an element of the tangent space of M![]() at ν (x), generated by the action of ξM
at ν (x), generated by the action of ξM![]() , which is essentially a virtual rate of change of the material microstructure.
, which is essentially a virtual rate of change of the material microstructure.
With these tools, we can define the link between changes of frames in the ambient space and the ones over M![]() . Formally, it is established by the existence of a family of differentiable homomorphisms {λ} mapping the group of diffeomorphisms of the ambient space over G, namely, {λ:=Diff(˜E3,˜E3)→G}
. Formally, it is established by the existence of a family of differentiable homomorphisms {λ} mapping the group of diffeomorphisms of the ambient space over G, namely, {λ:=Diff(˜E3,˜E3)→G}![]() . Changes in the ambient space governed by h∈Diff(˜E3,˜E3)
. Changes in the ambient space governed by h∈Diff(˜E3,˜E3)![]() imply changes ν
imply changes ν ![]() νh := gh (ν) on M
νh := gh (ν) on M![]() , with gh = λ (h). When {λ} is not empty, any smooth curve t→h(t)∈Diff(˜E3,˜E3)
, with gh = λ (h). When {λ} is not empty, any smooth curve t→h(t)∈Diff(˜E3,˜E3)![]() crossing at 0 the identity induces, consequently, a related curve t
crossing at 0 the identity induces, consequently, a related curve t ![]() νh (t) over M
νh (t) over M![]() . Differentiation at t = 0 defines the relevant ξM(ν)
. Differentiation at t = 0 defines the relevant ξM(ν)![]() . However, the family {λ} can be even empty in appropriate physical circumstances, and this case also has its significant consequences.
. However, the family {λ} can be even empty in appropriate physical circumstances, and this case also has its significant consequences.
In this section, the changes in observers considered in the ambient space ˜E3![]() are isometries (two observers differ from each other by a rigid-body motion: translation a(t)∈R3
are isometries (two observers differ from each other by a rigid-body motion: translation a(t)∈R3![]() and rotation Q (t) ∈ SO (3)). Hence, the homomorphisms in {λ} must account just for the effect of frame rotation in the physical space on the representation of microstructures on M
and rotation Q (t) ∈ SO (3)). Hence, the homomorphisms in {λ} must account just for the effect of frame rotation in the physical space on the representation of microstructures on M![]() , which is not altered by a rigid translation of the whole body. Formally, {λ} reduces to {λ : SO (3) → G}. The consequent analysis distinguishes two different cases: (1) SO (3) is a subgroup of Diff(M,M)
, which is not altered by a rigid translation of the whole body. Formally, {λ} reduces to {λ : SO (3) → G}. The consequent analysis distinguishes two different cases: (1) SO (3) is a subgroup of Diff(M,M)![]() ; (2) SO (3) is not included in Diff(M,M)
; (2) SO (3) is not included in Diff(M,M)![]() .
.
In both cases the rule governing how ˙ν![]() is altered under changes in observers is
is altered under changes in observers is
˙ν*=˙ν+A(ν)q,
with q the vector of rotational speed in Eq. (1.1) and, at any t in the time interval under scrutiny, A(ν)∈Hom(R3,TνM)![]() .
.
What changes from case 1 to case 2 is the meaning of the linear operator A(ν)![]() .
.
When SO (3) is a subgroup of Diff(M,M)![]() and the family {λ} is not empty, A(ν)
and the family {λ} is not empty, A(ν)![]() is the infinitesimal generator of the action of SO (3) over M
is the infinitesimal generator of the action of SO (3) over M![]() —in an analogous way the rigid velocity in Eq. (1.1) is given by the action of the Euclidean group (the one of rigid-body motions, once again a Lie group) over the ambient space ˜E3
—in an analogous way the rigid velocity in Eq. (1.1) is given by the action of the Euclidean group (the one of rigid-body motions, once again a Lie group) over the ambient space ˜E3![]() . Consider a differentiable map t
. Consider a differentiable map t ![]() Q (t) = exp (−eq (t)) ∈ SO (3), with e Ricci's symbol, and q(t)∈R3
Q (t) = exp (−eq (t)) ∈ SO (3), with e Ricci's symbol, and q(t)∈R3![]() . Denote by νq the value of ν after the action of Q (its specific form depends on the tensor rank of ν). By explicit computation of the time derivative of νq, we find that the vector q in Eq. (1.3) is the rate of q (t), namely, q:=dq(t)dt
. Denote by νq the value of ν after the action of Q (its specific form depends on the tensor rank of ν). By explicit computation of the time derivative of νq, we find that the vector q in Eq. (1.3) is the rate of q (t), namely, q:=dq(t)dt![]() , and we compute33
, and we compute33
A(ν)=dνqdq|q=0.
When SO (3) is not included in Diff(M,M)![]() and the set {λ} is not empty, by indicating by νλ(Q) the value of ν after the action of λ (Q) ∈ G (once again the explicit expression of νλ(Q) depends on the tensor nature of ν and λ (Q)), we find A(ν)
and the set {λ} is not empty, by indicating by νλ(Q) the value of ν after the action of λ (Q) ∈ G (once again the explicit expression of νλ(Q) depends on the tensor nature of ν and λ (Q)), we find A(ν)![]() is given by
is given by
A(ν)=dνλ(Q)dλdλ(Q)dq|q=0.
Expression (1.3) can be accepted, at least formally, even when we do not consider any link between changes in observers in the ambient space and on M![]() , i.e., when {λ} is empty. In this case, in formula (1.3) the vector q would not coincide with the rotation velocity vector in the ambient space ˜E3
, i.e., when {λ} is empty. In this case, in formula (1.3) the vector q would not coincide with the rotation velocity vector in the ambient space ˜E3![]() .
.
3.1.2 Class 2: changing the reference space by isometries
In all the ramifications of the previous class of changes in observers, the reference place is left invariant.34 We can have an enlarged view defining changes in observes that includes alterations of frames in the reference space in addition to what is done in the ambient space and over M![]() .
.
We presume then isometry-based changes in observers in ˜E3![]() and their consequences over M
and their consequences over M![]() exactly as in the previous class. In addition, we impose isometric changes of frame in the space E3
exactly as in the previous class. In addition, we impose isometric changes of frame in the space E3![]() where there is the reference place B
where there is the reference place B![]() . Formally, consider a vector field x
. Formally, consider a vector field x ![]() w over B
w over B![]() (it is a field assigning at every x∈B
(it is a field assigning at every x∈B![]() a vector in the tangent space to B
a vector in the tangent space to B![]() at the same point). w is what is perceived by the observer O
at the same point). w is what is perceived by the observer O![]() . w′ is what an observer O′
. w′ is what an observer O′![]() measures. The pullback of w′ into O
measures. The pullback of w′ into O![]() , indicated by w*, is given by
, indicated by w*, is given by
w*=w+ˉc(t)+ˉq(t)×(y−y0),
where ˉc![]() and ˉq
and ˉq![]() are, as in class 1, translational and rotational velocities. We impose the condition that c differs from ˉc
are, as in class 1, translational and rotational velocities. We impose the condition that c differs from ˉc![]() and q differs from ˉq
and q differs from ˉq![]() , a key point in the following developments.
, a key point in the following developments.
3.2 Diffeomorphism-based changes in observers
In principle, we can imagine that two observers may deform smoothly with respect to one another in the representation of ˜E3![]() , with consequences on M
, with consequences on M![]() dictated by the family of homomorphisms {λ} introduced above. We can also foresee changes in observers deforming smoothly the reference space E3
dictated by the family of homomorphisms {λ} introduced above. We can also foresee changes in observers deforming smoothly the reference space E3![]() . This way, we construct generalizations of the previous classes.
. This way, we construct generalizations of the previous classes.
3.2.1 Generalized class 1
O![]() and O′
and O′![]() differ in time by smooth deformations of the ambient space ˜E3
differ in time by smooth deformations of the ambient space ˜E3![]() . Formally, we have time-parameterized families of diffeomorphisms t↦ht:˜E3→˜E3
. Formally, we have time-parameterized families of diffeomorphisms t↦ht:˜E3→˜E3![]() , i.e., ht∈Diff(˜E3,˜E3)
, i.e., ht∈Diff(˜E3,˜E3)![]() , which are differentiable in time, with ht0
, which are differentiable in time, with ht0![]() the identity and t0 the initial instant for the change in observer. A vector field y↦ˉv:=ddtht(y)|t=t0
the identity and t0 the initial instant for the change in observer. A vector field y↦ˉv:=ddtht(y)|t=t0![]() is then defined over ˜E3
is then defined over ˜E3![]() , and, in particular, over the actual place Ba
, and, in particular, over the actual place Ba![]() of the body.35 Being a function of y∈Ba,ˉv
of the body.35 Being a function of y∈Ba,ˉv![]() enters directly a rule for the change in observer of the Eulerian representation v of the velocity. The rule is
enters directly a rule for the change in observer of the Eulerian representation v of the velocity. The rule is
v→v#:=v+ˉv.
Precisely, v# is the image in O![]() of the Eulerian velocity evaluated by O′
of the Eulerian velocity evaluated by O′![]() . However, since ˙y=v
. However, since ˙y=v![]() (Lagrangian and Eulerian representations of the velocity coincide), we can consider ˉv
(Lagrangian and Eulerian representations of the velocity coincide), we can consider ˉv![]() as the value of a field defined over the reference place, so instead of v→v#:=v+ˉv
as the value of a field defined over the reference place, so instead of v→v#:=v+ˉv![]() , we can write
, we can write
˙y→˙y#:=˙y+ˉv.
As regards the influence that such changes in ˜E3![]() might have on the representation of the microstructural shapes on M
might have on the representation of the microstructural shapes on M![]() , we have to consider the family of homomorphisms {λ:Diff(˜E3,˜E3)→G}
, we have to consider the family of homomorphisms {λ:Diff(˜E3,˜E3)→G}![]() . Consequently, with the notation introduced above, by indicating by νλ(ht)
. Consequently, with the notation introduced above, by indicating by νλ(ht)![]() the value of ν after the action of λ(ht):M→M
the value of ν after the action of λ(ht):M→M![]() , with ht:˜E3→˜E3
, with ht:˜E3→˜E3![]() , where ht is a diffeomorphism, we could then accept for changes in observers a relation of the type
, where ht is a diffeomorphism, we could then accept for changes in observers a relation of the type
˙ν#=˙ν+υ+A(ν)q,
with A(ν)![]() now given by
now given by
A(ν):=dνλ(ht)dλ(ht)dλ(ht)dt|t=0,
with υ a generic element of the linear space TνM![]() , and q a rigid rotational velocity of the physical space.
, and q a rigid rotational velocity of the physical space.
The previous relation is, however, formal. The key point is to understand whether a change in physical space induced by a diffeomorphism h (t) alters the features of the microstructure that we represent by M![]() in the specific mechanical model that we develop. In this sense, the choice of the class of changes in observers may depend on the physical situation at hand.
in the specific mechanical model that we develop. In this sense, the choice of the class of changes in observers may depend on the physical situation at hand.
Of course, we could just choose a general rule for changes in observers over M![]() of the type
of the type
˙ν#=˙ν+ˉυ,
with ˉυ(x)∈Tν(x)M![]() , as a general compact version of the previous relation for ˙ν#
, as a general compact version of the previous relation for ˙ν#![]() , which, in turn, evidences the influence of the change in observer in the physical space on the way we represent the microstructure over M
, which, in turn, evidences the influence of the change in observer in the physical space on the way we represent the microstructure over M![]() . Obviously, in the case of isometric changes in observers, ˙ν#=˙ν*
. Obviously, in the case of isometric changes in observers, ˙ν#=˙ν*![]() .
.
3.2.2 Generalized class 2
The generalization deals with changes in observer in the reference space induced by smooth deformations, precisely by time-parameterized maps ˆht:E3→E3![]() , with ˆht0
, with ˆht0![]() the identity, which are diffeomorphisms in space and are differentiable in time—once again t0 is the initial instant of the change in observer.
the identity, which are diffeomorphisms in space and are differentiable in time—once again t0 is the initial instant of the change in observer.
A new vector field is then defined over the reference space and is x↦ˉw:=ddtˆht(x)|t=t0![]() . Hence, by indicating by w# the image in O
. Hence, by indicating by w# the image in O![]() of the vector w evaluated by O′
of the vector w evaluated by O′![]() , we get
, we get
w↦w#:=w+ˉw.
In ˜E3![]() and over M
and over M![]() changes in observers are like in the generalized class 1.
changes in observers are like in the generalized class 1.
3.3 Notes on definitions and use of changes in observers
• Requirements of invariance under isometry-based changes in observers deal with what we call objectivity in the enlarged setting including M![]() . Their counterparts for the diffeomorphism-based classes are what we intend for covariance in the same framework.
. Their counterparts for the diffeomorphism-based classes are what we intend for covariance in the same framework.
• The diffeomorphism-based classes of changes in observers contain the relevant isometry-based versions. Then, a requirement of covariance is more stringent than the one of objectivity. At times, different choices may lead to different results, above all in the derivation of balance equations. For example, the requirement of invariance of the external power of actions under isometry-based changes in observers allows us to derive directly integral balances, while, in contrast, covariance brings us toward weak balances or pointwise balances under appropriate regularity conditions for the fields involved.
• In principle, it would be possible to exclude the representation of the manifold M![]() from the definition of the observer, considering ν as an “entity” insensitive to changes in observers. In this case, the evolution of ν would be represented by rules resulting independent of the observers. I shall come back to this issue.
from the definition of the observer, considering ν as an “entity” insensitive to changes in observers. In this case, the evolution of ν would be represented by rules resulting independent of the observers. I shall come back to this issue.
4 The relative power in the case of bulk mutations
4.1 External power of standard and microstructural actions
We call any subset b![]() of B
of B![]() with non-null volume measure and the same geometric regularity of B
with non-null volume measure and the same geometric regularity of B![]() a part—in other words b
a part—in other words b![]() is a fit region exactly as B
is a fit region exactly as B![]() is. When we imagine enucleating (the cut is just ideal) a generic part b
is. When we imagine enucleating (the cut is just ideal) a generic part b![]() of the body, we affirm commonly that b
of the body, we affirm commonly that b![]() interacts with the rest of the body and the external environment by bulk and contact actions. The former are a consequence of the interaction with the rest of the universe. The latter actions are exerted through the boundary ∂b
interacts with the rest of the body and the external environment by bulk and contact actions. The former are a consequence of the interaction with the rest of the universe. The latter actions are exerted through the boundary ∂b![]() of b
of b![]() . A representation of them follows by analyzing the body and its environment as elements of a universe of parts, a set partially ordered with respect to the relation “being part of” in which, in addition, we define two operations: meet and join. A part b
. A representation of them follows by analyzing the body and its environment as elements of a universe of parts, a set partially ordered with respect to the relation “being part of” in which, in addition, we define two operations: meet and join. A part b![]() is the join of two parts when it is the least envelop of them (which is still a part in the sense specified above). Also, b
is the join of two parts when it is the least envelop of them (which is still a part in the sense specified above). Also, b![]() is the meet of two parts when it is the greatest common part of the two factors. Meet and join assign to the set of parts of a body and its environment, a universe, the structure of an algebra, once we have included the empty set and an infinite set (what is called “material all” by Noll). Bulk and contact actions are then defined as vector-valued functions over the set of pairs of disjoint parts of a given universe (see Noll, 1973 for details). The extension of the procedure to a scheme in which we include a multifield and multiscale description of material microstructures, as sketched in previous sections, was proposed in Capriz and Virga (1990): that analysis requires not only a modified version of meet and join operations but also the embedding of M
is the meet of two parts when it is the greatest common part of the two factors. Meet and join assign to the set of parts of a body and its environment, a universe, the structure of an algebra, once we have included the empty set and an infinite set (what is called “material all” by Noll). Bulk and contact actions are then defined as vector-valued functions over the set of pairs of disjoint parts of a given universe (see Noll, 1973 for details). The extension of the procedure to a scheme in which we include a multifield and multiscale description of material microstructures, as sketched in previous sections, was proposed in Capriz and Virga (1990): that analysis requires not only a modified version of meet and join operations but also the embedding of M![]() in a linear space, a tool not necessary in the developments presented below.
in a linear space, a tool not necessary in the developments presented below.
Another way of defining the actions is through the power that they develop. A power is a functional which is additive over disjoint parts of a body and linear with respect to the rates involved (see Segev, 1994, for basic geometric issues on the matter). Among powers that we could define in principle, the one with the minimum entities involved is the power of all actions external to a generic part of the body.
Bulk and contact actions due to the deformation are on the actual shape of the body. For any part ba![]() of Ba
of Ba![]() , in traditional continuum mechanics the representation of the external power, Pextba(v)
, in traditional continuum mechanics the representation of the external power, Pextba(v)![]() , of all actions over ba
, of all actions over ba![]() is
is
Pextba(v):=∫bab‡a·vdy+∫∂bata·vdH2,
where dy and dH2![]() indicate volume and “surface” measures in Ba
indicate volume and “surface” measures in Ba![]() ; b‡a(y)∈T*yBa
; b‡a(y)∈T*yBa![]() represents body forces, the sum of inertial and noninertial components; and ta(y)∈T*yBa
represents body forces, the sum of inertial and noninertial components; and ta(y)∈T*yBa![]() indicates the traction through the boundary of ba
indicates the traction through the boundary of ba![]() . At any y∈∂ba
. At any y∈∂ba![]() , where the normal na (y) is defined uniquely (by assumption the condition is satisfied at all points of ∂ba
, where the normal na (y) is defined uniquely (by assumption the condition is satisfied at all points of ∂ba![]() but a finite number of corners and edges, as already mentioned), ta
but a finite number of corners and edges, as already mentioned), ta![]() depends only on y and na (y) at every instant. This is the standard Cauchy assumption (see the discussion about it in Fosdick & Virga, 1989). We consider here the normal to ∂ba
depends only on y and na (y) at every instant. This is the standard Cauchy assumption (see the discussion about it in Fosdick & Virga, 1989). We consider here the normal to ∂ba![]() as a covector, i.e., the normalized derivative of the function defining ∂ba
as a covector, i.e., the normalized derivative of the function defining ∂ba![]() through the locus of its zeros. The presumed regularity of ∂ba
through the locus of its zeros. The presumed regularity of ∂ba![]() allows such an interpretation.
allows such an interpretation.
An essential requirement for Pextba(v)![]() , an axiom indeed (see Noll, 1973), is its invariance under isometry-based changes in observers of class 1. Formally, we impose
, an axiom indeed (see Noll, 1973), is its invariance under isometry-based changes in observers of class 1. Formally, we impose
Pextba(v)=Pextba(v*)
for any translational (c (t)) and rotational (q (t)) velocities appearing in Eq. (1.2), and for any ba![]() . The assumption that the fields x
. The assumption that the fields x ![]() b‡a (y) and x↦ta(y)
b‡a (y) and x↦ta(y)![]() are integrable and the invariance condition imply the validity of the balance of forces,
are integrable and the invariance condition imply the validity of the balance of forces,
∫bab‡ady+∫∂batadH2=0,
and couples,
∫ba(y−y0)×b‡ady+∫∂ba(y−y0)×tadH2=0.
If we assume that b‡a is bounded and ta![]() is continuous with respect to y, the integral balance of forces implies the action–reaction principle, namely,
is continuous with respect to y, the integral balance of forces implies the action–reaction principle, namely,
ta(y,na)=−ta(y,−na),
and the Cauchy theorem, i.e., the linearity of ta![]() with respect to na, namely,
with respect to na, namely,
ta(y,na)=σ(y)na,
at every instant, which follows from the standard tetrahedron argument (see, e.g., Truesdell, 1991), and we have
σ(y)=3∑i=1ta(y,˜ei)⊗˜ei,
with ˜ei![]() the ith vector of a basis in a neighborhood of y. The assumption of continuity for ta(·,na)
the ith vector of a basis in a neighborhood of y. The assumption of continuity for ta(·,na)![]() has been variously weakened (Šilhavý, 1991, 2005), and we also have at our disposal notions of stress over manifolds (Segev, 1994, 2004; Segev & Falach, 2012). Here, we accept the stronger version for the sake of simplicity. We just remark that the essence of the Cauchy theorem is that σ is independent of na. The stress σ is a linear operator mapping covectors (normals in the interpretation above) to covectors, the traction ta
has been variously weakened (Šilhavý, 1991, 2005), and we also have at our disposal notions of stress over manifolds (Segev, 1994, 2004; Segev & Falach, 2012). Here, we accept the stronger version for the sake of simplicity. We just remark that the essence of the Cauchy theorem is that σ is independent of na. The stress σ is a linear operator mapping covectors (normals in the interpretation above) to covectors, the traction ta![]() , so it is of the form σ(y)=σji(y)˜ej⊗˜ei
, so it is of the form σ(y)=σji(y)˜ej⊗˜ei![]() , where ˜ei
, where ˜ei![]() is the ith vector of the dual basis in a neighborhood of y—such a basis is defined to be such that ˜ei·˜ej=δij
is the ith vector of the dual basis in a neighborhood of y—such a basis is defined to be such that ˜ei·˜ej=δij![]() , with δji the Kronecker index. We summarize this remark by writing simply σ(y)∈Hom(T*yBa,T*yBa)
, with δji the Kronecker index. We summarize this remark by writing simply σ(y)∈Hom(T*yBa,T*yBa)![]() .
.
The standard use of the Piola transform furnishes the Lagrangian representation of the balance equations in terms of (1) the first Piola–Kirchhoff stress P(x)∈Hom(T*xB,T*u(x)Ba)![]() , obtained by pulling back into the reference place B
, obtained by pulling back into the reference place B![]() the second component of σ, namely,
the second component of σ, namely,
P=(detF)σF−*,
where F−* := (F−1)*, and (2) the referential bulk actions
b‡:=(detF)b‡a.
Should we consider the normal as a vector instead of a covector, as above, in the definition of the first Piola–Kirchhoff stress the adjoint of F should be substituted by the transpose.
Alternatively, we could consider bulk and contact actions as the values over the cotangent bundle of Ba![]() , namely, T*Ba
, namely, T*Ba![]() , of fields defined over the reference place B
, of fields defined over the reference place B![]() , accepting from the beginning the Lagrangian description. In this case the expression of the external power reads
, accepting from the beginning the Lagrangian description. In this case the expression of the external power reads
Pexta(˙y):=∫bb‡·˙ydx+∫∂bt·˙ydH2,
where now, at every instant, we have fields x↦b‡(x)∈T*u(x)Ba![]() and x↦t(x,n(x))∈T*u(x)Ba
and x↦t(x,n(x))∈T*u(x)Ba![]() —assumed to be integrable over their domains—with n the normal to ∂b
—assumed to be integrable over their domains—with n the normal to ∂b![]() at all points to within a finite number of corners and edges. Of course, we have
at all points to within a finite number of corners and edges. Of course, we have
t(x,n(x))=ta(u(x),na(u(x))).
The requirement of invariance under isometry-based changes in observers of class 1 now gives
Pextb(˙y)=Pextb(˙y*)
for any translational (c (t)) and rotational (q (t)) velocities appearing in Eq. (1.1), and for any b![]() . Its immediate consequence is the validity of the integral balances of forces,
. Its immediate consequence is the validity of the integral balances of forces,
∫bb‡dx+∫∂btdH2=0,
and couples,
∫b(y−y0)×b‡dx+∫∂b(y−y0)×tdH2=0,
in the Lagrangian representation.
Under conditions of boundedness for b‡ and continuity for t![]() —not the weakest ones—we can use the balance of forces (1.6) to prove once again the action–reaction principle and the linearity of t(x,n)
—not the weakest ones—we can use the balance of forces (1.6) to prove once again the action–reaction principle and the linearity of t(x,n)![]() with respect to n, namely, the relation
with respect to n, namely, the relation
t(x,n)=P(x)n,
which in components is
ti(x,n)=PAi(x)nA.
We now have
P(x)=3∑K=1t(x,eK)⊗eK,
with eK the Kth vector of a basis in a neighborhood of x.
When we want to include the actions that develop power in the microstructural time rates, we may presume that they are subdivided into bulk and contact actions, exactly like the standard ones. Accepting, for example, the Lagrangian representation, we write an extended expression of Pextb(˙y)![]() , namely, Pextb(˙y,˙ν)
, namely, Pextb(˙y,˙ν)![]() , defined by
, defined by
Pextb(˙y,˙ν):=∫b(b‡·˙y+β‡·˙ν)dx+∫∂b(t·˙y+τ·˙ν)dH2,
where τ(x)∈T*˜ν(x)M![]() indicates microstructural contact actions, and β‡(x)∈T*˜ν(x)M
indicates microstructural contact actions, and β‡(x)∈T*˜ν(x)M![]() represents external bulk actions over the microstructure alone.36 The microstructural contact actions τ are due to nonhomogeneous microstructural changes across the boundary ∂b
represents external bulk actions over the microstructure alone.36 The microstructural contact actions τ are due to nonhomogeneous microstructural changes across the boundary ∂b![]() .
.
We require invariance of Pextb(˙y,˙ν)![]() with respect to isometry-based changes in observers in class 1, i.e., we impose
with respect to isometry-based changes in observers in class 1, i.e., we impose
Pextb(˙y,˙ν)=Pextb(˙y*,˙ν*)
for any choice of c and q in Eqs. (1.1) and (1.3), and for any part b![]() . We get first Eq. (1.6) and a different version of Eq. (1.7), namely,
. We get first Eq. (1.6) and a different version of Eq. (1.7), namely,
∫b((y−y0)×b‡+A*β‡)dx+∫∂b((y−y0)×t+A*τ)dH2=0
(see also Capriz & Mazzini, 1998; Mariano, 2002).