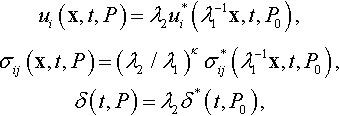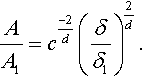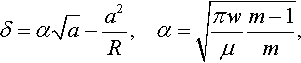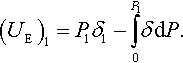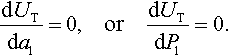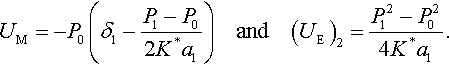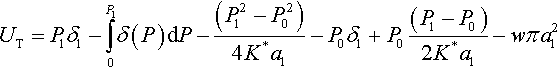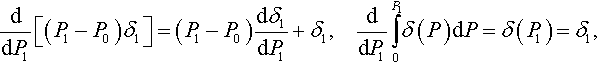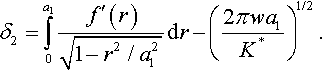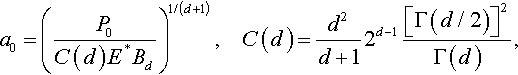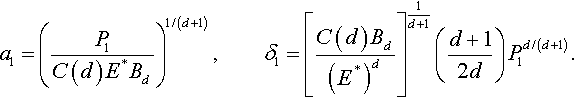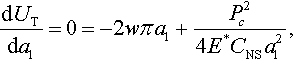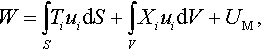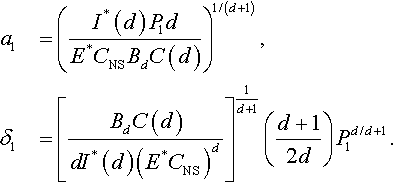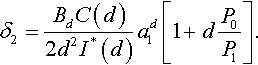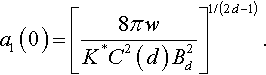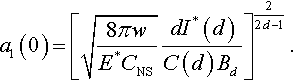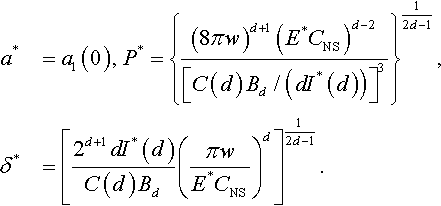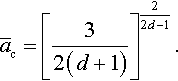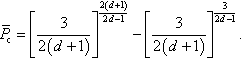The following condition has to be fulfilled for the contact problem to be self-similar: the contact region for one value of the external parameter has to be geometrically similar to the contact region for any other admissible value of the parameter. It is well known from mathematics (group theory) that any similarity transformation on a plane can be decomposed into four transformations: (1) shifting; (2) rotation; (3) dilation of coordinates; and (4) mirror symmetry. The reduction of variables using the Π theorem and reduction of variables using the property of quasi-homogeneous functions are possible if the dilation transformation of variables is used. It is evident that if a contact region has some axes of geometrical symmetry, then the use of mirror symmetry and rotation of the computation domain can be used for simplification of the numerical simulations; however these transformations should be excluded from the consideration as transformations of the contact region due to a change of the problem external parameter, because they have no physical meaning for contact problems.

Let us show that the problem of oblique indentation cannot be analyzed solely by the use of reduced coordinates (rescaling). Indeed, in the problem of oblique indentation, the nose of the indenter is shifted along the x₃ = 0 plane. However, if the growing contact region is geometrically similar to itself at an earlier stage and the center of the region is shifted, then two transformations are involved: shifting and dilation of coordinates. On the other hand, the use of reduced coordinates (rescaling) is applicable to the transformation of dilation of coordinates when the contact region is not shifted. Therefore, one cannot reduce the problem of oblique indentation to dilation with the fixed coordinate origin and use the reduced variables.

It should be noted that if one considers contact between axisymmetric bodies whose materials are isotropic or they satisfy the condition of rotational symmetry, then the problem has some self-similar features even if its solution is not self-similar. Indeed, the contact region is always a circle, i.e., it is changed by the homothetic transformation. However, the problem is more complicated for arbitrary 3D shapes or for general anisotropy of materials. Indeed, in contrast to the isotropic case, if a body of revolution contacts with an anisotropic medium, then the contact region can be noncircular. For example, it was experimentally observed in the problem of indentation of an anisotropic wooden specimen (balsa wood, 67% saturation) by a spherical indenter that the contact region differs from a circle and is close to an ellipse (Bowden & Tabor, 1964). However, even in this case the similarity approach based on the use of the dilation transformation of variables is still valid.

4.5.2 Dilation Similarity Transformations of Hertz-Type Contact

It was shown by Borodich (1989, 1990e, 1993a) that if one punch is replaced by another one using the following transformations then one solution of the contact problem can be transformed into another solution. Implicitly the transformations were used earlier (Borodich, 1984).

Transformation A. The function of the shape of the punch is transformed by homogeneous dilations λ along all axes, i.e.,

$x_i\to \lambda x_i.$

In this case, the punch is replaced by its scaled copy (see Fig. 3.4).

Transformation B. The function of the shape of the punch is transformed by dilation λ along the x₃ axis only, i.e.,

$x_1\to x_1,x_2\to x_2,x_3\to \lambda x_3.$

In this case, the punch is replaced by another one whose shape is just an extension along the x₃ axis of the original shape (see Fig. 3.5).

4.5.3 Similarity Theorems of Hertz-Type Contact

Corollary. If one looks for the punch shape such that it transforms under transformation A into itself, then it is readily seen that this is a 3D cone, B₁(θ)r.

One can see that the contact region is not changed under transformation B. Let us unify these two transformations. In this case the function of the shape f₁ of the punch is transformed by dilation λ₁ along the x₁ and x₂ axes and by λ₂ along the x₃ axis, i.e., the function of the shape f of the transformed punch is given by

$f\left(x_1,x_2\right)={\lambda }_2{f}_1\left({\lambda }_1^{-1}{x}_1,{\lambda }_1^{-1}{x}_2\right).$

  (3.115)

Then a formulation of the following theorem of similarity can be given.

Remarks.

1. Formally, Theorem 5 would be valid for other conditions of friction within the contact region, in particular conditions when regions of stick and slip are alternating. However, these conditions look rather unreal.

2. Theorem 5 shows that there exists a two-parameter transformation group of coordinate dilations such that it transforms one solution to the problem into another one. So, it gives a mathematical explanation for the existence of the similarity which was considered in papers where the distance between contacting bodies was determined by a positive, homogeneous function of degree d ≥ 1. Indeed, if the punch shape is described by a homogeneous function, then the two-parameter transformation group becomes a one-parameter transformation group and the punch under the considered transformation of coordinate dilation is transformed into itself. Thus, taking λ₁ = λ⁻¹ and λ₂ = λ^−d, one obtains the following theorem of similarity.

The similarity properties of all Hertz contact problems considered follow from Theorem 6 (see, e.g., Biwa & Storåkers, 1995; Borodich, 1988b, 1990a, 1990b, 1990c, 1990d, 1990e, 1993a; Galanov, 1981a, 1981b, 1982; Galanov & kravchenko, 1986; Hill et al., 1989).

Similarly to the case of the Hertz contact, the following theorem can be proved (Borodich, 1996, 1998a).

As already mentioned, the PH function b₀ can be fractal. However, even for such a fractal punch, the shape function f = b₂(x; p) = C₁x² [1 + εb₀(x; p)] has the derivative at the origin, f′(0) = 0. So, we can assume that the formulation of the contact problem is still valid for these fractal punches, and therefore Theorem 7 is also valid in the fractal case.

Often mathematical and physical fractals are confused and theorems proved for mathematical fractals are transferred without any adjustment to physical objects. One needs to realize that physical fractals exhibit the power-law behaviour only at intermediate scales δ, while mathematical ones assume that fractal dimension values of a set have to be calculated when δ → 0. This is one of the principal distinctions between physical and mathematical fractals. Hence, there are no mathematical fractals in nature. A mathematical fractal is just one of the possible models that reflect the power-law behavior of natural objects at some intermediate scales. It is wrong to expect that modeling of a rough surface by a mathematical fractal gives considerable advantages in studying an engineering problem. For these fractal curves or surfaces, one cannot use, at least in the usual sense, such a common notion as a normal vector to the surface. Hence, it is impossible to use the classic formulation of boundary value problems for a solid with mathematical fractal boundaries (Borodich, 2013).

It is evident that the solution to the contact problem for a PH punch has discrete self-similar properties, i.e., it is repeated in scaling form near all loads $p^{k\left(d+1\right)}{P}_0,k\in \mathbb{Z}$. Hence, it is possible to get the whole solution using the results of numerical simulation of the problem on a finite half-interval of external parameter (the so-called fundamental domain of the discrete group) only. In the above case, this fundamental domain is (P₁, p^{[2+κ(d−1)]} P₁].

It follows from Theorem 7 that the character of the contact does not depend on fine distinctions between shapes and the roughness functions b₀. The character of the self-similar solution depends on the degrees of homogeneity of the PH function of the punch shape and the operator F only. Thus, the solutions for all PH punches of degree d have the same character. One can conclude that the nonadhesive contact problems with PH roughness have some features of chaotic systems: the trend of the P-δ curve (the global characteristic of the solution) is independent of fine distinctions between PH functions describing roughness, while the stress field (the local characteristic) is sensitive to small perturbations of the punch shape. In particular, the character is the same for both fractal (prefractal) and smooth functions b₀. Particular cases of Theorem 7 in application to PH surfaces were considered by Borodich (1993b, 1998a) and Borodich and Galanov (2002).

It follows from similarity analysis of self-similar nonaxisymmetric contact problems that if the contacting pair is loaded by the force P₁, and the characteristic size of the contact region and the approach of solids are known for this load, they are equal to l(1, t, P₁) and δ(1, t, P₁) respectively. Then for the contact pair compressed by some force P, and whose initial gap is described by the function ch_d, c > 0, the size of the contact region and the approach may be defined by the following rescaling formulae:

$\begin{array}{ll}\delta \left(c,t,P\right)\hfill & =c^{\left(2-\kappa \right)/\left[2+\kappa \left(d-1\right)\right]}{\left(P/P_1\right)}^{d/\left[2+\kappa \left(d-1\right)\right]}\delta \left(1,t,P_1\right),\hfill \\ l\left(c,t,P\right)\hfill & =c^{-\kappa /\left[2+\kappa \left(d-1\right)\right]}{\left(P/P_1\right)}^{1/\left[2+\kappa \left(d-1\right)\right]}l\left(1,t,P_1\right).\hfill \end{array}$

  (3.116)

As mentioned above, these formulae provide an explanation for the Meyer scaling law.

4.6.2 Rescaling Formulae for Hardness and Nanoindentation

Let us denote by P₁, A₁, l₁, and δ₁, respectively, some initial load, the corresponding contact area, the characteristic size of the contact region, and the displacement. Then Eq. (3.116) can be rewritten as

$\frac{l}{l_1}=c^{\frac{-\kappa }{2+\kappa \left(d-1\right)}}{\left(\frac{P}{P_1}\right)}^{\frac{1}{2+\kappa \left(d-1\right)}},\frac{\delta }{{\delta }_1}=c^{\frac{2-\kappa }{2+\kappa \left(d-1\right)}}{\left(\frac{P}{P_1}\right)}^{\frac{d}{2+\kappa \left(d-1\right)}},$

  (3.117)

and as shown by Borodich et al. (2003), the rescaling formula for the contact area is

$\frac{A}{A_1}=c^{\frac{-2}{d}}{\left(\frac{\delta }{{\delta }_1}\right)}^{\frac{2}{d}}.$

  (3.118)

Further, for a fixed indenter, i.e., for c = 1, one can find that the hardness is the following function of the depth of indentation:

$\frac{H}{H_1}=\frac{P/A}{P_1/A_1}={\left(\frac{\delta }{{\delta }_1}\right)}^{\frac{\kappa \left(d-1\right)}{d}}.$

  (3.119)

Thus, for a fixed indenter, whose shape near the tip is described as a monomial function of degree d, one obtains from Eqs. (3.118) and (3.119)

$\delta ~A^{d/2},H~{\delta }^{\kappa \left(d-1\right)/d}.$

  (3.120)

Note that the fist of the relations in Eq. (3.120) is valid independently of the work-hardening exponent κ. The apparent hardness increases as a power-law function of degree κ(d − 1)/d and the hardness is constant only for d = 1, i.e., for ideally sharp 3D conical (conical or pyramidal) indenters.

Using Eq. (3.118), one can try to calibrate the indenter tip from an area-displacement curve. An example of such a curve was given by Doerner and Nix (1986). Applying formula (3.120) to this curve, Borodich et al. (2003) concluded that until about δ ≤ 90 nm the shape of the indenter used by Doerner and Nix (1986) could be described as a monomial function of degree d = 1.44.

The rescaling formulae (3.117), (3.118), and (3.120) were obtained assuming the homogeneity of material properties and that the stress–strain relation remains the same for any depth of indentation. This is not always true (see, e.g., a review by Ioffe, 1949). In addition, as already mentioned, plastic deformation exhibits a strong dependence on size below micrometer length scales (Gao et al., 1999), and models of indentation hardness based on the strain gradient plasticity (Nix & Gao, 1998) predict the hardness decreases as the depth of indentation increases. However, as we have already seen, nonideal indenter geometries (Borodich et al., 2003; Choi & Korach, 2011; Kindrachuk, Galanov, Kartuzov, & Dub, 2006; Kindrachuk et al., 2009; Ma, Zhou, Lau, Low, & deWit, 2002) may also affect the interpretation of the experimental results. I believe that two explanations are possible: (1) the hardness may decrease in accordance with Eq. (3.93) if dislocation scale effects are present and (2) the apparent hardness may increase according to Eq. (3.120) because the nominally sharp indenters are in fact not ideal. However, the former case is less common because not all materials are crystalline.

First, let us compare formulae (3.116) or formula (3.99) with experimental results obtained by Orlov and Pinegin (1971) for a polymeric material. Several terms are used in reference to this material: poly(methyl methacrylate), Plexiglas, and Perspex.

It is well known that poly(methyl methacrylate) is a viscoelastic (or hereditarily elastic) material. If one uses the homogeneous relations (3.106) and (3.107)

$\phi \left[\text{Γ}\left(t\right)\right]{\epsilon }_{\mathit{ij}}^{\text{D}}=\frac{{\sigma }_{\mathit{ij}}^{\text{D}}\left(t\right)}{2\mathcal{G}\left(t\right)}-{\displaystyle {\int }_0^{t}K\left(t,\tau \right){\sigma }_{\mathit{ij}}^{\text{D}}\left(\tau \right)\text{d}\tau },\phi \left[\text{Γ}\left(t\right)\right]={\text{Γ}}^{\kappa -1}\left(t\right)$

or the anisotropic homogeneous relations (3.108)

${\displaystyle \sum _{m=1}^n{Y}_m\left(I_1,\dots ,I_n\right)p_{\mathit{ij}}^{\left(m\right)}\left(\mathbf{x},t\right)}={\sigma }_{\mathit{ij}}\left(\mathbf{x},t\right)-{\displaystyle {\int }_0^t{K}_{\mathit{ijkl}}\left(t,\tau \right){\sigma }_{\mathit{kl}}\left(\mathbf{x},\tau \right)\text{d}\tau }$

as the constitutive relations for poly(methyl methacrylate), then one needs to take into account the following. The kernel K of the constitutive relations may be singular; in this case the diagram σ ~ ε obtained by the use of common experimental techniques would differ from the instantaneous diagram φ[Γ(t)]. The difference may be considerable even if the loading time is of the order of 0.1 s (Rabotnov, 1980). However, to apply formulae (3.116) or formula (3.99), one needs to know only the power κ. Assuming the instantaneous diagram can be obtained from experiments on very fast loading, one can take the results of dynamical experiments on poly(methyl methacrylate) (Perspex) presented by Kolsky (1949). Taking logarithms of the first nine points of the dynamic strain-stress curve and using the least-squares method for a direct line in the logarithmic coordinates, one can obtain κ = 0.7202 (Borodich, 1990e).

4.7.2 Variation of the Loading Time

Owing to viscoelasticity of the material, the characteristic size of the contact region depends on time. Table 3.1 shows the experimental relation between the diameter of the contact region l(P) = 2a and time for a spherical steel indenter of R = 60 mm under P₁ = 500 kgf and P₂ = 1000 kgf (Orlov & Pinegin, 1971, p. 53). If one takes κ = 0.7202 for poly(methyl methacrylate), then the formula (3.99) can be written as

$\frac{l\left(P_2\right)}{l\left(P_1\right)}={\left(P_2/P_1\right)}^{1/2.7202}=2^{1/2.7202}=1.29022\text{or}l\left(P_2\right)=1.29022·l\left(P_1\right).$

  (3.121)

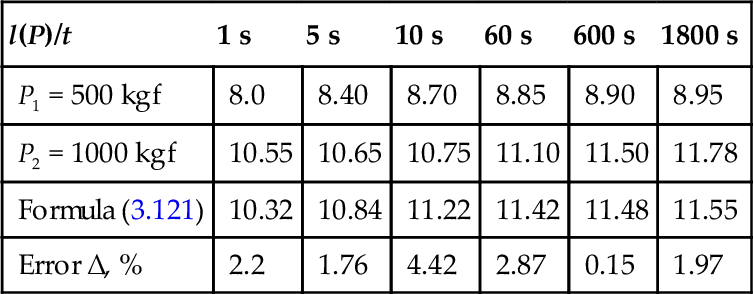
The error is found as

$\text{Δ}=\frac{l\left(P_1\right)·1.29022-l\left(P_2\right)}{l\left(P_2\right)}·100\%.$

One can see that there is excellent agreement between the experimental data and the predictions by Eq. (3.99) or Eq. (3.121).

4.7.3 Variation of the Indenter Size and the Load

Earlier, formula (3.99) was compared with data concerning indentation of an anisotropic wooden specimen by a spherical indenter (Bowden & Tabor, 1964). It was shown by Borodich (1989, 1990e, 1993a) that there is good agreement between experiments and the formula.

It is possible now to check if Eq. (3.99) is in agreement with experiments performed by Orlov and Pinegin (1971, p. 54).

The measurements were taken for a relatively fast loading, i.e., t was approximately 1 s or less. The loads were given in kilogram-force. It was taken that 1 kgf ≈ 10 N because this rounding will not affect the calculations since only the ratio P/P₁ is used in Eq. (3.99).

To use the rescaling formulae, one needs to know a solution (or an experimental result) for a certain value of the external parameter. It was taken that l(R₁, P₁) = 11.3 mm for the load P₁ = 12.9 kN, and that the sphere had radius R₁ = 38.1 mm (or D₁ = 76.2 mm) as presented by Orlov and Pinegin (1971, p. 54). Hence, only one experimental measurement was used to obtain all rescaling values in Table 3.2. One can see that formula (3.99) describes the experiments quite well.

Adhesion and adhesive contact problems have been studied for a long time. Adhesion is a universal physical phenomenon that usually has a negligible effect on surface interactions at the macroscale, whereas it becomes increasingly significant as the contact size decreases (Kendall, 2001). The term “adhesion” may have rather different meanings. It may be used to denote both the strong chemical bonds between surfaces and weak connections due to van der Waals forces. Other physical mechanisms of adhesion (e.g., adhesion due to electrical double layer charges) are also possible (Deryagin, Krotova, & Smilga, 1978). In addition, contact problems with nonslipping boundary conditions are often called adhesive contact problems (Mossakovskii, 1963; Spence, 1968).

Here forces of chemical bonding are not studied, and only molecular adhesion caused by van der Waals forces is considered. The distinction of these forces is somewhat artificial, because all of these forces are electrical in nature (Deryagin et al., 1978; Kiselev, Kozlov, & Zoteev, 1999; Parsegian, 2005); however, this distinction is very convenient because the interaction energies are rather different. The same distinction is usually introduced for studying phenomena of adsorption of a single molecule to a surface, where it is customary to divide adsorption into physical adsorption (physisorption) and chemisorption. The binding forces for physisorption are relatively weak, while the term “chemisorption” is used if the adsorption energy is large enough to be comparable to chemical bond energies. To study contact problems with molecular adhesion, one needs to know the work of adhesion w, which is equal to the energy needed to separate two dissimilar surfaces from contact to infinity (if the materials are identical, then adhesion is called cohesion). In other words, w is the work of adhesion that is equal to the tensile force integrated over the distance necessary to pull the two surfaces completely apart (Harkins, 1919).

5.1.2 Historical Preliminaries

Apparently, the first scientific discussion of the adhesion phenomenon is due to Robert Hooke. Observing liquors, syrups, and other “tenacious and glutinous bodies,” he wrote (Hooke, 1667) “it is evident, that the Parts of the tenacious body, as I may so call it, do stick and adhere so closely together, that though drawn out into long and very slender Cylinders, yet they will not easily relinquish one another… And this Congruity (that I may here a little further explain it) is both a Tenaceous and an Attractive power; for the Congruity, in the Vibrative motions, may be the cause of all kind of attraction, not only Electrical, but Magnetical also, and therefore it may be also of Tenacity and Glutinousness“.

In 1873 van der Waals discovered a property of molecules to attract each other and wrote that he had “come to the conclusion that attraction of the molecules decreases extremely quickly with distance, indeed that the attraction only has an appreciable value at distances close to the size of the molecules“ (van der Waals, 1910). Maxwell (1874) gave a very great appraisal of the van der Waals results and agreed that attraction is considered at short distances, but that molecules repel each other on a closer approach. Peter Lebedev gave the first electromagnetic explanation for van der Waals forces (Lebedew, 1894). However, only after the introduction of quantum mechanics by M. Planck were modern descriptions of the various kinds of attractive forces given by Debye, London, and Keesom (Parsegian, 2005). The attractive forces are collectively called van der Waals forces. The term includes attraction between two permanent dipoles (Keesom force), a permanent dipole and a corresponding induced dipole (Debye force), and two instantaneously induced dipoles (London dispersion force).

Bradley (1932) was the first to conside attraction between two absolutely rigid spheres. Taking into account only one of the components of the van der Waals forces, namely, the London dispersion force, he calculated pointwise the attraction of each point of one sphere to another one. Assuming additivity of the London forces, he calculated the total adhesive force between the spheres P_c. Although strictly speaking the London forces are not additive (Derjaguin, Abrikosova, & Livshitz, 1958), the assumption of additivity of the forces is usually considered as acceptable (Deryagin et al., 1978).

In 1934 Derjaguin published a series of papers (see, e.g., Derjaguin, 1934a, 1934b) where he studied the influence of adhesion on friction and contact between elastic solids. Developing his molecular theory of external friction, Derjaguin (1934a) referred to results of W Hardy from 1922, K. Terzagh from 1925, and G. Tomlinson from 1929; and developing his theory of adhesion, Derjaguin (1934b) referred not only to Tomlinson but also to Bradley (1932). Derjaguin (1934b) pointed out that to calculate adhesive interactions between particles, one needs to take into account the deformations of the particles. Derjaguin (1934b) presented the first attempt to consider the problem of adhesion between elastic spheres or between an elastic sphere and an elastic half-space. He assumed that the deformed shape of the sphere can be calculated by solving the Hertz contact problem, and suggested calculating the adhesive interaction by using only attraction between points at the surfaces of the solids and by introduction of the work of adhesion (this is the so-called Derjaguin approximation).

In fact, the Derjaguin approximation (see Derjaguin, 1934b, p. 156) can be formulated as follows:

1. instead of the pairwise summation of the interactions between the elements of solids, the volume molecular attractions are reduced to surface interactions;

2. the surface interactions are taken into account only between the closest elements of the surfaces lying on vertical straight lines; and

3. the interaction energy per unit area between small elements of curved surfaces is the same as the interaction energy per unit area energy between two parallel infinite planar surfaces.

The expression for adhesion between rigid spheres Pc was obtained by Bradley (1932) after rather lengthy calculations. He needed to perform pointwise calculations of the London forces similar to calculations of gravitational forces by I. Newton; however, the adhesive forces did not decrease as gravitational forces, i.e., as 1/r² (I. Newton learned of this law of gravity from a letter written by R. Hooke; see Arnold (1990)), but rather as 1/r⁷. The same result can be obtained in just one line using the Derjaguin approximation. Indeed, using the Hertz approximation, one can replace a sphere of radius R by a paraboloid of revolution δ = f(r) = B₂r², where B₂ = 1/(2R). Then, applying the Derjaguin approximation, one obtains

$\begin{array}{ll}{P}_{\text{c}}\hfill & ={\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_0^{\infty }{p}_{\text{a}}\left[z\left(r\right)\right]r\text{d}r\text{d}ɸ}}=2\pi R{\displaystyle {\int }_0^{\infty }{p}_{\text{a}}\left(z\right)·\text{d}z}=2\pi Rw,\hfill \\ w\hfill & ={\displaystyle {\int }_0^{\infty }{p}_{\text{a}}\left(z\right)\text{d}z}.\hfill \end{array}$

  (3.122)

Here p_a(z) is the adhesive force per unit area between flat surfaces separated by a distance z.

Starting from pioneering papers of Derjaguin (1934a, 1934b), the mechanics of adhesive contact between isotropic elastic solids developed into a well-established branch of science. The Derjaguin approximation is implicitly involved in many modern models of adhesive contact (however, these assumptions are usually used without referring to Derjaguin).

5.2.2 Sperling Model of Adhesive Contact

Unfortunately, some of Derjaguin’s assumptions and calculations were not correct. For example, Derjaguin’s assumption about the shape of deformed solids was not correct (in fact, he was not consistent in application of his approach). Nevertheless, his basic argument was correct because it equated the work done by the surface attractions against the work of deformation in the elastic spheres (see Kendall, 2001, p. 183).

In 1964 Sperling presented his Ph.D. thesis devoted mainly to the development of a model of adhesion between rough particles. In his thesis, Sperling (1964) discussed not only ideas introduced by Derjaguin (1934b), Lifshiz (Derjaguin et al., 1958; Parsegian, 2005), and Rumpf (1990), but also developed statistical models of adhesive contact between rough particles and studied the influence of plastic and viscoelastic effects on adhesion. It is known (see, e.g., Rabinovich, Adler, Ata, Singh, & Moudgil, 2000) that the Rumpf model is based on an application of the Derjaguin approximation to adhesion between rough rigid particles. However, adhesion between an elastic half-space and a sphere of radius R was also studied (see Sperling, 1964, pp. 69–78). Employing the Derjaguin idea that the virtual work done by the external load is equal to the sum of the virtual change of the potential elastic energy and the virtual work that will be consumed by the increase of the surface attractions (see (21) in Derjaguin, 1934b), Sperling wrote the following expression for the total potential energy U of the contact system:

$U=\frac{2\mu }{15R^2}\frac{m}{m-1}\left(3a^5+10R\delta a^3+15R^2{\delta }^{2}a\right)-\pi a^{2}w-P\delta +C,$

  (3.123)

where a is the contact radius, m = 1/ν, μ is the shear modulus of the material, C is an arbitrary constant, and P is the external load. In his calculations he used the solution presented by Jung (1950).

Sperling noted that equilibrium is observed when the energy is a minimum. By differentiating Eq. (3.124), he derived the following two expressions (see (88) and (89) in Sperling, 1964):

$\delta =\alpha \sqrt{a}-\frac{a^2}{R},\alpha =\sqrt{\frac{\pi w}{\mu }\frac{m-1}{m}},$

  (3.124)

and

$\delta =\beta \frac{1}{a}-\frac{a^2}{3R},\beta =\frac{P}{4\mu }\frac{m-1}{m}.$

  (3.125)

Expressions (3.124) and (3.125) and the corresponding dimensionless load-displacement curve were analyzed. In particular, it was found that the maximum value of the tensile force is equal to the separation force (see (93) in Sperling, 1964)

$F_{\text{sep}}=\frac{3}{2}\pi Rw,$

  (3.126)

and that at P = 0 the corresponding contact radius a₀ and displacement δ₀ are

$a_0={\left(2R^{2}M\right)}^{1/3},{\delta }_0=-4{\left(R{M}^2/27\right)}^{1/3},M=\frac{9\pi w}{8\mu }\frac{m-1}{m}.$

  (3.127)

Note that by using the Poisson ratio ν instead of m, one can present Eqs. (3.125) and (3.124) as

$\delta =\sqrt{\frac{2\pi wa}{E^{*}}}-\frac{a^2}{R}=\frac{P}{2E^{*}a}-\frac{a^2}{3R},$

  (3.128)

or

$P=-\frac{4E^{*}{a}^3}{3R}+\sqrt{8\pi E^{*}w{a}^3}.$

  (3.129)

5.2.3 The JKR Theory of Adhesive Contact

Johnson (1958) attempted to solve the adhesive contact problem for spheres by adding two simple stress distributions, namely, the Hertz stress field to a rigid flat-ended punch tensile stress distribution. Johnson argued that the infinite tension at the periphery of the contact would ensure that the spheres would peel apart when the compressive load was removed. Although Johnson’s conclusion about impossibility of adhesive contact was not correct, his suggestion to superpose the stress fields is very fruitful.

According to Kendall (2001, pp. 185–186), the JKR theory was developed historically in the following steps. In 1970 Kendall and Roberts discussed the experimental observations that the contact spots were larger than expected from the Hertz equation. They found “that the answer lay in applying Derjaguin’s method … to Johnson’s stress distribution.” Johnson presented a mathematical realization of this idea an evening later. Johnson et al. (1971) applied Derjaguin’s idea to equate the work done by the surface attractions against the work of deformation in the elastic spheres, to Johnson’s stress superposition, and created the famous JKR theory of adhesive contact. The JKR approach is based on the use of a geometrically linear formulation of the contact problem, and a combination of both the Hertz contact problem for two elastic spheres and the Boussinesq relation for a flat-ended cylindrical indenter.

If there were no surface forces of attraction, the radius of the contact area under a punch subjected to the external load P₀ would be a₀, and it could be found by solving the Hertz-type contact problem. However, in the presence of the forces of molecular adhesion, the equilibrium contact radius a₁ would be greater than a₀ under the same force P₀.

Johnson et al. (1971) suggested considering the total energy of the contact system U_T as made up of three terms: the stored elastic energy U_E, the mechanical energy in the applied load U_M, and the surface energy U_S. It is assumed that the contact system has come to its real state in two steps: (1) first it has a real contact radius a₁ and an apparent depth of indentation δ₁ under some apparent Hertz load P₁, and then (2) it is unloaded from P₁ to a real value of the external load P₀, keeping the contact radius a₁ constant (Fig. 3.6). The Boussinesq solution for contact between an elastic half-space and a flat punch of radius a₁ may be used in the latter step.

In this case, one can calculate U_E as the difference between the stored elastic energies (U_E)₁ and (U_E)₂ in the loading and unloading branches, respectively. Therefore,

${\left(U_{\text{E}}\right)}_1=P_1{\delta }_1-{\displaystyle {\int }_0^{P_1}\delta \text{d}P}.$

  (3.130)

Using the Boussinesq solution (Eq. 3.41), we obtain for the unloading branch

${\left(U_{\text{E}}\right)}_2={\displaystyle {\int }_{P_0}^{P_1}\frac{P}{2E^{*}{a}_1}\text{d}P}=\frac{P_1^2-P_0^2}{4E^{*}{a}_1}.$

  (3.131)

Thus, the stored elastic energy U_E is

$U_{\text{E}}={\left(U_{\text{E}}\right)}_1-{\left(U_{\text{E}}\right)}_2.$

  (3.132)

The mechanical energy in the applied load is given by

$U_{\text{M}}=-P_0{\delta }_2=-P_0\left({\delta }_1-\text{Δ}\delta \right),$

  (3.133)

where Δδ = δ₁ − δ₂ is the change in the depth of penetration due to unloading.

Since only the surface adhesive interactions within the contact region are taken into account (one disregards the adhesive forces acting outside the contact region), the surface energy can be written as

$U_{\text{S}}=-w\pi a_1^2.$

  (3.134)

The total energy U_T can be obtained by summation of Eqs. (3.132), (3.133), and (3.134), i.e.,

$U_{\text{T}}=U_{\text{E}}+U_{\text{M}}+U_S.$

  (3.135)

It is assumed in the JKR model that the equilibrium at contact satisfies the equation

$\frac{\text{d}{U}_{\text{T}}}{\text{d}{a}_1}=0,\text{or}\frac{\text{d}{U}_{\text{T}}}{\text{d}{P}_1}=0.$

  (3.136)

The above was applied to the case of the initial distance between contacting solids described by a paraboloid of revolution z = r²/(2R) (this is a very good approximation for a sphere). In the framework of the JKR theory, the following relations between the external load P₀ acting on the spheres and the adhesive contact radius a₁ were obtained:

$P_0=\left(4E^{*}/3R\right)a_1^3-\sqrt{8\pi w{E}^{*}{a}_1^3}$

  (3.137)

and

${\delta }_2=a_1^2/R-\sqrt{2\pi w{\left(E^{*}\right)}^{-1}{a}_1},$

  (3.138)

where R is the effective radius of the spheres (1/R = 1/R₁ + 1/R₂).

Equations (3.138) and (3.137) are exactly the same (up to the sign convention used by Sperling) as the Eqs. (3.128) and (3.129) that follows from the Sperling (1964) model. This is the reason that sometimes (see, e.g., Johnson & Pollock, 1994) the JKR theory is referred to as the JKRS theory.

It follows from the model that the instability point P_c of a P-δ curve is at the point where dP/dδ = 0, i.e.,

$P_{\text{c}}=-\frac{3}{2}\pi \mathit{wR},$

  (3.139)

and dP/dδ is infinite at another special point of the P-δ curve:

${\delta }_{\text{c}}=\frac{3}{4}{\left(\frac{{\pi }^2{w}^{2}R}{{\left(E^{*}\right)}^2}\right)}^{1/3}>0.$

  (3.140)

Evidently P_c is the same as F_sep from Eq. (3.126) up to the sign convention used by Sperling (1964).

5.2.4 The DMT, Maugis, and Other Theories of Adhesive Contact

As mentioned above, we concentrate here mainly on the JKR theory. The theory has been very well verified for elastomers and other materials (Maugis & Barquins, 1983). However, the adhesive forces can be taken into account by various other methods, e.g., (1) by pointwise integration of the interaction forces between points of the bodies, whose interaction energy is proportional to ρ⁻⁶, where ρ is the distance between the points; (2) by using the Derjaguin approximation; (3) by introducing an interaction potential between points on the surfaces, e.g., a Lennard–Jones potential (see, e.g., Borodich & Galanov, 2004; Muller, Yushchenko, & Derjaguin, 1980); or (4) by using piecewise-constant approximations of these potentials (Goryacheva & Makhovskaya, 2001, 2008; Johnson, 1997; Maugis, 1992; Zheng & Yu, 2007).

Nowadays there are several well-established classic models of adhesive contract, which include not only the JKR theory, but also the DMT theory and the Maugis transition solution between the JKR and DMT theories (Maugis, 1992). A detailed description of the theories is given by Maugis (2000); see also discussions by Johnson (1997) and Barthel (2008). However, one could get the wrong impression that the adhesive contact problems were not studied after the publication of the papers by Bradley (1932) and Derjaguin (1934a, 1934b) until 1971, when a famous paper was published by Johnson et al. (1971). In fact, this topic was an active area of research. See, e.g., an extended review by Krupp (1967) and references in the book by Rumpf (1990).

One can see that the adhesive force (Eq. 3.139) derived by Johnson et al. (1971) does not match the value (Eq. 3.122). This fact provided a reason for Derjaguin to criticize the JKR model. Perhaps his criticism was overdone, but one has to note that Derjaguin’s papers were not cited by Johnson et al. (1971). Derjaguin et al. (1975) presented an alternative to the JKR model, and this is usually referred to as the DMT model. The difference between the JKR and DMT theories was first explained by Tabor (1977), who noted that both theories have drawbacks: the DMT theory disregards the deformations of the shape of the contacting solids near the edge of the contact region, while the JKR theory disregards the attractive forces outside the contact region. He noted also that in the JKR model the contacting solids near the edge of the contact region form a “neck,” and hence the gap increases quickly and, in turn, the attractive force decreases very quickly. Tabor introduced a parameter μ that can be used to check whether the JKR model or the DMT models is applicable. Eventually, Muller et al. (1980) agreed with Tabor’s arguments, and using numerical simulations, they showed that the JKR theory and the DMT theory are at different limits of a parameter similar to the Tabor parameter. The historical development of the DMT theory is discussed in detail by Maugis (1992, 2000), Greenwood (1997, 2007), and Barthel (2008).

Calculating the Tabor–Muller–Maugis parameter (Maugis, 1992, 2000; Muller et al., 1980; Tabor, 1977; see also Greenwood, 2007)

$\mu ={\left(\frac{R_{\text{ef}}{w}^2}{{\left(E^{*}\right)}^2{z}_0^3}\right)}^{1/3},$

  (3.141)

one can check whether μ 1, and hence if the experiment is in the range of applicability of the JKR model, or whether μ 1, and hence if one needs to apply the DMT model. Here R_ef is the effective radius and z₀ is the equilibrium distance between atoms of the contacting pair, which is usually between 0.3 and 0.5 nm.

Using the Derjaguin idea that all adhesive interactions can be attributed to the surface, Muller et al. (1980) performed numerical simulations of adhesive contact using the Lennard–Jones potential. On the basis of the ideas discussed by Tabor (1977) and Muller et al. (1980), Maugis (1992, 2000) developed an analogy between the fracture mechanics approaches and the mechanics of frictionless adhesive contact. Maugis (1992) suggested modeling the attractive forces outside the contact area as a step function of some length ∇. The idea of the step-function approximation was borrowed by Maugis (1992) from Dugdale (1960). The Maugis theory considers the adhesive contact region as consisting of the following parts: in the inner part of radius a a close contact is maintained that is described by the Hertz and Boussinesq theory; in the outer part (the annulus a < r < a + ∇) adhesive attractive forces of constant intensity σ₀ are acting, but there is a gap between surfaces that increases from zero to some distance h₀. It is assumed that no attractive forces act in the region r > a + ∇. A very brief and precise description of the Maugis theory (the Maugis transition solution between the JKR and DMT theories) was given by Johnson (1997). As Johnson (1997) noted, to match the work of adhesion w and the maximum force σ₀ with those of the Lennard–Jones potential, one has to take h₀ = 0.971 z₀.

In fact, Maugis (1992) did not use the Tabor parameter because he introduced the parameter λ_M

${\lambda }_{\text{M}}=\frac{2}{0.97\pi }\sqrt[3]{\frac{4}{3}}\frac{{\delta }_{\text{c}}}{z_0}\approx 0.73\frac{{\delta }_{\text{c}}}{z_0}.$

  (3.142)

Maugis (2000) estimated that the DMT theory corresponds to small values of λ_M (λ_M < 0.1), while the JKR theory corresponds to large values of λ_M (λ_M > 5).

To describe a theory of adhesive contact in a dimensionless way, one needs to select characteristic scales of the contact problem for the force and the displacement at low loads and small displacements. These scales can be chosen arbitrary using the problem governing parameters w, E*, and the effective radius R_ef. The conditions P_c > 0 and δ_c > 0 defined by Eqs. (3.139) and (3.140) can be taken as such characteristic scales. If the JKR model is employed, then the force scale P_c has a clear physical meaning: it is the theoretical absolute value of the pull-off force in the framework of the JKR model. However, for other models, it is just a scaling parameter.

Maugis (1992) showed that for each value of the parameter λ_M, the graph of the functional relation P–δ is situated between the corresponding graphs for the JKR and DMT theories. Hence, the above-mentioned theories of adhesive contact of spheres can be represented as a dimensionless functional P–δ relation of the following type:

$F\left(\frac{P}{P_c},\frac{\delta }{{\delta }_{\text{c}}},{\lambda }_{\text{M}}\right)=0,P_{\text{c}}\ge 0,{\delta }_{\text{c}}\ge 0,$

  (3.143)

where F is given by the Maugis theory, which includes the JKR and DMT theories. The Maugis parameter λ_M represents the most suitable theory for the contacting materials and indenters.

The original DMT model did not have such a form. However, Maugis (2000) modified it, and the functional expression (3.143) for the DMT model in Maugis’s interpretation is

$F\left(\frac{P}{P_{\text{c}}},\frac{\delta }{{\delta }_{\text{c}}}\right)\equiv \frac{P}{P_{\text{c}}}-\frac{1}{\sqrt{3}}{\left(\frac{\delta }{{\delta }_{\text{c}}}\right)}^{3/2}+\frac{4}{3}=0.$

  (3.144)

The JKR model can be expressed as (Borodich et al., 2013; Maugis, 2000)

$F\left(\frac{P}{P_{\text{c}}},\frac{\delta }{{\delta }_{\text{c}}}\right)\equiv \{\begin{array}{l}\left(3\chi -1\right){\left(\frac{1+\chi }{9}\right)}^{1/3}-\frac{\delta }{{\delta }_{\text{c}}}=0,\chi \ge 0,\delta /{\delta }_{\text{c}}\ge -3^{-2/3},\hfill \\ -\left(3\chi -1\right){\left(\frac{1+\chi }{9}\right)}^{1/3}-\frac{\delta }{{\delta }_{\text{c}}}=0,\frac{2}{3}\ge \chi \ge 0,-1\le \delta /{\delta }_{\text{c}}<-3^{-2/3},\hfill \end{array}$

  (3.145)

where $\text{χ}=\sqrt{1+P/P_{\text{c}}}$.

The generality of the Maugis theory is the main reason that it is often considered as the general model of adhesive contact (Zheng & Yu, 2007; Zhou, Gao, & He, 2011). However, further generalizations are also possible. For example, Goryacheva and Makhovskaya (2008) suggested approximating the potential of the attractive forces in the outer part of the contact region as several step functions.

5.3.1 The JKR Theory for an Arbitrary Axisymmetric Indenter

Let us generalize the JKR model of contact with molecular adhesion and consider the case of the distances between the contacting solids being described as arbitrary convex axisymmetric functions.

For an arbitrary axisymmetric solid, one can calculate U_E as the difference between the stored elastic energies (U_E)₁ and (U_E)₂ in the loading OA and unloading AB branches, respectively (Fig. 3.6). Therefore, the stored elastic energy U_E is defined by Eq. (3.130), the mechanical energy in the applied load is described by Eq. (3.133), and the surface energy can be written as Eq. (3.134).

Taking into account the Boussinesq solution (Eq. 3.41), one obtains for the unloading branch

$\text{Δ}\delta =\frac{P_1-P_0}{2K^{*}{a}_1},\text{or}{P}_1-P_0=2K^{*}{a}_1\text{Δ}\delta ,$

  (3.146)

and therefore, one has

$U_{\text{M}}=-P_0\left({\delta }_1-\frac{P_1-P_0}{2K^{*}{a}_1}\right)\text{and}{\left(U_{\text{E}}\right)}_2=\frac{P_1^2-P_0^2}{4K^{*}{a}_1}.$

According to the Derjaguin assumptions, the adhesive interactions are reduced to the surface forces acting perpendicularly to the boundary of the half-space. The JKR theory considers only the adhesive forces acting within the contact region, which is always a circle, and the surface energy can be written as U_S = −π a²₁w. Hence, the total energy U_T can be written as

$U_{\text{T}}=P_1{\delta }_1-{\displaystyle {\int }_0^{P_1}\delta \left(P\right)\text{d}P}-\frac{\left(P_1^2-P_0^2\right)}{4K^{*}{a}_1}-P_0{\delta }_1+P_0\frac{\left(P_1-P_0\right)}{2K^{*}{a}_1}-w\pi a_1^2$

or

$U_{\text{T}}=\left(P_1-P_0\right){\delta }_1-{\displaystyle {\int }_0^{P_1}\delta \left(P\right)\text{d}P}-\frac{{\left(P_1-P_0\right)}^2}{4K^{*}{a}_1}-w\pi a_1^2.$

  (3.147)

Taking into account the expressions

$\frac{\text{d}}{\text{d}{P}_1}\left[\left(P_1-P_0\right){\delta }_1\right]=\left(P_1-P_0\right)\frac{\text{d}{\delta }_1}{\text{d}{P}_1}+{\delta }_1,\frac{\text{d}}{\text{d}{P}_1}{\displaystyle {\int }_0^{P_1}\delta \left(P\right)\text{d}P}=\delta \left(P_1\right)={\delta }_1,$

and

$\frac{\text{d}}{\text{d}{P}_1}\frac{{\left(P_1-P_0\right)}^2}{4K^{*}{a}_1}=\frac{\left(P_1-P_0\right)}{2K^{*}{a}_1}-\frac{{\left(P_1-P_0\right)}^2}{4K^{*}{a}_1^2}\frac{\text{d}{a}_1}{\text{d}{P}_1},$

and applying the equilibrium condition (3.136) to (3.147), one obtains

$\frac{\text{d}{U}_T}{\text{d}{P}_1}=\left(P_1-P_0\right)\frac{\text{d}{\delta }_1}{\text{d}{P}_1}-\frac{\left(P_1-P_0\right)}{2K^{*}{a}_1}+\left[\frac{{\left(P_1-P_0\right)}^2}{4K^{*}{a}_1^2}-2w\pi a_1\right]\left(\frac{\text{d}{a}_1}{\text{d}{P}_1}\right)=0.$

  (3.148)

Owing to the expressions (Eq. 3.77) of Theorem 1, one obtains from Eq. (3.148) that the equilibrium condition for the general JKR model is

$\frac{\text{d}{U}_T}{\text{d}{P}_1}=\left[\frac{{\left(P_1-P_0\right)}^2}{4K^{*}{a}_1^2}-2w\pi a_1\right]\frac{\text{d}{a}_1}{\text{d}{P}_1}=0,$

  (3.149)

or

${\left(P_1-P_0\right)}^2=8\pi w{K}^{*}{a}_1^3$

  (3.150)

Because of Eqs. (3.146) and (3.150), one has

$P_1-P_0=\sqrt{8\pi w{K}^{*}{a}_1^3}=2K^{*}{a}_1\text{Δ}\delta ,$

and hence the following expression is valid:

$\text{Δ}\delta =\sqrt{\frac{2\pi w{a}_1}{K^{*}}}.$

Thus, for an arbitrary convex body of revolution f(r), f(0) = 0, the general JKR theory leads to the following expressions:

$P_1=P_0+\sqrt{8\pi w{K}^{*}{a}_1^3},{\delta }_2={\delta }_1-\sqrt{\frac{2\pi w{a}_1}{K^{*}}}.$

  (3.151)

Taking into account formulae (3.49) and (3.52), the relations (3.151) can be written as

$P_0=P_1-\sqrt{8\pi w{K}^{*}{a}_1^3}=2K^{*}{\displaystyle {\int }_0^{a_1}\frac{r^2{f}^{\prime }\left(r\right)\text{d}r}{\sqrt{a_1^2-r^2}}}-\sqrt{8\pi w{K}^{*}{a}_1^3}$

  (3.152)

and

${\delta }_2={\displaystyle {\int }_0^{a_1}\frac{f^{\prime }\left(r\right)}{\sqrt{1-r^2/a_1^2}}\text{d}r}-{\left(\frac{2\pi w{a}_1}{K^{*}}\right)}^{1/2}.$

  (3.153)

We remember that according to the notation introduced by Johnson et al. (1971), the actual force, the actual contact radius, and the actual approach between contacting bodies are denoted by P₀, a₁, and δ₂, respectively.

5.3.2 The JKR Theory for Axisymmetric Monomial Indenters

For punches described by Eq. (3.53), the solution of the nonadhesive frictionless Hertz-type contact problem is given by

$a_0={\left(\frac{P_0}{C\left(d\right)E^{*}{B}_d}\right)}^{1/\left(d+1\right)},C\left(d\right)=\frac{d^2}{d+1}{2}^{d-1}\frac{{\left[\text{Γ}\left(d/2\right)\right]}^2}{\text{Γ}\left(d\right)},$

  (3.154)

and the contact radius a₁ and depth of indentation δ₁ under some apparent Hertz load P₁ are given by

$a_1={\left(\frac{P_1}{C\left(d\right)E^{*}{B}_d}\right)}^{1/\left(d+1\right)},{\delta }_1={\left[\frac{C\left(d\right)B_d}{{\left(E^{*}\right)}^d}\right]}^{\frac{1}{d+1}}\left(\frac{d+1}{2d}\right)P_1^{d/\left(d+1\right)}.$

  (3.155)

Using Eqs. (3.154) and (3.155), one obtains an exact formula giving a relation between the real load P₀ and the real radius of the contact region a₁ (Borodich, 2008; Borodich & Galanov, 2004; Borodich, Galanov, Keer, & Suarez-Alvarez, 2014; Borodich, Galanov, & Suarez-Alvarez, 2014; see also Galanov, 1993):

$P_0=P_1-\sqrt{8\pi w{K}^{*}{a}_1^3}=C\left(d\right)B_d{E}^{*}{a}_1^{d+1}-\sqrt{8\pi w{K}^{*}{a}_1^3}.$

  (3.156)

The real displacement of the punch is δ₂ = (δ₁ − Δδ), i.e.,

${\delta }_2=B_{d}C\left(d\right)\frac{d+1}{2d}{a}_1^d-{\left(\frac{2\pi w{a}_1}{E^{*}}\right)}^{1/2}.$

  (3.157)

In fact, Eqs. (3.156) and (3.157) are particular cases of Eqs. (3.152) and (3.153).

It is convenient to write the formula for the real displacement δ₂ in the case of a frictionless boundary condition as

${\delta }_2=\frac{B_{d}C\left(d\right)}{2d}{a}_1^d\left[1+d\frac{P_0}{P_1}\right].$

Zheng and Yu (2007) suggested writing relations (3.156) and (3.157) using the Euler beta function B(x, y) of variables x and y. Indeed, the expression (3.154) for C(d) can be written as

$C\left(d\right)=\frac{d^2}{d+1}\mathbf{B}\left(\frac{d}{2},\frac{1}{2}\right)=d\mathbf{B}\left(1+\frac{d}{2},\frac{1}{2}\right).$

Then one can write

$P_0=d{B}_d\mathbf{B}\left(1+\frac{d}{2},\frac{1}{2}\right)E^{*}{a}_1^{d+1}-\sqrt{8\pi w{E}^{*}{a}_1^3},$

  (3.158)

${\delta }_2=\frac{d{B}_d}{2}\mathbf{B}\left(\frac{d}{2},\frac{1}{2}\right)a_1^d-{\left(\frac{2\pi w{a}_1}{E^{*}}\right)}^{1/2}.$

  (3.159)

The Papkovich–Neuber formalism and the Galin solution were used in application to the mechanics of adhesive contact. In particular, Zheng and Yu (2007), Zhou et al. (2011) considered the JKR and Maugis–Dugdale contact problems for power-law-shaped solids. As Zheng and Yu (2007) noted, their solution to the JKR problem for power-law-shaped solids coincides with the solution obtained by Borodich and Galanov (2004). If one denotes Q = dB_d and Δγ = w, then formulae (33) and (34) presented by Zheng and Yu (2007) in dimensional form coincide with Eqs. (3.158) and (3.159). Naturally the solution of Zhou et al. (2011) for the JKR theory coincides with the solutions by Zheng and Yu (2007) and by Galanov (1993) and Borodich, Galanov (2004). Although just the formula for the contact load was presented in the short abstract by Borodich and Galanov (2004), both formulae were presented by Galanov (1993). However, Galanov (1993) and Galanov, Grigor’ev (1994) used a different way for normalization of the variables.

Hence, for an arbitrary convex body of revolution f(r), f(0) = 0, the JKR theory leads to Eq. (3.151) or Eq. (3.152) and Eq. (3.153) (compare with previous attempts to solve this problem by Maugis & Barquins, 1983, and Maugis, 1995).

5.4.1 The Nonslipping Boussinesq–Kendall Adhesive Contact Problem

Consider an axisymmetric flat-ended punch of radius a₁ that is vertically pressed into an elastic half-space. The frictionless case of this problem was considered by Boussinesq (1885), nonslipping contact was studied by Mossakovskii (1954), and frictionless contact with molecular adhesion was studied by Kendall (1971). Let us consider the problem with non-slipping boundary conditions and taking into account molecular adhesion (Borodich, 2011; Borodich, Galanov, & Suarez-Alvarez, 2014). Then the arguments of Kendall (1971) have to be slightly modified.

In this problem the boundary conditions for radial displacements within the contact region 0 ≤ r ≤ a₁ have the following form:

$u_r\left(r\right)=0,0\le r\le a_1.$

  (3.160)

The elastic material deforms according to the corrected Mossakovskii equation (Eq. 3.64), which can be presented as

$\delta =\frac{P}{2E^{*}{C}_{\text{NS}}{a}_1}.$

  (3.161)

As one can see from Eq. (3.41), the equation has the same form as the one for the frictionless case (the Boussinesq solution) with C_NS equal to unity.

The surface energy is given as above by Eq. (3.134). Using Eq. (3.161), one obtains that the stored elastic energy U_E and the mechanical energy of the applied load U_M are, respectively,

$U_{\text{E}}={\displaystyle {\int }_0^{P_0}P\text{d}\delta }=\frac{P^2}{4E^{*}{C}_{\text{NS}}{a}_1},U_{\text{M}}=-P_0\delta =-\frac{P^2}{2E^{*}{C}_{\text{NS}}{a}_1}.$

  (3.162)

The total energy U_T can be obtained by summation of all components given by Eq. (3.134) and Eq. (3.162):

$U_{\text{T}}=-w\pi a_1^2-\frac{P^2}{4E^{*}{C}_{\text{NS}}{a}_1}.$

  (3.163)

From the equilibrium equation (3.136), one has

$\frac{\text{d}{U}_{\text{T}}}{\text{d}{a}_1}=0=-2w\pi a_1+\frac{P_c^2}{4E^{*}{C}_{\text{NS}}{a}_1^2},$

  (3.164)

and hence one may obtain the adhesive force (the pull-off force) of a flat-ended circular punch of radius a₁ at the nonslipping boundary conditions:

$P_{\text{c}}=\sqrt{8\pi w{E}^{*}{C}_{\text{NS}}{a}_1^3}.$

  (3.165)

Thus, one can see from Eq. (3.165) that the adhesive force is proportional neither to the energy of adhesion nor to the area of the contact. Maugis (2000) came to the same conclusion for the frictionless Boussinesq–Kendall problem.

5.4.2 Energy Approach in the Nonslipping Case

Let us calculate the total energy of the system with nonslipping conditions. As explained above, it is attempted here to follow the original JKR approach as closely as possible, avoiding the resolution of interfacial tractions. However, one needs to provide the clear rationale for the extension of the frictionless JKR approach to the case of nonslipping contact conditions. The work W of the external forces, which include the surface tractions, the body forces, and the applied load, can be written as

$W={\displaystyle {\int }_S{T}_i{u}_i\text{d}S}+{\displaystyle {\int }_V{X}_i{u}_i\text{d}V}+U_{\text{M}},$

and according to Clapeyron’s theorem, it is stored in the linear-elastic body in the form of the strain energy (see, e.g., Lurie, 2005). Here T_i are the surface tractions, X_i are the body forces, and S and V are the surface and the body volume, respectively. The body forces in the problem under consideration are the adhesive forces. Because in the nonslipping case both the normal and radial tractions exist over the contact region, formally the work of radial surface tractions (U_E)₃ should be added to the expression for the stored elastic energy:

${\displaystyle {\int }_S{T}_i{u}_i\text{d}S}={\left(U_{\text{E}}\right)}_1-{\left(U_{\text{E}}\right)}_2+{\left(U_{\text{E}}\right)}_3,{\left(U_{\text{E}}\right)}_3={\displaystyle {\int }_S{T}_r{u}_r\text{d}S}.$

As already mentioned, one can use the superposition of two contact solutions for linear elastic materials if the contact region 0 ≤ r ≤ a₁ is fixed. Hence, the tangential stresses in the nonslipping contact problem can be obtained as the difference between the tangential stress field τ_M(r) of the Mossakovskii (or Mossakovskii–Spence) type problem (this is the Hertz-type contact problem with nonslipping boundary conditions) for the punch loaded by P₁ and the tangential stress field τ_B(r) of the Boussinesq–Mossakovskii contact problem after the unloading from P₁ to P₀, i.e., τ(r) = τ_M(r) − τ_B(r). Here the subscripts M and B denote variables associated with the Mossakovskii–Spence-type and the Boussinesq–Mossakovskii contact problems, respectively. Owing to the conditions (3.62), the differentials of the work done by the tangential tractions during increase of P from 0 to P₁ and then during decrease from P₁ to P₀ are zero, and hence the work of the tangential surface tractions (U_E)₃ = 0.

As already mentioned, the work of the external body forces in the problem under consideration is the work done by the adhesive forces. Here it is assumed that the Derjaguin approximation is valid, i.e., the adhesive interactions are reduced to the surface forces acting perpendicularly to the boundary of the half-space, and therefore the work of the surface adhesive forces on radial displacements is equal to zero. Thus, in the framework of the above assumptions, the JKR expression for the total energy is

$U_{\text{T}}={\left(U_{\text{E}}\right)}_1-{\left(U_{\text{E}}\right)}_2+U_{\text{M}}+U_{\text{S}},$

  (3.166)

and the problem is reduced to the classic JKR approach; however, the expressions for the components in Eq. (3.166) should be found from corresponding problems using the Mossakovskii–Spence formulation.

Comment. There are other approaches to problems of adhesive contact where the above assumptions are not accepted and the work of the surface adhesive forces on radial displacements is not equal to zero.

5.4.3 Nonslipping JKR Problem for Monomial Indenters

Let us assume the external parameter P of the Hertz-type contact problem is gradually increased. It follows from Theorem 6 for the Mossakovskii–Spence-type contact problems, i.e., the problem is axisymmetric, the materials are linear (κ = 1), and the boundary conditions are nonslipping (Eq. 3.62), that the following rescaling formulae are valid for the surface displacements u_r(r, 0, P):

$u_r\left(r,0,P\right)={\lambda }^{-d}{u}_r\left(\lambda r,0,P_I\right),\delta \left(P\right)={\lambda }^{-d}\delta \left(P_{\text{I}}\right),\left[\left(r\in G\left(P\right)\right)\right]\iff \left[\lambda r\in G\left(P_{\text{I}}\right)\right].$

Let r_* be a fixed radius and P_* be such a value of the external compressing force that a(P_*) = r_*. Then for P ≥ P_*,

$\left[r=a\left(P\right)\right]\iff \left[\lambda r=\lambda a=r_{*}=a\left(P_{*}\right)\right],\lambda ={\left(P_{*}/P\right)}^{1/\left(d+1\right)}=a_{*}/a.$

Then on the boundary plane (z = 0) within the contact region r ≤ r*, one has

$u_r\left(r,0,P\right)={\left(r/a_{*}\right)}^d{u}_r\left(a_{*},0,P_{*}\right)=C_0{r}^d,C_0=u_r\left(a_{*},0,P_{*}\right)a_{*}^{-d}.$

Hence, if it is assumed that there are nonzero radial displacements in the self-similar Mossakovskii–Spence-type contact problems, then s(r) = C₀r^d within the contact region. These conditions were considered by Spence (1968) and for d = 2 by Zhupanska (2009).

Thus, in the framework of the Mossakovskii–Spence formulation, the radial displacements u_r(r, 0, P) arise initially outside the contact region owing to bounded contact stresses (see Spence, 1968, fig. 1). Then the radial displacements can be treated as frozen-in displacements (Zhupanska, 2009) because the constant C₀ ensures that the radial strain at any given point of the contact zone does not change when the size of the contact region increases owing to an increase of the external parameter of the contact problem.

Let us consider as above axisymmetric monomial punches (Eq. 3.53) in the case of nonslipping contact conditions. If there were no surface forces, then the contact radius a₀ of a punch under the external load P₀ could be found from the solution given by Borodich and Keer (2004a):

$\begin{array}{ll}{a}_0\hfill & ={\left(\frac{I^{*}\left(d\right)P_{0}d}{E^{*}{C}_{\text{NS}}{B}_{d}C\left(d\right)}\right)}^{1/\left(d+1\right)},\hfill \\ I^{*}\left(d\right)\hfill & ={\displaystyle {\int }_0^1{t}^{d-1}\text{cos}\left[\frac{\text{ln}\left(3-4\nu \right)}{2\pi }\text{ln}\frac{1-t}{1+t}\right]\text{d}t.}\hfill \end{array}$

  (3.167)

The nonadhesive contact radius a₁ and depth of indentation δ₁ under some apparent load P₁ are given by

$\begin{array}{ll}{a}_1\hfill & ={\left(\frac{I^{*}\left(d\right)P_{1}d}{E^{*}{C}_{\text{NS}}{B}_{d}C\left(d\right)}\right)}^{1/\left(d+1\right)},\hfill \\ {\delta }_1\hfill & ={\left[\frac{B_{d}C\left(d\right)}{d{I}^{*}\left(d\right){\left(E^{*}{C}_{\text{NS}}\right)}^d}\right]}^{\frac{1}{d+1}}\left(\frac{d+1}{2d}\right)P_1^{d/d+1}.\hfill \end{array}$

  (3.168)

For incompressible materials, the Borodich–Keer formulae (3.167) and (3.168) are identical to the corresponding formulae of the Galin solution (3.154) and (3.155) because for ν = 0.5, one has I*(d) = 1/d and C_NS = 1.

Applying the techniques descried above, one can obtain an exact formula giving the relation between the load P and the radius of the contact region a:

$P_0=P_1-\sqrt{8\pi w{E}^{*}{C}_{\text{NS}}{a}_1^3}=\frac{E^{*}{C}_{\text{NS}}C\left(d\right)B_d}{d{I}^{*}\left(d\right)}{a}_1^{d+1}-\sqrt{8\pi w{E}^{*}{C}_{\text{NS}}{a}_1^3}.$

  (3.169)

As in the frictionless problem above, the real displacement of the punch is δ₂ = (δ₁ − Δδ), i.e.,

${\delta }_2=B_{d}C\left(d\right)\frac{d+1}{2d}\frac{1}{d{I}^{*}\left(d\right)}{a}_1^d-{\left(\frac{2\pi w{a}_1}{E^{*}{C}_{\text{NS}}}\right)}^{1/2}.$

  (3.170)

It is convenient to write the formula for the real displacement δ₂ in the case of the nonslipping boundary condition as

${\delta }_2=\frac{B_{d}C\left(d\right)}{2d^2{I}^{*}\left(d\right)}{a}_1^d\left[1+d\frac{P_0}{P_1}\right].$

5.5.1 Frictionless Adhesive Indentation

It follows from Eq. (3.156) that the radius a₁ of the contact region at P₀ = 0 is

$a_1\left(0\right)={\left[\frac{8\pi w}{K^{*}{C}^2\left(d\right)B_d^2}\right]}^{1/\left(2d-1\right)}.$

As is known, the choice of the characteristic parameters of the adhesive contact problem is rather arbitrary (Borodich & Galanov, 2008). The above value of the radius can be used as a characteristic size of the contact region in order to write dimensionless parameters.

Let us write the characteristic parameters of the adhesive contact problems as

$\begin{array}{ll}{a}^{*}\hfill & =a_1\left(0\right),P^{*}={\left\{\frac{{\left(8\pi w\right)}^{d+1}{\left(E^{*}\right)}^{d-2}}{{\left[C\left(d\right)B_d\right]}^3}\right\}}^{\frac{1}{2d-1}},\hfill \\ {\delta }^{*}\hfill & ={\left[\frac{2^{d+1}}{C\left(d\right)B_d}{\left(\frac{\pi w}{E^{*}}\right)}^d\right]}^{\frac{1}{2d-1}}.\hfill \end{array}$

  (3.171)

Then Eqs. (3.156) and (3.157) have the following forms:

$P_0/P^{*}={\left(a_1/a^{*}\right)}^{d+1}-{\left(a_1/a^{*}\right)}^{3/2}$

  (3.172)

and

$\frac{{\delta }_2}{{\delta }^{*}}=\frac{d+1}{d}{\left(\frac{a_1}{a^{*}}\right)}^d-{\left(\frac{a_1}{a^{*}}\right)}^{1/2}.$

  (3.173)

5.5.2 Nonslipping Adhesive Indentation

In this case, the radius a₁ of the contact region at P₀ = 0 can be obtained from Eqs. (3.169):

$a_1\left(0\right)={\left[\sqrt{\frac{8\pi w}{E^{*}{C}_{\text{NS}}}}\frac{d{I}^{*}\left(d\right)}{C\left(d\right)B_d}\right]}^{\frac{2}{2d-1}}.$