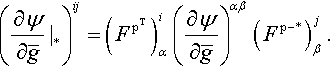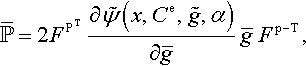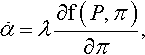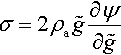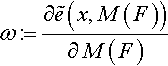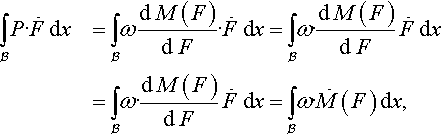4.2 Cauchy's theorem for microstructural contact actions

We assume that τ is a function of the point x and the normal n to $\partial \mathfrak{b}$ at all points where the normal itself is uniquely defined and at every instant. In other words, we presume the validity of Cauchy's postulate for the microstructural contact actions. A question is then whether we can prove the Cauchy theorem for τ.

A proof is given in Capriz and Virga (1990), but there the microstructure is represented in a manifold embedded into a linear space, with undoubted advantages. Here we want to maintain the representation of the microstructure in a manifold as abstract as possible, avoiding even the embedding of $\mathcal{M}$ into a linear space for it is not unique (a question already discussed in the introduction). We then follow another path as sketched below.

First, imagine freezing the macroscopic motion and allowing just the microstructure to vary in time. In other words, select $\stackrel{.}{y}=0$. The requirement of invariance of ${\mathcal{P}}_{\mathfrak{b}}^{\text{ext}}\left(0,\stackrel{.}{\nu }\right)$ implies just the validity of the integral balance

${\displaystyle {\int }_{\mathfrak{b}}{\mathcal{A}}^{*}{\beta }^{‡}\text{d}x}+{\displaystyle {\int }_{\partial \mathfrak{b}}{\mathcal{A}}^{*}\tau \text{d}{\mathcal{H}}^2=0}.$

  (1.8)

This has two main advantages:

1. The linear operator ${\mathcal{A}}^{*}$ projects both β^‡ and τ into ${\mathbb{R}}^3$ from $T^{*}\mathcal{M}$, which is, in general, a nonlinear space.

2. $\mathcal{A}$ does not depend on n. It is a function of $\tilde{\nu }\left(x\right)$ alone at every instant t.

These two aspects allow us to use the integral balance (1.8) in the standard way leading to Cauchy's theorem.

We presume first that both ${\mathcal{A}}^{*}\left(\tilde{\nu }(·)\right){\beta }^{‡}(·)$ and ${\mathcal{A}}^{*}\left(\tilde{\nu }(·)\right)\tau \left(·,n\right)$ are essentially bounded.³⁷ By the standard technique leading to the action–reaction principle (see, e.g., Truesdell, 1991) we can then prove that

${\mathcal{A}}^{*}\left(\tilde{\nu }\left(x\right)\right)\tau \left(x,n\right)=-{\mathcal{A}}^{*}\left(\tilde{\nu }\left(x\right)\right)\tau \left(x,-n\right),$

which is

${\mathcal{A}}^{*}\left(\tau \left(x,n\right)+\tau \left(x,-n\right)\right)=0,$

i.e., the sum τ (x, n) + τ (x, −n) belongs to the kernel of the linear operator ${\mathcal{A}}^{*}$. That sum is well defined: since $\tilde{\nu }(·)$ is continuous and single-valued, as assumed from the beginning, we have at x a unique value ν such that both τ (x, n) and τ (x, −n) belong to the same cotangent space $T_{\nu }^{*}\mathcal{M}$, which is a linear space.³⁸

We can exploit then the integral balance (1.8) reproducing the standard tetrahedron argument or exploit just two linearly independent vectors in space as in Truesdell (1991). What we find is that ${\mathcal{A}}^{*}\tau \left(x,n\right)={\mathcal{A}}^{*}\mathcal{S}\left(x\right)n$, i.e., at x there is a linear operator mapping n into the cotangent space $T_{\tilde{\nu }\left(x\right)}^{*}\mathcal{M}$ (we write in short $\mathcal{S}\left(x\right)\in \text{Hom}\left(T_x^{*}\mathcal{B},T_{\tilde{\nu }\left(x\right)}^{*}\mathcal{M}\right)$) such that

$\tau \left(x,n\right)=\mathcal{S}\left(x\right)n,$

  (1.9)

with $\mathcal{S}\left(x\right)\in \text{Hom}\left(T_x^{*}\mathcal{B},T_{\tilde{\nu }\left(x\right)}^{*}\mathcal{M}\right)$. Precisely, we get

$\mathcal{S}\left(x\right):={\displaystyle \sum _{K=1}^3\tau \left(x,e_A\right)\otimes e_A},$

where, as above, e_A is the Ath vector of a basis in a neighborhood of x. In components we have

${\tau }_{\alpha }\left(x,n\left(x\right)\right)={\mathcal{S}}_{\alpha }^A\left(x\right)n_A\left(x\right),$

where Greek indices indicate components over $\mathcal{M}$. We call $\mathcal{S}$ microstress to recall its role analogous to the standard stress and its microstructural origin.

Refinements seem possible:

• The construction of a framework determining the need for Cauchy's postulate for τ. (I refer to the appropriate generalization of the Hamel–Noll theorem (Truesdell, 1991).)

• The weakening of the continuity assumption along the lines indicated in Šilhavý (1991, 2005).

Difficulties arise when we consider $\tilde{\nu }(·)$ as a multivalued function over $\mathcal{M}$, with values determined modulo a permutation, as proposed for a refined description of material complexity in Focardi et al. (2014), where the conditions for the existence of the ground states for the relevant elastic energy are determined in this case.

4.3 The relative power: a definition

In the expressions of the power discussed above, the reference place $\mathcal{B}$ is presumed fixed once and for all. In the presence of bulk mutations in the matter, we can resort to the idea of having multiple reference shapes interpreted in one of the ways described in the introduction. Here our attention is on the definition of the vector field $x\mapsto w\left(x\right)\in T_x\mathcal{B}$, which we presume to be differentiable, a virtual velocity mimicking the incoming rearrangements of material elements that determine the mutation. In this case we can think of writing the external power relative to w. Moreover, since the vector field w (·) represents material mutations, we have to consider that during these mutations we have

1. changes in the energetic landscape and

2. actions in $\mathcal{B}$ power conjugated with the rupture of existing material bonds and/or the formation of new ones, and mutation-induced anisotropy.

In principle, in both cases we can have energy fluxes across boundaries inside the body and consequent emergence of anisotropies in the distribution of the energy itself. However, although we mention energy at this stage, we are not referring to specific constitutive classes. We need just to affirm that there is the free energy ψ and it changes in space and time when material mutations occur, nothing more. In particular, we write

$\psi =\tilde{\psi }\left(x,t,\varsigma \right),$

with ς the list of state variables that we do not specify. They have to be rendered explicit in discussing constitutive issues, but not here. Moreover, in addition to standard and microstructural actions, we should include the ones not associated with deformation or microstructural events described by $\stackrel{.}{\nu }$ (see the second item in the list above). A way to maintain distinct these new actions is to represent them as covector fields over $\mathcal{B}$ (vectors if we use the standard identification of ${\mathbb{R}}^3$ with its dual) of forces f and couples μ developing power on w and its curl, respectively. Further assumptions apply:

1. f may have just dissipative nature. It vanishes when the mechanical process is conservative.

2. μ has dissipative and conservative components, the latter appearing when the material mutations produce anisotropy without breaking and/or reforming material bonds.

By taking into account the representation of the contact actions in terms of stress and microstress in the Lagrangian configuration, I define the relative power, writing ${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right)$ for it, as the sum of the relative power of actions, indicated by ${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}-\text{a}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right)$, and another functional that I call the power of disarrangements, ${\mathcal{P}}_{\mathfrak{b}}^{\text{dis}}\left(w\right)$, determined by the energy fluxes and the configurational forces f and μ listed above. Precisely, ${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right)$ has the following form:

${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right):={\mathcal{P}}_{\mathfrak{b}}^{\text{rel}-\text{a}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right)+{\mathcal{P}}_{\mathfrak{b}}^{\text{dis}}\left(w\right),$

with

${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}-\text{a}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right):={\displaystyle {\int }_{\mathfrak{b}}{b}^{‡}·\left(\stackrel{.}{y}-\mathit{Fw}\right)\text{d}x+{\displaystyle {\int }_{\partial \mathfrak{b}}\mathit{Pn}·\left(\stackrel{.}{y}-\mathit{Fw}\right)\text{d}{\mathcal{H}}^2}}+{\displaystyle {\int }_{\mathfrak{b}}{\beta }^{‡}·\left(\stackrel{.}{\nu }-\mathit{Nw}\right)\text{d}x+{\displaystyle {\int }_{\partial \mathfrak{b}}\mathcal{S}n·\left(\stackrel{.}{\nu }-\mathit{Nw}\right)\text{d}{\mathcal{H}}^2}}$

and

${\mathcal{P}}_{\mathfrak{b}}^{\text{dis}}\left(w\right):={\displaystyle {\int }_{\partial \mathfrak{b}}\left(n·w\right)\psi \text{d}{\mathcal{H}}^2}-{\displaystyle {\int }_{\mathfrak{b}}\left({\partial }_x\psi +f\right)·w\text{d}x}+{\displaystyle {\int }_{\mathfrak{b}}\mu ·\text{curl}w\text{d}x.}$

In the previous expressions, ∂_xψ is the explicit derivative of $\tilde{\psi }\left(x,t,\varsigma \right)$ with respect to x, holding fixed all the other entries of the energy. It is an indicator of the loss of homogeneity in the energy landscape, altered by the mutation. The term (n · w) ψ is the energy density flux across the boundary $\partial \mathfrak{b}$, due to the mutation itself.

When w = 0 at every point (the body does not undergo bulk macroscopic mutations), ${\mathcal{P}}_{\mathfrak{b}}^{\text{dis}}\left(w\right)$ vanishes and ${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right)$ reduces to the external power ${\mathcal{P}}_{\mathfrak{b}}^{\text{ext}}\left(\stackrel{.}{y},\stackrel{.}{\nu }\right)$.

${\mathcal{P}}_{\mathfrak{b}}^{\text{dis}}\left(w\right)$ accounts for macroscopic mutations. The microscopic ones pertain to the terms

${\displaystyle {\int }_{\mathfrak{b}}{\beta }^{‡}·\stackrel{.}{\nu }\text{d}x}+{\displaystyle {\int }_{\partial \mathfrak{b}}\mathcal{S}n·\stackrel{.}{\nu }\text{d}{\mathcal{H}}^2}$

in ${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}-\text{a}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right)$. There is micro-to-macro interaction. It appears in the pointwise balance equations and the constitutive issues.

When we do not consider a multifield and multiscale representation of material microstructures and we describe bodies in the standard format, the relative power obviously reduces to

${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}}\left(\stackrel{.}{y},w\right):={\mathcal{P}}_{\mathfrak{b}}^{\text{rel}-\text{a}}\left(\stackrel{.}{y},w\right)+{\mathcal{P}}_{\mathfrak{b}}^{\text{dis}}\left(w\right),$

where ${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}-\text{a}}\left(\stackrel{.}{y},w\right)$ is derived from ${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}-\text{a}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right)$ by canceling microstructural actions and is given by

${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}-\text{a}}\left(\stackrel{.}{y},w\right):={\displaystyle {\int }_{\mathfrak{b}}{b}^{‡}·\left(\stackrel{.}{y}-\mathit{Fw}\right)\text{d}x+}{\displaystyle {\int }_{\partial \mathfrak{b}}\mathit{Pn}·\left(\stackrel{.}{y}-\mathit{Fw}\right)\text{d}{\mathcal{H}}^2},$

while ${\mathcal{P}}_{\mathfrak{b}}^{\text{dis}}\left(w\right)$ remains the same.

Notice that I have written ${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right)$ in terms of the first Piola–Kirchhoff stress P and the microstress $\mathcal{S}$ taking advantage of the discussion about their existence in previous sections. However, we could write ${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right)$ in its more primitive form including $\mathfrak{t}$ and τ in place of Pn and $\mathcal{S}n$. In this case the results below, emerging from a requirement of invariance of ${\mathcal{P}}_{\mathfrak{b}}^{\text{rel}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right)$ under changes in observers of class 2, would be enriched by the proof of the existence of P and $\mathcal{S}$, and their independence from n.

4.4 Kinetics

Microstructural inertia can appear, for example, in the case of bubbles migrating inside a liquid in motion, relative to it, and vibrating within it (see the remarks in Capriz & Giovine, 1997), or solids with an enormous number of cavities, each one containing a gyroscope (a case discussed in Milton & Willis, 2007).

In his book on continua with microstructure, Capriz (1989) writes the kinetic energy in a multifield and multiscale representation of bodies as the sum of the standard macroscopic kinetic energy and a microscopic component. By indicating with b in the apex position a covector corresponding to the vector decorated by the apex, we rewrite explicitly the sum as

$k\left({\stackrel{.}{y}}^{\mathfrak{b}},\nu ,{\stackrel{.}{\nu }}^{\mathfrak{b}}\right):=\frac{1}{2}\rho {\stackrel{.}{y}}^{\mathfrak{b}}·\stackrel{.}{y}+\kappa \left(\nu ,{\stackrel{.}{\nu }}^{\mathfrak{b}}\right),$

where κ is such that κ (ν, 0) = 0 and it admits a second derivative with respect to ${\stackrel{.}{\nu }}^{♭}$, which is positive definite, namely,

$\frac{\partial \kappa \left(\nu ,{\stackrel{.}{\nu }}^{\mathfrak{b}}\right)}{\partial {\stackrel{.}{\nu }}^{\mathfrak{b}}\partial {\stackrel{.}{\nu }}^{\mathfrak{b}}}·\left({\stackrel{.}{\nu }}^{\mathfrak{b}}\otimes {\stackrel{.}{\nu }}^{\mathfrak{b}}\right)\ge 0.$

The equality sign holds when ${\stackrel{.}{\nu }}^{♭}=0$.

In contrast with Capriz (1989), I presume that the dependence of $\kappa \left(\nu ,{\stackrel{.}{\nu }}^{♭}\right)$ must be considered deprived of the effects of macroscopic rigid-body motion. Microstructural inertia appears, should it exist, as a local microscopic fluctuation with respect to the macroscopic motion. Hence, we may consider κ as a function:

$\kappa \left(\nu ,{\stackrel{.}{\nu }}^{\mathfrak{b}}\right)=\mathfrak{h}\left(\nu ,{\stackrel{.}{\nu }}^{\mathfrak{b}}-{\left({\mathcal{A}}_q\right)}^{\mathfrak{b}}\right).$

The choice prevents an incongruence that would occur, in contrast, when κ is quadratic with respect to ${\stackrel{.}{\nu }}^{♭}$ and we calculate the total kinetic energy of the body during a rigid-body motion—a physically questionable extra inertia moment would appear if we do not use a form like $\mathfrak{h}$ (details are given in Mariano, 2002).

A standard assumption used below is that both b^‡ and β^‡ admit additive decompositions into inertial (bⁱⁿ and βⁱⁿ) and noninertial (b and β) components:

$b^{‡}=b^{\text{in}}+b,{\beta }^{‡}={\beta }^{\text{in}}+\beta .$

4.5 Invariance of the relative power under isometry-based changes in observers

Here I refer to changes in observers of class 2. The velocity w is defined on $\mathcal{B}$ (precisely, the map $x\mapsto w\left(x\right)\in T_x\mathcal{B}$ is a section of the tangent bundle to $\mathcal{B}$), so we have to use the rule (1.4) in the changes in observers.

Along the path, I shall assume that some fields are piecewise differentiable over $\mathcal{B}$ (in short, we say that they are of class PC¹) with bounded discontinuities over a surface Σ, oriented locally by the normal m, and not moving relative to $\mathcal{B}$ itself. For any field x a (x) of this type, taking values in a linear space, the limits a^± (x) := lim_ε↓0 a (x ± εn), x ∈ Σ, define the jump [a] of a as the difference [a] := a⁺ − a−, and the average 〈a〉 as $\langle a\rangle :=\frac{1}{2}\left(a^{+}+a^{-}\right)$. Given two fields x a₁ (x) and x a₂ (x) taking values in a linear space and such that a product a₁a₂ between them, distributive with respect to the sum, can be defined, we get the identity [a₁a₂] := [a₁] 〈a₂〉 + 〈a₁〉 [a₂].

The definition of [a] underlines the need of having a field taking values in a linear space. If it were not so, the difference would possibly not be defined. For this reason, in what follows, I shall consider the field x ν continuous across Σ. In fact, since $\mathcal{M}$ is here, in general, nonlinear, the jump [ν] of ν could not make sense. In contrast, the jump of $\stackrel{.}{\nu }$ and the jump of $\mathcal{S}$ are always defined, both being in linear spaces at every $x\in \mathcal{B}$.

I presume also that the derivatives of the map x ν suffer bounded discontinuities across Σ. Also, Σ is here unstructured: this means that it cannot sustain its own surface standard and microstructural tractions; in other words it is not endowed with its own surface energy.

Invariance of the relative power with respect to translations in ${\tilde{\mathcal{E}}}^3$ furnishes the integral balance of forces. We do not have the integral balance of microactions (or microforces if you want to use the term force in an extended sense) because translations are not available over $\mathcal{M}$ unless it is a priori selected as a linear space. Even in that case, however, if we accept changes in observers in class 2 (or class 1 in the absence of material mutations), a translation over $\mathcal{M}$ is not accounted for.

The integral balance of couples (1.11) includes the microactions. However, it does not mean that $\mathcal{S}$ and β^‡ are couples for they appear multiplied by the adjoint of the linear operator $\mathcal{A}$, which projects over the reference space their component over $\mathcal{M}$.

In principle, we could abandon the procedure based on the invariance of the relative power, or the external power alone, deciding to postulate the integral form of the balance equations. We would be then pushed to postulate an integral balance of microstructural actions, declaring it as “our first principle.” This way we would face the basic difficulty that in this case such a balance would be not defined in general for we take $\mathcal{M}$ as a manifold not necessarily coincident with a linear space. In fact, when $\mathcal{M}$ is a nonlinear manifold, the integrals in that balance would not be defined because the fields x β^‡ and $x\mapsto \mathcal{S}n$ take values in the cotangent bundle of $\mathcal{M}$, a nonlinear target space. A balance of microstructural actions could be formally defined only when $\mathcal{M}$ is a linear space. However, in any case its choice would introduce an assumption, namely, the structure of that integral balance, which is not necessary, as shown by the previous theorem (its proof can be developed by direct calculation). Moreover, if we presume such an integral balance a priori when $\mathcal{M}$ is linear, we should postulate the existence of the self-action z, which has been, in contrast, deduced with the procedure used in the previous theorem.

Another option could be a virtual power approach. We could assume the identity

${\mathcal{P}}_{\mathcal{B}}^{\text{rel}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right)={\mathcal{P}}_{\mathcal{B}}^{\text{rel}-\text{int}}\left(\stackrel{.}{y},\stackrel{.}{\nu },w\right),$

as a first principle, presuming its validity for any choice of (compactly supported) rate fields.⁴⁰ Such an assumption, however, is a way to affirm that we are postulating a priori the weak form of the pointwise balances of actions. We should then presume the existence of all ingredients appearing in the balance equations, having already in mind their structure. The difference between a procedure requiring the invariance of external power and the virtual power approach is not particularly appreciable in the standard setting for the elements appearing in the inner power are already present in the external one. In contrast, in the enriched setting discussed here, in postulating the inner power we should introduce a priori the self-action z without showing the need for its existence.

There is an indeterminacy in the pointwise balance of microactions (1.15). In fact, the addition to z of any z′ belonging to $\text{Ker}{\mathcal{A}}^{*}$ satisfies Eq. (1.16). Hence, it would appear in Eq. (1.15).⁴¹ The indeterminacy can be eliminated by covariance techniques (de Fabritiis & Mariano, 2005), i.e., by requiring at least invariance with respect to the generalized class 1. If we require such an invariance for the external power or the relative one, however, we do not obtain an appreciable result. Covariance requirements need the use of the balance of energy or the second law of thermodynamics.⁴² In this case, however, energy is involved, and the specification of the list of state variables is required. This way we would pay for the use of a more stringent invariance requirement by losing the hierarchical distinction between the derivation of the balance equations and the discussion of constitutive issues, the former determined without the need for the latter.

Invariance of the relative power with respect to translations and rotations in the reference space ${\mathcal{E}}^3$ determines integral balances of configurational forces and couples, the ones governing the bulk mutation. Hence, we are not forced to introduce a priori a stress $\mathbb{P}$ and bulk configurational forces and then to identify them with $\psi I-F^{*}P-N^{*}\mathcal{S}$ and −F*b^‡ − N*β^‡ by means of an additional procedure, the one described in Gurtin (1995, 2000a).

The assumption that f is solely dissipative reduces to the inequality f · w ≥ 0, the equality sign being valid only when w = 0, which implies that f is a linear function of w, with a positive coefficient. The result changes Eq. (1.17) into an evolution equation.

4.6 And if we disregard $\mathcal{M}$ during changes in the observers?

In principle we could consider ν to be observer-independent. In this case the invariance of the external power or the relative one with respect to isometry-based changes in the observer would not lead (under appropriate regularity) to the pointwise balances of microstructural actions (1.14) and (1.15), as is obvious from the procedure sketched above. Hence, ν would play a parametric role at equilibrium and its evolution should be prescribed a part, with the sole proviso of satisfying the second law of thermodynamics. This way we would enter the scheme of internal variables, intended just as entities describing the removal from thermodynamical equilibrium (see de Groot & Mazur, 1962 for a standard treatise on the matter from the point of view of nonequilibrium thermodynamics, above all with reference to chemical processes). The approach has been coupled with deformations in Coleman and Gurtin (1967), Halphen and Nguyon (1975), with a subsequent rich literature, in the majority of cases related to plasticity and/or damage (see, e.g., Krajcinovic, 1996). The balance of microstructural actions can be reduced to the evolution equation that appears in internal variable schemes in the absence of external body actions (including even possible rotational microstructural inertia), microstress, and when the self-action is the sum of conservative and dissipative components (see Mariano, 2002 for details). However, the relation is just formal: the difference in the use of the notion of an observer continues to distinguish the two approaches.

When there is no link between changes of frames in ${\tilde{\mathcal{E}}}^3$ and changes of atlas on $\mathcal{M}$, i.e., when {λ} is empty, the invariance procedure leading to the previous theorem would lead to a splitting of Eq. (1.11) into two integral balances:

${\displaystyle {\int }_{\mathfrak{b}}\left(y-y_0\right)\times b^{‡}\text{d}x}+{\displaystyle {\int }_{\partial \mathfrak{b}}\left(y-y_0\right)\times \mathit{Pn}\text{d}{\mathcal{H}}^2=0}$

and

${\displaystyle {\int }_{\mathfrak{b}}{\mathcal{A}}^{*}{\beta }^{‡}\text{d}x}+{\displaystyle {\int }_{\partial \mathfrak{b}}{\mathcal{A}}^{*}\mathcal{S}n\text{d}{\mathcal{H}}^2=0}.$

The first one is the standard balance of couples leading to the symmetry of PF* under the regularity condition mentioned in the theorem above. The second balance would produce once again (1.14) and

${\mathcal{A}}^{*}z+\left(\text{D}{\mathcal{A}}^{*}\right)\mathcal{S}=0.$

This circumstance stresses the role played in this setting by the notion of an observer and its changes.

4.7 Perspectives: low-dimensional defects, strain-gradient materials, covariance of the second law

In the presence of structured discontinuity surfaces, those endowed with their own surface energy for they are able to sustain surface standard and microstructural actions (it is a reasonable mathematical scheme for thin transition layers between phases, for example), the expression of the relative power has to be extended with the addition of two contributions: (1) the relative power of surface actions, and (2) the surface power of disarrangements containing fluxes of the surface energy and the surface counterparts of f and μ. The list of surface actions includes the standard surface stress and surface microstress and self-actions—the existence of the last actions is proven in Mariano (2002). The definition of the relative power in this case and the results emerging from the requirement of its invariance are given in Mariano (2014). However, a special case of that extended expression of the relative power in the conservative case emerges from the extension of Nöther's theorem, presented in de Fabritiis and Mariano (2005), to the elasticity of complex materials endowed with structured discontinuity surfaces. Different approaches can be followed to analyze the mechanics of structured discontinuity surfaces, with other assumptions and different procedures (Gurtin, 2000a; Gurtin & Struthers, 1990; Maugin & Trimarco, 1995; Simha & Bhattacharya, 2000). The reader will be able to distinguish the procedure requiring the smallest number of assumptions, a peculiarity allowing it to be a flexible tool to tackle nonstandard situations.

Analogous generalizations can be obtained in the presence of line defects endowed with their own line energy. This one is a scheme that we can adopt, for example, for the description of the dislocation core in metals. In this case, an expression of relative power in a setting where dissipation is essentially attributed to the counterparts of f and μ and to the self-action is given in Mariano (2012b).

We can define the relative power even for strain-gradient materials, including the hyperstress (a third-rank tensor). When we focus attention on the actions in the bulk alone, in the conservative setting of strain-gradient elasticity an expression for the relative power can be derived from the Nöther theorem (for it, see Kouranbaeva & Shkoller, 2000). The extension of the Nöther theorem to the case in which structured discontinuity surfaces appear in strain-gradient elasticity (e.g., think of two strain-gradient elastic materials glued to each other) is proven in Mariano (2007), where the surface hyperstress was introduced first. In the dissipative setting, the appropriate expression for the relative power including bulk and surface hyperstress is given in Mariano (2014).

Besides issues concerning low-dimensional defects endowed with their own energy in single-gradient or second-gradient field theories, another perspective deals with covariance in a dissipative setting. In fact, we can write a version of the second law of thermodynamics including the relative power and impose invariance under diffeomorphism-based changes in observers. The procedure requires (1) the specification of the list of state variables (it includes the metric in the reference place) and (2) a rule satisfied by the rate of change of the free energy under changes in observers (it affirms essentially that the energy changes tensorially, as assumed in elasticity in Marsden & Hughes, 1983). This way we deduce (1) the existence of the stresses, (2) the pointwise balances in the previous theorem, (3) the constitutive restrictions (among them we find that the conservative part of the Eshelby stress is the derivative of the free energy with respect to the material metric), and (4) the structure of the dissipation. Details in the case of elastic–plastic hardening materials are provided in the next section.

5.1 Multiplicative decomposition of F

Plasticity is the macroscopic emergence of the cooperation of microscopic structural changes in the matter. In this sense, the phenomenon is a mutation.

There are various manners of interpreting plastic phenomena. In this sense we can speak of theories of plasticity instead of a unique format.

A traditional approach is based on a multiplicative decomposition of the deformation gradient, F, into elastic, F^e, and plastic, F^p, factors:

$F=F^{\text{e}}{F}^{\text{p}}.$

For F^p we presume that

• det F^p > 0 at all x in $\mathcal{B}$, where F^p is defined,

• the field x F^p (x) is differentiable, and

• curl F^p ≠ 0.

With the last assumption we affirm that F^p is not intended as the spatial derivative of any deformation. F^p is only a linear operator that maps the tangent space to $\mathcal{B}$ at x onto another linear space that we imagine (and in this setting we cannot do more than imagine) as the tangent space to what is commonly called an intermediate configuration, determined by the structural changes in the material. This way we are factorizing the elastic-plastic process. The choice appears fictitious for elastic and plastic changes in the matter cooperate. However, the factorization of elastic and plastic phenomena seems to have microscopic justification at least in the case of crystals even without calling upon explicitly a notion of an intermediate configuration. Parry (2004) has shown that, for crystal lattices, a view based on the dislocation tensor and other elastic invariants⁴⁴ leads to a decomposition of the type F = F^e₁F^pF^e₂, which obviously reduces to the traditional one when F^e₂ coincides with the identity (see also Parry, 2001). Another justification constructed by considering deformations as $\mathit{SBV}\left(\mathcal{B}\right)$ maps⁴⁵ appears in Reina and Conti (2014).

When we accept the multiplicative decomposition F = F^eF^p, the right Cauchy–Green tensor in its version with both covariant components is

$C=F^{\text{p}*}{F}^{\text{e}*}\tilde{g}{F}^{\text{e}}{F}^{\text{p}}=F^{\text{p}*}{C}^{\text{e}}{F}^{\text{p}},$

with $C^{\text{e}}=F^{\text{e*}}\tilde{g}{F}^{\text{e}}$. The second-rank tensor C^e, endowed with a positive determinant, is the so-called elastic right Cauchy–Green tensor. Its components are covariant. Precisely, C^e is the pullback of the spatial metric $\tilde{g}$ through F^e.

The 1-contravariant, 1-covariant versions of C^e and C are, respectively, ${\tilde{C}}^{\text{e}}=F^{\text{eT}}{F}^{\text{e}}$ and $\tilde{C}=F^{\text{pT}}{\tilde{C}}^{\text{e}}{F}^{\text{p}}$. Also, the push-forward by F^p of the material metric, namely, the second-rank tensor $\overline{g}:=F^{\text{p}-*}g{F}^{\text{p}-1}$, is independent of any change of frame on $\mathcal{B}$, induced by diffeomorphisms of the reference space onto itself. The proof is elementary and can be found in Mariano (2013). Notice that ${\tilde{C}}^{\text{e}}={\tilde{g}}^{-1}{C}^{\text{e}}$ and $\tilde{C}={\tilde{g}}^{-1}C$.

The plastic factor of the deformation gradient maps the tangent spaces to $\mathcal{B}$ at different points onto distinct linear spaces. We do not have any information assuring us that we can glue together all the linear spaces obtained by means of F^p, varying x in $\mathcal{B}$, to construct the tangent bundle of a manifold that could be a fit region of the type $\mathcal{B}$, identified with what we call an intermediate configuration.

This is another way to interpret the assumption curl F^p ≠ 0, which excludes the possibility to individualize such a configuration that remains fictitious. In principle, it is even not necessary to imagine an intermediate (global) configuration, as I have already affirmed, although, point by point, the factorization F^eF^p implies a mapping from $T_x^{*}\mathcal{B}$ onto an unknown linear space determined by F^p. The linear spaces determined by F^p varying x in $\mathcal{B}$ could be interpreted as the tangent spaces of different configurations. Such an interpretation brings us back to the notes in the introduction dealing with virtual tangent spaces and multiple reference configurations.

5.2 Factorization of changes in observers

Consider changes in observers in the generalized class 2 presented previously, excluding what is pertinent to $\mathcal{M}$, which does not appear in this section. The velocity field $\overline{v}$ in the relation

$\stackrel{.}{y}\to {\stackrel{.}{y}}^{\#}:=\stackrel{.}{y}+\overline{v}$

is a function of x through y := u(x), so we write $\text{D}\overline{v}={\text{D}}_y\overline{v}F$. For $\text{D}\overline{v}$, according to Mariano (2013), I assume a multiplicative decomposition of the type

$\text{D}\overline{v}=\stackrel{·}{\overline{H^{\text{e}}{F}^{\text{p}}}}.$

  (1.22)

The presence of F^p does not reduce the generality of $\text{D}\overline{v}$, owing to the arbitrariness of H^e, a linear operator from the linear space individuated by F^p to the translation space over ${\tilde{\mathcal{E}}}^3$. Although it has no effects on the generality of changes in observers, the previous factorization of $\text{D}\overline{v}$ is crucial for the result on hardening plasticity presented here.

A relation given below is useful. To get it, we define

$L_H^{\text{e}}:={\stackrel{.}{H}}^{\text{e}}{F}^{\text{e}-1},L^{\text{p}}:={\stackrel{.}{F}}^{\text{p}}{F}^{\text{p}-1},$

and use the identity $\text{D}\overline{v}={\text{D}}_y\overline{v}F$ and Eq. (1.22). By computing ${\text{D}}_y\overline{v}$, we get⁴⁶

${\text{D}}_y\overline{v}=\stackrel{·}{\overline{H^{\text{e}}{F}^{\text{p}}}}{F}^{-1}=\text{Sym}{L}_H^{\text{e}}+\text{Skw}{L}_H^{\text{e}}+H^{\text{e}}{L}^{\text{p}}{F}^{\text{p}-1}.$

5.3 A version of the second law of thermodynamics involving the relative power

In accordance with Mariano (2013), I use here an isothermal version of the second law of thermodynamics (a mechanical dissipation inequality), which, for any part $\mathfrak{b}$ of $\mathcal{B}$ and any choice of the velocity fields, is given by

$\mathfrak{E}\left(\stackrel{.}{y},w;\psi ,\mathfrak{b}\right):=\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{\mathfrak{b}}\psi \text{d}x}-{\mathcal{P}}_{\mathfrak{b}}^{\text{rel}}\left(\stackrel{.}{y},w\right)\le 0,$

  (1.23)

where, we recall, ψ is the free energy and in the relative power we write $\mathfrak{t}$ instead of Pn in the surface integral including the contact actions.

The common expression of the mechanical dissipation inequality involves the external power alone. Here, we include the relative power, extending in this sense the standard inequality to account for the remodeling of the material structure induced by the plastic phenomena.

When this is the case—not here, however—the inequality can be further generalized by including the expression of the relative power that involves microstructural actions or hyperstresses in the presence of strain-gradient effects.

A direct description of the microstructures does not appear in this section for we are restricting the treatment to the standard framework of hardening plasticity just to exemplify how some general ideas discussed here work on a well-known ground.

5.4 Specific constitutive assumptions

The assumptions listed below apply:

H1 The state variables pertaining to the generic material element are F, F^p, and the hardening parameter α, a second-rank tensor taking into account hardening anisotropy and measuring how much during the plastic process the material goes far from thermodynamic equilibrium, where α plays only a parametric role, being considered an observer-independeni iniernal variable. Hence, the free energy is of the form

$\psi =\widehat{\psi }\left(x,F,F^{\text{p}},\alpha \right).$

It satisfies further assumptions:

H1.a For any linear operator $G\in \text{Hom}\left({\mathbb{R}}^3,{\mathbb{R}}^3\right)$ with det G = 1,

$\widehat{\psi }\left(x,F,F^{\text{p}}\right)=\widehat{\psi }\left(x,\mathit{FG},F^{\text{p}}G,\alpha \right).$

H1.b The free energy is objeciive. The requirement emerges naturally from the isotropy of the three-dimensional Euclidean space: if we rotate rigidly a frame in the physical space, the free energy of a material should not change. Elements of the orthogonal group SO (3) describe rotations, we recall.

Assumption H1.a is completely standard (see, e.g., Mielke, 2004; Ortiz & Repetto, 1999). This implies that

$\widehat{\psi }\left(x,F,F^{\text{p}},\alpha \right)=\overline{\psi }\left(x,F^{\text{e}},\overline{g},\alpha \right),$

where $\overline{g}:=F^{\text{p}-*}g{F}^{\text{p}-1}$, and we adopt the multiplicative decomposition of F. The previous restriction on the structure of the energy enlarges the common use of the invariance under the action of G, as described above, interpreted as a constraint leading to a structure of the free energy of the type $\widehat{\psi }\left(F,F^{\text{p}}\right)=\overline{\psi }\left(F^{\text{e}}\right)$ alone, not considering $\overline{g}$, which plays, in contrast, a role here, as we shall see below.
For any Q ∈ SO (3) that rotates frames in the space where the actual places are determined, since $\overline{g}$ has no components in that space and α is considered here to be observer-independent, just to follow the standard view on hardening, objectivity is written formally as

$\overline{\psi }\left(x,F^{\text{e}},\overline{g},\alpha \right)=\overline{\psi }\left(x,Q{F}^{\text{e}},\overline{g},\alpha \right),$

which implies

$\overline{\psi }\left(x,F^{\text{e}},\overline{g},\alpha \right)=\breve{\psi }\left(x,{\tilde{C}}^{\text{e}},\overline{g},\alpha \right).$

Since ${\tilde{C}}^{\text{e}}={\overline{g}}^{-1}{C}^{\text{e}}$, we can write

$\breve{\psi }\left(x,{\tilde{C}}^{\text{e}},\overline{g},\alpha \right)=\tilde{\psi }\left(x,C^{\text{e}},\overline{g},\alpha \right).$

H2 Under diffeomorphism-based changes in observers acting on both the ambient space and the reference space (it is the generalized class 2 in which we do not consider $\mathcal{M}$), we get

$\frac{\text{d}{\psi }^{\#}}{\text{d}t}=\frac{\text{d}\psi }{\text{d}t}+{\frac{\partial \psi }{\partial C^{\text{e}}}|}_{\downarrow \#}·2\text{Sym}{L}_H^{\text{e}}+{\frac{\partial \psi }{\partial \overline{g}}|}_{*}·{\mathcal{L}}_{\overline{w}g}+\frac{\partial \psi }{\partial \alpha }·\stackrel{.}{\alpha },$

where (·) |_* indicates the pullback in the reference place of (·), while (·) |_↓# is the push-forward of (·) in the current configuration with the additional lowering of the first index.⁴⁷
The push-forward of (·) in the current configuration, with the additional lowering of the first index, is given explicitly by

${\frac{\partial \psi }{\partial C^{\text{e}}}|}_{\downarrow \#}=\tilde{g}{F}^{\text{e}}\frac{\partial \psi }{\partial C^{\text{e}}}{F}^{\text{e}*},$

which is, in components,

${\left({\frac{\partial \psi }{\partial C^{\text{e}}}|}_{\downarrow \#}\right)}_i^j={\tilde{g}}_{\mathit{ik}}{\left(F^{\text{e}}\right)}_{\alpha }^k{\left(\frac{\partial \psi }{\partial C^{\text{e}}}\right)}^{\alpha \beta }{\left(F^{\text{e}*}\right)}_{\beta }^j.$

${\frac{\partial \psi }{\partial C^{\text{e}}}|}_{\downarrow \#}$ is then a 1-contravariant, 1-covariant tensor in the current place, an element of the dual space of Sym L^e_H.
The pullback in the reference place of (·) is given by

${\frac{\partial \psi }{\partial \overline{g}}|}_{*}=F^{{\text{p}}^{\text{T}}}\frac{\partial \psi }{\partial \overline{g}}{F}^{\text{p}-*},$

which is, in components,

${\left({\frac{\partial \psi }{\partial \overline{g}}|}_{*}\right)}^{\mathit{ij}}={\left(F^{{\text{p}}^{\text{T}}}\right)}_{\alpha }^i{\left(\frac{\partial \psi }{\partial \overline{g}}\right)}^{\alpha \beta }{\left(F^{\text{p}-*}\right)}_{\beta }^j.$

The term ${\mathcal{L}}_{\overline{w}}g$ indicates that the (virtual) velocity $\overline{w}$ alters the material metric g, dragging it. Indirectly, then, $\overline{w}$ induces changes in the metric $\overline{g}$ on the intermediate configuration, since $\overline{g}$ is the push-forward of g induced by F^p. Hence, instead of writing ${\left(\partial \psi /\partial \overline{g}\right)|}_{*}·{\mathcal{L}}_{\overline{w}}g$, we could consider the push-forward of ${\mathcal{L}}_{\overline{w}}g$ through F^p, multiplying it by $\partial \psi /\partial \overline{g}$, which would conceptually be the same thing.
The spatial metric $\tilde{g}$ can suffer alterations when the physical space is altered by a time-dependent family of diffeomorphisms having as an infinitesimal generator the (virtual) velocity $\overline{v}$. There is then an effect on ψ through C^e, the pullback through F^e of $\tilde{g}$ into the linear space determined by F^p and coinciding with $F^{\text{p}}{T}_x\mathcal{B}$. This is the reason justifying the introduction of the term (∂ψ/∂C^e) |_↓# in assumption H2.
In assumption H2 the factor ${\mathcal{L}}_{\overline{w}}g$ has no counterpart ${\mathcal{L}}_{\overline{v}}\tilde{g}$ in the current place because H^e is not the spatial derivative of any vector field. This aspect justifies the presence of the factor SymL^e_H.

H3 Contact actions depend on the same state variables entering the energy.⁴⁸

5.5 The covariance principle in a dissipative setting

Independently of the use of external, relative, or internal power, the isothermal version of the second law of thermodynamics is a certain expression lesser than or equal to zero, say, B ≤ 0. Another observer ${\mathcal{O}}^{\prime }$ always evaluates an inequality, say, B′ ≤ 0, with B ≠ B′, in general.

Thanks to assumption H2 and the linearity of the relative power with respect to the velocities $\stackrel{.}{y}$ and w, the pullback of B′ into $\mathcal{O}$ gives rise to an inequality of the type B* ≤ 0, with B* = B + B^†. The addendum B^† involves the velocity fields $\overline{v}$ and $\overline{w}$, entering the rules of changes in observers. Conversely, if we push forward B to the frames defining the observer ${\mathcal{O}}^{\prime }$, we find an inequality of the type B′ + B^‡ ≤ 0 because now the change in observer ${\mathcal{O}}^{\prime }\to \mathcal{O}$ is governed by the inverse of the previous maps, namely, h⁻¹ and ${\widehat{h}}^{-1}$. Hence, B^‡ is, in principle, different from B^†.

Previous remarks suggest a principle.

Essentially, the principle affirms that the dissipative nature of a process is indifferent to changes in observers.

5.6 The covariance result for standard hardening plasticity

The covariance principle in a dissipative setting is the key ingredient for proving the following theorem. It shows the covariant structure of the equations governing the standard description of hardening plasticity in the finite-strain regime.

The proof of this theorem can be developed by reproducing the analogous proof in Mariano (2013), with the minor variations required by the presence of α. It is left to the reader. Notice that with respect to what is presented in Mariano (2013), assumption H2 is varied by the insertion of the factor 2, which appears then in Eq. (1.29).

Evolution equations for ${\stackrel{.}{F}}^{\text{p}}$ and $\stackrel{.}{\alpha }$ can be derived by accepting the maximum dissipation principle. This is a standard view determining associate plasticity (Simo & Hughes, 1998), while the previous theorem is completely nonstandard.

To state the maximum dissipation principle, we need first to introduce an admissibility criterion. It can be expressed in terms of stress or strain. Here we adopt a standard representation in terms of stress P and thermodynamic flux π and write f(P, π) ≤ 0 for such a criterion, considering admissible the pairs (P, π) for which f satisfies the previous inequality.

The principle of maximum dissipation⁵⁰ prescribes that among all possible pairs (P, π) satisfying the admissibility criterion, the one that is physically realized maximizes the dissipation.

The expression for the dissipation here is the inequality (1.31). Maximizing it among admissible pairs (P, π) is tantamount to minimizing the Lagrangian

$\mathfrak{L}:=-\left(P·F^{\text{e}}{\stackrel{.}{F}}^{\text{p}}+\pi ·\stackrel{.}{\alpha }\right)+\lambda \text{f}\left(P,\pi \right)$

with respect to P and π. When f is differentiable, we get

${\stackrel{.}{F}}^{\text{p}}=\lambda F^{\text{e}-1}\frac{\partial \text{f}\left(P,\pi \right)}{\partial P}=\lambda F^{\text{p}}{F}^{-1}\frac{\partial \text{f}\left(P,\pi \right)}{\partial P}$

and

$\stackrel{.}{\alpha }=\lambda \frac{\partial \text{f}\left(P,\pi \right)}{\partial \pi },$

with λ ≥ 0, so we can identify the Lagrange multiplier λ with the rate of the plastic shift (Marsden & Hughes, 1983), and we have first λf(P, π) = 0, and then we can prove the consistency condition $\text{λ}\stackrel{.}{\text{f}}\left(P,\pi \right)=0$ (see Simo & Hughes, 1998 for the proof).

Another way of determining evolution laws for ${\stackrel{.}{F}}^{\text{p}}$ and $\stackrel{.}{\alpha }$ is, obviously, to prescribe them. The choice depends on the specific case that we are handling.

5.7 Doyle–ericksen formula in hardening plasticity

Relation (1.29) allows us to show that the Doyle–Ericksen formula, commonly derived and discussed in finite-strain elasticity (Doyle & Ericksen, 1956), holds also for elastic–plastic materials with hardening.

First, consider that Eq. (1.29) can be written as

$P=2\rho \tilde{g}{F}^{\text{e}}\frac{\partial {\tilde{\psi }}^{◊}\left(x,C^{\text{e}},\overline{g},\alpha \right)}{\partial C^{\text{e}}}{F}^{\text{p}-*},$

after defining ${\tilde{\psi }}^{◊}\left(x,C^{\text{e}},\overline{g}\right)$ as the free energy per unit mass, namely,

$\tilde{\psi }\left(x,C^{\text{e}},\overline{g},\alpha \right)=2\rho {\tilde{\psi }}^{◊}\left(x,C^{\text{e}},\overline{g},\alpha \right),$

ρ being the density of mass in the reference configuration.

We write ρ_a for the density of mass in the actual configuration. When mass is preserved, we have ρ = ρ_a det F.

Proof. Since by definition the right elastic Cauchy–Green tensor with all covariant components is defined by $C^{\text{e}}:=F^{\text{e}*}\tilde{g}{F}^{\text{e}}$, namely, $C_{\alpha \beta }^{\text{e}}={\left(F^{\text{e*}}\right)}_{\alpha }^i{\tilde{g}}_{\mathit{ij}}{\left(F^{\text{e}}\right)}_{\beta }^j$, we can consider C^e as a function of F^e and $\tilde{g}$, namely, $C^{\text{e}}={\tilde{C}}^{\text{e}}\left(F^{\text{e}},\tilde{g}\right)$. Since $\psi =\tilde{\psi }\left(x,C^{\text{e}},\overline{g}\right)$, as a result of G-invariance and objectivity requirements, we then have

$\frac{\partial \psi }{\partial \tilde{g}}=F^{\text{e}}\frac{\partial \tilde{\psi }\left(x,{\tilde{C}}^{\text{e}}\left(F^{\text{e}},\tilde{g}\right),\overline{g},\alpha \right)}{\partial C^{\text{e}}}{F}^{\text{e}*},$

so

$\frac{\partial \tilde{\psi }\left(x,C^{\text{e}},\overline{g},\alpha \right)}{\partial C^{\text{e}}}=F^{\text{e}-1}\frac{\partial \psi }{\partial \tilde{g}}{F}^{\text{e}-*}.$

From the definition of the first Piola–Kirchhoff stress, it then follows that

$\begin{array}{ll}\sigma \hfill & =\frac{1}{\text{det}F}P{F}^{*}=\frac{2\rho }{\text{det}F}\tilde{g}{F}^{\text{e}}\frac{\partial {\tilde{\psi }}^{◊}\left(x,C^{\text{e}},\overline{g},\alpha \right)}{\partial C^{\text{e}}}{F}^{\text{p}-*}{F}^{*}\hfill \\ \hfill & =2{\rho }_{\text{a}}\tilde{g}\frac{\partial \psi }{\partial \tilde{g}}{F}^{\text{e}-*}{F}^{\text{p}-*}{F}^{*}=2{\rho }_{\text{a}}\tilde{g}\frac{\partial \psi }{\partial \tilde{g}}{F}^{-*}{F}^{*},\hfill \end{array}$

which completes the proof.

5.8 Remarks and perspectives

• π does not appear in the power as an action conjugated with $\stackrel{.}{\alpha }$, with an eventual identification with $-\frac{\partial \tilde{\psi }}{\partial \alpha }$. For this reason π does not contribute to any balance equation. Hence, α is an internal variable in the sense of nonequilibrium thermodynamics (see, e.g., Capriz & Giovine, 1997; de Groot & Mazur, 1962).

• The previous remark inspires naturally (at least for me) another question: Can plasticity be described in the sense of the framework discussed in previous sections? In other words, can we associate with the plastic phenomena microstructural interactions satisfying their own balance equations? The approach would be in contrast with the choice of α, which is an unknown parameter useful just to measure the trend far from the neighborhood of thermodynamical equilibrium, where the mechanical behavior ceases to be elastic. In principle there is no obstacle to obtaining an affirmative answer. Of course it is matter of modeling because many choices of the nature of ν can be made, depending on the specific mechanism that we want to describe. An approach that connects the evolution of microdefects leading to plasticity with microactions satisfying their own balance is given in Dłużewsky (1996). The micromorphic scheme, the case when ν is a second-rank tensor (see Mindlin, 1964, for the linear case and also Green & Rivlin, 1964; Toupin, 1962, for the nonlinear setting), was adapted to plasticity in Fleck and Hutchinson (1997). Another example pertaining specifically to plasticity is given in Gurtin (2000b), where ν is identified with the slip velocity in single crystals. The subsequent pertinent literature is rather wide (see, e.g., Gudmundson, 2004; Gurtin & Anand, 2009; J. W Hutchinson, 2012; Reddy, Ebobisse, & McBride, 2008), and a specific essay could be dedicated to review it. The proposed models seem adequate (even particularly in certain cases) to capture various aspects of plastic phenomena and are often evidently useful to develop computations that may solve practical problems. And essentially the balance equations involving both macroscopic and microscopic actions (the latter associated with the mechanisms that the authors believe are essential to the description of specific aspects of the plastic flows) are in the most general cases deduced by resorting to the principle of virtual power as a basic source. To me this choice involves a foundational problem. In fact, when we start from the virtual power principle to find balance equations for a certain model, morally we have already in mind the exact structure of these balances. I have already stressed the point speaking in general about microstructures in previous sections. Proposing a virtual power principle is tantamount to assigning a priori the weak form of balance equations. Essentially, it could be the same to declare candidly in pointwise form the balances that one believes to be necessary for the analysis at hand. The question pertains to the internal actions appearing in these balances. When we assign the expression of the virtual power, we are postulating the existence of such inner actions (see, e.g., Gurtin & Anand, 2009). It could perhaps be useful to find that these actions are necessary, by means of some invariance procedure, for example, from the external power alone, as it appears in previous sections. Hence, to me a rather interesting question is the following: For what available models of plastic phenomena, based on balances of microactions, it is possible to prove the need for the existence of the inner actions that they involve (when they are involved) by means of some invariance procedure accepted as a first principle without postulating such actions? An answer could probably help in discriminating among models of the same phenomena.

• Beyond the question of the emergence of self-actions in the balance equations involving microactions, another issue to be discussed is the choice of ν to represent adequately plastic mechanisms. The issue could appear volatile when considered in full generality, for an answer depends on the specific material or phenomenon under analysis. However, in the case of crystalline materials, some details can be provided. For crystal lattices, Parry and Šilhavý (2000) have determined a basis for elastic invariants (see also Davini, 1996, for their definition). In a discussion we had in September 2001 at Taormina, Parry and I were in agreement that generic functions of the elastic invariants could be an adequate candidate for ν, but we neither followed up on our discussion nor wrote something about it. If we accept our remark and want to follow it, however, we have to handle it with care. In fact, a minimalistic choice for ν could be the dislocation density tensor, even without considering its gradient. The choice could be also appealing for it can be associated with geometric properties of the body manifold (its torsion). However, the same choice could be criticized. At the end of a 2001 paper entitled “Benefits and shortcomings of the continuous theory of dislocations,” Kröner (2001, p. 1132) wrote: “The greatest shortcoming is that the dislocation density tensor α, no matter whether introduced through differential geometry or in the conventional way, measures the average dislocation density only and, therefore, regards the internal mechanical state utmost incompletely. In principle, this shortcoming could be overcome by reorientation of dislocation theory towards a statistical theory, but only with highest expenditure of computations.” The remark suggests at least prudence in selecting a candidate for ν.

• Viewing plasticity in terms of the general framework of multiscale and multifield representations of material complexities, as introduced in previous sections, opens the way to models of strain-gradient effects in plastic phenomena. The necessity of the extension has been pointed out by crucial experiments (Fleck, Muller, Ashby, & Hutchinson, 1994), which have evidenced the effects due to the grain size in the torsion of thin metallic wires. These effects can be interpreted in terms of strain gradients. As a consequence, a number of related models of strain-gradient plasticity have been developed. Some of them have been quoted in the previous items, and at all times we have discussed the possibility of interpreting plastic phenomena in terms of a framework involving the balance of microactions due to microstructural events. A question is then the origin of the link between the analysis of the strain-gradient effects and the multifield setting. To give an adequate answer, we have to refer to a basic 1985 paper by Capriz (1985), with a preamble concerning a contemporary work by Dunn and Serrin (1985), who showed that the presence of the spatial derivatives of strain in the list of constitutive variables, defining the state of a material point, is compatible with the second law of thermodynamics when the standard inner power density $P·\stackrel{.}{F}$ is augmented by an addendum that depends on the same spatial derivatives of strain appearing in the list of state variables, decided from the beginning (such a description is rough, however it is sufficient to explain our argument here). Dunn and Serrin called such an addendum interstitial working, to remind us of the pioneering use of gradients of density made by Korteweg to describe capillary effects. However, notwithstanding the clear indication of the way to be followed to consider correctly strain-gradient effects, they did not go into the nature of the interstitial working with the aim of linking it with microstructural events. The link was established explicitly by Capriz (1985) for second-grade elasticity, i.e., in the case in which we consider the first derivative of F in the list of state variables. His remark is simple but has deep consequences. Let us consider the multifield and multiscale model-building framework discussed in previous sections. Imagine also that external bulk actions on the microstructure are absent, i.e., β = 0. If there is some physical reason to imagine an internal constraint of the type $\nu =\widehat{\nu }\left(F\right)$, in a conservative setting, the multifield and multiscale scheme accounting for material complexity reduces to second-grade elasticity and the necessary interstitial working is no more than the power of the microactions. Ofcourse, without considering the multifield framework used in Capriz (1985), for second-grade elasticity, we could introduce directly a hyperstress, a third-rank stress performing inner power in the spatial derivative of $\stackrel{.}{F}$, developing then the relevant mechanical structures. Such a stress emerges naturally in a conservative setting when we consider an elastic energy depending on F and DF, and we evaluate the first variation of it around minimizers, after proving their existence. In the nonconservative case, the existence of a hyperstress should be established, e.g., by a Cauchy-type theorem—an issue tackled, but not yet closed (the reader can find basic remarks in Fosdick & Virga, 1989; Nečas & Šilhavý, 1991; Noll & Virga, 1990). With respect to the actual state of the art, the interpretation in Capriz (1985) establishes a direct link between higher-order stresses and microstructural events, whatever they may be.

• The general multifield and multiscale framework for the mechanics of microstructures appears clearly useful when we turn our attention to strain-gradient plasticity and identify ν with F^p (the literature in this sense is rather wide—see the remarks in Gurtin & Anand, 2009) or even with the plastic part of the small-strain tensor (Fleck & Hutchinson, 1997). In accepting the identification of ν with F^p and following the guidelines proposed in previous sections, we would face the problem of interpreting changes in observers over $\mathcal{M}$, now the set including F^p, because F^p is a factor of the macroscopic deformation gradient F. The question deserves further investigations.

6.1 A remark on standard finite-strain elasticity

Consider the energy of an elastic simple body in the large-strain regime, disregarding body forces for the sake of simplicity:

$\mathcal{E}\left(u,\mathcal{B}\right):={\displaystyle {\int }_{\mathcal{B}}e\left(x,\text{D}u\left(x\right)\right)\text{d}x}.$

A result obtained by Coleman and Noll (1959) formalizes the physical incompatibility between the objectivity of the elastic energy density e (x, F) and its convexity with respect to F. In essence, it implies loss of uniqueness of equilibrium configurations under prescribed boundary conditions.

A requirement of polyconvexity of e with respect to F (the dependence suggested in Ball (1976/77)) reconciles analytical and physical instances. Polyconvexity means that we have to consider the elastic energy density as a convex function of the triple constituted by F, cof F, and det F. Also, when we take a polyconvex elastic energy and try to determine its minimizers, the minimizing sequences of F, cof F, and det F are independent of each other. The procedure assures that the strain compatibility of the elements in the sequence is preserved in the limit.

In discussing strain measures, we have already pointed out that det F and the entries of F and cof F can be put together in a unique geometric entity, the three-vector $M\left(F\right)\in {\text{Λ}}_3\left({\mathbb{R}}^3\times {\tilde{\mathbb{R}}}^3\right)$, with components the ones in the list (1, F,cof F,det F). Hence, we can consider the energy density as a convex function of M (F), as indicated in Giaquinta et al. (1989).

I have already remarked that M (F) does not always coincide with M (Du). The identity is ensured only when the strain is compatible. Considering e as a convex function of M (F) would then correspond to extending it even to incompatible strain states, a circumstance in agreement with the previous remark on minimizing sequences. Even in this case compatibility is recovered at the end of the minimizing procedure.

There is something more, however. The map F M (F) is not convex, nor is the subset of ${\text{Λ}}_3\left({\mathbb{R}}^3\times {\tilde{\mathbb{R}}}^3\right)$ containing elements of the type M (F)—write Σ_1,+,F for it. Hence, if we want to define a convex function of M (F), we must consider the convex hull of Σ_1,+,F, namely,

${\sum }_{1,+}:=\left\{M\in {\text{Λ}}_3\left({\mathbb{R}}^3\times {\tilde{\mathbb{R}}}^3\right)|M=\left(1,H,A,\mathfrak{a}\right),\mathfrak{a}>0\right\},$

with H and A the tensors defined in Section 2.5, and $\mathfrak{a}$ the scalar coinciding with det F when M = M (F). Once we have defined the energy density as a convex function over Σ_1,+, we add to it further conditions dictated by physics: the energy density increases to infinity when det F goes to zero or |M (F)| tends to infinity—infinite energy has to be paid for by shrinking to a point a volume or by stretching to infinity a string. These requirements imply an analytical property: the energy is coercive. It is crucial in determining the existence of equilibrium states (the ones reached by a requirement of minimality for the energy). Previous conditions imply also that the energy is coercive even when evaluated over the inverse map, i.e., when it is referred to the actual shape of the body.

When we accept

$e\left(x,F\right)=\tilde{e}\left(x,M\left(F\right)\right),$

the first Piola–Kirchhoff stress

$P=\frac{\partial e\left(x,F\right)}{\partial F}$

becomes

$P=\frac{\partial \tilde{e}\left(x,M\left(F\right)\right)}{\partial M\left(F\right)}\frac{\text{d}M\left(F\right)}{\text{d}F}.$

Since, by definition, M (F) is a third-rank, skew-symmetric tensor with all contravariant components (see Section 2.5), the components of the third-rank, skew-symmetric tensor

$\omega :=\frac{\partial \tilde{e}\left(x,M\left(F\right)\right)}{\partial M\left(F\right)}$

are all covariant, so ω is dual to M (F) and the product ω · M (F) is well defined in terms of duality pairing (see Section 2). Formally, we write $M\left(F\right)\in {\text{Λ}}_3\left({\mathbb{R}}^3\times {\tilde{\mathbb{R}}}^3\right)$ and $\omega \in {\text{Λ}}^3\left({\mathbb{R}}^3\times {\tilde{\mathbb{R}}}^3\right)$. The map x ω (x) is then a three-form over $\mathcal{B}$.

6.2 The current of a map and the inner work of elastic simple bodies

In the Lagrangian representation, consider the inner power of an elastic simple body undergoing large strains, namely,

${\displaystyle {\int }_{\mathcal{B}}P·\stackrel{.}{F}\text{d}x}.$

By taking into account the expressions in the previous section, we can write

$\begin{array}{ll}{\displaystyle {\int }_{\mathcal{B}}P·\stackrel{.}{F}\text{d}x}\hfill & ={\displaystyle {\int }_{\mathcal{B}}\omega \frac{\text{d}M\left(F\right)}{\text{d}F}·\stackrel{.}{F}\text{d}x}={\displaystyle {\int }_{\mathcal{B}}\omega ·\frac{\text{d}M\left(F\right)}{\text{d}F}\stackrel{.}{F}\text{d}x}\hfill \\ \hfill & ={\displaystyle {\int }_{\mathcal{B}}\omega ·\frac{\text{d}M\left(F\right)}{\text{d}F}\stackrel{.}{F}\text{d}x}={\displaystyle {\int }_{\mathcal{B}}\omega ·\stackrel{.}{M}\left(F\right)\text{d}x,}\hfill \end{array}$

and, in case of strain compatibility,

${\displaystyle {\int }_{\mathcal{B}}P·\stackrel{.}{F}\text{d}x}={\displaystyle {\int }_{\mathcal{B}}\omega ·\stackrel{.}{M}\left(\text{D}u\right)\text{d}x}.$

Since $\omega ·\stackrel{.}{M}\left(\text{D}u\right)$ is an inner power density, the integral

${\displaystyle {\int }_{\mathcal{B}}\omega ·M\left(\text{D}u\right)\text{d}x}$

has the meaning of inner work.

Once we fix u, we can allow ω to vary arbitrarily. The physical significance of such a choice is that of a virtual inner work obtained by testing virtual stresses over a given deformation. The remark clarifies the physical meaning of the functional G_u defined on smooth forms compactly supported over $\mathcal{B}\times {\tilde{\mathbb{R}}}^3$ by

$G_u\left(\omega \right):={\displaystyle {\int }_{\mathcal{B}}\omega \left(x,u\left(x\right)\right)·M\left(\text{D}u\left(x\right)\right)\text{d}x}$

and commonly called the current of u in geometric functional analysis (see the treatise Giaquinta et al., 1998). For any second-rank skew-symmetric tensor-valued map $x\mapsto \overline{\omega }\left(x\right)$, we define another functional, ∂ G_u, by

$\partial G_u\left(\overline{\omega }\right)=G_u\left(\text{d}\overline{\omega }\right),$

with d the exterior derivative. ∂ G_u is commonly called the boundary of G_u.

Summable maps u over $\mathcal{B}$ with a summable first distributional derivative, specifically elements of $W^{1,1}\left(\mathcal{B},{\tilde{\mathbb{R}}}^3\right)$, such that

• det Du (x) > 0 for almost every $x\in \mathcal{B}$,

• the map assigning to every x the modulus (intended in the standard sense of modulus of tensors) |M (Du (x))| is summable too,

• ∂ G_u = 0 on smooth, compactly supported 2-forms over $\mathcal{B}\times {\tilde{\mathbb{R}}}^3$, and

• for any $\tilde{f}\in C_c^{\infty }\left(\mathcal{B}\times {\widehat{\mathbb{R}}}^d\right)$

${\displaystyle {\int }_{\mathcal{B}}\tilde{f}\left(x,u\left(x\right)\right)\text{det D}u\left(x\right)\text{d}x}\le {\displaystyle {\int }_{{\tilde{\mathbb{R}}}^3}\underset{x\in \mathcal{B}}{\text{sup}}\tilde{f}\left(x,r\right)\text{d}r},$

  (1.32)

are called weak diffeomorphisms (Giaquinta et al., 1989).

Under the conditions ensuring coercivity, minimizers of the elastic energy in the finite-strain regime are found in a subclass of the space of weak diffeomorphisms with summability p > 1, as shown in Giaquinta et al. (1989).

The integral inequality (1.32) allows self-contact of the body boundary along the deformation and prevents self-penetration. The constraint $\partial G_u\left(\overline{\omega }\right)=0$ is stable when we superpose on u any other smooth deformation. It excludes the formation of holes and/or fractures. When such a condition is satisfied, u cannot be multivalued in any part of its domain, as occurs, for example, when a crack is nucleated and, eventually, opens and/or closes along a deformation. In other words, the graph of u is free of vertical components—verticality refers to the reference place $\mathcal{B}$ in the six-dimensional space ${\mathbb{R}}^3\times {\tilde{\mathbb{R}}}^3$, the first factor referred to the three-dimensional point space containing $\mathcal{B}$.

In this framework, if we want to model elastic–brittle behavior, we need to enlarge the functional setting at least weakening the constraint $\partial G_u\left(\overline{\omega }\right)=0$.

6.3 The griffith energy

When a fracture occurs in a body, energy is dissipated but energy is also localized along the crack margins, to ensure the stability of the matter. It was Josiah Willard Gibbs who insisted on the assignment of positive surface energy to interfaces to ensure stability of condensed matter structure. For fractures, in his pioneer work, Griffith (1920) presumed that the surface energy is proportional to the area of the crack margins. Hence, for an elastic–brittle solid undergoing bulk deformations, when a fracture occurs, the Griffith's energy, $\mathfrak{E}\left(u,\mathcal{B},\mathcal{C}\right)$, is

$\mathfrak{E}\left(u,\mathcal{B},\mathcal{C}\right):={\displaystyle {\int }_{\mathcal{B}}e\left(x,\text{D}u\left(x\right)\right)\text{d}x}+{\displaystyle {\int }_{\mathcal{C}}ɸ\text{d}{\mathcal{H}}^2},$