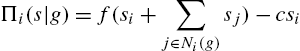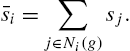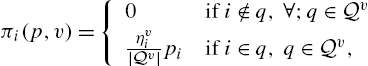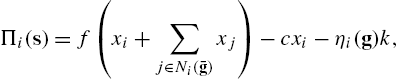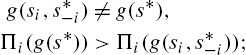Heterogeneity and Networks✶
Sanjeev Goyal Faculty of Economics and Christ's College, University of Cambridge, Cambridge, United Kingdom, [email protected]
Abstract
This chapter shows that networks can have large and differentiated effects on behavior and then argues that social and economic pressures facilitate the formation of heterogeneous networks. Thus networks can play an important role in understanding the wide diversity in human behavior and in economic outcomes.
Keywords
Networks; Network formation; Heterogeneity; Linking; Intermediation; Structural holes
1 Introduction and Overview
Social, economic and infrastructure networks are an important feature of an economy. Empirical research has highlighted the presence of great heterogeneity in these networks. We see this heterogeneity in Twitter (the number of followers ranges from less than ten to well over a million), in production networks (where real estate and finance form hubs), and in transport networks (airlines typically operate hub-spoke routes). This heterogeneity in connections raises two questions: one, how does network structure shape behavior at an individual and at the system level and two, what are the processes that give rise to such unequal networks? In this chapter I will argue one, that networks can have large and differentiated effects on behavior and two, that social and economic pressures facilitate the formation of heterogeneous networks. Thus networks can play an important role in understanding the diversity in economic outcomes that is observed empirically. I will draw heavily on two recent survey papers, Goyal (2016, 2017). Bramoulle et al. (2016) provide a panoramic overview of recent research on the economics of networks. Easley and Kleinberg (2010) offer a broad inter-disciplinary introduction to the study of networks.
The key methodological innovation of the early research on the economics of networks in the 1990s was the introduction of graph theory alongside purposeful agents. Two ideas were central: the study of how the network architecture shapes human behavior and the study of how purposeful individuals form links and thereby create networks. Over the past two decades, economists have developed a sophisticated understanding of the scope of these ideas and they are increasingly being used to address a wide range of applied questions.
To develop the main arguments in a straightforward way, I will concentrate on covering four research papers in some detail: a model of local strategic substitutes on a network Bramoulle and Kranton (2007), a model of trading in networks Choi et al. (2017), a model of simultaneous network formation and behavioral choice with local strategic substitutes Galeotti and Goyal (2010), and finally, a model of network formation where payoffs are determined by trade and intermediation benefits Goyal and Vega-Redondo (2007). In the first two papers the network is exogenous, and the latter two papers should be seen as a generalization in which the network is treated as endogenous.
The rest of the paper is organized as follows. Section 2 presents basic notation and terminology on networks. Section 3 discusses the theory of network formation, while Section 4 examines the effects of networks on behavior by presenting a framework that combines individual choice, networks and markets. Section 5 presents a discussion of models in which individuals choose actions as well as choose links, while Section 6 concludes.
2 Networks: Terminology
I begin by introducing some notation and a few basic concepts about networks. For a general overview of graph theory, see Bollobas (1998); for an introduction of network concepts to economics, see Goyal (2007), Jackson (2008) and Vega-Redondo (2007).
A network g comprises a collection of nodes ![]() with
with ![]() , and the links
, and the links ![]() ,
, ![]() , between them. A node may be an individual, a firm, a project, a city or a country, or even a collection of such entities. A link between them signifies a relation. In some instances it is natural to think of the link as bidirectional: examples include friendship, research collaboration and defense alliance. In other instances, a link is unidirectional: examples include investment in a project, citation, a web link, listening to a speech or following a tweet. In this section I will focus on undirected graphs; the concepts and terminology extend naturally to directed networks.
, between them. A node may be an individual, a firm, a project, a city or a country, or even a collection of such entities. A link between them signifies a relation. In some instances it is natural to think of the link as bidirectional: examples include friendship, research collaboration and defense alliance. In other instances, a link is unidirectional: examples include investment in a project, citation, a web link, listening to a speech or following a tweet. In this section I will focus on undirected graphs; the concepts and terminology extend naturally to directed networks.
In case ![]() in g,
in g, ![]() adds the link
adds the link ![]() , while if
, while if ![]() in g then
in g then ![]() . Similarly, if
. Similarly, if ![]() in g,
in g, ![]() deletes the link
deletes the link ![]() , while if
, while if ![]() in g, then
in g, then ![]() . Let
. Let ![]() denote the nodes with whom node i has a link; this set will be referred to as the neighbors of i. Let
denote the nodes with whom node i has a link; this set will be referred to as the neighbors of i. Let ![]() denote the number of connections/neighbors of node i in network g. Moreover, for any integer
denote the number of connections/neighbors of node i in network g. Moreover, for any integer ![]() , let
, let ![]() be the d-neighborhood of i in g: this is defined inductively,
be the d-neighborhood of i in g: this is defined inductively, ![]() and
and ![]() . So the 2-neighborhood of i includes the neighbors of i and the neighbors of the neighbors of i.
. So the 2-neighborhood of i includes the neighbors of i and the neighbors of the neighbors of i.
There is a path from i to j in g either if ![]() or there exist distinct nodes
or there exist distinct nodes ![]() different from i and j such that
different from i and j such that ![]() . A component is a maximal collection of nodes such that there is a path between every pair of nodes. A network g is said to be connected if there exists only one component, i.e., there is a path from any node i to every other node j.
. A component is a maximal collection of nodes such that there is a path between every pair of nodes. A network g is said to be connected if there exists only one component, i.e., there is a path from any node i to every other node j.
Let ![]() be a partition of nodes: two nodes belong to the same group if and only if they have the same degree. A network is said to be regular if every node has the same number of links i.e.,
be a partition of nodes: two nodes belong to the same group if and only if they have the same degree. A network is said to be regular if every node has the same number of links i.e., ![]()
![]() (and so all nodes belong to one group in the partition). The complete network,
(and so all nodes belong to one group in the partition). The complete network, ![]() , is a regular network in which
, is a regular network in which ![]() , while the empty network,
, while the empty network, ![]() , is a regular network in which
, is a regular network in which ![]() . Fig. 1 presents regular networks.
. Fig. 1 presents regular networks.
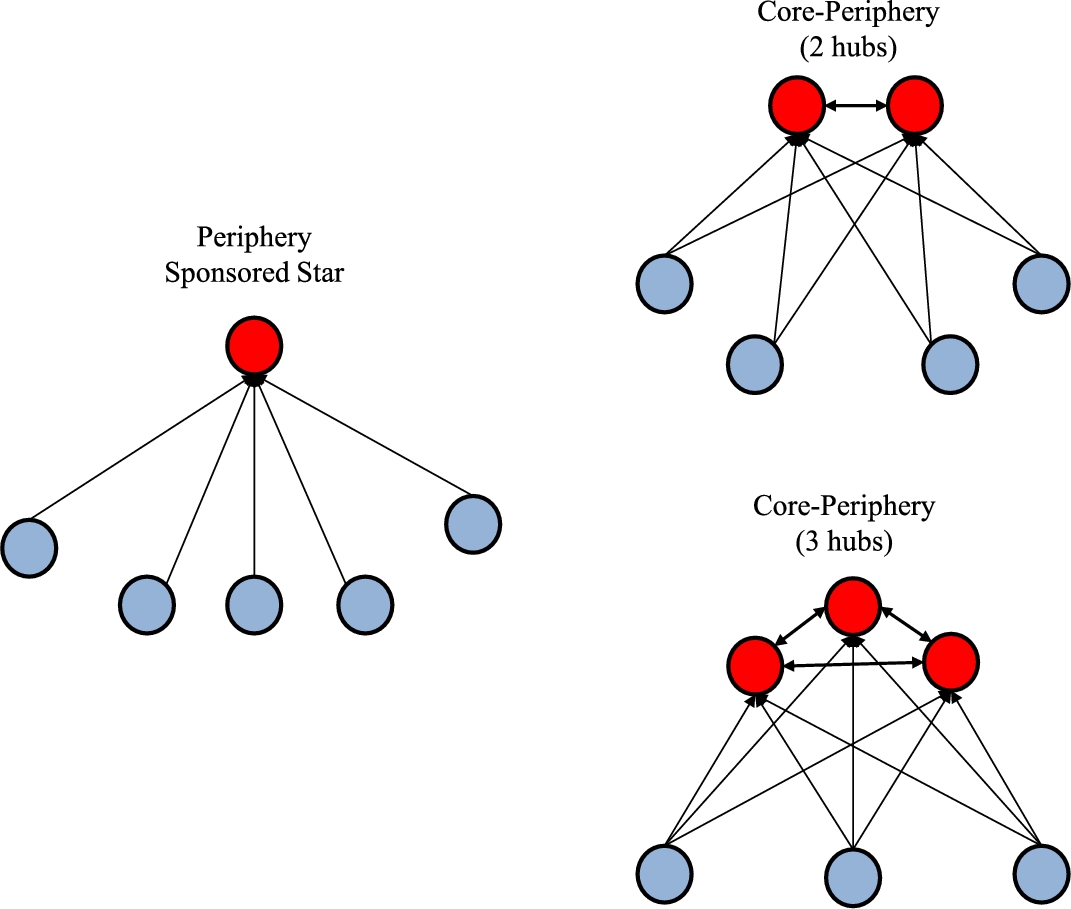
Once we step outside the class of regular networks, a wide variety of networks arise. A core-periphery network contains two groups: the periphery, ![]() , and the core,
, and the core, ![]() . Nodes in the periphery have a link only with nodes in the core; nodes in the core are fully linked with each other and have links with a subset of nodes in the periphery. The star (or hub-spoke) network is a special case in which the core contains a single node. The nested split graph is a partition of nodes
. Nodes in the periphery have a link only with nodes in the core; nodes in the core are fully linked with each other and have links with a subset of nodes in the periphery. The star (or hub-spoke) network is a special case in which the core contains a single node. The nested split graph is a partition of nodes ![]() into two or more sets such that for
into two or more sets such that for ![]() ,
, ![]() ,
, ![]() if and only if
if and only if ![]() , where
, where ![]() . Fig. 2 presents a range of such networks.
. Fig. 2 presents a range of such networks.

It is important to note that networks allow for a very rich range of possibility, that go beyond degrees. To bring out this point in a simple way, consider a degree-2 regular network and a (generalized) star network with the same number of links. This is presented in Fig. 3.

Now observe that as the number of nodes increases, ‘distance’ between the nodes is unbounded in the ring but it is bounded above by 2 in the star network. In the regular network, all nodes are essentially symmetric, while in the core-periphery network the hub nodes clearly have many more connections and are more ‘central’ than the other nodes.
3 The Theory of Network Formation
The finding that the social structure has large effects on individual behavior and payoffs suggests that individuals have an incentive to create networks that are advantageous to themselves. This observation has inspired the theory of network formation. In this section I briefly sketch the building blocks of the theory. The exposition borrows heavily from Goyal (2016, 2017).
The beginnings of the theory of network formation can be traced back to the work of Boorman (1975), Aumann and Myerson (1988) and Myerson (1991). The general framework and a systematic theory of network formation was first presented in Bala and Goyal (2000) and in Jackson and Wolinsky (1996). The two papers present complementary approaches to the process of network formation.1
I first take up the approach of unilateral link formation. This approach was introduced in Goyal (1993) and systematically studied in Bala and Goyal (2000). Consider a collection of individuals, each of whom can form a link with any subset of the remaining players. Link formation is unilateral: an individual can decide to form a link with another individual by paying for the link. It takes time and effort to sustain a link. A link with another individual allows access, in part and in due course, to the benefits available to the latter via his own links. Thus individual links generate externalities whose value depends on the level of decay/delay associated with indirect links. As links are created on an individual basis, the network formation process can be analyzed as a noncooperative game. The paper allows for general payoffs: utility increases in the number of people accessed and it decreases in the number of maintained links
There are interesting practical examples of this type of link formation – hyper-links across web-pages, citations, ‘following’ relations on Twitter, and gifts. But the principal appeal of this model is its simplicity. This simplicity allows for a systematic study of a number of central questions concerning social and economic networks.
Bala and Goyal (2000) provide a characterization of the architecture of equilibrium networks. The equilibrium networks have simple architectures: star (hub-spoke) networks and the cycle are salient. This prediction of great heterogeneity in connections and the presence of highly connected ‘hub’ nodes is an important theoretical contribution. In the star network, the central hub node will generally earn much larger payoffs as compared to the peripheral nodes. Thus, the theory provides a foundation for the idea that social structures may sustain great inequality.2
I turn next to two-sided or bilateral link formation. This approach was introduced and developed in Jackson and Wolinsky (1996). A link between two players requires the approval of both the players involved. This is the natural way to think about link formation in a number of social and economic contexts such as the formation of friendship ties, co-authorship, collaborations between firms, trading links between buyers and sellers, and free trade agreements between nations.
The simplest way to think of two sided link formation is to imagine an announcement game along the lines of the game sketched by Myerson (1991). Each player announces a set of intended links. A link between two individuals A and B is formed if both A and B announce an intention to create a link. In a context where links are two sided there are elements of “cooperation” involved in the formation of a link, and so solving such games calls for new concepts.
It is useful to begin the discussion with the familiar notion of Nash equilibrium as this will illustrate some of the conceptual issues that arise in the study of network formation with two-sided links. If every player announces that she wants to form no links then a best response is to announce no links. In other words, the empty network is a Nash equilibrium for any network formation game. To overcome this type of coordination failure, Jackson and Wolinsky (1996) propose the concept of pairwise stable networks.
A network is said to be pairwise stable if no individual wishes to delete a link and if no two unlinked individuals wish to form a link: Pairwise stability looks at the attractiveness of links in a network g, one at a time. Formally, every link present in a stable network must be profitable for the players involved in the link. For every link not present in the network it must be the case that if one player strictly gains from the link then the other player must be strictly worse off.
The second important contribution of the Jackson and Wolinsky (1996) paper was the finding that there is typically a tension between the requirement of strategic stability and of social efficiency. This highlights the presence of externalities in linking activity and remains a recurring theme in the subsequent research in this area.
The great attraction of pairwise stability is its simplicity. For any network it is relatively easy to check whether the two conditions are satisfied. The theoretical properties of this solution concept have been developed systematically and the solution concept has been widely applied. For a survey of this work, see Bloch and Dutta (2012) and Jackson (2008).
The theory of network formation has been and remains a very active field of research; for book length overviews, see Goyal (2007) and Jackson (2008). For a recent overview on network formation models and their applications, see Bramoulle et al. (2016).
4 Networks and Individual Behavior
This section introduces a framework for the study of behavior in networks. It will develop the argument that behavior in networks is shaped both by the nature of strategic interaction and by the structure of the network. These two forces can lead to significant heterogeneity in behavior and in payoffs for individuals, who are otherwise identical. I will draw heavily on Goyal (2007); for related surveys of this field, see Jackson and Zenou (2014) and Bramoulle and Kranton (2016).3
Games on networks consist of the set of players, the actions each of the players can choose, a description of the network of relationships between the players and a specification of how the actions and the network together define the payoffs accruing to each player.
The formulation of the strategies of players located in a network raises a number of considerations. Perhaps the first issue that needs to be discussed is whether players are obliged to choose the same action for all links or whether they have the freedom to choose link specific actions. It is reasonable to model individuals as choosing a single action in some contexts – such as consumer search about product prices or other characteristics. However, in some other contexts – an example would be effort in research projects – it is clear that individuals have the choice of putting different amounts of resources in different projects and frequently do exercise this option. However, the single action for all links model has the great merit of being very simple to work with and indeed most applications to date have worked with this formulation.
Suppose each player i takes an action ![]() in S, where S is a compact subset of
in S, where S is a compact subset of ![]() . The payoff (utility or reward) to player i under the profile of actions
. The payoff (utility or reward) to player i under the profile of actions ![]() is given by
is given by ![]() . In what follows,
. In what follows, ![]() refers to the profile of strategies of all players, other than player i.
refers to the profile of strategies of all players, other than player i.
We now turn to the role of networks in mediating effects of actions across players. A network has a number of different attributes – such as neighborhood size, distance, degree distribution – and it is clear that these attributes will play more or less important roles depending on the particular context under study. So there are many different ways in which network structure can be brought into the payoff function.
4.1 Local Interactions
Individuals are more affected by the actions of those who are “close by” – such as neighbors, friends, partners, and colleagues. The simplest case arises when only actions of neighbors matter and the actions of non-neighbors have no effects on an individual's payoffs. This is the case of pure local effects.4 This subsection studies a game with local effects. The next section takes up more general network effects.
A game with pure local effects exhibits positive externality if the payoffs are increasing in actions of neighbors, and it exhibits negative externality if they are decreasing in actions of neighbors. Turning next to strategic relations, a game with pure local effects is said to exhibit strategic complements or strategic substitutes depending on whether the marginal returns to own action for player i are increasing or decreasing in the efforts of her neighbors.
I now present a simple game on networks with local effects. Suppose each player chooses an action ![]() , where S is a compact interval in
, where S is a compact interval in ![]() . Following Bramoulle and Kranton (2007), suppose that the payoffs to a player i, in a network g, faced with a profile of efforts
. Following Bramoulle and Kranton (2007), suppose that the payoffs to a player i, in a network g, faced with a profile of efforts ![]() , are given by:
, are given by:
(1)
where ![]() is the marginal cost of effort. Assume that
is the marginal cost of effort. Assume that ![]() ,
, ![]() and
and ![]() . Define
. Define ![]() to be such that
to be such that ![]() . Moreover, the payoffs are an increasing function of others actions and the marginal payoffs are a decreasing function of others actions. Therefore, this is a game of positive externalities and strategic substitutes. ‘Local public goods’ is perhaps the natural interpretation of actions in this model.
. Moreover, the payoffs are an increasing function of others actions and the marginal payoffs are a decreasing function of others actions. Therefore, this is a game of positive externalities and strategic substitutes. ‘Local public goods’ is perhaps the natural interpretation of actions in this model.
The action set is compact, the payoffs are continuous in the actions of all players, and strictly concave in own action, and so it follows from standard considerations that a Nash equilibrium in pure strategies exists. We now examine how an equilibrium is sensitive to the structure of the network.
Define the sum of efforts of neighbors to be:
From the strict concavity of ![]() , it follows that if
, it follows that if ![]() then marginal returns to effort are lower than the marginal cost and so optimal effort is 0, while if
then marginal returns to effort are lower than the marginal cost and so optimal effort is 0, while if ![]() , then marginal returns from effort to player are strictly larger than marginal costs c and so optimal effort is positive, and given by
, then marginal returns from effort to player are strictly larger than marginal costs c and so optimal effort is positive, and given by ![]() .
.
So in equilibrium there are potentially two types of players: one, those who receive aggregate effort from their neighbors in excess of ![]() and exert no effort on their own, and two, players who receive less than
and exert no effort on their own, and two, players who receive less than ![]() aggregate effort from their neighbors and contribute exactly the difference between what they receive and
aggregate effort from their neighbors and contribute exactly the difference between what they receive and ![]() . An implication is that an individual will choose
. An implication is that an individual will choose ![]() if and only if each of her neighbors choose 0. So we start by examining specialized equilibria, i.e., outcomes in which every player chooses either
if and only if each of her neighbors choose 0. So we start by examining specialized equilibria, i.e., outcomes in which every player chooses either ![]() or 0.
or 0.
We will use the concept of independent sets. An independent set of a network g is a set of players ![]() such that for any
such that for any ![]() ,
, ![]() , i.e., no two players in I are directly linked. A maximal independent set is an independent set that is not contained in any other independent set.
, i.e., no two players in I are directly linked. A maximal independent set is an independent set that is not contained in any other independent set.
Every network contains a maximal independent set: number the players ![]() . Now start by placing player 1 in I, and look for players
. Now start by placing player 1 in I, and look for players ![]() . If player
. If player ![]() , then include her in the independent set, I, if not then include her in the complement set
, then include her in the independent set, I, if not then include her in the complement set ![]() . Suppose, to fix ideas that,
. Suppose, to fix ideas that, ![]() . Next consider player 3: if player
. Next consider player 3: if player ![]() , then include her in I, while if she is then include her in
, then include her in I, while if she is then include her in ![]() . Move next to player 4 and proceed likewise until you reach player n. At each stage, a player is included in the set if she is not a neighbor of any player who is already included in the set. This process is well defined, and will lead to a maximal set of players I such that for any pair of players
. Move next to player 4 and proceed likewise until you reach player n. At each stage, a player is included in the set if she is not a neighbor of any player who is already included in the set. This process is well defined, and will lead to a maximal set of players I such that for any pair of players ![]() ,
, ![]() .
.
Observe that in the empty network there exists a unique maximal independent set and this is the set of all players N. In the complete network, on the other hand, there are n distinct maximal sets, each of which contains a single player. In the star network, there are two maximal independent sets: a set that contains only the central player and a set that contains all the peripheral players.
Maximal independent sets have an intimate connection with specialized Nash equilibria: assign the action ![]() to every member of a maximal independent set and assign action 0 to every player who is not a member of this maximal independent set. This configuration constitutes an equilibrium in view of the characterization provided in Proposition 1.
to every member of a maximal independent set and assign action 0 to every player who is not a member of this maximal independent set. This configuration constitutes an equilibrium in view of the characterization provided in Proposition 1.
Moreover, it is immediate that in any non-empty network, a maximal independent set must be a strict subset of the set of players N. Thus every such network is characterized by extreme heterogeneity in effort levels – with some players being experts and contributing ![]() while others contribute 0 – across otherwise identical individuals.
while others contribute 0 – across otherwise identical individuals.
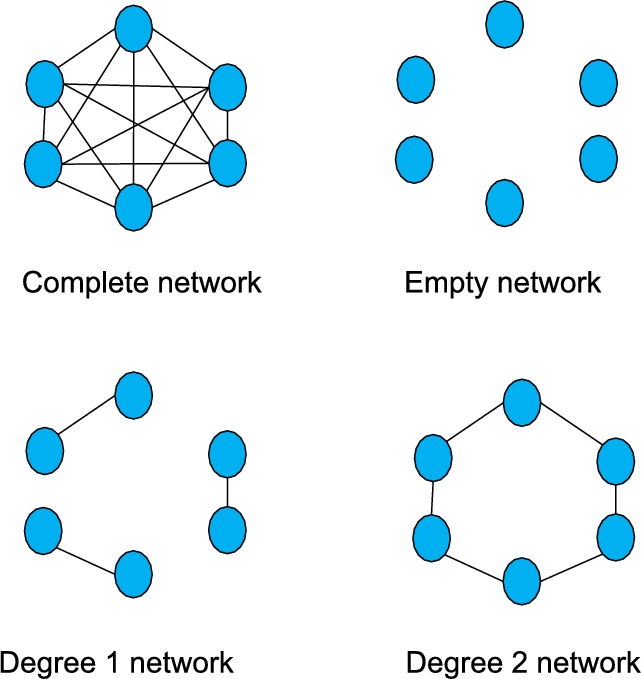
This result gives us a first impression of how networks matter: when we move from the empty network to any non-empty network this gives rise to the possibility of significant free riding, with a subset of players exerting maximal effort while others exert no effort at all. For instance, in the star network there are two specialized equilibria: one, where the central player chooses ![]() and all the peripheral players choose 0; two, every peripheral player chooses
and all the peripheral players choose 0; two, every peripheral player chooses ![]() , and the central player chooses 0. Fig. 4 illustrates these equilibria.
, and the central player chooses 0. Fig. 4 illustrates these equilibria.
We now turn to the possibility of outcomes in which everyone contributes positively. Define an equilibrium strategy profile in which all players choose positive effort as a distributed equilibrium. It is easy to see that there does not always exist such an equilibrium. Take the star network. In a distributed equilibrium it must be the case that for every player i, ![]() and
and ![]() . Let
. Let ![]() denote the central player's effort. For any peripheral player l, Proposition 1 says that
denote the central player's effort. For any peripheral player l, Proposition 1 says that ![]() , while for the central player,
, while for the central player, ![]() . These equalities cannot be simultaneously satisfied since
. These equalities cannot be simultaneously satisfied since ![]() for every peripheral player in a distributed equilibrium.
for every peripheral player in a distributed equilibrium.
Distributed equilibria, however, arise naturally in regular networks: there exists a symmetric distributed equilibrium ![]() such that
such that ![]() . Every player chooses
. Every player chooses ![]() .
.
Turning next to the distribution of payoffs: in a specialized equilibrium the active players will earn ![]() , while the free riders will earn at least
, while the free riders will earn at least ![]() . If c is large then networks can give rise to large heterogeneity in payoffs.
. If c is large then networks can give rise to large heterogeneity in payoffs.
This subsection focused on games of pure local effects: we showed how networks can generate large behavioral heterogeneity and correspondingly large payoff inequality. The study of games with local effects remains an active field of research, see e.g., Gagnon and Goyal (2017). We now turn to an example of general network effects.
4.2 Trading in Networks
Supply, service and trading chains are a defining feature of the modern economy. They are prominent in agriculture, in transport and communication networks, in international trade, and in finance. The routing of economic activity, the allocation of surplus and the efficiency of the system depend on the prices set by these different intermediaries. The goal here is to propose a simple model of price setting in a network of intermediaries.
By way of motivation, consider a tourist who wishes to travel by train from London to see the Louvre in Paris. The first leg of the journey is from home to St. Pancras Station. There are a number of different taxi companies, bus services and the Underground. Once at St. Pancras Station, the only service provider to Paris Nord Station is Eurostar. Upon arriving at Paris Nord, there are a number of alternatives (bus, Metro and taxi) to get to the Louvre. The network consists of alternative paths each constituted of local transport alternatives in London and in Paris and the Eurostar Company. Each of the service providers sets a price. The traveler picks the cheapest ‘path’. Fig. 5 represents this example.

Building on this example, Choi et al. (2017) propose the following model: there is a source node, ![]() , and a destination node,
, and a destination node, ![]() . A path between the two is a sequence of interconnected nodes, each occupied by an intermediary. The source node and the destination node and all the paths between them together define a network. The passage from source to destination generates a surplus. First let us consider the simple case where this surplus is known and set it equal to 1. Intermediaries (who have zero cost) simultaneously post a price. The prices determine a total cost for every path between
. A path between the two is a sequence of interconnected nodes, each occupied by an intermediary. The source node and the destination node and all the paths between them together define a network. The passage from source to destination generates a surplus. First let us consider the simple case where this surplus is known and set it equal to 1. Intermediaries (who have zero cost) simultaneously post a price. The prices determine a total cost for every path between ![]() and
and ![]() . The tourist moves along a least cost path: so an intermediary earns payoffs only if she is located on it. This completes the description of a game on a network.
. The tourist moves along a least cost path: so an intermediary earns payoffs only if she is located on it. This completes the description of a game on a network.
To build some intuition for how networks matter, let us consider two simple networks. The first network has two paths between ![]() and
and ![]() , each with a distinct intermediate node. The two intermediaries compete in price: this is a simple game of strategic complements. Standard arguments – a la Bertrand – tell us that both firms will set a price equal to 0. The second network contains a single line with two nodes between
, each with a distinct intermediate node. The two intermediaries compete in price: this is a simple game of strategic complements. Standard arguments – a la Bertrand – tell us that both firms will set a price equal to 0. The second network contains a single line with two nodes between ![]() and
and ![]() . The two intermediaries are now engaged in bilateral Nash Bargaining and the strategies are strategic substitutes (assuming that the sum of demands must equal the value of surplus). As in the Nash bargaining model, there are a number of possible outcomes.
. The two intermediaries are now engaged in bilateral Nash Bargaining and the strategies are strategic substitutes (assuming that the sum of demands must equal the value of surplus). As in the Nash bargaining model, there are a number of possible outcomes.
Turning to the general model, every intermediary i simultaneously posts a price ![]() . Let
. Let ![]() denote the price profile. The network g and the price profile p define a cost for every path q between
denote the price profile. The network g and the price profile p define a cost for every path q between ![]() and
and ![]() :
:
(2)
Let ![]() be the set of all paths between
be the set of all paths between ![]() and
and ![]() . Payoffs arise out of active intermediation: an intermediary i obtains
. Payoffs arise out of active intermediation: an intermediary i obtains ![]() only if he lies on a feasible least cost path. A least cost path
only if he lies on a feasible least cost path. A least cost path ![]() is one such that
is one such that ![]() . Define
. Define ![]() . A path q is feasible if
. A path q is feasible if ![]() , where v is the value of economic ‘good’ generated by the path. All paths generate the same value v. If there are multiple least cost paths, one of them is chosen randomly to be the active path. Given g, p and v, denote by
, where v is the value of economic ‘good’ generated by the path. All paths generate the same value v. If there are multiple least cost paths, one of them is chosen randomly to be the active path. Given g, p and v, denote by ![]() the set of feasible least cost paths, and intermediary i's payoff is given by:
the set of feasible least cost paths, and intermediary i's payoff is given by:
(3)
where ![]() is the number of paths in
is the number of paths in ![]() that contain intermediary i.
that contain intermediary i.
A node is said to be critical if it lies on all paths between ![]() and
and ![]() . Choi et al. (2017) develop the following characterization of equilibrium pricing.
. Choi et al. (2017) develop the following characterization of equilibrium pricing.
Observe that if there is trade and there exist critical traders then intermediaries must extract all surplus: if not then a critical trader can raise its price and increase profits strictly. However, critical traders are not necessary for surplus extraction. This is because of possible coordination failures along chains of traders that enhance the market power of non-critical traders. These coordination problems give rise to multiple equilibria.5
This multiplicity and the possibility of very different allocations of surplus motivates an experimental study of pricing. Choi et al. (2017) choose networks that allow us to examine the roles of coordination, competition and market power. These networks are depicted in Fig. 6.
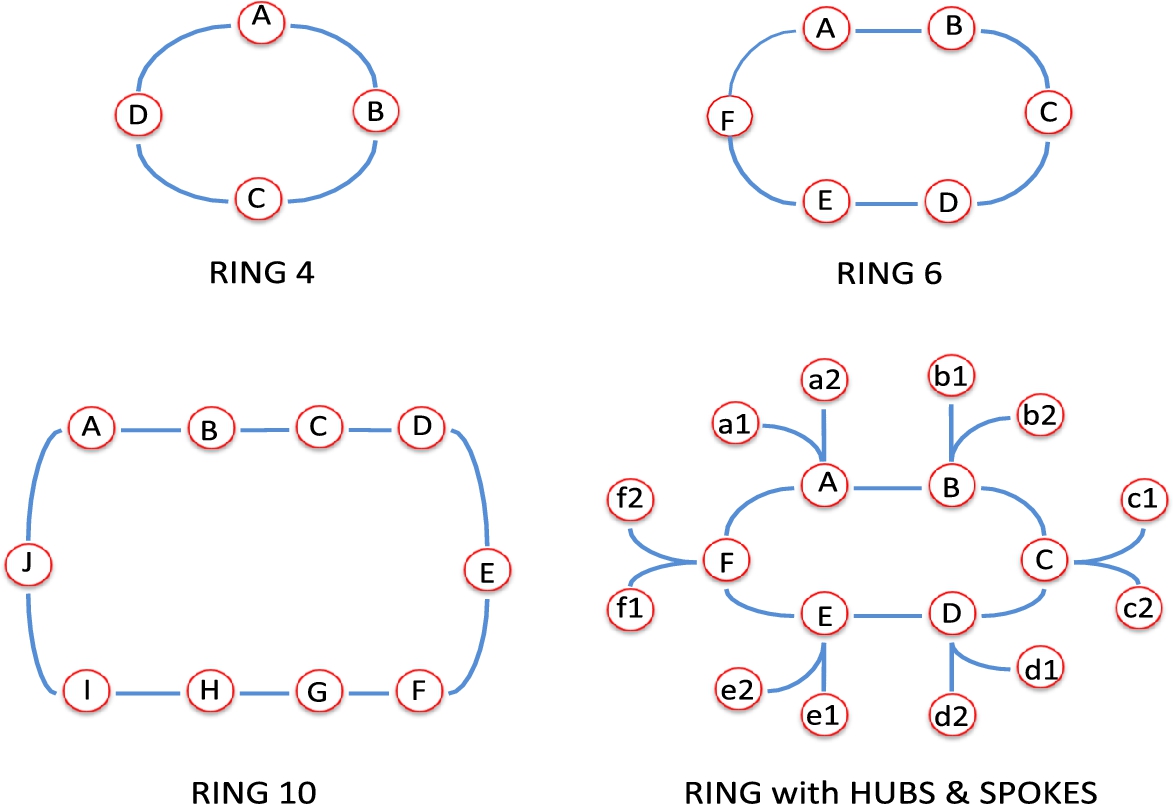
The ring networks with four, six and ten traders allow us to focus on coordination and competition. For every choice of ![]() and
and ![]() , there are always two competing paths of intermediaries. In Ring 4, for any non-adjacent pair, there are two paths with a single intermediary each. Ring 6 and Ring 10 allow for situations with a higher (and possibly unequal) number of intermediaries on either path.
, there are always two competing paths of intermediaries. In Ring 4, for any non-adjacent pair, there are two paths with a single intermediary each. Ring 6 and Ring 10 allow for situations with a higher (and possibly unequal) number of intermediaries on either path.
The Ring with Hubs and Spokes network allows for a study of the impact of market power: for instance, if ![]() is located at
is located at ![]() and
and ![]() is located at
is located at ![]() , intermediary A is a pure monopolist, while if
, intermediary A is a pure monopolist, while if ![]() is
is ![]() instead, then the intermediaries A and B play a symmetric Nash demand game. This network also creates the space for both market power and competition to come into play. For instance, if
instead, then the intermediaries A and B play a symmetric Nash demand game. This network also creates the space for both market power and competition to come into play. For instance, if ![]() is located at
is located at ![]() and
and ![]() is located at
is located at ![]() , then there are two competing paths: a shorter path (through A, F, and E) and a longer path (through A, B, C, D, and E). Traders A and E are the only critical intermediaries.
, then there are two competing paths: a shorter path (through A, F, and E) and a longer path (through A, B, C, D, and E). Traders A and E are the only critical intermediaries.
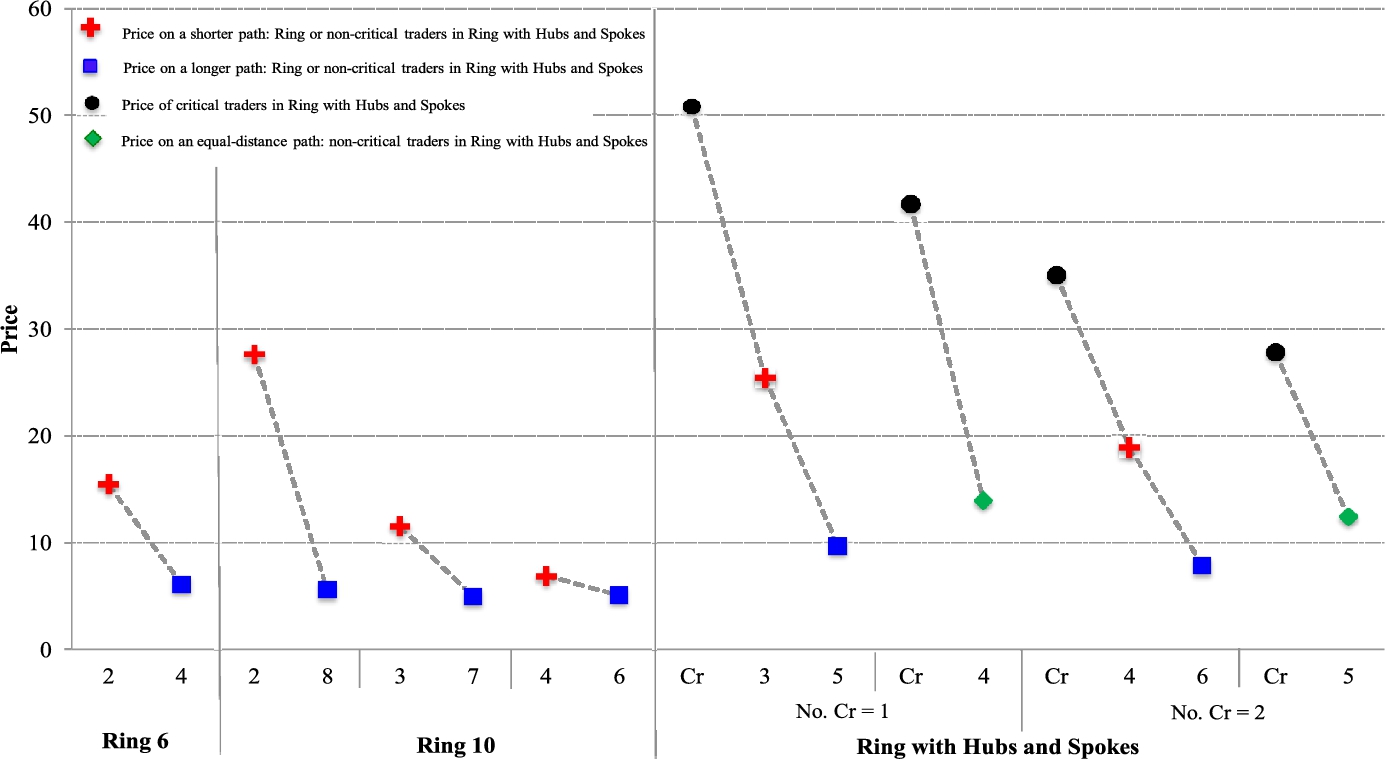
Fig. 7 presents intermediation costs in different treatments. To put these experimental variations into perspective, observe that in Ring 4, there is a unique equilibrium that corresponds to the Bertrand outcome. In every other network, whenever there are at least two intermediaries on every path, there exist both efficient and inefficient equilibria.6

In Ring 4, intermediation costs are around five percent of the surplus. In the other rings, intermediation costs vary between ten and twenty percent of the surplus. The overall conclusion is that intermediation costs in all ring networks are modest and, between the two efficient equilibria, are much closer to the one with zero intermediation cost, especially in the smaller rings.
In the Ring with Hubs and Spokes, when ![]() and
and ![]() are served by a sole critical intermediary, the authors find a surplus extraction of 99 percent! Finally, when there are two competing paths and critical traders, the intermediation cost ranges between 62 percent and 83 percent. In the case without critical intermediaries, this cost falls sharply to around 28 percent, which is comparable to the low-cost outcome found in Rings. These observations are summarized as follows:
are served by a sole critical intermediary, the authors find a surplus extraction of 99 percent! Finally, when there are two competing paths and critical traders, the intermediation cost ranges between 62 percent and 83 percent. In the case without critical intermediaries, this cost falls sharply to around 28 percent, which is comparable to the low-cost outcome found in Rings. These observations are summarized as follows:
I turn now to the issue of how surplus is divided between critical and non-critical intermediaries. Table 1 presents the average fraction of intermediation costs charged by critical traders, conditional on exchange. The number within parentheses is the number of group observations. Looking at the last 20 rounds, we observe that 67 percent to 80 percent of intermediation costs go to the critical trader(s). In all the cases, regardless of whether an exchange takes place along the shorter or longer path, the number of non-critical traders is at least as large as the number of critical traders. This is consistent with the pricing behavior of different intermediaries, as reported in Fig. 8.7 This leads to:
Table 1
Surplus division among intermediaries
| Network | (#Cr,#Paths, d(q),d(q′)) | Rounds | ||
|---|---|---|---|---|
| 1 ∼ 20 | 21 ∼ 41 | 41 ∼ 60 | ||
| Ring with hubs and spokes | (1, 2, 3, 5) | 0.56 | 0.68 | 0.72 |
| (20) | (26) | (25) | ||
| (1, 2, 4, 4) | 0.48 | 0.56 | 0.67 | |
| (16) | (13) | (10) | ||
| (2, 2, 4, 6) | 0.73 | 0.77 | 0.80 | |
| (16) | (19) | (24) | ||
| (2, 2, 5, 5) | 0.65 | 0.67 | 0.74 | |
| (8) | (8) | (11) | ||

Notes. The number in a cell is the average fraction of costs charged by critical traders. The number of observations is reported in parentheses. #Cr denotes the number of critical intermediaries, #Paths denotes the number of paths connecting buyer and seller, ![]() denotes the length of path q between buyer and seller.
denotes the length of path q between buyer and seller.
The experiments establish that subjects avoid coordination problems. As a result, trade always takes place, critical traders make large profits while non-critical traders make very little profits.
The results are sharp but it is possible to argue that criticality is too demanding: a node that lies on most (but not all) paths has the same status as compared to a node that lies on only one path. Moreover, all critical paths have equal status in the model. It may be argued that the location in the path – upstream or downstream – should matter. Related work with alternative pricing protocols develops these points. For auctions, see Kotowski and Leister (2014) and Gottardi and Goyal (2012); for bargaining, see Condorelli et al. (2016), Gofman (2011), and Manea (2017); for bid-and-ask prices, see Acemoglu and Ozdaglar (2007), Blume et al. (2007) and Gale and Kariv (2009).8
In this section I have considered games with local and global effects. For a general discussion on the nature of strategic interaction in networks, see Goyal (2007). An early paper that consider games on a network with a combination of local and global (market) effects is Goyal and Moraga-Gonzalez (2001). For more recent surveys on the subject, see Jackson and Zenou (2014) and Bramoulle and Kranton (2016). An important message from this literature is that, by varying the strategic structure of payoffs, we can bring different elements of networks into play. The two examples discussed in this section illustrate this general point. In the public goods game, maximal independent sets are important for understanding behavior, while in the pricing game it is criticality (and related notions of betweenness centrality) that are relevant. Moreover, the discussion also shows how heterogeneity in network properties can have powerful effects on choice, on payoffs, and on welfare.
5 Combining Actions and Link Formation
This section will present models that combine choices on actions and linking. I will draw upon original papers by Galeotti and Goyal (2010) and Goyal and Vega-Redondo (2007), and a recent survey paper by Vega-Redondo (2016).
We invest time in acquiring information ourselves, but we also link with others and learn from them. I start with some general observations on patterns of communication. The classical early work of Lazarsfeld et al. (1948) and Katz and Lazersfeld (1955) found that personal contacts play a dominant role in disseminating information which in turn shapes individuals decisions. In particular, they identified 20 percent of their sample of 4,000 individuals as the primary source of information for the rest. The Law of the Few subsumes these empirical findings: in social groups, a majority of individuals get most of their information from a very small subset of the group, viz., the influencers. Moreover, research suggests that there are minor differences between the observable economic and demographic characteristics of the influencers and the others. This suggests that individual interactions may play an important role in sustaining such high levels of heterogeneity.
5.1 The Law of the Few
Motivated by these observations, and building on Bala and Goyal (2000) and Bramoulle and Kranton (2007), Galeotti and Goyal (2010) propose the following model of activity and interactions. Suppose individuals choose to personally acquire information and to form connections with others to access the information these contacts acquire. Their main finding is that every (strict) equilibrium of the game exhibits the ‘Law of the Few’. The network has a core-periphery architecture; the players in the core acquire information personally, while the peripheral players acquire no information personally but form links and get all their information from the core players. The core group is small relative to the number of individuals.9 Fig. 9 presents a collection of core-periphery networks.
As usual, let ![]() with
with ![]() be the set of players and let i and j be typical members of this set. Each player i chooses a level of personal information acquisition
be the set of players and let i and j be typical members of this set. Each player i chooses a level of personal information acquisition ![]() and a set of links with others to access their information, which is represented as a (row) vector
and a set of links with others to access their information, which is represented as a (row) vector ![]() , where
, where ![]() , for each
, for each ![]() . We will suppose that
. We will suppose that ![]() and that
and that ![]() . We say that player i has a link with player j if
. We say that player i has a link with player j if ![]() . A link between player i and j allows both players to access the information personally acquired by the other player. The set of strategies of player i is denoted by
. A link between player i and j allows both players to access the information personally acquired by the other player. The set of strategies of player i is denoted by ![]() . Define
. Define ![]() as the set of strategies of all players. A strategy profile
as the set of strategies of all players. A strategy profile ![]() specifies the personal information acquired by each player,
specifies the personal information acquired by each player, ![]() , and the network of relations
, and the network of relations ![]() .
.
The network of relations g is a directed graph; let G be the set of all possible directed graphs on n vertices. Define ![]() as the set of players with whom i has formed a link. Let
as the set of players with whom i has formed a link. Let ![]() . The closure of g is an undirected network denoted by
. The closure of g is an undirected network denoted by ![]() , where
, where ![]() for each i and j in N. In words, the closure of a directed network involves replacing every directed edge of g by an undirected one. Define
for each i and j in N. In words, the closure of a directed network involves replacing every directed edge of g by an undirected one. Define ![]() as the set of players directly connected to i. The undirected link between two players reflects bilateral information exchange between them.
as the set of players directly connected to i. The undirected link between two players reflects bilateral information exchange between them.
The payoffs to player i under strategy profile ![]() are:
are:
(4)
where ![]() reflects the cost of information and
reflects the cost of information and ![]() is the cost of linking with one other person. As in Section 3, assume that
is the cost of linking with one other person. As in Section 3, assume that ![]() is twice continuously differentiable, increasing, and strictly concave in y. Also assume that there is a
is twice continuously differentiable, increasing, and strictly concave in y. Also assume that there is a ![]() such that
such that ![]() .
.
It is easy to see, using arguments from Section 3, that every player must access at least ![]() information. Moreover, the perfect substitutability of own and neighbors' information and the linearity in the costs of acquiring information imply that if a player personally acquires information then the sum of the information he acquires and the information acquired by his neighbors must equal
information. Moreover, the perfect substitutability of own and neighbors' information and the linearity in the costs of acquiring information imply that if a player personally acquires information then the sum of the information he acquires and the information acquired by his neighbors must equal ![]() . We next observe that if some player acquires
. We next observe that if some player acquires ![]() , and if
, and if ![]() , then it is optimal for all other players to acquire no information personally and to form a link with this player. For a strategy profile
, then it is optimal for all other players to acquire no information personally and to form a link with this player. For a strategy profile ![]() , let us define
, let us define ![]() as the set of players who acquire information personally, and let
as the set of players who acquire information personally, and let ![]() be the information that i accesses from his neighbors. So we know how much information everyone must access. Now we turn to the distribution of personal information acquisition, the aggregate information acquired in a social group and the structure of social communication. Galeotti and Goyal (2010) establish:
be the information that i accesses from his neighbors. So we know how much information everyone must access. Now we turn to the distribution of personal information acquisition, the aggregate information acquired in a social group and the structure of social communication. Galeotti and Goyal (2010) establish:
Galeotti and Goyal (2010) provide the following intuitive explanation for this result. In this model, returns from information are increasing and concave while the costs of personally acquiring information are linear. This implies that on his own an individual would acquire a certain amount of information, which for the purposes of this discussion is normalized so that ![]() . The second element in this model is the substitutability of information acquired by different individuals. This implies that if A acquires information on his own and receives information from player B then in the aggregate he must have access to 1 unit of information (else he could strictly increase his payoff by modifying personal information acquisition). The third and key element is that links are costly and rationally chosen by individuals. The implication of this is that if A finds it optimal to maintain a link with B then so must every other player. Hence, the group of individuals who acquire information must be completely linked and the aggregate information acquired in the society must equal exactly 1. Moreover, since linking is costly, A will only link with B if B acquires a certain minimum amount of information. Since total information acquired is 1, it follows that there is an upper bound to the number of people who will acquire information: this upper bound is independent of the number of players n. And so the proportion of information acquirers will be negligible in a large group. Finally, we observe that since the aggregate information acquired in the group is 1, everyone who does not personally acquire information must be linked to all those who acquire information, yielding the core-periphery network.
. The second element in this model is the substitutability of information acquired by different individuals. This implies that if A acquires information on his own and receives information from player B then in the aggregate he must have access to 1 unit of information (else he could strictly increase his payoff by modifying personal information acquisition). The third and key element is that links are costly and rationally chosen by individuals. The implication of this is that if A finds it optimal to maintain a link with B then so must every other player. Hence, the group of individuals who acquire information must be completely linked and the aggregate information acquired in the society must equal exactly 1. Moreover, since linking is costly, A will only link with B if B acquires a certain minimum amount of information. Since total information acquired is 1, it follows that there is an upper bound to the number of people who will acquire information: this upper bound is independent of the number of players n. And so the proportion of information acquirers will be negligible in a large group. Finally, we observe that since the aggregate information acquired in the group is 1, everyone who does not personally acquire information must be linked to all those who acquire information, yielding the core-periphery network.
The result mentioned above is derived in a setting where individuals are ex-ante identical. A recurring theme in the empirical work is that influencers have demographic characteristics which are similar to those of others. But this work also finds that they have distinctive attitudes which include higher attention to general market information and enjoyment in acquiring information, see e.g., Feick and Price (1987). This motivates a study of the consequences of small heterogeneity in individual characteristics. Our main finding is that if an individual has a slight cost advantage in acquiring information (or a greater preference for information) then in equilibrium this person is always the unique hub. Small heterogeneities thus help select individuals who play dramatically different roles in social organization.
A natural way to model this difference is to suppose that some players have slightly lower costs of acquiring information. Galeotti and Goyal (2010) consider a situation where ![]() for all
for all ![]() , while
, while ![]() , where
, where ![]() is a small number. Let
is a small number. Let ![]() . Clearly, as long as
. Clearly, as long as ![]() ,
, ![]() , and
, and ![]() as
as ![]() . They establish the following result on strict Nash equilibria:
. They establish the following result on strict Nash equilibria:
This result shows that a very small difference in the cost of acquiring information is sufficient to separate the player who will acquire information and act as a hub from those who will acquire little or no information personally and will only form connections.
Following on Galeotti and Goyal (2010) the intuition for this result may be explained as follows: First, observe that for the low cost player the optimal information level is greater than the optimal information level for other players, i.e., ![]() . From the arguments developed in Proposition 2 we know that aggregate information acquired by all players other than player 1 will be at most
. From the arguments developed in Proposition 2 we know that aggregate information acquired by all players other than player 1 will be at most ![]() . This implies that in equilibrium, player 1 must acquire information personally,
. This implies that in equilibrium, player 1 must acquire information personally, ![]() . If
. If ![]() , the best reply of every other player is to acquire no information and to form a link with player 1. In case
, the best reply of every other player is to acquire no information and to form a link with player 1. In case ![]() we know, from arguments in Proposition 1, that
we know, from arguments in Proposition 1, that ![]() and so there is a player
and so there is a player ![]() with
with ![]() and
and ![]() . If some player wants to link with i then so must everyone else. But then player i accesses all information
. If some player wants to link with i then so must everyone else. But then player i accesses all information ![]() ; since
; since ![]() , this contradicts Proposition 1. Thus no player must have a link with player
, this contradicts Proposition 1. Thus no player must have a link with player ![]() in equilibrium. Hence, i must form a link with player 1, and, from the optimality of linking, so must every other player. Finally, since every player is choosing positive effort, the equilibrium values of
in equilibrium. Hence, i must form a link with player 1, and, from the optimality of linking, so must every other player. Finally, since every player is choosing positive effort, the equilibrium values of ![]() and
and ![]() can be derived from the two equations
can be derived from the two equations ![]() and
and ![]() .
.
We briefly note that payoffs may be very unequal in the core-periphery networks: so in the case of a single hub for instance the central player earns ![]() , while the spokes each earn
, while the spokes each earn ![]() . In the event that
. In the event that ![]() is much larger than k, the payoff of the hub players is much smaller than the spokes. On the other hand in the case of multiple hubs, it is possible the hubs earn a great deal more than the spokes. So information investment activity and linking can lead to very specialized patterns of behavior and very heterogeneous networks.
is much larger than k, the payoff of the hub players is much smaller than the spokes. On the other hand in the case of multiple hubs, it is possible the hubs earn a great deal more than the spokes. So information investment activity and linking can lead to very specialized patterns of behavior and very heterogeneous networks.
5.2 Intermediation Rents and Network Formation
In the trading game, we showed that intermediaries earn large payoffs if and only if they are ‘critical’. In this section, we consider a network formation game in which traders seek to link with each other to carry out exchange and also to extract intermediation rents by becoming critical. We wish to understand whether criticality is sustainable in such an environment and how the payoffs are distributed.
The discussion here is based on Goyal and Vega-Redondo (2007). Suppose traders can exchange goods and that this creates a surplus of 1. Networks are relevant because this exchange can be undertaken only if these traders know each other personally or there is a sequence of personal connections which indirectly link the two traders. In the case where traders know each other they each get one-half of the surplus. If they are linked indirectly then the allocation of the surplus depends on the competition between the intermediary agents. Following the discussion in Section 3, suppose that competition between paths between any two players j and k leads to full dissipation of market power: in other words intermediaries only make money if they are critical. We have thus combined the model of trading in networks above with a model of network formation.
We will consider a game of network formation in which players propose links. So a strategy for player i is ![]() , where
, where ![]() . A link is formed between players i and j if both propose a link to each other, i.e.,
. A link is formed between players i and j if both propose a link to each other, i.e., ![]() . Denote by
. Denote by ![]() the set of players who are critical to connect j and k in network g and let
the set of players who are critical to connect j and k in network g and let ![]() . Then, for any strategy profile
. Then, for any strategy profile ![]() , the (net) payoffs to player i are given by:
, the (net) payoffs to player i are given by:
(5)
where ![]() stands for the indicator function specifying whether i is critical for j and k,
stands for the indicator function specifying whether i is critical for j and k, ![]() refers to the number of players with whom player i has a link, and
refers to the number of players with whom player i has a link, and ![]() is the cost per link.
is the cost per link. ![]() refers to the component of individual i in network g.
refers to the component of individual i in network g.
I now discuss the incentives to form and delete links and the nature of pairwise stable networks. It is easily seen that the star, the cycle containing all players and hybrid cycle-stars (in which there is a cycle and all players outside the cycle have a single link to a single node in the cycle) are all pairwise stable. In the star the center earns a payoff of ![]() , and has no incentive to a delete a single link so long as
, and has no incentive to a delete a single link so long as ![]() . Two spokes have no incentive to form a link between them if
. Two spokes have no incentive to form a link between them if ![]() , while no spoke has an incentive to delete a link if
, while no spoke has an incentive to delete a link if ![]() . Thus a star is pairwise stable so long as
. Thus a star is pairwise stable so long as ![]() .
.
In a cycle every player gets a payoff of ![]() . An additional link is clearly not attractive since it does not create any extra surplus while it increases costs. Deleting one link is not attractive for an individual player as it makes a neighboring player critical for all transactions, which lowers individual payoffs by at least
. An additional link is clearly not attractive since it does not create any extra surplus while it increases costs. Deleting one link is not attractive for an individual player as it makes a neighboring player critical for all transactions, which lowers individual payoffs by at least ![]() . This clearly exceeds the cost c, for large enough n. Similar arguments can be used to show that hybrid cycle-star networks are pairwise stable (for some range of costs).
. This clearly exceeds the cost c, for large enough n. Similar arguments can be used to show that hybrid cycle-star networks are pairwise stable (for some range of costs).
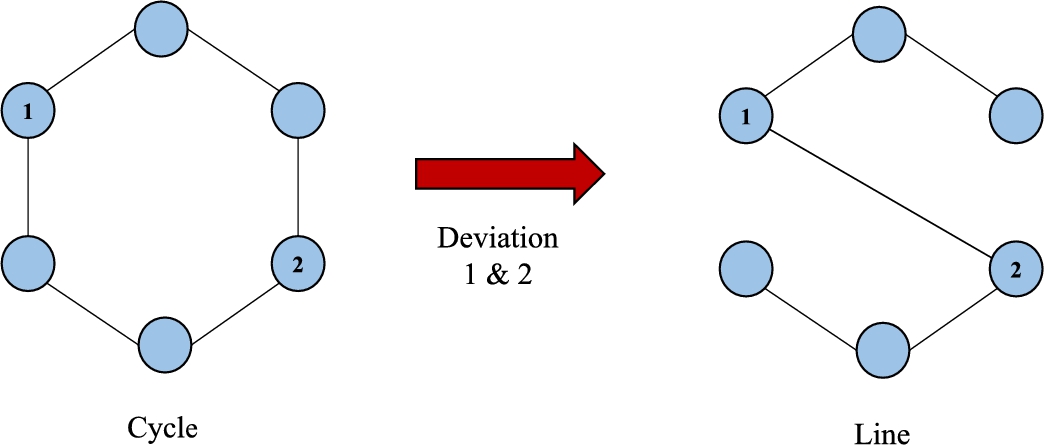
I now turn to deviations that involve greater coordination. Consider the case of two players choosing to add a link between themselves and delete a subset of links with others. To see how this may have large effects, consider the cycle network containing all players. Consider two players that are far apart in the cycle and establish a direct link. By simultaneously breaking one link each, they can produce a line and become central in it. In a line, they must pay intermediation costs to a number of others, but at the same time they both occupy prominent centrality positions in the line network. This deviation is illustrated in Fig. 10.
Under some circumstances such deviations may be profitable and they have the effect of sharply restricting the set of ‘equilibrium’ networks. This possibility leads to a consideration of strict bilateral equilibrium networks. Goyal and Vega-Redondo (2007) propose the following definition.10
Goyal and Vega-Redondo (2007) provide the following (partial) characterization of strict bilateral equilibrium networks.
There are four arguments in the proof. The first argument exploits access and intermediation advantages to show that an equilibrium network is either connected or empty. The second argument demonstrates agglomeration pressures: a minimal network with long paths cannot be sustained. This is because players located at the ‘end’ of the network benefit from connecting to a central player in order to save on intermediation costs (cutting path lengths) while a central player is ready to incur the cost of an additional link because this enhances her intermediation payoffs because she shares the intermediation rents with fewer other players. This deviation is illustrated in Fig. 11.

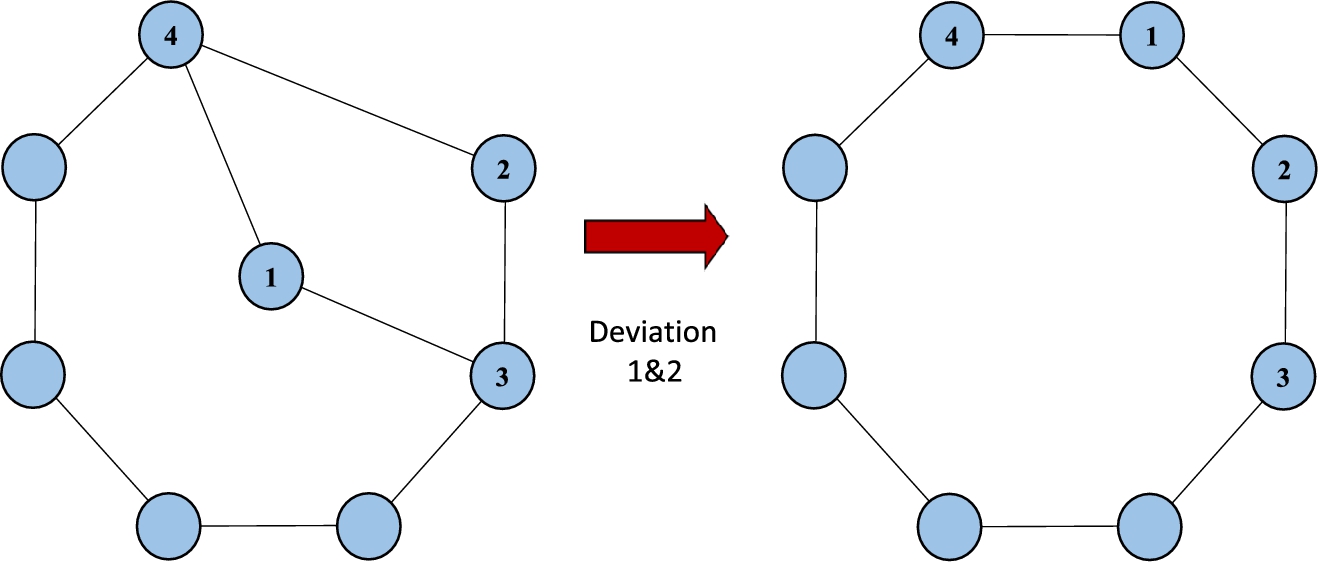
The third argument builds on the above example of bilateral deviations to show that a cycle or a hybrid cycle-star network is not sustainable. The fourth argument rules out networks with two or more cycles. It is here that the requirement of strictness is invoked. Fig. 12 illustrates how players 1 and 2 are indifferent between the network with two cycles and a network in which there is only one cycle.
Proposition 5 covers large societies and assumes that ![]() . Goyal and Vega-Redondo (2007) show that in small societies too strategic pressures will create the potential for a ‘structural hole’ and there will be players who earn large intermediation payoffs by spanning them. In case
. Goyal and Vega-Redondo (2007) show that in small societies too strategic pressures will create the potential for a ‘structural hole’ and there will be players who earn large intermediation payoffs by spanning them. In case ![]() , the star is not an equilibrium, since peripheral players have a strict incentive to link up. For large societies, the above arguments show that no other network is a strict bilateral equilibrium. Thus if
, the star is not an equilibrium, since peripheral players have a strict incentive to link up. For large societies, the above arguments show that no other network is a strict bilateral equilibrium. Thus if ![]() then there exist no strict bilateral equilibria.
then there exist no strict bilateral equilibria.
I conclude this discussion with a comment on payoff inequality. In the star network the central player earns ![]() while each of the peripheral players makes
while each of the peripheral players makes ![]() . The payoff difference between the central player and the peripheral player is large, and in particular, the ratio of the two payoffs is unbounded, as n gets large.
. The payoff difference between the central player and the peripheral player is large, and in particular, the ratio of the two payoffs is unbounded, as n gets large.
The discussion above shows that strategic linking pushes toward an extreme form of market power with a single critical node. One ingredient of the model that plays an important role in the analysis is that only a critical node can earn intermediation rents. In a recent paper, van der Leij et al. (2016) extend this model to allow for smoother competition between paths: here multiple paths may earn intermediation rents depending on a competition parameter δ, that allows in the one extreme for full collusion and in the other extreme for Bertrand competition (as in the model above). They also show that small initial differences in size of banks can feedback to create a core-periphery network with large banks in the core. In particular, their model can reproduce the observed core-periphery structure in the Dutch interbank market for reasonable parameter values.
5.3 Related Work
For a more extensive survey of games with actions and linking, see Vega-Redondo (2016). Here I would like to briefly mention the closely related line of work on link formation in a setting where actions are strategic complements, Koenig et al. (2014). The basic game has linear quadratic payoffs, as in the paper by Ballester et al. (2006). I briefly discuss this paper now.
Koenig et al. (2014) show that if individuals form links to maximize centrality, then the linking process leads to nested split graphs: these are networks with a clear hierarchical structure (for an illustration, see Fig. 2). There is a top group of high effort players, who are linked to all players choosing efforts below them. The second level effort players are in turn linked to all players choosing effort below them, and so forth. For an early derivation of nested graphs in a model of network formation, see Goyal and Joshi (2003). A similar structure is also identified in related papers by Hiller (2012) and Baetz (2014), who study a setting like Galeotti and Goyal (2010), except that actions are strategic complements (and not substitutes).
An important general message from this literature is that, in a rich variety of settings, purposeful linking activity leads to sharply structured networks with significant heterogeneity in degree, in behavior across nodes, and in individual payoffs.
6 Concluding Remarks
We started with the observation that heterogeneity is a defining feature of real world social, economic and infrastructure networks. I have tried to argue, with the help of simple models, how heterogeneous networks give rise to very widely varying forms of behavior and potentially significant inequality. Furthermore, I have presented models that combine activity in networks with linking behavior to show how heterogeneous network structures are a natural outcome in a wide range of circumstances. Thus networks are important for understanding the diversity in economic outcomes that has been empirically noted.