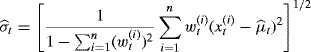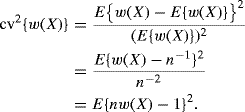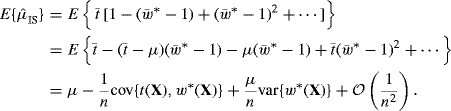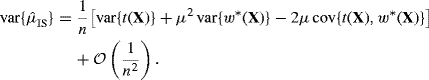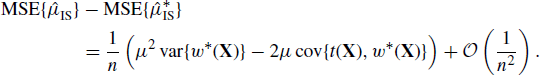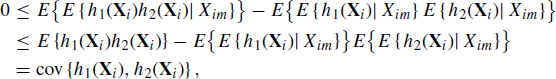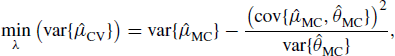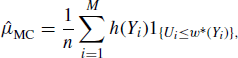Chapter 6
Simulation and Monte Carlo Integration
This chapter addresses the simulation of random draws X1, . . ., Xn from a target distribution f. The most frequent use of such draws is to perform Monte Carlo integration, which is the statistical estimation of the value of an integral using evaluations of an integrand at a set of points drawn randomly from a distribution with support over the range of integration [49].
Estimation of integrals via Monte Carlo simulation can be useful in a wide variety of settings. In Bayesian analyses, posterior moments can be written in the form of an integral but typically cannot be evaluated analytically. Posterior probabilities can also be written as the expectation of an indicator function with respect to the posterior. The calculation of risk in Bayesian decision theory relies on integration. Integration is also an important component in frequentist likelihood analyses. For example, marginalization of a joint density relies upon integration. Example 5.1 illustrates an integration problem arising from the maximum likelihood fit of a generalized linear mixed model. A variety of other integration problems are discussed here and in Chapter 7.
Aside from its application to Monte Carlo integration, simulation of random draws from a target density f is important in many other contexts. Indeed, Chapter 7 is devoted to a specific strategy for Monte Carlo integration called Markov chain Monte Carlo. Bootstrap methods, stochastic search algorithms, and a wide variety of other statistical tools also rely on generation of random deviates.
Further details about the topics discussed in this chapter can be found in [106, 158, 374, 383, 417, 432, 469, 539, 555, 557].
6.1 Introduction to the Monte Carlo Method
Many quantities of interest in inferential statistical analyses can be expressed as the expectation of a function of a random variable, say E{h(X)}. Let f denote the density of X, and μ denote the expectation of h(X) with respect to f. When an i.i.d. random sample X1, . . ., Xn is obtained from f, we can approximate μ by a sample average:
as n→ ∞, by the strong law of large numbers (see Section 1.6). Further, let ![]() , and assume that h(X)2 has finite expectation under f. Then the sampling variance of
, and assume that h(X)2 has finite expectation under f. Then the sampling variance of ![]() is
is ![]() , where the expectation is taken with respect to f. A similar Monte Carlo approach can be used to estimate σ2 by
, where the expectation is taken with respect to f. A similar Monte Carlo approach can be used to estimate σ2 by
When σ2 exists, the central limit theorem implies that ![]() has an approximate normal distribution for large n, so approximate confidence bounds and statistical inference for μ follow. Generally, it is straightforward to extend (6.1), (6.2), and most of the methods in this chapter to cases when the quantity of interest is multivariate, so it suffices hereafter to consider μ to be scalar.
has an approximate normal distribution for large n, so approximate confidence bounds and statistical inference for μ follow. Generally, it is straightforward to extend (6.1), (6.2), and most of the methods in this chapter to cases when the quantity of interest is multivariate, so it suffices hereafter to consider μ to be scalar.
Monte Carlo integration provides slow ![]() convergence. With n nodes, the quadrature methods described in Chapter 5 offer convergence of order
convergence. With n nodes, the quadrature methods described in Chapter 5 offer convergence of order ![]() or better. There are several reasons why Monte Carlo integration is nonetheless a very powerful tool.
or better. There are several reasons why Monte Carlo integration is nonetheless a very powerful tool.
Most importantly, quadrature methods are difficult to extend to multidimensional problems because general p-dimensional space is so vast. Straightforward product rules creating quadrature grids of size np quickly succumb to the curse of dimensionality (discussed in Section 10.4.1), becoming harder to implement and slower to converge. Monte Carlo integration samples randomly from f over the p-dimensional support region of f, but does not attempt any systematic exploration of this region. Thus, implementation of Monte Carlo integration is less hampered by high dimensionality than is quadrature. However, when p is large, a very large sample size may still be required to obtain an acceptable standard error for ![]() . Quadrature methods also perform best when h is smooth, even when p = 1. In contrast, the Monte Carlo integration approach ignores smoothness. Further comparisons are offered in [190].
. Quadrature methods also perform best when h is smooth, even when p = 1. In contrast, the Monte Carlo integration approach ignores smoothness. Further comparisons are offered in [190].
Monte Carlo integration replaces the systematic grid of quadrature nodes with a set of points chosen randomly from a probability distribution. The first step, therefore, is to study how to generate such draws. This topic is addressed in Sections 6.2 and 6.3. Methods for improving upon the standard estimator given in Equation (6.1) are described in Section 6.4.
6.2 Exact Simulation
Monte Carlo integration motivates our focus on simulation of random variables that do not follow a familiar parametric distribution. We refer to the desired sampling density f as the target distribution. When the target distribution comes from a standard parametric family, abundant software exists to easily generate random deviates. At some level, all of this code relies on the generation of standard uniform random deviates. Given the deterministic nature of the computer, such draws are not really random, but a good generator will produce a sequence of values that are statistically indistinguishable from independent standard uniform variates. Generation of standard uniform random deviates is a classic problem studied in [195, 227, 383, 538, 539, 557].
Rather than rehash the theory of uniform random number generation, we focus on the practical quandary faced by those with good software: what should be done when the target density is not one easily sampled using the software? For example, nearly all Bayesian posterior distributions are not members of standard parametric families. Posteriors obtained when using conjugate priors in exponential families are exceptions.
There can be additional difficulties beyond the absence of an obvious method to sample f. In many cases—especially in Bayesian analyses—the target density may be known only up to a multiplicative proportionality constant. In such cases, f cannot be sampled and can only be evaluated up to that constant. Fortunately, there are a variety of simulation approaches that still work in this setting.
Finally, it may be possible to evaluate f, but computationally expensive. If each computation of f(x) requires an optimization, an integration, or other time-consuming computations, we may seek simulation strategies that avoid direct evaluation of f as much as possible.
Simulation methods can be categorized by whether they are exact or approximate. The exact methods discussed in this section provide samples whose sampling distribution is exactly f. Later, in Section 6.3, we introduce methods producing samples from a distribution that approximates f.
6.2.1 Generating from Standard Parametric Families
Before discussing sampling from difficult target distributions, we survey some strategies for producing random variates from familiar distributions using uniform random variates. We omit justifications for these approaches, which are given in the references cited above. Table 6.1 summarizes a variety of approaches. Although the tabled approaches are not necessarily state of the art, they illustrate some of the underlying principles exploited by sophisticated generators.
Table 6.1 Some methods for generating a random variable X from familiar distributions.

6.2.2 Inverse Cumulative Distribution Function
The methods for the Cauchy and exponential distributions in Table 6.1 are justified by the inverse cumulative distribution function or probability integral transform approach. For any continuous distribution function F, if U ~ Unif(0, 1), then X = F−1(U) = inf {x : F(x) ≥ U} has a cumulative distribution function equal to F.
If F−1 is available for the target density, then this strategy is probably the simplest option. If F−1 is not available but F is either available or easily approximated, then a crude approach can be built upon linear interpolation. Using a grid of x1, . . ., xm spanning the region of support of f, calculate or approximate ui = F(xi) at each grid point. Then, draw U ~ Unif(0, 1) and linearly interpolate between the two nearest grid points for which ui ≤ U ≤ uj according to
(6.3) ![]()
Although this approach is not exact, we include it in this section because the degree of approximation is deterministic and can be reduced to any desired level by increasing m sufficiently. Compared to the alternatives, this simulation method is not appealing because it requires a complete approximation to F regardless of the desired sample size, it does not generalize to multiple dimensions, and it is less efficient than other approaches.
6.2.3 Rejection Sampling
If f(x) can be calculated, at least up to a proportionality constant, then we can use rejection sampling to obtain a random draw from exactly the target distribution. This strategy relies on sampling candidates from an easier distribution and then correcting the sampling probability through random rejection of some candidates.
Let g denote another density from which we know how to sample and for which we can easily calculate g(x). Let e(·) denote an envelope, having the property e(x) = g(x)/α ≥ f(x) for all x for which f(x) > 0 for a given constant α ≤ 1. Rejection sampling proceeds as follows:
The draws kept using this algorithm constitute an i.i.d. sample from the target density f; there is no approximation involved. To see this, note that the probability that a kept draw falls at or below a value y is
(6.4) 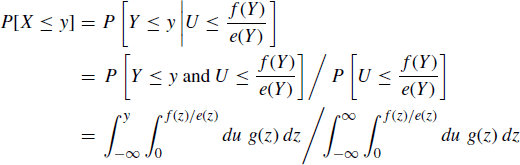
which is the desired probability. Thus, the sampling distribution is exact, and α can be interpreted as the expected proportion of candidates that are accepted. Hence α is a measure of the efficiency of the algorithm. We may continue the rejection sampling procedure until it yields exactly the desired number of sampled points, but this requires a random total number of iterations that will depend on the proportion of rejections.
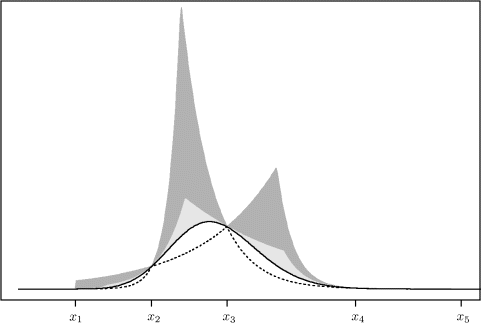
Recall the rejection rule in step 3 for determining the fate of a candidate draw, Y = y. Sampling U ~ Unif(0, 1) and obeying this rule is equivalent to sampling U|y ~ Unif(0, e(y)) and keeping the value y if U < f(y). Consider Figure 6.1. Suppose the value y falls at the point indicated by the vertical bar. Then imagine sampling U|Y = y uniformly along the vertical bar. The rejection rule eliminates this Y draw with probability proportional to the length of the bar above f(y) relative to the overall bar length. Therefore, one can view rejection sampling as sampling uniformly from the two-dimensional region under the curve e and then throwing away any draws falling above f and below e. Since sampling from f is equivalent to sampling uniformly from the two-dimensional region under the curve labeled f(x) and then ignoring the vertical coordinate, rejection sampling provides draws exactly from f.
Figure 6.1 Illustration of rejection sampling for a target distribution f using a rejection sampling envelope e.
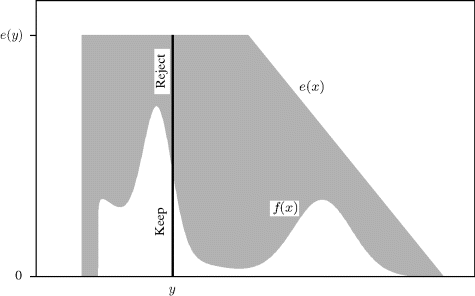
The shaded region in Figure 6.1 above f and below e indicates the waste. The draw Y = y is very likely to be rejected when e(y) is far larger than f(y). Envelopes that exceed f everywhere by at most a slim margin produce fewer wasted (i.e., rejected) draws and correspond to α values near 1.
Suppose now that the target distribution f is only known up to a proportionality constant c. That is, suppose we are only able to compute easily q(x) = f(x)/c, where c is unknown. Such densities arise, for example, in Bayesian inference when f is a posterior distribution known to equal the product of the prior and the likelihood scaled by some normalizing constant. Fortunately, rejection sampling can be applied in such cases. We find an envelope e such that e(x) ≥ q(x) for all x for which q(x) > 0. A draw Y = y is rejected when U > q(y)/e(y). The sampling probability remains correct because the unknown constant c cancels out in the numerator and denominator of (6.5) when f is replaced by q. The proportion of kept draws is α/c.
Multivariate targets can also be sampled using rejection sampling, provided that a suitable multivariate envelope can be constructed. The rejection sampling algorithm is conceptually unchanged.
To produce an envelope we must know enough about the target to bound it. This may require optimization or a clever approximation to f or q in order to ensure that e can be constructed to exceed the target everywhere. Note that when the target is continuous and log-concave, it is unimodal. If we select x1 and x2 on opposite sides of that mode, then the function obtained by connecting the line segments that are tangent to log f or log q at x1 and x2 yields a piecewise exponential envelope with exponential tails. Deriving this envelope does not require knowing the maximum of the target density; it merely requires checking that x1 and x2 lie on opposite sides of it. The adaptive rejection sampling method described in Section 6.2.3.2 exploits this idea to generate good envelopes.
To summarize, good rejection sampling envelopes have three properties: They are easily constructed or confirmed to exceed the target everywhere, they are easy to sample, and they generate few rejected draws.
Example 6.1 (Gamma Deviates) Consider the problem of generating a Gamma(r, 1) random variable when r ≥ 1. When Y is generated according to the density
for t(y) = a(1 + by)3 for −1/b< y < ∞, ![]() , and
, and ![]() , then X = t(Y) will have a Gamma(r, 1) distribution [443]. Marsaglia and Tsang describe how to use this fact in a rejection sampling framework [444]. Adopt (6.6) as the target distribution because transforming draws from f gives the desired gamma draws.
, then X = t(Y) will have a Gamma(r, 1) distribution [443]. Marsaglia and Tsang describe how to use this fact in a rejection sampling framework [444]. Adopt (6.6) as the target distribution because transforming draws from f gives the desired gamma draws.
Simplifying f and ignoring the normalizing constant, we wish to generate from the density that is proportional to q(y) = exp {a log {t(y)/a} − t(y) + a}. Conveniently, q fits snugly under the function e(y) = exp { − y2/2}, which is the unscaled standard normal density. Therefore, rejection sampling amounts to sampling a standard normal random variable, Z, and a standard uniform random variable, U, then setting X = t(Z) if
(6.7) ![]()
and t(Z) > 0. Otherwise, the draw is rejected and the process begun anew. An accepted draw has density Gamma(r, 1). Draws from Gamma(r, 1) can be rescaled to obtain draws from Gamma(r, λ).
In a simulation when r = 4, over 99% of candidate draws are accepted and a plot of e(y) and q(y) against y shows that the two curves are nearly superimposed. Even in the worst case (r = 1), the envelope is excellent, with less than 5% waste.
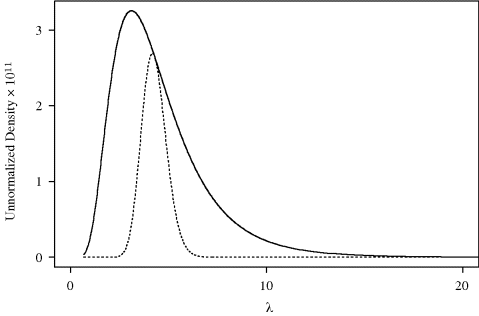
Example 6.2 (Sampling a Bayesian Posterior) Suppose 10 independent observations (8, 3, 4, 3, 1, 7, 2, 6, 2, 7) are observed from the model Xi|λ ~ Poisson (λ). A lognormal prior distribution for λ is assumed: log λ ~ N(log 4, 0.52). Denote the likelihood as L(λ|x) and the prior as f(λ). We know that ![]() maximizes L(λ|x) with respect to λ; therefore the unnormalized posterior, q(λ|x) = f(λ)L(λ|x) is bounded above by e(λ) = f(λ)L(4.3|x). Figure 6.2 shows q and e. Note that the prior is proportional to e. Thus, rejection sampling begins by sampling λi from the lognormal prior and Ui from a standard uniform distribution. Then λi is kept if Ui < q(λi|x)/e(λi) = L(λi|x)/L(4.3|x). Otherwise, λi is rejected and the process is begun anew. Any kept λi is a draw from the posterior. Although not efficient—only about 30% of candidate draws are kept—this approach is easy and exact.
maximizes L(λ|x) with respect to λ; therefore the unnormalized posterior, q(λ|x) = f(λ)L(λ|x) is bounded above by e(λ) = f(λ)L(4.3|x). Figure 6.2 shows q and e. Note that the prior is proportional to e. Thus, rejection sampling begins by sampling λi from the lognormal prior and Ui from a standard uniform distribution. Then λi is kept if Ui < q(λi|x)/e(λi) = L(λi|x)/L(4.3|x). Otherwise, λi is rejected and the process is begun anew. Any kept λi is a draw from the posterior. Although not efficient—only about 30% of candidate draws are kept—this approach is easy and exact.
Figure 6.2 Unnormalized target (dotted) and envelope (solid) for rejection sampling in Example 6.2.
6.2.3.1 Squeezed Rejection Sampling
Ordinary rejection sampling requires one evaluation of f for every candidate draw Y. In cases where evaluating f is computationally expensive but rejection sampling is otherwise appealing, improved simulation speed is achieved by squeezed rejection sampling [383, 441, 442].
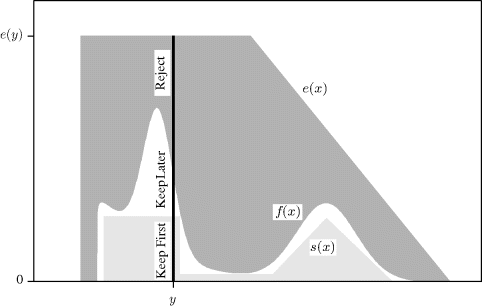
This strategy preempts the evaluation of f in some instances by employing a nonnegative squeezing function, s. For s to be a suitable squeezing function, s(x) must not exceed f(x) anywhere on the support of f. An envelope, e, is also used; as with ordinary rejection sampling, e(x) = g(x)/α ≥ f(x) on the support of f.
The algorithm proceeds as follows:
Note that when Y = y, this candidate draw is kept with overall probability f(y)/e(y), and rejected with probability [e(y) − f(y)]/e(y). These are the same probabilities as with simple rejection sampling. Step 3 allows a decision to keep Y to be made on the basis of an evaluation of s, rather than of f. When s nestles up just underneath f everywhere, we achieve the largest decrease in the number of evaluations of f.
Figure 6.3 illustrates the procedure. When a candidate Y = y is sampled, the algorithm proceeds in a manner equivalent to sampling a Unif(0, e(y)) random variable. If this uniform variate falls below s(y), the candidate is kept immediately. The lighter shaded region indicates where candidates are immediately kept. If the candidate is not immediately kept, then a second test must be employed to determine whether the uniform variate falls under f(y) or not. Finally, the darker shaded region indicates where candidates are ultimately rejected.
Figure 6.3 Illustration of squeezed rejection sampling for a target distribution, f, using envelope e and squeezing function s. Keep First and Keep Later correspond to steps 3 and 4 of the algorithm, respectively.
As with rejection sampling, the proportion of candidate draws kept is α. The proportion of iterations in which evaluation of f is avoided is ![]() .
.
Squeezed rejection sampling can also be carried out when the target is known only up to a proportionality constant. In this case, the envelope and squeezing function sandwich the unnormalized target. The method is still exact, and the same efficiency considerations apply.
Generalizations for sampling multivariate targets are straightforward.
6.2.3.2 Adaptive Rejection Sampling
Clearly the most challenging aspect of the rejection sampling strategy is the construction of a suitable envelope. Gilks and Wild proposed an automatic envelope generation strategy for squeezed rejection sampling for a continuous, differentiable, log-concave density on a connected region of support [244].
The approach is termed adaptive rejection sampling because the envelope and squeezing function are iteratively refined concurrently with the generation of sample draws. The amount of waste and the frequency with which f must be evaluated both shrink as iterations increase.
Let ![]() (x) = log f(x), and assume f(x) > 0 on a (possibly infinite) interval of the real line. Let f be log-concave in the sense that
(x) = log f(x), and assume f(x) > 0 on a (possibly infinite) interval of the real line. Let f be log-concave in the sense that ![]() (a) − 2
(a) − 2 ![]() (b) +
(b) + ![]() (c) < 0 for any three points in the support region of f for which a < b < c. Under the additional assumptions that f is continuous and differentiable, note that
(c) < 0 for any three points in the support region of f for which a < b < c. Under the additional assumptions that f is continuous and differentiable, note that ![]() ′(x) exists and decreases monotonically with increasing x, but may have discontinuities.
′(x) exists and decreases monotonically with increasing x, but may have discontinuities.
The algorithm is initiated by evaluating ![]() and
and ![]() ′ at k points, x1 < x2 < . . . < xk. Let Tk = {x1, . . ., xk}. If the support of f extends to −∞, choose x1 such that
′ at k points, x1 < x2 < . . . < xk. Let Tk = {x1, . . ., xk}. If the support of f extends to −∞, choose x1 such that ![]() ′(x1) > 0. Similarly, if the support of f extends to ∞, choose xk such that
′(x1) > 0. Similarly, if the support of f extends to ∞, choose xk such that ![]() ′(xk) < 0.
′(xk) < 0.
Define the rejection envelope on Tk to be the exponential of the piecewise linear upper hull of ![]() formed by the tangents to
formed by the tangents to ![]() at each point in Tk. If we denote the upper hull of
at each point in Tk. If we denote the upper hull of ![]() as
as ![]() , then the rejection envelope is
, then the rejection envelope is ![]() . To understand the concept of an upper hull, consider Figure 6.4. This figure shows
. To understand the concept of an upper hull, consider Figure 6.4. This figure shows ![]() with a solid line and illustrates the case when k = 5. The dashed line shows the piecewise upper hull, e*. It is tangent to
with a solid line and illustrates the case when k = 5. The dashed line shows the piecewise upper hull, e*. It is tangent to ![]() at each xi, and the concavity of
at each xi, and the concavity of ![]() ensures that
ensures that ![]() lies completely above
lies completely above ![]() everywhere else. One can show that the tangents at xi and xi+1 intersect at
everywhere else. One can show that the tangents at xi and xi+1 intersect at
(6.8) ![]()
for i = 1, . . ., k − 1. Therefore,
and i = 1, . . ., k, with z0 and zk defined, respectively, to equal the (possibly infinite) lower and upper bounds of the support region for f. Figure 6.5 shows the envelope ek exponentiated to the original scale.
Figure 6.4 Piecewise linear outer and inner hulls for ![]() (x) = log f(x) used in adaptive rejection sampling when k = 5.
(x) = log f(x) used in adaptive rejection sampling when k = 5.
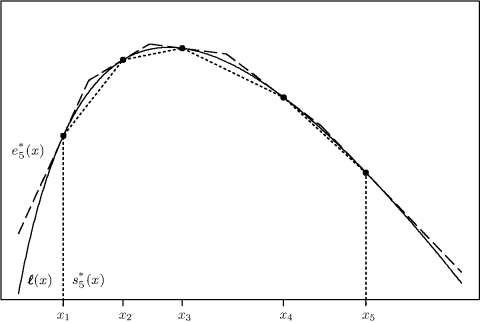
Figure 6.5 Envelopes and squeezing function for adaptive rejection sampling. The target density is the smooth, nearly bell-shaped curve. The first method discussed in the text, using the derivative of ![]() , produces the envelope shown as the upper boundary of the lighter shaded region. This corresponds to Equation (6.9) and Figure 6.4. Later in the text, a derivative-free method is presented. That envelope is the upper bound of the darker shaded region and corresponds to (6.11) and Figure 6.6. The squeezing function for both approaches is given by the dotted curve.
, produces the envelope shown as the upper boundary of the lighter shaded region. This corresponds to Equation (6.9) and Figure 6.4. Later in the text, a derivative-free method is presented. That envelope is the upper bound of the darker shaded region and corresponds to (6.11) and Figure 6.6. The squeezing function for both approaches is given by the dotted curve.
Define the squeezing function on Tk to be the exponential of the piecewise linear lower hull of ![]() formed by the chords between adjacent points in Tk. This lower hull is given by
formed by the chords between adjacent points in Tk. This lower hull is given by
and i = 1, . . ., k − 1. When x < x1 or x > xk, let ![]() . Thus the squeezing function is
. Thus the squeezing function is ![]() . Figure 6.4 shows a piecewise linear lower hull,
. Figure 6.4 shows a piecewise linear lower hull, ![]() , when k = 5. Figure 6.5 shows the squeezing function sk on the original scale.
, when k = 5. Figure 6.5 shows the squeezing function sk on the original scale.
Figures 6.4 and 6.5 illustrate several important features of the approach. Both the rejection envelope and the squeezing function are piecewise exponential functions. The envelope has exponential tails that lie above the tails of f. The squeezing function has bounded support.
Adaptive rejection sampling is initialized by choosing a modest k and a corresponding suitable grid Tk. The first iteration of the algorithm proceeds as for squeezed rejection sampling, using ek and sk as the envelope and squeezing function, respectively. When a candidate draw is accepted, it may be accepted without evaluating ![]() and
and ![]() ′ at the candidate if the squeezing criterion was met. However, it may also be accepted at the second stage, where evaluation of
′ at the candidate if the squeezing criterion was met. However, it may also be accepted at the second stage, where evaluation of ![]() and
and ![]() ′ at the candidate is required. When a candidate is accepted at this second stage, the accepted point is added to the set Tk, creating Tk+1. Updated functions ek+1 and sk+1 are also calculated. Then iterations continue. When a candidate draw is rejected, no update to Tk, ek, or sk is made. Further, we see now that a new point that matches any existing member of Tk provides no meaningful update to Tk, ek, or sk.
′ at the candidate is required. When a candidate is accepted at this second stage, the accepted point is added to the set Tk, creating Tk+1. Updated functions ek+1 and sk+1 are also calculated. Then iterations continue. When a candidate draw is rejected, no update to Tk, ek, or sk is made. Further, we see now that a new point that matches any existing member of Tk provides no meaningful update to Tk, ek, or sk.
Candidate draws are taken from the density obtained by scaling the piecewise exponential envelope ek so that it integrates to 1. Since each accepted draw is made using a rejection sampling approach, the draws are an i.i.d. sample precisely from f. If f is known only up to a multiplicative constant, the adaptive rejection sampling approach may still be used, since the proportionality constant merely shifts ![]() ,
, ![]() , and
, and ![]() .
.
Gilks and co-authors have developed a similar approach that does not require evaluation of ![]() ′ [237, 240]. We retain the assumptions that f is log-concave with a connected support region, along with the basic notation and setup for the tangent-based approach above.
′ [237, 240]. We retain the assumptions that f is log-concave with a connected support region, along with the basic notation and setup for the tangent-based approach above.
For the set of points Tk, define Li(·) to be the straight line function connecting (xi, ![]() (xi)) and (xi+1,
(xi)) and (xi+1, ![]() (xi+1)) for i = 1, . . ., k − 1. Define
(xi+1)) for i = 1, . . ., k − 1. Define
with the convention that L0(x) = Lk(x) =∞. Then ![]() is a piecewise linear upper hull for
is a piecewise linear upper hull for ![]() because the concavity of
because the concavity of ![]() ensures that Li(x) lies below
ensures that Li(x) lies below ![]() (x) on (xi, xi+1) and above
(x) on (xi, xi+1) and above ![]() (x) when x < xi or x > xi+1. The rejection sampling envelope is then
(x) when x < xi or x > xi+1. The rejection sampling envelope is then ![]() .
.
The squeezing function remains as in (6.10). Iterations of the derivative-free adaptive rejection sampling algorithm proceed analogously to the previous approach, with Tk, the envelope, and the squeezing function updated each time a new point is kept.
Figure 6.6 illustrates the derivative-free adaptive rejection sampling algorithm for the same target shown in Figure 6.4. The envelope is not as efficient as when ![]() ′ is used. Figure 6.5 shows the envelope on the original scale. The lost efficiency is seen on this scale, too.
′ is used. Figure 6.5 shows the envelope on the original scale. The lost efficiency is seen on this scale, too.
Figure 6.6 Piecewise linear outer and inner hulls for ![]() (x) = log f(x) used in derivative-free adaptive rejection sampling when k = 5.
(x) = log f(x) used in derivative-free adaptive rejection sampling when k = 5.
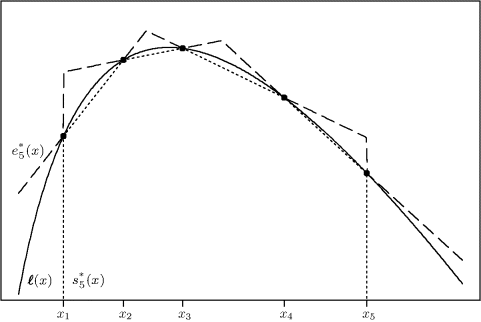
Regardless of the method used to construct ek, notice that one would prefer the Tk grid to be most dense in regions where f(x) is largest, near the mode of f. Fortunately, this will happen automatically, since such points are most likely to be kept in subsequent iterations and included in updates to Tk. Grid points too far in the tails of f, such as x5, are not very helpful.
Software for the tangent-based approach is available in [238]. The derivative-free approach has been popularized by its use in the WinBUGS software for carrying out Markov chain Monte Carlo algorithms to facilitate Bayesian analyses [241, 243, 610]. Adaptive rejection sampling can also be extended to densities that are not log-concave, for example, by applying Markov chain Monte Carlo methods like those in Chapter 7 to further correct the sampling probabilities. One strategy is given in [240].
6.3 Approximate Simulation
Although the methods described above have the appealing feature that they are exact, there are many cases when an approximate method is easier or perhaps the only feasible choice. Despite how it might sound, Approximation is not a critical flaw of these methods because the degree of approximation can be controlled by user-specified parameters in the algorithms. The simulation methods in this section are all based to some extent on the sampling importance resampling principle, which we discuss first.
6.3.1 Sampling Importance Resampling Algorithm
The sampling importance resampling (SIR) algorithm simulates realizations approximately from some target distribution. SIR is based upon the notion of importance sampling, discussed in detail in Section 6.4.1. Briefly, importance sampling proceeds by drawing a sample from an importance sampling function, g. Informally, we will call g an envelope. Each point in the sample is weighted to correct the sampling probabilities so that the weighted sample can be related to a target density f. For example, the weighted sample can be used to estimate expectations under f.
Having graphed some univariate targets and envelopes in the early part of this chapter to illustrate basic concepts, we shift now to multivariate notation to emphasize the full generality of techniques. Thus, X = (X1, . . ., Xp) denotes a random vector with density f(x), and g(x) denotes the density corresponding to a multivariate envelope for f.
For the target density f, the weights used to correct sampling probabilities are called the standardized importance weights and are defined as
for a collection of values x1, . . ., xm drawn i.i.d. from an envelope g. Although not necessary for general importance sampling, it is useful to standardize the weights as in (6.12) so they sum to 1. When f = cq for some unknown proportionality constant c, the unknown c cancels in the numerator and denominator of (6.12).
We may view importance sampling as approximating f by the discrete distribution having mass ![]() on each observed point xi for i = 1, . . ., m. Rubin proposed sampling from this distribution to provide an approximate sample from f [559, 560]. The SIR algorithm therefore proceeds as follows:
on each observed point xi for i = 1, . . ., m. Rubin proposed sampling from this distribution to provide an approximate sample from f [559, 560]. The SIR algorithm therefore proceeds as follows:
A random variable X drawn with the SIR algorithm has distribution that converges to f as m → ∞. To see this, define ![]() , let Y1, . . ., Ym ~ i.i.d. g, and consider a set
, let Y1, . . ., Ym ~ i.i.d. g, and consider a set ![]() . Then
. Then
(6.13) ![]()
The strong law of large numbers gives
(6.14) ![]()
as m→ ∞. Further,
(6.15) ![]()
as m→ ∞. Hence,
(6.16) ![]()
as m→ ∞. Finally, we note that
(6.17) ![]()
by Lebesgue's dominated convergence theorem [49, 595]. The proof is similar when the target and envelope are known only up to a constant [555].
Although both SIR and rejection sampling rely on the ratio of target to envelope, they differ in an important way. Rejection sampling is perfect, in the sense that the distribution of a generated draw is exactly f, but it requires a random number of draws to obtain a sample of size n. In contrast, the SIR algorithm uses a pre-determined number of draws to generate an n-sample but permits a random degree of approximation to f in the distribution of the sampled points.
When conducting SIR, it is important to consider the relative sizes of the initial sample and the resample. These sample sizes are m and n, respectively. In principle, we require n/m → 0 for distributional convergence of the sample. In the context of asymptotic analysis of Monte Carlo estimates based on SIR, where n→ ∞, this condition means that m→ ∞ even faster than n→ ∞. For fixed n, distributional convergence of the sample occurs as m→ ∞, therefore in practice one obviously wants to initiate SIR with the largest possible m. However, one faces the competing desire to choose n as large as possible to increase the inferential precision. The maximum tolerable ratio n/m depends on the quality of the envelope. We have sometimes found ![]() tolerable so long as the resulting resample does not contain too many replicates of any initial draw.
tolerable so long as the resulting resample does not contain too many replicates of any initial draw.
The SIR algorithm can be sensitive to the choice of g. First, the support of g must include the entire support of f if a reweighted sample from g is to approximate a sample from f. Further, g should have heavier tails than f, or more generally g should be chosen to ensure that f(x)/g(x) never grows too large. If g(x) is nearly zero anywhere where f(x) is positive, then a draw from this region will happen only extremely rarely, but when it does it will receive a huge weight.
When this problem arises, the SIR algorithm exhibits the symptom that one or a few standardized importance weights are enormous compared to the other weights, and the secondary sample consists nearly entirely of replicated values of one or a few initial draws. When the problem is not too severe, taking the secondary resample without replacement has been suggested [220]. This is asymptotically equivalent to sampling with replacement, but has the practical advantage that it prevents excessive duplication. The disadvantage is that it introduces some additional distributional approximation in the final sample. When the distribution of weights is found to be highly skewed, it is probably wiser to switch to a different envelope or a different sampling strategy altogether.
Since SIR generates X1, . . ., Xn approximately i.i.d. from f, one may proceed with Monte Carlo integration such as estimating the expectation of h(X) by ![]()
![]() as in (6.1). However, in Section 6.4 we will introduce superior ways to use the initial weighted importance sample, along with other powerful methods to improve Monte Carlo estimation of integrals.
as in (6.1). However, in Section 6.4 we will introduce superior ways to use the initial weighted importance sample, along with other powerful methods to improve Monte Carlo estimation of integrals.
Example 6.3 (Slash Distribution) The random variable Y has a slash distribution if Y = X/U where X ~ N(0, 1) and U ~ Unif(0, 1) independently. Consider using the slash distribution as a SIR envelope to generate standard normal variates, and conversely using the normal distribution as a SIR envelope to generate slash variates. Since it is easy to simulate from both densities using standard methods, SIR is not needed in either case, but examining the results is instructive.
The slash density function is
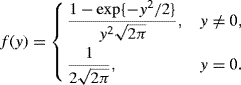
This density has very heavy tails. Therefore, it is a fine importance sampling function for generating draws from a standard normal distribution using SIR. The left panel of Figure 6.7 illustrates the results when m = 100, 000 and n = 5000. The true normal density is superimposed for comparison.
Figure 6.7 The left panel shows a histogram of approximate draws from a standard normal density obtained via SIR with a slash distribution envelope. The right panel shows a histogram of approximate draws from a slash density obtained via SIR using a normal envelope. The solid lines show the target densities.
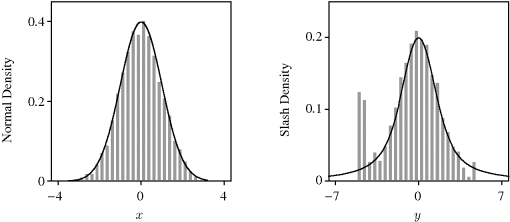
On the other hand, the normal density is not a suitable importance sampling function for SIR use when generating draws from the slash distribution because the envelope's tails are far lighter than the target's. The right panel of Figure 6.7 (where, again, m = 100, 000 and n = 5000) illustrates the problems that arise. Although the tails of the slash density assign appreciable probability as far as 10 units from the origin, no candidate draws from the normal density exceeded 5 units from the origin. Therefore, beyond these limits, the simulated tails of the target have been completely truncated. Further, the most extreme candidate draws generated have far less density under the normal envelope than they do under the slash target, so their importance ratios are extremely high. This leads to abundant resampling of these points in the tails. Indeed, 528 of the 5000 values selected by SIR are replicates of the three lowest unique values in the histogram. ![]()
Example 6.4 (Bayesian Inference) Suppose that we seek a sample from the posterior distribution from a Bayesian analysis. Such a sample could be used to provide Monte Carlo estimates of posterior moments, probabilities, or highest posterior density intervals, for example. Let f(θ) denote the prior, and L(θ|x) the likelihood, so the posterior is f(θ|x) = cf(θ)L(θ|x) for some constant c that may be difficult to determine. If the prior does not seriously restrict the parameter region favored by the data via the likelihood function, then perhaps the prior can serve as a useful importance sampling function. Sample θ1, . . ., θm i.i.d. from f(θ). Since the target density is the posterior, the ith unstandardized weight equals L(θi|x). Thus the SIR algorithm has a very simple form: Sample from the prior, weight by the likelihood, and resample.
For instance, recall Example 6.2. In this case, importance sampling could begin by drawing λ1, . . ., λm ~ i.i.d. Lognormal(log 4, 0.52). The importance weights would be proportional to L(λi|x). Resampling from λ1, . . ., λm with replacement with these weights yields an approximate sample from the posterior. ![]()
6.3.1.1 Adaptive Importance, Bridge, and Path Sampling
In some circumstances, one initially may be able to specify only a very poor importance sampling envelope. This may occur, for example, when the target density has support nearly limited to a lower-dimensional space or surface due to strong dependencies between variables not well understood by the analyst. In other situations, one may wish to conduct importance sampling for a variety of related problems, but no single envelope may be suitable for all the target densities of interest. In situations like this, it is possible to adapt the importance sampling envelope.
One collection of ideas for envelope improvement is termed adaptive importance sampling. An initial sample of size m1 is taken from an initial envelope e1. This sample is weighted (and possibly resampled) to obtain an initial estimate of quantities of interest or an initial view of f itself. Based on the information obtained, the envelope is improved, yielding e2. Further importance sampling and envelope improvement steps are taken as needed. When such steps are terminated, it is most efficient to use the draws from all the steps, along with their weights, to formulate suitable inference. Alternatively, one can conduct quick envelope refinement during several initial steps, withholding the majority of simulation effort to the final stage and limiting inference to this final sample for simplicity.
In parametric adaptive importance sampling, the envelope is typically assumed to belong to some family of densities indexed by a low-dimensional parameter. The best choice for the parameter is estimated at each iteration, and the importance sampling steps are iterated until estimates of this indexing parameter stabilize [189, 381, 490, 491, 606]. In nonparametric adaptive importance sampling, the envelope is often assumed to be a mixture distribution, such as is generated with the kernel density estimation approach in Chapter 10. Importance sampling steps are alternated with envelope updating steps, adding, deleting, or modifying mixture components. Examples include [252, 657, 658, 680]. Although potentially useful in some circumstances, these approaches are overshadowed by Markov chain Monte Carlo methods like those described in Chapter 7, because the latter are usually simpler and at least as effective.
A second collection of ideas for envelope improvement is relevant when a single envelope is inadequate for the consideration of several densities. In Bayesian statistics and certain marginal likelihood and missing data problems, one is often interested in estimating a ratio of normalizing constants for a pair of densities. For example, if fi(θ|x) = ciqi(θ|x) is the ith posterior density for θ (for i = 1, 2) under two competing models, where qi is known but ci is unknown, then r = c2/c1 is the posterior odds for model 1 compared to model 2. The Bayes factor is the ratio of r to the prior odds.
Since it is often difficult to find good importance sampling envelopes for both f1 and f2, one standard importance sampling approach is to use only a single envelope to estimate r. For example, in the convenient case when the support of f2 contains that of f1 and we are able to use f2 as the envelope, r = E{q1(θ|x)/q2(θ|x)}. However, when f1 and f2 differ greatly, such a strategy will perform poorly because no single envelope can be sufficiently informative about both c1 and c2. The strategy of bridge sampling employs an unnormalized density, qbridge, that is, in some sense, between q1 and q2 [457]. Then noting that
we may employ importance sampling to estimate the numerator and the denominator, thus halving the difficulty of each task, since qbridge is nearer to each qi than the qi are to each other. These ideas have been extensively studied for Bayesian model choice [437].
In principle, the idea of bridging can be extended by iterating the strategy employed in (6.18) with a nested sequence of intermediate densities between q1 and q2. Each neighboring pair of densities in the sequence between q1 and q2 would be close enough to enable reliable estimation of the corresponding ratio of normalizing constants, and from those ratios one could estimate r. In practice, it turns out that the limit of such a strategy amounts to a very simple algorithm termed path sampling. Details are given in [222].
6.3.2 Sequential Monte Carlo
When the target density f becomes high dimensional, SIR is increasingly inefficient and can be difficult to implement. Specifying a very good high-dimensional envelope that closely approximates the target with sufficiently heavy tails but little waste can be challenging. Sequential Monte Carlo methods address the problem by splitting the high-dimensional task into a sequence of simpler steps, each of which updates the previous one.
Suppose that X1:t = (X1, . . ., Xt) represents a discrete time stochastic process with Xt being the observation at time t and X1:t representing the entire history of the sequence thus far. The Xt may be multidimensional, but for simplicity we adopt scalar notation here when possible. Write the density of X1:t as ft. Suppose that we wish to estimate at time t the expected value of h(X1:t) with respect to ft using an importance sampling strategy.
A direct application of the SIR approach from Section 6.3.1 would be to draw a sample of x1:t sequences from an envelope gt and then calculate the importance weighted average of this sample of h(x1:t) values. However, this overlooks a key aspect of the problem. As t increases, X1:t and the expected value of h(x1:t) evolve. At time t it would be better to update previous inferences than to act as if we had no previous information. Indeed, it would be very inefficient to start the SIR approach from scratch at each time t. Instead we will develop a strategy that will enable us to append the simulated Xt to the X1:t−1 previously simulated and to adjust the previous importance weights in order to estimate the expected value of h(X1:t). Such an approach is called sequential importance sampling [419].
The attractiveness of such incremental updating is particularly apparent when sequential estimation must be completed in real time. For example, when applied to object tracking, sequential importance sampling can be used to estimate the current location of an object (e.g., a missile) from noisy observations made by remote sensors (e.g., radar). At any time, the true location is estimated from the current observation and the sequence of past observations (i.e., the estimated past trajectory). As tracking continues at each time increment, the estimation must keep up with the rapidly incoming data. A wide variety of sequential estimation techniques have been applied to tackle this tracking problem [95, 239, 287, 447].
Applications of sequential importance sampling are extremely diverse, spanning sciences from physics to molecular biology, and generic statistical problems from Bayesian inference to the analysis of sparse contingency tables [108, 109, 167, 419].
6.3.2.1 Sequential Importance Sampling for Markov Processes
Let us begin with the simplifying assumption that X1:t is a Markov process. In this case, Xt depends only on Xt−1 rather than the whole history X1:t−1. Then the target density ft(x1:t) may be expressed as
Suppose that we adopt the same Markov form for the envelope, namely
Using the ordinary nonsequential SIR algorithm (Section 6.3.1), at time t one would sample from gt(x1:t) and reweight each x1:t value by ![]() . Using (6.19) and (6.20), we see that
. Using (6.19) and (6.20), we see that ![]() , where u1 = f1(x1)/g1(x1) and ui = fi(xi|xi−1)/gi(xi|xi−1) for i = 2, . . ., t.
, where u1 = f1(x1)/g1(x1) and ui = fi(xi|xi−1)/gi(xi|xi−1) for i = 2, . . ., t.
Given x1:t−1 and ![]() , we can take advantage of the Markov property by sampling only the next component, namely Xt, appending the value to x1:t−1, and adjusting
, we can take advantage of the Markov property by sampling only the next component, namely Xt, appending the value to x1:t−1, and adjusting ![]() using the multiplicative factor ut. Specifically, when the target and envelope distributions are Markov, a sequential importance sampling approach for obtaining at each time a sequence x1:t and corresponding weight
using the multiplicative factor ut. Specifically, when the target and envelope distributions are Markov, a sequential importance sampling approach for obtaining at each time a sequence x1:t and corresponding weight ![]() is given in the steps below. A sample of n such points and their weights can be used to approximate ft(x1:t) and hence the expected value of h(X1:t). The algorithm is:
is given in the steps below. A sample of n such points and their weights can be used to approximate ft(x1:t) and hence the expected value of h(X1:t). The algorithm is:
For obtaining an independent sample of n draws ![]() , i = 1, . . ., n, the above algorithm can be carried out by treating the n sequences one at a time or as a batch. Using this sample of size n, the weighted average
, i = 1, . . ., n, the above algorithm can be carried out by treating the n sequences one at a time or as a batch. Using this sample of size n, the weighted average ![]() serves as the estimate of
serves as the estimate of ![]() .
.
It is not necessary to standardize the weights at the end of each cycle above, although when we seek to estimate ![]() the normalization is natural. Section 6.4.1 discusses weight normalization in a more general context. Section 6.3.2.5 describes a generalization of sequential importance sampling that involves resampling with normalized weights between cycles.
the normalization is natural. Section 6.4.1 discusses weight normalization in a more general context. Section 6.3.2.5 describes a generalization of sequential importance sampling that involves resampling with normalized weights between cycles.
Example 6.5 (Simple Markov Process) Let Xt|Xt−1 ~ ft denote a Markov process where
For each t we wish to obtain an importance-weighted sample of ![]() with importance weights
with importance weights ![]() for i = 1, . . ., n. Suppose we wish to estimate σt the standard deviation of Xt using the weighted estimator
for i = 1, . . ., n. Suppose we wish to estimate σt the standard deviation of Xt using the weighted estimator
where ![]() .
.
Using sequential importance sampling, at stage t we can begin by sampling from a normal envelope ![]() . Due to the Markov property, the weight updates are
. Due to the Markov property, the weight updates are
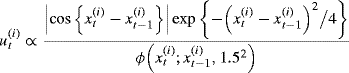
where ϕ(z; a, b) denotes the normal density for z with mean a and variance b.
Thus to update the (t − 1)th sample, the ![]() are drawn, appended to the corresponding past sequences to form
are drawn, appended to the corresponding past sequences to form ![]() , with the respective weights updated according to
, with the respective weights updated according to ![]() . We may then estimate σt using (6.22). At t = 100 we find
. We may then estimate σt using (6.22). At t = 100 we find ![]() . By comparison, when Xt|xt−1 ~ N(xt−1, 22), then no sequential importance sampling is needed and the analogous
. By comparison, when Xt|xt−1 ~ N(xt−1, 22), then no sequential importance sampling is needed and the analogous ![]() . Thus, the cosine term in (6.21) contributes additional variance to the distribution ft.
. Thus, the cosine term in (6.21) contributes additional variance to the distribution ft.
This example is sufficiently simple that other approaches are possible, but our sequential importance sampling approach is very straightforward. However, as t increases, the weights develop an undesirable degeneracy discussed in Section 6.3.2.3. Implementing the ideas there makes this example more effective. ![]()
6.3.2.2 General Sequential Importance Sampling
The task of obtaining an approximate sample from ft(x1:t) was greatly simplified in Section 6.3.2.1 because of the Markov assumption. Suppose now that we want to achieve the same goal in a case where the Markov property does not apply. Then the target density is
noting x1:1 = x1. Similarly, let us drop the Markov property of the envelope, permitting
The importance weights then take the form
(6.25) ![]()
and the recursive updating expression for the importance weights is
(6.26) ![]()
for t > 1. Example 6.6 presents an application of the approach described here for non-Markov sequences. First, however, we consider a potential problem with the sequential weights.
6.3.2.3 Weight Degeneracy, Rejuvenation, and Effective Sample Size
As the importance weights are updated at each time, it is increasingly likely that the majority of the total weight will be concentrated in only a few sample sequences. The reason for this is that each component of a sequence must be reasonably consistent with each corresponding conditional density ft(xt|x1:t−1) as time progresses. Each instance when an unusual (i.e., unlikely) new component is appended to a sample sequence, this proportionally reduces the weight for that entire sequence. Eventually few—if any—sequences have avoided such pitfalls. We say that the weights are increasingly degenerate as they become concentrated on only a few sequences X1:t. Degenerating weights degrade estimation performance.
To identify such problems, the effective sample size can be used to measure the efficiency of using the envelope g with target f [386, 418]. This assesses the degeneracy of the weights.
Degeneracy of the weights is related to their variability: as weights are increasingly concentrated on a few samples with the remaining weights near zero, the variance of the weights will increase. A useful measure of variability in the weights is the (squared) coefficient of variation (CV) given by
Next we will identify how this quantity can be incorporated into a measure of weight degeneracy.
The effective sample size can be interpreted as indicating that the n weighted samples used in an importance sampling estimate are worth a certain number of unweighted i.i.d. samples drawn exactly from f. Suppose that n samples have normalized importance weights ![]() for i = 1, . . ., n. If z of these weights are zero and the remaining n − z are equal to 1/(n − z), then estimation effectively relies on the n − z points with nonzero weights.
for i = 1, . . ., n. If z of these weights are zero and the remaining n − z are equal to 1/(n − z), then estimation effectively relies on the n − z points with nonzero weights.
In this case, the coefficient of variation in (6.27) can be estimated as
(6.28) 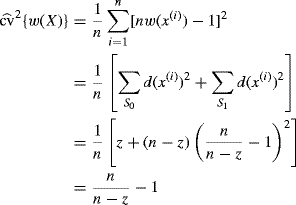
where d(x(i)) = nw(x(i)) − 1 and the samples are partitioned based on whether the weight is 0 or 1 using ![]() and
and ![]() . Therefore
. Therefore ![]() . Moreover, by the nature of the weights we are considering, it is intuitive that the effective sample size should be n − z since that is the number of nonzero weights. Thus we can measure the effective sample size as
. Moreover, by the nature of the weights we are considering, it is intuitive that the effective sample size should be n − z since that is the number of nonzero weights. Thus we can measure the effective sample size as
Larger effective sample sizes are better, while smaller ones indicate increasing degeneracy. The notation ![]() is used to stress that the effective sample size is a measure of the quality of g as an envelope for f. In the case where the weights have not been standardized, the equivalent expression is
is used to stress that the effective sample size is a measure of the quality of g as an envelope for f. In the case where the weights have not been standardized, the equivalent expression is
(6.30) ![]()
Applying (6.29) to calculate ![]() from the standardized weights is straightforward since
from the standardized weights is straightforward since
(6.31) 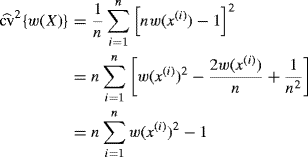
so
(6.32) ![]()
In the case of sequential importance sampling, we may monitor ![]() to assess importance weight degeneracy. Typically, the effective sample size will decrease as time progresses. At time t when the effective sample size falls below some threshold, the collection of sequences
to assess importance weight degeneracy. Typically, the effective sample size will decrease as time progresses. At time t when the effective sample size falls below some threshold, the collection of sequences ![]() , i = 1, . . ., n, should be rejuvenated. The simplest rejuvenation approach is to resample the sequences with replacement with probabilities equal to the
, i = 1, . . ., n, should be rejuvenated. The simplest rejuvenation approach is to resample the sequences with replacement with probabilities equal to the ![]() and then reset all weights to 1/n. Inclusion of this multinomial resampling step is sometimes called sequential importance sampling with resampling [421] and is closely related to the notion of particle filters which follows in Section 6.3.2.5. We illustrate the approach in several examples below. A variety of more sophisticated approaches for reducing degeneration and implementing rejuvenation are cited in Sections 6.3.2.4 and 6.3.2.5.
and then reset all weights to 1/n. Inclusion of this multinomial resampling step is sometimes called sequential importance sampling with resampling [421] and is closely related to the notion of particle filters which follows in Section 6.3.2.5. We illustrate the approach in several examples below. A variety of more sophisticated approaches for reducing degeneration and implementing rejuvenation are cited in Sections 6.3.2.4 and 6.3.2.5.
Figure 6.8 illustrates the concepts discussed in the last two subsections. Time increases from left to right. The five shaded boxes and corresponding axes represent some hypothetical univariate conditional densities (like histograms turned sideways) for sampling the Xt|x1:t−1. For each t, let gt be a uniform density over the range for Xt covered by the shaded boxes. Starting at t = 1 there are points ![]() for i
for i ![]() {1, 2, 3}, represented by the three small circles on the leftmost edge of Figure 6.8. Their current weights are represented by the sizes of the circles; initially the weights are equal because g1 is uniform. To initiate a cycle of the algorithm, the three points receive weights proportional to f1(x1)/g1(x1). The weighted points are shown just touching the x1 axis. The point in the dominant region of f1 receives proportionally more weight than the other two, so its circle has grown larger. The effect is dampened in the figure because the weights are rescaled for visual presentation to prevent the circles from growing too large to fit in the graph or too small to see.
{1, 2, 3}, represented by the three small circles on the leftmost edge of Figure 6.8. Their current weights are represented by the sizes of the circles; initially the weights are equal because g1 is uniform. To initiate a cycle of the algorithm, the three points receive weights proportional to f1(x1)/g1(x1). The weighted points are shown just touching the x1 axis. The point in the dominant region of f1 receives proportionally more weight than the other two, so its circle has grown larger. The effect is dampened in the figure because the weights are rescaled for visual presentation to prevent the circles from growing too large to fit in the graph or too small to see.
Figure 6.8 Illustration of sequential importance sampling. Time progresses from left to right. Samples are indicated by solid lines. Densities are shaded boxes. Points are shown with circles; the area of the circle is an indication of the sequence's weight at that time. The dashed line indicates an instance of weight regeneration through sequence resampling. See the text for a detailed discussion.
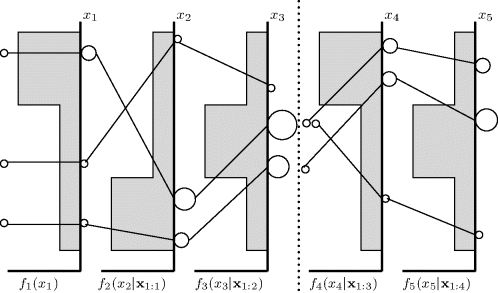
At time t = 2, new uniform draws are appended to the current points, thereby forming sequences of length 2. The lines between the first two density graphs indicate which x2 is appended to which x1. At this point, the sequence reaching the middle x2 point has the largest weight because its x1 point had high weight at the first stage and its x2 sits in a region of high density according to f2(x2|x1). The bottom path also had increased weight because its x2 landed in the same high-density region for t = 2. Again, g2 has not influenced the weights because it is uniform.
At the next time step, the sequences have grown by appending sampled x3 values, and they have been reweighted according to f3(x3|x1:2). At this point, suppose that the weights are sufficiently degenerate to produce an effective sample size ![]() small enough to trigger regeneration of the weights. This event is indicated by the dashed vertical line. To fix the problem, we resample three sequences with replacement from the current ones with probabilities proportional to their respective weights. In the figure, two sequences will now progress from the middle x3, one from the bottom x3, and none from the top x3. The latter sequence becomes extinct, to be replaced by two sequences having the same past up to t = 3 but different futures beyond that. Finally, the right portion of the figure progresses as before, with additional samples at each t and corresponding adjustments to the weights.
small enough to trigger regeneration of the weights. This event is indicated by the dashed vertical line. To fix the problem, we resample three sequences with replacement from the current ones with probabilities proportional to their respective weights. In the figure, two sequences will now progress from the middle x3, one from the bottom x3, and none from the top x3. The latter sequence becomes extinct, to be replaced by two sequences having the same past up to t = 3 but different futures beyond that. Finally, the right portion of the figure progresses as before, with additional samples at each t and corresponding adjustments to the weights.
Example 6.6 (High-Dimensional Distribution) Although the role of t has been emphasized here as indexing a sequence of random variables Xt for t = 1, 2, . . ., sequential importance sampling can also be used as a strategy for the generic problem of sampling from a p-dimensional target distribution fp for fixed p. We can accumulate an importance weighted sample from this high-dimensional distribution one dimension at a time by sampling from the univariate conditional densities as suggested by (6.23) and (6.24). After p steps we obtain the ![]() and their corresponding weights needed to approximate a sample from fp.
and their corresponding weights needed to approximate a sample from fp.
For example, consider a sequence of probability densities given by ft(x1:t) = kt exp { − ||x1:t||3/3} for some constants kt, where || · || is the Euclidean norm and t = 1, . . ., p. Here X1:p is the random variable having density fp. Although ft(x1:t) is a smooth unimodal density with tails somewhat lighter than the normal distribution, there is no easy method for sampling from it directly. Note also that the sequence of random variables X1:t is not Markov because for each t the density of Xt|X1:t−1 depends on all prior components of X1:t. Thus this example requires the general sequential importance sampling approach described in Section 6.3.2.2.
Let us adopt a standard normal distribution for the envelope. The tth conditional density can be expressed as ft(xt|x1:t−1) = ft(x1:t)/ft−1(x1:t−1). The sequential importance sampling strategy is given by:
Note that the resampling strategy in step 5 attempts to rejuvenate the sample periodically to reduce degeneracy; hence the algorithm is called sequential importance sampling with resampling.
As an example, set p = 50, n = 5000, and α = 0.2. Over the 50 stages, step 5 was triggered 8 times. The median effective sample size during the process was about 2000. Suppose we simply drew 5000 points from a 50-dimensional standard normal envelope and importance reweighted these points all at once. This one-step approach yielded an effective sample size of about 1.13. Increasing the sample size to n = 250, 000 only increases the effective sample size to 1.95 for the one-step approach. High-dimensional space is too vast to stumble across many p-dimensional draws with high density using the one-step approach: good points must be generated sequentially one dimension at a time. ![]()
6.3.2.4 Sequential Importance Sampling for Hidden Markov Models
Another class of distributions to which sequential importance sampling can be applied effectively is generated by hidden Markov models. Consider a Markov sequence of unobservable variables X0, X1, X2, . . . indexed by time t. Suppose that these variables represent the state of some Markov process, so the distribution of Xt|x1:t−1 depends only on xt−1. Although these states are unobservable, suppose that there is also an observable sequence of random variables Y0, Y1, Y2, . . . where Yt is dependent on the process state at the same time, namely Xt. Thus we have the model
![]()
for t = 1, 2, . . . and px and py are density functions. This is called a hidden Markov process.
We wish to use the observed y1:t as data to estimate the states x1:t of the hidden Markov process. In the importance sampling framework ft(x1:t|y1:t) is the target distribution.
Note that there is a recursive relationship between ft and ft−1. Specifically,
Suppose that at time t we adopt the envelope gt(xt|x1:t−1) = px(xt|xt−1). Then the multiplicative update for the importance weights can be expressed as
The final equality results from the substitution of (6.33) into (6.34).
This framework can be recast in Bayesian terms. In this case, X1:t are considered parameters. The prior distribution at time t is ![]() . The likelihood is obtained from the observed data density, equaling
. The likelihood is obtained from the observed data density, equaling ![]() . The posterior ft(x1:t|y1:t) is proportional to the product of the prior and the likelihood, as obtained recursively from (6.33). Thus the importance weight update at time t is the likelihood obtained from the new data yt at time t. The sequential factorization given here is akin to iterating Example 6.4 in which we sampled from the prior distribution and weighted by the likelihood. A similar strategy is described by [113], where the procedure is generalized to sample dimensions in batches.
. The posterior ft(x1:t|y1:t) is proportional to the product of the prior and the likelihood, as obtained recursively from (6.33). Thus the importance weight update at time t is the likelihood obtained from the new data yt at time t. The sequential factorization given here is akin to iterating Example 6.4 in which we sampled from the prior distribution and weighted by the likelihood. A similar strategy is described by [113], where the procedure is generalized to sample dimensions in batches.
Example 6.7 (Terrain Navigation) An airplane flying over uneven terrain can use information about the ground elevation beneath it to estimate its current location. As the plane follows its flight path, sequential elevation measurements are taken. Simultaneously, an inertial navigation system provides an estimated travel direction and distance. At each time point the previously estimated location of the plane is updated using both types of new information. Interest in such problems arises in, for example, military applications where the approach could serve as an alternative or backup to global satellite systems. Details on the terrain navigation problem are given by [30, 31, 287].
Let the two-dimensional variable Xt = (X1t, X2t) denote the true location of the plane at time t, and let dt denote the measured drift, or shift in the plane location during the time increment as measured by the inertial navigation system. The key data for terrain navigation come from a map database that contains (or interpolates) the true elevation m(xt) at any location xt.
Our hidden Markov model for terrain navigation is
(6.35) ![]()
where ![]() t and δt are independent random error processes representing the error in drift and elevation measurement, respectively, and Yt is the observed elevation. We treat dt as a known term in the location process rather than a measurement and allow any measurement error to be subsumed into
t and δt are independent random error processes representing the error in drift and elevation measurement, respectively, and Yt is the observed elevation. We treat dt as a known term in the location process rather than a measurement and allow any measurement error to be subsumed into ![]() t.
t.
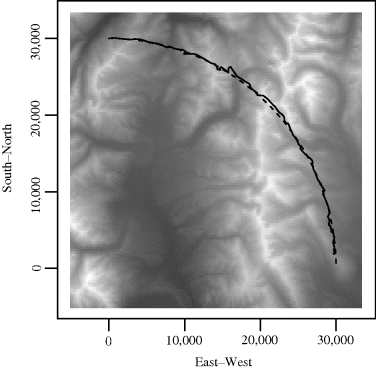
Figure 6.9 shows a topographic map of a region in Colorado. Light shading corresponds to higher ground elevation and the units are meters. Let us suppose that the plane is following a circular arc specified by 101 angles θt (for t = 0, . . ., 100) equally spaced between π/2 and 0, with the true location at time t being xt = (cos θt, sin θt) and the true drift dt being the difference between the locations at times t and t − 1. Let us assume that measurement error in the elevation process can be modeled as δt ~ N(0, σ2) where we assume σ = 75 here.
Figure 6.9 Results of Example 6.7 showing an image of ground elevations for a region of Colorado, where lighter shades correspond to higher elevations. The dashed line is the true, unknown, flight path and the solid line is the estimated path. The two are nearly the same.
Suppose that random error in location ![]() t has a distribution characterized by
t has a distribution characterized by ![]() where
where ![]() and
and ![]() where we take q = 400 and
where we take q = 400 and ![]() . This distribution gt(
. This distribution gt(![]() t) effectively constitutes the importance sampling envelope gt(xt|xt−1). This complicated specification is more simply described by saying that
t) effectively constitutes the importance sampling envelope gt(xt|xt−1). This complicated specification is more simply described by saying that ![]() t has a bivariate normal distribution with standard deviations q and kq, rotated so that the major axis of density contours is parallel to the tangent of the flight path at the current location. A standard bivariate normal distribution would be an alternative choice, but ours simulates the situation where uncertainty about the distance flown during the time increment is greater than uncertainty about deviations orthogonal to the direction of flight.
t has a bivariate normal distribution with standard deviations q and kq, rotated so that the major axis of density contours is parallel to the tangent of the flight path at the current location. A standard bivariate normal distribution would be an alternative choice, but ours simulates the situation where uncertainty about the distance flown during the time increment is greater than uncertainty about deviations orthogonal to the direction of flight.
In this example, we maintain n = 100 sampled trajectories ![]() , although this number would be much greater in a real application. To initiate the model we sample from a bivariate normal distribution centered at x0 with standard deviations of 50. In real life, one could imagine that the initialization point corresponds to the departure airport or to some position update provided by occasional detection stations along the flight path, which provide highly accurate location data allowing the current location to be “reinitialized.”
, although this number would be much greater in a real application. To initiate the model we sample from a bivariate normal distribution centered at x0 with standard deviations of 50. In real life, one could imagine that the initialization point corresponds to the departure airport or to some position update provided by occasional detection stations along the flight path, which provide highly accurate location data allowing the current location to be “reinitialized.”
The sequential importance sampling algorithm for this problem proceeds as follows:
Note that this algorithm incorporates the resampling option to reduce weight degeneracy.
In this algorithm, each sequence ![]() represents one possible path for the airplane, and these complete paths have corresponding importance weights
represents one possible path for the airplane, and these complete paths have corresponding importance weights ![]() . Figure 6.9 shows the result. The dashed line is the true flight path and the solid line is the estimated path calculated as in step 5 above, using the elevation data yt.
. Figure 6.9 shows the result. The dashed line is the true flight path and the solid line is the estimated path calculated as in step 5 above, using the elevation data yt.
The results show very good tracking of the true locations. Of course, the result is dependent on n and the magnitudes of noise in the state and observation processes. Performance here also benefits from the fact that Colorado terrain is very distinctive with large variation in elevations. In flat areas the procedure is less effective. Although the Colorado Rocky Mountains are rarely flat, there are long ridges and valleys that have relatively constant elevation, thereby tempting the algorithm to pursue false directions. The algorithm will also struggle when the terrain exhibits localized topological features (e.g., hilltops) that resemble each other and are repeated across a region of the map. In that case, some ![]() may jump to the wrong hilltop.
may jump to the wrong hilltop.
Although estimation performance is good in our example, maintenance of a large effective sample size was poor. A majority of the iterations included a rejuvenation step. The data for this example are available from the book website. ![]()
The sequential importance sampling technique evolved from a variety of methods for sequential imputation and Monte Carlo analysis of dynamic systems [34, 386, 416, 418, 430]. Considerable research has focused on methods to improve or adapt gt and to slow weight degeneracy [90, 95, 168, 239, 260, 386, 417, 419, 679].
6.3.2.5 Particle Filters
As we have discussed above, sequential importance sampling is often of little help unless resampling steps are inserted in the algorithm at least occasionally to slow weight degeneracy that is signaled by diminishing effective sample sizes. Particle filters are sequential Monte Carlo strategies that emphasize the need for preventing degeneracy [90, 167, 239, 274, 379]. They have been developed primarily within the framework of hidden Markov models as described in Section 6.3.2.4. At time t, the current sample of sequences is viewed as a collection of weighted particles. Particles with high weights enjoy increasing influence in Monte Carlo estimates, while underweighted particles are filtered away as t increases.
Particle filters can be seen as generalizations of sequential importance sampling, or as specific strategies for sequential importance sampling with resampling. The distinct names of these approaches hide their methodological similarity. As noted previously, sequential importance sampling can be supplemented by a resampling step where the x1:t are resampled with replacement with probability proportional to their current weights and then the weights are reset to 1/n. In the simplest case, this would be triggered when the effective sample size diminished too much. Adopting a particle filter mindset, one would instead resample at each t. An algorithm described as a particle filter is often characterized by a stronger focus on resampling or adjustment of the new draws between or within cycles to prevent degeneracy.
Resampling alone does not prevent degeneracy. Although low-weight sequences are likely to be discarded, high-weight sequences are merely replicated rather than diversified. Particle filters favor tactics like perturbing or smoothing samples at each t. For example, with a particle filter one might supplement the resampling step by moving samples according to a Markov chain transition kernel with appropriate stationary distribution [239]. Alternatively, one could smooth the resampling step via a weighted smoothed bootstrap [175], for example, by replacing the simple multinomial resampling with sampling from an importance-weighted mixture of smooth densities centered at some or all the current particles [252, 273, 611, 658]. Another strategy would be to employ an adaptive form of bridge sampling (see Section 6.3.1.1) to facilitate the sequential sampling steps [260]. The references in Section 6.3.2.4 regarding improvements to sequential importance sampling are also applicable here.
The simplest particle filter is the bootstrap filter [274]. This approach relies on a simple multinomial importance-weighted resample at each stage, rather than waiting for the weights to degenerate excessively. In other words, sequences are resampled with replacement with probability proportional to their current weights, then the weights are reset to 1/n. The sequential importance sampling strategy we have previously described would wait until resampling was triggered by a low effective sample size before conducting such a resample.
Example 6.8 (Terrain Navigation, Continued) The bootstrap filter is easy to implement in the terrain navigation example. Specifically, we always resample the current collection of paths at each t.
Thus, we replace step 6 in Example 6.7 with
where those substeps are (a), (b), and (c) listed under step 6 in that example. The estimated flight path is qualitatively indistinguishable from the estimate in Figure 6.9. ![]()
6.4 Variance Reduction Techniques
The simple Monte Carlo estimator of ∫h(x)f(x)dx is
![]()
where the variables X1, . . ., Xn are randomly sampled from f. This approach is intuitively appealing, and we have thus far focused on methods to generate draws from f. In some situations, however, better Monte Carlo estimators can be derived. These approaches are still based on the principle of averaging Monte Carlo draws, but they employ clever sampling strategies and different forms of estimators to yield integral estimates with lower variance than the simplest Monte Carlo approach.
6.4.1 Importance Sampling
Suppose we wish to estimate the probability that a die roll will yield a one. If we roll the die n times, we would expect to see about n/6 ones, and our point estimate of the true probability would be the proportion of ones in the sample. The variance of this estimator is 5/36n if the die is fair. To achieve an estimate with a coefficient of variation of, say, 5%, one should expect to have to roll the die 2000 times.
To reduce the number of rolls required, consider biasing the die by replacing the faces bearing 2 and 3 with additional 1 faces. This increases the probability of rolling a one to 0.5, but we are no longer sampling from the target distribution provided by a fair die. To correct for this, we should weight each roll of a one by 1/3. In other words, let Yi = 1/3 if the roll is a one and Yi = 0 otherwise. Then the expectation of the sample mean of the Yi is 1/6, and the variance of the sample mean is 1/36n. To achieve a coefficient of variation of 5% for this estimator, one expects to need only 400 rolls.
This improved accuracy is achieved by causing the event of interest to occur more frequently than it would in the naive Monte Carlo sampling framework, thereby enabling more precise estimation of it. Using importance sampling terminology, the die-rolling example is successful because an importance sampling distribution (corresponding to rolling the die with three ones) is used to oversample a portion of the state space that receives lower probability under the target distribution (for the outcome of a fair die). An importance weighting corrects for this bias and can provide an improved estimator. For very rare events, extremely large reductions in Monte Carlo variance are possible.
The importance sampling approach is based upon the principle that the expectation of h(X) with respect to its density f can be written in the alternative form
or even
where g is another density function, called the importance sampling function or envelope.
Equation (6.36) suggests that a Monte Carlo approach to estimating E{h(X)} is to draw X1, . . ., Xn i.i.d. from g and use the estimator
where ![]() are unstandardized weights, also called importance ratios. For this strategy to be convenient, it must be easy to sample from g and to evaluate f, even when it is not easy to sample from f.
are unstandardized weights, also called importance ratios. For this strategy to be convenient, it must be easy to sample from g and to evaluate f, even when it is not easy to sample from f.
Equation (6.37) suggests drawing X1, . . ., Xn i.i.d. from g and using the estimator
where ![]() are standardized weights. This second approach is particularly important in that it can be used when f is known only up to a proportionality constant, as is frequently the case when f is a posterior density in a Bayesian analyses.
are standardized weights. This second approach is particularly important in that it can be used when f is known only up to a proportionality constant, as is frequently the case when f is a posterior density in a Bayesian analyses.
Both estimators converge by the same argument applied to the simple Monte Carlo estimator given in (6.1), as long as the support of the envelope includes all of the support of f. In order for the estimators to avoid excess variability, it is important that f(x)/g(x) be bounded and that g have heavier tails than f. If this requirement is not met, then some standardized importance weights will be huge. A rare draw from g with much higher density under f than under g will receive huge weight and inflate the variance of the estimator.
Naturally, g(X) often will be larger than f(X) when X ~ g, yet it is easy to show that E{f(X)/g(X)} = 1. Therefore, if f(X)/g(X) is to have mean 1, this ratio must sometimes be quite large to counterbalance the predominance of values between 0 and 1. Thus, the variance of f(X)/g(X) will tend to be large. Hence, we should expect the variance of h(X)f(X)/g(X) to be large, too. For an importance sampling estimate of μ to have low variance, therefore, we should choose the function g so that f(x)/g(x) is large only when h(x) is very small. For example, when h is an indicator function that equals 1 only for a very rare event, we can choose g to sample in a way that makes that event occur much more frequently, at the expense of failing to sample adequately uninteresting outcomes for which h(x) = 0. This strategy works very well in cases where estimation of a small probability is of interest, such as in estimation of statistical power, probabilities of failure or exceedance, and likelihoods over combinatorial spaces like those that arise frequently with genetic data.
Also recall that the effective sample size given in (6.29) can be used to measure the efficiency of an importance sampling strategy using envelope g. It can be interpreted as indicating that the n weighted samples used in an importance sampling estimate are worth ![]() unweighted i.i.d. samples drawn exactly from f and used in a simple Monte Carlo estimate [386, 417]. In this sense, it is an excellent way to assess the quality of the envelope g. Section 6.3.2.2 provides further detail.
unweighted i.i.d. samples drawn exactly from f and used in a simple Monte Carlo estimate [386, 417]. In this sense, it is an excellent way to assess the quality of the envelope g. Section 6.3.2.2 provides further detail.
The choice between using the unstandardized and the standardized weights depends on several considerations. First consider the estimator ![]() defined in (6.38) using the unstandardized weights. Let
defined in (6.38) using the unstandardized weights. Let ![]() . When X1, . . ., Xn are drawn i.i.d. from g, let
. When X1, . . ., Xn are drawn i.i.d. from g, let ![]() and
and ![]() denote averages of the
denote averages of the ![]() and t(Xi), respectively. Note
and t(Xi), respectively. Note ![]() . Now,
. Now,
(6.40) ![]()
and
(6.41) ![]()
Thus ![]() is unbiased, and an estimator of its Monte Carlo standard error is the sample standard deviation of t(X1), . . ., t(Xn) divided by n.
is unbiased, and an estimator of its Monte Carlo standard error is the sample standard deviation of t(X1), . . ., t(Xn) divided by n.
Now consider the estimator ![]() defined in (6.39) that employs importance weight standardization. Note that
defined in (6.39) that employs importance weight standardization. Note that ![]() . Taylor series approximations yield
. Taylor series approximations yield
Thus, standardizing the importance weights introduces a slight bias in the estimator ![]() . The bias can be estimated by replacing the variance and covariance terms in (6.42) with sample estimates obtained from the Monte Carlo draws; see also Example 6.12.
. The bias can be estimated by replacing the variance and covariance terms in (6.42) with sample estimates obtained from the Monte Carlo draws; see also Example 6.12.
The variance of ![]() is similarly found to be
is similarly found to be
Again, a variance estimate for ![]() can be computed by replacing the variances and covariances in (6.43) with sample estimates obtained from the Monte Carlo draws.
can be computed by replacing the variances and covariances in (6.43) with sample estimates obtained from the Monte Carlo draws.
Finally, consider the mean squared errors (MSE) of ![]() and
and ![]() . Combining the bias and variance estimates derived above, we find
. Combining the bias and variance estimates derived above, we find
Assuming without loss of generality that μ > 0, the leading terms in (6.44) suggest that the approximate difference in mean squared errors is negative when
(6.45) ![]()
where cv { · } denotes a coefficient of variation. This condition can be checked using sample-based estimators as discussed above. Thus, using the standardized weights should provide a better estimator when ![]() and
and ![]() are strongly correlated. In addition to these considerations, a major advantage to using the standardized weights is that it does not require knowing the proportionality constant for f. Hesterberg warns that using the standardized weights can be inferior to using the raw weights in many settings, especially when estimating small probabilities, and recommends consideration of an improved importance sampling strategy we describe below in Example 6.12 [326]. Casella and Robert also discuss a variety of uses of the importance weights [100].
are strongly correlated. In addition to these considerations, a major advantage to using the standardized weights is that it does not require knowing the proportionality constant for f. Hesterberg warns that using the standardized weights can be inferior to using the raw weights in many settings, especially when estimating small probabilities, and recommends consideration of an improved importance sampling strategy we describe below in Example 6.12 [326]. Casella and Robert also discuss a variety of uses of the importance weights [100].
Using the standardized weights is reminiscent of the SIR algorithm (Section 6.3.1), and it is sensible to compare the estimation properties of ![]() with those of the sample mean of the SIR draws. Suppose that an initial sample Y1, . . ., Ym with corresponding weights
with those of the sample mean of the SIR draws. Suppose that an initial sample Y1, . . ., Ym with corresponding weights ![]() is resampled to provide n SIR draws X1, . . ., Xn, where n < m. Let
is resampled to provide n SIR draws X1, . . ., Xn, where n < m. Let
![]()
denote the SIR estimate of μ.
When interest is limited to estimation of μ, the importance sampling estimator ![]() ordinarily should be preferred over
ordinarily should be preferred over ![]() . To see this, note
. To see this, note
![]()
Therefore the SIR estimator has the same bias as ![]() . However, the variance of
. However, the variance of ![]() is
is
(6.46) 
Thus the SIR estimator provides convenience at the expense of precision.
An attractive feature of any importance sampling method is the possibility of reusing the simulations. The same sampled points and weights can be used to compute a variety of Monte Carlo integral estimates of different quantities. The weights can be changed to reflect an alternative importance sampling envelope, to assess or improve performance of the estimator itself. The weights can also be changed to reflect an alternative target distribution, thereby estimating the expectation of h(X) with respect to a different density.
For example, in a Bayesian analysis, one can efficiently update estimates based on a revised posterior distribution in order to carry out Bayesian sensitivity analysis or sequentially to update previous results via Bayes' theorem in light of new information. Such updates can be carried out by multiplying each existing weight ![]() by an adjustment factor. For example, if f is a posterior distribution for X using prior p1, then weights equal to
by an adjustment factor. For example, if f is a posterior distribution for X using prior p1, then weights equal to ![]() for i = 1, . . ., n can be used with the existing sample to provide inference from the posterior distribution using prior p2.
for i = 1, . . ., n can be used with the existing sample to provide inference from the posterior distribution using prior p2.
Example 6.9 (Network Failure Probability) Many systems can be represented by connected graphs like Figure 6.10. These graphs are composed of nodes (circles) and edges (line segments). A signal sent from A to B must follow a path along any available edges. Imperfect network reliability means that the signal may fail to be transmitted correctly between any pair of connected nodes—in other words, some edges may be broken. In order for the signal to successfully reach B, a connected path from A to B must exist. For example, Figure 6.11 shows a degraded network where only a few routes remain from A to B. If the lowest horizontal edge in this figure were broken, the network would fail.
Figure 6.10 Network connecting A and B described in Example 6.9.
Figure 6.11 Network connecting A and B described in Example 6.9, with some edges broken.
Network graphs can be used to model many systems. Naturally, such a network can model transmission of diverse types of signals such as analog voice transmission, electromagnetic digital signals, and optical transmission of digital data. The model may also be more conceptual, with each edge representing different machines or people whose participation may be needed to achieve some outcome. Usually, an important quantity of interest is the probability of network failure given specific probabilities for the failure of each edge.
Consider the simplest case, where each edge is assumed to fail independently with the same probability, p. In many applications p is quite small. Bit error rates for many types of signal transmission can range from 10−10 to 10−3 or even lower [608].
Let X denote a network, summarizing random outcomes for each edge: intact or failed. The network considered in our example has 20 potential edges, so X = (X1, . . ., X20). Let b(X) denote the number of broken edges in X. The network in Figure 6.10 has b(X) = 0; the network in Figure 6.11 has b(X) = 10. Let h(X) indicate network failure, so h(X) = 1 if A is not connected to B, and h(X) = 0 if A and B are connected. The probability of network failure, then, is μ = E{h(X)}. Computing μ for a network of any realistic size can be a very difficult combinatorial problem.
The naive Monte Carlo estimate of μ is obtained by drawing X1, . . ., Xn independently and uniformly at random from the set of all possible network configurations whose edges fail independently with probability p. The estimator is computed as
(6.47) ![]()
Notice that this estimator has variance μ(1 − μ)/n. For n = 100, 000 and p = 0.05, simulation yields ![]() with a Monte Carlo standard error of about 1.41 × 10−5.
with a Monte Carlo standard error of about 1.41 × 10−5.
The problem with ![]() is that h(X) is very rarely 1 unless p is unrealistically large. Thus, a huge number of networks may need to be simulated in order to estimate μ with sufficient precision. Instead, we can use importance sampling to focus on simulation of X for which h(X) = 1, compensating for this bias through the assignment of importance weights. The calculations that follow adopt this strategy, using the nonstandardized importance weights as in (6.38).
is that h(X) is very rarely 1 unless p is unrealistically large. Thus, a huge number of networks may need to be simulated in order to estimate μ with sufficient precision. Instead, we can use importance sampling to focus on simulation of X for which h(X) = 1, compensating for this bias through the assignment of importance weights. The calculations that follow adopt this strategy, using the nonstandardized importance weights as in (6.38).
Suppose we simulate ![]() by generating network configurations formed by breaking edges in Figure 6.10, assuming independent edge failure with probability p∗ > p. The importance weight for
by generating network configurations formed by breaking edges in Figure 6.10, assuming independent edge failure with probability p∗ > p. The importance weight for ![]() can be written as
can be written as
(6.48) ![]()
and the importance sampling estimator of μ is
(6.49) ![]()
Let ![]() denote the set of all possible network configurations, and let
denote the set of all possible network configurations, and let ![]() denote the subset of configurations for which A and B are not connected. Then
denote the subset of configurations for which A and B are not connected. Then
(6.50) ![]()
(6.51) ![]()
(6.52) 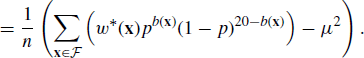
Now, for a network derived from Figure 6.10, failure only occurs when b(X) ≥ 4. Therefore,
(6.53) 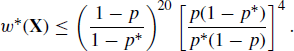
When p∗ = 0.25 and p = 0.05, we find ![]() . In this case,
. In this case,
(6.54) 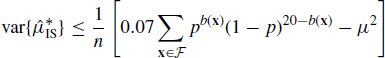
(6.55) 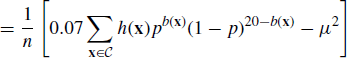
(6.56) ![]()
Thus ![]() is substantially smaller than
is substantially smaller than ![]() . Under the approximation that cμ − μ2 ≈ cμ for small μ and relatively larger c, we see that
. Under the approximation that cμ − μ2 ≈ cμ for small μ and relatively larger c, we see that ![]()
![]() .
.
With the naive simulation strategy using p = 0.05, only 2 of 100, 000 simulated networks failed. However, using the importance sampling strategy with p∗ = 0.2 yielded 491 failing networks, producing an estimate of ![]() with a Monte Carlo standard error of 1.57 × 10−6.
with a Monte Carlo standard error of 1.57 × 10−6.
Related Monte Carlo variance reduction techniques for network reliability problems are discussed in [432]. ![]()
6.4.2 Antithetic Sampling
A second approach to variance reduction for Monte Carlo integration relies on finding two identically distributed unbiased estimators, say ![]() and
and ![]() , that are negatively correlated. Averaging these estimators will be superior to using either estimator alone with double the sample size, since the estimator
, that are negatively correlated. Averaging these estimators will be superior to using either estimator alone with double the sample size, since the estimator
(6.57) ![]()
has variance equal to
where ρ is the correlation between the two estimators and σ2/n is the variance of either estimator using a sample of size n. Such pairs of estimators can be generated using the antithetic sampling approach [304, 555].
Given an initial estimator, ![]() , the question is how to construct a second, identically distributed estimator
, the question is how to construct a second, identically distributed estimator ![]() that is negatively correlated with
that is negatively correlated with ![]() . In many situations, there is a convenient way to create such estimators while reusing one simulation sample of size n rather than generating a second sample from scratch. To describe the strategy, we must first introduce some notation. Let X denote a set of i.i.d. random variables, {X1, . . ., Xn}. Suppose
. In many situations, there is a convenient way to create such estimators while reusing one simulation sample of size n rather than generating a second sample from scratch. To describe the strategy, we must first introduce some notation. Let X denote a set of i.i.d. random variables, {X1, . . ., Xn}. Suppose ![]() , where h1 is a real-valued function of m arguments, so h1(Xi) = h1(Xi1, . . ., Xim). Assume E{h1(Xi)} = μ. Let
, where h1 is a real-valued function of m arguments, so h1(Xi) = h1(Xi1, . . ., Xim). Assume E{h1(Xi)} = μ. Let ![]() be a second estimator, with the analogous assumptions about h2.
be a second estimator, with the analogous assumptions about h2.
We will now prove that if h1 and h2 are both increasing in each argument (or both decreasing), then cov{h1(Xi), h2(Xi)} is positive. From this result, we will be able to determine requirements for h1 and h2 that ensure that ![]() is negative.
is negative.
The proof proceeds via induction. Suppose the above hypotheses hold and m = 1. Then
for any random variables X and Y. Hence, the expectation of the left-hand side of (6.59) is also nonnegative. Therefore, when X and Y are independent and identically distributed, this nonnegative expectation implies
Now, suppose that the desired result holds when Xi is a random vector of length m − 1, and consider the case when Xi = (Xi1, . . ., Xim). Then, by hypothesis, the random variable
(6.61) ![]()
Taking the expectation of this inequality gives
where the substitution of terms in the product on the right side of (6.62) follows from the fact that each ![]() for j = 1, 2 is a function of the single random argument Xim, for which the result (6.60) applies.
for j = 1, 2 is a function of the single random argument Xim, for which the result (6.60) applies.
Thus, we have proven by induction that h1(Xi) and h2(Xi) will be positively correlated in these circumstances; it follows that ![]() and
and ![]() will also be positively correlated. We leave it to the reader to show the following key implication: If h1 and h2 are functions of m random variables U1, . . ., Um, and if each function is monotone in each argument, then cov{h1(U1, . . ., Um), h2(1 − U1, . . ., 1 − Um)} ≤ 0. This result follows simply from our previous proof after redefining h1 and h2 to create two functions increasing in their arguments that satisfy the previous hypotheses. See Problem 6.5.
will also be positively correlated. We leave it to the reader to show the following key implication: If h1 and h2 are functions of m random variables U1, . . ., Um, and if each function is monotone in each argument, then cov{h1(U1, . . ., Um), h2(1 − U1, . . ., 1 − Um)} ≤ 0. This result follows simply from our previous proof after redefining h1 and h2 to create two functions increasing in their arguments that satisfy the previous hypotheses. See Problem 6.5.
Now the antithetic sampling strategy becomes apparent. The Monte Carlo integral estimate ![]() can be written as
can be written as
(6.63) 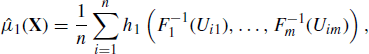
where Fj is the cumulative distribution function of each Xij (j = 1, . . ., m) and the Uij are independent Unif(0, 1) random variables. Since Fj is a cumulative distribution function, its inverse is nondecreasing. Therefore, ![]() is monotone in each Uij for j = 1, . . ., m whenever h1 is monotone in its arguments. Moreover, if Uij ~ Unif (0, 1), then 1 − Uij ~ Unif (0, 1). Hence,
is monotone in each Uij for j = 1, . . ., m whenever h1 is monotone in its arguments. Moreover, if Uij ~ Unif (0, 1), then 1 − Uij ~ Unif (0, 1). Hence, ![]() is monotone in each argument and has the same distribution as
is monotone in each argument and has the same distribution as ![]() . Therefore,
. Therefore,
(6.64) 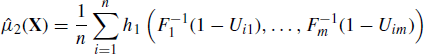
is a second estimator of μ having the same distribution as ![]() . Our analysis above allows us to conclude that
. Our analysis above allows us to conclude that
(6.65) ![]()
Therefore, the estimator ![]() will have smaller variance than
will have smaller variance than ![]() would have with a sample of size 2n. Equation (6.58) quantifies the amount of improvement. We accomplish this improvement while generating only a single set of n random numbers, with the other n derived from the antithetic principle.
would have with a sample of size 2n. Equation (6.58) quantifies the amount of improvement. We accomplish this improvement while generating only a single set of n random numbers, with the other n derived from the antithetic principle.
Example 6.10 (Normal Expectation) Suppose X has a standard normal distribution and we wish to estimate μ = E{h(X)} where h(x) = x/(2x − 1). A standard Monte Carlo estimator can be computed as the sample mean of n = 100, 000 values of h(Xi) where X1, . . ., Xn ~ i.i.d. N(0, 1). An antithetic estimator can be constructed using the first n = 50, 000 draws. The antithetic variate for Xi is simply −Xi, so the antithetic estimator is ![]() . In the simulation,
. In the simulation, ![]() , so the antithetic approach is profitable. The standard approach yielded
, so the antithetic approach is profitable. The standard approach yielded ![]() with a Monte Carlo standard error of 0.0016, whereas the antithetic approach gave
with a Monte Carlo standard error of 0.0016, whereas the antithetic approach gave ![]() with a standard error of 0.0003 [estimated via (6.58) using the sample variance and correlation]. Further simulation confirms a more than fourfold reduction in standard error for the antithetic approach.
with a standard error of 0.0003 [estimated via (6.58) using the sample variance and correlation]. Further simulation confirms a more than fourfold reduction in standard error for the antithetic approach. ![]()
Example 6.11 (Network Failure Probability, Continued) Recalling Example 6.9, let the ith simulated network, Xi, be determined by standard uniform random variables Ui1, . . ., Uim, where m = 20. The jth edge in the ith simulated network is broken if Uij < p. Now h(Xi) = h(Ui1, . . ., Uim) equals 1 if A and B are not connected, and 0 if they are connected. Note that h is nondecreasing in each Uij; therefore the antithetic approach will be profitable. Since Xi is obtained by breaking the jth edge when Uij < p for j = 1, . . ., m, the antithetic network draw, say ![]() , is obtained by breaking the jth edge when Uij > 1 − p, for the same set of Uij used to generate Xi. The negative correlation induced by this strategy will ensure that
, is obtained by breaking the jth edge when Uij > 1 − p, for the same set of Uij used to generate Xi. The negative correlation induced by this strategy will ensure that ![]() is a superior estimator to
is a superior estimator to ![]() .
. ![]()
6.4.3 Control Variates
The control variate strategy improves estimation of an unknown integral by relating the estimate to some correlated estimator of an integral whose value is known. Suppose we wish to estimate the unknown quantity μ = E{h(X)} and we know of a related quantity, θ = E{c(Y)}, whose value can be determined analytically. Let (X1, Y1), . . ., (Xn, Yn) denote pairs of random variables observed independently as simulation outcomes, so cov {Xi, Xj} = cov {Yi, Yj} = cov {Xi, Yj} = 0 when i ≠ j. The simple Monte Carlo estimators are ![]() and
and ![]() . Of course,
. Of course, ![]() is unnecessary, since θ can be found analytically. However, note that
is unnecessary, since θ can be found analytically. However, note that ![]() will be correlated with
will be correlated with ![]() when cor {h(Xi), c(Yi)} ≠ 0. For example, if the correlation is positive, an unusually high outcome for
when cor {h(Xi), c(Yi)} ≠ 0. For example, if the correlation is positive, an unusually high outcome for ![]() should tend to be associated with an unusually high outcome for
should tend to be associated with an unusually high outcome for ![]() . If comparison of
. If comparison of ![]() with θ suggests such an outcome, then we should adjust
with θ suggests such an outcome, then we should adjust ![]() downward accordingly. The opposite adjustment should be made when the correlation is negative.
downward accordingly. The opposite adjustment should be made when the correlation is negative.
This reasoning suggests the control variate estimator
(6.66) ![]()
where λ is a parameter to be chosen by the user. It is straightforward to show that
(6.67) ![]()
Minimizing this quantity with respect to λ shows that the minimal variance,
is obtained when
This optimal λ depends on unknown moments of h(Xi) and c(Yi), but these can be estimated using the sample (X1, Y1), . . ., (Xn, Yn). Specifically, using
(6.70) 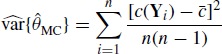
and
(6.71) 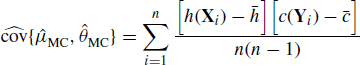
in (6.69) provides an estimator ![]() , where
, where ![]() and
and ![]() . Further, plugging such sample variance and covariance estimates into the right-hand side of (6.68) provides a variance estimate for
. Further, plugging such sample variance and covariance estimates into the right-hand side of (6.68) provides a variance estimate for ![]() .
.
In practice, ![]() and
and ![]() often depend on the same random variables, so Xi = Yi. Also, it is possible to use more than one control variate. In this case, we may write the estimator as
often depend on the same random variables, so Xi = Yi. Also, it is possible to use more than one control variate. In this case, we may write the estimator as ![]() when using m control variates.
when using m control variates.
Equation (6.68) shows that the proportional reduction in variance obtained by using ![]() instead of
instead of ![]() is equal to the square of the correlation between
is equal to the square of the correlation between ![]() and
and ![]() . If this result sounds familiar, you have astutely noted a parallel with simple linear regression. Consider the regression model E{h(Xi)|Yi = yi} = β0 + β1c(yi) with the usual regression assumptions and estimators. Then
. If this result sounds familiar, you have astutely noted a parallel with simple linear regression. Consider the regression model E{h(Xi)|Yi = yi} = β0 + β1c(yi) with the usual regression assumptions and estimators. Then ![]() and
and ![]()
![]() . In other words, the control variate estimator is the fitted value on the regression line at the mean value of the predictor (i.e., at θ), and the standard error of this control variate estimator is the standard error for the fitted value from the regression. Thus, linear regression software may be used to obtain the control variate estimator and a corresponding confidence interval. When more than one control variate is used, multiple linear regression can be used to obtain
. In other words, the control variate estimator is the fitted value on the regression line at the mean value of the predictor (i.e., at θ), and the standard error of this control variate estimator is the standard error for the fitted value from the regression. Thus, linear regression software may be used to obtain the control variate estimator and a corresponding confidence interval. When more than one control variate is used, multiple linear regression can be used to obtain ![]() (i = 1, . . ., m) and
(i = 1, . . ., m) and ![]() [555].
[555].
Problem 6.5 asks you to show that the antithetic approach to variance reduction can be viewed as a special case of the control variate method.
Example 6.12 (Control Variate for Importance Sampling) Hesterberg suggests using a control variate estimator to improve importance sampling [326]. Recall that importance sampling is built upon the idea of sampling from an envelope that induces a correlation between ![]() and
and ![]() . Further, we know
. Further, we know ![]() . Thus, the situation is well suited for using the control variate
. Thus, the situation is well suited for using the control variate ![]() . If the average weight exceeds 1, then the average value of
. If the average weight exceeds 1, then the average value of ![]() is also probably unusually high, in which case
is also probably unusually high, in which case ![]() probably differs from its expectation, μ. Thus, the importance sampling control variate estimator is
probably differs from its expectation, μ. Thus, the importance sampling control variate estimator is
(6.72) ![]()
The value for λ and the standard error of ![]() can be estimated from a regression of
can be estimated from a regression of ![]() on
on ![]() as previously described. Like
as previously described. Like ![]() , which uses the standardized weights, the estimator
, which uses the standardized weights, the estimator ![]() has bias of order
has bias of order ![]() , but will often have lower mean squared error than the importance sampling estimator with unstandardized weights
, but will often have lower mean squared error than the importance sampling estimator with unstandardized weights ![]() given in (6.38).
given in (6.38). ![]()
Example 6.13 (Option Pricing) A call option is a financial instrument that gives its holder the right—but not the obligation—to buy a specified amount of a financial asset, on or by a specified maturity date, for a specified price. For a European call option, the option can be exercised only at the maturity date. The strike price is the price at which the transaction is completed if the option is exercised. Let S(t) denote the price of the underlying financial asset (say, a stock) at time t. Denote the strike price by K, and let T denote the maturity date. When time T arrives, the holder of the call option will not wish to exercise his option if K > S(T) because he can obtain the stock more cheaply on the open market. However, the option will be valuable if K < S(T) because he can buy the stock at the low price K and immediately sell it at the higher market price S(T). It is of interest to determine how much the buyer of this call option should pay at time t = 0 for this option with strike price K at maturity date T.
The Nobel Prize–winning model introduced by Black, Scholes, and Merton in 1973 provides a popular approach to determining the fair price of an option using a stochastic differential equation [52, 459]. Further background on option pricing and the stochastic calculus of finance includes [184, 406, 586, 665].
The fair price of an option is the amount to be paid at time t = 0 that would exactly counterbalance the expected payoff at maturity. We'll consider the simplest case: a European call option on a stock that pays no dividends. The fair price of such an option can be determined analytically under the Black–Scholes model, but estimation of the fair price via Monte Carlo is an instructive starting point. According to the Black–Scholes model, the value of the stock at day T can be simulated as
where r is the risk-free rate of return (typically the return rate of the U.S. Treasury bill that matures on day (T − 1), σ is the stock's volatility [an annualized estimate of the standard deviation of log {S(t+1)/S(t)} under a lognormal price model], and Z is a standard normal deviate. If we knew that the price of the stock at day T would equal S(T), then the fair price of the call option would be
discounting the payoff to present value. Since S(T) is unknown to the buyer of the call, the fair price to pay at t = 0 is the expected value of the discounted payoff, namely E{C}. Thus, a Monte Carlo estimate of the fair price to pay at t = 0 is
(6.75) 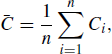
where the Ci are simulated from (6.73) and (6.74) for i = 1, . . ., n using an i.i.d. sample of standard normal deviates, Z1, . . ., Zn.
Since the true fair price, E{C}, can be computed analytically in this instance, there is no need to apply the Monte Carlo approach. However, a special type of European call option, called an Asian, path-dependent, or average-price option, has a payoff based on the average price of the underlying stock throughout the holding period. Such options are attractive for consumers of energies and commodities because they tend to be exposed to average prices over time. Since the averaging process reduces volatility, Asian options also tend to be cheaper than standard options. Control variate and many other variance reduction approaches for the Monte Carlo pricing of options like these are examined in [59].
To simulate the fair price of an Asian call option, simulation of stock value at maturity is carried out by applying (6.73) sequentially T times, each time advancing the stock price one day and recording the simulated closing price for that day, so
for a sequence of standard normal deviates, {Z(t)}, where t = 0, . . ., T − 1. The discounted payoff at day T of the Asian call option on a stock with current price S(0) is defined as
where ![]() and the S(t) for t = 1, . . ., T are the random variables representing future stock prices at the averaging times. The fair price to pay at t = 0 is E{A}, but in this case there is no known analytic solution for it. Denote the standard Monte Carlo estimator for the fair price of an Asian call option as
and the S(t) for t = 1, . . ., T are the random variables representing future stock prices at the averaging times. The fair price to pay at t = 0 is E{A}, but in this case there is no known analytic solution for it. Denote the standard Monte Carlo estimator for the fair price of an Asian call option as
(6.78) 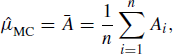
where the Ai are simulated independently as described above.
If ![]() is replaced in (6.77) by the geometric average of the price of the underlying stock throughout the holding period, an analytic solution for E{A} can be found [370]. The fair price is then
is replaced in (6.77) by the geometric average of the price of the underlying stock throughout the holding period, an analytic solution for E{A} can be found [370]. The fair price is then
(6.79) 
where
where Φ is the standard normal cumulative distribution function, and N is the number of prices in the average. Alternatively, one could estimate the fair price of an Asian call option with geometric averaging using the same sort of Monte Carlo strategy described above. Denote this Monte Carlo estimator as ![]() .
.
The estimator ![]() makes an excellent control variate for estimation of μ. Let
makes an excellent control variate for estimation of μ. Let ![]() . Since we expect the fair price of the two Asian options (arithmetic and geometric mean pricing) to be very highly correlated, a reasonable initial guess is to use λ = − 1.
. Since we expect the fair price of the two Asian options (arithmetic and geometric mean pricing) to be very highly correlated, a reasonable initial guess is to use λ = − 1.
Consider a European call option with payoff based on the arithmetic mean price during the holding period. Suppose that the underlying stock has current price S(0) = 100, strike price K = 102, and volatility σ = 0.3. Suppose there are N = 50 days to maturity, so simulation of the maturity price requires 50 iterations of (6.76). Assume the risk-free rate of return is r = 0.05. Then the analogous geometric mean price option has a fair price of 1.83. Simulations show that the true fair value of the arithmetic mean price option is roughly μ = 1.876. Using n = 100, 000 simulations, we can estimate μ using either ![]() or
or ![]() , and both estimators tend to give answers in the vicinity of μ. But what is of interest is the standard error of estimates of μ. We replicated the entire Monte Carlo estimation process 100 times, obtaining 100 values for
, and both estimators tend to give answers in the vicinity of μ. But what is of interest is the standard error of estimates of μ. We replicated the entire Monte Carlo estimation process 100 times, obtaining 100 values for ![]() and for
and for ![]() . The sample standard deviation of the values obtained for
. The sample standard deviation of the values obtained for ![]() was 0.0107, whereas that of the
was 0.0107, whereas that of the ![]() values was 0.000295. Thus, the control variate approach provided an estimator with 36 times smaller standard error.
values was 0.000295. Thus, the control variate approach provided an estimator with 36 times smaller standard error.
Finally, consider estimating λ from the simulations using (6.69). Repeating the same experiment as above, the typical correlation between ![]() and
and ![]() was 0.9999. The mean of
was 0.9999. The mean of ![]() was −1.0217 with sample standard deviation 0.0001. Using the
was −1.0217 with sample standard deviation 0.0001. Using the ![]() found in each simulation to produce each
found in each simulation to produce each ![]() yielded a set of 100
yielded a set of 100 ![]() values whose standard deviation was 0.000168. This represents a 63-fold improvement in the standard error over
values whose standard deviation was 0.000168. This represents a 63-fold improvement in the standard error over ![]() .
. ![]()
6.4.4 Rao–Blackwellization
We have been considering the estimation of μ = E{h(X)} using a random sample X1, . . ., Xn drawn from f. Suppose that each Xi = (Xi1, Xi2) and that the conditional expectation E{h(Xi)|xi2} can be solved for analytically. To motivate an alternate estimator to ![]() , we may use the fact that
, we may use the fact that ![]() , where the outer expectation is taken with respect to the distribution of Xi2. The Rao–Blackwellized estimator can be defined as
, where the outer expectation is taken with respect to the distribution of Xi2. The Rao–Blackwellized estimator can be defined as
(6.80) 
and has the same mean as the ordinary Monte Carlo estimator ![]() . Notice that
. Notice that
(6.81) ![]()
follows from the conditional variance formula. Thus, ![]() is superior to
is superior to ![]() in terms of mean squared error. This conditioning process is often called Rao–Blackwellization due to its use of the Rao–Blackwell theorem, which states that one can reduce the variance of an unbiased estimator by conditioning it on the sufficient statistics [96]. Further study of Rao–Blackwellization for Monte Carlo methods is given in [99, 216, 507, 542, 543].
in terms of mean squared error. This conditioning process is often called Rao–Blackwellization due to its use of the Rao–Blackwell theorem, which states that one can reduce the variance of an unbiased estimator by conditioning it on the sufficient statistics [96]. Further study of Rao–Blackwellization for Monte Carlo methods is given in [99, 216, 507, 542, 543].
Example 6.14 (Rao–Blackwellization of Rejection Sampling) A generic approach that Rao–Blackwellizes rejection sampling is described by Casella and Robert [99]. In ordinary rejection sampling, candidates Y1, . . ., YM are generated sequentially, and some are rejected. The uniform random variables U1, . . ., UM provide the rejection decisions, with Yi being rejected if ![]() , where
, where ![]() . Rejection sampling stops at a random time M with the acceptance of the nth draw, yielding X1, . . ., Xn. The ordinary Monte Carlo estimator of μ = E{h(X)} can then be reexpressed as
. Rejection sampling stops at a random time M with the acceptance of the nth draw, yielding X1, . . ., Xn. The ordinary Monte Carlo estimator of μ = E{h(X)} can then be reexpressed as
which presents the intriguing possibility that ![]() somehow can be improved by using all the candidate Yi draws (suitably weighted), rather than merely the accepted draws.
somehow can be improved by using all the candidate Yi draws (suitably weighted), rather than merely the accepted draws.
Rao–Blackwellization of (6.82) yields the estimator
(6.83) 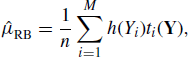
where the ti(Y) are random quantities that depend on Y = (Y1, . . ., YM) and M according to
Now tM(Y) = 1 since the final candidate was accepted. For previous candidates, the probability in (6.84) can be found by averaging over permutations of subsets of the realized sample [99]. We obtain
(6.85) 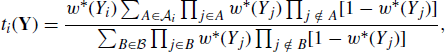
where ![]() is the set of all subsets of {1, . . ., i − 1, i + 1, . . ., M − 1} containing n − 2 elements, and
is the set of all subsets of {1, . . ., i − 1, i + 1, . . ., M − 1} containing n − 2 elements, and ![]() is the set of all subsets of {1, . . ., M − 1} containing n − 1 elements. Casella and Robert [99] offer a recursion formula for computing the ti(Y), but it is difficult to implement unless n is fairly small.
is the set of all subsets of {1, . . ., M − 1} containing n − 1 elements. Casella and Robert [99] offer a recursion formula for computing the ti(Y), but it is difficult to implement unless n is fairly small.
Notice that the conditioning variables used here are statistically sufficient since the conditional distribution of U1, . . ., UM does not depend on f. Both ![]() and
and ![]() are unbiased; thus, the Rao–Blackwell theorem implies that
are unbiased; thus, the Rao–Blackwell theorem implies that ![]() will have smaller variance than
will have smaller variance than ![]() .
. ![]()
Problems
6.1. Consider the integral sought in Example 5.1, Equation (5.7), for the parameter values given there. Find a simple rejection sampling envelope that will produce extremely few rejections when used to generate draws from the density proportional to that integrand.
6.2. Consider the piecewise exponential envelopes for adaptive rejection sampling of the standard normal density, which is log-concave. For the tangent-based envelope, suppose you are limited to an even number of nodes at ±c1, . . ., ± cn. For the envelope that does not require tangent information, suppose you are limited to an odd number of nodes at 0, ± d1, . . ., ± dn. The problems below will require optimization using strategies like those in Chapter 2.
6.3. Consider finding σ2 = E{X2} when X has the density that is proportional to q(x) = exp { − |x|3/3}.
(6.86) 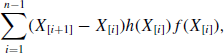
(6.87) 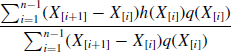
6.4. Figure 6.12 shows some data on the number of coal-mining disasters per year between 1851 and 1962, available from the website for this book. These data originally appeared in [434] and were corrected in [349]. The form of the data we consider is given in [91]. Other analyses of these data include [445, 525].
Figure 6.12 Number of coal-mining disasters per year between 1851 and 1962.
The rate of accidents per year appears to decrease around 1900, so we consider a change-point model for these data. Let j = 1 in 1851, and index each year thereafter, so j = 112 in 1962. Let Xj be the number of accidents in year j, with X1, . . ., Xθ ~ i.i.d. Poisson(λ1) and Xθ+1, . . ., X112 ~ i.i.d. Poisson(λ2). Thus the change-point occurs after the θth year in the series, where θ ![]() {1, . . ., 111}. This model has parameters θ, λ1, and λ2. Below are three sets of priors for a Bayesian analysis of this model. In each case, consider sampling from the priors as the first step of applying the SIR algorithm for simulating from the posterior for the model parameters. Of primary interest is inference about θ.
{1, . . ., 111}. This model has parameters θ, λ1, and λ2. Below are three sets of priors for a Bayesian analysis of this model. In each case, consider sampling from the priors as the first step of applying the SIR algorithm for simulating from the posterior for the model parameters. Of primary interest is inference about θ.
6.5. Prove the following results.
![]()
6.6. Consider testing the hypotheses H0 : λ = 2 versus Ha : λ > 2 using 25 observations from a Poisson(λ) model. Rote application of the central limit theorem would suggest rejecting H0 at α = 0.05 when Z ≥ 1.645, where ![]() .
.
6.7. Consider pricing a European call option on an underlying stock with current price S(0) = 50, strike price K = 52, and volatility σ = 0.5. Suppose that there are N = 30 days to maturity and that the risk-free rate of return is r = 0.05.
6.8. Consider the model given by X ~ Lognormal (0, 1) and log Y = 9 + 3 log X + ![]() , where
, where ![]() ~ N(0, 1). We wish to estimate E{Y/X}. Compare the performance of the standard Monte Carlo estimator and the Rao–Blackwellized estimator.
~ N(0, 1). We wish to estimate E{Y/X}. Compare the performance of the standard Monte Carlo estimator and the Rao–Blackwellized estimator.
6.9. Consider a bug starting at the origin of an infinite lattice L and walking one unit north, south, east, or west at each discrete time t. The bug cannot stay still at any step. Let x1:t denote the sequence of coordinates (i.e., the path) of the bug up to time t, say ![]() with x0 = (0, 0). Let the probability distribution for the bug's path through time t be denoted ft(x1:t) = f1(x1)f2(x2|x1), . . ., ft(xt|x1:t−1).
with x0 = (0, 0). Let the probability distribution for the bug's path through time t be denoted ft(x1:t) = f1(x1)f2(x2|x1), . . ., ft(xt|x1:t−1).
Define Dt(x1:t) to be the Manhattan distance of the bug from the origin at time t, namely ![]() . Let
. Let ![]() denote the number of times the bug has visited the lattice point
denote the number of times the bug has visited the lattice point ![]() up to and including time t. Thus Rt(xt) counts the number of visits to the current location.
up to and including time t. Thus Rt(xt) counts the number of visits to the current location.
The bug's path is random, but the probabilities associated with moving to the adjacent locations at time t are not equal. The bug prefers to stay close to home (i.e., near the origin), but has an aversion to revisiting its previous locations. These preferences are expressed by the path distribution ft(x1:t) ∝ exp { − (Dt(xt) + Rt(xt)/2)}.