4

Material Control/Inventory Control

4.1 INTRODUCTION

Material control is a way of regulating the purchase, storage and use of materials required for production because material constitutes an important factor of production. Material also forms an important part in determining the cost of a product. Material control is given importance to ensure uninterrupted production and to minimize the investment of funds in material. Thus, material control is aimed at having proper control over production, production cost, investment in material and increase in profitability.

4.2 OBJECTIVES OF MATERIAL CONTROL

The fundamental purpose of material control is to obtain the requisite quantity of material at the right price, at the right quantity, at the right quality and from the right source. The other objectives of material control are as follows:

1. Regular supply of material: Material control ensures regular supply of material to the factory so that production may not be held up for want of material.
2. Minimum possibility of overstocking and understocking: When the right quantity of stock is ordered, questions of overstocking or understocking do not arise.
3. Minimum wastage: Proper material management and control reduces wastage of material.
4. Getting material at reasonable prices: Material control enables a company to purchase material at reasonable prices.
5. Availability of up-to-date information: With material control, up-to-date information regarding material can be obtained for better planning and decision making.

4.2.1 Essentials of a good material control system

Since material forms a major part of the cost of a product, proper controlling and recording is essential:

1. The quality of the material purchased must depend on the product manufactured.
2. The price of the material should be minimum; otherwise the cost of the product would go up.
3. The production process should not be interrupted for want of material.
4. The material should be neither overstocked nor understocked.
5. The loss of and wastage of material should be avoided during production.
6. Wastage of stored goods should be avoided.

4.3 REQUIREMENTS OF MATERIAL CONTROL

The requirements of material control are as follows:

• Proper coordination of all departments involved
• Determining the purchase procedure to ensure that purchases are made after making suitable enquiries
• Use of standard forms for placing the order
• Preparation of budgets concerning materials, supplies and equipment
• Storage of all materials and supplies in a location having proper safeguards
• Ensuring continuous stock checking
• Operation of a system of stores control and issue
• Development of a system of controlling accounts and subsidiary records
• Regular reports of materials purchased, issues from stock inventory balances, obsolete stock and goods returned by defective units

4.4 DUTIES OF A STOREKEEPER

The duties of a storekeeper are as follows:

• To exercise general control over all activities in the stores department.
• To ensure safekeeping as to both the quality and quantity of materials.
• To maintain proper records.
• To initiate purchase requisition notes for the replacement of stock.
• To initiate action for stopping further purchase when the stock level approaches the maximum limit.
• To check and receive purchased materials forwarded by the receiving department and to arrange for their storage in appropriate places.
• To reserve a particular material for a specific job when so required.
• To issue materials only in required quantities against authorized requisition notes/material lists.
• To check book balances with the actual stock at frequent intervals by way of internal control over wrong issues, pilferage, etc.

4.5 LEVELS OF STOCK

Material control means maintaining a right level of stock by taking into account the production requirement and the financial resources of a business. The inflow and outflow of materials have to be regulated in such a manner that neither is production adversely affected for want of material nor is there unnecessary blocking of capital funds due to overstocking of raw materials. This implies there is always a limit to the minimum and maximum quantities of materials to be stored.

In order that the correct quantity of materials is purchased and stocked, the storekeeper applies some scientific techniques of material control. Fixing of certain levels for materials is one such technique.

4.5.1 Minimum stock level

The minimum level or minimum stock is that level of stock below which stock should not be allowed to fall. In case the stock of any item falls below this level, there is the danger of stopping production and, therefore, the management should give top priority to the acquisition of new supplies.

It is the level below which the stock of an item should not normally be allowed to fall. In the case of stock falling below this level, there is a danger of stopping production of the item. This level is also known as “safety stock” because such stock is normally not touched. This level is fixed after considering (a) rate of consumptions and (b) time required to acquire the stock:

 

 

The main factors considered in fixing the minimum level of inventory are as follows:

1. Information about maximum consumption and maximum delivery period for each item to determine its reorder level.
2. Average rate of consumption for each inventory item.
3. Average delivery period for each item; this period can be calculated by averaging the maximum and minimum periods.

4.5.2 Maximum stock level

The maximum stock limit is the upper level of inventory and the quantity that must not be exceeded without specific instruction from the management. In other words, the maximum stock level is that quantity of material above which the stock of any item should not normally be allowed to go.

It is the level above which the stock of any item should not generally be allowed to go. This level of stock is maintained for avoiding overstocking of materials and its associated risks. This level is fixed after considering (a) rate of consumption, (b) amount of capital needed and available, (c) storage space available, (d) insurance costs, (e) cost of storing above normal cost and (f) risk of wastage and deterioration:

 

 

The important considerations that govern the fixing of maximum level for various inventory items are as follows:

1. The fixing of maximum level of an inventory item requires information about its reorder level. The reorder level itself depends upon its maximum rate of consumption and maximum delivery period. It is in fact the product of maximum consumption of the inventory item and its maximum delivery period.
2. Knowledge about minimum consumption and minimum delivery period for each inventory item should also be known.
3. The determination of maximum level also requires the figure of economic order quantity.

4. The availability of funds and storage space, nature of items and price of items per unit are also important for fixing the maximum level.
5. In the case of imported materials, due to their irregular supply the maximum level should be high.

4.5.3 Reorder level

The reorder level of stock is the point at which stock of a particular item has diminished to a point where it needs to be replenished. It is the level at which a new order for a material is to be placed. It is the level at which a purchase requisition is made. It is the level between maximum and minimum. It is also known as the ordering level. This level is fixed after considering rate of consumption (r), minimum level (b), delivery time (c) and variation in delivery time (d).

 

4.5.4 Danger level

This is the level at which issue of material is stopped. This level indicates emergency of stock position. The storekeeper at this level obtains material at any cost. But issues are made only under specific instructions.

Danger level is a level of stock fixed usually below the minimum level. When the stock reaches danger level, an urgent action for purchase is initiated. When stock reaches the minimum level, the storekeeper must make special arrangements to get fresh material so that production is not interrupted due to the shortage of material.

4.5.5 Average stock level

It is the normal level of stock held by a firm:

4.6 ECONOMIC ORDER QUANTITY

Economic order quantity (EOQ) is the size of the order that gives maximum economy in purchasing any material and ultimately contributes towards maintaining the material at the optimum level and at the minimum cost. In other words, it is the ideal quantity of a material to be purchased at a time. The quantity is fixed in such a way that carrying cost and ordering cost are minimized. Carrying cost refers to the cost of holding the materials in the store. Ordering cost refers to the cost of placing orders for the purchase of materials.

EOQ is essentially an accounting formula that determines the point at which the combination of order costs and inventory carrying costs is the least. The result is the most cost-effective quantity to order. In purchasing this is known as the order quantity, whereas in manufacturing it is known as the production lot size.

EOQ is the number of units that a company should add to its inventory with each order to minimize the total costs of inventory, such as holding costs, order costs and shortage costs. EOQ is used as part of a continuous review inventory system, in which the level of inventory is monitored at all times and a fixed quantity is ordered each time the inventory level reaches a specific reorder point.

4.6.1 How does EOQ work?

Not all companies use EOQ. Companies that deal with a large volume of stock use EOQ. It is used in industries where the ordering of stock is repetitive. Another type of business also uses EOQ, that is, business that has multiple orders and has to plan for their components. Businesses that have a steady demand for stock adopt EOQ.

When implementing EOQ

1. Ensure that data regarding costs have been collected.
2. Use a software application when stock to be ordered is in large quantities.
3. Adjust the EOQ formula as and when required.

The underlying assumptions of EOQ are

1. The ordering cost is constant.
2. The rate of demand is constant.
3. The lead time is fixed.
4. The purchase price of the item is constant, that is, no discount is available.
5. The replenishment is made instantaneously, and the whole batch is delivered at once.

4.6.2 How to calculate EOQ?

EOQ is calculated as follows:

 

A = annual consumption

B = buying cost per order

or

C = cost per unit

S = storage and carrying cost

 

C = annual usage of material

O = cost of placing one order

I = annual carrying cost of one unit

 

Annual usage is expressed in units. Order cost is the sum of the fixed costs that are incurred each time an item is ordered. Carrying cost is the cost associated with having the inventory at hand.

4.7 ABC ANALYSIS

ABC analysis is a business term used to define an inventory categorization technique often used in materials management. It is also known as selective inventory control. It is a part of inventory management, in which items included in the inventory are classified into different categories such as items of higher value occupying lesser space, those of lower value occupying more space and others.

ABC analysis provides a mechanism for identifying items that have significant impact on overall inventory cost, while also providing a mechanism for identifying different categories of stock that require different management and controls. When carrying out an ABC analysis, inventory items are valued (item cost multiplied by quantity issued/consumed in a period) with the results and then ranked. The results are then grouped typically into three bands. These bands are called ABC codes.

ABC analysis is similar to the Pareto principle in that the ‘A class’ group typically accounts for a large proportion of the overall value but a small percentage of the overall volume of inventory.

ABC codes

1. 'A class’ inventory will typically contain items that account for 80% of total value, or 20% of total items.
2. 'B class’ inventory will have around 15% of total value or 30% of total items.
3. 'C class’ inventory will account for the remaining 5% of total value or 50% of total items.

Another breakdown of ABC classes

1. A—approximately 10% of items or 66.6% of value
2. B—approximately 20% of items or 23.3% of value
3. C—approximately 70% of items or 10.1% of value

Under this system, materials are classified into three categories in the order of their respective values. Materials that are costly are grouped into ‘A’ category. Materials that are moderate in value are grouped into ‘B’ category, and materials that are cheap are grouped into ‘C’ category. In other words, high-priced materials are grouped into the A category, medium-priced materials are grouped into the B category and low-priced materials are grouped into the ‘C’ category.

Materials in the A category form a small part of the total inventory. Utmost care should be taken in storing and using these materials. Materials in the B category form a medium part of the total inventory. Moderate care and control should be exercised in storing and using these materials. Materials in the C category form a large part of the total inventory. Such materials need not be given much importance as such.

Category	Percentage of items	Percentage of cost
A	8	75
B	25	20
C	67	5
Total	100	100

4.8 JUST-IN-TIME ANALYSIS—THE ORIGIN

Just-in-time (JIT) analysis was developed by Toyota's Vice President Taiichi Ohno. The JIT concept was first transferred to the United States around 1980 at Kawasaki's Lincoln, Nebraska. Since then many corporations in the United States have followed suit and have begun implementing JIT. But even today the concept is just beginning to be understood and used by many industrial enterprises throughout the world.

JIT analysis is nothing but just-in-time inventory system. It is the purchase of material in such a way that materials are delivered before their use. Timely deliveries have special significance in JIT analysis.

JIT is an inventory strategy that strives to improve a business's return on investment by reducing in-process inventory and associated carrying costs. Ability to provie quick notice that stock depletion requires personnel to order new stock is critical to inventory reduction at the centre of JIT. This saves warehouse space and costs. However, the complete mechanism for making this work is often misunderstood.

The benefits of JIT are

1. Reduced setup time. Cutting setup time allows the company to reduce inventory for ‘changeover’ time.
2. The flow of goods from warehouses to shelves improves. Small lot sizes reduce delay in the supply of inventories, which simplifies inventory flow and its management.
3. Employees with multiple skills are used more efficiently. Having employees trained to work on different parts of the process allows companies to move workers to where they are needed.
4. Production scheduling and work hour consistency is synchronized with demand. If there is no demand for a product at a time, it is not made.
5. Increased emphasis on supplier relationships. A company without inventory does not want a supply system problem that creates a part shortage. This makes supplier relationships extremely important.
6. Supplies come in at regular intervals throughout the production day. Supply is synchronized with production demand and the maximum amount of inventory at hand at any time.

4.9 VED ANALYSIS

VED analysis is used mainly for the control of spare parts, where V stands for vital, E stands for essential and D stands for desirable. Absence of vital spare parts will immediately affect production, absence of essential spare parts will affect production after a few hours or so and absence of desirable spare parts will affect production only after a week or so.

It is the analysis for monitoring and controlling stores and spare parts inventory by classifying them into three categories, viz, vital, essential and desirable. The mechanics of VED analysis is similar to that of ABC analysis. Whereas in ABC classification inventories are classified on the basis of their consumption value and in HML analysis the unit value is the basis, criticality of inventories is the basis for vital, essential and desirable categorization.

VED analysis is done to determine the criticality of an item and its effect on production and other services. It is specially used for the classification of spare parts. If a part is vital it is given ‘V’ classification, if it is essential then it is given ‘E’ classification and if it is not so essential the part is given ‘D’ classification. For V items, a large stock of inventory is generally maintained, whereas for D items minimum stock is enough.

VED Analysis

VED analysis can be defined as the analysis of maintenance spares into

 

V items—items of vital importance

E items—items of essential importance

D items—items of desirable importance

4.10 PERPETUAL INVENTORY SYSTEM

Perpetual inventory means the system of records, whereas continuous stocktaking means the physical checking of those records with actual stocks. The perpetual inventory method has the following advantages:

• The stocktaking task, which is long and costly, is avoided under this method.
• The management may be informed daily of the number of units and the value of each kind of material at hand.

• The investment in materials and supplies may be kept at the lowest point in conformity with operating requirements.
• A system of internal check is always in operation. This results in detailed and reliable checks on the stores.
• It is not necessary to stop production so as to carry out a complete physical stocktaking.
• Perpetual inventory records provide details about the cost of material for individual products, jobs processes, production orders or departments.
• Discrepancies and errors are promptly discovered and remedial action can be taken to avoid their occurrence in the future.
• This method has a moral effect on the staff, makes them disciplined and careful and acts as a check against dishonest actions.
• The disadvantages of excessive stock are avoided.

4.11 PERIODIC INVENTORY SYSTEM

Under the periodic method, the entire book inventory is verified at a given date by an actual count of materials at hand. This physical inventory is usually taken near the end of the accounting period. This method provides for the recording of purchases, purchase returns and purchase allowances on a daily basis.

The costs of goods sold are computed by deducting closing inventory from the sum of opening inventory and purchases made during the current period. It is assumed that goods not on hand at the end of the accounting period have been sold. There is no system and accounting for shrinkage, losses, theft and waste throughout the accounting period and they can be discovered only after the end of the period.

Taking a physical inventory at the end of a year is an important task in the periodic inventory system. It must be ensured that all items are counted accurately. Counting procedures usually involve teams of people assigned to specific sections of the factory and to inventory storage areas. Large items are counted individually, whereas small items are weight-counted. Counted items are tagged to prevent double counting and information from the tags concerning each item's description and quantity is recorded on the inventory sheet.

Periodic inventory system refers to knowing the level of every item of stock at all times. It is a method of recording stores’ balances after every receipt and issue. This system implies continuous maintenance of stock.

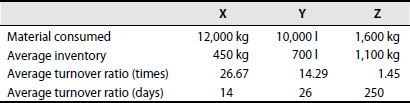
4.12 STOCK/MATERIAL TURNOVER RATIO

Material turnover (MT) ratio refers to the rate of consumption of materials. It indicates the fast- and slow-moving materials. A high ratio indicates that an item is fast moving and investment in it is low. A lower ratio indicates the item is not consumed in more quantity and the locking of working capital in undesirable items.

 

Illustration 1

Find out the EOQ and the number of orders per year.

Annual usage:	1,000 units
Cost of material per unit:		Rs 20
Cost of placing one order:	Rs 40

Annual carrying cost of one unit; 10% of inventory value.

 

Solution:

The answer is five orders per year.

 

Problem 1. Find out the EOQ and the number of orders per year

Annual usage:	2,000 units
Cost of material per unit:		Rs 20
Cost of placing one order:	Rs 40

Annual carrying cost of one unit; 10% of inventory value.

 

Illustration 2

Monthly consumption	4,200 units
Cost per unit	Rs 63
Ordering cost	Rs 125 per order
Inventory carrying cost	20% of the average inventory

Calculate EOQ.

Solution:

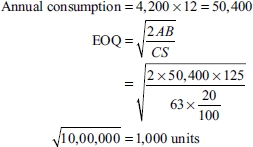
Problem 2.

Monthly consumption	6,200 units
Cost per unit	Rs 63
Ordering cost per order	Rs 125
Inventory carrying cost	20% of the average inventory

Calculate EOQ.

Illustration 3

Consumption of material per annum	Rs 12,500
Ordering cost per order	Rs 100
Carrying and storage cost	10% of the average inventory

Calculate EOQ.

Solution:

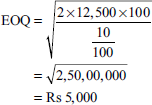
Problem 3.

Consumption of material per annum	Rs 14,500
Ordering cost per order	Rs 100
Carrying and storage cost	10% of the average inventory

Calculate EOQ.

Illustration 4

A factory consumes 30 units of material per day, which is supplied by a wholesaler in lots of 480 units each at Rs 4,800 per lot. On an average the factory works for 300 days in a year. Each order involves handling charges of Rs 400 and freight charges of Rs 600. The storage cost is Rs 1.40 per unit per annum. Carrying cost is 0.50% per month. Calculate EOQ.

Solution:

Where

A = annual usage of material

B = buying cost per order

C = cost per unit

S = storage and carrying cost

1. Annual usage = 30 units per day × 300 working days = 9,000 units
2. Buying cost = Handling charges + Freight = 400 + 600 = Rs 1,000
3. 

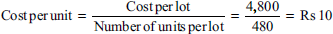
(s) Storage and carrying cost:

∴ Number of units to be ordered each time to minimize overall inventory cost = 3,000 units

(b) Frequency of placing orders:

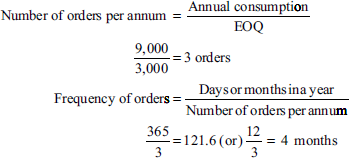
Problem 4. A factory consumes 30 units of material per day, which is supplied by a wholesaler in lots of 480 units each at Rs 6,800 per lot. On an average the factory works for 300 days in a year. Each order involves handling charges of Rs 400 and freight charges of Rs 600. The storage cost is Rs 1.40 per unit per annum. Carrying cost is 0.50% per month. Calculate EOQ.

Illustration 5

A company is able to obtain quantity discount on its order of material in the following manner:

Price per tonne	Tonnes
Rs 6.00	Less than 100
Rs 5.80	100 and less than 600
Rs 5.20	600 and less than 1,200
Rs 4.60	1,200 and less than 2,000
Rs 4.00	2,000 and above

Annual demand is 3,000 tonnes. Storage cost is 10% per annum. Delivery cost per order is Rs 6. Calculate EOQ.

Solution:

 

Where

A = annual usage

B = buying cost per order

C = cost per unit

S = storage and carrying cost per unit

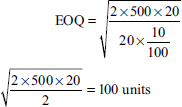
Tabular method

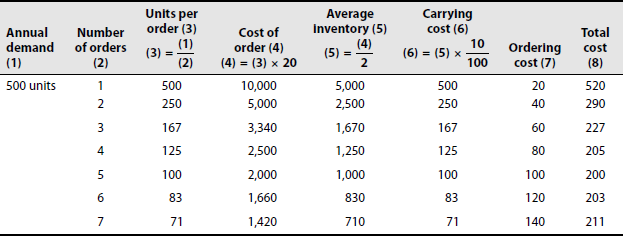
It can be observed from the aforementioned table that when five orders are placed for 100 units each time, the total cost is the lowest. So EOQ = 100 units per order.

Problem 5. A company is able to obtain quantity discount on its order of material in the following manner:

Price per tonne	Tonnes
Rs 7.00	Less than 100
Rs 6.80	100 and less than 600
Rs 6.20	600 and less than 1,200
Rs 5.60	1,200 and less than 2,000
Rs 5.00	2,000 and above

Annual demand is 3,000 tonnes. Storage cost is 10% per annum. Delivery cost per order is Rs 6. Calculate EOQ.

Illustration 6

Calculate EOQ using tabular method.

Annual consumption	3,000 units
Ordering cost	Rs 6 per order
Price per unit	Rs 4
Carrying cost per annum	10%

Solution:

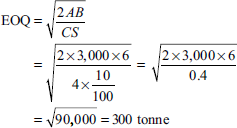
Problem 6. Calculate EOQ using tabular method.

Annual consumption	700 units
Ordering cost	Rs 20 per order
Price per unit	Rs 20
Carrying cost per annum	10%

Illustration 7

ARR Limited got an offer on its order of materials as under

Price per tonne	Tonnes
1,400	Less than 800
1,380	800 and less than 1,600
1,360	1,600 and less than 2,500
1,340	2,500 and less than 3,500
1,320	3,500 and above

The annual requirement for material is 6,000 tonne. The ordering cost per order is Rs 1,200 and the stockholding cost is estimated at 20% of material cost per annum. The purchase quantity options to be considered are 600, 900, 1,800, 2,400 and 3,600 tonne. You are required to compute the most economical purchase level. What will be your answer to the question if no discounts are offered and the price per tonne is Rs 2,100.

Solution: Computation of the most economical purchase level is as follows:

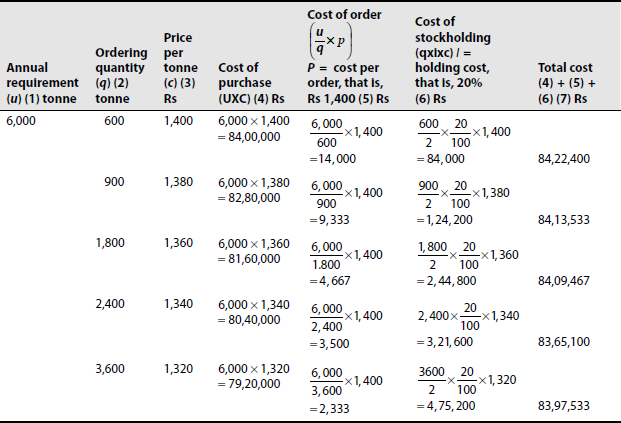
From the aforementioned table we see that the minimum cost is Rs 83,65,100. When the order quantity is 2,400 tonne, the most economical purchase level is 2,400 tonne.

(b)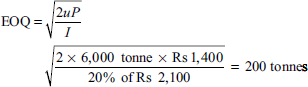

Problem 7. ARR Limited got an offer on its order of materials as unde

Price per tonne	Tonne
2,400	Less than 800
2,380	800 and less than 1,600
2,360	1,600 and less than 2,500
2,340	2,500 and less than 3,500
2,320	3,500 and above

The annual requirement for material is 6,000 tonne. The ordering cost per order is Rs 1,200 and the stockholding cost is estimated at 20% of material cost per annum. The purchase quantity options to be considered are 600, 900, 1,800, 2,400 and 3,600 tonne. You are required to compute the most economical purchase level. What will be your answer to the question if no discounts are offered and the price per tonne is Rs 2,100.

Illustration 8

Calculate inventory turnover ratio and express in number of days the average inventory held.

Value of material	Rs 2/kg
Opening stock		1,200 kg
Purchases	1,400 kg
Closing stock	600 kg

Solution:

Problem 8. Calculate inventory turnover ratio and express in number of days the average inventory held.

Value of material	Rs 2/kg
Opening stock		1,400 kg
Purchases	1,600 kg
Closing stock	800 kg

Illustration 9

Calculate the material turnover ratio from the following particulars:

	Material A	Material B
	Rs	Rs
Opening stock	8,000	10,000
Purchases	60,000	70,000
Closing stock	4,000	8,000

Solution:

For material A,

For material B,

Problem 9. Calculate the material turnover ratio from the following particulars:

	Material A	Material B
	Rs	Rs
Opening stock	10,000	12,000
Purchases	70,000	80,000
Closing stock	4,000	8,000

Illustration 10

Calculate the material turnover ratio from the following particulars and determine the fast-moving item:

	Material X	Material Y
	Rs	Rs
Materials on 1 January 2005	40,000	60,000
Materials on 31 December 2005	10,000	20,000
Materials purchased	1,40,000	2,10,000

Solution:

For material X,

For material Y,

 

Comment: The inventory turnover ratio of material X is higher than that of Y. Therefore, material X is fast moving compared with material Y.

Problem 10. Calculate the material turnover ratio from the following particulars and determine the fast-moving item:

	Material X	Material Y
	Rs	Rs
Materials on 1 January 2005	40,000	60,000
Materials on 31 December 2005	10,000	20,000
Materials purchased	1,40,000	2,10,000

Illustration 11

Material X is used as follows:
Maximum usage in a month	800 units
Minimum usage in a month	200 units
Average usage in a month	400 units
Head time: maximum—8 months, minimum—4 months
Reorder quantity	1,200 numbers
Maximum reorder period for emergency purchases	1 month

Calculate (a) reorder level, (b) maximum level, (c) minimum level, (d) average level and (e) danger level.

Solution: The terms lead time and reorder period mean the same thing. Usage and consumption are also used as alternative terms.

1. Reorder level = Maximum consumption × Maximum reorder period

                  = 800 units × 8 months

                  = 6,400 units

2. Maximum stock level = Reorder level + Reorder quantity) − (Minimum consumption × Minimum reorder period)

                               = 6,400 + 1,200 − (200×4)

                               = 7,600 − 800 = 6,800 units

3. Minimum cost stock level = Reorder level − Normal consumption × Normal reorder period)
   

    

4. 
5. Danger level = Average consumption × Maximum reorder period for emergency purchases

                  = 400 × 1 = 400 units

Problem 11.

Material X is used as follows:
Maximum usage in a month	900 units
Minimum usage in a month	200 units
Average usage in a month	400 units
Head time: maximum—8 months, minimum—4 months
Reorder quantity	1,200 numbers
Maximum reorder period for emergency purchases	1 month

Calculate (a) reorder level, (b) maximum level, (c) minimum level, (d) average level and (e) danger level.

Illustration 12

Two materials X and Y are used as follows:

Particulars	Material X	Material Y
Reorder quantity	2,200	2,000
Reorder period	2–4 week	4–6 week
Normal usage	400 units/week	300 units/week
Minimum usage	300 units/week	200 units/week
Maximum usage	600 units/week	400 units/week

Calculate (a) reorder level, (b) maximum level, (c) minimum level, (d) average level

Solution:

1. Reorder level = Maximum consumption × Maximum reorder period

       Material X = 600 units × 4 weeks = 2,400 units

       Material Y = 400 units × 6 weeks = 2,400 units

2. Maximum level = Reorder level + Reorder quantity − Minimum consumption × Minimum reorder period]

      Material X = 2,400 + 2,200 [300 × 2]

                      = 4,600 − 600 = 4,000 units

      Material Y = 2,400 + 2,000 [200 × 4]

                      = 4,400 − 800 = 3,600 units

3. 
4. 

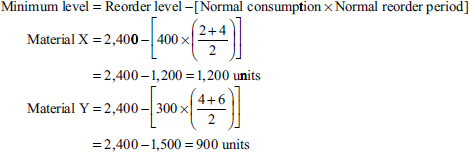
Problem 12. Two materials X and Y are used as follows:

Particulars	Material X	Material Y
Reorder quantity	2,400	2,200
Reorder period	2–4 weeks	4–6 weeks
Normal usage	400 units/week	300 units/week
Minimum usage	300 units/week	200 units/week
Maximum usage	600 units/week	400 units/week

Illustration 13

Calculate (a) EOQ, (b) reorder level, (c) maximum level and (d) minimum level from the following information:

Normal usage	250 units per day
Minimum usage		150 units per day
Maximum usage	350 units per day
Reorder period		60–70 days
Annual usage	75,000 units
Cost of purchase per order	Rs 1.50
Cost per unit	Rs 2
Carrying cost per annum	20%

Solution:

1. Economic ordering quantity:
   

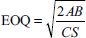
   Where

   A = annual usage

   B = buying cost per order

   C = cost per unit

   S = storage and carrying cost

   
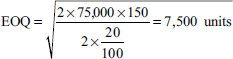
2. Reorder level = Maximum consumption × Maximum reorder period

                   = 350 units × 70 days

                   = 24,500 units

3. Maximum level = Reorder level + Reorder quantity − Minimum consumption × Minimum reorder period]

                      = 24,500 + 7,500 − (150 × 60)

                      = 32,000 − 9,000

                      = 23,000

4. Minimum level = Reorder level − [Normal consumption × Normal reorder period]
   

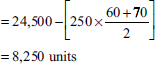
Problem 13. Calculate (a) EOQ, (b) reorder level, (c) maximum level and (d) minimum level from the following information:

Normal usage	350 units per day
Minimum usage		250 units per day
Maximum usage	450 units per day
Reorder period		60–70 days
Annual usage	75,000 units
Cost of purchase per order	Rs 1.50
Cost per unit	Rs 2
Carrying cost per annum	20%

Illustration 14

Two components X and Y are used as follows:

Normal usage	50 units each per week
Minimum usage		25 units each per week
Maximum usage	100 units each per week
Reorder quantity	X—500 units, Y—700 units
Reorder period		X—4–6 weeks, Y—2–4 weeks

Calculate for each component the (1) reorder level, (2) minimum level (3) maximum level and (4) average level.

Solution:

1. Reorder level = Maximum consumption × Maximum reorder level

   Component X = 100 units × 6 weeks = 600 units

   Component Y = 100 units × 4 weeks = 400 units

2. 
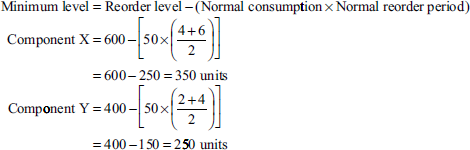
3. Maximum level = Reorder level + Reorder quantity − [Minimum consumption × Minimum reorder period]

     Component X = 600 + 500 − [25 × 4]

                          = 1,100 − 100 = 1,000 units

     Component Y = 400 + 700 − [25 × 2]

                          = 1,100 − 50 = 1,050 units

4. 

Problem 14. Two components X and Y are used as follows:

Normal usage	75 units each per week
Minimum usage		50 units each per week
Maximum usage	200 units each per week
Reorder quantity	X—500 units, Y—700 units
Reorder period		X—4–6 weeks, Y—2–4 weeks

Calculate for each component the (1) reorder level, (2) minimum level, (3) maximum level and (4) average level.

Illustration 15

Two components X and Y are used as follows:

Normal usage	600 units each per week
Maximum usage	800 units each per week
Minimum usage		250 units each per week
Reorder quantity	X—4,500 units, Y—7,500 units
Reorder period		X—4–6 weeks, Y—2–4 weeks

Calculate for each component the (a) reorder level, (b) minimum level, (c) maximum level and (d) average stock level.

 

Solution:

1. Reorder level = Maximum consumption × Maximum reorder period

   Component X = 800 units × 6 weeks = 4,800 units

   Component Y = 800 units × 4 weeks = 3,200 units

2. 
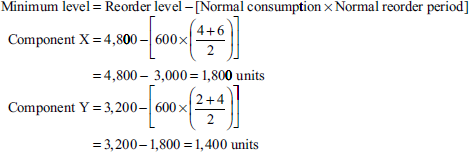
3. Maximum level = Reorder level + Reorder quantity − [Minimum consumption × Minimum reorder period]

     Component X = 4,800 + 4,500 − [25 × 4]

                          = 9,300 − 1,000 = 8,300 units

     Component Y = 3,200 + 7,500 − [25 × 2]

                          = 10,700 − 500 = 10,200 units

4. 

Problem 15. Two components X and Y are used as follows:

Normal usage	800 units each per week
Maximum usage	900 units each per week
Minimum usage		450 units each per week
Reorder quantity	X—4,500 units, Y—7,500 units
Reorder period		X—4–6 weeks, Y—2–4 weeks

Illustration 16

Two components A and B are used as follows:

Normal usage	100 units each per week
Minimum usage	50 units each per week
Maximum usage	200 units each per week
Reorder quantity	A—800 units, B—1,000 units
Reorder period	A—6–8 weeks, B—3–5 weeks

Calculate for each component the (a) minimum level, (b) maximum level and (c) average stock level.

Solution:

Reorder level = Maximum consumption × Maximum reorder period

Component A = 200 × 8 = 1,600 units

Component B = 200 × 5 = 1,000 units

1. Minimum level = Reorder level − Normal consumption × Normal reorder period]
   
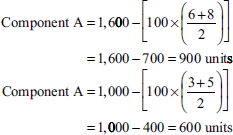
2. Maximum level = Reorder level + Reorder quantity − [Minimum consumption × Minimum reorder period]

     Component A = 1,600 + 800 − [25 × 6]

                         = 2,400 − 300 = 2,100 units

     Component B = 1,000 + 1,000 − [25 × 3]

                         = 2,000 − 150 = 1,850 units

3. 

Problem 16. Two components A and B are consumed as follows:

Normal usage	200 units each per week
Minimum usage	100 units each per week
Maximum usage	300 units per each week
Reorder quantity	A—800 units, B—1,000 units
Reorder period	A—6–8 weeks, B—3–5 weeks

Calculate for each component the (a) minimum level, (b) maximum level and (c) average stock level.

Illustration 17

From the following particulars, calculate (a) reorder level, (b) minimum level and (c) maximum level:

Normal usage	150 units per day
Minimum usage		70 units per day
Maximum usage	150 units per day
Economic order quantity	8,000 units
Reorder period		25–30 days

Solution:

1. Reorder level = Maximum consumption × Maximum reorder period

                   = 150 × 30 = 4,500 units

2. 
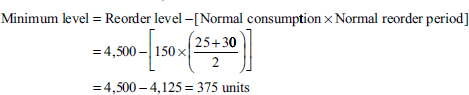
3. Maximum level = Reorder level + Reorder quantity − (Minimum consumption × Minimum reorder period)

                      = 4,500 + 8,000 − [70 × 25

                      = 12,500 − 1,750 = 10,750 units

Problem 17. From the following particulars, calculate (a) reorder level, (b) minimum level and (c) maximum level:

Normal usage	300 units per day
Minimum usage		100 units per day
Maximum usage	250 units per day
Economic order quantity	8,000 units
Reorder period		25–30 days

Illustration 18

Calculate (a) EOQ, (b) maximum level, (c) minimum level and (d) reordering level from the following data:

Reorder period		4–6 weeks
Maximum consumption		150 units per week
Minimum consumption		50 units per week
Normal consumption	100 units per week
Annual consumption	36,000 units
Cost per unit	Re 1
Ordering cost	Rs 25

Inventory carrying cost is 20% of unit value.

 

Solution:

1. Economic ordering quantity:
   

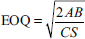
   Where

   A = annual usage

   B = buying cost per order

   C = cost per unit

   S = storage and carrying cost

   
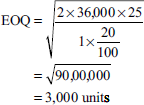
2. Reorder level = Maximum consumption × Maximum reorder period

                   = 150 × 6 = 900 units

3. Maximum level = Reorder level + Reorder quantity − (Minimum consumption × Minimum reorder period)

                      = 900 + 3,000 − [50 × 4

                      = 3,900 − 200 = 3,700 units

4. 

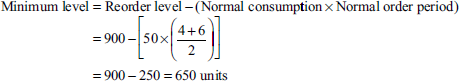
Problem 18. Calculate (a) EOQ, (b) maximum level, (c) minimum level and (d) reordering level from the following data:

Reorder period		4–6 weeks
Maximum consumption		250 units per week
Minimum consumption		100 units per week
Normal consumption	200 units per week
Annual consumption	36,000 units
Cost per unit	Re 1
Ordering cost	Rs 25

Inventory carrying cost is 20% of unit value.

Illustration 19

In a manufacturing firm, a material is used as follows:

Maximum consumption		14,000 units per week
Minimum consumption		3,000 units per week
Normal consumption	10,000 units per week
Reorder quantity	52,000 units
Average consumption		8,000 units per week
Emergency delivery time	2 weeks
Minimum	6 weeks; maximum: 10 weeks

Calculate (a) reorder level, (b) minimum level, (c) maximum level, (d) average stock level and (e) danger level.

Solution:

1. Reorder level = Maximum consumption × Maximum reorder period = 14,000 × 10 = 1, 40,000
2. 
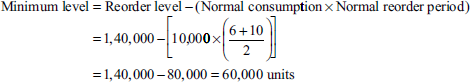
3. Maximum level = Reorder level + Reorder quantity − [Minimum consumption × Minimum reorder period]

                      = 1,40,000 + 52,000 − [3000 × 6]

                      = 1,92,000 − 18,000 = 1,74,000 units

4. 
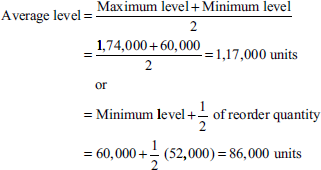
5. Danger level = Average consumption × Emergency delivery time

                  = 8,000 units × 2 weeks = 16,000 units

Problem 19. In a manufacturing firm, a material is used as following:

Maximum consumption		16,000 units per week
Minimum consumption		5,000 units per week
Normal consumption	12,000 units per week
Reorder quantity	52,000 units
Average consumption		8,000 units per week
Emergency delivery time	2 weeks
Minimum	6 weeks; maximum: 10 weeks

Calculate (a) reorder level, (b) minimum level, (c) maximum level, (d) average stock level and (e) danger level.

Illustration 20

In manufacturing its products, a company uses three raw materials, A, B and C, for which the following particulars apply:

Weekly production varies from 225 to 275 units, averaging 250. What would you expect the quantities of (a) minimum stock of A, (b) maximum stock of B, (c) reorder level of C and (d) average stock of A to be?

Solution:

1. Minimum stock of A
   
2. Maximum stock of B

   Maximum stock of B = Reorder level + Reorder quantity − (Minimum consumption × Minimum reorder period)

                                     6,700 + 6,000 − (1,125 × 3) = 9,325 lb

   (Minimum production per week = 225 units

   Usage per unit of product = 5 lb

   ∴ Minimum consumption of material per week = 225 × 5 = 1,125 lb)

3. Reorder level of C

   Reorder level of C = Maximum consumption × Maximum reorder period

                              2,200 × 4 = 8,800 lb

   (Maximum production per week = 275 units)

   Usage per unit = 8 lb

   ∴ Maximum consumption of material C = 275 × 8 = 2,200 lb

4. Average stock level of A
   

Problem 20. In manufacturing its products, a company uses three raw materials, A, B and C, for which the following particulars apply:

Weekly production varies from 225 to 275 units, averaging 250. What would you expect the quantities of (a) minimum stock of A, (b) maximum stock of B, (c) reorder level of C and (d) average stock of A to be?

4.13 ADVANCED-TYPE SOLVED PROBLEMS

Illustration 1

Develop the formula for economic order quantity.

Solution:

A = annual consumption

B = buying cost per order

CS = carrying cost per unit

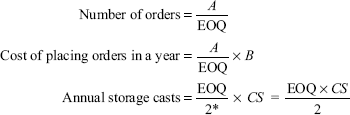
^*Since on an average 50% of E will be in stock.

At the EOQ level, total storage costs are equal to total order placing costs.

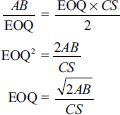
Illustration 2

If the minimum stock level and average stock level of raw material A are 4,000 and 9,000 units, respectively, find its reorder quantity.

Solution:

Minimum stock level of material	A4,000 units
Average stock of material	A9,000 units
Average stock level	minimum stock level + ½ reorder quantity
½ Reorder quantity	9,000–4,000
	5,000 units
Reorder quantity	10,000 units

Illustration 3

G Ltd produces a product that has a monthly demand of 4,000 units. The product requires a component X, which is purchased at Rs 10 for every finished product one unit at component is required. The ordering cost is Rs 60 and the holding cost is 10% per annum. You are required to calculate

1. EOQ.
2. If the minimum lot size to be supplied is 4,000 units, what is the extra cost the company has to incur?
3. What is the minimum carrying cost the company has to incur?

Solution:

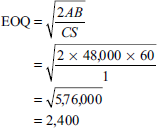
(i) If the order size is 4,000 units

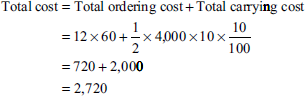
When the order size is 2,400

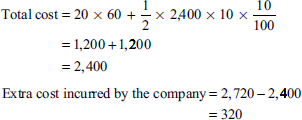
The carrying or storage cost depends upon the size of the order. Its value will be minimum when the order size is the lowest. In the question, the two order sizes are 2,400 units and 4,000 units. Hence, 2,400 units is the least of the two order sizes. At this size, the carrying cost will be minimum. The minimum carrying cost in this case will be as follows:

 

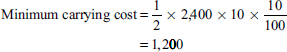
Illustration 4

A gardener is deciding on the EOQ for two brands of lawn fertilizers: Super Grow and Nature's Own. The following information is collected:

	Fertilizer
Particulars	Super Grow	Nature's Own
Annual demand	2,000 bags	1,280 bags
Relevant ordering cost per purchase order	600	700
Annual relevant carrying cost per bag	240	280

You are required to calculate

1. Compute EOQ for Super Grow and Nature's Own.
2. For the EOQ, what is the sum of the total annual relevant ordering costs, total annual relevant ordering costs and total annual relevant carrying costs for Super Grow and Nature's Own?
3. For the EOQ, compute the number of deliveries per year for Super Grow and Nature's Own.

Solution:

1. Calculation of EOQ:

   Super Grow:

    

   

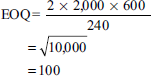
   Nature's Own:

    

   
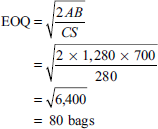
2. Total annual relevant costs for Super Grow:

    

   

    

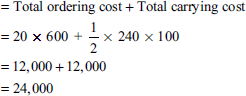
   Total annual relevant costs for Nature's Own:

    

   
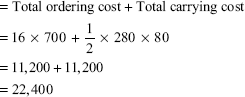
3. Number of deliveries for Super Grow:

    

   

   Number of Deliveries:

    

   

Illustration 5

In a company, weekly minimum and maximum consumptions of material A are 25 and 75 units, respectively. The reorder quantity as fixed by the company is 300 units. The material is received within 4–6 weeks from the issue of supply order. Calculate minimum level and maximum level of material A.

Minimum level = Reorder level − Average consumption × Average reorder period)

                      = 455 − (50 units × 4 weeks)

                      = 650 units

  Reorder level = Maximum usage × Maximum reorder period

                      = 75 units × 6 weeks

                      = 450 units

Illustration 6

About 50 items are required every day for a machine. A fixed cost of Rs 25 per order is incurred for playing an order. The inventory carrying cost per item amounts to Rs 0.01 per day. The lead period is 32 days. Compute (i) economic order quantity and (ii) reorder level.

Solution:

Annual consumption	= 50 × 365 = 18,250 units
Order cost	= 25
Inventory carrying cost per item per annum	= 0.01 × 365
	= 3.65

1.  

   
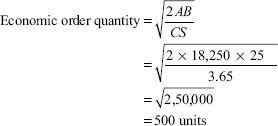
2. Reorder level = Maximum usage × Maximum reorder period

                   = 50 × 32

                   = 1,600 items

Illustration 7

A company uses three raw materials A, B and C for a particular product for which the following data apply:

Weekly production varies from 175 to 225 units, averaging 200 units, of the said product. What would be the values of the following quantities?

1. Minimum stock of A?
2. Maximum stock of B?
3. Reorder level of C?
4. Average stock level of A?

Solution:

1. Minimum stock of A = Reorder level − Average usage × Average delivery period)

                              = 8,000 − (2,000 × 2)

                              = 4,000 kg

2. Maximum stock of B = Reorder level + Reorder quantity − (Minimum usage × Minimum delivery period)

                               = 4,750 + 5,000 − (700 × 3)

                               = 4,750 + 5,000 − 2,100

                               = 7,650

3. Reorder level of C = Maximum usage × Maximum delivery period

                           = 4 × 1,350

                           = 5,400kg

4. 

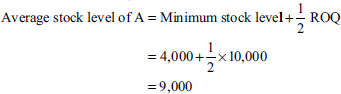
CHAPTER SUMMARY

After reading this chapter, you should be able to understand the importance of material for production. You should have also understood the levels, essentials and techniques of material control.

KEY FORMULAE

1. 

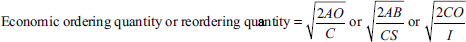
   Where

   First formula:

   A = annual consumption

   O = ordering cost per order

   C = carrying cost per unit per year

   Second formula:

   B = buying cost per order

   C = cost per unit

   S = storage and carrying cost

   Third formula:

   C = annual usage of material

   O = cost of placing one order

   I = annual carrying cost of one unit

2. Reorder level = maximum delivery period × maximum usage or consumption
3. Minimum level or minimum stock level = ROL − (normal usage × average delivery period)
4. Maximum level or maximum stock level = ROL + ROQ − (minimum consumption × minimum delivery period)
5. Average stock level = minimum level + maximum level/2

   or

   Average stock level = minimum level + ½ of ROQ or EOQ

6. Danger level = average consumption × maximum delivery period
7. Inventory turnover ratio = value of material consumed/value of average stock
8. 
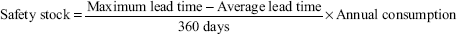
9. Reorder level = safety stock + lead time consumption
10. Recorder level = minimum stock + average consumption × average delivery period
11. Carrying cost = ½ × order size × inventory carrying cost per order

EXERCISE FOR YOUR PRACTICE

Objective-Type Questions

I. State whether the following statements are true or false:

1. Continuous stock taking should not be resorted to since it results in the disruption of work.
2. ABC analysis concentrates more on important items.
3. The terms material and inventory should not be used synonymously.
4. EOQ is a reorder quantity.
5. When maximum stock level is fixed, the stock at hand should never exceed this level.
6. Perpetual inventory system means a continuous stocktaking system.
7. Under ABC analysis, A stands for high-value items.
8. There are two aspects, namely, accounting aspect and operational aspect, of material control.
9. Stock verification sheets are maintained to record the results of physical verification.
10. Material control covers three stages, namely, purchasing, storing and issuing.

[Ans: 1—false, 2—true, 3—true, 4—false, 5—false, 6—false, 7—true, 8—true, 9—true, 10—true]

II. Choose the correct answer:

1. Under ABC analysis, A stands for
   1. Low-value item
   2. Minimum-value item
   3. High-value item
   4. None of the above
2. Stock verification sheets are maintained to record the results of
   1. Annual consumption
   2. Physical verification
   3. Both a and b
   4. None of the above
3. Formula for average stock level
   1. Minimum + maximum level/2
   2. Minimum level + 1/2 of ROQ or EOQ
   3. Both a and b
4. Reorder level = safety stock +______
   1. Short time consumption
   2. Lead time consumption
   3. Average consumption
   4. None of the above
5. _____analysis is used mainly for the control of spare parts
   1. VED analysis
   2. JIT analysis
   3. Periodic inventory system
   4. Perpetual inventory system
6. Timely deliveries have special significance in
   1. VED analysis
   2. JIT analysis
   3. Periodic inventory system
   4. Perpetual inventory system
7. If the quality of materials purchased is too low, the product will be of
   1. Superior quality
   2. Inferior quality
   3. Both a and b
   4. None of the above

8. Higher cost of finished product would make the product
   1. Competitive
   2. Uncompetitive
   3. Comparative
   4. None of the above
9. Physical inventory is usually taken near
   1. Beginning of the accounting period
   2. End of the accounting period
   3. Middle of the accounting period
   4. None of the above
10. The cost of goods sold is computed by deducting
    1. Opening inventory
    2. Closing inventory
    3. Both a and b
    4. None of the above

    Ans: 1—(c), 2—(b), 3—(c), 4—(b), 5—(a), 6—(b), 7—(b), 8—(b), 9—(b), 10—(b).

DISCUSSION QUESTIONS

Short Answer-Type Questions

1. What do you mean by material control?
2. What do you mean by minimum stock level?
3. Explain the concept of EOQ. What is its importance in cost accounts?
4. What is reorder level?
5. What is ABC analysis?
6. Give short notes on JIT and VED analyses

Essay-Type Questions

1. Explain the importance of material control.
2. What are the objectives and requirements of material control?
3. Bring out the major duties of a storekeeper.
4. Write a detailed note on perpetual inventory system.
5. Write elaborately on periodic inventory system.

PROBLEMS

1. The following figures are taken from the books of a firm for the year ended on 1994. The valuation of inventory is Re 1 per kilogram or litre.
   
2. Calculate the material turnover ratio for the material items mentioned in the previous problem and express in number of days the average inventory held.

   Ans:

3. From the following data, find EOQ:

   Annual usage	6,000 units
   Cost per unit	Re 0.30
   Buying cost	Rs 7 per order
   Carrying cost	15% of average inventory holding

   [Ans: 1,366 units]

4. A manufacturer buys certain equipment from outside suppliers at Rs 30 per unit. Total annual needs are 800 units. The following further data are available:

   Annual return on investments		10%
   Rent, insurance, taxes per unit per year		Re 1
   Cost of placing an order	Rs 100

   Determine the economic order quantity

   [Ans: 200 units]

5. From the following information, find EOQ and the number of orders placed in a year:

   Annual consumption	120 units
   Buying cost per order	Rs 20
   Price per unit	Rs 100

   Storage and carrying cost as a percentage of average inventory 12%.

   [Ans: 20 units, 6 orders]

6. Find EOQ given the following:

   Monthly usage	150 units
   Buying cost	Rs 2 per order
   Cost per unit	0.32 paise
   Storage cost	25% per annum

   (Osmania, B.Com.)

   [Ans: EOQ = 300 units]

7. Calculate EOQ for the following data:

   Annual consumption	600 units
   Order cost	Rs 12 per order
   Cost price per unit	Rs 20
   Storage and carrying cost	20%

   (Madras, 1990)

   [Ans: EOQ = 60 units]

8. Calculate EOQ from the following particulars:

   Annual usage	20,000 units
   Buying cost per order	Rs 10
   Cost per unit	Rs 100
   Cost of carrying inventory	10% of cost

   (Madras, 1996)

   [Ans: EOQ = 200 units]

9. From the following information, determine EOQ:

   Annual consumption	90,000 units
   Cost per unit	Rs 50
   Buying cost per order	Rs 10
   Cost of carrying inventory	10% of cost

   (Madras, 1996)

   [Ans: EOQ = 600 units]

10. Calculate EOQ from the following particulars:

    Annual usage	6,000 units
    Cost of materials per unit	Rs 20
    Cost of placing and receiving one order	Rs 60
    Annual carrying cost	Rs 2 per unit

    (Madras,)

    [Ans: EOQ = 600 units]

    Hint: Carrying cost of Rs 2 per unit can be directly used in the formula without any reference to cost per unit.

     

11. From the following data, you are required to determine EOQ:

    Annual usage	8,000 units
    Cost per unit	Re 0.30
    Buying cost	Rs 7 per order

    Storage and carrying costs as percentage of average inventory holding 15%.

    [Ans: 1,578 units]

12. Find EOQ from the following particulars:

    Annual usage	Rs 1,20,000
    Cost of placing and receiving one order	Rs 60
    Annual carrying cost	10% of inventory value

    (Madras, 1995)

    [Ans: EOQ = Rs 12,000]

13. You are required to compute the economic ordering quantity with the help of the following details:

    Material usage per month	Rs 1,600
    Buying cost per order	Rs 40
    Storage and carrying cost	15% of inventory value

    [Ans: EOQ = Rs 3,200]

14. From the following, for material A calculate (a) reorder level and (b) minimum level:

    Reorder quantity	4,000 units
    Minimum stock level to allow for emergencies		5 weeks
    Average delivery time from suppliers	4 weeks
    Maximum stock level allowed by management		20 weeks
    Average rate of consumption per week		250 units
    Minimum consumption in 4 weeks	800 units

    (B.Com., Madras)

    [Ans: (a) 2,250; (b) 1,250]

15. From the following information, calculate (a) maximum stock level, (b) minimum stock level, (c) reorder level and (d) average stock level:

    Minimum consumption		240 units per day
    Maximum consumption		420 units per day
    Normal consumption	300 units per day
    Reorder quantity	3,600 units
    Reorder period		10–15 days
    Normal reorder period	12 days

    (Madras, 1995)

    [Ans: (a) 7,500 units; (b) 2,700 units; (c) 6,300 units; (d) 5,100 units or 4,500 units]

16. From the following information, calculate maximum, minimum and average stock levels:

    Normal consumption per day	500 kg
    Minimum consumption per day		200 kg
    Maximum consumption per day		800 kg
    Lead time	10–16 days
    Reorder quantity		3,000 kg

    (Madras, 1990)

    [Ans: maximum stock level = 13,800 units; minimum stock level = 6,300 units;
    average stock level = 10,050 units or 7,800 units]

17. From the following information, calculate maximum, minimum, and average stock levels:

    Normal consumption per day	500 kg
    Minimum consumption per day		200 kg
    Maximum consumption per day		800 kg
    Lead time	10–16 days
    Reorder quantity		3,000 kg

    (B.Com., Calicut)

    [Ans: 13,800 kg; 6,300 kg; 7,800 kg]

    In a manufacturing firm, a material is used as follows:

    Maximum consumption		12,000 units per week
    Minimum consumption		4,000 units per week
    Normal consumption	8,000 units per week
    Reorder quantity	48,000 units
    Minimum	4 weeks
    Maximum	6 weeks

    Calculate (a) reorder level, (b) minimum level, (c) maximum level and (d) average stock level.

    (B.Com., Bangalore)

    [Ans: (a) 72,000; (b) 32,000; (c) 1,04,000; (d) 56,000 or 38,000]

18. From the following data for the last 12 months, compute reorder level, minimum level and average stock level of a stock item:

    Maximum usage in a month	300 kg
    Minimum usage in a month	200 kg
    Average usage in a month	225 kg
    Time lag in the procurement of materials	maximum—6 months, minimum—2 months
    Reordering quantity	750 kg

    (Madras, 1998)

    [Ans: reorder level = 1,800 units; minimum level = 900 units;
    average stock level = 1,275 units (900 + 375)]

19. In a manufacturing concern, material X is used as follows:

    Maximum consumption		9,000 units per week
    Minimum consumption		3,000 units per week
    Normal consumption	6,000 units per week
    Reorder quantity	36,000 units
    Time required for delivery	4–6 weeks
    Time required for emergent supplies	1 week

    Calculate (a) reorder level, (b) minimum level, (c) maximum level, (d) danger level and (e) average stock level.

    (B.Com., Madurai)

    [Ans: (a) 54,000 units; (b) 24,000 units; (c) 78,000 units; (d) 6,000 units; (e) 42,000 units]

20. Calculate minimum stock level, maximum stock level and reordering level from the following details:

    Minimum consumption		100 units per day
    Maximum consumption		150 units per day
    Normal consumption	120 units per day
    Reorder period		10–15 days
    Reorder quantity	1,500 units
    Normal reorder period	12 days

    (Madras, 1998)

    [Ans: minimum stock level = 810 units; maximum stock level = 2,750 units;
    reordering level = 2,250 units]

21. Calculate maximum level, minimum level and reordering level from the following data:

    Reorder quantity	1,500 units
    Reorder period		4–6 weeks
    Maximum consumption	400 units per week
    Normal consumption	300 units per week
    Minimum consumption	250 units per week

    (ICWA)

    [Ans: maximum level = 2,900 units; minimum level = 900 units; reorder level = 2,400 units]

22. Calculate reorder level, minimum stock level, maximum stock level and average stock level from the following information:

    Normal usage	300 units per week
    Maximum usage		450 units per week
    Minimum usage		150 units per week
    Reorder period		4–6 weeks
    Reorder quantity	2,400 units

    (Madras, 1997)

    [Ans: reorder level = 2,700 units; minimum stock level = 1,200 units; maximum stock level =
    4,500 units; average stock level = 2,850 units or 2,400 units]

23. From the following information, calculate reorder level, maximum stock level and minimum stock level:

    Reorder quantity	4,000 units
    Minimum stock level to allow for emergencies	4 weeks
    Average delivery time from suppliers	4 weeks
    Maximum stock level allowed by management	20 weeks
    Average rate of consumption per week	250 units
    Minimum consumption in 4 weeks	800 units

    (Madras, 1992)

    [Ans: reorder level = 2,000 units (250 × (4 + 4)); maximum stock level = 5,200 units;
    minimum stock level = 1,000 units]

24. From the following data for the last 12 months, compute the average stock level for a component:

    Maximum usage in a month	300 numbers
    Minimum usage in a month	200 numbers
    Average usage in a month	225 numbers
    Time lag in the procurement of materials:
    Maximum	6 months
    Minimum	2 months
    Reorder quantity	760 numbers

    (Madras, 1991)

    

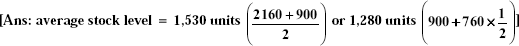
25. Two components X and Y are used as follows:

    Normal usage	4,500 units each per week
    Minimum usage		2,250 units each per week
    Maximum usage	6,750 units each per week
    Reorder quantity
    X		19,500 units
    Y		21,000 units
    Reorder period
    X		3–5 weeks
    Y		2–4 weeks

    Calculate for each of the components (a) reorder level, (b) minimum level and (c) maximum level.

     

    (Madras, B.A., 1995)

    [Ans: (a) X—33,750 units; (b) X—15,750 units; (c) A—46,400 units, X—27,000 units,
    Y—13,500 units, B—43,500 units]

26. The following information pertaining to a firm is available:

    Annual consumption	12,000 units (360 days)
    Cost per unit	Re 1
    Cost per order	Rs 12
    Inventory carrying cost	20% per annum
    Lead time (maximum, normal and minimum):	30—15—5 (days)
    Daily consumption (maximum, normal and minimum)	45—33—15 (units)

    Calculate inventory levels.

     

    (Madras, 1999)

    [Ans: reorder level = 1,350 units; EOQ = 1,200 units; maximum level = 2,475 units;
    minimum level = 855 units]

27. The following information is available for component D:

    Maximum stock level	8,400 units
    Budgeted consumption:
    Maximum	1,500 units per month
    Minimum	800 units per month
    Estimated delivery period:
    Maximum	4 months
    Minimum	2 months
    You are required to calculate
    (a) reorder level and
    (b) reorder quantity

    (Madras, 1989)

    [Ans: (a) 6,000 units; (b) 4,000 units]

28. From the following data, find (a) reorder level and (b) reorder quantity:

    Maximum stock level	16,800 units
    Budgeted consumption
    Maximum	3,000 units per month
    Minimum	1,600 units per month
    Estimated delivery period
    Maximum	4 months
    Minimum	2 months

    [Ans: (a) 12,000 units; (b) 8,000 units]

EXAMINATION PROBLEMS

1. Calculate economic ordering quantity from the following particulars:

   Annual requirement	1,600 units
   Cost of material per unit	Rs 40
   Cost of placing and receiving one order	Rs 50
   Annual carrying cost of inventory is 10% of inventory value.

   (Madras, 1986)

   [Ans: EOQ = 200 units]

2. Calculate EOQ from

   Annual consumption	600 units
   Ordering cost	Rs 12 per order
   Carrying cost	20%
   Price per unit	Rs 20

   (B.Com., Punjab)

   [Ans: 60 units]

3. Calculate the economic ordering quantity from the following information:

   Consumption of material per annum	10,000 kg
   Ordering cost per order		Rs 50
   Cost per kilogram of raw material	Rs 2
   Store cost	8% on inventory

   (Madras, 1988)

   [Ans: EOQ = 2,500 kg]

4. A manufacturer buys certain equipment from outside suppliers at Rs 30 per unit. Total annual needs are 80,000 units. The following further data are available:

   Annual return on investment	10%
   Rent, insurance, taxes per unit per year	Rs 13
   Cost of placing an order	Rs 100

   Determine EOQ.

   (Bharathidasan, 1992)

   

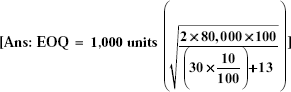
5. A car-making company buys 2,000 steel parts at Rs 140 per part for assembly. The buying cost per order is Rs 35. The inventory carrying cost is Rs 14 per unit per year, calculated as follows:

   Return on investment is 8%	11.20
   Rent, taxes, insurances, handling charges, etc.	Rs 2.80.

   Calculate the EOQ.

   

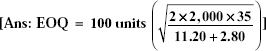
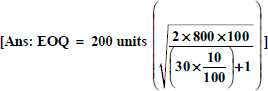
6. A manufacturer buys certain equipment from outside suppliers at Rs 30 per unit. Total annual needs are 800 units. The following further data are available:

   Annual return on investment	10%
   Rent, insurance, taxes per unit per year	Re 1
   Cost of placing an order	Rs 100

   Determine the EOQ.

   (Madras, 1994)

   

7. An engineering company consumes 50,000 units of a component per year. The ordering, receiving and handling costs are Rs 3 per order, whereas the trucking costs are Rs 12 per order. Further details are as follows:

   Interest	Re 0.06 per unit per year
   Deterioration cost	Re 0.004 per unit per annum
   Storage cost	Rs 1,000 per annum for 5,000 units

   Calculate the EOQ.

   (Madras, 1996)

   

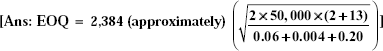
8. Calculate EOQ. Also state the number of orders to be placed in a year.

   Consumption of material per annum	10,000 kg
   Cost of material per kilogram Rs	2
   Order placing costs per order Rs	50

   Storage costs 8% on average inventory.

   (Madras, 1991)

   [Ans: EOQ = 2,500 kg, number of orders to be placed = 4]

9. From the following particulars, calculate EOQ and the number of orders per annum.

   Annual requirement	1,600 units
   Cost of materials per unit	Rs 40
   Cost of placing and receiving one order		Rs 50
   Annual carrying cost of inventory	10% of the inventory value

   (Madras, 1987)

   [Ans: EOQ = 200 units, number of orders per annum = 8]

10. Find EOQ when the annual consumption is 6,000 kg. Ordering cost is Rs 120 per order. Price per kilogram is Rs 20 and the carrying cost is 20%. Also ascertain the frequency of placing orders.

     

    (Bharathidasan, B.Com.)

    [Ans: EOQ = 600 kg, number of orders = 10 per annum, frequency =
    one order per 36.5 or 37 days, or one order per 1.2 months]

    10a. Find EOQ, given the following:

    Monthly usage	150 units
    Buying cost	Rs 2 per order
    Cost per unit	Re 0.32 paise
    Storage cost	25% per annum

    (Osmania, B.Com.)

    [Ans: EOQ = 300 units]

11. Two components X and Y are used as follows:

    Normal usage	50 units each per week
    Minimum usage		25 units each per week
    Maximum usage	75 units each per week
    Reorder quantity	X—400 units, Y—600 units
    Reorder period		X—4–6 weeks, Y—2–4 weeks

    Calculate for each component (a) reorder level, (b) minimum level, (c) maximum level and (d) average level.

    (M.Com., Calicut)

    [Ans: (a) reorder level X = 450 units, Y = 300 units; (b) minimum level X = 200 units,
    Y = 150 units; (c) maximum level X = 750 units, Y = 850 units;
    (d) average stock X = 400 units, Y = 450 units]

12. Two components X and Y are used as follows:

    Normal usage	600 units each per week
    Maximum usage	900 units each per week
    Minimum usage		300 units each per week
    Reorder quantity	X—4,800 units, Y—7,200 units
    Reorder period		X—4–6 weeks, Y—2–4 weeks

    Calculate for each component (a) reorder level, (b) minimum level, (c) maximum level and (d) average stock level.

    (B.Com., Andhra)

    

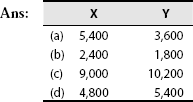
13. Two components A and B are consumed as follows:

    Normal usage	100 units per week each
    Minimum usage	50 units per week each
    Maximum usage	150 units per week each
    Reorder quantity	A—400 units, B—600 units
    Reorder period	A—6–8 weeks, B—3–5 weeks

    Calculate for each component (a) minimum level, (b) maximum level and (c) average stock level.

     

    (B. Com., Madurai)

    

14. From the following particulars, calculate (a) reorder level, (b) minimum level and (c) maximum level:

    Normal usage	100 units per day
    Minimum usage		60 units per day
    Maximum usage	130 units per day
    EOQ	5,000 units
    Reorder period	25–30 days

    (B. Com., Kerala)

    [Ans: (a) 3,900 units; (b) 1,150 units; (c) 7,400 units]

15. Calculate (a) EOQ, (b) maximum level, (c) minimum level and (d) reordering level from the following data:

    Reorder period		4–6 weeks
    Maximum consumption		100 units per week
    Minimum consumption	50 units per week
    Normal consumption	75 units per week
    Annual consumption	36,000 units
    Cost per unit	Re 1
    Ordering cost	Rs 25

    Inventory carrying cost is 20% of unit value.

     

    [Ans: (a) 3,000 units; (b) 3,400 units; (c) 225 units; (d) 600 units]

    15a. In a manufacturing firm, a material is used as follows:

    Maximum consumption		12,000 units per week
    Minimum consumption		4,000 units per week
    Normal consumption	8,000 units per week
    Reorder quantity	48,000 units
    Minimum	4 weeks
    Maximum	6 weeks

    Calculate (a) reorder level, (b) minimum level, (c) maximum level and (d) average stock level.

     

    (B. Com., Bangalore)

    [Ans: (a) 72,000; (b) 32,000; (c) 1,04,000; (d) 56,000 or 38,000]

16. The following figures are taken from the records of a company for the year 2001. The valuation of inventory is Rs 2 per kilogram:

     

    

     

    Calculate the material turnover ratio of the two materials X and Y and express in number of days the average inventory held. Also, determine which of the two materials is fast moving.

     

    

    X is fast moving.