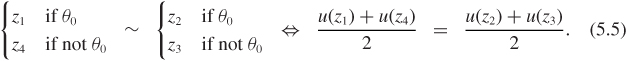5
Ramsey and Savage

In the previous two chapters we have studied the von Neumann–Morgenstern expected utility theory (NM theory) where all uncertainties are represented by objective probabilities. Our ultimate goal, however, is to understand problems where decision makers have to deal with both the utility of outcomes, as in the NM theory, and the probabilities of unknown states of the world, as in de Finetti’s coherence theory.

For an example, suppose your roommate is to decide between two bets: bet (i) gives $5 if Duke and not UNC wins this year’s NCAA final, and $0 otherwise; bet (ii) gives $10 if a fair die that I toss comes up 3 or greater. The NM theory is not rich enough to help in deciding which lottery to choose. If we agree that the die is fair, lottery (ii) can be thought of as a NM lottery, but what about lottery (i)? Say your roommate prefers lottery (ii) to lottery (i). Is it because of the rewards or because of the probabilities of the two events? Your roommate could be almost certain that Duke will win and yet prefer (ii) because he or she desperately needs the extra $5. Or your roommate could believe that Duke does not have enough of a chance of winning.

Generally, based on agents’ preferences, it is difficult to understand their probability without also considering their utility, and vice versa. “The difficulty is like that of separating two different co-operating forces” (Ramsey 1926, p. 172). However, several axiom systems exist that achieve this. The key is to try to hold utility considerations constant while constructing a probability, and vice versa. For example, you can ask your roommate whether he or she would prefer lottery (i) to (iii), where you win $0 if Duke wins this year’s NCAA championship, and you win $5 otherwise. If your roommate is indifferent then it has to be that he or she considers Duke winning and not winning to be equally likely. You can then use this as though it were a NM lottery in constructing a utility function for different sums of money.

In a fundamental publication titled Truth and probability, written in 1926 and published posthumously in 1931, Frank Plumpton Ramsey developed the first axiom system on preferences that yields an expected utility representation based on unique subjective probabilities and utilities (Ramsey 1926). A full formal development of Ramsey’s outline had to wait until the book The foundations of statistics, by Leonard J. Savage, “The most brilliant axiomatic theory of utility ever developed” (Fishburn 1970). After summarizing Ramsey’s approach, in this chapter we give a very brief overview of the first five chapters of Savage’s book. As his book’s title implies, Savage set out to lay the foundation to statistics as a whole, not just to decision making under uncertainty. As he points out in the 1971 preface to the second edition of his book:

We will return to this topic in Chapter 7, when discussing the motivation for the minimax approach.

Featured readings:

Ramsey, F. (1926). The Foundations of Mathematics, Routledge & Kegan Paul, London, chapter Truth and Probability, pp. 156–211.

Savage, L. J. (1954). The foundations of statistics, John Wiley & Sons, Inc., New York.

Critical reviews of Savage’s work include Fishburn (1970), Fishburn (1986), Shafer (1986), Lindley (1980), Drèze (1987), and Kreps (1988). A memorial collection of writings also includes biographical materials and transcriptions of several of Savage’s very enjoyable lectures (Savage 1981b).

5.1 Ramsey’s theory

In this section we review Ramsey’s theory, following Muliere & Parmigiani (1993). A more extensive discussion is in Fishburn (1981). Before we present the technical development, it is useful to revisit some of Ramsey’s own presentation. In very few pages, Ramsey not only laid out the game plan for theories that would take decades to unfold and are still at the foundation of our field, but also anticipated many of the key difficulties we still grapple with today:

Ramsey develops his theory for outcomes that are numerically measurable and additive. Outcomes are not monetary nor necessarily numerical, but each outcome is assumed to carry a value. This is a serious restriction and differs significantly from NM theory and, later, Savage, but it makes sense for Ramsey, whose primary goal was to develop a logic of the probable, rather than a general theory of rational behavior. The set of outcomes is Z. As before we consider a subject that has a weak order on outcome values. Outcomes in the same equivalence class with respect to this order are indicated by z₁ ~ z₂, while strict preference is indicated by ≻.

The general strategy of Ramsey is: first, find a neutral proposition with subjective probability of one-half, then use this to determine a real-valued utility of outcomes, and finally, use the constructed utility function to measure subjective probability.

Ramsey considers an agent making choices between options of the form “z₁ if θ is true, z₂ if θ is not true.” We indicate such an option by

The outcome z and the option

belong to the same equivalence class, a property only implicitly assumed by Ramsey, but very important in this context as it represents the equivalent of reflexivity.

In Ramsey’s definition, an ethically neutral proposition is one whose truth or falsity is not “an object of desire to the subject.” More precisely, a proposition θ₀ is ethically neutral if two possible worlds differing only by the truth of θ₀ are equally desirable. Next Ramsey defines an ethically neutral proposition with probability based on a simple symmetry argument: if for every pair of outcomes (z₁, z₂),

The existence of one such proposition is postulated as an axiom:

Axiom R1 There is an ethically neutral proposition believed to degree 1/2.

The next axiom states that preferences among outcomes do not depend on which ethically neutral proposition with probability is chosen. There is no loss of generality in taking : the same construction could have been performed with a proposition of arbitrary probability, as long as such probability could be measured based solely on preferences.

Axiom R2 The indifference relation (5.3) still holds if we replace θ₀ with any other ethically neutral event .

Axiom R2a If θ is an ethically neutral proposition with probability , we have that if

then z₁ ≻ z₂ if and only if z₃ ≻ z₄, and z₁ ~ z₂ if and only if z₃ ~ z₄.

Axiom R3 The indifference relation between actions is transitive.

Axiom R4 If

and

then

Axiom R5 For every z₁, z₂, z₃, there exists a unique outcome z such that

Axiom R6 For every pair of outcomes (z₁, z₂), there exists a unique outcome z such that

This is a fundamental assumption: as χ_z ~ z, this implies that there is a unique certainty equivalent to a. We indicate this by z*(a).

Axiom R7 Axiom of continuity: Any progression has a limit (ordinal).

Axiom R8 Axiom of Archimedes.

Ramsey’s original paper provides little explanation regarding the last two axioms, which are reported verbatim here. Their role is to make the space of outcomes rich enough to be one-to-one with the real numbers. Sahlin (1990) suggests that continuity should be the analogue of the standard completeness axiom of real numbers. Then it would read like “every bounded set of outcomes has a least upper bound.” Here the ordering is given by preferences.

We can imagine formalizing the Archimedean axiom as follows: for every z₁ ≻ z₂ ≻ z₃, there exist z and z′ such that

and

Axioms R1–R8 are sufficient to guarantee the existence of a real-valued, one-toone, utility function on outcomes, designated by u, such that

Ramsey did not complete the article before his untimely death at 26, and the posthumously published draft does not include a complete proof. Debreu (1959) and Pfanzagl (1959), among others, designed more formal axioms based on which they obtain results similar to Ramsey’s.

In (5.4), an individual’s preferences are represented by a continuous and strictly monotone utility function u, determined up to a positive affine transformation. Continuity stems from Axioms R2a and R6. In particular, consistent with the principle of expected utility,

Having defined a way of measuring utility, Ramsey can now derive a way of measuring probability for events other than the ethically neutral ones. Paraphrasing closely his original explanation, if the option of z* for certain is indifferent with that of z₁ if θ is true and z₂ if θ is false, we can define the subject’s probability of θ as the ratio of the difference between the utilities of z* and z₂ to that between the utilities of z₁ and z₂, which we must suppose the same for all the z*, z₁, and z₂ that satisfy the indifference condition. This amounts roughly to defining the degree of belief in θ by the odds at which the subject would bet on θ, the bet being conducted in terms of differences of value as defined.

Ramsey also proposed a definition for conditional probabilities of θ₁ given that θ₂ occurred, based on the indifference between the following actions:

Similarly to what we did with called-off bets, the conditional probability is the ratio of the difference between the utilities of z₁ and z₂ to that between the utilities of z₃ and z₄, which we must again suppose the same for any set of z that satisfies the indifference condition above. Interestingly, Ramsey observes:

This comment is an ancestor of the concern we discussed in Section 2.2, about temporal coherence. We will return to this issue in Section 5.2.3.

Finally, he proceeds to prove that the probabilities so derived satisfy what he calls the fundamental laws, that is the Kolmogorov axioms and the standard definition of conditional probability.

5.2 Savage’s theory

5.2.1 Notation and overview

We are now ready to approach Savage’s version of this story. Compared to the formulations we encountered so far, Savage takes a much higher road in terms of the mathematical generality, dealing with continuous variables and general outcomes and parameter spaces. Let Z denote the set of outcomes (or consequences, or rewards) with a generic element z. Savage described an outcome as “a list of answers to all the questions that might be pertinent to the decision situation at hand” (Savage 1981a). As before, Θ is the set of possible states of the world. Its generic element is θ. An act or action is a function a : Θ → Z from states to outcomes. Thus, a(θ) is the consequence of taking action a if the state of the world turns out to be θ. The set of all acts is A. Figure 5.1 illustrates the concept. This is a good place to point out that it is not in general obvious how well the consequences can be separated from the states of the world. This difficulty motivates most of the discussion of Chapter 6 so we will postpone it for now.

Figure 5.1 Two acts for modeling the decision of whether or not to take an umbrella to work.

Before we dive into the axioms, we outline the general plan. It has points in common with Ramsey’s except it can count on the NM theory and maneuvers to construct the probability first, to be able to leverage it in constructing utilities:

1. Use preferences over acts to define a “more probable than” relationship among states of the world (Axioms 1–5).

2. Use this to construct a probability measure on the states of the world (Axioms 1–6).

3. Use the NM theory to get an expected utility representation.

One last reminder: there are no compound acts (a rather artificial, but very powerful construct) and no physical chance mechanisms. All probabilities are subjective and will be derived from preferences, so we will have some hard work to do before we get to familiar places.

We follow the presentation of Kreps (1988), and give the axioms in his same form, though in slightly different order. When possible, we also provide a notation of the name the axiom has in Savage’s book—those are names like P1 and P2 (for postulate). Full details of proofs are given in Savage (1954) and Fishburn (1970).

5.2.2 The sure thing principle

We start, as usual, with a binary preference relation and a set of states that are not so boring to generate complete indifference.

These are Axioms P1 and P5 in Savage.

A cornerstone of Savage’s theory is the sure thing principle:

Implementing this principle requires a few more steps, necessary to define more rigorously what it means to “prefer a₁ to a₂ knowing that the event Θ₀ obtained.” Keep in mind that the deck we are playing with is a set of preferences on acts, and those are functions defined on the whole set of states Θ. To start thinking about conditional preferences, consider the acts shown in Figure 5.2. Acts a₁ and a₂ are different from each other on the set Θ₀, and are the same on its complement . Say we prefer a₁ to a₂. Now look at versus . On Θ₀ this is the same comparison we had before. On and are again equal to each other, though their actual values have changed from the previous comparison. Should we also prefer to ? Axiom S3 says yes: if two acts are equal on a set (in this case ), the preference between them is not allowed to depend on the common value taken in that set.

Figure 5.2 The acts that are being compared in Axiom S3. Curves that are very close to one another and parallel are meant to be on top of each other, and are separated by a small vertical shift only so you can tell them apart.

Axiom S3 Suppose that in A and Θ₀ ⊆ Θ are such that

1. and for all θ in Θ₀; and

2. a₁(θ) = a₂(θ) and for all θ in .

Then a₁ ≻ a₂ if and only if .

This is Axiom P2 in Savage, and resembles the independence axiom NM2, except that here there are no compound acts and the mixing is done by the states of nature.

Axiom S3 makes it possible to define the notion, fundamental to Savage’s theory, of conditional preference. To define preference conditional on Θ₀, we make the two acts equal outside of Θ₀ and then compare them. Because of Axiom S3, it does not matter how they are equal outside of Θ₀.

Definition 5.1 (Conditional preference) We say that a₁ ≻ a₂ given Θ₀ if and only if , where and and .

Figure 5.3 describes schematically this definition. The setting has the flavor of a called-off bet, and it represents a preference stated before knowing whether Θ₀ occurs or not. Problem 5.1 helps you tie this back to the informal definition of the sure thing principle given in Savage’s quote. In particular, within the Savage axiom system, if a ≻ a′ on Θ₀ and a ≻ a′ on , then a ≻ a′.

Figure 5.3 Schematic illustration of conditional preference. Acts and do not necessarily have to be constant on . Again, curves that are very close to one another and parallel are meant to be on top of each other, and are separated by a small vertical shift only so you can tell them apart.

5.2.3 Conditional and a posteriori preferences

In Sections 2.1.4 and 5.1 we discussed the correspondence between conditional probabilities, as derived in terms of called-off bets, and beliefs held after the conditioning event is observed. A similar issue arises here when we consider preferences between actions, given that the outcome of an event is known. This is a critical concern if we want to make a strong connection between axiomatic theories and statistical practice. Pratt et al. (1964) comment that while conditional preferences before and after the conditioning event is observed can reasonably be equated, the two reflect two different behavioral principles. Therefore, they suggest, an additional axiom is required. Restating their axiom in the context of Savage’s theory, it would read like:

Before/after axiom The a posteriori preference a₁ ≻ a₂ given knowledge that Θ₀ has occurred holds if and only if the conditional preference a₁ ≻ a₂ given Θ₀ holds.

Here the conditional preference could be defined according to Definition 5.1. This axiom is not part of Savage’s formal development.

5.2.4 Subjective probability

In this section we are going to focus on extracting a unique probability distribution from preferences. We do this in stages, first defining qualitative probabilities, or “more likely than” statements, and then imposing additional restrictions to derive the quantitative version. Dealing with real-valued Θ makes the analysis somewhat complicated. We are showing the tip of a big iceberg here, but the submerged part is secondary to the main story of our book. Real analysis aficionados will enjoy it, though: Kreps (1988) has an entire chapter on it, and so does DeGroot (1970). Interestingly, DeGroot uses a similar technical development, but assumes utilities and probabilities (as opposed to preferences) as primitives in the theory, thus bypassing entirely the need to axiomatize preferences.

The first definition we need is that of a null state. If asked to compare two acts conditional on a null state, the agent will always be indifferent. Null states will turn out to have a subjective probability of zero.

Definition 5.2 (Null state) Θ₀ ⊆ Θ is called null if a ~ a′ given Θ₀ for all a, a′ in A.

The next two axioms are making sure we can safely hold utility-like considerations constant in teasing probabilities out of preferences. The first, Axiom S4:

Axiom S4 If:

1. Θ₀ is not null; and

2. a(θ) = z₁ and a′(θ) = z₂, for all θ ∊ Θ₀,

then a ≻ a′ given Θ₀ if and only if z₁ ≻ z₂.

This is Axiom P3 in Savage. Figure 5.4 describes schematically this condition.

Next, Axiom S5 goes back to the simple binary comparisons we used in the preface of this chapter to understand your roommate probabilities. Say he or she prefers a₁: $10 if Duke wins the NCAA championship and $0 otherwise to a₂: $10 if UNC wins and $0 otherwise. Should your roommate’s preferences remain the same if you change the $10 to $8 and the $0 to $1? Axiom S5 says yes, and it makes it a lot easier to separate the probabilities from the utilities.

Figure 5.4 Schematic illustration of Axiom S4.

Axiom S5 Suppose that in A, and Θ₀, Θ₁ ⊆ Θ are such that:

1. z₁ ≻ z₂ and ;

2. a₁(θ) = z₁ and and a₁(θ) = z₂ and ;

3. and and and ;

then if and only if .

Figure 5.5 describes schematically this axiom. This is Axiom P4 in Savage.

We are now equipped to figure out, from a given set of preferences between acts, which of two events an agent considers more likely, using precisely the simple comparison considered in Axiom S5.

Definition 5.3 (More likely than) For any two Θ₀, Θ₁ in Θ, we say that Θ₀ is more likely than Θ₁ (denoted by Θ₀ ≻ Θ₁) if for every z₁, z₂ such that z₁ ≻ z₂ and a, a′ defined as

then a ≻ a′.

Figure 5.5 The acts in Axiom S5.

This is really nothing but our earlier Duke/UNC example dressed up in style. For your roommate, a Duke win must be more likely than a UNC win.

If we tease out this type of comparison for enough sets, we can define what is called a qualitative probability. Formally:

Definition 5.4 (Qualitative probability) The binary relation ≻ between sets is a qualitative probability whenever:

1. ≻ is asymmetric and negatively transitive;

2. Θ₀ ≻ ∅ for all Θ₀ (subset of Θ);

3. Θ ≻ ∅; and

4. if Θ₀ ∩ Θ₂ = Θ₁ ∩ Θ₂ = ∅, then Θ₀ ≻ Θ₁ if and only if Θ₀ ∪ Θ₂ ≻ Θ₁ ∪ Θ₂.

As you may expect, we have done enough work to get a qualitative probability out of the preferences:

Theorem 5.1 If S1–S5 hold then the binary relation ≻ on Θ is a qualitative probability.

Qualitative probabilities are big progress, but Savage is aiming for the good old quantitative kind. It turns out that if you have a quantitative probability, and you say that an event Θ₀ is more likely than Θ₁ if Θ₀ has a larger probability than Θ₁, then you define a legitimate qualitative probability. In general, however, the qualitative probabilities will not give you quantitative ones without additional technical conditions that can actually be a bit strong.

One way to get more quantitative is to be able to split up the set Θ into an arbitrarily large number of equivalent subsets. Then the quantitative probability of each of these must be the inverse of this number. De Finetti (1937) took this route for subjective probabilities, for example. Savage steps in this direction somewhat reluctantly:

To follow this thought one more step, we could impose the following sort of condition: given any two sets, you can find a partition fine enough that you can take the less likely of the two sets, and merge it with any element of the partition without altering the fact that it is less likely. More formally:

Definition 5.5 (Finite partition condition) If Θ₀, Θ₁ in Θ are such that Θ₀ ≻ Θ₁, then there exists a finite partition {E₁, ..., E_n} of Θ such that Θ₀ ≻ Θ₁ ∪ E_k, for every k = 1, ..., n.

This would gets us to the finish line as far as the probability part is concerned, because we could prove the following.

Theorem 5.2 The relationship ≻ is a qualitative probability and satisfies the axiom on the existence of a finite partition if and only if there exists a unique probability measure π such that

1. Θ₀ ≻ Θ₁ if and only if π(Θ₀) > π(Θ₁);

2. for all Θ₀ ⊆ Θ and k ∊ [0, 1], there exists Θ₁ ⊆ Θ, such that π(Θ₁) = kπ(Θ₀).

See Kreps (1988) for details.

Savage approaches this slightly differently and embeds the finite partition condition into his Archimedean axiom, so that it is stated directly in terms of preferences—a much more attractive approach from the point of view of foundations than imposing restrictions on the qualitative probabilities directly. The requirement is that you can split up the set Θ in small enough pieces so that your preference will be unaffected by an arbitrary change of consequences within any one of the pieces.

Axiom S6 (Archimedean axiom) For all a₁, a₂ in A such that a₁ ≻ a₂ and z ∊ Z, there exists a finite partition of Θ such that for all Θ₀ in the partition:

1. for θ ∊ Θ₀ and for ; then ; or

2. for θ ∊ Θ₀ and for ; then .

This is P6 in Savage. Two important consequences of this are that there are no consequences that are infinitely better or worse than others (similarly to NM3), and also that the set of states of nature is rich enough that it can be split up into very tiny pieces, as required by the finite partition condition. A discrete space may not satisfy this axiom for all acts.

It can in fact be shown that in the context of this axiom system the Archimedean condition above guarantees that the finite partition condition is met:

Theorem 5.3 If S1–S5 and S6 hold then ≻ satisfies the axiom on the existence of a finite partition of Θ.

It then follows from Theorem 5.2 that the above gives a necessary and sufficient condition for a unique probability representation.

5.2.5 Utility and expected utility

Now that we have a unique π on Θ, and the ability to play with very fine partitions of Θ, we can follow the script of the NM theory to derive utilities and a representation of preferences. To be sure, one more axiom is needed, to require that if you prefer a to having any consequence of a′ for sure, then you prefer a to a′.

Axiom S7 For all Θ₀ ⊆ Θ:

1. If a ≻ a′(θ) given Θ₀ for all θ in Θ₀, then a ≻ a′ given Θ₀.

2. If a′(θ) ≻ a given Θ₀ for all θ in Θ₀, then a′ ≻ a given Θ₀.

This is Axiom P7 in Savage, and does a lot of the work needed to apply the theory to general consequences. Similar conditions, for example, can be used to generalize the NM theory beyond the finite Z we discussed in Chapter 3.

We finally laid out all the conditions for an expected utility representation.

Theorem 5.4 Axioms (S1–S7) are sufficient for the following conclusions:

1. ≻ as defined above is a qualitative probability, and there exists a unique probability measure π on Θ such that Θ₀ ≻ Θ₁ if and only if π(Θ₀) > π(Θ₁).

2. For all Θ₀ ⊆ Θ and k ∊ [0, 1], there exists a subset Θ₁ of Θ₀ such that π(Θ₁) = kπ(Θ₀).

3. For π given above, there is a bounded utility function u : Z → ℜ such that a ≻ a′ if and only if

   

   Moreover, this u is unique up to a positive affine transformation.

When the space of consequences is denumerable, we can rewrite the expected utility of action a in a form that better highlights the parallel with the NM theory. Defining

p(z) = π{θ : a(θ) = z}

we have the familiar

except now p reflects a subjective opinion and not a controlled chance mechanism.

Wakker (1993) discusses generalizations of this theorem to unbounded utility.

5.3 Allais revisited

In Section 3.5 we discussed Allais’ claim that sober decision makers can still violate the NM2 axiom of independence. The same example can be couched in terms of Savage’s theory. Imagine that the lotteries of Figure 3.3 are based on drawing at random an integer number θ between 1 and 100. Then for any decision maker that trusts the drawing mechanism to be random π(θ) = 0.01. The lotteries can then be rewritten as shown in Table 5.1.

This representation is now close to Savage’s sure thing principle (Axiom S3). If a number between 12 and 100 is drawn, it will not matter, in either situation, which lottery is chosen. So the comparisons should be based on what happens if a number between 1 and 11 is drawn. And then the comparison is the same in both situations. Savage thought that this conclusion “has a claim to universality, or objectivity” (Savage 1954). Allais obviously would disagree. If you want to know more about this debate, which is still going on now, good references are G¨ardenfors and Sahlin (1988) Kahneman et al. (1982), Seidenfeld (1988), Kahneman and Tversky (1979), Tversky (1974), Fishburn (1982), and Kreps (1988).

While this example is generally understood to be a challenge to the sure thing principle, we would like to suggest that there also is a connection with the “before/after axiom” of Section 5.2.3. This axiom requires that the preferences for two acts, after one learns that θ is for sure 11 or less, should be the same as those expressed if the two actions are made equal in all cases where θ is 12 or more—irrespective of what the common outcome is. There are individuals who, like Allais, are reversing the preferences depending on the outcome offered if θ is 12 or more. But we suppose that the same individuals would agree that a ≻ a′ if and only if b ≻ b′ once it is known for sure that θ is 11 or less. The two comparisons are now identical for sure! So it seems that agents such as those described by Allais would also be likely to violate the “before/after axiom.”

Table 5.1 Representation of the lotteries of the Allais paradox in terms of Savage’s theory. Rewards are in units of $100 000. Probabilities of the three columns are respectively 0.01, 0.10, and 0.89.

	θ = 1	2 ≤ θ ≤ 11	12 ≤ θ ≤ 100
a	5	5	5
a′	0	25	5
b	5	5	0
b′	0	25	0

5.4 Ellsberg paradox

The next example is due to Ellsberg. Suppose that we have an urn with 300 balls in it: 100 of these balls are red (R) and the rest are either blue (B) or yellow (Y). As in the Allais example, we will consider two pairs of actions and we will have to choose between lotteries a and a′, and then between lotteries b and b′. Lotteries are depicted in Table 5.2.

Suppose a decision maker expresses a preference for a over a′. In action a the probability of winning is 1/3. We may conclude that the decision maker considers blue less likely than yellow, and therefore believes to have a higher chance of winning the prize in a. In fact, this is only slightly more complicated than the sort of comparison that is used in Savage’s theory to construct the qualitative probabilities.

What Ellsberg observed is that this is not necessarily the case. Many of the same decision makers also prefer b′ to b. In b′ the probability of winning the prize is 2/3. If one thought that blue is less likely than yellow, it would follow that the probability of winning the prize in lottery b is more than 2/3, and thus that b is to be preferred to b′.

In fact, the observed preferences violate Axiom S3 in Savage’s theory. The actions are such that

a(R) = b(R)	and	a′(R) = b′(R)
a(B) = b(B)	and	a′(B) = b′(B)
a(Y) = a′(Y)	and	b(Y) = b′(Y).

So we are again in the realm of Axiom S3, and it should be that if a ≻ a′, then b ≻ b′.

Why is there a reversal of preferences in Ellsberg’s experience? The answer seems to be that many decision makers prefer gambles where the odds are known to gambles where the odds are, in Ellsberg’s words, ambiguous. Gärdenfors and Sahlin comment:

Table 5.2 Actions available in the Ellsberg paradox. In Savage’s notation, we have Θ = {R, B, Y} and Z = {0, 1000}. There are 300 balls in the urn and 100 are red (R), so most decision makers would agree that π(R) = 1/3 while π(B) and π(Y) need to be derived from preferences.

	R	B	Y
a	1000	0	0
a′	0	1000	0
b	1000	0	1000
b′	0	1000	1000

Ellsberg himself affirms that the apparently contradictory behavior presented in the previous example is not random at all:

More readings on the Ellsberg paradox are in Fishburn (1983) and Levi (1985). See also Problem 5.4.

5.5 Exercises

Problem 5.1 Savage’s “informal” definition of the sure thing principle, from the quote in Section 5.2.2 is: If the person would not prefer a₁ to a₂ either knowing that the event Θ₀ obtained, or knowing that the event , then he does not prefer a₁ to a₂. Using Definition 5.1 for conditional preference, and using Savage’s axioms directly (and not the representation theorem), show that Savage’s axioms imply the informal sure thing principle above; that is, show that the following is true: if a ≻ a′ on Θ₀ and a ≻ a′ on , then a ≻ a′. Optional question: what if you replace Θ₀ and with Θ₀ and Θ₁, where Θ₀ and Θ₁ are mutually exclusive? Highly optional question for the hopelessly bored: what if Θ₀ and Θ₁ are not mutually exclusive?

Problem 5.2 Prove Theorem 5.1.

Problem 5.3 One thing we find unconvincing about the Allais paradox, at least as originally stated, is that it refers to a situation that is completely hypothetical for the subject making the decisions. The sums are huge, and subjects never really get anything, or at most they get $10 an hour if the guy who runs the study had a decent grant. But maybe you can think of a real-life situation where you expect that people may violate the axioms in the same way as in the Allais paradox.

We are clearly not looking for proofs here—just a scenario, but one that gets higher marks than Allais’ for realism. If you can add even the faintest hint that real individuals may violate expected utility, you will have a home run. There is a huge bibliography on this, so one fair way to solve this problem is to become an expert in the field, although that is not quite the spirit of this exercise.

Problem 5.4 (DeGroot 1970) Consider two boxes, each of which contains both red balls and green balls. It is known that one-half of the balls in box 1 are red and the other half are green. In box 2, the proportion θ of red balls is not known with certainty, but this proportion has a probability distribution over the interval 0 ≤ θ ≤ 1.

(a) Suppose that a person is to select a ball at random from either box 1 or box 2. If that ball is red, the person wins $1; if it is green the person wins nothing. Show that under any utility function which is an increasing function of monetary gain, the person should prefer selecting the ball from box 1 if, and only if, E_θ[θ] < 1/2.

(b) Suppose that a person can select n balls (n ≥ 2) at random from either of the boxes, but that all n balls must be selected from the same box; suppose that each selected ball will be put back in the box before the next ball is selected; and suppose that the person will receive $1 for each red ball selected and nothing for each green ball. Also, suppose that the person’s utility function u of monetary gain is strictly concave over the interval [0, n], and suppose that E_θ[θ] = 1/2. Show that the person should prefer to select the balls from box 1.

Hint: Show that, if the balls are selected from box 2, then for any given value of θ, E_θ[u] is a concave function of π on the interval 0 ≤ θ ≤ 1. This can be done by showing that

Then apply Jensen’s inequality to g(θ) = E_θ[u].

(c) Switch red and green and try (b) again.

Note: The function f is concave if f(αx+(1 – α)y) ≥ αf(x) + (1 – α)f(y). Pictorially, concave functions are ∩-shaped. Continuously differentiable concave functions have second derivatives ≤ 0. Jensen’s inequality states that if g is a convex (concave) function, and θ is a random variable, then E[g(θ)] ≥ (≤) g(E[θ]).

Comment: This is a very nice example, and is related to the Ellsberg paradox. The idea there is that in the situation of case (a), according to the expected utility principle, if E_θ[θ] = 1/2 you should be indifferent between the two boxes. But empirically, most people still prefer box 1. What do you think?

Problem 5.5 Suppose you are to choose among two experiments A and B. You are interested in estimating a parameter based on squared error loss using the data from the experiment. Therefore you want to choose the experiment that minimizes the posterior variance of the parameter. If the posterior variance depends on the data that you will collect, expected utility theory recommends that you take an expectation. Suppose experiment A has an expected posterior variance of 1 and B of 1.03, so you prefer A. But what if you looked at the whole distribution of variances, for different possible data sets, and discovered that the variances you get from A range from 0.5 to 94, while the variances you get from B range from 1 to 1.06? (The distribution for experiment A would have to be quite skewed, but that is not unusual.)

Is A really a good choice? Maybe not (if 94 is not big enough, make it 94 000). But then, what is it that went wrong with our choice criterion? Is there a fault in the expected utility paradigm, or did we simply misspecify the losses and leave out an aspect of the problem that we really cared about? Write a few paragraphs explaining what you would do, why, and whether there may be a connection between this example and any of the so-called paradoxes we discussed in this chapter.