6
State independence

Savage’s theory provides an axiomatization that yields unique probabilities and utilities, and provides a foundation for Bayesian decision theory. A key element in this enterprise is the definition of constant outcomes: that is, outcomes that have the same value to the decision maker irrespective of the states of the world. Go back to the Samarkand story of Chapter 4: you are about to ship home a valuable rug you just bought for $9000. At which price would you be indifferent between buying a shipping insurance for the full value of the rug, or taking the risk? Compared to where we were in Chapter 4, we can now answer this question with or without an externally given probability for the rug to be lost. Implicitly, however, all the approaches we have available so far assume that the only relevant state of the world for this decision is whether the rug will be lost. For example, we assume we can consider the value of the sum of money paid for the rug, or the value of the sum necessary to buy insurance, as fixed quantities that do not change with the state of the world. But what if the value of the rug to us depended on how much we can resell it for in New York? Or what if we had to pay for the insurance in the currency of Uzbekistan? Both of these considerations may introduce additional elements of uncertainty that make it hard to know the utility of the relevant outcomes without specifying the states of a “bigger world” that includes the exchange rates and the sale of the rug in addition to the shipment outcome. Our solutions only apply to the “small world” whose only states are whether the rug will be lost or not. They are good to the extent that the small world is a good approximation of bigger worlds. Savage (1954, Sec. 5.5) thought extensively about this issue and included in his book a very insightful section, pertinently called “Small worlds.” Elsewhere, he comments:

To elaborate on this point, in this chapter we move away from Savage’s theory and consider another formulation of subjective expected utility theory, developed by Anscombe and Aumann (1963). Though this theory is somewhat less general than Savage’s, here too we have both personal utilities on outcomes and personal probabilities on unknown states of the world. A real nugget in this theory is the clear answer given to the question of independence of utilities and states of the world. We outline this theory in full, and present an example, due to Schervish et al. (1990), that illustrates the difficulties in the definition of small worlds.

Featured articles:

Anscombe, F. J. & Aumann, R. J. (1963). A definition of subjective probability, Annals of Mathematical Statistics 34: 199–205.

Useful background readings are Kreps (1988) and Fishburn (1970).

6.1 Horse lotteries

We start by taking a finite set Θ to be the set of all possible states of the world. This will simplify the mathematics and help us home in to the issue of state independence more cleanly. For simplicity of notation we will label states with integers, so that Θ = {1, 2, ..., k}. Also, Z will be the set of prizes or rewards. We will assume that Z is finite, which will enable us to use results from the NM theory. The twist in this theory comes with the definition of acts. We start with simple acts:

Definition 6.1 (Simple act) A simple act is a function a : Θ → Z.

So far so good: these are defined as in Savage. Although we are primarily interested in simple acts, we are going to build the theory in terms of more complicated things called horse lotteries. The reason is that in this way we can exploit the machinery of the NM theory to do most of the work in the representation theorems. Let us suppose that we have a randomization device that lets us define objective lotteries like in the NM theory. Let P be the set of probability functions on Z. Anscombe and Aumann (1963) consider acts to be any function from states of the world to one of these probability distributions. They termed these acts “horse lotteries” to suggest that you may get one of k von Neumann and Morgenstern lotteries depending on which horse (θ) wins a race. Formally

Definition 6.2 (Act, or horse lottery) An act is a function a : Θ → P.

Then every a ∊ A can be written as a list of functions:

a = (a(1), a(2), ..., a(k))

and a(θ) ∊ P, θ = 1, ..., k. We also use the notation a(θ, z) to denote the probability that lottery a(θ) assigns to outcome z.

This leads to a very clean system of axioms and proofs but it is a little bit artificial and it requires the notion of an objective randomization. In this regard, Anscombe and Aumann write:

The theory, as in NM theory, will require compound acts. These are defined as earlier, state by state. Formally:

Definition 6.3 (Compound acts) For a and a′ from A and for α ∊ [0, 1], define the act a″ = αa + (1 – α)a′ by

Figure 6.1 illustrates this notation. In the figure, Θ = {1, 2} and Z = {10, 15, 20, 25, 30}. So, a(1) = (0.5, 0.3, 0.2, 0.0, 0.0), while a′(2) = (0.0, 0.0, 0.6, 0.0, 0.4). If we define a compound act of the form a″ = 0.6a + 0.4a′, we have a″(1) = (0.3, 0.18, 0.32, 0.2, 0.0) and a″(2) = (0.0, 0.0, 0.84, 0.0, 0.16).

Figure 6.1 Two Anscombe–Aumann actions a and a′ and their compound action with α = 0.6. Here 1 and 2 are the two possible states of the world.

6.2 State-dependent utilities

Now we are able to introduce a set of axioms with respect to preferences (that is, ≻) among elements of A.

Axiom AA1 ≻ on A is a preference relation.

Axiom AA2 If a ≻ a′ and α ∊ (0, 1], then

αa + (1 – α)a″ ≻ αa′ + (1 – α)a″

for every a″ ∊ A.

Axiom AA3 If a ≻ a′ ≻ a″, then ∃ α, β ∊ (0, 1) such that

αa + (1 – α)a″ ≻ a′ ≻ βa + (1 – β)a″.

These axioms are the same as NM1, NM2, and NM3 except that they apply to the more complicated acts that we are considering here.

Based on results from the NM representation theorem, there is a function f : A → ℜ that represents ≻ and satisfies

f(αa + (1 – α)a′) = αf(a) + (1 – α)f (a′).

Using this fact and a little more work (Kreps 1988), one can establish the following result.

Theorem 6.1 Axioms AA1, AA2, and AA3 are necessary and sufficient for the existence of real-valued u₁, ..., u_k, such that

Also, if is another collection of functions satisfying such a condition, then ∃ α > 0 and β_θ, θ = 1, ..., k, such that .

This theorem is great progress, but we are still far from the standard expected utility representation. The reason is that the functions u depend on both θ and z. These are usually called state-dependent utilities (you have a different utility function in every state of the world) and they are a mix of what we usually call utility (the state-independent ones) and what we call probability. Specifically, if we allow utilities to differ across states, the uniqueness of personal probability no longer holds, and there are multiple probability distributions that satisfy the representation of Theorem 6.1. For example, the representation of Theorem 6.1 can be interpreted to mean that ku_θ(z) is the (state-dependent) utility and π(θ) = 1/k are the personal probabilities. Alternatively, for any other probability distribution π* such that π*(θ) > 0 for every state, we can define

and still conclude that a ≻ a′ if and only if

We can therefore represent the given preferences with multiple combinations of probabilities and state-dependent utilities.

6.3 State-independent utilities

The additional condition that is needed to disentangle the probability from the utility is state independence. Specifically, we need one more definition and two more axioms. A state θ is called null if we no longer care about the outcome of the lottery once θ has occurred. This translates into the condition that we are indifferent between any two acts that differ only in what happens if θ occurs. Formally we have:

Definition 6.4 (Null state) The state θ is said to be null if a ~ a′ for all pairs a and a′ such that a(θ′) = a′(θ′) for all θ′ ≠ θ.

Here are the two new axioms. AA4 is just a structural condition to avoid wasting time with really boring problems where one is indifferent to everything. AA5 is a more serious weapon.

Axiom AA4 There exist a and a′ in A such that a′ ≻ a.

Axiom AA5 Take any a ∊ A and any two probability distributions p and q on Z. If

(a(1), ..., a(θ – 1), p, a(θ + 1), ..., a(k)) ≻ (a(1), ..., a(θ – 1), q, a(θ + 1), ..., a(k))

for some state θ, then for all non-null θ′

(a(1), ..., a(θ′ – 1), p, a(θ′ + 1), ..., a(k)) ≻ (a(1), ..., a(θ′ – 1), q, a(θ′ + 1), ..., a(k)).

AA5 is a monotonicity axiom which asks us to consider two comparisons: in the first, the two actions are identical except that in state θ one has lottery p and the other q. In the second, the two actions are again identical, except that now it is in state θ′ that one has lottery p and the other q. Suppose that one prefers the action with lottery p in the first comparison. The axiom requires that the preference will hold in the second comparison as well. So the preference for p over q is independent of the state. So Axiom AA5 says that preferences should be state independent. Along with AA1–AA4, this condition will provide a representation theorem, discussed in the next section, with unique probabilities and unique utilities up to an affine transformation.

Before we move to the details of this representation, consider this example, reported by Schervish et al. (1990), that shows what could go wrong with AA5. Suppose an agent, who expresses preferences according to Anscombe–Aumann’s axioms and has linear utility for money (that is, u(cz) = cu(z)), is offered to choose among three simple acts a₁, a₂, a₃ whose payoffs are described in Table 6.1 depending on the states of nature θ₁, θ₂, θ₃. Assuming that the agent has state-independent utility, the expected utility of lottery a_i is u(1)π(θ_i), i = 1, 2, 3. Furthermore, if all three horse lotteries are equivalent for the agent, then it must be that he or she considers the states to be equally likely, that is π(θ_i) = 1/3, i = 1, 2, 3.

Table 6.1 Payoffs for six horse lotteries in the dollar/yen example.

	θ1	θ2	θ3
a1	$1	0	0
a2	0	$1	0
a3	0	0	$1
a4	¥100	0	0
a5	0	¥125	0
a6	0	0	¥150

Now imagine that the agent is also indifferent among lotteries a₄, a₅, a₆ of Table 6.1. Again assuming state-independent linear utility for yen payoffs and assuming that for the agent the lotteries are equivalent, we conclude that π*(θ₁)u(100) = π*(θ₂)u(125) = π*(θ₃)u(150), or π(θ₁) = 1.25π(θ₂) = 1.5π(θ₃) which implies π*(θ₁) = 0.4054, π*(θ₂) = 0.3243, and π*(θ₃) = 0.2703.

So this is in seeming contradiction with the indifference among a₁, a₂, a₃. However, the agent is not necessarily inconsistent, but may simply not be willing to follow axiom AA5. For example, the states could represent exchange rates between dollars and yen (θ₁ = {1 dollar is worth 100 yen}, θ₂ = {1 dollar is worth 125 yen}, and θ₃ = {1 dollar is worth 150 yen}). Then AA5 would be untenable. The reward set is Z = {$1, ¥100, ¥125, ¥150}. In order to make comparisons among the rewards in Z you must know the state of nature.

You can see that if the agent is (and in this case for a good reason) not ready to endorse AA5, we are left with the question of which is the agent’s “personal” probability? The uniqueness of the probability depends on the choice of what counts as a “constant” of utility—the dollar or the yen. Schervish et al. (1990), who concocted this example, have an extensive discussion of related issues. They also make an interesting comment on the implications of AA5 for statistical decision theory and all the good stuff in Chapter 7:

6.4 Anscombe–Aumann representation theorem

We now are now ready to discuss the Anscombe–Aumann representation theorem and its proof.

Theorem 6.2 Axioms AA1–AA5 are necessary and sufficient for the existence of a nonconstant function u : Z → ℜ and a probability distribution π on Θ such that

Moreover, the probability distribution π is unique, and u is unique up to a positive linear transformation.

This sounds like magic. Where did the probability come from? The proof sheds some light on this. Look out for a revealing point when personal probabilities materialize from the weights in the affine transformations that define the class of solutions to the NM theorem. Our proof follows Kreps (1988).

Proof: The proof in the ⇒ direction is the most interesting. It starts by observing that axioms AA1–AA3 imply a representation as given by Theorem 6.1. Axiom AA4 implies that there is at least one nonnull state, say θ₀. For any two probability distributions p and q on Z, any nonnull state θ and an arbitrary a, we have, that

if and only if

(a(1), ..., a(θ – 1), p, a(θ + 1), ..., a(k)) ≻ (a(1), ..., a(θ – 1), q, a(θ + 1), ..., a(k))

if and only if (by application of Axiom AA5)

(a(1), ..., a(θ₀ – 1), p, a(θ₀ + 1), ..., a(k)) ≻ (a(1), ..., a(θ₀ – 1), q, a(θ₀ + 1), ..., a(k))

if and only if (by the representation in Theorem 6.1)

For simple lotteries, the result on uniqueness in NM theory guarantees that there are constants α_θ > 0 and β_θ such that

α_θu_θ0(.) + β_θ = u_θ(.).

In particular, for null states, α_θ = 0 (because a state θ is null if and only if u_θ is constant). We can define u(z) = u_θ0(z) (and α_θ0 = 1, β_θ0 = 0) which, along with the representation obtained with Theorem 6.1, implies

or, equivalently,

Subtracting the sum of β_θ and dividing the remaining elements on both sides of the inequality by the positive quantity ∑_θ′ α_θ′ completes the proof if we take π(θ) = α_θ/∑_θ′ α_θ′.

The proof of the uniqueness part of the theorem is left as an exercise. The proof that axioms AA1–AA5 are necessary for the representation in Theorem 6.2 is a worked exercise.

Anscombe–Aumann’s representation theorem assumes that the set of possible states of the world Θ is finite. An extension of this representation theorem to arbitrary Θ is provided by Fishburn (1970).

6.5 Exercises

Problem 6.1 (Schervish 1995, problem 31, p. 212) Suppose that there are k ≥ 2 horses in a race and that a gambler believes that π_i is the probability that horse i will win (). Suppose that the gambler has decided to wager an amount a to be divided among these k horses. If he or she wagers a_i on horse i and that horse wins, the utility of the gambler is log(c_ia_i), where c₁, ..., c_k are known positive numbers. Find values a₁, ..., a_k that maximize the expected utility.

Problem 6.2 Prove the uniqueness of π and u in Theorem 6.2.

Problem 6.3 Prove that if there is a function u : Z → ℜ, and a probability distribution π on Θ such that

then ≻ satisfies axioms AA1–AA3 and AA5, assuming AA4.

Solution

We do this one axiom at a time.

Axiom AA1 ≻ on A is a preference relation.

We know that ≻ is a preference relation if ∀ a, a ∊ A, (i) a ≻ a′, a ≻ a′, or a ~ a′, and (ii) a ≻ a′ and a′ ≻ a″, then a ≻ a″. We are going to call U, U′, and so on the expected utilities associated with actions a, a′, and so on. For example,

1. Since the U are real numbers, U > U′, U′ > U, or U = U′, and from (6.1) a ≻ a′, a′ ≻ a, or a ~ a′.

2. Since a ≻ a′ ⇒ U > U′ and a′ ≻ a″ ⇒ U′ > U″. Consequently, U > U′, by transitivity on ℜ.

Axiom AA2 If a ≻ a′ and α ∊ (0, 1], then

αa + (1 – α)a″ ≻ αa′ + (1 – α)a″, for every a″ ∊ A.

If a ≻ a′ then

for all α ∊ (0, 1]. Therefore,

or

and it follows from (6.1) that

αa + (1 – α)a″ ≻ αa′ + (1 – α)a″.

Axiom AA3 If a ≻ a′ ≻ a″, then ∃ α, β ∊ (0, 1) such that

αa + (1 – α)a″ ≻ a′ ≻ βa + (1 – β)a″.

From (6.1), if a ≻ a′ ≻ a″,

where U, U′, U″ ∊ ℜ. By continuity on ℜ, there exist α, β ∊ (0, 1] such that

βU + (1 – β)U″ < U′ < αU + (1 – α)U″

or

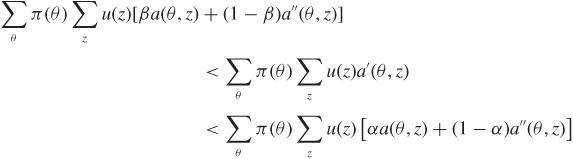
and then αa + (1 – α)a″ ≻ a′ ≻ βa + (1 – β)a″.

Axiom AA5 If a ∊ A and p, q ∊ P are such that

(a(1), ..., a(i – 1), p, a(i + 1), ..., a(k)) ≻ (a(1), ..., a(i – 1), q, a(i + 1), ..., a(k))

for some i, then for all nonnull j

(a(1), ..., a(j – 1), p, a(j + 1), ..., a(k)) ≻ (a(1), ..., a(j – 1), q, a(j + 1), ..., a(k)).

Redefine

a =	(a(1), ..., a(i – 1), p, a(i + 1), ..., a(k))
a′ =	(a(1), ..., a(i – 1), q, a(i + 1), ..., a(k))
a″ =	(a(1), ..., a(j – 1), p, a(j + 1), ..., a(k))
a″ =	(a(1), ..., a(j – 1), q, a(j + 1), ..., a(k))

where i and j are nonnull states. Suppose that

a ≻ a′ but a′″ ≻ a″.

Then from (6.1) a ≻ a′ if and only if

Since a(θ) = a′(θ), θ = 1, 2, ..., i – 1, i + 1, ..., k, a(i) = p, and a′(i) = q we can see that

or p ≻ q, in NM terminology. Analogously,

which is a contradiction, since p must be preferred to q in any nonnull state. Therefore, a″ ≻ a′″.

Problem 6.4 (Kreps 1988, problem 5, p. 112) What happens to this theory if the outcome space Z changes with the state? That is, suppose that in state θ the possible outcomes are given by a set Z_θ. How much of the development above can you adapt to this setting? If you know that there are at least two prizes that lie in each of the Z_θ, how much of this chapter’s development can you carry over?

Hint: Spend a finite amount of time on this and then write down your thoughts.