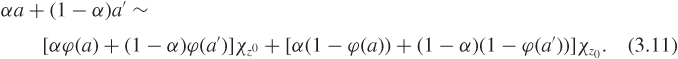3
Utility
Broadly defined, the goal of decision theory is to help choose among actions whose consequences cannot be completely anticipated, typically because they depend on some future or unknown state of the world. Expected utility theory handles this choice by assigning a quantitative utility to each consequence, a probability to each state of the world, and then selecting an action that maximizes the expected value of the resulting utility. This simple and powerful idea has proven to be a widely applicable description of rational behavior.
In this chapter, we begin our exploration of the relationship between acting rationally and ranking actions based on their expected utility. For now, probabilities of unknown states of the world will be fixed. In the chapter about coherence we began to examine the relationship between acting rationally and reasoning about uncertainty using the laws of probability, but utilities were fixed and relegated to the background. So, in this chapter, we will take a complementary perspective.
The pivotal contribution to this chapter is the work of von Neumann and Morgenstern. The earliest version of their theory (here NM theory) is included in the appendix of their book Theory of Games and Economic Behavior. The goal of the book was the construction of a theory of games that would serve as the foundation for studying the economic behavior of individuals. But the theory of utility that they constructed in the process is a formidable contribution in its own right. We will examine it here outside the context of game theory.
Featured articles:
Bernoulli, D. (1954). Exposition of a new theory on the measurement of risk, Econometrica 22: 23–36.
Jensen, N. E. (1967). An introduction to Bernoullian utility theory: I Utility functions, Swedish Journal of Economics 69: 163–183.
The Bernoulli reference is a translation of his 1738 essay, discussing the celebrated St. Petersburg’s paradox. Jensen (1967) presents a classic version of the axiomatic theory of utility originally developed by von Neumann and Morgenstern (1944). The original is a tersely described development, while Jensen’s account crystallized the axioms of the theory in the form that was adopted by the foundational debate that followed. Useful general readings are Kreps (1988) and Fishburn (1970).
3.1 St. Petersburg paradox
The notion that mathematical expectation should guide rational choice under uncertainty was formulated and discussed as early as the seventeenth century. An issue of debate was how to find what would now be called a certainty equivalent: that is, the fixed amount of money that one is willing to trade against an uncertain prospect, as when paying an insurance premium or buying a lottery ticket. Huygens (1657) is one of the early authors who used mathematical expectation to evaluate the fair price of a lottery. In his time, the prevailing thought was that, in modern terminology, a rational individual should value a game of chance based on the expected payoff.
The ideas underlying modern utility theory arose during the Age of Enlightenment, as the evolution of the initial notion that the fair value is the expected value. The birthplace of utility theory is usually considered to be St. Petersburg. In 1738, Daniel Bernoulli, a Swiss mathematician who held a chair at the local Academy of Science, published a very influential paper on decision making (Bernoulli 1738). Bernoulli analyzed the behavior of rational individuals in the face of uncertainty from a Newtonian perspective, viewing science as an operational model of the human mind. His empirical observation, that thoughtful individuals do not necessarily take the financial actions that maximize their expected monetary return, led him to investigate a formal model of individual choices based on the direct quantification of value, and to develop a prototypical utility function for wealth. A major contribution has been to stress that:
no valid measurement of the value of risk can be given without consideration of its utility, that is the utility of whatever gain accrues to the individual. ... To make this clear it is perhaps advisable to consider the following example. Somehow a very poor fellow obtains a lottery ticket that will yield with equal probability either nothing or twenty thousand ducats. Would he not be ill advised to sell this lottery ticket for nine thousand ducats? To me it seems that the answer is in the negative. On the other hand I am inclined to believe that a rich man would be ill advised to refuse to buy the lottery ticket for nine thousand ducats. (Bernoulli 1954, p. 24, an English translation of Bernoulli 1738).
Bernoulli’s development is best known in connection with the notorious St. Petersburg game, a gambling game that works, in Bernoulli’s own words, as follows:
Perhaps I am mistaken, but I believe that I have solved the extraordinary problem which you submitted to M. de Montmort, in your letter of September 9, 1713 (problem 5, page 402). For the sake of simplicity I shall assume that A tosses a coin into the air and B commits himself to give A 1 ducat if, at the first throw, the coin falls with its cross upward; 2 if it falls thus only at the second throw, 4 if at the third throw, 8 if at the fourth throw, etc. (Bernoulli 1954, p. 33)
What is the fair price of this game? The expected payoff is
that is infinitely many ducats. So a ticket that costs 20 ducats up front, and yields the outcome of this game, has a positive expected payoff. But so does a ticket that costs a thousand ducats, or any finite amount. If expectation determines the fair price, no price is too large. Is it rational to be willing to spend an arbitrarily large sum of money to participate in this game? Bernoulli’s view was that it is not. He continued:
The paradox consists in the infinite sum which calculation yields as the equivalent which A must pay to B. This seems absurd since no reasonable man would be willing to pay 20 ducats as equivalent. You ask for an explanation of the discrepancy between mathematical calculation and the vulgar evaluation. I believe that it results from the fact that, in their theory, mathematicians evaluate money in proportion to its quantity while, in practice, people with common sense evaluate money in proportion to the utility they can obtain from it. (Bernoulli 1954, p. 33)
Using this notion of utility, Bernoulli offered an alternative approach: he suggested that one should not act based on the expected reward, but on a different kind of expectation, which he called moral expectation. His starting point was that any gain brings a utility inversely proportional to the whole wealth of the individual. Analytically, Bernoulli’s utility u of a gain Δ in wealth, relative to the current wealth z, can be represented as
where c is some positive constant. For Δ sufficiently small we obtain
Integrating this differential equation gives
where z0 is the constant of integration and can be interpreted here as the wealth necessary to get a utility of zero. The worth of the game, said Bernoulli, is the expected value of the gain in wealth based on (3.1). For example, if the initial wealth is 10 ducats, the worth is
Bernoulli computed the value of the game for various values of the initial wealth. If you own 10 ducats, the game is worth approximately 3 ducats, 6 ducats if you own 1000.
Bernoulli moved rational behavior away from linear payoffs in wealth, but still needed to face the obstacle that the logarithmic utility is unbounded. Savage (1954) comments on an exchange between Gabriel Cramer and Daniel Bernoulli’s uncle Nicholas Bernoulli on this issue:
Daniel Bernoulli’s paper reproduces portions of a letter from Gabriel Cramer to Nicholas Bernoulli, which establishes Cramer’s chronological priority to the idea of utility and most of the other main ideas of Bernoulli’s paper. ... Cramer pointed out in his aforementioned letter, the logarithm has a serious disadvantage; for, if the logarithm were the utility of wealth, the St. Petersburg paradox could be amended to produce a random act with an infinite expected utility (i.e., an infinite expected logarithm of income) that, again, no one would really prefer to the status quo. ... Cramer therefore concluded, and I think rightly, that the utility of cash must be bounded, at least from above. (Savage 1954, pp. 91–95)
Bernoulli acknowledged this restriction and commented:
The mathematical expectation is rendered infinite by the enormous amount which I can win if the coin does not fall with its cross upward until rather late, perhaps at the hundredth or thousandth throw. Now, as a matter of fact, if I reason as a sensible man, this sum is worth no more to me, causes me no more pleasure and influences me no more to accept the game than does a sum amounting only ten or twenty million ducats. Let us suppose, therefore, that any amount above 10 millions, or (for the sake of simplicity) above 224 = 166, 777, 216 ducats be deemed by me equal in value to 224 ducats or, better yet, that I can never win more than that amount, no matter how long it takes before the coin falls with its cross upward. In this case, my expectation is
Thus, my moral expectation is reduced in value to 13 ducats and the equivalent to be paid for it is similarly reduced – a result which seems much more reasonable than does rendering it infinite. (Bernoulli 1954, p. 34)
We will return to the issue of bounded utility when discussing Savage’s theory. In the rest of this chapter we will focus on problems with a finite number of outcomes, and we will not worry about unbounded utilities. For the purposes of our discussion the most important points in Bernoulli’s contribution are: (a) the distinction between the outcome ensuing from an action (in this case the number of ducats) and its value; and (b) the notion that rational behavior may be explained and possibly better guided by quantifying this value. A nice historical account of Bernoulli’s work, including related work from Laplace to Allais, is given by Jorland (1987). For additional comments see also Savage (1954, Sec. 5.6), Berger (1985) and French (1988).
3.2 Expected utility theory and the theory of means
3.2.1 Utility and means
The expected utility score attached to an action can be considered as a real-valued summary of the worthiness of the outcomes that may result from it. In this sense it is a type of mean. From this point of view, expected utility theory is close to theories concerned with the most appropriate way of computing a mean. This similarity suggests that, before delving into the details of utility theory, it may be interesting to explore some of the historical contributions to the theory of means. The discussion in this section in based on Muliere and Parmigiani (1993), who expand on this theme.
As we have seen while discussing Bernoulli, the notion that mathematical expectation should guide rational choice under uncertainty was formulated and discussed as early as the seventeenth century. After Bernoulli, the debate on moral expectation was important throughout the eighteenth century. Laplace dedicated to it an entire chapter of his celebrated treatise on probability (Laplace 1812). Interestingly, Laplace emphasized that the appropriateness of moral expectation relies on individual preferences for relative rather than absolute gains:
[With D. Bernoulli], the concept of moral expectation was no longer a substitute but a complement to the concept of mathematical expectation, their difference stemming from the distinction between the absolute and the relative values of goods. The former being independent of, the latter increasing with the needs and desires for these goods. (Laplace 1812, pp. 189–190, translation by Jorland 1987)
It seems fair to say that choosing the appropriate type of expectation of an uncertain monetary payoff was seen by Laplace as the core of what is today identified as rational decision making.
3.2.2 Associative means
After a long hiatus, this trend reemerged in the late 1920s and the 1930s in several parts of the scientific community, including mathematics (functional equations, inequalities), actuarial sciences, statistics, economics, philosophy, and probability. Not coincidentally, this is also the period when both subjective and axiomatic probability theories were born. Bonferroni proposed a unifying formula for the calculation of a variety of different means from diverse fields of application. He wrote:
The most important means used in mathematical and statistical applications consist of determining the number 
that relative to the quantities z1, ..., zn with weights w1, ..., wn, is in the following relation with respect to a function ψ:
I will take z1, ..., zn to be distinct and the weights to be positive. (Bonferroni 1924, p. 103; our translation and modified notation for consistency with the remainder of the chapter)
Here ψ is a continuous and strictly monotone function. Various choices of ψ yield commonly used means: ψ(z) = z gives the arithmetic mean, ψ(z) = 1/z, z > 0, the harmonic mean, ψ(z) = zk the power mean (for k ≠ 0 and z in some real interval I where ψ is strictly monotone), ψ(z) = log z, z > 0, the geometric mean, ψ(z) = ez the exponential mean, and so forth.
To illustrate the type of problem behind the development of this formalism, let us consider one of the standard motivating examples from actuarial sciences, one of the earliest fields to be concerned with optimal decision making under uncertainty. Consider the example (Bonferroni 1924) of an insurance company offering life insurance to a group of N individuals of which w1 are of age z1, w2 are of age z2, ..., and wn are of age zn. The company may be interested in determining the mean age of the group so that the probability of complete survival of the group after a number y of years is the same as that of a group of N individuals of equal age . If these individuals share the same survival function Q, and deaths are independent, the mean satisfies the relationship
which is of the form (3.2) with ψ(z) = log Q(z + y) – log Q(z).
Bonferroni’s work stimulated activity on characterizations of (3.2); that is, on finding a set of desirable properties of means that would be satisfied if and only if a mean of the form (3.2) is used. Nagumo (1930) and Kolmogorov (1930), independently, characterized (3.2) (for wi = 1) in terms of these four requirements:
continuity and strict monotonicity of the mean in the zi;
reflexivity (when all the zi are equal to the same value, that value is the mean);
symmetry (that is, invariance to labeling of the zi); and
associativity (invariance of the overall mean to the replacement of a subset of the values with their partial mean).
3.2.3 Functional means
A complementary approach stemmed from the problem-driven nature of Bonferroni’s solution. This approach is usually associated with Chisini (1929), who suggests that one may want to identify a critical aspect of a set of data, and compute the mean so that, while variability is lost, the critical aspect of interest is maintained. For example, when computing the mean of two speeds, he would argue, one can be interested in doing so while keeping fixed the total traveling time, leading to the harmonic mean, or the total fuel consumption, leading to an expression depending, for example, on a deterministic relationship between speed and fuel consumption.
Chisini’s proposal was formally developed and generalized by de Finetti (1931a), who later termed it functional. De Finetti regarded this approach as the appropriate way for a subject to determine the certainty equivalent of a distribution function. In this framework, he reinterpreted the axioms of Nagumo and Kolmogorov as natural requirements for such choice. He also extended the characterization theorem to more general spaces of distribution functions.
In current decision-theoretic terms, determining the certainty equivalent of a distribution of uncertain gains according to (3.2) is formally equivalent to computing an expected utility score where ψ plays the role of the utility function. De Finetti commented on this after the early developments of utility theory (de Finetti 1952). In current terms, his point of view is that the Nagumo–Kolmogorov characterization of means of the form (3.2) amounts to translating the expected utility principle into more basic axioms about the comparison of probability distributions.
It is interesting to compare this later line of thinking to the treatment of subjective probability that de Finetti was developing in the early 1930s (de Finetti 1931b, de Finetti 1937), and that we discussed in Chapter 2. There, subjective probability is derived based on an agent’s fair betting odds for events. Determining the fair betting odds for an event amounts to declaring a fixed price at which the agent is willing to buy or sell a ticket giving a gain of S if the event occurs and a gain of 0 otherwise. Again, the fundamental notion is that of certainty equivalent. However, in the problem of means, the probability distribution is fixed, and the existence of a well-behaved ψ (that can be thought of as a utility) is derived from the axioms. In the foundation of subjective probability, the utility function for money is fixed at the outset (it is actually linear), and the fact that fair betting odds behave like probabilities is derived from the coherence requirement.
3.3 The expected utility principle
We are now ready to formalize the problem of choosing among actions whose consequences are not completely known. We start by defining a set of outcomes (also called consequences, and sometimes rewards), which we call Z, with generic outcome z. Outcomes are potentially complex and detailed descriptions of all the circumstances that may be relevant in the decision problem at hand. Examples of outcomes include schedules of revenues over time, consequences of correctly or incorrectly rejecting a scientific hypothesis, health states following a treatment or an intervention, consequences of marketing a drug, change in the exposure to a toxic agent that may result from a regulatory change, knowledge gained from a study, and so forth. Throughout the chapter we will assume that only finitely many different outcomes need to be considered.
The consequences of an action depend on the unknown state of the world: an action yields a given outcome in Z corresponding to each state of the world θ in some set Θ. We will use this correspondence as the defining feature of an action; that is, an action will be defined as a function a from Θ to Z. The set of all actions will be denoted here by A. A simple action is illustrated in Table 3.1.
In expected utility theory, the basis for choosing among actions is a quantitative evaluation of both the utility of the outcomes and the probability that each outcome will occur. Utilities of consequences are measured by a real-valued function u on Z, while probabilities of states of the world are represented by a probability distribution π on Θ. The weighted average of the utility with respect to the probability is then used as the choice criterion.
Throughout this chapter, the focus is on the utility aspect of the expected utility principle. Probabilities are fixed; they are regarded as the description of a well-understood chance mechanism.
Table 3.1 A simple decision problem with three possible actions, four possible outcomes, expressed as cash flows in pounds, and three possible states of the world. You can revisit it in Problem 3.3.
|
|
States of nature |
||
|
|
θ = 1 |
θ = 2 |
θ = 3 |
|
a1 |
£100 |
£110 |
£120 |
Actions |
a2 |
£90 |
£100 |
£120 |
|
a3 |
£100 |
£110 |
£100 |
An alternative way of describing an action in the NM theory is to think of it as a probability distribution over the set Z of possible outcomes. For example, if action a is taken, the probability of outcome z is
that is the probability of the set of states of the world for which the outcome is z if a is chosen. If Θ is a subset of the real line, say (0, 1), and π a continuous distribution, by varying a(θ) we can generate any distribution over Z, as there are only finitely many elements in it. We could, for example, assume without losing generality that π is uniform, and that the “well-understood chance mechanism” is a random draw from (0, 1). We will, however, maintain the notation based on a generic π, to facilitate comparison with Savage’s theory, discussed in Chapter 5.
In this setting the expected utility principle consists of choosing the action a that maximizes the expected value
of the utility. Equivalently, in terms of the outcome probabilities,
An optimal action a*, sometimes called a Bayes action, is one that maximizes the expected utility, that is
Utility theory deals with the foundations of this quantitative representation of individual choices.
3.4 The von Neumann–Morgenstern representation theorem
3.4.1 Axioms
Von Neumann & Morgenstern (1944) showed how the expected utility principle captured by (3.4) can be derived from conditions on ordinal relationships among all actions. In particular, they provided necessary and sufficient conditions for preferences over a set of actions to be representable by a utility function of the form (3.4). These conditions are often thought of as basic rationality requirements, an interpretation which would equate acting rationally to making choices based on expected utility. We examine them in detail here.
The set of possible outcomes Z has n elements {z1, z2, ..., zn}. As we have seen in Section 3.3, an action a implies a probability distribution over Z, which is also called lottery, or gamble. We will also use the notation pi for p(zi), and p = (p1, ..., pn). For example, if Z = {z1, z2, z3}, the lotteries corresponding to actions a and a′, depicted in Figure 3.1, can be equivalently denoted as p = (1/2, 1/4, 1/4) and p′ = (0, 0, 1).
The space of possible actions A is the set of all functions from Θ to Z. A lottery does not identify uniquely an element of A, but all functions that lead to the same probability distribution can be considered equivalent for the purpose of the NM theory (we will meet an exception in Chapter 6 where we consider state-dependent utilities).
As in Chapter 2, the notation ≺ is used to indicate a binary preference relation on A. The notation a ≺ a′ indicates that action a′ is strictly preferred to action a.
Figure 3.1 Two lotteries associated with a and a′, and the lottery associated with compound action a″ with α = 1/3.
Indifference between two outcomes (neither a ≺ a′ nor a′ ≺ a) is indicated by a ~ a′. The notation a ≾ a′ indicates that a′ is preferred or indifferent to a. The relation ≺ over the action space A is called a preference relation if it satisfies these two properties:
Completeness: for any two a and a′ in A, one and only one of these three relationships must be satisfied:
a ≺ a′, or
a ≻ a′, or
neither of the above.
Transitivity: for any a, a″, and a″ in A, the two relationships a ≾ a′ and a′ ≾ a″ together imply that a ≾ a″.
Completeness says that, in comparing two actions, “I don’t know” is not allowed as an answer. Considering how big A is, this may seem like a completely unreasonable requirement, but the NM theory will not really require the decision maker to actually go through and make all possible pairwise comparisons: it just requires that the decision maker will find the axioms plausible no matter which pairwise comparison is being considered. The “and only one” part of the definition builds in a property sometimes called asymmetry.
Transitivity is a very important assumption, and is likely to break down in problems where outcomes have multiple dimensions. Think of a sport analogue. “Team A is likely to beat team B” is a binary relation between teams. It could be that team A beats team B most of the time, that team B beats team C most of the time, and yet that team C beats team A more often than not. Maybe team C has offensive strategies that are more effective against A than B, or has a player that can erase A’s star player from the game. The point is that teams are complex and multidimensional and this can generate cyclical, or non transitive, binary relations. Transitivity will go a long way towards turning our problem into a one-dimensional one and paving the way for a real-valued utility function.
A critical notion in what follows is that of a compound action. For any two actions a and a′, and for α ∊ [0, 1], a compound action a″ = αa + (1 – α)a′ denotes the action that assigns probability αp(z) + (1 – α)p′(z) to outcome z. For example, in Figure 3.1, a″ = (1/3)a + (2/3)a′ which implies that p″ = (1/6, 1/12, 9/12). The notation αa + (1 – α)a′ is a shorthand for pointwise averaging of the probability distributions implied by actions a and a′, and does not indicate that the outcomes themselves are averaged. In fact, in most cases the summation operator will not be defined on Z.
The axioms of the NM utility theory, in the format given by Jensen (1967) (see also Fishburn 1981, Fishburn 1982, Kreps 1988), are
NM1 ≺ is complete and transitive.
NM2 Independence: for every a, a′, and a″ in A and α ∊ (0, 1], we have
a ≻ a′ implies (1 – α)a″ + αa ≻ (1 – α)a″ + αa′.
NM3 Archimedean: for every a, a′, and a″ in A such that a ≻ a′ ≻ a″ we can find α, β ∊ (0, 1) such that
αa + (1 – α)a″ ≻ a′ ≻ βa + (1 – β)a″.
The independence axiom requires that two composite actions should be compared solely based on components that may be different. In economics this is a controversial axiom from both the normative and the descriptive viewpoints. We will return later on to some of the implications of this axiom and the criticisms it has drawn. An important argument in favor of this axiom as a normative axiom in statistical decision theory is put forth by Seidenfeld (1988), who argues that violating this axiom amounts to a sequential form of incoherence.
The Archimedean axiom requires that, when a is preferred to a′, it is not preferred so strongly that mixing a with a″ cannot lead to a reversal of preference. So a cannot be incommensurably better than a′. Likewise, a″ cannot be incommensurably worse than a′. A simple example of a violation of this axiom is lexicographic preferences: that is, preferences that use some dimensions of the outcomes as a primary way of establishing preference, and use other dimensions only as tie breakers if the previous dimensions are not sufficient to establish a preference. Look at the worked Problem 3.1 for more details.
In spite of the different context and structural assumptions, the axioms of the Nagumo–Kolmogorov characterization and the axioms of von Neumann and Morgenstern offer striking similarities. For example, there is a parallel between the associativity condition (substituting observations with their partial mean has no effect on the global mean) and the independence condition (mixing with the same weight an option to two other options will not change the preferences).
3.4.2 Representation of preferences via expected utility
Axioms NM1, NM2 and NM3 hold if and only if there is a real valued utility function u such that the preferences for the options in A can be represented as in expression (3.4). A given set of preferences identifies a utility function u only up to a linear transformation with positive slope. This result is formalized in the von Neumann–Morgenstern representation theorem below.
Theorem 3.1 Axioms NM1, NM2, and NM3 are true if and only if there exists a function u such that for every pair of actions a and a′
and u is unique up to a positive linear transformation.
An equivalent representation of expression (3.7) is
Understanding the proof of the von Neumann–Morgenstern representation theorem is a bit of a time investment but it is generally worthwhile, as it will help in understanding the implications and the role of the axioms as well as the meaning of utility and its relation to probability. It will also lead us to an intuitive elicitation approach for individual utilities.
To prove the theorem we will start out with a lemma, the proof of which is left as an exercise.
Lemma 1 If the binary relation ≻ satisfies Axioms NM1, NM2, and NM3, then:
If a ≻ a′ then
βa + (1 – β)a′ ≻ αa + (1 – α)a′ if and only if 0 ≤ α < β ≤ 1.
, a ≻ a″ imply that there is a unique α* ∊ [0, 1] such that a′ ~ α*a + (1 – α*)a″.a ~ a′, α ∊ [0, 1] imply that
αa + (1 – α)a″ ~ αa′ + (1 – α)a″, ∀ a″ ∊ A.
Taking this lemma for granted we will proceed to prove the von Neumann–Morgenstern theorem. Parts (a) and (c) of the lemma are not too surprising. The heavyweight is (b). Most of the weight in proving (b) is carried by the Archimedean axiom. If you want to understand more look at Problem 3.6.
We will prove the theorem in the ⇒ direction. The reverse is easier and is left as an exercise. There are two important steps in the proof of the main theorem. First we will show that the preferences can be represented by some real-valued function ϕ; that is, that there is a ϕ such
a ≻ a′ ⇔ ϕ(a) > ϕ(a′).
This means that the problem can be captured by a one-dimensional “score” representing the worthiness of an action. Considering how complicated an action can be, this is no small feat. The second step is to prove that this ϕ must be of the form of an expected utility.
Let us start by defining χz as the action that gives outcome z for every θ. The implied p assigns probability 1 to z (see Figure 3.2).
A fact that we will state without detailed proof is that, if preferences satisfy Axioms NM1, NM2, and NM3, then there exists z0 (worst outcome) and z0 (best outcome) in Z such that
for every a ∊ A. One way to prove this is by induction on the number of outcomes. To get a flavor of the argument, try the case n = 2.
Figure 3.2 The lottery implied by χz2, which gives outcome z2 with certainty.
We are going to rule out the trivial case where the decision maker is indifferent to everything, so that we can assume that z0 and z0 are also such that χz0 ≻ χz0. Lemma 1, part (b) guarantees that there exists a unique α ∊ [0, 1] such that
a ~ αχz0 + (1 – α)χz0.
We define ϕ(a)asthevalueof α that satisfies the condition above. Consider now another action a′ ∊ A. We have
from Lemma 1, part (a) ϕ(a) > ϕ(a′) if and only if
ϕ(a)χz0 + (1 – ϕ(a))χz0 ≻ ϕ(a′)χz0 + (1 – ϕ(a′))χz0,
which in turn holds if and only if
a ≻ a′.
So we have proved that ϕ(.), the weight at which we are indifferent between the given action and a combination of the best and worst with that weight, provides a numerical representation of the preferences.
We now move to proving that ϕ(.) takes the form of an expected utility. Now, from applying Lemma 1, part (c) to the indifference relations (3.9) and (3.10) we get
αa + (1 – α)a′ ~ α[ϕ(a)χz0 + (1 – ϕ(a))χz0] + (1 – α)[ϕ(a′)χz0 + (1 – ϕ(a′))χz0].
We can reorganize this expression and obtain
By definition ϕ(a) is such that
a ~ ϕ(a)χz0 + (1 – ϕ(a))χz0.
Therefore ϕ(αa + (1 – α)a′) is such that
αa + (1 – α)a′ ~ ϕ(αa + (1 – α)a′)χz0 + (1 – ϕ(αa + (1 – α)a′))χz0.
Combining the expression above with (3.11) we can conclude that
ϕ(αa + (1 – α)a′) = αϕ(a) + (1 – α)ϕ(a′),
proving that ϕ(.) is an affine function.
We now define u(z) = ϕ(χz). Again, by definition of ϕ,
χz ~ u(z)χz0 + (1 – u(z))χz0.
Eventually we would like to show that ϕ(a) = ∑z∈Z u(z)p(z), where the p are the probabilities implied by a. We are not far from it. Consider Z = {z1, ..., zn}. The proof is by induction on n.
If Z = {z1} take a = χz1. Then, χz0 and χz0 are equal to χz1 and therefore, ϕ(a) = u(z1)p(z1).
Now assume that the representation holds for actions giving positive mass to Z = {z1, ..., zm−1} only and consider the larger outcome space Z = {z1, ..., zm−1, zm}. Say zm is such that p(zm) > 0; that is, zm is in the support of p. (If p(zm) = 0 we are covered by the previous case.) We define
Here, p′ has support of size (m – 1). We can reexpress the definition above as
p(z) = p(zm)Izm + (1 – p(zm))p′(z),
where I is the indicator function, so that
a ~ p(zm)χzm + (1 – p(zm))a′.
Applying ϕ on both sides we obtain
ϕ(a) = p(zm)ϕ(χzm) + (1 – p(zm))ϕ(a′) = p(zm)u(zm) + (1 – p(zm))ϕ(a′).
We can now apply the induction hypothesis on a′, since the support of p′ is of size (m – 1). Therefore,
Using the definition of p′ it follows that
which completes the proof.
3.5 Allais’ criticism
Because of the centrality of the expected utility paradigm, the von Neumann–Morgenstern axiomatization and its derivatives have been deeply scrutinized and criticized from both descriptive and normative perspectives. Empirically, it is well documented that individuals may willingly violate the independence axiom (Allais 1953, Kreps 1988, Kahneman et al. 1982, Shoemaker 1982). Normative questions have also been raised about the weak ordering assumption (Seidenfeld 1988, Seidenfeld et al. 1995).
In a landmark paper, published in 1953, Maurice Allais proposed an example that challenged both the normative and descriptive validities of expected utility theory. The example is based on comparing the hypothetical decision situations depicted in Figure 3.3. In one situation, the decision maker is asked to choose between lotteries a and a′. In the next, the decision maker is asked to choose between lotteries b and b′. Consider these two choices before you continuing reading. What would you do?
In Savage’s words:
Many people prefer gamble a to gamble a′, because, speaking qualitatively, they do not find the chance of winning a very large fortune in place of receiving a large fortune outright adequate compensation for even a small risk of being left in the status quo. Many of the same people prefer gamble b′ to gamble b; because, speaking qualitatively, the chance of winning is nearly the same in both gambles, so the one with the much larger prize seems preferable. But the intuitively acceptable pair of preferences, gamble a preferred to gamble a′ and gamble b′ to gamble b, is not compatible with the utility concept. (Savage 1954, p. 102, with a change of notation)
Why is it that these preferences are not compatible with the utility concept? The pair of preferences implies that any utility function must satisfy
u(5) > |
0.1u(25) + 0.89u(5) + 0.01u(0) |
0.1u(25) + 0.9u(0) > |
0.11u(5) + 0.89u(0). |
Here arguments are in units of $100 000. You can easily check that one cannot have both inequalities at once. So there is no utility function that is consistent with gamble a being preferred to gamble a′ and gamble b′ to gamble b.
Figure 3.3 The lotteries involved in the so-called Allais paradox. Decision makers often prefer a to a′ and b′ to b—a violation of the independence axiom in the NM theory.
Specifically, which elements of the expected utility theory are being criticized here? Lotteries a and a′ can be viewed as compound lotteries involving another lottery a*, which is depicted in Figure 3.4. In particular,
a = |
0.11a + 0.89a |
a′ = |
0.11a* + 0.89a. |
By the independence axiom (Axiom NM2 in the NM theory) we should have
a ≻ a′ if and only if a ≻ a*.
Observe, on the other hand, that
Figure 3.4 Allais Paradox: Lottery a*.
If we obey the independence axiom, we should also have b ≻ b′. Therefore, preferences for a over a′, and b′ over b, violate the independence axiom.
3.6 Extensions
Expected utility maximization has been a fundamental tool in guiding practical decision making under uncertainty. The excellent publications by Fishburn (1970), Fishburn (1989) and Kreps (1988) provide insight, details, and references. The literature on the extensions of the NM theory is also extensive. Good entry points are Fishburn (1982) and Gärdenfors and Sahlin (1988). A general discussion of problems involved in various extensions can be found in Kreps (1988).
Although in our discussion of the NM theory we used a finite set of outcomes Z, similar results can be obtained when Z is infinite. For example, Fishburn (1970, chapter 10) provides generalization to continuous spaces by requiring additional technical conditions, which effectively allow one to define a utility function that is measurable, along with a new dominance axiom, imposing that if a is preferred to every outcome in a set to which p′ assigns probability 1, then a′ should not be preferred to a, and vice versa. A remaining limitation of the results discussed by Fishburn (1970) is the fact that the utility function is assumed to be bounded. Kreps (1988) observes that the utility function does not need to be bounded, but only such that plus and minus infinity are not possible expected utilities under the considered class of probability distributions. He also suggests an alternative version for the Archimedean Axiom NM3 that, along with the other axioms, provides a generalization of the von Neumann–Morgenstern representation theorem in which the utility is continuous over a real-valued outcome space.
3.7 Exercises
Problem 3.1 (Kreps 1988) Planners in the war room of the state of Freedonia can express the quality of any war strategy against arch-rival Sylvania by a probability distribution on the three outcomes: Freedonia wins; draws; loses (z1, z2, and z3). Rufus T. Firefly, Prime Minister of Freedonia, expresses his preferences over such probability distributions by the lexicographic preferences
a ≻ a′
whenever
where p = (p1, p2, p3) is the lottery associated with action a and 
the lottery associated with action a′.
Which of the three axioms does this binary relation satisfy (if any) and which does it violate?
Solution
NM1 First, let us check whether the preference relation is complete.
If
then a ≻ a′ (by the definition of the binary relation).If
then a′ ≻ a.If
then(iii.1) if
then a ≻ a′,(iii.2) if
then a′ ≻ a,(iii.3) if
then it must also be that 
and the two actions are the same.
Therefore, the binary relation is complete. Let us now check whether it is transitive, by considering actions such that a′ ≻ a and a″ ≻ a′.
Suppose
and 
. Then, clearly, 
and therefore a″ ≻ a.Suppose
, 
, and 
. We have 
and therefore a″ ≻ a.Suppose
, 
, and 
. It follows that 
. Thus, a″ ≻ a.Suppose
, 
, and 
and 
. We now have 
and 
. Therefore, a″ ≻ a.
From (i)–(iv) we can conclude that the binary relation is also transitive. So Axiom NM1 is not violated.
NM2 Take α ∊ (0, 1]:
Suppose a ≻ a′ due to
. For any value of α ∊ (0, 1] we have 
. Thus, αa + (1 – α)a″ ≻ αa′ + (1 – α)a″.Suppose a ≻ a′ because
and 
. For any value of α ∊ (0, 1] we have:(ii.1)
.(ii.2)
.From (ii.1) and (ii.2) we can conclude that αa + (1 – α)a″ ≻ αa′ + (1 – α)a″.
Therefore, from (i) and (ii) we can see that the binary relation satisfies Axiom NM2.
NM3 Consider a, a′, and a″ in A and such that a ≻ a′ ≻ a″.
Suppose that a ≻ a′ ≻ a″ because
.Since
, ∃α, β ∊ (0, 1) such that 
since this is a property of real numbers. So, αa+(1–α)a″ ≻ a′ ≻ βa + (1 – β)a″.Suppose that a ≻ a′ ≻ a″ because
(and 
).Since
, ∀ α, β ∊ (0, 1): 
. Also, 
implies that ∃ α, β ∊ (0, 1) such that 
. Thus, αa + (1 – α)a″ ≻ a′ ≻ βa + (1 – β)a″.Suppose that a ≻ a′ ≻ a″ because of the following conditions:
,
and 
.
We have
. This implies that 
. Therefore, we cannot have a′ ≻ αa + (1 – α)a″.
By (iii) we can observe that Axiom NM3 is violated.
Problem 3.2 (Berger 1985) An investor has 1000$ to invest in speculative stocks. The investor is considering investing a dollars in stock A and (1000 – a) dollars in stock B. An investment in stock A has a 0.6 chance of doubling in value, and a 0.4 chance of being lost. An investment in stock B has a 0.7 chance of doubling in value, and a 0.3 chance of being lost. The investor’s utility function for a change in fortune, z, is u(z) = log(0.0007z + 1) for –1000 ≤ z ≤ 1000.
What is Z (for a fixed a)? (It consists of four elements.)
What is the optimal value of a in terms of expected utility? (Note: This perhaps indicates why most investors opt for a diversified portfolio of stocks.)
Solution
Z = {−1000, 2a – 1000, 1000 – 2a, 1000}.
Based on Table 3.2 we can compute the expected utility, that is
U =
0.12 log(0.3) + 0.18 log(0.0014a + 0.3)
+ 0.28 log(1.7 – 0.0014a) + 0.42 log(1.7).
Now, let us look for the value of a which maximizes the expected utility (that is, the optimum value a*). We have
Table 3.2 Rewards, utilities, and probabilities for Problem 3.2, assuming that the investment in stock A is independent of the investment of stock B.
z
–1000
2a – 1000
1000 – 2a
1000
Utility
log(0.3)
log(0.0014a + 0.3)
log(1.7 – 0.0014a)
log(1.7)
Probability
(0.4) (0.3)
(0.6) (0.3)
(0.4) (0.7)
(0.6) (0.7)
Setting the derivative equal to zero and evaluating it at a* leads to the following equation:
By solving this equation we obtain a* = 344.72. Also, since the second derivative
we conclude that a* = 344.72 maximizes the expected utility U.
Problem 3.3 (French 1988) Consider the actions described in Table 3.1 in which the consequences are monetary payoffs. Convert this problem into one of choosing between lotteries, as defined in the von Neumann–Morgenstern theory. The decision maker holds the following indifferences with reference lotteries:
£100 ~ £120 with probability 1/2; £90 with probability 1/2;
£110 ~ £120 with probability 4/5; £90 with probability 1/5.
Assume that π(θ1) = π(θ3) = 1/4 and π(θ2) = 1/2. Which is the optimal action according to the expected utility principle?
Problem 3.4 Prove part (a) of Lemma 1.
Problem 3.5 (Berger 1985) Assume that Mr. A and Mr. B have the same utility function for a change, z, in their fortune, given by u(z) = z1/3. Suppose now that one of the two men receives, as a gift, a lottery ticket which yields either a reward of r dollars (r > 0) or a reward of 0 dollars, with probability 1/2 each. Show that there exists a number b > 0 having the following property: regardless of which man receives the lottery ticket, he can sell it to the other man for b dollars and the sale will be advantageous to both men.
Problem 3.6 Prove part (b) of Lemma 1. The proof is by contradiction. Define
α* = sup{α ∊ [0, 1] : a′ ≿ αa + (1 – α)a″}
and consider separately the three cases:
α*a + (1 – α*)a″ ≻ a′ ≻ a″
a ≻ a′ ≻ α*a + (1 – α*)a″
a′ ~ α*a + (1 – α*)a″.
The proof is in Kreps (1988). Do not look it up, this was a big enough hint.
Problem 3.7 Prove the von Neumann–Morgenstern theorem in the ⇐ direction.
Problem 3.8 (From Kreps 1988) Kahneman and Tversky (1979) give the following example of a violation of the von Neumann–Morgenstern expected utility model. Ninety-five subjects were asked:
Suppose you consider the possibility of insuring some property against damage, e.g., fire or theft. After examining the risks and the premium, you find that you have no clear preference between the options of purchasing insurance or leaving the property uninsured.
It is then called to your attention that the insurance company offers a new program called probabilistic insurance. In this program you pay half of the regular premium. In case of damage, there is a 50 percent chance that you pay the other half of the premium and the insurance company covers all the losses; and there is a 50 percent chance that you get back your insurance payment and suffer all the losses...
Recall that the premium is such that you find this insurance is barely worth its cost.
Under these circumstances, would you purchase probabilistic insurance?”
And 80 percent of the subjects said that they would not. Ignore the time value of money. (Because the insurance company gets the premium now, or half now and half later, the interest that the premium might earn can be consequential. We want you to ignore such effects. To do this, you could assume that if the insurance company does insure you, the second half of the premium must be increased to account for the interest the company has forgone. While if it does not, when the company returns the first half premium, it must return it with the interest it has earned. But it is easiest simply to ignore these complications altogether.) The question is: does this provide a violation of the von Neumann–Morgenstern model, if we assume (as is typical) that all expected utility maximizers are risk neutral?