13
Changes in utility as information

In previous chapters we discussed situations in which a decision maker, before making a decision, has the opportunity to observe data x. We now turn to the questions of whether this observation should be made and how worthwhile it is likely to be. Observing x could give information about the state of nature and, in this way, lead to a better decision; that is, a decision with higher expected utility. In this chapter we develop this idea more formally and present a general approach for assessing the value of information. Specifically, the value of information is quantified as the expected change in utility from observing x, compared to the “status quo” of not observing any additional data. This approach permits us to measure the information provided by an experiment on a metric that is tied to the decision problem at hand. Our discussion will follow Raiffa and Schlaifer (1961) and DeGroot (1984).

In many areas of science, data are collected to accumulate knowledge that will eventually contribute to many decisions. In that context the connection outlined above between information and a specific decision is not always useful. Motivated by this, we will also explore an idea of Lindley (1956) for measuring the information in a data set, which tries to capture, in a decision-theoretic way, “generic learning” rather than specific usefulness in a given problem.

Featured articles:

Lindley, D. V. (1956). On a measure of the information provided by an experiment, Annals of Mathematical Statistics 27: 986–1005.

DeGroot, M. H. (1984). Changes in utility as information, Theory and Decision 17: 287–303.

Useful references are Raiffa and Schlaifer (1961) and Raiffa (1970).

13.1 Measuring the value of information

13.1.1 The value function

The first step in quantifying the change in utility resulting from a change in knowledge is to describe the value of knowledge in absolute terms. This can be done in the context of a specific decision problem, for a given utility specification, as follows. As in previous chapters, let a* denote the Bayes action, that is a* maximizes the expected utility

As usual, a is an action, u is the utility function, θ is a parameter with possible values in a parameter space Θ, and π is the decision maker’s prior distribution. Expectation (13.1) is taken with respect to π. We need to keep track of this fact in our discussion, and we do so using the subscript π on U. The amount of utility we expect to achieve if we decide to make an immediate choice without experimentation, assuming we choose the best action under prior π, is

This represents, in absolute terms, the “value” to the decision maker of solving the problem as well as possible, given the initial state of knowledge. We illustrate V(π) using three stylized statistical decision problems:

1. Consider an estimation problem where a represents a point estimate of θ and the utility is

   u(a(θ)) = −(θ – a)²,

   that is the negative of the familiar squared error loss. The optimal decision is a* = E[θ] as we discussed in Chapter 7. Computing the expectation in (13.2) gives

   

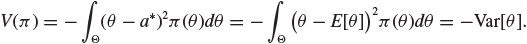
   The value of solving the problem as well as possible given the knowledge represented by π is the negative of the variance of θ.

2. Next, consider the discrete parameter space Θ = {1, 2, ...} and imagine that the estimation problem is such that we gain something only if our estimate is exactly right. The corresponding utility is

   u(a(θ)) = I_{a=θ},

   where, again, a represents a point estimate of θ. The expected utility is maximized by a* = mode(θ) ≡ θ⁰ (use your favorite tie-breaking rule if there is more than one mode) and

   V(π) = π(θ⁰).

   The value V is now the largest mass of the prior distribution.

3. Last, consider forecasting θ when forecasts are expressed as a probability distribution, as is done, for example, for weather reports. Now a is the whole probability distribution on θ. This is the problem we discussed in detail in Chapter 10 when we talked about scoring rules. Take the utility to be

   u(a(θ)) = log(a(θ)).

   This utility is a proper local scoring rule, which implies that the optimal decision is a*(θ) = π(θ). Then,

   

   The negative of this quantity is also known as the entropy (Cover and Thomas 1991) of the probability distribution π(θ). A high value of V means low entropy, which corresponds to low variability of θ.

In all these examples the value V of the decision problem is directly related to a measure of the strength of the decision maker’s knowledge about θ, as reflected by the prior π. The specific aspects of the prior that determine V depend on the characteristics of the problem. All three of the above problems are statistical decisions. In Section 13.2.2 we discuss in detail an example using a two-stage decision tree similar to those of Chapter 12, in which the same principles are applied to a practical decision problem.

The next question for us to consider is how V changes as the knowledge embodied in π changes. To think of this concretely, consider example 2 above, and suppose priors π₁ and π₂ are as follows:

θ	π1	π2
−1	0.5	0.1
0	0.4	0.4
1	0.1	0.5

For a decision maker with prior π₁, the optimal choice is –1 and V(π₁) = 0.5. For one with prior π₂, the optimal choice is 1 and V(π₁) = 0.5. For a third with prior απ₁ + (1 – α)π₂ with, say, α = 0.5, the optimal choice is 0, with V(απ₁ + (1 – α)π₂) = 0.4, a smaller value. The third decision maker is less certain about θ than any of the previous two. In fact, the prior απ₁ + (1 – α)π₂ is hedging bets between π₁ and π₂ by taking a weighted average. It therefore embodies more variability than either one of the other two. This is why the third decision maker expects to gain less than the others from having to make an immediate decision, and, as we will see later, may be more inclined to experiment.

You can check that no matter how you choose α in (0, 1), you cannot get V to be above 0.5, so the third decision maker expects to gain less no matter what α is. This is an instance of a very general inequality which we consider next.

Theorem 13.1 The function V(π) is convex; that is, for any two distributions π₁ and π₂ on θ and 0 < α < 1

Proof: The main tool here is a well-known inequality from calculus, which says that sup{f₁(x) + f₂(x)} ≤ sup f₁(x) + sup f₂(x). Applying this to the left hand side of (13.3) we get

We will use this theorem later when measuring the expected change in V that results from observing additional data.

13.1.2 Information from a perfect experiment

So far we quantified the value of solving the decision problem at hand based on current knowledge, as captured by π. At the opposite extreme we can consider the value of solving the decision problem after having observed an ideal experiment that reveals the value of θ exactly. We denote experiments in general by E, and this ideal experiment by E^∞. We define a_θ as an action that would maximize the decision’s maker utility if θ was known. Formally, for a given θ,

Because θ is unknown, so is a_θ. For any given θ, the difference

measures the gap between the best that can be achieved under the current state of knowledge and the best that can be achieved if θ is known exactly. This is called conditional value of perfect information, since it depends on the specific θ that is chosen. What would the value be to the decision maker of knowing θ exactly? Because different θ will change the utility by different amounts, it makes sense to answer this question by computing the expectation of (13.5) with respect to the prior π, that is

which is called expected value of perfect information. Using equations (13.2), (13.4), and (13.5) we can, equivalently, rewrite

The first term on the right hand side of equation (13.7) is the prior expectation of the utility of the optimal action given perfect information on θ. Section 13.2.2 works through an example in detail.

13.1.3 Information from a statistical experiment

From a statistical viewpoint, interesting questions arise when one can perform an experiment E which may be short of ideal, but still potentially useful. Say E consists of observing a random variable x, with possible values in the sample space X, and whose probability density function (or probability mass) is f(x|θ). The tree in Figure 13.1 represents two decisions: whether to experiment and what action to take. We can solve this two-stage decision problem using dynamic programming, as we described in Chapter 12. The solution will tell us what action to take, whether we should perform the experiment before reaching that decision, and, if so, how the results should affect the subsequent choice of an action.

Suppose the experiment has cost c. The largest value of c such that the experiment should be performed can be thought of as the value of the experiment for this decision problem. From this viewpoint, an experiment has value only if it may affect subsequent decisions. How large this value is depends on the utilities assigned to the final outcome of the decision process, on the strength of the dependence between x and θ, and on the probability of observing the various outcomes of x. We now make this more formal.

The “No Experiment” branch of the tree was discussed in Section 13.1.1. In summary, if we do not experiment, we choose an action a that maximizes the expected utility (13.1). The amount of utility we expect to gain is given by (13.2). When we have the option to perform an experiment, two questions can be considered:

1. After observing x, how much did we learn about θ?

2. How much do we expect to learn from x prior to observing it?

Figure 13.1 Decision tree for a generic statistical decision problem with discrete x. The decision node on the left represents the choice of whether or not to experiment, while the ones on the right represent the terminal choice of an action.

Question 2 is the relevant one for solving the decision tree. Question 1 is interesting retrospectively, as a quantification of observed information: answering question 1 would provide a measure of the observed information about θ provided by observing x. To simplify the notation, let π_x denote the posterior probability density function (or posterior probability mass in the discrete case) of θ, that is π_x = π(θ|x). A possible answer to question 1 is to consider the observed change in expected utility, that is

However, it is possible that the posterior distribution of θ will leave the decision maker with more uncertainty about θ or, more generally, with a less favorable scenario. Thus, with definition (13.8), the observed information can be both positive and negative. Also, it can be negative in situations where observing x was of great practical value, because it revealed that we knew far less about θ than we thought we did.

Alternatively, DeGroot (1984) proposed to define the observed information as the expected difference, calculated with respect to the posterior distribution of θ, between the expected utility of the Bayes decision and the expected utility of the decision a* that would be chosen if observation x had not been available. Formally

where a* represents a Bayes decision with respect to the prior distribution π. The observed information is always nonnegative, as V(π_x) = max_a U_πx(a). Expression (13.9) is also known as the conditional value of sample information (Raiffa and Schlaifer 1961) or conditional value of imperfect information (Clemen and Reilly 2001).

Let us explore further the definition of observed information in two of the stylized cases we considered earlier.

1. We have seen that in an estimation problem with utility function u(a(θ)) = −(θ – a)², we have V(π) = −Var(θ). The observed information (using equation (13.9)) is

   

   that is the square of the change in mean from the prior to the posterior.

2. Take now u(a(θ)) = I_{a=θ}, and let θ⁰ and be the modes for π and π_x, respectively. As we saw, V(π) = π(θ⁰). Then

   

   the difference in the posterior probabilities of the posterior and prior modes. This case is illustrated in Figure 13.2.

We can now move to our second question: how much do we expect to learn from x prior to observing it? The approach we will follow is to compute the expectation of the observed information, with respect to the marginal distribution of x. Formally

Figure 13.2 Observed information for utility u(a(θ)) = I_{a=θ}, when Θ = {1, 2, 3}. Observing x shifts the probability mass and also increases the dispersion, decreasing the point mass at the mode. In this case the value V of the decision problem is higher before the experiment, when available evidence indicated θ = 1 as a very likely outcome, than it is afterwards. However, the observed information is positive because the experiment suggested that the decision a = θ = 1, which we would have chosen in its absence, is not likely to be a good one.

An important simplification of this expression can be achieved by expanding the expectation in the second term of the right hand side:

where m(x) is the marginal distribution of x. Replacing the above into the definition of V(E), we get

This expression is also known as the expected value of sample information (Raiffa and Schlaifer 1961). Note that this is the same as the expectation of (13.8).

Now, because E_x[π_x] = π, we can write

From the convexity of V (Theorem 13.1) and Jensen’s inequality, we can then derive the following:

Theorem 13.2 V(E) ≥ 0.

This inequality means that no matter what decision problem one faces, expected utility cannot be decreased by taking into account free information. This very general connection between rationality and knowledge was first brought out by Raiffa and Schlaifer (1961), and Good (1967), whose short note is very enjoyable to read. Good also points out that in the discrete case considered in his note, the inequality is strict unless there is a dominating action: that is, an action that would be chosen no matter how much experimentation is done. Later, analysis of Ramsey’s personal notes revealed that he had already noted Theorem 13.2 in the 1920s (Ramsey 1991).

We now turn to the situation where the decision maker can observe two random variables, x₁ and x₂, potentially in sequence. We define E₁ and E₂ as the experiments corresponding to observation of x₁ and x₂ respectively, and define E₁₂ as the experiment of observing both. Let π_x1x2 be the posterior after both random variables are observed. Let be an optimal action when the prior is π and be an optimal action when the prior is π_x1. The observed information if both random variables are observed at the same time is, similarly to expression (13.9),

If instead we first observe x₁ and revise our prior to π_x1, the additional observed information from observing that x₂ can be defined is

In both cases the final results depend on both x₁ and x₂, but in the second case, the starting point includes knowledge of x₁.

Taking the expectation of (13.14) we get that the expected information from E₁₂ is

Next, taking the expectation of (13.15) we get that the expected conditional information is

This measures the expected value of observing x₂ conditional on having already observed x₁. The following theorem gives an additive decomposition of the expected information of the two experiments.

Theorem 13.3

Proof:

V(E12)	= Ex1x2[V(πx1x2)] – V(π)
	= Ex1x2[V(πx1x2)] – Ex1[V(πx1)] + Ex1[V(πx1)] – V(π)
	= V(E2|E1) + V(E1).

It is important that additivity is in V(E₂|E₁) and V(E₁), rather than V(E₂) and V(E₁). This reflects the fact that we accumulate knowledge incrementally and that the value of new information depends on what we already know about an unknown. Also, in general, V(E₂|E₁) and V(E₁) will not be the same even if x₁ and x₂ are exchangeable.

13.1.4 The distribution of information

The observed information V_x depends on the observed sample and it is unknown prior to experimentation. So far we focused on its expectation, but it can be useful to study the distribution of V_x, both for model validation and design of experiments.

We illustrate this using an example based on normal data. Suppose that a random quantity x is drawn from a N(θ, σ²) distribution, and that the prior distribution for θ is . The posterior distribution of θ given x is a distribution where, as given in Appendix A.4,

and the marginal distribution of x is . Earlier we saw that with the utility function u(a(θ)) = −(θ – a)², we have

V_x(E) = (E[θ|x] – E[θ])².

Thus, in this example, V_x(E) = (μ_x – μ₀)². The difference in means is

Since , we have

Therefore,

Knowing the distribution of information gives us a more detailed view of what we can anticipate to learn from an observation. Features of this distribution could be used to discriminate among experiments that have the same expected utility. Also, after we make the observation, comparing the observed information to the distribution expected a priori can provide an informal overall diagnostic of the joint specification of utility and probability model. Extreme outliers would lead to questioning whether the model we specified was appropriate for the experiment.

13.2 Examples

13.2.1 Tasting grapes

This is a simple example taken almost verbatim from Savage (1954). While obviously a bit contrived, it is useful to make things concrete, and give you numbers to play around with. A decision maker is considering whether to buy some grapes and, if so, in what quantity. To his or her taste, grapes can be classified as of poor, fair, or excellent quality. The unknown θ represents the quality of the grapes and can take values 1, 2, or 3, indicating increasing quality. The decision maker’s personal probabilities for the quality of the grapes are stated in Table 13.1.

The decision maker can buy 0, 1, 2, or 3 pounds of grapes. This defines the basic or terminal acts in this example. The utilities of each act according to the quality of the grapes are stated in Table 13.2. Buying 1 pound of grapes maximizes the expected utility U_π(a). Thus, a* = 1 is the Bayes action with value V(π) = 1.

Table 13.1 Prior probabilities for the quality of the grapes.

Quality	1	2	3
Prior probability	1/4	1/2	1/4

Table 13.2 Utilities associated with each action and quality of the grapes.

a	θ			Uπ(a)
	1	2	3
0	0	0	0	0
1	–1	1	3	1
2	–3	0	5	1/2
3	–6	–2	6	–1

Table 13.3 Joint probabilities (multiplied by 128) of quality θ and outcome x.

x	θ
	1	2	3
1	15	5	1
2	10	15	2
3	4	24	4
4	2	15	10
5	1	5	15

Table 13.4 Expected utility of action a (in pounds of grapes) given outcome x. For each x, the highest expected utility is in italics.

a	x
	1	2	3	4	5
0	0/21	0/27	0/32	0/27	0/21
1	–7/21	11/27	32/32	43/27	49/21
2	–40/21	–20/27	8/32	44/27	72/21
3	–94/21	–78/27	–48/32	18/27	74/21

Suppose the decision maker has the option of tasting some grapes. How much should he or she pay for making this observation? Suppose that there are five possible outcomes of observation x, with low values of x suggesting low quality. Table 13.3 shows the joint distribution of x and θ.

Using Tables 13.2 and 13.3 it can be shown that the conditional expectation of the utility of each action given each possible outcome is as given in Table 13.4. The highest value of the expected utility V(π_x), for each x, is shown in italics. Averaging with respect to the marginal distribtion of x from Table 13.3, E_x[V(π_x)] = 161/128 ≈ 1.26. The decision maker would pay, if necessary, up to V(E) = E_x[V(π_x)] – V(π) ≈ 1.26 – 1.00 = 0.26 utilities for tasting the grapes before buying.

13.2.2 Medical testing

The next example is a classic two-stage decision tree. We will use it to illustrate in a simple setting the value of information analysis, and to show how the value of information varies as a function of prior knowledge about θ. Return to the travel insurance example of Section 7.3. Remember you are about to take a trip overseas. You are not sure about the status of your vaccination against a certain mild disease that is common in the country you plan to visit, and need to decide whether to buy health insurance for the trip. We will assume that you will be exposed to the disease, but you are uncertain about whether your present immunization will work. Based on aggregate data on tourists like yourself, the chance of developing the disease during the trip is about 3% overall. Treatment and hospital abroad would normally cost you, say, 1000 dollars. There is also a definite loss in quality of life in going all the way to a foreign country and being grounded at a local hospital instead of making the most out of your experience, but we are going to ignore this aspect here. On the other hand, if you buy a travel insurance plan, which you can do for 50 dollars, all your expenses will be covered. This is a classical gamble versus sure outcome situation.

Table 13.5 Hypothetical monetary consequences of buying or not buying an insurance plan for the trip to an exotic country.

Actions	Events
	θ1: ill	θ2: not ill
Insurance	–50	–50
No insurance	–1000	0

Table 13.5 presents the outcomes for this decision problem. We are going to analyze this decision problem assuming both a risk-neutral and a risk-averse utility function for money. In the risk-neutral case we can simply look at the monetary outcome, so when we talk about “utility” we refer to the risk-averse case. We will start by working out the risk-neutral case first and come back to the risk-averse case later.

If you are risk neutral, based on the overall rate of disease of 3% in tourists, you should not buy the insurance plan because this action has an expected loss of 30 dollars, which is better than a loss of 50 dollars for the insurance plan. Actually, you would still choose not to buy the insurance for any value of π(θ₁) less than 0.05, as the observed expected utility (or expected return) is

How much money could you save if you knew exactly what will happen? That amount is the value of perfect information. The optimal decision under perfect information is to buy insurance if you know you will become ill and not to buy it if you know you will stay healthy. In the notation of Section 13.1.2

The returns that go with the two cases are

so that the expected return under perfect information is –50 π(θ₁). In our example, −50 × 0.03 = −1.5. The difference between this amount and the expected return under current information is the expected value of perfect information. For a general prior, this works out to be

An alternative way of thinking about the value of perfect information as a function of the initial prior knowledge on θ is presented in Figure 13.3. The expected utility of not buying the insurance plan is –1000 π(θ₁), while the expected utility of buying insurance is –50. The expected value of perfect information for a given π(θ₁) is the difference between the expected return with perfect information and the maximum between the expected returns with and without insurance. The expected value of perfect information increases for π(θ₁) < 0.05 and it decreases for π(θ₁) ≥ 0.05.

When π(θ₁) = 0.03, the expected value of perfect information is 950 × 0.03 = 28.5. In other words, you would be willing to spend up to 28.5 dollars for an infallible medical test that can predict exactly whether you are immune or not. In practice, it is rare to have access to perfect information, but this calculation gives you an upper bound for the value of the information given by a reliable although not infallible, test. We turn to this case now.

Figure 13.3 The expected utility of no insurance (solid line) and insurance (dashed line) as a function of the prior π(θ₁). The dotted line, a weighted average of the two, is the expected utility of perfect information, that is E_θ[u(a_θ(θ))]. The gap between the dotted line and the maximum of the lower two lines is the expected value of perfect information. As a function of the prior, this is smallest at the extremes, where we think we know a lot, and greatest at the point of indifference between the two actions, where information is most valued.

Suppose you have the option of undergoing a medical test that can inform you about whether your immunization is likely to work. After the test, your individual chances of illness will be different from the overall 3%. This test costs c dollars, so from what we know about the value of perfect information, c has to be less than or equal to 28.5 for you to consider this possibility. The result x of the test will be either 1 (for high risk or bad immunization) or 0 (for low risk or good immunization). From past experience, the test is correct in 90% of the subjects with the bad immunization and 77% of subjects with good immunization. In medical terms, these figures represent the sensitivity and specificity of the test (Lusted 1968). Formally they translate into f(x = 1|θ₁) = 0.9 and f(x = 1|θ₂) = 0.23. Figure 13.4 shows the solution of this decision problem using a decision tree, assuming that c = 10. The optimal strategy −10 is to buy the test. If x = 1, then the best strategy is buying the insurance. Otherwise, it is best not to buy it. If no test was made, then not buying the insurance would be best, as observed earlier.

Figure 13.4 Solved decision tree for the two-stage insurance problem.

The test result x can alter your course of action and therefore it provides valuable information. The expected value of the information in x is defined by equation (13.12). Not considering cost for the moment, if x = 1 the optimal decision is to buy the insurance and that has conditional expected utility of –50; if x = 0 the optimal decision is not to buy insurance, which has conditional expected utility of −4. So in our example the first term in expression (13.12) is

Ex[V(πx)]	= −50 × m(X = 1) – 4 × m(X = 0)
	= −50 × 0.25 – 4 × 0.75
	= −15.5,

and thus the expected value of the information provided by the test is V(E) = −15.5 – (–30) = 14.5. This difference exceeds the cost, which is 10 dollar, which is why according to the tree it is optimal to buy the test.

We now explore, as we had done in Figure 13.3, how the value of information changes as a function of the prior information on θ. We begin by evaluating V(π_x) for each of the two possible experimental outcomes. From (13.19)

and

Replacing Bayes’ formula for π(θ₁|x) and solving the inequalities, we can rewrite these as

and

Averaging these two functions with respect to the marginal distribution of x we get

The intermediate range in this expression is the set of priors such that the optimal solution can be altered by the results of the test. By contrast, values outside this interval are too far from the indifference point π(θ₁) = 0.05 for the test to make a difference: the two results of the test lead to posterior probabilities of illness that are both on the same side of 0.05, and the best decision is the same.

Subtracting (13.19) from (13.21) gives the expected value of information

Figure 13.5 graphs V(E) and V(E^∞) versus the prior π(θ₁). At the extremes, evidence from the test is not sufficient to change a strong initial opinion about becoming or not becoming ill, and the test is not expected to contribute valuable information. As was the case with perfect information, the value of the test is largest at the point of indifference π(θ₁) = 0.05.

As a final exploration of this example, let us imagine that you are slightly averse to risk, as opposed to risk neutral. Specifically, your utility function for a change in wealth of z dollars is of the form

Figure 13.5 Expected value of information versus prior probability of illness. The thin line is the expected value of perfect information, and corresponds to the vertical gap between the dotted line and the maximum of the lower two lines in Figure 13.3. The thicker line is the expected value of the information provided by the medical test.

In the terminology of Chapter 4 this is a constantly risk-averse utility. To elicit your utility you consider a lottery where you win $1010 with probability 0.5, and nothing otherwise, and believe that you are indifferent between $450 and the lottery ticket. Then you set u(0) = 0, u(1010) = 1, and u(450) = 0.5. Solving for the parameters of your utility function gives a = b = 2.813 721 8 and λ = 0.000 434 779. Using equation (13.23) we can extrapolate the utilities to the negative monetary outcomes in the decision tree of Figure 13.4. Those are

Outcomes in dollars	–10	–50	–60	–1000	–1010
Utility	–0.012	–0.062	–0.074	–1.532	–1.551

Solving the tree again, the best decision in the absence of testing continues to be do not buy the insurance plan. In the original case, not buying the insurance plan was the best decision as long as π(θ₁) was less than 0.05. Now such a cutoff has diminished to about 0.04 (give or take rounding error) as a result of your aversion to the risk of spending a large sum for the hospital bill. Finally, the overall optimal strategy is still to buy the test and buy insurance only if the test is positive.

The story about the trip abroad is fictional, but it captures the essential features of medical diagnosis and evaluation of the utility of a medical test. Real applications are common in the medical decision-making literature (Lusted 1968, Barry et al. 1986, Sox 1996, Parmigiani 2002). The approach we just described for quantification of the value of information in medical diagnosis relies on knowing probabilities such as π(θ) and f(x|θ) with certainty. In reality these will be estimates and are also uncertain. While for a utility-maximizing decision maker it is appropriate to average out this uncertainty, there are broader uses of a value of information analysis, such as supporting decision making by a range of patients and physicians who are not prepared to solve a decision tree every time they order a test, or to support regulatory decisions. With this in mind, it is interesting to represent uncertainty about model inputs and explore the implication of such uncertainty on the conclusions. One approach to doing this is probabilistic sensitivity analysis (Doubilet et al. 1985, Critchfield and Willard 1986), which consists of drawing a random set of inputs from a distribution that reflects the uncertainty about them (for example, is consistent with confidence intervals reported in the studies that were used to determine those quantities), and evaluating the value of information for each.

Figure 13.6 shows the results of probabilistic sensitivity analysis applied to a decision analysis of the value of genetic testing for a cancer-causing gene called BRCA1 in guiding preventative surgery decisions. Details of the underlying modeling assumptions are discussed by Parmigiani et al. (1998). Figure 13.6 reminds us of Figure 13.5 with additional noise. There is little variability in the range of priors for which the test has value, while there is more variability in the value of information to the left of the mode. As was the case in our simpler example above, the portions of the curve on either side of the mode are affected by different input values.

In Figure 13.6 we show variability in the value of information as inputs vary. In general, uncertainty about inputs translates into uncertainty about optimal decisions at all stages of a multistage problem. Because of this, in a probabilistic sensitivity analysis of the value of diagnostic information it can be interesting to separately quantify and convey the uncertainty deriving directly from randomness in the input, and the uncertainty deriving from randomness in the optimal future decisions. In clinical settings, this distinction can become critical, because it has implications for the appropriateness of a treatment. A detailed discussion of this issue is in Parmigiani (2004).

Figure 13.6 Results of a probabilistic sensitivity analysis of the additional expected quality adjusted life resulting from genetic testing for the cancer-causing gene BRCA1. Figure from Parmigiani et al. (1998).

13.2.3 Hypothesis testing

We now turn to a more statistical application of value of information analysis, and work out in detail an example of observed information in hypothesis testing. Assume that x₁, ..., x₉ form a random sample from a N(θ, 1) distribution. Let the prior for θ be N(0, 4) and the goal be that of testing the null hypothesis H₀ : θ < 0 versus the alternative hypothesis H₁ : θ ≥ 0. Set π(H₀) = π(H₁) = 1/2. Let a_i denote the action of accepting hypothesis H_i, i = 0, 1, and assume that the utility function is that shown in Table 13.6.

Table 13.6 Utility function for the hypotheses testing example.

Actions	States of nature
	H0	H1
a0 = accept H0	0	–1
a1 = accept H1	–3	0

The expected utilities for each decision are:

with V(π) = sup_a∈A U_π(a) = −1/2. Based on the initial prior, the best decision is action a₀. The two hypotheses are a priori equally likely, but the consequences of a wrong decision are worse for a₁ than they are for a₀.

Using standard conjugate prior algebra, we can derive the posterior distribution of θ, which is

which in turn can be used to compute the posterior probabilities of H₀ and H₁ as

where Θ(x) is the cumulative distribution function of the standard normal distribution. After observing xⁿ = (x₁, ..., x₉), the expected utilities of the two alternative decisions are:

• for decision a₀:

• for decision a₁:

and a₀ is optimal if U_πx(a₀) > U_πx(a₁), that is if

or, equivalently, if . Therefore,

Also,

Therefore, the observed information is

In words, small values of result in the same decision that would have been made a priori, and does not contribute to decision making. Values larger than 0.2279 lead to a reversal of the decision and are informative. For very large values the difference in posterior expected utility of the two decisions approaches one. The resulting observed information is shown in Figure 13.7.

Figure 13.7 Observed information for the hypothesis testing example, as a function of the sample mean.

Finally, we can now evaluate the expected value of information. Using the fact that , we have

In expectation, the experiment is worth 0.416. Assuming a linear utility and constant cost for the observations, this implies that the decision maker would be interested in the experiment as long as observations had unit price lower than 0.046.

13.3 Lindley information

13.3.1 Definition

In this section, we consider in more detail the decision problem of Chapter 10 and example 3 that is reporting a distribution regarding an unknown quantity θ with values in Θ. This can be thought of as a Bayesian way of modeling a situation in which data are not gathered to solve a specific decision problem but rather to learn about the world or to provide several decision makers with information that can be useful in multiple decision problems. This information is embodied in the distribution that is reported.

As seen in our examples in Sections 13.1.1 and 13.1.3, if a denotes the reported distribution and the utility function is u(a(θ)) = log a(θ) the Bayes decision is a* = π, where π is the current distribution on θ. The value associated with the decision problem is

Given the outcome of experiment E, consisting of observing x from the distribution f(x|θ), we can use the Bayes rule to determine π_x. By the argument above, the value associated with the decision problem after observing x is

and the observed information is

Prior to experimentation, the expected information from E is, using (13.12),

This is called Lindley information, and was introduced in Lindley (1956). We use the notation I(E) for consistency with his paper. Lindley information was originally derived from information-theoretic, rather than decision-theoretic, arguments, and coincides with the expected value with respect to x of the Kullback–Leibler (KL) divergence between π_x and π, which is given by expression (13.26).

In general, if P and Q are two probability measures defined on the same space, with p and q their densities with respect to the common measure ν, the KL divergence between P and Q is defined as

(see Kullback and Leibler 1951, Kullback 1959). The KL divergence is nonnegative but it is not symmetric. In decision-theoretic terms, the reason is that it quantifies the loss of representing uncertainty by Q when the truth is P, and that may differ from the loss of representing uncertainty by P when the truth is Q. For further details on properties of the KL divergence see Cover and Thomas (1991) or Schervish (1995).

13.3.2 Properties

Suppose that the experiment E₁₂ consists of observing x₁ and x₂, and that the partial experiments of observing just x₁ and just x₂ are denoted by E₁ and E₂, respectively. Observing x₂ after x₁ has previously been observed has expected information I_x1x2 (E₂|E₁). As discussed in Section 13.1.3, the expected information of E₂ after E₁ has been performed is the average of I_x1x2(E₂|E₁) with respect to x₁ and x₂ and it is denoted by I(E₂|E₁). We learned from Theorem 13.3 that the overall information in E₁₂ can be decomposed into the sum of the information contained in the first experiment and the additional information gained by the second one given the first. A special case using Lindley information is given by the next theorem. It is interesting to revisit it because here the proof clarifies how this decomposition can be related directly to the decomposition of a joint probability into a marginal and a conditional.

Theorem 13.4

Proof: From the definition of Lindley information we have

Also, from the definition of the information provided by E₂ after E₁ has been performed, we have

Adding expressions (13.32) and (13.33) we obtain

which is the desired result.

The results that follow are given without proof. Some of the proofs are good exercises. The first result guarantees that the information measure for any experiment is the same as the information for the corresponding sufficient statistic.

Theorem 13.5 Let E₁ be the experiment consisting of the observation of x, and let E₂ be the experiment consisting of the observation of t(X), where t is a sufficient statistic. Then I(E₁) = I(E₂).

The next two results consider the case in which x₁ and x₂ are independent, conditional on θ, that is f(x₁, x₂|θ) = f(x₁|θ)f(x₂|θ).

Theorem 13.6 If x₁ and x₂ are conditionally independent given θ, then

with equality if, and only if, x₁ and x₂ are unconditionally independent.

This proposition says that the information provided by the second of two conditionally independent observations is, on average, smaller than that provided by the first. This naturally reflects the diminishing returns of scientific experimentation.

Theorem 13.7 If x₁ and x₂ are independent, conditional on θ, then

with equality if, and only if, x₁ and x₂ are unconditionally independent.

In the case of identical experiments being repeated sequentially, we have a more general result along the lines of the last proposition. Let E₁ be any experiment and let E₂, E₃, ... be conditionally independent and identical repetitions of E₁. Let also

Theorem 13.8 I(E⁽ⁿ⁾) is a concave, increasing function of n.

Proof: We need to prove that

By applying equation (13.31) we have I(E⁽ⁿ⁺¹⁾) = I(E_n+1|E⁽ⁿ⁾) + I(E⁽ⁿ⁾). Next, using the fact that Lindley information is nonnegative, we obtain I(E⁽ⁿ⁺¹⁾) – (E⁽ⁿ⁾) ≥ 0, which proves the left side inequality.

Using again equation (13.31) on both I(E⁽ⁿ⁺¹⁾) and I(E⁽ⁿ⁾) we can observe that the right side inequality is equivalent to I(E_n+1|E⁽ⁿ⁾) ≤ I(E_n|E⁽ⁿ⁻¹⁾). As E_n+1 ≡ E_n, the inequality becomes I(E_n+1|E⁽ⁿ⁾) ≤ I(E_n+1|E⁽ⁿ⁻¹⁾). Also, since E⁽ⁿ⁾ = (E⁽ⁿ⁻¹⁾, E_n) we can rewrite the inequality as I(E_n+1|E⁽ⁿ⁻¹⁾, E_n) ≤ I(E_n+1|E⁽ⁿ⁻¹⁾). The proof of this inequality follows from an argument similar to that of (13.31).

As the value of V is convex in the prior, increased uncertainty means decreased value of stopping before experimenting. We would then expect that increased uncertainty means increased value of information. This is in fact the case.

Theorem 13.9 For fixed E, I(E) is a concave function of π(θ).

This means that if π₁ and π₂ are two prior distributions for θ, and 0 ≤ α ≤ 1, then the information provided by an experiment E with a mixture prior π₀(θ) = απ₁(θ) + (1 – α)π₂(θ) is at least as large as the linear combination of the information provided by the experiment under priors π₁ and π₂. In symbols, I₀(E) ≥ αI₁(E) + (1 – α)I₂(E) where I_i(E) is the expected information provided by E under prior π_i for i = 0, 1, 2.

13.3.3 Computing

In realistic applications closed form expressions for I are hard to derive. Numerical evaluation of expected information requires Monte Carlo integration (see, for instance, (Gelman et al. (1995)). The idea is as follows. First, simulate points θ_i from π(θ) and, for each, x_i from f(x|θ_i), with i = 1, ..., I. Using the simulated sample obtain the Monte Carlo estimate for E_θE_x|θ[log[f(x|θ)]], that is

Next, evaluate E_x[log(m(x))], again using Monte Carlo integration, by calculating

When the marginal is not available in closed form, this requires another Monte Carlo integration to evaluate m(x_i) for each i as

where the θ_j are drawn from π(θ). Using these quantities, Lindley information is estimated by taking the difference between (13.38) and (13.39). Carlin and Polson (1991) use an implementation of this type. Müller and Parmigiani (1993) and Müller and Parmigiani (1995) discuss computational issues in the use of Markov-chain Monte Carlo methods to evaluate information-theoretic measures such as entropy, KL divergence, and Lindley information, and introduce fast algorithms for optimization problems that arise in Bayesian design. Bielza et al. Insua (1999) extend those algorithms to multistage decision trees.

13.3.4 Optimal design

An important reason for measuring the expected information provided by a prospective experiment is to optimize the experiment with respect to some design variables (Chaloner and Verdinelli 1995). Consider a family of experiments E_D indexed by the design variable D. The likelihood function for the experiment E_D is f_D(x|θ), x ∊ X. Let π_D(θ|x) denote the posterior distribution resulting from the observation of x and let m_D(x) denote the marginal distribution of x. If D is the sample size of the experiment, we know that I(E_D) is monotone, and choosing a sample size requires trading off information against other factors like cost.

In many cases, however, there will be a natural trade-off built into the choice of D and I(E_D) will have a maximum. Consider this simple example. Let the random variable Y have conditional density f(y|θ). We are interested in learning about θ, but cannot observe y exactly. We can only observe whether or not it is greater than some cutpoint D. This problem arises in applications in which we are interested in estimating the rate of occurrence of an event, but it is impractical to monitor the phenomenon studied continuously. What we observe is then a Bernoulli random variable x that has success probability F(D|θ). Choices of D that are very low will give mostly zeros and be uninformative, while choices that are very high will give mostly ones and also turn out uninformative. The best D is somewhere in the center of the distribution of y, but where exactly?

To solve this problem we first derive general optimality conditions. Let us assume that D is one dimensional, continuous, or closely approximated by a continuous variable, and that f_D(θ|x) is differentiable with respect to D. Lindley information is

Define

The derivative of I(E_D) with respect to D turns out to be

To see that (13.40) holds, differentiate the integrand of I(E_D) to get

It follows from differentiating Bayes’ rule that

Thus

It can be proved that the following area conditions hold:

Equation (13.40) follows from this.

With simple manipulations, (13.40) can be rewritten as

This expression parallels the alternative expression for (13.29), given by Lindley (1956):

Equations (13.40) and (13.41) can be used in calculating the optimal D whenever Lindley information enters as a part of the design criterion. For example, if D is sample size, and the cost of observation c is fixed, then the real-valued approximation to the optimal sample size satisfies

Returning to the optimal cutoff problem, in which c = 0, we have

which gives

Similarly, if F(x) is the marginal cdf of x,

with

By inserting (13.45) through (13.47) into (13.41), we obtain

Now, by dividing both sides by f(D) we obtain that a necessary condition for D to be optimal is

in words, we must choose the cutoff so that the expected conditional logit is equal to the marginal logit. Expectation is taken with respect to the posterior distribution of θ given that x is at the cutoff point.

13.4 Minimax and the value of information

Theorem 13.2 requires that actions should be chosen according to the expected utility principle. What happens if an agent is minimax and a is chosen accordingly? In that case, the minimax principle can lead to deciding without experimenting, in instances where it is very hard to accept the conclusion that the new information is worthless. The point was first raised by Savage, as part of his argument for the superiority of the regret (or loss) form over the negative utility form of the minimax principle:

While Savage considered this objection not to be relevant for the regret case, one can show that the same criticism applies to both forms. One can construct examples where the minimax regret principle attributes the same value V to an ancillary statistic and to a consistent estimator of the state of nature for arbitrary n. In other instances (Hodges and Lehmann 1950) the value is highest for observing an inconsistent estimator of the unknown quantity, even if a consistent estimator is available.

A simple example will illustrate the difficulty with minimax (Parmigiani 1992). This is constructed so that minimax is well behaved in the negative utility version of the problem, and not so well behaved in the regret (or loss) version. Examples can be constructed where the reverse is true. A box contains two marbles in one of three possible configurations: both marbles are red, the first is blue and the second is red, or both are blue. You can choose between two actions, whose consequences are summarized in the table below, whose entries are negative payoffs (a 4 means you pay $4):

	RR	BR	BB
a1	2	0	4
a2	4	4	0

A calculation left as an exercise would show that the minimax action for this problem is a mixed strategy that puts weight 2/3 on a₁ and 1/3 on a₂, and has risk 2 + 2/3 in states RR and BB and 1 + 1/3 in state BR.

Suppose now that you have the option to see the first marble at a cost of $0.1. To determine whether the observation is worthwhile, you look at its potential use. It would not be very smart to choose act a₂ after seeing that the first marble is red, so the undominated decision functions differ only in what they recommend to do after having seen that the first marble is blue. Call a₁(B) the function choosing a₁, and a₂(B) that choosing a₂. Then the available unmixed acts and their consequences are summarized in the table

	RR	BR	BB
a1	2	0	4
a2	4	4	0
a1(B)	2.1	0.1	4.1
a2(B)	2.1	4.1	0.1

As you can see, a₁(B) is not an admissible decision rule, because it is dominated by a₁, but a₂(B) is admissible. The equalizer strategy yields an even mixture of a₁ and a₂(B) which has average loss of $2.05 in every state. So with positive probability, minimax applied to the absolute losses prescribes to make the observation.

Let us now consider the same regret form of the loss table. We get that by shifting each column so that the minimum is 0, which gives

	RR	BR	BB
a1	0	0	4
a2	2	4	0

The minimax strategy for this table is an even mixture of a₁ and a₂ and has risk 1 in state RR and 2 in the others. If you have the option of experimenting, the unmixed table is

	RR	BR	BB
a1	0	0	4
a2	2	4	0
a1(B)	0.1	0.1	4.1
a2(B)	0.1	4.1	0.1

In minimax decision making, you act as though an intelligent opponent decided which state occurs. In this case, state RR does not play any role in determining the minimax procedure, being dominated by state BR from the point of view of your opponent. You have no incentive to consider strategies a₁(B) and a₂(B): any mixture of one of these with the two acts that do not include observation will increase the average loss over the value of 2 in either column.

So in the end, if you follow the minimax regret principle you never perform the experiment. The same conclusion is reached no matter how little the experiment costs, provided that the cost is positive. The assumption that you face an opponent whose gains are your losses makes you disregard the fact that, in some cases, observing the first marble gives you the opportunity to choose an act with null loss, and only makes you worry that the marble may be blue, in which case no further cue is obtained. This concern can lead you to “ignore extensive evidence,” to put it in Savage’s terms. What makes the negative utility version work the opposite way is the “incentive” given to the opponent to choose the state where the experiment is valuable to you.

Chernoff (1954) noticed that an agent minimizing the maximum regret could in some cases choose action a₁ over action a₂ when these are the only available options, but choose a₂ when some other option a₃ is made available. This annoying feature originates from the fact that turning a payoff table into a regret table requires subtracting constants to each column, and these constants can be different when new rows appear. In our example, the added rows arise from the option to experiment: the losses of a rule based on an experiment are linear combinations of entries already present in the same column as payoffs for the terminal actions, and cannot exceed the maximum loss when no experimentation is allowed. This is a different mechanism whereby minimax decision making to “ignore extensive evidence” compared to the earlier example from Chernoff, because the constants for the standardization to regret are the same after one adds the two rows corresponding to experimental options.

13.5 Exercises

Problem 13.1 Prove equation (13.7).

Problem 13.2 (Savage 1954) In the example of Section 13.2.1 suppose the decision maker could directly observe the quality of the grapes. Show that the decision maker’s best action would then yield 2 utilities, and show that it could not possibly lead the decision maker to buy 2 pounds of grapes.

Problem 13.3 Using simulation, approximate the distribution of V_x(E) in the example in Section 13.1.4. Suppose each observation costs $230. Compute the marginal cost-effectiveness ratio for performing the experiment in the example (versus the status quo of no experimentation). Use the negative of the loss as the measure of effectiveness.

Problem 13.4 Derive the four minimax strategies advertised in Section 13.4.

Problem 13.5 Consider an experiment consisting of a single Bernoulli observation, from a population with success probability θ. Consider a simple versus simple hypothesis testing situation in which A = {a₀, a₁}, Θ = {0.50, 0.75}, and with utilities as shown in Table 13.7. Compute V(E) = E_x[V(π_x)] – V(π).

Problem 13.6 Show that I is invariant to one-to-one transformations of the parameter θ.

Problem 13.7 Let f(x|θ) = pf₁(x|θ)+(1–p)f₂(x|θ). Let E, E₁, E₂ be the experiments of observing a sample from f(x|θ), f₁(x|θ) and f₂(x|θ) respectively. Show that

Problem 13.8 Consider a population of individuals cross-classified according to binary variables x₁ and x₂. Suppose that the overall proportions of individuals with characteristics x₁ and x₂ are known to be p₁ and p₂ respectively. Say p₁ < p₂ < 1 – p₂ < 1 – p₁. However, the proportion ω of individuals with both characteristics is unknown. We are considering four experiments:

1. Random sample of individuals with x₁ = 1

2. Random sample of individuals with x₁ = 0

3. Random sample of individuals with x₂ = 1

4. Random sample of individuals with x₂ = 0.

Table 13.7 Utilities for Problem 13.5.

Actions	States of nature
	0.50	0.75
a0	0	–1
a1	–1	0

Using the result stated in Problem 13.7 show that experiment 1 has the highest information on ω irrespective of the prior.

Hint: Work with the information on θ = ω/p₁ and then translate the result in terms of ω.

Problem 13.9 Prove Theorem 13.5.

Hint: Use the factorization theorem about sufficient statistics.

Problem 13.10 Prove Theorem 13.6. Use its result to prove Theorem 13.7.

Problem 13.11 Consider an experiment E that consists of observing n conditionally independent random variables x₁, ..., x_n, with x_i ~ N(θ, σ²), with σ known. Suppose also that a priori . Show that

You can use facts about conjugate priors from Bernardo and Smith (2000) or Berger (1985). However, please rederive I.

Problem 13.12 Prove Theorem 13.9.

Hint: As in the proof of Theorem 13.1, consider any pair of prior distributions π₁ and π₂ of θ and 0 < α < 1. Then, calculate Lindley information for any experiment E with prior distribution απ₁ + (1 – α)π₂ for the unknown θ.