Lemma 1.65. Let p be an odd prime and e ≥ 2. For all a ∈ ℤ, we have
Proof: For e = 2, the statement is trivial. So, let e > 2. Inductively, we have ![]() ≡ 1 + ape−2 mod pe−1. Hence, there is a number b ∈ ℤ such that
≡ 1 + ape−2 mod pe−1. Hence, there is a number b ∈ ℤ such that ![]() + ape−2 + bpe−1. Using
+ ape−2 + bpe−1. Using ![]() for 1 ≤ k < p, we obtain
for 1 ≤ k < p, we obtain
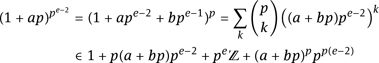
Now, ![]() because p > 2, and thus
because p > 2, and thus ![]() mod pe follows.
mod pe follows.
□
Lemma 1.66. Let e ≥ 3. Then for all a ∈ ℤ, we have (1 + 4a)2e−3 ≡ 1 + 2e−1a mod 2e.Proof: The statement is trivial for e = 3. Let e > 3. Then by inductive hypothesis, we may assume that (1+4a)2e−4 = 1+2e−2a+ 2e−1b for b ∈ ℤ. Using e ≤ 2e−4,we obtain
We now use these two lemmas to show that certain elements in (ℤ/peℤ)∗ have a large order.
Theorem 1.67. Let p be an odd prime. Then, for all e ≥ 1 the group (ℤ/peℤ)∗ is cyclic. For e ∈ {1, 2}, the group (ℤ/2eℤ)∗ is cyclic, too. If e > 2, then (ℤ/2eℤ)∗ is isomorphic to the additive group ℤ/2ℤ×ℤ/2e−2ℤ and therefore not cyclic.
Proof: The multiplicative group of a finite field is cyclic. This shows the assertion for all cases where e = 1. Now let p be odd and e ≥ 2. We choose a generator g of (ℤ/pℤ)∗. Then, gp−1 = 1 + ap and (p + g)p−1 = 1 + bp for suitable integers a and b. Suppose that p | a and p | b. Then, gp ≡ g mod p2 and (p + g)p ≡ p + g mod p2, which leads to a contradiction as follows:
Thus, without loss of generality, we may assume that gcd(a, p) = 1; otherwise we could take p + g as generating element of (ℤ/pℤ)∗. Lemma 1.65 yields (1 + ap)pe−1 ≡ 1 + ape mod pe+1 and therefore (1 + ap)pe−1 ≡ 1 mod pe. In particular, the order of 1+ap in (ℤ/peℤ)∗ divides pe−1.Again from Lemma1.65, we conclude that (1+ap)pe−2 ≡ 1 + ape−1 ≢ 1 mod pe. Therefore, the order of gp−1 in (ℤ/peℤ)∗ is pe−1 and, thus, the order of g is (p − 1)pe−1. Consequently, (ℤ/peℤ)∗ is cyclic.
The group (ℤ/4ℤ)∗ is cyclic because it is of order 2. We now come to the case p = 2 and e > 2. Lemma 1.66 implies 52e−2 = (1 + 4)2e−2 ≡ 1 + 2e mod 2e+1 and thus 52e−2 ≡ 1 mod 2e. Quite similarly, one can show that 52e−3 ≡ 1 + 2e−1≢ 1 mod 2e. Therefore, the order of the number 5 in (ℤ/2eℤ)∗ is 2e−2. Let G be the subgroup of (ℤ/2eℤ)∗ generated by 5. Suppose that −1 ∈ G; in other words, we have 5n ≡ −1 mod 2e for some n ∈ ℕ. Then, −1 ≡ 5n ≡ 1 mod 4, a contradiction. This shows G ∩ −G = 0. From |G ∪ −G| = 2e−1 = |(ℤ/2eℤ)∗| we obtain G ∪ −G = (ℤ/2eℤ)∗. In particular, the group homomorphism ℤ/2ℤ × ℤ/2e−2ℤ → (ℤ/2eℤ)∗, (a, b) ↦ (−1)a5b is surjective and hence bijective.
□
1.11 Quadratic reciprocity
Let ![]() q be a finite field. An element a ∈
q be a finite field. An element a ∈ ![]() q is a square or a quadratic residue if there exists b ∈
q is a square or a quadratic residue if there exists b ∈ ![]() q with b2 = a. In this case, we call b a square root of a. If b is a square root of a, then so is −b. Since quadratic equations over fields have at most two solutions, b and −b are the only square roots of a. In general, not all elements of a field are squares. As a simple example, consider 3 = {0, 1, −1}, where −1 is not a square. The following theorem, named after Euler, gives an effective criterion to test whether a ∈ q is a square.
q with b2 = a. In this case, we call b a square root of a. If b is a square root of a, then so is −b. Since quadratic equations over fields have at most two solutions, b and −b are the only square roots of a. In general, not all elements of a field are squares. As a simple example, consider 3 = {0, 1, −1}, where −1 is not a square. The following theorem, named after Euler, gives an effective criterion to test whether a ∈ q is a square.
Theorem 1.68 (Euler’s criterion). Let q be a finite field and q ∈ ℕ be odd. Then the mapping ![]() is a surjective homomorphism of (multiplicative) groups. Moreover
is a surjective homomorphism of (multiplicative) groups. Moreover
Proof: If a is a square, then there exists ![]() with b2 = a. From Corollary 1.5, we obtain
with b2 = a. From Corollary 1.5, we obtain ![]() Now, let a not be a square. By Theorem 1.56, the multiplicative group
Now, let a not be a square. By Theorem 1.56, the multiplicative group ![]() is cyclic. Let g be a generator of this group and choose k ∈ ℕ such that a = g2k+1. From gq−1 = 1, we conclude
is cyclic. Let g be a generator of this group and choose k ∈ ℕ such that a = g2k+1. From gq−1 = 1, we conclude ![]() because the polynomial X2 − 1 has no other roots. Since the order of g is q − 1, we obtain
because the polynomial X2 − 1 has no other roots. Since the order of g is q − 1, we obtain ![]() and thus
and thus
Now we have shown that in all cases ![]() and 1 occurs if and only if a is a square. This also shows that the mapping is a homomorphism. For surjectivity, we note that
and 1 occurs if and only if a is a square. This also shows that the mapping is a homomorphism. For surjectivity, we note that ![]() and
and ![]() for all generators g of
for all generators g of ![]()
□
Euler’s criterion implies that there are as many squares as nonsquares in ![]() if q is odd. We take a look at squares in prime fields ℤ/pℤ. At first glance, the fields ℤ/pℤ and ℤ/qℤ for different primes p and q do not seem to have very much in common. But, surprisingly, both structures are tightly connected by their quadratic residues. This is what the law of quadratic reciprocity is about.
if q is odd. We take a look at squares in prime fields ℤ/pℤ. At first glance, the fields ℤ/pℤ and ℤ/qℤ for different primes p and q do not seem to have very much in common. But, surprisingly, both structures are tightly connected by their quadratic residues. This is what the law of quadratic reciprocity is about.
Let n be an arbitrary odd number and a ∈ ℤ coprime to n. The mapping x ↦ ax mod n defines a permutation on the set {0, . . . , n − 1}. We let
and call ![]() the Jacobi symbol (named after Carl Gustav Jacob Jacobi, 1804–1851); it is the sign of the permutation x ↦ ax mod n. The connection between quadratic residues and signs of permutations is given by the following result of Yegor Ivanovich Zolotarev (1847–1878).
the Jacobi symbol (named after Carl Gustav Jacob Jacobi, 1804–1851); it is the sign of the permutation x ↦ ax mod n. The connection between quadratic residues and signs of permutations is given by the following result of Yegor Ivanovich Zolotarev (1847–1878).
Theorem 1.69 (Zolotarev’s lemma). Let p be an odd prime and a ∈ ℤ such that p ∤ a. Then, a is a square modulo p if and only if ![]()
Proof: Lemma 1.15 shows
The last congruence follows from Fermat’s little theorem. Euler’s criterion yields the result.
□
By Zolotarev’s lemma, also the commonly used Legendre symbol (named after Adrien-Marie Legendre, 1752–1833) can be defined using the Jacobi symbol. Usually, the same notation is used. However, only odd primes p are considered. Moreover, the domain of ![]() is extended to all a ∈ ℤ by having
is extended to all a ∈ ℤ by having ![]() for p | a. From Euler’s criterion, we obtain for the Legendre symbol
for p | a. From Euler’s criterion, we obtain for the Legendre symbol ![]() the property
the property ![]() mod p for all a ∈ ℤ.
mod p for all a ∈ ℤ.
Now, we formulate the law of quadratic reciprocity in Theorem 1.70 (a), along with its two supplements (b) and (c) and the two multiplication rules (d) and (e) for the Jacobi symbol.
Theorem 1.70 (Law of quadratic reciprocity). Let m ∈ ℤ, and let n ∈ ℕ be odd with gcd(m, n) = 1. Then the following statements hold:
Proof: (a) We first assume that m, n ≥ 1 and that m is odd. The permutation x ↦ x+1 mod m has the sign 1 because the elements 0, . . . , m−2 all have an inversion with m − 1 and there are no other inversions. By sequential application of the mappings, we see that sgn(x ↦ x + y0 mod m) = 1 holds for all y0 ∈ ℤ. Let P = {0, . . . , m − 1} × {0, . . . , n − 1}.We define mappings μ and ν on P by
□
For every fixed y', the mapping νy' : (x, y') → (nx + y' mod m, y') is a permutation on the set {0, . . . , m − 1} × {y'} and its sign is ![]() The mapping νy' also defines a permutation of the same sign on the set P if every value (x, y) with y ≠ y' is mapped to itself. Now ν is the sequential application of all ' νyfor 0 ≤ y' < n. This yields sgn
The mapping νy' also defines a permutation of the same sign on the set P if every value (x, y) with y ≠ y' is mapped to itself. Now ν is the sequential application of all ' νyfor 0 ≤ y' < n. This yields sgn![]() Analogously, μ is a permutation with sgn
Analogously, μ is a permutation with sgn![]() Thus
Thus
By the Chinese remainder theorem, we can regard μ∘ ν−1 as a permutation π on the set {0, . . . , mn − 1}. For (x, y) ∈ P, it maps nx + y to x + my. We now count the inversions of π. These are the pairs ((x, y), (x' , y')) ∈ P2 satisfying nx + y < nx' + y' and x + my > x' + my. The last two requirements are equivalent to x < x' and y > y'. Therefore, π has ![]() inversions. This shows
inversions. This shows
Now, we have shown (a) for positive numbers because ![]()
(b)Using Lemma 1.15, we obtain
(d)This property holds according to Theorem 1.16 because sgn is a homomorphism. In particular, the law of quadratic reciprocity (a) holds for all odd numbers m ∈ ℤwith gcd(m, n) = 1.
(c)From what we have already shown, we conclude
The assertion follows by induction on n.
(e)By the Chinese remainder theorem, there exists r ∈ ℕ with r ≡ 1 mod 4 and r ≡ m mod n. Thus
This completes the proof.
□
The proof of the law of quadratic reciprocity, we presented here goes back to George Rousseau [89]. The law of quadratic reciprocity yields the following algorithm for computing the Jacobi symbol:

Note that, in this algorithm, only the four least significant bits of the numbers m and n are used to find out whether powers of −1 evaluate to 1 or −1.
1.1. Show that every semigroup has at most one neutral element.
1.2. Show that in a monoid every element has at most one inverse.
1.3. Show that in a finite monoid M each left inverse is also right inverse, that is, ba = 1 implies ab = 1 for all a, b ∈ M.
1.4. Show that for infinite monoids, the claim of Exercise 1.3 does not hold in general.
1.5. Let S be a semigroup. An element a ∈ S is called regular if there exists b ∈ S such that aba = a. Show that for every regular element a ∈ S, there is an element c ∈ S with both aca = a and cac = c.
1.6. Let S be a finite semigroup. Recall that an element e ∈ S is idempotent if it satisfies e2 = e. Show:
(a)For each x ∈ S, the set { xk | k ≥ 1} ⊆ S contains a unique idempotent element. This element is some power xℓ with 1 ≤ ℓ ≤ |S|.
1.7. Let φ: M → G be a homomorphism from a finite semigroup M onto a group G and H be a smallest subsemigroup of M such that φ(H) = G. Show that H is a group.
1.8. A semigroup S is inverse if for every x ∈ S there exists a unique element ![]() such that
such that ![]() and
and ![]()
(a)Show ![]() for idempotents e, f of an inverse semigroup.
for idempotents e, f of an inverse semigroup.
(b)Show that the idempotents in an inverse semigroup forma commutative subsemigroup.
1.9. Let S be a finite semigroup with n elements and a1, . . . , an ∈ S be arbitrary. Show that there exists an index i ∈ {1, . . . , n} and an element b ∈ S with a1 ⋅⋅ ⋅ ai = a1 ⋅⋅ ⋅ aib.
1.10. Specify a finite monoid M and a submonoid U of M such that | U| does not divide |M|.
1.11. Let X and Y be nonempty sets, S a semigroup, and φ: Y × X → S a mapping. Show that the operation ∘ with (x, s, y) ∘ (x' , s' , y) = (x, s ⋅ φ(y, x) ⋅ s' , y) defines a semigroup on the set X × S × Y, the so-called Rees sandwich semigroup named after David Rees (1918–2013).
1.12. Show that, in a group, only the neutral element is idempotent. Moreover, a finite monoid is a group if and only if it has exactly one idempotent.
1.13. Let G be a semigroup. Prove the following assertions:
(a)Suppose there is an element e ∈ G with the following properties:
–For all g ∈ G, we have eg = g (left neutral element).
–For all g ∈ G, there exists h ∈ G with hg = e (left inverse elements). Then, G is a group.
(b)Suppose there is an element e ∈ G with the following properties:
–For all g ∈ G, we have ge = g (right neutral element).
–For all g, ∈ G there exists h ∈ G with hg = e (left inverse elements). Then, G is not necessarily a group.
(c)If for all a, b ∈ G the equations ax = b and ya = b have solutions x, y ∈ G, then G is a group.
1.14. Let G be a group and S ⊆ G a subset.
(a)Show that the following properties are equivalent:
(i)S is a subgroup of G.
(ii) S ≠ 0 and xy−1 ∈ S for all x, y ∈ S.
(b)Let S be finite. Show that the following properties are equivalent:
(i)S is a subgroup of G.
(ii) S ≠ 0 and xy ∈ S for all x, y ∈ S.
(c)Specify a group G and an infinite subset S ⊆ G such that S is not a subgroup of G, but it has the property xy ∈ S for all x, y ∈ S.
1.15. Let G and H be groups and φ: G → H be a mapping. Show that the following properties are equivalent:
(i)φ is a group homomorphism, that is, for all x, y ∈ G, we have φ(1G) = 1H, φ(x−1) = φ(x)−1, and φ(xy) = φ(x)φ(y).
(ii) For all x, y ∈ G, we have φ(xy) = φ(x)φ(y).
1.16. LetMbe a monoid satisfying m2 = 1 for all m ∈ M. Show that M is a commutative group.
1.17. Show that in a commutative group G the elements of odd order form a subgroup.
1.18. Let G be a group and H be a subgroup of G. Show that the implication xH = yH ⇒ xHx−1 = yHy−1 holds for all x, y ∈ G.
1.19. Let G be a (possibly infinite) group and H a subgroup satisfying [G : H] = n < ∞, that is, H has finite index. Prove the following assertions:
(a)For all g ∈ G there exists i ∈ {1, . . . , n} such that gi ∈ H.
(b)N = ⋂x∈G xHx−1 is the largest normal subgroup of G contained in H. Furthermore, G/N is finite.
1.20. Show that the relation given by the normal subgroup property is not transitive.
1.21. Let G be a group. Show that the bijective function f : G → G with f(a) = a−1 is a group homomorphism if and only if G is commutative.
1.22. Let G and H be groups, let f : G → H be a group homomorphism and let a ∈ G be an element of finite order. Show that the order of f(a) divides the order of a.
1.23. Show that every finite domain R is a skew field.
1.24. Let R be a commutative ring. Show that for a subset I ⊆ R, the following statements are equivalent:
(i)I is an ideal.
(ii) I is an additive subgroup such that R /I with the operations
forms a ring, where I is the neutral element with respect to addition and 1 + I is the neutral element with respect to multiplication.
(iii) I is the kernel of a ring homomorphism.
1.25. Let R be a ring and I and J be ideals in R with I ⊆ J. Show that R/J and (R/I)/(J/I) are isomorphic.
1.26. Let R be a ring and I and J be ideals of R. Which of the following sets are ideals of R?
| (i)I + J | (ii) I ⋅ J | (iii) I ∪ J | (iv) I ∩ J |
1.27. Show that in the ring ℤ[X], the ideal 〈6, X2 − 2〉 = 6ℤ[X]+(X2−2)ℤ[X] is neither a principal ideal nor maximal.
1.28. Determine the order of the element 3 in the multiplicative group (ℤ/16ℤ)∗.
1.29. Count the elements in (ℤ/60ℤ)∗ with even order.
1.30. Let m, n > 1 be natural numbers with gcd(m, n) > 1. Show that the additive groups (ℤ/mℤ) × (ℤ/nℤ) and ℤ/mnℤ are not isomorphic.
1.31. Find s ∈ ℕwith 51 ⋅ s ≡ 1 mod 98.
1.32. Find the two smallest numbers n1, n2 ∈ ℕsuch that the following congruences for i = 1, 2 are satisfied: ni ≡ 2 mod 3, ni ≡ 3 mod 4 and ni ≡ 6 mod 7.
1.33. Show that ![]() mod 60 for all n ∈ ℕ.
mod 60 for all n ∈ ℕ.
1.34. Show that 5 is the only prime number of the form z4 +4 with z ∈ ℤ. Hint: Use polynomial division to determine a polynomial p such that z4 + 4 = (z2 − 2z + 2) ⋅ p(z).
1.35. Compute gcd(X6 + X5 + X3 + X, X8 + X7 + X6 + X4 + X3 + X + 1) in the polynomial ring ![]() 2[X] over the two-element field
2[X] over the two-element field ![]() 2.
2.
1.36. Let f(X) = X5+X2 +1 ∈ ![]() 2[X]. Show that f(X) is irreducible over the two-element field
2[X]. Show that f(X) is irreducible over the two-element field ![]() 2.
2.
1.37. Let t ≥ 1. The polynomial f(X) ∈ ℝ[X] is called t-thin if it is the sum of at most t terms of the form aiXi. Then, f(X) =Σi≥0 aiXi and ai ≠ 0 for at most t indices i. Show that the number of positive real roots of f(X) ≠ 0 is bounded by t − 1.
1.38. Let 0 ≠ f (X) = Σi aiXi ∈ ℝ[X] be a polynomial of degree d. The number of sign changes of f(X) is the number of sign changes in the sequence (a0, . . . , ad); and this is defined as the number of sign changes in the subsequence that remains if all aj with aj = 0 are omitted. The number of sign changes in the sequence (0, 1, 0, −3, 4, 0, 2, −1) thus is that of (1, −3, 4, 2, −1), which is 3.
(a)Let 0 < λ ∈ ℝ be a positive real number. Show that the number of sign changes of g(X) = (X − λ)f(X) is strictly greater than the number of sign changes of f(X).
(b)(Descartes’ rule of signs; named after René Descartes, 1596–1650) The number of positive real roots (with multiplicities) of f(X) is bounded by the number of sign changes in the sequence (a0, . . . , ad).
1.39. Let f(X) = Xn + an−1Xn−1 + ⋅⋅ ⋅ + a0 ∈ ℤ[X]. Show that if r ∈ ℚ is a root of f(X), then r ∈ ℤ and r divides a0.
1.40. (Eisenstein’s criterion; named after F. Gotthold M. Eisenstein, 1823–1852) Let f(X) = anXn + ⋅⋅ ⋅ + a0X0 ∈ ℤ[X] with n ≥ 1 and an ≠ 0. Suppose there exists a prime number p such that p ∤ an and p | an−1, ..., p | a0, but p2 ∤ a0. Show that f(X) is irreducible over ℚ.
1.41. Prove the following statements using Eisenstein’s criterion from the previous exercise:
(a)Let p be a prime number and f(X) = Xn − p for n ≥ 1. Then, f(X) is irreducible over ℚ and thus in particular ![]()
(b)Let p be a prime number and f(X) = Xp−1 + Xp−2 +⋅ ⋅⋅ +1. Then, f(X) is irreducible over ℚ.
Hint: f(X) can be written as ![]() and f(X) is irreducible over ℚ if and only if f(X + 1) is.
and f(X) is irreducible over ℚ if and only if f(X + 1) is.
1.42. We extend formal power series to series of the form
Claim: The series ![]() satisfies S(X) = 0.
satisfies S(X) = 0.
Proof: X ⋅ S(X) = S(X) and therefore S(X) ⋅ (1 − X) = 0. On the other hand, (1 − X) ⋅ Σi≥0 X i = 1. From these facts, we obtain
Where is the error in this proof?
1.43. Consider the set ![]() with addition defined by (a +
with addition defined by (a + ![]() and multiplication by
and multiplication by ![]()
![]() Show that, with these operations,
Show that, with these operations, ![]() is a field.
is a field.
1.44. Let F be a field, E a field extension of F and α ∈ E a root of the polynomial p(X) ∈ F[X] with deg(p) ≥ 1. Prove that there is a unique polynomial m(X) ∈ F[X] with the leading coefficient 1 and the property
The polynomial m(X) is called the minimal polynomial of α.
1.45. Let a ∈ ℤand p an odd prime with p ∤ a. Let m be the order of a in (ℤ/pℤ)∗ and n the order of a in (ℤ/peℤ)∗ for e ≥ 1. Show that m | n and ![]()
1.46. Let ![]() be a field with q elements for an odd number q. Show that a ∈ is a square if and only if X − a ∈ [X] divides the polynomial X(q−1)/2 − 1.
be a field with q elements for an odd number q. Show that a ∈ is a square if and only if X − a ∈ [X] divides the polynomial X(q−1)/2 − 1.
Summary
Notions
–semigroup, monoid
–Abelian, commutative
–homomorphism
–isomorphism
–group, inverse element
–generated substruct. 〈X〉
–coset
–order of a group
–order of an element
–index [G : H]
–cyclic group
–generating element
–kernel ker(φ), image im(φ)
–normal subgroup
–quotient group G /H
–symmetry group
–symmetric group
–inversion
–sign sgn(π)
–transposition
–(commutative) ring
–zero ring
–skew field
–field
–subring, subfield
–ring homomorphism
–ideal, quotientring
–principal ideal
–maximal ideal
–zero divisor
–(integral) domain
–characteristic char(R)
–prime field
–Frobenius homomorphism
–formal power series
–polynomials R [X]
–zero polynomial
–degree deg(f)
–leading coefficient
–derivative f '
–root, multiplicity
–irreducible
–Noetherian ring
–field extension
–splitting field
–algebraic closure
–finite field q
–Jacobi symbol
–Legendre symbol
Methods and results
–partitioning into cosets
–Lagrange’s theorem: |G| = [G : H]⋅ |H|
–g|G| = 1. Moreover: gn = 1 ⇔ order of g divides n
–groups of prime order are cyclic
–subgroups of cyclic groups are cyclic
–G Abelian group, g, h ∈ G with coprime orders m, n ⇒ gh is of order mn
–Cauchy’s theorem: p prime divisor of |G| ⇒ G has an element of order p
–normal subgroups are exactly the kernels of group homomorphisms
–subgroups of index 2 are normal subgroups
–homomorphism theorem for groups: φ: G → H homomorphism ⇒ G/ ker(φ) ≅ im(φ)
–structure of the symmetry group of a regular polygon
–π permutation on {1, . . . , n}. Then, sgn(π) = (−1)# of inversions ![]()
–sgn: Sn → {−1, 1} is a homomorphism
–π is product of m transpositions ⇒ sgn(π) = (−1)m
–each permutation is the product of transpositions
–homomorphism theorem for rings: φ: R → S homomorphism ⇒ R/ ker(φ) ≅ im(φ)
–ring homomorphisms φ: F → R with F a field and R ≠ {0} are injective
–R commutative. Then: I ⊆ R maximal ideal ⇔ R/I field
–R domain ⇒ char(R) = 0 or char(R) = p prime
–binomial theorem: ![]()
–R commutative, char(R) = p prime ⇒ x ↦ xp is a homomorphism on R
–Fermat’s little theorem: R commutative, char(R) = p prime ⇒ ∀a ∈ R: ap = a
–Bézout’s lemma: For all k,ℓ ∈ ℤ there exist a, b ∈ ℤ with gcd(k, ℓ) = ak + bℓ.
–extended Euclidean algorithm
–k ∈ (ℤ/nℤ)∗ ⇔ gcd(k, n) = 1 ⇔ the mapping x ↦ kx on ℤ/nℤ is bijective
–n is prime ⇔ ℤ/nℤ is a field
–ideals in ℤ are generated by a single element
–k | ℓ ⇔ ℓℤ ⊆ kℤ; kℤ + ℓℤ = gcd(k, ℓ)ℤ; kℤ ∩ ℓℤ = lcm(k, ℓ)ℤ
–Chinese remainder theorem: For gcd(k, ℓ) = 1, the mapping ℤ/kℓℤ → ℤ/kℤ × ℤ/ℓℤ defined by x mod kℓ ↦ (x mod k, x mod ℓ) is a homomorphism of rings.
–computing Euler’s totient function: φ(pk) = (p − 1)pk−1 for p prime, φ(kℓ) = φ(k)φ(ℓ) for gcd(k, ℓ) = 1
–Euler’s theorem: gcd(a, n) = 1 ⇒ aφ(n) ≡ 1 mod n
–Σd|n φ(d) = n
–G cyclic group of order n, d | n ⇒ G has φ(d) elements of order d
–R![]() X
X![]() integral domain ⇔ R integral domain
integral domain ⇔ R integral domain
–f ∈ R![]() X
X![]() invertible ⇔ f(0) ∈ R invertible
invertible ⇔ f(0) ∈ R invertible
–deg(f + g) ≤ max(deg(f), deg(g))
–deg(f ⋅ g) ≤ deg(f) + deg(g) with equality in the case of integral domains
–(f + g)' = f ' + g; (f ⋅ g)' = f ' ⋅ g + f ⋅ g'
–polynomial division
–F field⇒every ideal in K [X] is principal
