Proof: Let and for p, q, u, υ ∈ k[x, y]. Then, pυ coincides with uq at infinitely many points P ∈ E (k). By Lemma 5.2, we see that pυ = uq and thus r = t. If r = p/q for p, q ∈ k[x, y], then we can multiply both the numerator and the denominator by q. This shows that every rational function r(x, y) can be written as

□

with u(x), υ(x), w(x) ∈ k[x] and w(x) ≠ 0.

The order of a point (see Theorem 5.3) is a concept which can also be applied to rational functions. For r = p/q ∈ k(x, y) and P ∈ E (k), let dp and dq be the orders of p and q at P, respectively. The difference d = dp − dq is a well-defined integer and we call d ∈ ℤ the order of r at P. For d ≥ 0, the image r(P) is defined; this is the case for almost all points of the curve. For d > 0 we speak of a zero or root, and for d < 0 we speak of a pole. By Theorem 5.4, rational functions without poles are polynomials.

If the field k has characteristic p > 2 and if A and B belong to a finite field extension q of the prime field p, then we consider the Frobenius automorphism k → k, a ↦ aq. For a ∈ k, we have a = aq if and only if a ∈ q. In particular, Aq = A and Bq = B. Hence, sq(x) = s(xq). It follows that the Frobenius mapping

is well defined and bijective because for all x, y ∈ k, we have y2 = s(x) if and only if y2q = sq(x) = s(xq). Whenever we mention the Frobenius mapping ϕq in the remainder of this section, we implicitly assume that A, B ∈ q and that q is a prime power.

Let ρ : E (k) → E (k) be a partial function such that there exist rational functions r(x, y), t(x, y) ∈ k(x, y) which satisfy ρ(P) = (r(P), t(P)) for all points P in the domain of ρ. We call ρ a rational morphism if it is defined almost everywhere. The domain of ρ must not contain the poles of r or t. Note that ρ uniquely determines the two rational functions r(x, y) and t(x, y). The composition of rational morphisms is again a rational morphism. The Frobenius mapping ϕq is a typical example of a rational morphism; it is therefore called the Frobenius morphism. Moreover, ϕq is defined everywhere and it is bijective.

We give two important examples of rational morphisms. For every point T = (a, b) ∈ E(k), the translation τ defined by τ(P) = P + T is rational because for all (x, y) ∈ E(k) {T, −T}, we have τ(x, y) = (xT , yT) with

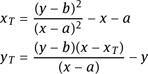
It is just as easy to see that σ(P) = 2P is a rational morphism. A point (x, y) ∈ E (k) with y ≠ 0 satisfies σ(x, y) = (x̂, ŷ) for

The morphism σ also defines a group homomorphism. This leads to the following notion. An endomorphism of E (k) is a group homomorphism of E ̃(k) into itself, which is either trivial (i.e., it maps E(k) to ) or it coincides with a rational morphism almost everywhere. We immediately see that nontrivial endomorphisms have a finite kernel because the image of almost every point is in E (k) and, thus, different from O.

Lemma 5.15. If endomorphism α and β coincide at almost all points of E (k), then α = β.

Proof: We may assume that α and β are nontrivial. Let P ∈ E (k). We show that α(P) = β(P). For almost every point T ∈ E(k), we have α(P + T) = β(P + T) ≠ , and almost all points T ∈ E (k) satisfy α(T) = β(T) ≠ . We can therefore choose some point T which satisfies both properties. Since α and β are homomorphisms, we obtain

□

If we set ϕq() = , then the following theorem shows that ϕq is an endomorphism.

Theorem 5.16. The Frobenius morphism ϕq is an endomorphism.

Proof: See Exercise 5.9.

□

Theorem 5.17. The endomorphisms form a ringwith the operations defined by (α + β)(P) = α(P) + β(P) and (α ⋅ β)(P) = α(β(P)).

Proof: The endomorphisms of an Abelian group form a ring with these operations. Thus, we only have to show the closure as rational morphisms. This is clear for composition. See Exercise 5.7 for addition.

□

The following lemma provides a normal form of endomorphisms.

Lemma 5.18. Let α be a nontrivial endomorphism. Then there exist polynomials p(x), q(x), u(x), υ(x) ∈ k[x] such that for almost all points (x, y) ∈ E (k). Moreover, neither p(x)/q(x) nor u(x)/υ(x) is constant.

Proof: See Exercise 5.8.

□

Theorem 5.19. Let α be an endomorphism with α(P) = (r(P), t(P)) for almost all points P ∈ E (k). Then the following properties hold:

Proof: By Lemma 5.18, we can assume that and Therefore, almost all (x, y) ∈ E (k) satisfy

We may assume that u (x) and υ(x) have no common roots. Since all roots in the denominator υ(x) appear twice, but x3+Ax+B only has simple roots, has to have a pole at all roots of υ(x). Thus, υ(x) = 0 implies q(x) = 0. In other words, if r(P) is defined, then t(P) is defined. The rational morphism ρ given by ρ(P) = (r(P), t(P)) is therefore defined at all points where r does not have a pole.

For property (a) it remains to show that ρ(P) = α(P) holds for all points P ∈ E(k) such that ρ(P) is defined. This is done by applying the proof technique from Lemma 5.15; the main difference is that we cannot assume ρ to be an endomorphism. For almost all points T ∈ E(k), the mapping P ↦ ρ(P + T) − ρ(T) for P ∈ E(k) is a rational morphism, that is, there exist rational functions r̂, t̂ ∈ k(x, y) such that the rational morphism ρT = (r̂, t̂̂) coincides with this mapping at almost all points P. The image ρT(P) is defined if and only if both r̂(P) and t̂( P) are defined. Note that ρT(P) could be defined even if ρ(P + T) is undefined; for instance, this could be the case for P = −T. Let T be a point such that ρ(T) is defined and it satisfies ρ(T) = α(T). For almost all points P ∈ E(k), we have

This shows that ρT coincides with α at almost all P and, hence, ρT coincides with ρ at almost all points P. By Lemma 5.14, we obtain r̂ = r and t̂ = t, that is, ρT = ρ. Consider a point P ∈ E(k) in the domain of ρ. There exists a point T such that ρ(P+T) = α(P+T) and ρ(T) = α(T). This yields ρ(P) = ρT(P) = α(P), as desired.

For property (b), we show that ρ(P) is defined if and only if α(P) ≠ O. The implication from left to right follows from property (a). For the other direction, let α(P) ≠ . We find a point T such that ρ(P + T) = α(P + T) and ρ(T) = α(T), and this yields α(P) = ρT(P) = ρ(P). In particular, ρ(P) is defined.

□

Let α be an endomorphism with for almost all (x, y) ∈ E(k) such that the polynomials p(x) and q(x) have no common roots. The degree of α is

Note that, by Lemma 5.14, the degree of a nontrivial endomorphism is well defined. We call α separable if one of the derivatives p(x) or q(x) is not the zero function. The Frobenius endomorphism ϕq has degree q, but it is not separable. A direct computation shows that multiplication by 2, that is α(P) = 2P, is separable (Exercise 5.10). The degree of α is 4. This can be computed directly but it also follows from the next theorem.

Theorem 5.20. The following properties hold for each nontrivial endomorphism α:

Proof: We start with the proof of surjectivity. Let P ∈ E(k). Obviously P = (P + T) − T for all T ∈ E(k). If both (P + T) and T belong to the image of α, then so does P. It therefore suffices to show that for almost every point P ∈ E(k) there exists Q ∈ E (k) with α(Q) = P. In particular, we do not need to consider the three points P with P = −P.

Let p(x), q(x), u(x), υ(x) ∈ k[x] be the polynomials given by Lemma 5.18. Moreover, we assume that p(x) and q(x) have no common roots. For almost all points (c, d) ∈ E(k), the property α(c, d) = (a, b) implies p(c)/q(c) = a. In particular, c is a root of p(x) − aq(x). We therefore consider polynomials of the form p(x) − aq(x) for a ∈ k.

For almost all a ∈ k, we have deg(α) = degx(p(x) − aq(x)). Note that deg(α) ≥ 1 since p/q is not constant. If P = (a, b) ∈ E(k) is a point such that the polynomial p(x) − aq(x) is not constant, then there exists a root c of this polynomial. For this root, we find some element d ∈ k such that Q = (c, d) and −Q = (c, −d) are the only points on the curve E (k) with c as first component. By Theorem 5.19, the first component of α(Q) is Hence, there are only two possibilities: either α(Q) = P and α(−Q) = −P or α(Q) = −P and α(−Q) = P. Note that Q ≠ −Q since we only consider points P with P ≠ −P. This shows that every root of p(x) − aq(x) accounts for a unique point Q with α(Q) = P; we might have to replace d by −d. In particular, this shows that α is surjective. In addition, since p(x)−aq(x) has at most deg(α) roots, this shows that |ker(α)| = |α−1(P)| ≤ deg(α). If α is not separable, then the derivative p'(x)− aq'(x) of p(x)− aq(x) is zero. In particular, p(x)− aq(x) has multiple roots; this yields |ker(α)| < deg(α).

For the remainder of this proof, let α be separable. Let C ⊆ k be the set of roots of the polynomial p(x)q' (x) − p'(x)q(x). It remains to be shown that there exists a ∈ k such that the polynomial p(x) − aq(x) has no multiple roots and its degree is deg(α). Since there are infinitely many a such that the degree of p(x) − aq(x) is deg(α), there is such an a ∈ k {0} with a ≠ p(ĉ)/q(ĉ) for all ĉ ∈ C. Suppose that p(x) − aq(x) has a multiple root c, that is, p(c) − aq(c) = 0 and p'(c) − aq(c) = 0. The multiplication of the two equations p(c) = aq(c) and aq'(c) = p'(c) yields ap(c)q' (c) = ap'(c)q(c). Since a ≠ 0, we obtain c ∈ C. This contradicts the choice of a because a = p(c)/q(c). If P = (a, b) is a point on the curve, then |ker(α)| = |α−1(P)| ≥ deg(α). This completes the proof of the theorem.

□

Remark 5.21. From Exercise 5.11, the mapping P ↦ ϕq(P) − P defines the surjective endomorphism (ϕq − 1), and its kernel consists of the elliptic curve Ẽ(q).

To prove Hasse’s theorem, the following path can be taken. First, show that (ϕq − 1) is separable. Thus, the problem of determining |Ẽ(q)| is reduced to giving a bound for the degree of (ϕq − 1). This is rather difficult and technical. The proof typically uses the concept of Weil pairings and is, for example, presented in [108]. Weil pairings were defined in 1940 by André Weil (1906–1998).

◊

Further reading

There is a huge number of scientific articles and textbooks on elliptic curves. Silverman’s book [97] is a standard reference. However, for the proofs, the author often refers, without further explanation, to the book by Robin Hartshorne (born 1938) on algebraic geometry [48], which treats the area in a very general way and uses the concept of schemes as defined by Alexander Grothendieck (1928–2014). Hartshorne’s book was not written to be an introduction to the theory of elliptic curves and, therefore, is not suitable for that purpose. A good introduction to the theory of elliptic curves is, for example, book by Washington [108]. We would further like to mention [57, 65]. Cryptographic applications of elliptic curves are also treated in textbooks such as [58] by Neal Koblitz (born 1948). However, this book does not prove the group structure. (The proof of the group structure of elliptic curves as given here uses the method of “divisors” and requires no knowledge beyond the scope of the current book.) Koblitz and Victor Saul Miller (born 1947) are considered to be co-founders of elliptic curve cryptography (ECC), see [56] and [76]. Since the mid-1980s, cryptography using elliptic curves has developed rapidly and become the most established method in practice other than the RSA cryptosystem.

Exercises

5.1. A general elliptic curve is defined by an equation of the following type:

5.2. Show that the polynomial X 3 + AX + B has multiple zeros if and only if 4A3 + 27B2 = 0. Make sure that your reasoning is also valid for characteristic 2 and 3.

5.3. Let p ≥ 3 be prime and let E be an elliptic curve over p defined by Y2 = X3 + AX + B. For a ∈ p we let

Show that

5.4. Let E be the curve defined by Y2 = X3 + X + 6 over the field 11.

5.5. Let E be the curve defined by Y2 = X3 + X over the field 5.

Note: In the following exercises, let E (k) always be an elliptic curve given by the equation Y2 = X3 + AX + B over an algebraically closed field k of characteristic different from 2. Moreover, let 4A3 + 27B2 ≠ 0.

5.6. Show that { P ∈ Ẽ(k) | 3P = } is isomorphic to the group ℤ/3ℤ × ℤ/3ℤ.

5.7. Show that, for endomorphisms α and β of an elliptic curve, α + β defined by (α + β)(P) = α(P) + β(P) is also a rational morphism.

5.8. Let α be a nontrivial endomorphism. Show that there exist polynomials p(x), q(x), u(x), υ(x) ∈ k[x] such that for almost all (x, y) ∈ E(k). In addition, show that neither p(x)/q(x) nor u(x)/υ(x) is constant.

5.9. Show that the Frobenius morphism ϕq is an endomorphism.

Hint: Use that E ̃(k) = Pic0(E(k)) by Theorem 5.5.

5.10. Show that the endomorphism α(P) = 2P of E (k) is separable.

5.11. Show that the mapping P ↦ ϕq(P) − P defines a surjective endomorphism (ϕq − 1) and that the kernel consists of the elliptic curve E ̃(q) over q.

Summary

Notions

Methods and results