3 Number theoretic algorithms

Many cryptosystems rely on fast arithmetic in various algebraic structures. For instance, when creating the private and the public key for Rivest–Shamir–Adleman (RSA), you have to find large prime numbers p and q, as well as to invert modulo (p − 1)(q − 1); then, a fast algorithm for exponentiation is required for encryption and decryption. In addition, we want fast algorithms for multiplication and division for the elementary operations of computing the product of two numbers modulo n. On the other hand, the security of many cryptosystems relies on the difficulty of some number theoretic problems. For instance, RSA is secure only as long as there is no efficient algorithm for integer factorization. It is therefore important to know how factorization algorithms work and to be aware of the cases when factorization is easy. Similarly, the ElGamal cryptosystem relies on the difficulty of the discrete logarithm. When solving equations in finite fields, it is important to extract roots; this is a recurring subproblem in various other settings. Before we consider some algorithms for the above problems, we will start with two basic tools for estimating the (worst-case or the expected) running time of an algorithm.

3.1 Runtime analysis of algorithms

Throughout this chapter, let ℝ≥0 be the set of nonnegative real numbers. We start with some techniques concerning the runtime analysis of algorithms. To this end, for any function f : ℝ≥0 →ℝ≥0, we define the function class

as the set of functions growing at most as fast as f. The O-notation was popularized by Edmund Georg Hermann Landau (1877–1938).

Master theorem

In the runtime estimation of recursive algorithms, you often have to deal with recurrences. We present asymptotic estimates for a large class of such recurrences.

Lemma 3.1. Let a ≥ 0, b > 1, and f, g : ℝ≥0 →ℝ≥0 with f(1) ≤ g(1). If f(n) ≤ a⋅ f(n/b)+ g(n) for all n ≥ b, then for all k ∈ ℕ.

Proof: For k = 0, the claim is true. Now, let k > 0. By definition, we have f(bk) ≤ a ⋅ f(bk−1) + g(bk). The inductive hypothesis for k − 1 yields

□

Distinguishing different cases depending on the specific values of the parameters a and b and the specific function g, we obtain the following theorem. Here, log n = max(1, log2 n).

Theorem 3.2 (Master theorem). Let a, b, c ∈ ℝ≥0 with b > 1 and let f : ℝ≥0 → ℝ≥0 be nondecreasing with f(n) ≤ a ⋅ f(n/b) + (nc). Then

Proof: Suppose that f(1) ≤ d and f(n) ≤ a ⋅ f(n/b) + dnc for some d > 0. The function h(n) = f(n)/d satisfies h(1) ≤ 1 and h(n) ≤ a ⋅ h(n/b) + nc. If h satisfies the claim of the theorem, so does f . It therefore suffices to deal with the case f(1) ≤ 1 and f(n) ≤ a ⋅ f(n/b) + nc. Furthermore, it is enough to consider n = bk with k ∈ ℕ: the function f is nondecreasing and since p(bn) ∈ (p(n)) for the functions p on the right-hand side, we can bound the value on n by the value on the next b-power. With g(n) = nc, Lemma 3.1 yields

If a < bc, the limit of the geometric series yields a constant factor

For a = bc, we have f(n) ≤ nc ⋅ (k + 1) ∈ (nc log n). The remaining case is a > bc:

Thus, the proof is complete for all cases.

The following example gives another typical approach for solving recurrences. The idea is to verify an educated guess.

□

Example 3.3. Let f : ℝ≥0 → ℝ≥0 be a nondecreasing function such that f(n) ≤ for some d ≥ 1. If we had then f(n) ∈ (n log n) by the master theorem. The “+4” should not change the asymptotics, and we therefore conjecture that for some sufficiently large constant k ≥ 4d we have f(n) ≤ kn log2 n for all n ≥ 1. Here, “sufficiently large” means that the conjecture holds for all n between 1 and 256d, that is, the base case is true. Let now n > 256d and suppose the conjecture holds for values smaller than n. Then

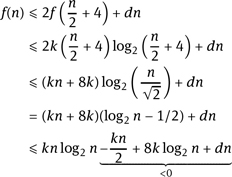
Thus, f(n) ≤ kn log2 n as desired.

◊

Birthday paradox

The birthday paradox can be quite helpful in the consideration of randomized algorithms. The idea is that, in a random sequence of elements from an n-element set, there is a high probability of two identical elements occurring within the first elements. Taking as basic set the 366 possible birthdays, it can be shown that the probability of two people having the same birthday in a group of 23 people is greater than 1/2. Since the number 23 seems surprisingly small, this situation is usually described by the name birthday paradox.

Let N be an n-element set. We consider a random sequence of length m consisting of elements of N. The probability that the first i + 1 items in the sequence are all different is

Thus, the probability that all m items are different can also be written as

Here, a uniform distribution of the elements is assumed; however, if certain elements are more likely than others, then the probability of a match is even greater. With the inequality (1 + x) ≤ ex, we can estimate the probability to have no duplicates as follows:

With increasing m, the term approaches 0. For a probability below 1/2 will be reached. The birthday paradox is the basis for runtime estimations in so-called ρ algorithms.

3.2 Fast exponentiation

Let M be a monoid. Fast exponentiation means: on input a ∈ M and n ∈ ℕ find the element an applying as few monoid operations as possible. Naively, one could determine an by the recursive rule an = a ⋅ an−1 with n − 1 operations. But if n is given in binary, this leads to an exponential algorithm. If n is an even number, one can determine an from an/2 by squaring. The fast exponentiation method now tries to square as often as possible. Moreover, it should not be necessary to store more than constantly many monoid elements. This is achieved by the following algorithm:

If n is odd, then an = a ⋅ an−1, and n − 1 is even. Therefore, n can be halved in each iteration. If â and n̂ are the initial values of a and n, respectively, then the loop invariant is e ⋅ an = ân̂ . In each execution of the while loop at most two monoid operations are performed, so this algorithm requires at most 2 ⌊log2 n⌋ + 2 operations. The maximum number of operations is reached on numbers of the form n = 2k − 1. In the case of M = ℤ/mℤ, with modular multiplication as the operation, the above algorithm is also called fast modular exponentiation. This is meant to emphasize that you do not compute the number an ∈ ℤ first and then reduce modulo m, but that all intermediate results are computed modulo m. Therefore, these numbers are limited by m, whereas an can already become very large for rather small numbers a and n.

We note that for cryptographic applications, in order to make sure that you cannot deduce any information about the input by measuring the execution time or the energy consumption, it is often desirable for the running time not to depend on n but only on the number of digits of n. For this purpose, the first line of the while loop could be replaced by

Remark 3.4. The above approach is not always optimal. Consider the computation of a15. Using fast exponentiation, we need six operations: squaring three times yields the elements a2, a4, a8; and with three further multiplications,we obtain a15 = a ⋅a2 ⋅ a4 ⋅ a8. If, on the other hand, we compute the five elements a2, a3 = a ⋅ a2, a6 = (a3)2, a12 = (a6)2 and a15 = a12 ⋅a3 with one operation each, then these five multiplications lead to the desired result. The general approach of this kind is usually referred to as addition chains. An addition chain for n ∈ ℕ{0} is a sequence (a0, . . . , ak) of natural numbers with the properties a0 = 1, ak = n, and each number ai (for i ≥ 1) is the sum of two (not necessarily different) preceding numbers. Here, the length k is the number of monoid operations required to compute an by this addition chain. The addition chain for 15 that results from fast exponentiation, is (1, 2, 3, 4, 7, 8, 15). The alternate computation with five multiplications uses the addition chain (1, 2, 3, 6, 12, 15). The main algorithmic disadvantage (except that one has to construct optimal addition chains, which, however, does not require monoid operations) is that, in general, all intermediate results need to be stored. At best, nearly half of the required monoid operations can be saved using addition chains; see Section 4.6.3 in [55].

◊

3.3 Binary GCD

We have seen, in Section 1.5.1, how to compute the greatest common divisor with a logarithmic number of recursive calls. The algorithm presented there can be applied to arbitrary rings which admit a Euclidean division, so-called Euclidean domains. This includes polynomial rings over fields; see Theorem 1.44. However, in many settings, the operation “ℓ mod k” is considered to be expensive in the sense that it uses significantly more time and energy than, for instance, addition and subtraction. The binary gcd (the procedure bgcd below) efficiently computes the greatest common divisor of two natural numbers such that all divisions and multiplications are by the number 2. Assuming that we represent natural numbers in binary, these are nothing but bitwise shifts.

The number of recursive calls is in O(log k +log ℓ) since, after at most two calls, at least one of the arguments is divided by 2. Note that 2 is a common divisor of k and ℓ if and only if both of them are even. Since gcd(k, ℓ) = gcd(k − ℓ, ℓ), the correctness of the algorithm follows. It is possible to extend the binary gcd such that, on input k and ℓ, it additionally computes numbers a and b with ak + bℓ = gcd(k, ℓ). Moreover, this extension also does not use arbitrary division and multiplication; see Exercise 3.3.

3.4 Probabilistic recognition of primes

For many applications, such as the RSA cryptosystem, very large prime numbers are needed. This leads to the question of how to rapidly check a given (large) number n for primality. In the next chapter, we will present a deterministic polynomial time algorithm for this problem. However, its running time cannot compete with the probabilistic methods presented here. The two main procedures in this section – the Solovay–Strassen and the Miller–Rabin primality test – work in rounds. In each round, a number a ∈ {1, . . . , n − 1} is selected at random and, depending on a, the output is either that n is composite or that n is probably prime. If the output is that n is composite, then n is actually composite. But whenever the output says that n is probably prime, then n could still be composite. However, both methods have the property that, for a composite number n, with probability at least 1/2, the chosen a reveals n as composite. Therefore, after k independent rounds, a composite number is discovered with a probability of at least 1 − 2−k. If after 100 rounds each time the output claimed that n may be prime, then the error probability is less than

3.4.1 Fermat primality test and Carmichael numbers

On input n, the Fermat test consists of two steps. First, it randomly chooses a ∈ {1, . . . , n − 1}. Then, it computes b = an−1 mod n. If n is prime, then Fermat’s little theorem yields b = 1. Thus, if b ≠ 1, then n is composite. Otherwise, if b = 1, then n might be prime, but we do not know for sure. It could therefore be helpful to repeat the procedure in order to possibly reveal n as composite.

Carmichael numbers are named after Robert Daniel Carmichael (1879–1967). A Carmichael number is a composite number n satisfying an−1 ≡ 1 mod n for all a ∈ (ℤ/nℤ)∗. This means that the Fermat test fails for such numbers because there is no real chance to find a suitable a which proves that n is composite (of course, there is always the tiny chance to choose a ∉ (ℤ/nℤ)∗ and find a divisor of n). There are infinitely many Carmichael numbers [2]. The first three Carmichael numbers are 561, 1105, and 1729. The Carmichael numbers are the Knödel numbers K1. They are named after Walter Knödel (born 1926) who was the founding Dean of the Department of Computer Science at the University of Stuttgart. A number n belongs to Krif an−r ≡ 1 mod n for all a ∈ (ℤ/nℤ)∗. The following theorem collects some basic properties of Carmichael numbers. A natural number n is square-free if m2 ∤ n for all integers m ≥ 2, that is, no prime power of exponent greater than 1 appears in the prime factorization of n.

Theorem 3.5. Let n be a Carmichael number. Then the following properties hold:

Proof: (a) Note that n ≥ 4. If n is even, then mod n, a contradiction. (b) Suppose that n = pdu for some prime number p such that p ∤ u and d ≥ 2. Then wee have

This yields (pd−1 + 1)n ≡ 1 mod pd and (pd−1 + 1)n−1 ≢ 1 mod pd. Let b ≡ pd−1 + 1 mod pd and b ≡ 1 mod u. Then, b is an element in (ℤ/nℤ)∗ satisfying bn−1 ≢ 1 mod n, a contradiction.

(c)Assume that n = pq for two prime numbers p ≠ q. Let g ∈ ℤ/nℤ be a generator modulo p and congruent 1 modulo q. The order of g is p − 1. On the other hand, gn−1 = 1 since n is a Carmichael number. This yields

and thus p − 1 | q − 1. Symmetrically, we have q − 1 | p − 1 and thus p = q, a contradiction. Therefore, n has at least three different prime factors.

3.4.2 Solovay–Strassen primality test

Robert Martin Solovay (born 1938) and Volker Strassen (born 1936) combined Euler’s criterion and the law of quadratic reciprocity to obtain a probabilistic primality test, the Solovay–Strassen test. The basic idea is the following. To assure the primality of a given odd number n ≥ 3, in each round you verify that mod for a randomly chosen a ∈ (ℤ/nℤ)∗. More precisely, one round of the Solovay–Strassen test works as follows:

For the computation of b, we use fast exponentiation and c is computed using the algorithm for the Jacobi symbol. Note that b ∈ {1, −1} implies a ∈ (ℤ/nℤ)∗. If n is prime,then the output is “n is probably prime” by Euler’s criterion and Zolotarev’s lemma. We now show that, in every round, composite numbers are detected with probability greater than 1/2. If n survived k rounds of this procedure, then the probability that n is prime is at least 1 − 2−k. There are no exceptions for this test such as Carmichael numbers for the Fermat test.

Theorem 3.6. Let mod n } for an odd number n ≥ 3. Then, E (n) is a subgroup of (ℤ/nℤ)∗ and we have

Proof: E (n) contains the element 1; so it is not empty and, by Theorem 1.70 (d), E (n) is a group. The direction from right to left follows from Euler’s criterion (Theorem 1.68) and Zolotarev’s lemma (Theorem 1.69). For the remaining direction, suppose that E (n) = (ℤ/nℤ)∗ for a composite number n. In particular, n is a Carmichael number. From Theorem 3.5, n is square-free. We can write n = pu for a prime number p ≥ 3 with p ∤ u. Let a be not a square modulo p and congruent 1 modulo u. In particular, a ∈ (ℤ/nℤ)∗. Then, we have

From E(n) = (ℤ/nℤ)∗, we obtain mod n and therefore mod u. This is a contradiction to a ≡ 1 mod u.

□

If n is an odd and composite number, then the index of the subgroup E (n) in (ℤ/nℤ)∗ is at least 2. Thus, more than half of the elements of {1, . . . , n − 1} are not in E(n). All such elements lead to a round of the Solovay–Strassen test in which n is detected as composite.

3.4.3 Miller–Rabin primality test

The initial situation is as follows: let n ≥ 3 be an odd number. After a certain number of trial divisions, we suspect that n could be prime. The Miller–Rabin test is named after Gary Lee Miller and Michael Oser Rabin. In every round, it either refutes the primality or it yields the result that n is prime with a probability of at least 3/4. The Miller–Rabin test refines the Fermat test and it can also handle Carmichael numbers. It can even be efficiently performed for large numbers and, by repeating it independently, it can be made sufficiently reliable for all practical purposes, such as cryptographic applications.

Given an odd number n ≥ 3, the Miller–Rabin test works as follows:

First, let n be prime. Then by Fermat’s little theorem, we have an−1 ≡ 1 mod n for all a ∈ {1, . . . , n − 1}. If b ≡ 1 mod n, the output is “n is probably prime.” So let b ≢ 1 mod n. Since mod n, the sequence ( ) contains an element c whose square in ℤ/nℤ is equal to 1, and c itself is not 1. But ℤ/nℤ is a field in which the polynomial X2 − 1 only has the two roots 1 and −1. Therefore, −1 occurs in the list. This shows that in any case the output is “n is probably prime” whenever n is actually prime.

It remains to consider the case where n is composite. In Theorem 3.11, we show that then in at most 1/4 of all cases the output is “n is probably prime.”

Proposition 3.7. Let n = rst ∈ ℕ for pairwise coprime numbers r, s, t ≥ 1 such that r, s ≥ 3 are odd. Let u be odd, ℓ ≥ 1 and

for k = min{ 2ℓ−1u | ∀a ∈ G: a2ℓ' u ≡ 1 mod rs }. Then, H ≠ G.

Proof: Since ℓ ≥ 1, we have −1 ∈ G and thus k ∈ ℕ. By construction of k there exists a ∈ G with a2k ≡ 1 mod rs and ak ≢ 1 mod rs. Without loss of generality, let ak ≢ 1 mod r. From the Chinese remainder theorem, there exists b with b ≡ a mod r and b ≡ 1 mod st. We have b2k ≡ 1 mod rs and hence b ∈ G. On the other hand, b ∉ H because bk ≢ ±1 mod rs. This shows H ≠ G.

□

Using Proposition 3.7, one can easily prove an error probability of at most 1/2 for the Miller–Rabin test: for any odd composite number n, we can consider the groups

for k = min{ 2ℓ−1u | ∀a ∈ G: a2ℓ' u ≡ 1 mod n }. Remember that n − 1 = 2ℓu for an odd number u. All elements a ∈ (ℤ/nℤ)∗ H lead to the output “n is composite.” If G ≠ (ℤ/nℤ)∗, then we also have H ≠ (ℤ/nℤ)∗. Otherwise, n is a Carmichael number and by Theorem 3.5, we can write n = rs for odd coprime numbers r, s ≥ 3. Proposition 3.7 yields H ≠ G. Therefore, in any case, the index of H in (ℤ/nℤ)∗ is at least 2. This gives an error probability of 1/2. Proving the error probability 1/4 is slightly more involved.

Lemma 3.8. Let n = pd ≠ 9 for some odd prime p. At most 1/5 of all elements a ∈ (ℤ/nℤ)∗ yield the output “n is probably prime” in the Miller–Rabin test.

Proof: The group (ℤ/nℤ)∗ is cyclic of order (p − 1)pd−1. Let g be a generator of (ℤ/nℤ)∗. We have gcd((p − 1)pd−1, n − 1) = p − 1. Therefore, we have (gk)n−1 ≡ 1 mod n if and only if pd−1 | k. Hence, exactly p − 1 elements a ∈ (ℤ/nℤ)∗ satisfy an−1 ≡ 1 mod n. If an−1 ≢ 1 mod n, then

and the output is “n is composite.” Unless p = 3 and d = 2, we have 1/pd−1 ≤ 1/5.

□

Lemma 3.9. Let n = rs for odd coprime numbers r, s ≥ 3 and suppose that n is not a Carmichael number. At most 1/4 of all elements a ∈ (ℤ/nℤ)∗ yield the output “n is probably prime” in the Miller–Rabin test.

Proof: Let

for Note that H is a subgroup of G which, in turn, is a subgroup of (ℤ/nℤ)∗. Since n is not a Carmichael number, we have G ≠ (ℤ/nℤ)∗, and Proposition 3.7 shows H ≠ G. Therefore, the index of H in (ℤ/nℤ)∗ is at least 4.

Next, we show that the output “n is probably prime” implies a ∈ H. If b = 1, then a ∈ H. Let now b2i ≡ −1 mod n for i < ℓ. Then, mod rs and thus a ∈ G. In particular, the element a is considered in the definition of k and thus, 2iu divides k. This shows a ∈ H. Therefore, all elements a ∈ (ℤ/nℤ)∗ H lead to the output “n is composite.”

□

In the case of n being a Carmichael number, we use the property that n has at least three different prime factors for applying Proposition 3.7 twice.

Lemma 3.10. Let n be a Carmichael number. At most 1/4 of all elements a ∈ (ℤ/nℤ)∗ yield the output “n is probably prime” in the Miller–Rabin test.

Proof: By Theorem 3.5, we have n = rst for coprime numbers r, s, t ≥ 3. Let G = (ℤ/nℤ)∗ and ℓ' ∈ ℕ minimal such that

Since −1 ∈ G, we have ℓ' ≥ 1. We define Let

Note that J is a subgroup of H and H is a subgroup of G. Proposition 3.7 shows H ≠ G. If J ≠ H, then the index of J in G is at least 4, and we are done, since all a ∈ G J yield the output “n is composite.” So let J = H, that is, ah ≡ ±1 mod rs implies ah ≡ ±1 mod n for all a ∈ G. If ah ≡ −1 mod n, then ah ≡ −1 mod rs; now, the element â defined by â ≡ a mod rs and â ≡ 1 mod t is in H J, a contradiction. This shows J = { a ∈ (ℤ/nℤ)∗ | ah ≡ 1 mod n }. Let m ∈ ℕ be minimal with J = {a ∈ (ℤ/nℤ)∗ | a2mu ≡ 1 mod n }. We set k = 2m−1u. By Proposition 3.7

is a proper subgroup of J. Hence, the index of K in G is at least 4.

It remains to show that the output “n is probably prime” implies a ∈ K. If b = 1, then a ∈ K. Let now b2i ≡ −1 mod n for i < ℓ. Then, b2i ≡ −1 mod rs and thus i < ℓ. It follows that a ∈ H = J. In particular, a is considered in the definition of m. We conclude i < m and a ∈ K. Therefore, all a ∈ G K yield the output “n is composite.”

□

Theorem 3.11. Let n ≥ 3 be odd and composite. At most 1/4 of all elements a ∈ {1, . . . , n − 1} yield the output “n is probably prime” in the Miller–Rabin test.

Proof: All elements a ∈ {1, . . . , n − 1} with a ∉ (ℤ/nℤ)∗ yield the output “n is composite.” For n ≠ 9, the claim therefore follows from the Lemmas 3.8, 3.9 and 3.10. For n = 9, the Miller–Rabin test considers eight possible choices for a, but only a = 1 and a = −1 lead to the output “n is possibly prime.”

□

This shows that the Miller–Rabin test yields a given level of certainty with half as many rounds as the Solovay–Strassen test.

3.4.4 Applications of the Miller–Rabin scheme

Proposition 3.7 does not require that 2ℓu = n − 1. This allows us to extend the Miller–Rabin scheme to other settings. Let n ≥ 3 be odd. Suppose that ℓ ≥ 1 and that u is odd. We can arbitrarily choose a ∈ {1, . . . , n − 1}, set b = au mod n, and then consider the sequence Let

for Proposition 3.7 shows H ≠ G. For every element a ∉ H one of the following properties holds:

Thus, for a random element a ∈ {1, . . . , n − 1} one of these two conditions is satisfied in at least half of the cases. If condition (a) is satisfied because a is not invertible modulo n, then we find a nontrivial divisor of n, namely gcd(a, n). If, in contrast, condition (a) is satisfied for a ∈ (ℤ/nℤ)∗, then G =(ℤ/nℤ)∗. If mod n and condition (b) holds, then there is an element such that c2 ≡ 1 mod n and c ≢ ±1 mod n. But then (c − 1)(c + 1) ≡ 0 mod n, and gcd(c − 1, n) is a nontrivial divisor of n. In particular, half of all elements a ∈ {1, . . . , n − 1} yield either a divisor of n or the result G ≠ (ℤ/nℤ)∗. If φ(n) divides 2ℓu, then G = (ℤ/nℤ)∗ and we can use the Miller–Rabin scheme as a probabilistic method for factorizing n. For example, if all prime factors of φ(n) are elements of the set {p1, . . . , pm}, then n can be factored by choosing ℓ and u such that holds.

Security of the secret key in RSA

Using the Miller–Rabin scheme, we will show that the secret key for the RSA cryptosystem is secure. For the RSA algorithm, two sufficiently large primes p and q are determined and n = pq is computed. Then numbers e, s ≥ 3 with es ≡ 1 mod φ(n) are computed. The public key is the pair (n, e), and the secret key is s. Encryption is done by x ↦ xe mod n; decryption can be accomplished by y ↦ ys mod n. If it is possible to factorize n, then it is possible, from the knowledge of e, to determine the secret key s efficiently. However, it is generally believed that there is no efficient method for factorizing large numbers, and that it is therefore not feasible to factorize n. We want to show that with the knowledge of the secret key s, it is easily possible to determine the factors of n. Since it is assumed that the latter cannot be performed efficiently, there can be no efficient method to determine s with the knowledge of the public key (n, e).

Let s ∈ ℕ be a number with (xe)s = xes ≡ x mod n for all x ∈ ℤ. Then, aes−1 ≡ 1 mod n for all a ∈ (ℤ/nℤ)∗. Wewrite es−1 = 2ℓu with an odd u. From Proposition 3.7, using the same notation, we obtain H ⊊ G = (ℤ/nℤ)∗. In particular, the following procedure yields a factor of n with high probability:

As we saw above, this procedure finds a divisor of n with a probability of at least 1/2 in each iteration. Under the assumption that one cannot factorize n efficiently, this shows that it is not possible for an attacker to derive the secret key from the public key in the RSA cryptosystem.

3.4.5 Miller–Rabin versus Solovay–Strassen

The Solovay–Strassen test plays a minor role in practice and it cannot compete with the Miller–Rabin test, the latter being conceptually and algorithmically simpler. The Solovay–Strassen test loses because, for a fixed choice of a, whenever the Solovay–Strassen test deduces that n is composite, then so does the Miller–Rabin test. We show this in Theorem 3.12.

Let n ≥ 3 be odd and a ∈ ℤ with gcd(a, n) = 1. The number n is a pseudoprime to base a if an−1 ≡ 1 mod n (and so, n with the choice of a passes the Fermat test); n is an Eulerian pseudoprime to base a if mod n is true (and so, n with the choice of a passes the Solovay–Strassen test); finally, n is a strong pseudoprime to base a if n − 1 = 2ℓu for an odd u and one of the following conditions is satisfied:

On this choice of a, strong pseudoprimes pass the Miller–Rabin test. The less bases there are such that a composite number n is an (Eulerian or strong, respectively) pseudoprime, the more likely the respective primality test will detect that n is composite. Carmichael numbers are pseudoprimes to all bases.

If n is an Eulerian pseudoprime to base a, then a(n−1)/2 mod n ∈ {1, −1} and therefore an−1 = (a(n−1)/2)2 ≡ 1 mod n. So n is a pseudoprime to base a. Thus, the Solovay–Strassen test on composite numbers never performs worse (and on Carmichael numbers it always performs better) than the Fermat test. The next theorem shows that the Miller–Rabin test performs even better; see also Exercise 3.4.

Theorem 3.12. Every strong pseudoprime n to base a is also an Eulerian pseudoprime to base a.

Proof: Let a ∈ (ℤ/nℤ)∗ such that the output of the Miller–Rabin test is “n is probably prime.” We need to show that the Solovay–Strassen test gives the same output. We write n − 1 = 2ℓu with u odd. Note that ℓ ≥ 1 since n is odd. Let b = au mod n. Since and u is odd, we have

It therefore remains to show that mod n. If b = 1, then this is true. Let now b2k−1 ≡ −1 mod n for some k ∈ {1, . . . , ℓ}. In particular, the order of b modulo n is 2k.

We let n = p1 ⋅⋅ ⋅ pt for not necessarily distinct primes pi. Let pi − 1 = 2ℓi ui for ui odd. By reordering, we can assume that ℓ1 ≤ ⋅⋅ ⋅ ≤ ℓt. We have b2k ≡ 1 ≢ −1 ≡ b2k−1 mod pi for all i. Therefore, the order of b modulo pi is 2k, and we obtaink ≤ ℓ1. Let s be the number of exponents ℓi with k = ℓi. For i ≤ s we have pi − 1 = 2kui = 2k(1 + 2zi) = 2k + 2k+1zi ≡ 2k mod 2k+1, and if i > s, then 2k+1 | pi − 1 and thus pi ≡ 1 mod 2k+1. This yields