□

Generalizing nondeterministic automata, we now allow rational sets as labels. An M-automaton with rational labels is a tuple A = (Q, δ, I, F), where Q, I, F are have the same meaning as in the definition of nondeterministic automata and δ is a subset of Q×RAT(M)×Q. A run ofAis a sequence of the form q0u1q1 ⋅⋅ ⋅ unqn with qi ∈ Q, ui ∈ M and for all i ∈ {1, . . . , n} there is a transition (qi−1, Li , qi)∈ δ with ui ∈ Li. Accepting runs and the accepted set L(A) of A are defined as above. As before, A is called finite if δ is a finite set. Of course, this does not mean that a rational set L ∈ RAT(M) which occurs as a label of a transition has to be finite.

Next, we want to show that nondeterministic automata accept rational sets. We do so by changing labels of transitions; see the proof of the next lemma. The method is often referred to as state elimination.

Lemma 7.13. Let A be a finite M-automaton with rational labels. Then L(A) ∈ RAT(M).

Proof: Let A = (Q, δ, I, F). Without loss of generality Q = {q2, . . . , qn} with n ≥ 2. Since the class of rational sets is closed under union, we can assume that for all qi , qj ∈ Q at most one transition (qi , Li,j, qj)∈ δ exists. We add two new states q0 and q1 to Q and obtain the set of states Q' = {q0, . . . , qn}. Define

The automaton B = (Q' , δ' , {q0}, {q1}) is equivalent to A. Moreover, B satisfies the following invariants; the initial state q0 has no incoming transitions, the final state q1 has no outgoing transitions and for qi , qj ∈ Q' there is at most one transition (qi , Li,j, qj)∈ δ. Moreover, Li,j ∈ RAT(M). In the following, we let Li,j = 0 if there is no transition from qi to qj.

We continue the process of “state elimination” as long as n > 1. If this is the case, we construct an automaton C = (Q,' δ,' q0, q1) equivalent to B with Q' = {q0, . . . , qn−1} such that C also satisfies the three invariants of B. First, we remove the state qn and all its adjacent transitions, then we replace each transition (qi , Li,j, qj)∈ δ' with i, j < n by where

The procedure is also visualized in the following picture:

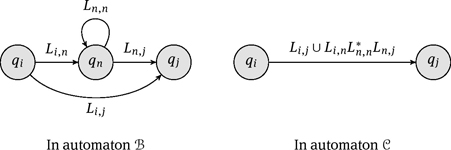
By repeatedly eliminating states, we can assume that in B we eventually have n = 1. By construction, we obtain L(B) = L0,1 ∈ RAT(M).

□

Theorem 7.14. Let M be a monoid and L ⊆ M. Then the following statements are equivalent:

Proof: The implication (a) ⇒ (b) is Lemma 7.11, and (b) ⇒ (c) can be seen with Lemma 7.12. For (c) ⇒ (d) one replaces all transitions (p, u, q) by (p, {u}, q). Finally, (d)⇒(a) is Lemma 7.13.

Lemma 7.15. Every rational subset L ⊆ Mis contained in a finitely generated submonoid of M.

Proof: Since every nondeterministic finite automaton Ahas only finitely many edges, only finitely many labels U ⊆ M can occur. In particular, L(A) ⊆ U∗ ⊆ M. Therefore, by Theorem 7.14 every rational subset L of M is contained in a finitely generated submonoid of M.

□

A consequence of the previous lemma is that M is a rational subset of M if and only if M is finitely generated. In particular, the class of rational subsets is not closed under inverse homomorphisms, because the homomorphism ψ: M → {1} yields the subset M as preimage of the rational subset {1}. However, rational subsets are closed under homomorphisms, because in nondeterministic automata one can replace every label by its homomorphic image.

The next theorem of Dawson James McKnight, Jr. (1928–1981) characterizes finitely generated monoids by the inclusion of REC(M) into RAT(M), see [74].

Theorem 7.16 (McKnight). A monoid M is finitely generated if and only if REC(M) ⊆ RAT(M).

Proof: The recognizable set M by Lemma 7.15 can only be rational if Mis finitely generated. The converse follows from Theorem 7.14 because, if M is finitely generated, then we can view a finite M-automaton (in the sense of Section 7.1) as a nondeterministic spelling automaton.

□

If M is a free monoid over a finite alphabet, then the rational sets inside M are also called regular. In the next section, we deal with regular languages. We will see that the regular languages and the recognizable sets coincide; this is Kleene’s theorem.

7.3 Regular languages

We have seen that the classes of recognizable and rational subsets are incomparable, in general. Finite subsets of M are always rational, but they are not recognizable, for example, in infinite groups; see Remark 7.1. On the other hand, the recognizable set ℕ over the monoid of natural numbers ℕwith multiplication as operation is not rational since the monoid (ℕ, ⋅, 1) is not finitely generated.

In the following, we will stick to the convention of speaking about languages and words whenwemean subsets and elements in finitely generated free monoids. We now show that the properties of being regular, rational and recognizable are equivalent for finitely generated free monoids. This result is known as Kleene’s theorem on regular languages [54].

Theorem 7.17 (Kleene). Let Σ be a finite alphabet. Then REC(Σ∗) = RAT(Σ∗).

Proof: The inclusion REC(Σ∗)⊆ RAT(Σ∗) follows from Theorem 7.16. Now, let L ⊆ Σ∗ be rational. From Theorem 7.14, we know that a spelling nondeterministic finite Σ∗- automaton A = (Q, δ, I, F) with n = |Q| states exists which accepts the language L. Using the so-called subset construction, we design an equivalent deterministic automaton with at most 2n states. The result of this construction is the subset automaton B. The states of B are subsets of Q, which explains the upper bound 2n. The construction starts by defining I ⊆ Q as the unique initial state in B. Suppose that P ⊆ Q has already been defined as a state of B. For each letter a ∈ Σ define

We add the set P ⋅ a to the set of states of B if it is not there already, making more and more subsets of Q become states of B.

For all words w ∈ Σ∗, the state I ⋅ w of B consists of all states q ∈ Q of A for which a run of A on w, starting in some initial state p ∈ I and ending at q, exists. The proof of this fact is carried out by induction on the length of w. Accordingly, we define the final states of B as the set of subsets which contain at least one final state of A. So, B defines the desired deterministic automaton, which accepts L.

□

Let Σ be a finite alphabet, then we denote by REG(Σ∗) the family of regular languages. Theorem 7.17 says REG(Σ∗) = REC(Σ∗) = RAT(Σ∗). By general closure properties of recognizable and rational sets, Theorem 7.2 and Remark 7.10, we obtain the following assertion.

Corollary 7.18. Let Σ be a finite alphabet. Then REG(Σ∗) is a Boolean algebra. If φ: Σ∗ → Γ∗ is any homomorphism to a finitely generated monoid, then we have φ(REG(Σ∗))⊆ REG(Γ∗) and φ−1(REG(Γ∗))⊆ REG(Σ∗).

The corresponding constructions in Corollary 7.18 are effective. This means, if regular languages L and K are given, for example, by rational expressions, then we can effectively construct a recognizing homomorphism or a rational expression for, say, L K. The next theorem states another useful closure property for regular languages, but effectiveness is not always guaranteed.

Theorem 7.19. Let Σ be a finite alphabet, L ∈ REG(Σ∗) be a regular language and K ⊆ Σ∗ be any language. Then the quotient

is regular. Moreover, if K is regular, and if L and K are specified by accepting finite automata, then we can effectively find an automaton accepting LK−1.

Proof: Let us assume that L is given by some finite automaton with state space Q and set of final states F. In order to define an accepting automaton for LK−1 we enlarge the set of final states to the new set

It is clear that the new automaton accepts the quotient LK−1. If K is given by a finite automaton, then we can use, for example, the product automaton construction to compute F.

The effectiveness in Theorem 7.19 is given if K belongs to a class of formal languages where first, the class is closed under intersection with regular sets and second, we can decide emptiness. So, Theorem 7.19 is effective for “context-free” but not for “context-sensitive” languages; see for example [51].

Over a finitely generated free monoid Σ∗ the concepts of deterministic and nondeterministic finite automata are equivalent. Henceforth, we say that a nondeterministic finite automaton (Q, δ, I, F) is spelling if the transition relation δ is a subset of Q×Σ×Q. We also use the notation NFA as an abbreviation for a spelling automaton. We use the abbreviation ε-NFA if δ ⊆ Q × (Σ ∪ {ε}) × Q. The subset construction in the proof of Theorem 7.17 shows that for every ε-NFA with n states there exists an equivalent deterministic one with at most 2n states. Equivalence means that they both accept the same language L ⊆ Σ∗. Minimization leads to the minimal automaton AL and its transition monoid is the syntactic monoid Synt(L); it is the smallest recognizing monoid for L. This construction yields because first, AL has at most 2n states (and this bound is tight) and second, for an automaton A with s states, the transition monoid has at most ss states (and this bound is tight again). However, if we start with an ε-NFA with n states which accepts a language L, then the proof of the next theorem shows that we can realize a recognizing homomorphism inside the monoid of Boolean n × n-matrices. This yields |Synt . To see the difference, consider n = 3. The number is greater than 10 million, but Another advantage of using n × n-matrices is that they can be multiplied efficiently.

Theorem 7.20. Let Σ be finite and A an ε-NFA over Σ∗ with n states. Then, the syntactic monoid of L = L(A) has at most elements.

Proof: Let A = (Q, δ, I, F) where without loss of generality Q = {1, . . . , n}. By assumption, we have δ ⊆ Q × (Σ ∪ {ε}) × Q. Removing ε-transitions does not increase the set of states. Thus, without loss of generality we may assume δ ⊆ Q × Σ × Q. For each letter a ∈ Σ, we define a Boolean n × n-matrix Aa ∈ n×n by letting the entry to be 1 if otherwise. The Boolean values ' = {0, 1} with the disjunction ∨ as addition and the conjunction ∧ as multiplication form a semiring, and, hence, the Boolean n × n-matrices with multiplication forma monoid n×n. Thus, the mapping a ↦ φ(a) = Aa defines a homomorphism φ from Σ∗ to n×n. If w = a1 ⋅⋅ ⋅ am is a word and φ(w) = B = Aa1 ⋅⋅ ⋅ Aam, then Bi,j = 1 is true if and only if there is a path from i to j labeled by w. Moreover, for P = {B ∈ n×n | ∃i ∈ I, j ∈ F : Bi,j = 1 }, we obtain φ−1(P) = L. Therefore, φ recognizes the language L. By Theorem 7.4, the syntactic monoid is the homomorphic image of a submonoid of n×n. Therefore, it contains at most 2n2 elements.

□

An important consequence of Kleene’s theorem is that the class of regular languages is closed under finite intersection and complementation. As shown by the following example, RAT(M) is not closed under finite intersection, in general. Moreover, if RAT(M) is not closed under finite intersection, then it is not closed under complementation by the rules of De Morgan (Augustus De Morgan, 1806–1871).

Example 7.21 (Nonclosure under finite intersection). Let M = {a, c}∗ × b∗. Algebraically M is a direct product of two free monoids. Let L = (a, b)∗(c, 1)∗ and K = (a, 1)∗(c, b)∗. The sets L, K ⊆ M are rational. We can represent the intersection L ∩ K by the set { (ancn, bn) | n ∈ ℕ}. Consider the projection π : M → {a, c}∗ which erases the second component. This is a homomorphism and the image of (ancn, bn)∈ M is ancn. Thus, π(L ∩ K) = { ancn | n ∈ ℕ}. It is clear that for m ≠ n the words am and an are not syntactically equivalent. This is true for all four languages L, K, L ∩ K ⊆ M, and π(L ∩ K). Hence, none of them is recognizable. The point is that {a, c}∗ is free. Hence by Kleene’s theorem, π(L ∩ K) is not rational. Since the rational subsets are closed under homomorphic, L ∩ K is not rational.

◊

7.4 Star-free languages

A fundamental result by Schützenberger relates star-free languages (defined in the following) to finite aperiodic monoids [92].Here, a monoid N is called aperiodic if there exists n ∈ ℕ such that un+1 = un for all u ∈ N. Aperiodic monoids are orthogonal to groups. A nontrivial group is never aperiodic; and if in an aperiodic monoid M an element u has a right-inverse υ with uυ = 1, then u = υ = 1. Indeed, if uυ = 1, then unυn = 1 for all n ∈ ℕ. Now, if in addition un+1 = un for some n, then u = u unυn = un+1υn = unυn = 1. (The situation for υ is symmetric.) Thus, aperiodic monoids are also called group-free.

Local divisors

We begin with a useful construction on monoids, which simplifies the proof of Theorem 7.22 and is also the main tool in Section 7.5. Local divisors also show up in Section 7.6. For further applications, we refer to [23–30].

Let M be a monoid and c ∈ M. We define a new operation ∘ on its subset cM ∩ Mc by

Assume that xc = x'c and cy = cy'. Then xc ∘ cy = xcy = x'cy = x'cy' = x'c ∘ cy'. This shows that ∘ is well defined. Let cx = xc and cy be elements of cM ∩ Mc. Then cx ∘ cy = x'c ∘ cy = x'cy = cxy. Computation rules of M carry over to cM ∩ Mc. In particular, the operation ∘ on cM ∩ Mc is associative, because the operation of M is associative. Thus, Mc = (cM ∩ Mc, ∘, c) is a monoid with c as its neutral element; it is called the local divisor of M at c. If xn = xn+1 for all x ∈ M, then a straightforward computation shows that we have yn = yn+1 for all y in the local divisor Mc, too. Indeed, let cx = yc ∈ cM ∩ Mc and n ∈ ℕ. Taking the fold power of xc in the monoid Mc, we obtain xnc. Thus, any local divisor of an aperiodic monoid is aperiodic. Actually, Mc is the homomorphic image of the submonoid { x ∈ M | xc ∈ cM } under the mapping φ(x) = xc. The mapping φ is a homomorphism since φ(x)φ(y) = (xc) ∘ (yc) = xyc = φ(xy) and φ(1) = c, which is the neutral element in Mc. Moreover, since each y ∈ Mc = cM ∩Mc can be written as y = xc, we obtain φ(x) = y and φ is surjective. Hence, Mc is indeed a “divisor” in the sense of Section 7.5. Moreover, if c is idempotent (i.e., c2 = c), then Mc is isomorphic to the so-called local submonoid cMc of M. These two properties coined the notion of local divisor. If M is aperiodic and 1 ≠ c ∈ M, then we have seen cm ≠ 1 for all m ∈ M. Therefore, |cM ∩ Mc| < |M|. This is the crucial property that make local divisors attractive for induction.

SF = AP

As an application of the algebraic approach for recognizable languages, we present a decidable characterization of star-free languages. Decidability means that for any standard way to represent a regular language L, say, for example, by an accepting NFA, there is an algorithm which returns “yes” if and only if L is star free. Moreover, in the positive case it gives a star-free expression for L.

The family SF(M) of star-free sets over M is inductively defined as follows:

Since SF(M) is closed under finite union and complementation, SF(M) is closed under finite intersection, too. In contrast to a regular expression, a star-free expression may use complementation, but but no Kleene star. This explains its name “star-free.”

Consider the singletons {aa} and {ab} in {a, b}∗. Singletons are star free by definition. In Example 7.25, we will see that {aa}∗ is not a star-free language, whereas {ab}∗ is star free (if a ≠ b). Thus, a star in the syntactic description does not tell us whether the corresponding language is star free or not. The example {aa}∗ also shows that the class of star-free languages is not closed under Kleene star. Regular star-free languages are regular. However, over arbitrary monoids, the class of rational sets and the class of star-free sets are incomparable, in general.

The next theorem by Schützenberger is often considered the second most important fundamental theorem on regular languages (after Kleene’s theorem).

Theorem 7.22 (Schützenberger). Let L ⊆ Σ∗ be a language over a finite alphabet Σ. Then the following assertions are equivalent:

The remainder of this section is devoted to the proof of this theorem. For a finite alphabet Σ, the class of regular star-free languages SF(Σ∗) can alternatively be defined as follows: first, 0 ∈ SF(Σ∗), second, if a ∈ Σ, then {a} ∈ SF(Σ∗), and third, for languages K, L ⊆ SF(Σ∗) the languages K ∪ L, Σ∗ L, and KL are elements of SF(Σ∗). Let Γ ⊆ Σ, then Γ∗ is star free

Moreover, SF(Γ∗) ⊆ SF(Σ∗) because given a star-free expression for L ∈ SF(Γ∗), we can substitute every complementation Γ∗ K by (Σ∗ K)∩ Γ∗. We can replace an intersection by using complementation, union, and complementation. This yields a star free expression for L over the alphabet Σ.

Lemma 7.23. The syntactic monoid of a star-free language is aperiodic.

Proof: We show that for every star-free language L ∈ SF(Σ∗), there exists a number n(L) ∈ℕsuch that for all x, y, u ∈ Σ∗:

□

We set n(0) = 1, and for a ∈ Σ, we define n({a}) = 2. Now let K, L ∈ SF(Σ∗) be languages for which n(L) and n(K) are suitably defined already. Then, we let n(Σ∗ L) = n(L), as well as n(K ∪ L) = max(n(K), n(L)) and n(KL) = n(K)+ n(L)+1. We only prove the correctness of n(KL); the according proofs for the other constructions are similar. Let w = xun(K)+n(L)+2y ∈ KL. We assume that the splitting of w = w1w2 into w1 ∈ K and w2 ∈ L is done within one of the u-factors. Splittings inside x or y are easier. Let u = uu, w1 = xun1u' ∈ K and w2 = uun2 y ∈ L with n1 +1+ n2 = n(K)+ n(L)+2. We have either n1 ≥ n(K)+1 or n2 ≥ n(L)+1.Without loss of generality, let n1 ≥ n(K)+1. By our assumptions, xun1−1u' ∈ K and hence xun(K)+n(L)+1y ∈ KL. Analogously, one can show that xun(K)+n(L)+1y ∈ KL implies xun(K)+n(L)+2y ∈ KL.

The difficult part in the proof of Schützenberger’s theorem is handled next. We present the proof from [62].

Lemma 7.24. If L ⊆ Σ∗ is recognized by a finite aperiodic monoid M, then L is star free.

Proof: Let φ: Σ∗→M be a homomorphism recognizing L.Wehave L =⋃p∈φ(L) φ−1(p). Therefore, it suffices to show for all p ∈ M, that φ−1(p) is star free. Let Σ1 = {a ∈ Σ | φ(a) = 1 }. In aperiodic monoids uυw = 1 implies uυ = 1 and this implies υ = 1. Hence,

□

Next, let p ≠ 1. For c ∈ Σ with φ(c) ≠ 1, we define Σc = Σ {c}. Restricting φ to the domain now yields the homomorphism with w ↦ φ(w). Since each word w with φ(w) ≠ 1 contains a letter c with φ(c) ≠ 1, we obtain

The language contains the prefix before the first c and corresponds to the suffixes after the last c. By induction on the size of the alphabet, we obtain that and are elements of It remains to show that for p ∈ φ(c)M∩Mφ(c) the language φ−1 (p)∩cΣ∗∩Σ∗c is star free. Let We define a substitution

where Here, T∗ denotes the free monoid over the set T rather than the Kleene star. The mapping σ replaces maximal c-free factors υ by φc(υ). Let ψ: T∗ → Mφ(c) be the homomorphism into the local divisor of M at φ(c), that results from T → M φ(c) with φc(w) → φ(cwc) by the universal property of free monoids (Theorem 6.1). For w = cυ1cυ2 ⋅⋅ ⋅ cυk ∈ {ε} ∪ cΣ∗ with and k ≥ 0, we have

Thus,

and hence φ−1(p) ∩ cΣ∗ ∩ Σ∗c = σ−1ψ−1(p) ⋅ c. Therefore, it is sufficient to show that σ−1ψ−1(p) ∈ SF(Σ∗). Recall that we have φ(c) ≠ 1, hence |Mφ(c)| < |M| since M is aperiodic. By induction on the size of the recognizing monoid, we obtain ψ−1(p) ∈ SF(T∗), and by induction on the size of the alphabet φ−c 1 (t) ∈ SF(Σ∗) for all t ∈ T. By structural induction, we now show that σ−1(K) ∈ SF(Σ∗) for every language K ∈ SF(T∗):

The last relation holds because of σ(cw1cw2) = σ(cw1)σ(cw2).

□

Proof of Theorem 7.22: If L is recognized by a finite aperiodic monoid, then, by Lemma 7.24, L is star free. If L is star free, then by Lemma 7.23 Synt(L) is aperiodic. With Kleene’s theorem (Theorem 7.17), we obtain SF(Σ∗) ⊆ RAT(Σ∗) and that all star-free languages are recognizable. By Theorem 7.9, Synt(L) is finite. Since Synt(L) recognizes the language L, there is some finite aperiodic monoid recognizing L. Schützenberger’s theorem follows.

Given a regular expression for L, we can effectively compute the corresponding syntactic monoid. Given a finite monoid we can check whether x|M|+1 = x|M| for all x ∈ M. This last condition expresses that a finite monoid is aperiodic. Thus, whether a given regular language is star free can be checked using this method.

Example 7.25. Let Σ = {a, b}. The language L = (ab)∗ ∈ RAT(Σ∗) is star free, because

The syntactic monoid of L has six elements {1, a, b, ab, ba, 0}. It is aperiodic because x3 = x2 for all elements x. In contrast, the syntactic monoid of the language (aa)∗ ∈ RAT({a}∗) is the group ℤ/2ℤ, so (aa)∗ is not star free.

◊

Star-free languages play a central role in formal verification. In this area, specifications are formulated using some simple logical formalism; and many popular logics turn out to have exactly the same expressive power as star-free languages. For a survey, refer to [24].

7.5 Krohn–Rhodes theorem

Krohn and Rhodes studied the structure of finite monoids via decompositions. In 1965, they showed that every finite monoid can be represented as a wreath product of flip–flops and finite simple groups [59]; here, a flip–flop is a three element monoid. A representation as a wreath product of flip–flops and finite simple groups is called a Krohn–Rhodes decomposition. The most common presentation of the Krohn–Rhodes theorem uses so-called transformation monoids; see [29, 38, 60, 87, 101]. The concept of transformation monoids is a mixture of automata and monoids. Gérard Lallement (1935–2006) published a proof of the Krohn–Rhodes theorem in 1971, which only uses monoids in the traditional sense [63]; unfortunately, his proof had a flaw, and the corrected version relies on a more technical notion of wreath products [64]. The proof presented here only uses monoids in the traditional sense, too, but it is inspired by a similar proof using transformation monoids [29]. The main technique is local divisors as introduced in Section 7.4. As a byproduct of this approach, we do not use any semigroups which are not monoids.

We start this section with an introduction to some useful terminology, including divisors and wreath products. In order to prove that a monoid T divides some given wreath product, it is often more illustrative to apply the so-called wreath product principle. Then, we consider flip–flops and their generalizations; monoids where every nonneutral element is a right zero. We present a decomposition technique for arbitrary finite groups into simple groups. A group G is simple if {1} and G are its only normal subgroups. The induction parameter in our proof of the Krohn–Rhodes theorem is the number of elements x satisfying {x} ≠ Mx ≠ M, that is, the elements which are neither a right zero nor invertible. We decompose a monoid M into a local divisor Mc and an augmented submonoid N#. The latter is a monoid extension of N, where, for every element x ∈ N, there exists a unique right zero such that for all x, y ∈ N. Moreover, the right zeros of N are also right zeros in N #

We need the following notions to state the Krohn–Rhodes theorem; further details aregiven in the following. AmonoidM is a divisor of a monoid N ifM is a homomorphic image of a submonoid of N. Let MN be the set of all mappings f : N → M. The wreath product M ≀ N is the set MN × N with the composition (f, a)(g, b) = (h, ab) where the mapping h : N → M is defined by h(x) = f(x)g(xa) for x ∈ N. The flip–flop monoid U2 = {1, a, b} with neutral element 1 is defined by xa = a and xb = b for all x ∈ U2.

Theorem 7.26 (Krohn, Rhodes). Let M be a finite monoid. Let CM be the closure of U2 and all simple group divisors of M under wreath products. Then M divides a monoid in CM.

A simple group divisor is a divisor which is a simple group. Another way of stating the Krohn–Rhodes theorem is by saying that every finite monoid M divides a sequence of wreath products where each factor is either the flip–flop U2 or a simple group divisor of M; such a sequence is called a Krohn–Rhodes decomposition of M. We note that the wreath product ≀ on monoids is not associative, that is, in general (M ≀ N) ≀ T is not isomorphic to M ≀ (N ≀ T). The corresponding operation on transformation monoids is associative.

Throughout this section, for a finite monoid M, we let CM be the smallest class of finite monoids containing U2 and the simple group divisors of M such that the wreath product of any two monoids in CM is again in CM. After some preparatory work (on divisors and wreath products), we prove the Krohn–Rhodes theorem by showing that it holds for bigger and bigger classes of monoids until, at the end of this section, we are able to give the proof for arbitrary monoids.

Divisors and surjective partial homomorphisms

Let M and N be monoids. If a submonoid U of N and a surjective homomorphism φ: U → M exist, then M is a divisor of N. In this case, we write M ≺ N. The intuitive idea is that N is more powerful than M (for instance, in the sense that every language recognizable by M is also recognizable by N). A group divisor is a divisor which forms a group. In many cases, it is more convenient to work with surjective partial homomorphisms to prove M ≺ N. A partial mapping ψ: N → M is a partial homomorphism if ψ(nn) is defined whenever both ψ(n) and ψ(n) are defined, and then we have ψ(nn) = ψ(n)ψ(n' ). As usual, the partial homomorphism ψ is surjective if for every m ∈ M there exists n ∈ N with ψ(n) = m. As shown in the following lemma, a surjective partial homomorphism is a mere reformulation of division.

Lemma 7.27. We have M ≺ N if and only if there exists a surjective partial homomorphism ψ: N → M.

Proof: First, let M ≺ N. Then there is a submonoid U of N and a surjective homomorphism ψ: U → M. The mapping ψ is a surjective partial homomorphism from N to M. For the other direction, let ψ: N → M be a partial homomorphism. The domain of ψ is a subsemigroup U of N. If U contains the neutral element 1 of N, then ψ(n) = ψ(n ⋅ 1) = ψ(n)ψ(1) for all n ∈ U. This shows that ψ(1) is neutral for all elements ψ(n). Since ψ is surjective, we obtain ψ(1) = 1.Hence, ψ: U → Mis a surjective homomorphism. If 1 ∉ U, let φ: U ∪ {1} → M be defined by φ(1) = 1 and φ(n) = ψ(n) for n ∈ U. Then U ∪ {1} is a submonoid of N and φ is a surjective homomorphism.

□

We freely apply Lemma 7.27 without further reference.

Lemma 7.28. If M ≺ N and N ≺ T, then M ≺ T.

Proof: Let ψ1 : N → M and ψ2 : T → N be surjective partial homomorphisms. Then their composition ψ1 ∘ ψ2 : T → M is a surjective partial homomorphism.

□

Wreath products

For a monoid M and an arbitrary set X, let MX = {f : X → M | f is a mapping }. For f, g ∈ MX, we define f ∗ g by (f ∗ g)(x) = f(x) g(x). The set MX can be interpreted as a product of |X| copies of M, and ∗ is the pointwise operation on the components. In particular, MX forms a monoid with ∗ as the operation.

Let M and N be two monoids. For g : N → M and a ∈ N the mapping ag: N → M is defined by (ag)(x) = g(xa). Note that a(f ∗ g) = af ∗ ag. We can now define an operation on MN × N as follows. For pairs (f, a) and (g, b) in MN × N, we set

For the set MN × N with this operation, we write

and call it the wreath product of M and N. Next, we show that M ≀ N forms a monoid. The neutral element is (ι, 1) with ι(x) = 1 for all x ∈ N. Consider (f, a), (g, b), (h, c) ∈MN × N. Then the following computation shows that the operation in M ≀ N is associative:

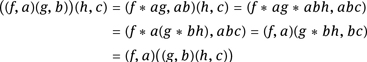
Next, we show that the direct product is a divisor of the wreath product.

Lemma 7.29. Let M and N be two monoids. Then M × N ≺ M ≀ N.

Proof: Let U be the submonoid ofMN ×N consisting of all the elements (f, a) such that f is constant, that is, there exists m ∈ M with f(x) = m for all x ∈ N. A surjective homomorphism φ: U → M × N is given by φ(f, a) = (f(1), a). Note that f(1) = f(x) for all x ∈ N since f is constant. This yields φ((f, a) (g, b)) = φ(f ∗ ag, ab) = (f(1) g(a), ab) = (f(1) g(1), ab) = (f(1), a) (g(1), b) = φ(f, a) φ(g, b).