For all subsets I ⊆ {1, . . . , n} and nodes b in G, we introduce an arc from b to b'' = (b − AeI )/2, provided b'' ∈ ℤn and ‖b‖1 ≤ ‖A‖1. The label of this arc is 2x + eI and denotes the affine mapping x ↦ 2x + eI.

This construction is “sound”: by following the arcs we cannot transform an unsolvable linear Diophantine system into a solvable one.

Next, we prove “completeness”: if b is any node in G and x ∈ ℕn is a vector solving Ax = b, then there exists a path in the graph G from b to the final node 0 such that h(0) = x, where h is the label of that path, interpreted as composition of mappings. We show this claim by induction on ‖x‖1.

The assertion is trivial for ‖x‖1 = 0, because then we must have x = b = 0. Thus, we may assume that at least one component xi of x = (x1, . . . , xn) is positive. As above, let I = {i ∈ {1, . . . , n} | xi is odd } and eI be the characteristic vector of I. Then b' = b − AeI ∈ 2ℤn and x'' = (x − eI)/2 ∈ ℕn satisfy Ax'' = b'' where b'' = b/2. Thus, we only need to show that b'' is a node in G, that is, ‖b‖1 ≤ ‖A‖1. This is immediate: we have ‖b‖1 ≤ ‖A‖1 and hence

We are done by induction because ‖x‖1 < ‖x‖1.

What we have shown is that on input (A, c) we can effectively construct a finite labeled graph G (of singly exponential size) with final state 0 and initial state c which, when viewed as a nondeterministic finite automaton, accepts a rational set R of affine mappings from ℕn to itself such that

Clearly, Ax = c has a solution if and only if R ≠ Ø.

Actually, the graph G is not optimal, as it might contain unreachable nodes and as it always has a selfloop around 0 labeled by x ↦ 2x, even if Ax = c has only finitely many solutions. This is something we do not like because the graph should be acyclic if there are finitely many solutions, only. We prefer to have a graph that encodes solutions in a more efficient way; it should be empty if there are no solutions and it should have no directed cycles if there are only finitely many solutions. For example, in the case that Ax = 0 where A is invertible, so x = 0 is the only solution, the graph we have constructed (and hence the rational set) contains the infinite set of mappings x ↦ 2ℓx for ℓ ∈ ℕ. We can remove the selfloop around 0 by introducing additional arcs. If we are at node 0 and x = 0, then we are at a final node and there is no need to use the selfloop x ↦ 2x at 0. Therefore, it is enough to consider a nonzero solution x of Ax = 0. Since x ≠ 0, there is some index 0 ≤ i ≤ n such that xi > 0. Then x' = x − e{i} ∈ ℕn solves Ax' = −Ae{i}, and we have ‖−Ae{i}‖1 ≤ ‖A‖1. Hence, −Ae{i} is a node in G. Thus, we simply add the n arcs from 0 to the nodes −Ae{i} for 1 ≤ i ≤ n and each such arc is labeled by x + e{i}.

This yields a new NFA '' which accepts the rational language R' = L('). The graph ' for the linear Diophantine system ((1, −1), 2) (representing x1 − x2 = 2) is depicted in Figure 7.3. We retain for R' the first two properties of R, but we also obtain a desirable third property

We can then trim the NFA by removing any node that does not lie on a path from initial to final states.

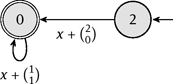
Example 7.65. For simplicity, let r = 1 and n = 2; there is only one equation with two variables. We consider the linear Diophantine system is Ax = 2 were A = (1, −1). We have ‖A‖1 = ‖2‖1 = 2. Hence G has five states: −2, . . . ,2, where 2 is initial and 0 is final. Replacing the loop around state 0 by arcs labeled x + e{i} yields the graph which is depicted in Figure 7.3. The state −2 does not lie on any path from the initial to final vertices; so removing the state −2 produces a smaller G. However, this is not the smallest NFA describing the set of all solutions. For example, an ad hoc construction shown in Figure 7.4 also describes all solutions; it has only two states.

Fig. 7.3. The NFA ' (before trimming) describing all solutions x ∈ ℕ2 of (1, −1)x = 2.

Fig. 7.4. The “minimal” NFA ? describing all solutions x ∈ ℕ2 of (1, −1)x = 2.

◊

Exercises

7.1. Consider the syntactic monoid Synt(L) for L = {anbn ∈ Σ∗ | n ∈ ℕ} with Σ = {a, b}∗ and a ≠ b. For u ∈ Σ∗ let [u] ∈ Synt(L) denote the syntactic congruence class of the word u.

7.2. A semigroup S is cyclic if there is an element x ∈ S with S = {xk | k ≥ 1 }. Determine all cyclic semigroups with n elements.

7.3. Let φ: Σ∗ → M be a homomorphism into a finite monoid M. Show that a number n ≥ 1 exists with φ(Σn) = φ(Σ2n). The smallest such number is called the stabilization index of φ.

7.4. Let M be a monoid and let L ⊆ M be recognizable. Show that the language { u ∈ M | uu ∈ L } is recognizable, too.

7.5. (Mezei’s theorem) Let M1 and M2 be monoids. Showthat L ⊆ M1×M2 is recognizable if and only if L is a finite union of languages of the form K1×K2 with K1 ∈ REC(M1) and K2 ∈ REC(M2).

7.6. Let A = (Q, ⋅, q0 , F) be a deterministic M-automaton. Then the complement automaton is B = (Q, ⋅, q0 , Q F). Show L(B) = M L(A).

7.7. Let A1 = (Q1, ⋅, q1, F1) and A2 = (Q2, ⋅, q2, F2) be two deterministic M-automata. For an arbitrary subset F ⊆ Q1 × Q2, one can construct the product automaton B = (Q1 × Q2, ⋅, (q1, q2), F) with (p, q) ⋅ a = (p ⋅ a, q ⋅ a).

7.8. Let Σ = {a, b} and L = ((ab)∗a ∪ abb)∗ ∈ RAT(Σ∗).

7.9. Minimize the following automaton.

7.10. (Brzozowski’s automata minimization) Let Σ be a finite alphabet. For a spelling nondeterministic finite Σ∗-automaton A = (Q, δ, I, F) let Aρ denote the automaton (Q, δρ , F, I), where δρ = {(q, a, p) | (p, a, q) ∈ δ } (the symbol ρ stands for reverse). The nondeterministic automaton Aρ accepts the mirror language L(A)ρ = { an ⋅⋅ ⋅ a1 | a1 ⋅⋅ ⋅ an ∈ L(A), ai ∈ Σ }. Finally, by ?(A) we denote the subset automaton of A. Show that for any deterministic finite Σ∗-automaton A = (Q, δ, q0, F), in which all states are reachable, the automaton ?(Aρ) is the minimal Σ∗-automaton for the language L(A)ρ.

Remark: This means that for each spelling nondeterministic automaton after the four operations mirror – subset construction – mirror – subset construction one ends up with the equivalent minimal automaton. This amazing observation is due to Brzozowski (born 1935) [11].

7.11. A nonempty class of finite monoids V is a variety (also called a pseudovariety in the terminology of universal algebra) if the following two closure properties are satisfied. (i) N ∈ V and N' ≺ N implies N' ∈ V. (ii) N1, N2 ∈ V implies N1 × N2 ∈ V. For any monoid M let ?(M) be the set of all subsets of M which are recognized by a monoid from the variety V. Show:

7.12. Let Σ be a finite alphabet and L ⊆ Σ∗. Show that the following properties are equivalent:

7.13. Let M be a finite monoid and C the smallest family of finite monoids containing U2 and being closed under wreath products and divisors. Show:

7.14. Let M and N be monoids and let φ: A∗ → M ≀N be a homomorphism. Show that there exist homomorphisms ? : A∗ → N and such that φ(u) = φ(υ) whenever ν(u) = ν(υ) and μ(σν(u)) = μ(σν(υ)).

7.15. Let M and N be monoids. A surjective partial mapping ψ: N → M is a covering if for each m ∈ M at least one element m̂ ∈ N exists with

for all n ∈ N, for which ψ(n) is defined. The element m̂ is called a cover of m. Show that M is a divisor of N if and only if there exists a covering ψ: N → M.

7.16. Give a covering from Un × U2 to Un+1.

7.17. Let M be a monoid generated by A; let c ∈ A and let N be the submonoid of M generated by A {c}. Give a covering from (UN × Mc) ≀ (N# × U1) to M.

7.18. Recall that Green’s relation Dis defined in an arbitrary monoid M as L ∘R. Show that D is an equivalence relation; that is, show L ∘ R = R ∘ L.

7.19. Let φ: Σ+ → S be a homomorphism into a finite semigroup S and let L ⊆ Σω. Show that L is recognized by φ if and only if the following equality holds:

7.20. Let φ: Σ+ → S be a homomorphism to a finite semigroup S. Define the relation ∼φ on Σω by letting α ∼φ β if there are factorizations α = u1u2 ⋅⋅ ⋅ and β = υ1υ2 ⋅⋅ ⋅ such that ui, υi ∈ Σ+ and φ(ui) = φ(υi). Show that φ recognizes L if and only if from α ∈ L and α ∼φ β it follows that β ∈ L.

7.21. In Remark 7.50, we discussed several variants of Büchi automata: acceptance either by states or transitions and allowing that labels on transitions are words instead of letters. We may also allow a set of initial states and/or that there are no incoming arcs into initial states. Show that these variants do not change the expression power of Büchi automata.

Summary

Notions

Methods and results