Here, ⊕ is the bitwise exclusive-or. All these mappings can easily be computed (assuming that this is the case for ck), but they are difficult to invert if we have a good encryption function. More robust statements are usually not available. On the one hand, this is because such statements about the security of encryption functions are not known; however on the other hand, it is also important how ⊕ and ck behave relative to each other. If, for example, ck(x) = x ⊕ k, then all of the above compression functions are easy to invert.

Merkle–Damgård construction

We now assume that we have a collision resistant compression function g : 2n →n; for example, we may use one of the functions defined above, if we have a sufficiently good encryption function. Using g, we intend to construct a collision resistant hash function h : ∗ → n. For this purpose, we use the Merkle–Damgård-construction designed by Ralph C. Merkle (born 1952) and Ivan Bjerre Damgård (born 1956). To simplify the presentation, we assume that we only compute hash values of messages with less than 2n bits. For the typical value of n = 128, this number is greater than the estimated number of atoms in the universe. Collisions with more than 2128 bits could not be written down anyway.

So let x ∈ ∗ be any word with less than 2n bits. We add as few zeros as possible on the right of x in order to obtain a word x' whose length is divisible by n. Let ℓx ∈ n be the binary encoding of the length of x; we allow leading zeros such that ℓx has length n. The length of the word x̄ = xℓx is divisible by n. We can therefore write x̄ = x1 ⋅⋅ ⋅ xs with xi ∈ n and s ≥ 1. Note that xs = ℓx. Now, we let H0 = 0n ∈ n and Hi = g(Hi−1 ⋅ xi) for i ≥ 1; here, ⋅ denotes the concatenation operation. The hash value of x is defined as

Suppose, we know two different words x, y ∈ ∗ of length less than 2n satisfying h(x) = h(y). We show that, under this assumption, we are able to find a collision for g; to do that, we define x̄ = x1 ⋅⋅ ⋅ xs and ȳ = y1 ⋅⋅ ⋅ yt as extensions of x and y as defined above, with xi , yi ∈ n. Let H 0, . . . , H s be the intermediate values in the computation of the hash value of x, and G0, . . . , Gt those for y. Without loss of generality, let s ≤ t. If Hs−i−1 ≠ Gt−i−1 and Hs−i = Gt−i, then

is a collision of g, as both words are mapped by g to Hs−i. If this situation does not occur, then, since Hs = h(x) = h(y) = Gt, the property Hs−i = Gt−i holds for all i ∈ {0, . . . , s}. Under this assumption, we show that there is an index i ∈ {0, . . . , s−1} with xs−i ≠ yt−i. If, on the contrary, we have xs−i = yt−i for all 0 ≤ i < s, then in particular ℓx = xs = yt = ℓy. Consequently, x and y have the same length, resulting in s = t and x = y; this is a contradiction. Thus, an index i ∈ {0, . . . , s−1} with xs−i ≠ yt−i exists. Then, (Hs−i−1 ⋅ xs−i, Gs−i−1 ⋅ ys−i) is a collision of g. Therefore, if g is collision resistant, then h is collision resistant.

2.12 Digital signatures

In 1991, the Digital Signature Algorithm (DSA) was proposed by the US National Institute of Standards and Technology (NIST). To send an appropriately signed message, a random number generator and an efficient primality test are required. Additionally, one relies on well-known secure hash functions, like the ones described in the previous section. A hash function computes a small fixed-length value from an arbitrarily long bit string. In the scenario of DSA, hash values with bit length 160 are needed.

We now describe the nine steps Alice has to perform in order to sign a message according to the DSA standard. The first five steps are independent of the message content:

It might be unclear what mod p means and why Alice succeeds in finding such an element g. We know that the multiplicative group is cyclic, and since q | p − 1, it has a unique subset U of order q. In fact, Alice needs a generator g of U. For each the element is in U, which is guaranteed by Fermat’s little theorem. If g ≢ 1 mod p, then g is a generator because q is prime. The chance of finding a generator of U is very high: the homomorphism with f ↦ f k is surjective and all elements of U aremet equally often. Therefore, the probability for g to generate the group U is 1 − 1/q.

The method’s security depends on the fact that no efficient algorithm is known for computing x ∈ {1, . . . , q − 1} from y ∈ {1, . . . , p − 1}. The only known method is to compute the discrete logarithm of y to base g. The order q has a binary length of 160 bits and should thus be too large to do that.

After these general preliminaries, we now describe the steps that Alice needs to perform when sending a signed message m to Bob.

The last step is possible because ℓ ∈ (ℤ/qℤ)∗. The signature of the message m is the pair (r, s), and Alice sends (m, r, s) to Bob. The signature is a bit string of length 320, that is 40 bytes.

If Bob receives a message m with signature (r, s), he verifies the signature as follows. He computes the hash value h and then u = s−1h mod q and υ = s−1r mod q. Then, he checks whether the following congruence holds:

If the congruence is satisfied, he accepts the signature. In order to see that all correctly built signatures are accepted, we consider the following lines. From Alice’s computations, we know that sℓ ≡ h + xr mod q. This yields

and consequently r ≡ (guyυ mod p) mod q, as desired. Note that the signature (r, s) only fits to one single hash value h. Thus, it is not possible to eavesdrop on a signature (r, s) and use it for a different message m' with the hash value h' ≠ h.

Suppose that Oscar tries to fake a signature. We may assume that he is using the correct hash value h for the message m. The problem for Oscar is that, after the values (h, r, s) have been chosen, the values of ℓ mod q and x mod q directly determine each other. So, Oscar can then compute ℓ if and only if he can compute x. If he has no information about x at all, then for him all elements gℓ ∈ U are equally likely. For solving the congruence r ≡ (gℓ mod p) mod q, nothing better is known than computing the discrete logarithm of y to base g. In order to prevent the public key (q, p, g, y) from being compromised, one can use certification agencies for signing the public key.

As a second method for digital signatures, let us mention RSA signatures. The idea here is to reverse the order of encryption and decryption in a cryptosystem. The RSA algorithm works correctly, because the encryption function c and the decryption function d aremutually inverse functions. Bob knows Alice’s public RSA key and can compute the encryption function c, but only Alice knows the decryption function d. If Alice wants to send a signed message m to Bob, then she computes the hash value h(m) and sends the pair (m, d(h(m))) to Bob. Bob, receiving a message (m, s) from Alice, computes h(m) and accepts if h(m) = c(s). If the message indeed originates from Alice, then c(s) = c(d(h(m))) = h(m).

2.13 Secret sharing

Secret sharing is about the following situation: Alice wants to distribute a secret s among n people in such a way that t of these people together are able to reconstruct s; however, if less than t people meet, it must not be possible for them to gain any information about s. Mechanisms like this are often used in access controls for systems or information: for instance, one can imagine a company with twenty employees to have a very important customer data base. This data base is encrypted with a key s. The owner, Alice, does not want any single employee to gain access to the data base because he could steal the file and sell it to a competitor. But if three or more employees meet, they should be able to work with the customer data base. It should not matter at all which three of the twenty employees are trying to access entries of the customer file. Another useful property is the ability to add another person with access to the secret s. In the above example, Alice could hire more employees.

We first consider a mechanical solution of this problem. Suppose that the secret is hidden behind some door. Alice could build a door with several locks such that each lock has to be unlocked before the door opens. For every lock, she can produce arbitrarily many keys. Let {1, . . . , n} be the set of employees, and let A1, . . . , Am be the subsets of {1, . . . , n} with t − 1 elements. We note that Alice builds m locks, each one labeled by a subset Aj.

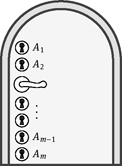
An employee i ∈ {1, . . . , n} gets the key to lock Aj if and only if i ∉ Aj. Therefore, if B = Aj is a meeting of t − 1 employees, then none of the employees in B has the key to the lock Aj. In particular, no subset of less than t employees can open the door. On the other hand, if B is a subset of at least t employees, then B Aj ≠ 0 for all j ∈ {1, . . . , m}. This shows that every key is in the possession of some member in B and thus, the group B can open the door.

In order to implement this method without physical locks, Alice could fix a large finite commutative group G, for instance, Alice could use G = ℤ/nℤ. We assume that the secret is an element s ∈ G. Every key to the virtual lock Aj is a pair (j, gj) where gj is a random element in G, except for gm, which is chosen as Then, all keys together can recover On the other hand, if some key is missing, then all elements in G could be the secret key (with the same probability if the elements gj are chosen independently and uniformly at random). The purpose of the first component in the keys is to (easily) allow gj = gk for j =k.

If Alice hires a new employee n + 1, she has to install new locks. The labels of these locks are subsets Bj of {1, . . . , n + 1} with n + 1 ∈ Bj and |Bj| = t − 1. Thus, in the physical setting, the new employee n + 1 gets the keys to all the old locks, and the keys to the new locks are distributed accordingly among the old employees. In the virtual implementation, Alice has to choose a new element gj ∈ G for every lock but one, including the old locks. The remaining key is chosen such that the sum yields s. If Alice keeps the old keys for the locks A1, . . . , Am, then the new employee can recover the secret s all on his own by summing up his keys.

The large number of keys and the difficulties when adding participants are serious drawbacks. These problems are solved by an approach developed by Shamir [94].

Shamir’s secret sharing scheme

We assume that the secret s is a natural number: for instance, s could encode a password in decimal. Alice first chooses a prime number p which should be much larger than n and s. The prime number p is published. Now, Alice constructs a random polynomial a(X) by choosing coefficients a1, . . . , at−1 ∈ p independently and uniformly at random. These coefficients together with the secret s define the polynomial

The degree of a is smaller than t, and at 0, the polynomial a evaluates to a(0) = s. Next, Alice communicates the information (i, a(i)) to person i using a secure channel. If t or more of these people work together, they can reconstruct the coefficients of the polynomial a with their t values and, thus, the secret s. For instance, they may use Lagrange interpolation. For t pairwise different elements x1, . . . , xt ∈ p, the ith Lagrange polynomial ℓi(X) is defined by

Thus, ℓi is a polynomial of degree t − 1, and

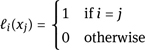
If a(x1), . . . , a(xt ) are known, we can determine ã (X) = Σ1≤i≤t a(xi)ℓi(X). The polynomial a(X)−ã(X) has zeros in each of x1, . . . , xt. Since the degree of a(X)−ã(X) is at most t − 1, it has to be the zero polynomial. We conclude a(X) = ã(X). This shows that t or more people can reconstruct the secret s. It is also easy to see that further people can be added easily.

We still have to show that less than t people are not able to obtain information about the secret s. For this, let t − 1 different points (xi , a(xi)) ∈ (p {0}) × p for i ∈ {1, . . . , t−1} be known. If less than t−1 points are known, even less information is available. By Lagrange interpolation, there are p polynomials ã(X) ∈ p[X] of degree less than t satisfying ã(xi) = a(xi) for all i ∈ {1, . . . , t − 1}. Each of these polynomials would result in a different secret s̃ = ã(0). Since each such polynomial ã(X) is equally likely, every secret s̃ is equally likely. We note that if we had used ℤ or ℚ instead of p, then the possible elements s̃ could not all have the same probability; in addition, the coefficients ai could not be chosen uniformly at random.

2.14 Digital commitment

The following conversation between Alice, an employee of the investment advisory company Ruin Invest, and a potential customer Bob was intercepted.4

Bob: Tell me five shares you recommend for purchase. If they all rise during the next month, then I will be your customer.

Alice: If I told you the shares, then you could invest without paying us. I suggest you look at our recommendations of the last month. You will be amazed what gains you would have made on a purchase.

Bob: How can I be sure that you really recommended these shares? You could just pick five winners. If you now tell me ongoing shares, I know you cannot change your choice. I would not cheat and invest in the shares you recommended.

Alice: We do not cheat either, and we will tell you the recommended shares of the last month.

The mutual distrust leads to a problem here. As a mechanical solution, the current recommendation could be deposited in a sealed envelope at a safe place. Then the choice could be checked afterward. An electronic version to solve this problem is referred to as digital commitment. Alice commits herself to an information t (here just 1 bit). Using a symmetric encryption method, the following steps are performed:

Thus, Alice has committed herself to xt. Later on, Bob can verify Alice’s choice:

How can Alice cheat? She could try to find a key k' resulting in a desired t. But then also dk' (y) = xt' has to hold for the random string x. With a randomly selected key k, this corresponds to a known plaintext attack, which a good cryptosystem should be able to withstand. Bob is in an even worse position because, besides the secret text y, he only knows a prefix of the plaintext (namely, x).

A public collision resistant hash function f can also be used to make a commitment. The protocol for this is as follows:

Now again Alice has committed herself to t. Later, Bob can verify Alice’s information t:

Since f is difficult to invert, Bob cannot determine the bit t before he receives x1x2t (especially because several preimages of f(x1x2t) could have the prefix x1). Disclosing a part of the random information makes it possible to check whether Alice chose special strings that would make it easier to find a collision. So Alice has to disclose the “true” value of t. The main advantage of this protocol is that Bob does not have to send any messages: for instance, Alice could use a radio station, newspaper ads, a web page or her Twitter account.

Example 2.5. Alice and Bob have a telephone conversation. They want to decide who has to attend the cryptography course the next day to take notes. For this purpose, each of them flips a coin. If both have the same result (both have heads or both have tails), then Alice has to attend the course; otherwise Bob has to go. If Alice tells Bob the result of her coin toss, he could choose his result such that Alice has to go; conversely, the same situation occurs if Bob is the first to tell the result of his coin toss. Therefore, they agree on the following protocol. Alice commits to a bit t, then Bob tells Alice his coin toss result in form of a bit t. Finally, Alice reveals her bit t, and both of them know who will attend the course.

◊

2.15 Shamir’s attack on the Merkle–Hellman cryptosystem

The Merkle–Hellman cryptosystem is based on the knapsack problem, which is one of the classical NP-complete problems [44]. The cryptosystem was developed by Merkle and Hellman and published in 1978 [75]. Their hope was to have designed a secure cryptosystem that is based on a provably hard problem (unless P = NP). This hope did not last long: soon after its presentation, it was destroyed by Shamir.

In the following, we describe the Merkle–Hellman scheme in its original form and, after that, we explain Shamir’s method for breaking it. The presentation essentially follows [95], but in a somewhat less technical (and less general) way.

The input to the knapsack problem is a sequence (s1, . . . , sn , c) of natural numbers in binary, and the question is whether there is a subset I ⊆ {1, . . . , n} such that

We understand c to be the capacity of a knapsack and si the size of the i th piece. Then, we want to know whether it is possible to fill the knapsack completely. The algorithmic difficulty arises from the binary encoding of the numbers, because when the numbers are given in unary, then the problem is solvable in polynomial time; see Exercise 2.18. On the other hand, the problem becomes very simple in some special cases, even if the inputs are in binary.

We call a sequence of positive real numbers (s1, . . . , sn) superincreasing if sj > for all 1 ≤ j ≤ n. The sequence si = 2i for i ∈ ℕ is superincreasing, whereas the Fibonacci sequence F i is not. The knapsack problem for superincreasing sequences is solvable in linear time: when considering si in the order from n down to 1, one has to include i in I if and only if the remaining capacity suffices. In particular, solutions are unique.

The Merkle–Hellman cryptosystem

The cryptographic idea is to hide the property of being superincreasing by a modulo computation. The Merkle–Hellman cryptosystem consists of two parts: one private and one public. Alice secretly chooses a superincreasing sequence (s1, . . . , sn) and a modulus m. This number has to satisfy Preferably, m should be prime because Alice needs two more secret numbers u, w ∈ {2, . . . , m − 1} such that uw ≡ 1 mod m. Concretely, it was suggested to have n = 100 and the numbers si having n+i−1 bitswhilemshould have 2n bits. In order to hide the order of the numbers si ,Alice chooses a permutation π on {1, . . . , n}. She publishes a sequence (a1, . . . , an) with values 0 < ai < m and

aπ(i) = siu mod m

Then, ai is a number with 2n bits. Bob encrypts a bit string (x1, . . . , xn) ∈ n of length n by the sum

Bob sends y to Alice on a public channel. It follows y < n22n, so y consists of about 2n + log n bits. Alice receives y and computes c = yw mod m. She knows

and by the choice of m this yields c = Σi≤n xπ(i)si. Since (s1, . . . , sn) is superincreasing, she can reconstruct the sequence (xπ(1), . . . , xπ(n)) ∈ n and therefore she knows all the xi for 1 ≤ i ≤ n.

Shamir’s attack

We will show that the Merkle–Hellman system in the form just described is insecure and can be broken. The crucial observation is that it is neither necessary to compute the permutation π nor the sequence (s1, . . . , sn) nor the numbers m, or w. The attacker aims for a permutation σ, a superincreasing sequence of positive rational numbers (r1, . . . , rn, 1), and a number V with 0 < V < 1 such that

ri ≡ aσ(i)V mod 1

Here, a ≡ b mod 1 means that the difference a − b is an integer. If the aim is achieved, it follows that

Since and because the sequence of the ri is superincreasing, an attacker obtains all xσ(i) efficiently. We may have π ≠ σ, but the interest is in the sequence (x1, . . . , xn), only. Since σ and the xσ(i) are known, the xi can be computed.

It is not clear how an attacker can achieve this task, but there is a very important aid: the attacker knows that σ, the sequence (r1, . . . , rn), and the number V exist: consider σ = π, ri = si/m, and V = w/m. We fix the unknown value υ = w/m and we try to approach υ with our value V.

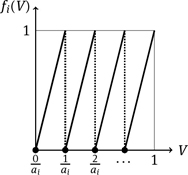
For each index i ∈ {1, . . . , n}, we consider the function fi : [0, 1) → [0, 1) with fi(V) = aiV mod 1. As usual, we have [0, 1) = { x ∈ ℝ| 0 ≤ x < 1 }. The graph of this function is a sawtooth wave. There are exactly ai zeros 0, 1/ai, . . . , (ai − 1)/ai; and, except for the jumps, the slope is always ai. In the following, numbers of the form q /ai with 0 ≤ q < ai are called positions.

At the point υ, the function fπ(i) evaluates to

Since (s1, . . . , sn, 1) is superincreasing, this means that the permutation π is determined by the order of the values fi (υ).This is the crucial observation that makes breaking the Merkle–Hellman method possible. The problem is now reduced to finding a sufficiently good approximation of the value υ.

There are less than n4 possibilities for the initial sequence (π(1), . . . , π(4)). Without loss of generality, we can assume to be in a phase of the attack where the values π(1), . . . , π(4) are correct. If the initial sequence is not correct, it is not clear whether the aim will be achieved. If the aim is not achieved, then we try the next possibility for π(1), . . . , π(4). If the aim is achieved with an incorrect hypothesis for π(1), . . . , π(4), this does not matter. Thus, after a maximum of four exchanges in the sequence (a1, . . . , an),we can assume that we have π(j) = j for 1 ≤ j ≤ 4; and, without restriction, a1, . . . , a4 correspond to the smallest values s1, . . . , s4.

Let J = {1, 2, 3, 4}. We choose λ ≥ 0 with aj > 22n+j−λ for all j ∈ J. The attack is easier if λ is small. If a1, . . . , a4 were uniformly distributed, then we would expect λ ≤ 8. From a practical viewpoint, this justifies assuming that λ is a small constant. Actually, a weaker assumption suffices in the mathematical analysis. Later, we see that the attack is successful with high probability as long as λ is sublinear.

Next, we consider for each j ∈ J a natural number cj with 0 < cj < aj and

where 0 ≤ εj < 1/aj. We have ajυ = cj + ajεj and thus ajυ mod 1 = sj/m = ajεj < 1 for all j ∈ J (because π(j) = j for j ∈ J). From the estimations m > 22n − 1, aj > 22n+j−λ and sj < 2n+j−1 (from the bit length of sj), we conclude 22n−1+2n+j−λεj < 2n+j−1 and thus

Let ℓ ∈ J be such that for all j ∈ J. In the following, we assume that cℓ ≠ 0. We discuss this again later and provide a justification for the assumption. For the time being, we can consider the case cℓ ≠ 0 as the case to treat first. From (2.1) and (2.2), we obtain

Because of cℓ ≠ 0, the following system of Diophantine inequalities in the four unknowns cj with j ∈ J has an integer solution:

By υ, we know that at least one solution of the system (2.3) is guaranteed. For the following,weonlyneedthevalue cℓ and the index ℓ ∈ J. However, we need to compute all possible solutions for each ℓ ∈ J and thus, a priori, we obtain a list cℓ,1, cℓ,2, cℓ,3, . . . . The number of ℓ ∈ J is only 4, but the respective lists could become too long and thus cause the attack to fail. But the following heuristic shows that one does not have to be afraid of the lists becoming too long. On the contrary, we can assume that we will find exactly one ℓ and only one cℓ ≠ 0, and even this only if we investigate the correct set {π(1), . . . , π(4)}. In all other cases, it is likely that no solution will be found (which then also shows that {π(1), . . . , π(4)} was not chosen correctly).

To explain the heuristic, we assume for the moment that the numbers aj for j ∈ J are independently and uniformly distributed random variables. If we fix a position 0 < p/aℓ < 1, then the probability for the interval

to have a nonempty intersection with each set of positions ℕ/aj for j ∈ J{ℓ}, is at most (2−n+λ)3 = 2−3n+3λ. Summing up over all positions, we obtain the result that there exists a solution with a probability which is at most 2−n+3λ. If λ is sublinear, then this probability converges to zero. (For λ ∈ O(1), the probability approaches zero exponentially fast.) A problem with the estimation is that the values aj are not independent and, for the right choices of {π(1), . . . , π(4)} and ℓ, there exists some solution. However, in many cases there is only one (or very few) solutions. Moreover, from the user perspective, wemust deal with the case where the solution (cj)j∈J ∈ ℕ4 is unique. This solution can be found by standard methods in polynomial time as there is only a constant number of inequalities.

Should there be, contrary to expectations, several solutions, an attacker might find all solutions by checking them one by one. For simplicity, we may assume that {π(1), . . . , π(4)} is correct and for this choice exactly one solution cℓ of the system (2.3) with ℓ ∈ J exists and that cℓ and ℓ ∈ J are known.

Defining α = cℓ/aℓ and ε = 2−3n+λ, from Equation (2.1), we obtain the property υ ∈ [α, α + ε]. For each index 1 ≤ i ≤ n, at most one position p/ai can be within the interval [α, α+ε] because the distance between p/ai and (p+1)/ai is too large for ε. The graph of the function fi with fi(V) = aiV mod 1 within the interval [α, α+ε] therefore consists of at most two segments, which can easily be computed. There are at most (n2) intersections, and we partition the interval [α, α + ε] in at most (n2) subintervals such that no intersections and no positions are in the interior of the subintervals. Since (0, s1/ m, . . . , sn/ m, 1) is superincreasing, υ has to be in the interior of such a subinterval. This is a good occasion to reintegrate the previously excluded case cℓ = 0, which leads to the special case α = 0. Within the interval [0, ε], there are no intersections at all, and we only get one additional interval (0, ε) with the possibility υ ∈ (0, ε). Now, let (β, β+δ) be the interior of a subinterval (where now we allow β = 0 and δ = ε). The graph of each function fi yields a unique segment within (β, β + δ). Thus, the segments are linearly ordered from bottom to top and this defines a permutation σ.

For every V ∈ (β, β + δ), the corresponding permutation σ has the property

Only very few of these sequences (aσ(1)V mod 1, . . . , aσ(n)V mod 1, 1) will be superincreasing. However, at the latest during the attack phase, in which the guess of {π(1), . . . , π(4)} and cℓ is correct, the existence of such a sequence in one of the subintervals is guaranteed. In this phase, it is the interval (β, β + δ) with υ ∈ (β, β + δ). Here, σ coincides with π. Of course, we do not know at all whether we are in the right phase or at the right β. But we know that this is possible and we just want to check whether (aσ(1)V mod 1, . . . , aσ(n)V mod 1, 1) is superincreasing.

First, for 1 ≤ i ≤ n, we define natural numbers ci by ⌊aiβ⌋. Then, for V ∈ (β, β+δ), we have aiV mod 1 = ai − ci.

For each interval (β, β + δ) with associated permutation σ we obtain the following n + 3 linear inequalities in the indeterminate V:

Writing this in a clearer form, we obtain

For any choice of β, this yields two rational numbers 0 ≤ L, R ≤ 1 with the solution set V ∈ (L, R). In the correct phase and if υ ∈ (β, β + δ) is true, then υ lies inside such an interval (L, R). Thus, it is guaranteed to find an interval with L < R.

We take and define rσ(i) = aσ(i)V − cσ(i). Then the aim of the attack is reached because the sequence (0, r1, . . . , rn, 1) is superincreasing. We can now decrypt all messages.

We have a look again at the complexity of the attack. In the worst case, we have to test (n4) cases to find π(1), . . . , π(4). For each of these possibilities, solutions (cj)j∈J ∈ ℕ4 are found in polynomial time, provided they exist. One can assume that once solutions exist, they are unique. But even a very generous estimate, a polynomial number of solutions would not detract from the fundamental strength of the attack. Next, for each choice of π(1), . . . , π(4) and each solution (cj)j∈J ∈ ℕ4 only (n2) intervals are considered. Each of these intervals defines a system of linear inequalities in one variable V. These are only polynomially many. At least one of these systems of equations defines a superincreasing sequence (rσ(1), . . . , rσ(n), 1). The Merkle–Hellman encryption is ineffective.

As noted by Shamir, there is another weak point of the Merkle–Hellman cryptosystem: the attack can start long before the transmission of the first message, because the calculations can start as soon as Alice publishes the parameters. We might have days or weeks to find σ and a superincreasing sequence (rσ(1), . . . , rσ(n)). The selected parameters can be verified by encrypting self-chosen plaintexts.

Exercises

2.1. Decrypt the communication between Frederick the Great and Voltaire on page 49.

2.2. Is it true that every encryption function with a finite set of ciphertexts (for fixed key k) has to be surjective?

2.3. Let n = 7 ⋅ 11 = 77 and e = 43.

2.4. (Multiple exponent attack) A message x was encrypted using the two RSA keys (551, 5) and (551, 13). The resulting ciphers are 514 and 438, respectively. Determine the plaintext x.

2.5. (Multi-prime RSA) Let p1, . . . , pm be m different prime numbers, let n = p1 ⋅⋅ ⋅ pm, and let s ⋅ e ≡ 1 mod φ(n). Messages x, y ∈ {0, . . . , n − 1} are encrypted by c(x) = xe mod n and decrypted by d(y) = ys mod n. Show that the method is correct, that is, d(c(x)) = x holds for all x ∈ {0, . . . , n − 1}.

2.6. Let n = 11 ⋅ 23 = 253.

2.7. Let n = 2 ⋅ 23 + 1 = 47 and g = 5.

2.8. Let h : X→Y be a compression function. For y ∈Y, we define ‖y‖=|{ x | h(x)=y }|. Furthermore, let N be the number of collisions of h and m = Σy∈Y ‖y‖/|Y| the average size of ‖y‖. Show the following relationships:

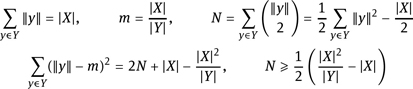
2.9. Let h1 : {0, 1}2m → {0, 1}m be a collision resistant compression function. The functions hi : {0, 1}2im→{0, 1}m for i>1aredefinedby hi(x1x2)=h1(hi−1(x1)hi−1(x2)) for x1, x2 ∈ {0, 1}2i−1m. Show that the hi are collision resistant, too.