8 Discrete infinite groups

This chapter concerns some fundamental issues in combinatorial group theory with a focus on discrete infinite groups. The idea is to prepare the reader for more advanced books such as [7, 8, 15] or the classics like [69] or [93]. In particular, we discuss amalgamated products, HNN extensions, and their normal forms. We cover free groups and their rational subsets, and show that automorphism groups of finitely generated free groups are finitely generated themselves. The proof is based on simple transformations of finite edge-labeled graphs, which have an interpretation in terms of Whitehead automorphisms. Finally, we take a quick look at geometric aspects by determining the algebraic structure of SL(2, ℤ) as the amalgamated product of ℤ/6ℤ and ℤ/4ℤ over their subgroups of order 2, and by determining the algebraic structure of the modular group PSL(2, ℤ) as the free product of ℤ/3ℤand ℤ/2ℤ. The notion of confluent string rewriting is central to our approach.

8.1 Classical algorithmic problems

The most fundamental algorithmic problems for finitely presented groups, formulated in about 1910 by Max Dehn (1878–1952) [21], are as follows:

It turns out that these problems are undecidable, but this was not known until the mid-1950s. Undecidability of the word problem in finitely presented groups was shown independently in Russia by Pyotr Sergeyevich Novikov (1901–1975) and in the West by William Werner Boone (1929–1983). A modern proof for the (difficult) undecidability result of the word problem can be found in [100]. The word problem is a special instance of the conjugacy problem, and once we know that the word problem is undecidable, it is fairly easy to see that the isomorphism problem is undecidable, too. The isomorphism problem was actually raised first by Heinrich Franz Friedrich Tietze (1880–1964) in [104].

8.2 Residually finite monoids

In this chapter, we discuss some sufficient criteria for the decidability of the word problem: for example, if we can embed a finitely generated group G into a group of invertible n × n matrices over some suitable ring or field, say, over the rationals ℚ, then the word problem can be solved “easily” by computing the product of matrices. Checking that a product of matrices over the rationals A1 ⋅⋅ ⋅ Ak is the identity matrix can be further reduced to computing the product of matrices with integer coefficients where, moreover, each matrix has determinant 1. Thus, the word problem in G can be effectively reduced to the computation of products of matrices in the special linear group SL(n, ℤ). Given a product A = A1 ⋅⋅ ⋅ Ak with Ai ∈ SL(n, ℤ) such that A = (aij) is not the identity, we have either aii ≠ 1 for some i or aij ≠ 0 for some i, j with i ≠ j (or both). Hence, there is some prime p such that aii ≢ 1 mod p or aij ≢ 0 mod p. In other words, if A = (aij) ≠ 1 in SL(n, ℤ), then the canonical homomorphism of SL(n, ℤ) onto the finite group SL(n, ℤ/pℤ)witnesses A ≠ 1 because (aij mod p) ≠ 1 in SL(n, ℤ/pℤ). This leads to the notion of residual finiteness which we define for monoids.

We say that a monoid M is residually finite if, for each m, n ∈ M with m ≠ n, there exists some homomorphism h : M → N onto a finite monoid N such that h(m) ≠ h(n). If M = G is a group, this is equivalent to saying that for each g ≠ 1 there exists a homomorphism h : G → N onto a finite group G such that h(g) ≠ 1 (which is the classical definition of residually finite groups). We have just seen that SL(n, ℤ) is residually finite; and, as a consequence, all subgroups of SL(n, ℤ) are residually finite, too.

A group G is called Hopfian if each surjective homomorphism from G to G is an automorphism. The notion of Hopfian group is named after Heinz Hopf (1894–1971). Exercise 8.9 shows that all finitely generated residually finite groups are Hopfian. It is known that SL(n, ℤ) is finitely generated for all n ≥ 1; therefore, all SL(n, ℤ) are Hopfian. We study SL(2, ℤ) more closely in Section 8.12.

8.3 Presentations

The notion of a presentation using a semi-Thue system provides an important technical tool to study various algorithmic problems for monoids and groups, including the word problem.

Throughout this section, Γ denotes an alphabet. Here an alphabet is a (possibly infinite) set of elements, called letters. We follow the notation from Chapter 6. A word is a sequence of letters w = a1 ⋅⋅ ⋅ am with m ∈ ℕ and ai ∈ Γ for 1 ≤ i ≤ m. The integer m is the length of the word w, which is denoted by |w|. The empty word has length 0, and frequently we denote it by 1 or ε. The set Γ∗ of all words in Γ becomes a free monoid, where the multiplication is the concatenation (a1 ⋅⋅ ⋅ am) ⋅ (b1 ⋅⋅ ⋅ bn) = a1 ⋅⋅ ⋅ amb1 ⋅⋅ ⋅ bn.

If Γ is equipped with a linear order <, then this order induces a lexicographic order on Γ∗. The words are then arranged as in a dictionary: if a, b ∈ Γ with a < b, then a word of the form pau is prior to each word of the form pbυ. One problem with this order is that, prior to b, there are infinitely many words which start with a. This problem can be avoided by considering the length-lexicographic (or shortlex) order, where we have u < υ if |u| < |υ|, and if |u| = |υ| then we order u and υ with respect to the lexicographic order. If Γ is finite, then there are only finitely many words prior to u ∈ Γ∗. Thus, using a shortlex-ordered lexicon, we can find any u ∈ Γ∗ in a finite amount of time.

If Mis any monoid, then we may uniquely extend each mapπ : Γ → M to a monoid homomorphism π : Γ∗ → M such that π(a1 ⋅⋅ ⋅ am) = π(a1) ⋅⋅ ⋅ π(am). Hence, we have a free choice for letters to assign monoid elements, and for each choice we obtain a unique homomorphism. This explains the term free monoid for Γ∗, which was already more specifically described in Theorem 6.1. If a homomorphism π : Γ∗ → M is surjective, then we say that π is a presentation of M; M is called finitely generated if there exists a presentation where Γ is finite. In other words, there is a finite subset of M such that every element of M can be written as a word over this finite subset. Given a presentation π : Γ∗ → M the word problem of M is the set WP(M) = { (u, υ) ∈ Γ∗ × Γ∗ | π(u) = π(υ) }. The word problem is decidable if there is an algorithm that decides membership in WP(M). In finitely generated monoids, the existence of such an algorithm is actually a property of M and not of π. Indeed, let ψ: Γ∗ → M be another homomorphism. For each a ∈ Γ, there is a word wa ∈ Γ∗ with π(wa) = ψ(a). Hereweuse the fact that π is surjective. To check whether ψ(u) = ψ(υ), we first compute (in linear time) words Wu, Wυ ∈ Γ∗ with π(Wu) = ψ(u) and π(Wυ) = ψ(υ). We then use the existing algorithm for π to test whether π(Wu) = π(Wυ).

8.4 Rewriting systems

The concept of a rewriting system is rather general. It consists of a set X and a binary relation ⇒ ⊆ X × X. We write x ⇒ y to express that (x, y) belongs to the relation ⇒. We then say that x can be rewritten in one step to y or that y can be derived in one step from x. Rewriting systems are particularly useful if they satisfy the Church–Rosser property, which is explained below. The property is named after Alonzo Church (1903–1995) and John Barkley Rosser, Sr. (1907–1989).

8.4.1 Termination and confluence

If ⇒ ⊆ X × X is a rewriting system, then we use the following notation:

(a)⇐⇒ symmetric closure,

A critical pair arises, therefore, from the presence of two left components that overlap. A semi-Thue system S is locally confluent if and only if, for each critical pair (u, υ), there exists w with If, in particular, two rules with non-overlapping left components are applicable in a word, then it is clear that both resulting words can be transferred with one rewriting step to the same word. If S is finite, then there are only finitely many critical pairs. This leads to the following decidability result.

Theorem 8.5. It is decidable whether a finite and terminating semi-Thue system S ⊆ Γ∗ × Γ∗ is confluent and, hence, whether it is convergent.

Proof: Since S is finite, there are only finitely many critical pairs. For each such pair (u, υ), we compute ∈ IRR(S) and ∈ IRR(S). This is possible because S is finite and terminating. If S is confluent, then there exists some w ∈ Γ∗ with Now, û and v̂ are irreducible w.r.t. S, which gives that w = û = v̂ as words. Thus, if û ≠ v̂, then S is not confluent. On the other hand, the equality û = v̂ for all critical pairs is sufficient to guarantee local confluence. Since S is terminating, local confluence implies confluence, hence convergence.

□

Since local confluence and termination imply confluence, Theorem 8.5 reduces the problem of deciding convergence (= confluence + termination) of a finite semi-Thuesystem to the problem of deciding termination. The latter problem is, however, undecidable, because the halting problem for Turing machines can be reduced to the problem of deciding termination of some finite semi-Thue system. The reduction is fairly straightforward and left to the interested reader.

A monoid M is finitely presented if it is isomorphic to a quotient monoid Γ∗/S, where S and Γ are finite. The existence of a finite system S with Γ∗/S = M does not depend on the choice of the surjective homomorphism π : Γ∗ → M, but it only depends on M. To see this, we consider a finite S and another surjective homomorphism ψ: Γ∗ → M which induces Γ∗/S' = M, and for which Γ' is finite. We want to show that in S' there is a finite subset S' with Γ∗/S'' = Γ∗/S. First, we have a homomorphism φ: Γ∗ → Γ∗ such that ψ(φ(u)) = π(u) for all u ∈ Γ∗. This follows from the universal property of free monoids (see Theorem 6.1). For all a' ∈ Γ, there is a word ua ∈ Γ∗ with because ψ(a) is equal to some π(ua). Furthermore, for all (ℓ, r) ∈ S we have since Γ∗/S' = M. But then there already exists a finite subset S'' ⊆ S' with for all a' ∈ Γ, and we obtain for all (ℓ, r) ∈ S because Γ and S are finite. We obtain a sequence of homomorphisms:

where arrows are labeled by the respective homomorphisms that induce these maps. The composition of the homomorphisms gives the bijection induced by π. Hence, is injective. Since for all a' ∈ Γ, this map is also surjective. This shows Γ∗/S'' = Γ∗/S, and thus the assertion.

The next example leads to the concept of a free group.

Example 8.6 (Free groups). Let where is a disjoint copy of Σ. We extend the map a ↦ a to an involution on Γ by for all a ∈ Γ and put Consider now the strongly confluent and convergent system

The system defines the free group with basis Σ by

The cardinality of Σ is called the rank of F (Σ). If G is any group, and φ(a) ∈ G is defined for all a ∈ Σ, then we put and obtain a homomorphism φ: Γ∗ → G with for all a ∈ Γ. This means that we may extend each map φ: Σ → G uniquely to a group homomorphism φ: F (Σ) = Γ∗/S → G, that is, F (Σ) is “free” on Σ. We also recognize that all words from Σ∗ are irreducible and, hence, we obtain an embedding Σ∗ ⊆ F (Σ), which, a priori, is not initially apparent. For a free group with generators a1, . . . , an, we also write F (a1, . . . , an) instead of F ({a1, . . . , an}). Free groups have been investigated by mathematicians since the end of the 19th century. A systematic study began with papers by Walther Franz Anton Ritter von Dyck9(1856–1934) [36, 37]. Dyck’s name also appears in formal language theory. The term Dyck language was coined, to the best of our knowledge, in [17]. A Dyck language is the set of all words that have a correct bracketing over a given alphabet of “brackets.” The set of “brackets” forms an alphabet with involution and there are two types of Dyck languages. In the asymmetric type, we distinguish between opening and closing brackets. Thus, if there are (asymmetric) brackets (, ), [, ], then ( [ ][ ] ) ( ) is a well-formed Dyck word, but ( [ ] ] [ ) ( ) is not. In the symmetric version, there is no distinction between “opening” and “closing” brackets; and we recognize the word problem of a free group. Indeed, if the symmetric brackets are given by, for example, then is a Dyck word if and only if w is the neutral element in the free group F (a, b).

◊

As a historical side remark: Dyck did not use the presentation chosen here. He presented the free group F (a, b) on two generators in a more sophisticated way by using three letters a, b, c without explicit inverse letters. His rewriting system was

For Σ = {a, b}, the inclusion {a, b} ⊆ {a, b, c} induces a canonical isomorphism and an alternative presentation of the free group. There are two equivalent views

Just as the standard presentation for a free group in Example 8.6, the system SDyck is also strongly confluent. In addition, SDyck is fully symmetric and it provides the minimal number of monoid generators.

In classical group theory, a group G is called finitely presented if there is a finitely generated free group F (Σ) and finitely many defining elements r1, . . . , rm such that G is isomorphic to F(Σ)/{r1 = 1, . . . , rm = 1}. From the definition, it is clear that a group G is finitely presented if and only if G is finitely presented as a monoid.

Example 8.7 (Free Products). Let I be an index set and Mi be monoids with Γi = Mi {1} for i ∈ I. Then each Mi has a convergent presentation given by its multiplication table ?i; see Example 8.2. We may assume without restriction that the Γi are pairwise disjoint; and we let Γ = ∪i∈IΓi be their union. It follows that the union ? = ∪i∈I?i is terminating and locally confluent, because it is confluent on all critical pairs. Thus, Mis convergent. The irreducible normal forms are the words w = a1 ⋅⋅ ⋅ an where n ≥ 0, aj ∈ Γ for 1 ≤ j ≤ n, and for all i ∈ I and 1 ≤ j < n, we have that aj ∈ Γi

implies aj+1 ∉ Γi. The resulting monoid

is called the free product over the Mi. It has the universal property: if (hi : M i → N)i∈I is a family of homomorphisms to some monoid N, then a unique homomorphism h : ∗i∈IMi → N exists such that each hi is the restriction of h to Mi; and, moreover, each homomorphism h : ∗i∈I Mi → N is of this form. If I = {1, 2}, then we also write M1 ∗ M 2 for its free product.

◊

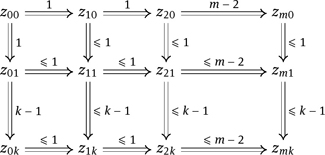
Example 8.8. Let p, q ∈ ℤ with 0 < p ≤ |q|. The Baumslag–Solitar group BS(p, q) is given by two group generators a, t, and a single defining relation tap t−1 = aq. As monoid generators, we use the alphabet with involution Γ = {a, ā, t, t̄ } where c̄̄ = c. Moreover, we identify c̄m with c−m for m ∈ ℤ. We present BS(p, q) using the following convergent semi-Thue system:

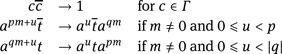
Local confluence of S is straightforward. Termination follows fromthe fact that letters t, t̄ move to the left by jumps over b blocks where b ∈ {a, ā}. Let us take a closer look. If we apply, say, a rule apm+ut̄ → aut̄aqm, then left of t̄, we either decrease the number of a̅’s (note that p can be negative) or the number of a̅’s is not changed, but the number of a’s is decreased. A more careful analysis for termination is given later in the more general context of HNN extensions in Theorem 8.19.

The irreducible normal forms correspond to sequences

where the following conditions are satisfied:

The computation of normal forms yields a polynomial time algorithm for the word problem if each a block is represented as am where m ∈ ℤand m is written in binary.

◊

The family BS (p, q) (see Example 8.8) of one-relator groups was introduced by Gilbert Baumslag (1933–2014) and Donald Solitar (1932–2008). This rich family provides standard examples for various phenomena in group theory: for instance, the group BS(2, 3) is not Hopfian, that is, there is a surjective homomorphism of BS(2, 3) onto itself, which is not injective. Such a homomorphism is given by t ↦ t and a ↦ a2; see Exercise 8.10.

Example 8.9. In [105], Stephan Waack (born 1954) considered an extension of the Baumslag–Solitar group BS(1, 2) with group generators a, s, t and defining relations sas−1 = tat−1 = a2. This defines the Waack group W. It is a special case of a generalized Baumslag–Solitar group [42].

The group W has another presentation with generators a, r, t and relations tat−1 = a2 and rar−1 = a. To see this, let r = s−1t. Then a, r, t generate W as well; and it holds

Thus, the equation rar−1 = a is valid in W. Conversely we have s = tr−1. Hence, from rar−1 = a we can deduce

This shows the first claim by so-called Tietze transformations.

Second, let us show that we can present W by a convergent semi-Thue system, too. We start with the set of monoid generators Γ = {a, a, t, t, r, r}. As above, we let for all c ∈ Γ. The rewriting system S has the following rules for all c ∈ Γ and b ∈ {a, a}:

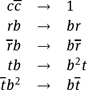
As for Baumslag–Solitar groups, the system S leads to a polynomial time algorithm to solve the word problem in W.

◊

Actually, polynomial time is not the smallest complexity class for the word problem in Baumslag–Solitar groups BS(p, q) or for the Waack group W. The word problem can be solved in the complexity class “logspace.” More precisely, one can show that the word problems in the groups BS (p, q) (for p > 1) and W have the same complexity as the word problem in free groups up to NC1 reductions [106, 109]. The result in [109] is actually stronger: the conjugacy problem in generalized Baumslag–Solitar groups is solvable in “logspace.”

8.5 Solving the word problem in finitely presented monoids

There is no universal algorithm for solving the word problem. Different methods apply to different classes of groups. As expected, the main tool in this chapter is related to confluent rewriting.

Proposition 8.10. Let M be a finitely presented monoid that has a presentation as M = Γ∗/S by a finite convergent semi-Thue system S ⊆ Γ∗ × Γ∗. Then M has a decidable word problem.

Proof: Recall that S is convergent if and only if it is terminating and confluent. Since S is finite and terminating we can, on input u, υ ∈ Γ∗, effectively compute irreducible normal forms ∈ IRR(S) and ∈ IRR(S). Since S is confluent, we have (and hence u = υ in M) if and only if û and v̂ are identical as words in Γ∗.

It is not necessary that a finite rewriting system be convergent everywhere to decide the word problemin a group G. It is sufficient if the system is terminating (everywhere) and confluent on all words which represent the identity in G. This idea was already present in Dehn’s work; his method is nowadays known as Dehn’s algorithm. This led to the theory of small cancellation groups [69], and later to the notion of hyperbolic group due to Mikhail Leonidovich Gromov (born 1943) [47].

In the early 1980s, it was asked whether, for every finitely presented monoid M with a decidable word problem, there exists some finite convergent semi-Thue system S ⊆ Γ∗ × Γ∗ such that M is isomorphic to Γ∗/S. At that time, no method was known to show that a finitely presented monoid M with a decidable word problem does not have a finite convergent presentation. Later, Craig Cecil Squier (1946–1992) found a homological finiteness condition that provides such a method [98].

Let us present another classical tool to attack word problems. It shows decidability for a rather large class of groups. The proof of Proposition 8.11 is an exercise, but it does not give any practical algorithm.

Proposition 8.11. Let M be a residually finite and finitely presented monoid. Then M has a decidable word problem.

Proof: See Exercise 8.2.

□

We have seen above that the special linear groups SL(n, ℤ) are residually finite, and below, in Corollary 8.39, we see that, as a consequence, free groups are residually finite, too. However, there is also a nice direct proof for this fact.

Proposition 8.12. Free groups are residually finite.

Proof: Let F = F (Σ) be a free group with the basis Σ ⊆ F and as in Example 8.6 (with a = a−1). Let n ≥ 1 and w = a1 ⋅⋅ ⋅ an ∈ Γ∗ with ai ∈ Γ and Thus, we have w ≠ 1 in F; and the set of prefixes P = { a1 ⋅⋅ ⋅ ai | 0 ≤ i ≤ n } is a finite set with at least two elements: the empty word and the nonempty word w. For each a ∈ Σ, we define a partial injection φa which maps a1 ⋅⋅ ⋅ ai to a1 ⋅⋅ ⋅ aia in case a1 ⋅⋅ ⋅ aia ∈ P. If φa is defined for S ⊆ P, then S is in bijection with φa(S). Hence, P S is in bijection with P φa(S), too; and we are able to extend φa to a bijection ψa, which is defined everywhere on P. As a consequence, the mapping a ↦ ψa defines a homomorphism h from F (Σ) to the finite permutation group of the set P. We have h(w) ≠ id P since h(w) maps the empty word in P to the nonempty word w ∈ P.

□

Example 8.13. The Waack group W from Example 8.9 is finitely presented and has a decidable word problem, but it is not residually finite. Indeed, consider the presentation with monoid generators Γ = {a, a̅, t, t̄, r, r̄} and the convergent system S as in Example 8.9. The words tat and rt̄atr̄ are both irreducible w.r.t. S, but different. Now let φ: W → N be any homomorphism to a finite monoid. We may assume that φ is surjective and N is a finite group. Let 〈a〉 be the cyclic subgroup of N, which is generated by φ(a). Let us identify g ∈ W with φ(g) ∈ N using abuse of language. Then the conjugation tat−1 = a2 is an automorphism of 〈a〉; and every element in 〈a〉 is the square of some other element in 〈a〉. In particular, a = a2k in 〈a〉 for some k ∈ ℕ. Hence, in N we have

Thus, the nontrivial element t−1atrt−1a−1tr−1 in W is mapped to 1 for every homomorphism to a finite monoid. Hence, W is not residually finite.

◊

8.6 Free partially commutative monoids and groups

In computer science, partial commutation is a natural concept to investigate concurrent systems. This goes back to the work of Robert Marion Keller (born 1944) [53]. The idea is that concurrency or independence of events a and b is described by commutativity ab = ba. In this connection, Antoni Mazurkiewicz (born 1934) coined the notion of trace monoid [72]. He considered a finite alphabet Σ and a relation I ⊆ Σ × Σ, which is assumed to be irreflexive and symmetric. The relation I is called an independence relation since it reflects the abstract behavior of events which occur independently of each other; and therefore (a, b) ∈ I should imply that ab and ba have the same effect. It is also the semantic explanation why I is irreflexive: an action a is not independent of itself. The resulting trace monoid is

Frequently, we also call M (Σ, I) the free partially commutative monoid over (Σ, I). The latter term also suits better to express the algebraic structure of M (Σ, I).

Example 8.14. Let (Σ, I) be a finite graph.

◊

We extend the relation I to a relation I ⊆ Σ∗ × Σ∗ by setting (u, υ) ∈ I if all letters in u are in the relation I to all letters in υ. Put any linear order ≤ on Σ and consider the semi-Thue system S in (8.3), which is infinite as soon as I ≠ 0. In the exercises, we discuss the existence of finite convergent systems which represent M (Σ, I):