Implementation Considerations
This appendix discusses in some detail what’s involved in efficient implementation of the various “temporal” operators introduced in the body of the book. Among other things, it presents a series of transformation laws for the crucial operators PACK and UNPACK, and it sketches the details of certain implementation algorithms for those operators. Those algorithms have the desirable property that it should never be necessary to materialize the result of an UNPACK operation in its entirety. The appendix also describes an intuitively attractive graphical representation for these operations. It then considers algorithms for efficient implementation of the various U_ algebraic operators (U_MINUS, etc.) and U_update operators (U_INSERT, etc.).
Keywords: PACK and UNPACK implementation; “temporal” operator implementation; graphical representation of PACK and UNPACK
There are only two qualities in the world: efficiency and inefficiency.
—George Bernard Shaw:
John Bull’s Other Island (1907)
Our primary aim in this book has been to show how the relational model can be used to address the problem of temporal data management or, more generally, any problem for which the interval abstraction is applicable. In other words, our concern has been with getting the underlying theory right. In this appendix, by contrast, we take a look at the pragmatic issue of implementation—though we should say immediately that some of the ideas we’ll be discussing are still somewhat logical, not physical, in nature, and are thus still model issues in a way. To be specific, we’ll be considering among other things certain transformation laws (which we’ll refer to as just transforms for short) that apply to certain of the relational operators—PACK and UNPACK in particular—and those transforms can certainly be regarded as characteristics of, or logical consequences of, the underlying model. We’ll also sketch the details of certain implementation algorithms for all of those operators.
Of course, we make no claim that what follows is the last word on the matter. Indeed, it wouldn’t be the last word even if we were to expand it to include all of our own thoughts on the subject. New and better techniques are constantly being invented in this field as in others, and we welcome the possibility of innovations on the part of other workers in this area.
PACK and UNPACK
We begin by listing some simple transforms that apply to the PACK and UNPACK operators in particular (with additional commentary in certain cases). Let r be an arbitrary relation. Then:
Now let r have interval attributes A1, A2, …, An (n ≥ 1), and let ACL be a commalist of attribute names containing just those names A1, A2, …, An in sequence as shown. Then:
3. PACK ( PACK r ON ( ACL ) ) ON ( ACL ) ≡ PACK r ON ( ACL )
4. PACK ( UNPACK r ON ( ACL ) ) ON ( ACL ) ≡ PACK r ON ( ACL )
5. UNPACK ( UNPACK r ON ( ACL ) ) ON ( ACL ) ≡ UNPACK r ON ( ACL )
6. UNPACK ( PACK r ON ( ACL ) ) ON ( ACL ) ≡ UNPACK r ON ( ACL )
Now let BCL be an arbitrary permutation of ACL. Then:
Note that an analogous transform does not apply to PACK, in general.
Next, recall from Chapter 10 that PACK r ON (ACL) for n > 1 is defined to require a preliminary UNPACK r ON (ACL). In other words:
PACK r ON ( ACL ) ≡ PACK (… ( PACK ( PACK r' ON ( A1 ) ) ON ( A2 ) ) … ) ON ( An )
where r' is
UNPACK r ON ( A1 , A2 , … , An )
However, there’s no need to do the preliminary UNPACK on A1. In other words, the following is another valid transform:
where r" is
UNPACK r ON ( A2 , … , An )
As an important special case of Transform 8, we can ignore the implicit initial UNPACK entirely when packing on just a single attribute (as in fact we already know).
Now let r be a relation with an interval attribute A, and let B be all of the attributes of r apart from A. Let r1, r2, …, rk be a partitioning of r on B—i.e., a grouping of the tuples of r into distinct sets (partitions) r1, r2, …, rk such that (a) all B values in partition ri are the same and (b) B values in partitions ri and rj (i ≠ j) are different. Then, using the n-adic form of D_UNION (“disjoint union”), we have:
9. PACK r ON ( A ) ≡ D_UNION { PACK r1 ON ( A ), PACK r2 ON ( A ) , ……… , PACK rk ON ( A ) }
10. UNPACK r ON ( A ) ≡ D_UNION { UNPACK r1 ON ( A ), UNPACK r2 ON ( A ) , ……… , UNPACK rk ON ( A ) }
We’ll make use of Transform 9 in particular in our discussion of the SPLIT operator, later. We close the present discussion by observing that if
a. r is a relation with an interval attribute A and B is all of the attributes of r apart from A (as for Transforms 9 and 10 above), and
b. r is represented in storage by a stored file f such that there’s a one to one correspondence between the tuples of r and the stored records of f, and
then PACK r ON (A) and UNPACK r ON (A) can both be implemented in a single pass over f. The PACK case is particularly important, and we therefore offer some further comments in connection with it.
Suppose we’re processing that stored file f in “BEGIN (A) within B” order. Consider a particular B value b; by definition, all stored records having B = b will be grouped together. Therefore, when we’re processing that particular group of stored records, as soon as we encounter one whose A value neither meets nor overlaps the A value from the immediately preceding record, we can emit an output record (and similarly when we reach the end of the entire group). The PACK implementation can thus be pipelined—i.e., the result can be computed “one tuple at a time” (more correctly, one record at a time), and there’s no need for the invoker to wait for the entire result to be materialized before carrying out further work.
The foregoing observations are pertinent to many of the implementation algorithms to be discussed in the sections to follow. In particular, those observations imply that whenever such an algorithm talks about inserting a tuple into some result that’s being built up gradually, it might be possible for the implementation to return just the tuple in question—or the record, rather—to the invoker; thus, the overall result (usually representing some relation in some unpacked form) might never need to be physically materialized in its entirety.
In addition to the foregoing considerations, if f is indeed sorted on B as suggested, then that fact permits an obvious and efficient implementation for the operation of partitioning r on B. This point is worth making explicitly because several of the algorithms to be discussed in the sections that follow make use of such partitioning.
The various U_ operators discussed in Chapter 11 are all defined in terms of PACK and UNPACK. An efficient implementation of these latter operators is thus highly desirable. We now take a closer look at this issue.
PACK
The basic problem with PACK from an implementation standpoint is that it’s defined in terms of a preliminary series of UNPACKs, and UNPACK has the potential to be extremely expensive in execution, in terms of both space and time. Following reference [76], therefore, we now proceed to show how:
a. Certain of those preliminary UNPACKs can be “optimized away” entirely, and
b. Others can be replaced internally by a more efficient operator called SPLIT.
It’s convenient to begin by introducing an operator that we’ll call PACK' (“pack prime”). Informally, PACK' is the same as PACK, except that it doesn’t do the preliminary unpacking that’s required by the formal definition of PACK as such. (In our implementation algorithms, therefore, we’ll take care to use PACK' in place of PACK only when we know it’s safe to do so—in particular, when we know the input relation is appropriately unpacked already.) Here first is the definition of PACK' when the packing is to be done on the basis of just a single attribute:1
PACK' r ON ( A ) ≡
WITH ( r1 := r GROUP { A } AS X, r2 := EXTEND r1 : { X := COLLAPSE ( X ) } ) :r2 UNGROUP Y
This definition is identical to the one we gave for the regular PACK operator in Chapter 9, where we were concerned with packing on the basis of a single attribute only. In other words, PACK' is identical to PACK if the packing is on the basis of a single attribute—naturally, since no preliminary unpacking is necessary when packing on the basis of just one attribute, as we already know.
Next, we define PACK' on attributes A1, A2 , … , An (n > 1), in that order, thus:
PACK' r ON ( A1 , A2 , … , An ) ≡
PACK' ( … ( PACK' ( PACK' r ON ( A1 ) ) ON ( A2 ) ) … ) ON ( An )
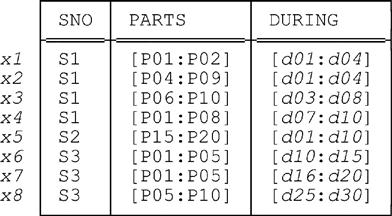
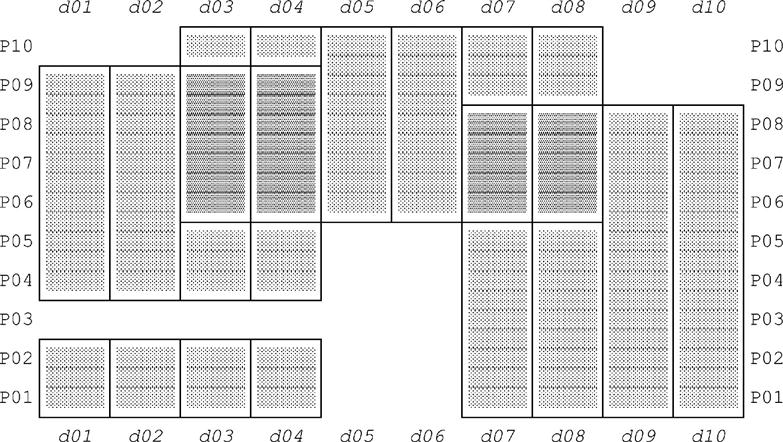
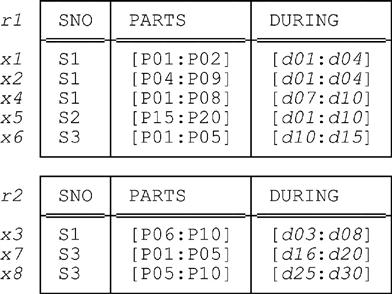
Here’s an example. Consider Fig. E.1, which shows a sample value for relvar S_PARTS_DURING—a relvar that, as you’ll recall from Chapter 6 and elsewhere, has two interval attributes, PARTS and DURING.2 We’ve labeled the tuples in the figure for purposes of subsequent reference. Observe that the relation in the figure does involve certain redundancies; for example, tuples x3 and x4 both tell us among other things that supplier S1 was able to supply part P06 on day d08.
Of course, we can eliminate those redundancies—also any circumlocutions that might be present—by replacing the current value of S_PARTS_DURING by the result of evaluating the following expression (which uses PACK, not PACK', please note):
PACK S_PARTS_DURING ON ( PARTS, DURING )
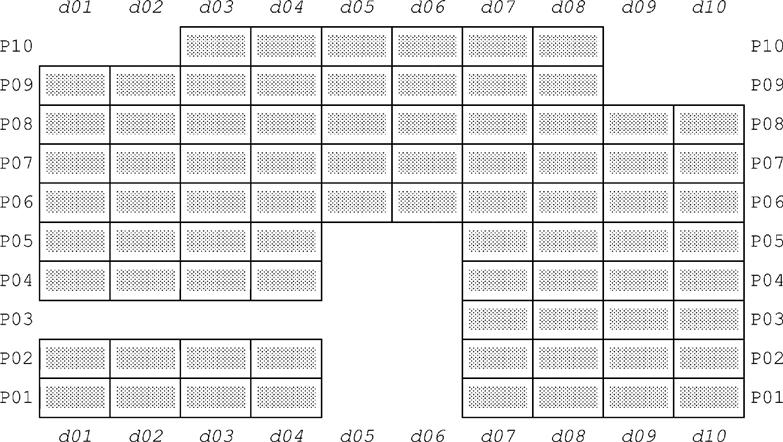
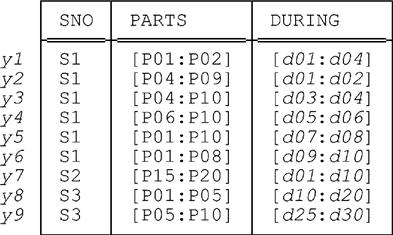
Given the relation shown in Fig. E.1, the result is shown in Fig. E.2.
Next, we note that (thanks to Transform 4) the foregoing PACK expression is logically equivalent to this longer one:
PACK
( UNPACK S_PARTS_DURING ON ( DURING, PARTS ) )
ON ( PARTS , DURING )
Note: We’ve deliberately specified the attributes in the sequence DURING then PARTS (for the UNPACK) and PARTS then DURING (for the PACK), for reasons that’ll become clear in just a moment. Of course, the sequence makes no difference anyway in the case of UNPACK.
We now observe that the argument to PACK in the foregoing longer expression is guaranteed to be appropriately unpacked, and we can therefore safely replace that PACK by PACK' instead, thus:
PACK'
( UNPACK S_PARTS_DURING ON ( DURING , PARTS ) )
ON ( PARTS , DURING )
This expression in turn is logically equivalent to:
WITH ( t1 := UNPACK S_PARTS_DURING ON ( DURING ) ,
t2 := UNPACK t1 ON ( PARTS ) ,
t3 := PACK' t2 ON ( PARTS ) ) :
PACK' t3 ON ( DURING )
However, we can replace t2 by t1 in the third step here (dropping the second step entirely), thanks to the following identity:
PACK' ( UNPACK t1 ON ( PARTS ) ) ON ( PARTS ) ≡ PACK' t1 ON ( PARTS )
(This identity is clearly valid, because (a) PACK' is identical to PACK if the operation is performed on the basis of a single attribute, and (b) we know from Transform 4 that the identity that results if we replace PACK' by PACK on both sides is valid.) So the overall expression can be simplified to just:
WITH ( t1 := UNPACK S_PARTS_DURING ON ( DURING ) ,
t3 := PACK' t1 ON ( PARTS ) ) :
PACK' t3 ON ( DURING )
So we’ve succeeded in optimizing away one of the UNPACKs, and the operation is thus more efficient than it was before.
Can we get rid of the second UNPACK as well? Well, we’ve already indicated that the answer to this question is yes, but the details are a little more complicated than they were for the first one. Basically, the idea is to avoid unpacking “all the way,” as it were (i.e., unpacking all the way down to unit intervals); instead, we “unpack” (or split, rather) only as far as is truly necessary—which is to say, down only to certain disjoint subintervals. The effect is to produce a result with (in general) fewer tuples than a full UNPACK would produce; however, that result is still such as to allow us “to focus on the information content … without having to worry about the many different ways in which that information might be bundled together into clumps,” as we put it in Chapter 8.
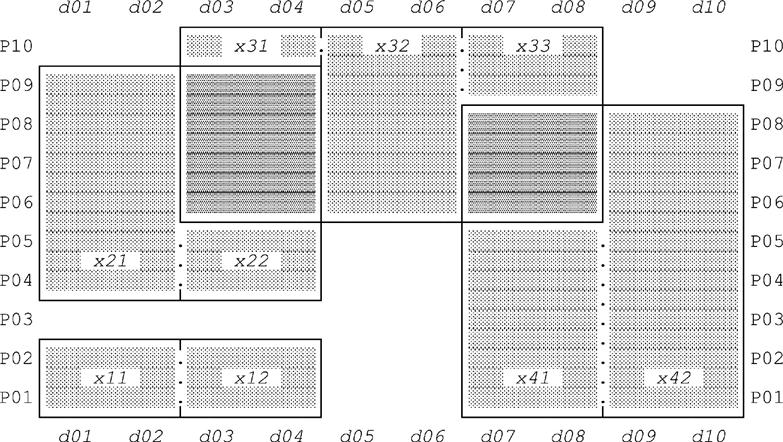
By way of example, consider tuple x3 from Fig. E. 1:

This tuple can be split into the following three tuples (note the tuple labels):
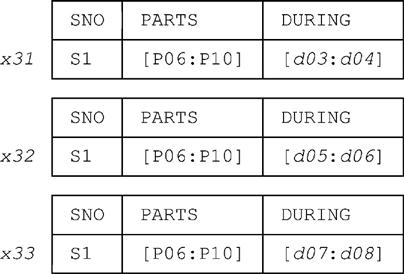
Of course, tuples x31-x33 together represent the same information as the original tuple x3 did.
Why exactly would we want to split tuple x3 in the way just shown? In order to answer this question, consider first the relation—let’s call it X—that’s the restriction of the relation in Fig. E.1 to just the tuples for supplier S1:

Note that the tuple to be split, tuple x3, has DURING value i = [d03:d08]. Intuitively speaking, then, we split tuple x3 the way we did because:
■ Interval i consists of the six points d03, d04, d05, d06, d07, and d08.
■ Of these six, the four points d03, d04, d07, and d08 (only) are boundary points—i.e., begin or end points—for the DURING value in at least one tuple in X.
■ Those boundary points divide interval i into precisely the subintervals [d03:d04], [d05:d06], and [d07:d08]. Hence the indicated split.
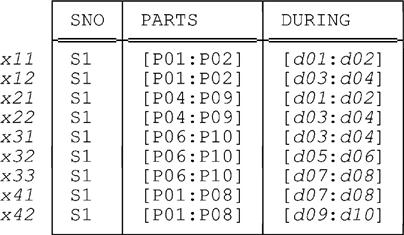
Here then is our general algorithm for splitting all of the tuples in some given relation. Note: We’ll state and illustrate the algorithm initially with reference to the simple relation X shown above, containing just the tuples for supplier S1 (i.e., tuples x1-x4) from Fig. E.1; then we’ll extend the algorithm to deal with an arbitrary relation, using the relation in Fig. E.1 as the basis for an extended example.
Step 1: Create an ordered list L consisting of all points p such that p is equal to either b or e+1 for some DURING value [b:e] in X. In our example, L is the list
d01, d03, d05, d07, d09, d11
Step 2: Let x be some tuple in X. Create an ordered list Lx consisting of all points p from L such that b ≤ p ≤ e+1, where [b:e] is the DURING value in x. For example, in the case of tuple x3, Lx is the list
d03, d05, d07, d09
Step 3: For every consecutive pair of points b and e appearing in Lx, produce a tuple obtained from tuple x by replacing the DURING value in x by the interval [b:e−1]. For tuple x3, this step yields the three tuples x31-x33 shown earlier. We say that tuple x3 has been split with respect to the points in L.
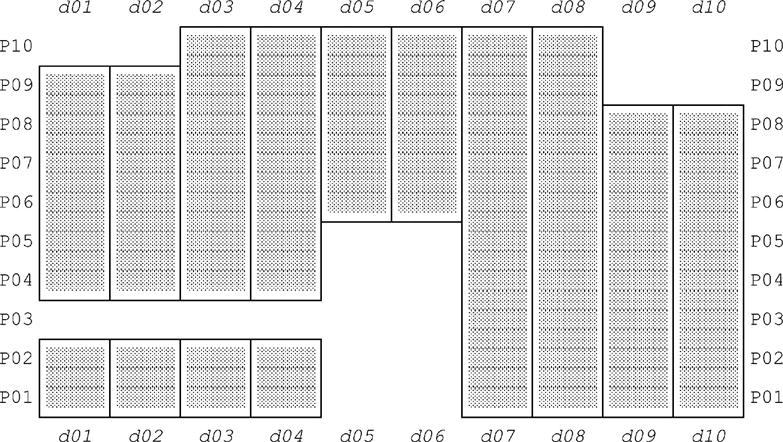
If we now repeat Steps 2 and 3 for every tuple in X and construct a relation containing all and only the tuples thus produced, we obtain the relation Y shown in Fig. E.3. We’ll express this fact for the purposes of this appendix by saying that Y is obtained by evaluating the expression
SPLIT X ON ( DURING ) PER L
In other words, we’ll assume for the purposes of this appendix that we have available to us an operator called SPLIT whose syntax is SPLIT r ON (A) PER L, where r is a relation, A is an interval attribute of R, and L is a list of values of the point type underlying the interval type of attribute A.
And now the expression
PACK' Y ON ( PARTS, DURING )
gives us all of the tuples to be found for supplier S1 in the result of packing S_PARTS_DURING on (PARTS, DURING)—in other words, tuples y1-y6 as shown in Fig. E.2—without performing any UNPACKs, as such, at all.
Aside: The foregoing algorithm does have the slightly unfortunate effect in the example of first splitting tuple x1 into tuples x11 and x12 and then recombining those two tuples to obtain tuple x1 again—or tuple y1, rather, as it’s labeled in Fig. E.2. It would be possible to revise the algorithm in such a way as to avoid such unnecessary splitting and recombining, but care would be needed to ensure that the revisions did in fact decrease the overall execution time and not increase it. We omit further discussion of this possibility here. End of aside.
To complete our discussion of SPLIT: Clearly, in order to split every tuple in the original S_PARTS_DURING relation, what we need to do is partition that relation on attribute SNO (in our example, we obtain three partitions, one for each of suppliers S1, S2, and S3), and then repeat Steps 1-3 above with each partition in turn taking on the role of X.
Having explained SPLIT, we can now present an efficient algorithm for implementing PACK—PACK, not PACK'—in terms of SPLIT on a relation r with two interval attributes A1 and A2. Let B be all of the attributes of r apart from A1 and A2. Then:
Step 1: Initialize result to empty.
Step 2: Partition r on B. Let the resulting partitions be r1, r2, …, rk.
Step 3: Execute the following:
do for each ri ( i = 1 , 2 , … , k ) ;
if COUNT ( ri ) = 1 then result := result D_UNION ri ; else do Steps 4 and 5 ;
end do ;
Step 4: Create an ordered list L consisting of all points p such that p is equal to either b = BEGIN (A2) or e+1 = POST (A2) for some A2 value [b:e] in ri.
Step 5: Execute the following:
WITH ( t1 := SPLIT ri ON ( A2 ) PER L ,
t2 := PACK' t1 ON ( A1 ) ,
t3 := PACK' t2 ON ( A2 ) ) :
result := result D_UNION t3 ;
We observe that, in comparison with an implementation involving explicit UNPACKS, the foregoing algorithm (a) is considerably faster and (b) requires substantially less space, because it’s applied to each partition of the original relation separately. Additional implementation techniques, such as the use of suitable indexes (on the final result as well as on the original relation and intermediate results), can be used to improve execution time still further. Details of such additional techniques are beyond the scope of this appendix, however. Note: The foregoing remarks also apply, mutatis mutandis, to the algorithms we’ll be presenting in later sections for U_UNION, U_MINUS, and so on. We won’t repeat them in those later sections, however, letting this one paragraph do duty for all.
We close this discussion by observing that the implementation algorithm for PACK becomes much simpler in the important special case in which the packing is done on the basis of just a single attribute, because in that case no splitting or unpacking is needed at all. That is, if r is a relation with an interval attribute A and B is all of the attributes of r apart from A, then we can implement PACK r ON (A) by simply implementing PACK' r ON (A). And if r is represented in storage by a stored file f such that there’s a one to one correspondence between the tuples of r and the stored records of f, then an efficient way to implement PACK' r ON (A) is to sort f into “BEGIN (A) within B” order and then perform the packing in a single pass over f as noted earlier in this section.
UNPACK
Again let r be a relation with two interval attributes A1 and A2 and let B be all of the attributes of r apart from A1 and A2. Consider the expression:
UNPACK r ON ( A1, A2 )
The first thing we do is PACK (yes, pack) r on (A1,A2), using the efficient implementation for PACK described above. Let r' be the result of this step. Then we execute the following pseudocode algorithm:
result := empty ;
do for each tuple t ∈ r' ;
do for each p1 ∈ ( A1 FROM t ) ;
do for each p2 ∈ ( A2 FROM t ) ;
insert tuple { A1 [p1:p1] , A2 [p2:p2] , B ( B FROM t ) } into result ;end do ;
end do ;
end do ;
Of course, we’re assuming here that materialization of the unpacked form of r on (A1,A2) is actually required. In practice, it’s to be hoped that various transforms can be used to optimize away the need for such materialization, in which case it’ll be sufficient to perform just the preliminary PACK step. In other words, it might not be necessary to produce the unpacked form at all, if (as will usually be the case) the result of the original UNPACK is to be passed as an argument to some operator Op and the desired overall result can be obtained by applying Op (or some other operator Op') directly to r' (= PACK r ON (A1,A2)) instead of r. In particular, it should never be necessary to materialize the result of unpacking a relation on the basis of just one attribute, except in the unlikely case in which the user explicitly requests the result of such materialization—to be displayed, for instance.
A Graphical Representation
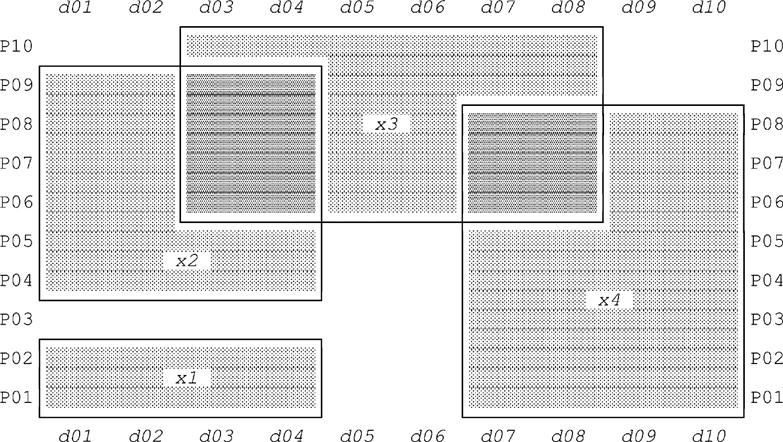
The graphical representation introduced in Chapter 10 in connection with the notion of packing relations on two (or more?) attributes can be used to illustrate certain of the ideas discussed in the previous section, and some readers might find such illustrations helpful. Consider once again the relation X from a few pages back, which contained just the tuples x1-x4 (the ones for supplier S1) from Fig. E.1:

Fig. E.4 shows a graphical representation of the PARTS and DURING components of the four tuples in this relation. The redundancy, or overlap, among those tuples—indicated by darker shading—is very obvious from that figure.
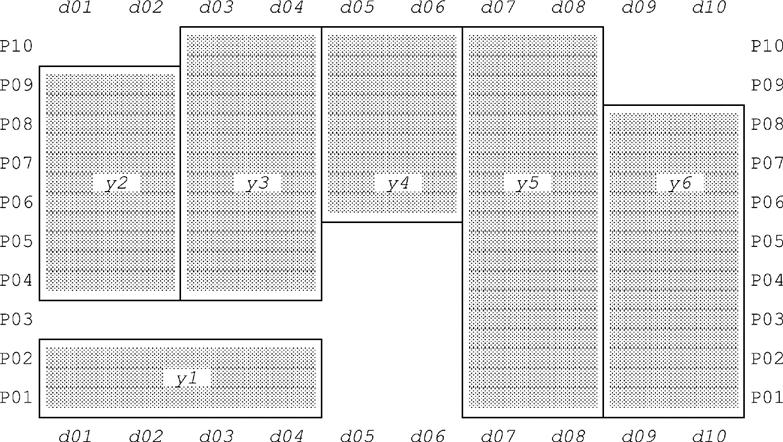
Fig. E.5 shows a similar graphical representation for the corresponding “packed tuples” y1-y6 from Fig. E.2. Here it’s obvious that the overlaps have disappeared.
In like manner, for supplier S3,3 figures analogous to Figs. E.4 and E.5 would show that:
a. Tuples x6 and x7 (see Fig. E.1) correspond to adjacent—not overlapping—rectangles (adjacent here meaning, more precisely, that the right edge of the rectangle for x6 and the left edge of the rectangle for x7 exactly coincide).
b. Packing those two tuples yields tuple y8 (see Fig. E.2), corresponding to a single combined rectangle.
Now recall the following expression which, given the relation of Fig. E.1 as input, yields the relation of Fig. E.2 as output:
WITH ( t1 := UNPACK S_PARTS_DURING ON ( DURING ) ,
t2 := UNPACK t1 ON ( PARTS ) ,
t3 := PACK' t2 ON ( PARTS ) ) :
PACK' t3 ON ( DURING )
Figs. E.6, E.7, and E.8 show graphical representations of t1, t2, and t3, respectively (tuples for supplier S1 only in every case). As for the result of the overall expression, we’ve already seen the graphical representation for that (for supplier S1, at least) in Fig. E.5.
Finally, if once again X is the relation containing tuples x1-x4 only and L is the list d01, d03, d05, d07, d09, d11, then Fig. E.9 is a graphical representation of the result of the expression
SPLIT X ON ( DURING ) PER L
(see Fig. E.3).
Algebraic Operators
Now we turn our attention to the “U_” operators (U_union and the rest). All of these operators are defined to do a preliminary UNPACK on their relation operand(s); as always, however, we want to avoid actually having to perform those UNPACKs if we possibly can. Fortunately, there are several transforms and algorithms available to help us in this connection, which we now proceed to describe.4
U_UNION
First of all, it’s easy to see that UNPACK distributes over regular UNION:
UNPACK ( r1 UNION r2 ) ON ( ACL ) ≡ ( UNPACK r1 ON ( ACL ) ) UNION ( UNPACK r2 ON ( ACL ) )
Hence we have:
USING ( ACL ) : r1 UNION r2
![]() PACK
PACK
( ( UNPACK r1 ON ( ACL ) ) UNION ( UNPACK r2 ON ( ACL ) ) )
ON ( ACL )
≡ PACK
( UNPACK ( r1 UNION r2 ) ON ( ACL ) )
ON ( ACL )
≡ PACK ( r1 UNION r2 ) ON ( ACL )
Thus, we can implement the original U_union by directly applying the PACK algorithm described in the section “PACK and UNPACK” to the regular union of r1 and r2. No unpacking is required. (We mentioned this point in passing in Chapter 11, as you might recall.)
We can improve matters still further—in particular, we can avoid actually materializing the union of r1 and r2—by means of the following algorithm (a modified version of the PACK algorithm discussed earlier). Let r1 and r2 each have interval attributes A1 and A2 and let B be all of the attributes apart from A1 and A2 in each. Then:
Step 1: Initialize result to empty.
Step 2: Let r be the result of r1 UNION r2 (but see the note following Step 5). Partition r on B into z1, z2, …, zk.5
Step 3: For each zi (i = 1, 2, …, k), do Steps 4 and 5.
Step 4: Create an ordered list L consisting of all points p such that p is equal to either BEGIN (A2) or POST (A2) for some A2 value in zi.
Step 5: Execute the following:
WITH ( t1 := SPLIT zi ON ( A2 ) PER L ,
t2 := PACK' t1 ON ( A1 ) ,
t3 := PACK' t2 ON ( A2 ) ) :
result := result D_UNION t3 ;
Note: Although Step 2 above refers explicitly to r as the union of r1 and r2, there’s no need to check for appearances of the same tuple in both r1 and r2, as the invocations of PACK' in Step 5 will eliminate any duplicates. In fact, there’s no need for r to be physically materialized at all; instead, the implementation can simply perform a search on r1 and r2 to find the tuples that belong to any given partition zi (indeed, Steps 4 and 5 effectively do just that). In this connection, we remind you that sorting can be useful in the implementation of partitioning.
Further improvements are possible. In particular, Step 5 can sometimes be simplified to just
result := result D_UNION zi ;
For example, suppose relations r1 and r2 are as shown in Fig. E.10 (note that they’re both restrictions of the relation in Fig. E.1), and consider, e.g., tuple x5. Since that tuple has an SNO value that appears in r1 and not r2, it can be inserted directly into the result without any need for the SPLIT and the two PACK' operations. In appropriate circumstances, it should be possible to insert sets containing any number of tuples directly into the result in this manner.
This brings us to the end of our discussion of U_UNION. We’ve considered this operator in some detail in order to give some idea as to the range of implementation and optimization possibilities that might be available in general. In our discussions of the other operators below, we won’t usually try to be so comprehensive.
U_MINUS
Consider the expression
USING ( A1, A2 ) : r1 MINUS r2
where r1 and r2 are as for U_UNION above. Here’s the implementation algorithm:
Step 1: Initialize result to empty.
Step 2: Partition r1 on B into r11, r12, …, r1h. For each r1i (i = 1, 2, …, h), define r2i as r2 MATCHING r1i{B} (thus, r2i consists of all r2 tuples with the same B value as the tuples in r1i).
Step 3: For each i (i = 1, 2, …, h), do Steps 4 and 5.
Step 4: Create an ordered list L1 consisting of all points p1 such that p1 is either BEGIN (A1) or POST (A1) for some A1 value in r1i UNION r2i. Also, create an ordered list L2 consisting of all points p2 such that p2 is either BEGIN (A2) or POST (A2) for some A2 value in r1i UNION r2i.
Step 5: Execute the following:
WITH ( t1 := SPLIT r1i ON ( A1 ) PER L1 ,
t2 := SPLIT t1 ON ( A2 ) PER L2 ,
t3 := SPLIT r2i ON ( A1 ) PER L1 ,
t4 := SPLIT t3 ON ( A2 ) PER L2 ,
t5 := t2 MINUS t4 ,
t6 := PACK' t5 ON ( A1 ) ,
t7 := PACK' t6 ON ( A2 ) ) :
result := result D_UNION t7 ;
U_INTERSECT
U_INTERSECT is a special case of U_JOIN, and the same techniques apply. See the subsection immediately following.
U_JOIN
We observe first that—as we saw in Exercise 11.3 in Chapter 11—U_JOIN can be defined without any explicit reference to UNPACK at all, as follows (we assume for simplicity that the packing and unpacking is to be done on the basis of a single attribute A):
USING ( A ) : r1 JOIN r2 ≡
WITH ( t1 := r1 RENAME { A AS X } , t2 : = r2 RENAME { A AS Y } ,t3 := t1 JOIN t2 ,
t4 := t3 WHERE X OVERLAPS Y,
t5 := EXTEND t4 : { A := X INTERSECT Y } , t6 := T5 { ALL BUT X , Y } ) :PACK t6 ON ( A )
We now exploit the ideas underlying the foregoing definition in the following algorithm for implementing the expression
USING ( A1, A2 ) : r1 JOIN r2
We assume that r1 has attributes A, B, A1, and A2; r2 has attributes A, C, A1, and A2; and A1 and A2 are interval attributes.
Step 1: Initialize result to empty.
Step 2: Execute the following pseudocode algorithm:
let a be an A value that appears both in some tuple ∈ r1 and in some tuple ∈ r2 ;
do for each such a ;
do for each tuple t1 ∈ r1 with A = a ;
do for each tuple t2 ∈ r2 with A = a ;
with ( a11 := A1 FROM t1, a21 := A2 FROM t1 ,
a12 := A1 FROM t2 , a22 := A2 FROM t2 ) :
if a11 OVERLAPS a12 AND a21 OVERLAPS a22
then insert tuple
{ A a r B ( B FROM t1 ), C ( C FROM t2 ) ,
A1 ( a11 INTERSECT a12 ) , A2 ( a21 INTERSECT a22 ) } into result ;
end if ;
end do ;
end do ;
end do ;
Step 3: Using the PACK algorithm described earlier, execute the following:
result := PACK result ON ( A1, A2 ) ;
Note: If the U_JOIN is performed on the basis of just a single attribute and the input relations r1 and r2 are already packed on that attribute, then Step 3 here is unnecessary.
U_project
The expression
USING ( ACL ) : r { BCL }
is defined to be equivalent to
PACK ( ( UNPACK r ON ( ACL ) ) { BCL } ) ON ( ACL )However, there’s no need to perform the initial UNPACK shown in this definition. In other words, the foregoing expression can be further simplified to just
PACK ( r { BCL } ) ON ( ACL )Thus, the implementation algorithm is:
Step 1: Initialize result to empty.
Step 2: Execute the following pseudocode algorithm:
do for each tuple t ∈ r ;
add tuple t { BCL } to result ;
end do ;
Step 3: Execute the following:
result := PACK result ON ( ACL ) ;
■ In practice we would expect the “add tuple” statement in Step 2 to be subject to pipelining, whereby the added tuple is immediately input to the next step—in this case Step 3.
■ As a consequence, result in Step 2 must be understood as a bag of tuples, not a relation, because it might contain duplicates (but any such duplicates will be removed by the PACK in Step 3).
■ Note, therefore, that we’ve taken the liberty in Step 3 of applying a relational operator, PACK, to something that isn’t necessarily a relation.
■ Finally, note also the use of tuple projection (“t {BCL}”) in Step 2.
U_restrict
The expression
USING ( ACL ) : r WHERE bx
is defined to be equivalent to
PACK ( ( UNPACK r ON ( ACL ) ) WHERE bx ) ON ( ACL )
In the (unusual) special case where bx mentions no attribute in ACL, this latter expression can be simplified to just
PACK ( r WHERE bx ) ON ( ACL )
The implementation algorithm for this simple case is immediate:
WITH ( t1 := r WHERE bx ) : PACK t1 ON ( ACL )
Furthermore, if relation r is already packed on ACL, the PACK step is unnecessary.
More usually, of course, bx will mention at least one attribute in ACL, and such cases appear to pose a significant challenge to our aim of avoiding materialization of unpacked forms. We illustrate the problem by considering the simple case where bx is nothing more than a comparison between an attribute A in ACL and a literal. Bear in mind the important point that within bx the attribute reference A denotes a unit interval.
Consider the following example of a U_restriction:
USING ( A ) : r WHERE A ⊆ [b:e]
This U_restriction is logically equivalent to the following U_JOIN:
USING ( A ) : r JOIN RELATION { TUPLE { A [b:e] } }And we’ve already seen shown that U_JOIN can be implemented without unpacking. But it does seem rather a challenge to expect an implementation that recognizes the foregoing equivalence to do the same thing for all expressions that happen to be equivalent to that U_JOIN invocation. By way of illustration, note that all of the following are equivalent to A ⊆ [b:e]:
And so on (note in particular that POINT FROM i, BEGIN (i) and END (i) are all equivalent when i is a unit interval).
When bx contains logical connectives, we can find equivalent expressions using relational counterparts of those connectives. For example, negation suggests MINUS, or (perhaps better) its generalization NOT MATCHING. Thus we have:
■ USING ( A ) : r WHERE NOT ( A ⊆ [b:e] )
≡
USING ( A ) : r NOT MATCHING RELATION { TUPLE { A [b:e] } }
■ USING ( A ) : r WHERE A ⊆ [b1:e1] OR A ⊆ [b2:e2]
≡
USING ( A ) : r JOIN ( RELATION { TUPLE { A [b1:e1] } } UNION RELATION { TUPLE { A [b2:e2] } } )
≡
USING ( A ) : r JOIN RELATION { TUPLE { A [b1:e1] }, TUPLE { A [b2:e2] } }
■ USING ( A1, A2 ) : r WHERE A1 ⊆ [b1:e1] AND A2 ⊆ [b2:e2]
≡
USING ( A1 , A2 ) : r JOIN RELATION { TUPLE { A1 [b1:e1] , A2 [b2:e2] } }
As you can see, these various alternative formulations are really no more complicated than the U_restrictions they correspond to; thus, users might not complain if they’re forced to use them themselves (for performance reasons) when the implementation fails to rise to the aforementioned challenge.
We close this subsection by noting an example where the final PACK step isn’t needed:
USING ( A1, A2 ) : r WHERE A1 = A2
Before reading on, you might like to try verifying this claim for yourself. Explanation: Let s be the result of (UNPACK r ON (A1,A2)) WHERE A1 = A2 and let B be all of the attributes of s apart from A1 and A2. Let tuples t1 and t2 of s be such that B FROM t1 = B FROM t2 and A1 FROM t1 = A1 FROM t2. Then it follows from the stated WHERE condition that t1 and t2 are the same tuple. Thus, t1 can’t be “merged” with any other tuples in the packing process, and the fact that s = PACK s ON (A1,A2) follows immediately.
By the way, the foregoing example isn’t completely unrealistic. Suppose A1 represents stated time intervals and A2 logged time intervals; then relation s tells us the times at which the database’s record was in synch with our beliefs at those times. For example, if r is the relvar S_DURING_LOG (see the section “Logged Times” in Chapter 17), then a tuple for supplier S1 in s would be telling us that throughout the unit interval [d:d] the database said we believed S1 was under contract throughout that same unit interval [d:d]. However, we’d surely prefer to see the maximal intervals throughout which the database and our beliefs were in synch. Such a result could be obtained by means of an expression of the form:
USING ( A1 , A2 ) : r JOIN ( r { ALL BUT A1 } RENAME { A2 AS A1 } )And we know how to implement U_JOIN without unpacking.
U_EXTEND
The expression
USING ( ACL ) : EXTEND r : { B := exp }is defined to be equivalent to
PACK
( EXTEND ( UNPACK r ON ( ACL ) ) : { B := exp } )
ON ( ACL )
In the special case where exp mentions no attribute in ACL, this expression can be simplified to just
PACK ( EXTEND r : { B := exp } ) ON ( ACL )The implementation algorithm for this simple case is immediate:
WITH ( t1 := EXTEND r : { B := exp } ) : PACK t1 ON ( ACL )Furthermore, if relation r is already packed on ACL, the PACK step is unnecessary.
In fact, the foregoing observations also apply when exp mentions just one of the attributes in ACL. For example, in
USING ( A ) : EXTEND r : { LA := COUNT ( A ) }the USING specification is completely redundant—the expression reduces to just
PACK ( EXTEND r : { LA := 1 } ) ON ( A )And if relation r is already packed on ACL, then (as before) the PACK step is unnecessary.
Aside: Actually it’s quite difficult to come up with examples any more complicated than the one just shown. For example, consider:
WITH ( A2 := [d03:d07],
r2 := r1 WHERE A1 MERGES A2 ) :
USING ( A1 ) : EXTEND r2 : { XA := A1 UNION A2 }
If A1 = [d01:d02] in some tuple of r2, then one of the resulting assignments to XA becomes XA := [d01:d01] UNION [d03:d07], which fails. If evaluation does succeed, however, then the same result can be achieved by replacing the U_EXTEND invocation by PACK ( EXTEND r2 : { XA := A1 UNION A2 } ) ON ( A1 ). End of aside.
However, when we consider examples where exp mentions two or more attributes in ACL, we run into difficulties. For one thing, it remains the case that genuinely useful examples don’t readily come to mind; for another, the simple but contrived examples that do come to mind seem to be such that unpacked form can’t be completely avoided. For example, let relation s be the result of
USING ( A1, A2 ) : EXTEND r : { TV := ( A1 = A2 ) }If, in some tuple t of s, TV = TRUE, then the values of A1 and A2 in t are the same unit interval and t thus appears in the unpacked form of s. For consider, if t is the tuple {A1 [d02:d02], A2 [d02:d02], TV TRUE}, then s can’t contain a tuple {A1 [d02:d02], A2 [dx:dx], TV TRUE}, where dx ≠ d02 and [dx:dx] MERGES [d02:d02]. For that reason, there’s a certain amount of unavoidable unpacking involved in the following pseudocode algorithm.
Step 1: Initialize t1 to empty.
Step 2: Execute the following:
do for each tuple t ∈ ( r WHERE A1 OVERLAPS A2 ) :
do for each point p in ( A1 FROM t ) INTERSECT ( A2 FROM t ) :
u := tuple { A1 [p:p] , A2 [p:p] , B B } ;
if NOT ( u ∈ t1 )
then
add u to t1 ;
end do ;
end do ;
Step 3: Execute the following:
result := WITH ( t2 := USING ( A1 , A2 ) : r MINUS t1 ,
t3 := EXTEND t1 : { TV := TRUE } ,
t4 := EXTEND t2 : { TV := FALSE } ) :
t3 D_UNION t4 ;
No final PACK is needed here because t1 and t2 are both in packed form, from which it follows that t3 and t4 are also in packed form, and therefore, because they’re disjoint, so is result. However, t1, materialized in Step 2, is in unpacked form.
U_GROUP
It’s easiest to explain the implementation of U_GROUP in terms of a concrete example. Let the current value of relvar SP_DURING be as follows:
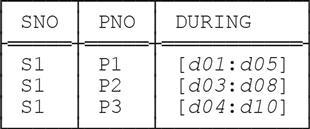
Consider the expression:
USING ( DURING ) : SP_DURING GROUP { PNO } AS PNO_RELThis expression is defined to be equivalent to:
PACK
( UNPACK SP_DURING ON ( DURING ) ) GROUP { PNO } AS PNO_REL )ON ( DURING )
Here then is the implementation algorithm:
Step 1: Initialize result to empty.
Step 2: Partition SP_DURING on SNO. In the example, this step yields a single partition, for supplier S1.
Step 3: For each resulting partition p, do Steps 4 to 6 below.
Step 4: Split the tuples in p. For the single partition in the example (for supplier S1), this step yields:
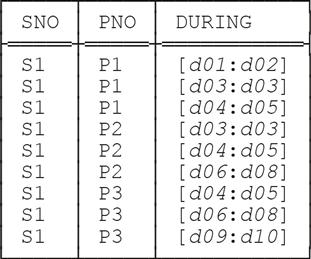
Step 5: Apply the specified grouping, to yield px, say. In the example, this step yields—

—where relations pr1, pr2, pr3, pr4, and pr5 are as follows:
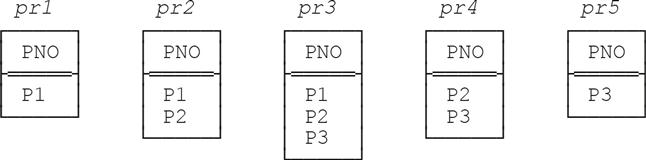
Step 6: result := result D_UNION ( PACK px ON ( DURING ) ) ;
U_UNGROUP
The implementation algorithm for U_UNGROUP is very similar to that for U_GROUP, except that no splitting is needed in Step 4 and (of course) UNGROUP is used instead of GROUP in Step 5. We omit the details here.
U_comparisons
First we consider “U_=”. The expression
USING ( ACL ) : r1 = r2
is defined to be equivalent to
( UNPACK r1 ON ( ACL ) ) = ( UNPACK r2 ON ( ACL ) )
Here’s the implementation algorithm:
WITH ( t1 := PACK r1 ON ( ACL ) ,
t2 := PACK r2 ON ( ACL ) ) :
t1 = t2
Note: The two PACKs here are correct—they’re not typographical errors for UNPACK.
Turning now to “U_⊆”, the expression
USING ( ACL ) : r1 ⊆ r2
is defined to be equivalent to
( UNPACK r1 ON ( ACL ) ) ⊆ ( UNPACK r2 ON ( ACL ) )
which is in turn equivalent to
IS_EMPTY ( USING ( ACL ) : r1 MINUS r2 )
And we know how to implement U_MINUS without unpacking. As for “U_⊇”, the expression USING (ACL ) : r1 ⊇ r2 is of course equivalent to USING (ACL) : r2 ⊆ r1.
Update Operators
We assume throughout this section that relvar R has heading {A,B,A1,A2} and key {A,A1,A2}, where A1 and A2 are interval attributes and B is all of the attributes of R apart from A, A1, and A2. We further assume that R is subject to the U_key constraint USING (A1,A2): KEY {A,A1,A2}, and hence in particular that the value of R is packed on (A1,A2) at all times.
Intuitively, the basic idea with respect to all three of U_INSERT, U_DELETE, and U_UPDATE is that it’s not necessary to unpack (or split, rather) and subsequently repack all of the tuples involved in the operation—it’s sufficient to split and repack just those tuples that are relevant, as we’ll see.
U_INSERT
Let the set of tuples to be inserted into R be the tuples in relation r.
Step 1: If R and r together contain distinct tuples t1 and t2 such that
( ( A FROM t1 ) = ( A FROM t2 ) ) AND
( ( A1 FROM t1 ) OVERLAPS ( A1 FROM t2 ) ) AND
( ( A2 FROM t1 ) OVERLAPS ( A2 FROM t2 ) )
then signal error: WHEN / THEN constraint violation. (Of course, U_INSERTs, U_DELETEs, and U_UPDATEs can all fail on a variety of constraint violations. We don’t show the code to deal with such errors in general, but we do mention WHEN / THEN constraints, in connection with U_INSERT in particular, because of their fundamental nature—also because they’re conceptually easy to deal with.)
Step 2: Partition r on {A,B}. For each resulting partition pr, do Steps 3 to 5.
Step 3: Let t1 be a tuple of R such that there exists some tuple t2 in pr such that
( ( A FROM t1 ) = ( A FROM t2 ) ) AND
( ( B FROM t1 ) = ( B FROM t2 ) ) AND
( ( A1 FROM t1 ) MEETS ( A1 FROM t2 ) OR
( A2 FROM t1 ) MEETS ( A2 FROM t2 ) )
Let r1 be the set of all such tuples t1.
Step 4: Delete all tuples of r1 from R.
Step 5: Let r2 be the result of USING (A1,A2): r1 UNION pr. Insert all tuples of r2 into R. Note that no key uniqueness checking will be needed in this step.
U_DELETE
We deliberately don’t consider the completely general case here, but limit ourselves to U_DELETEs of the following “almost completely general” form:
USING ( A1 , A2 ) : DELETE R WHERE A1 ⊆ a1 AND A2 ⊆ a2 AND ( bx ) ) ;
Step 1: Let r1 be the set of all tuples t1 of R satisfying
( ( A1 FROM t1 ) OVERLAPS a1 ) AND
( ( A2 FROM t1 ) OVERLAPS a2 ) AND
( bx )
Step 2: Let tuple t1 of r1 be as follows:
TUPLE { A a , B b , A1 i1 , A2 i2 }
Let r2 be the set of all tuples t2 of the form
TUPLE { A a , B b , A1 ( i1 INTERSECT a1 ) , A2 ( i2 INTERSECT a2 ) }
Step 3: Let r3 be the result of
USING ( A1 , A2 ) : r1 MINUS r2
Step 4: Delete all tuples of r1 from R.
Step 5: Use the algorithm for U_INSERT to insert the tuples of r3 into R.
Note: As we saw in Chapter 16, PORTION DELETE is often likely to be preferred over U_DELETE. As some commercial implementations already support an SQL version of this operator (see Chapter 19), however, we see no need to present an implementation algorithm here.
U_UPDATE
We deliberately don’t consider the completely general case here, but limit ourselves to U_UPDATEs of the “almost completely general” form:
USING ( A1 , A2 ) : UPDATE R WHERE A1 ⊆ a1 AND A2 ⊆ a2 AND ( bx ) : { attribute assignments } ;The following algorithm is very similar to that for U_DELETE:
Step 1: Let r1 be the set of all tuples t1 of R satisfying
( ( A1 FROM t1 ) OVERLAPS a1 ) AND
( ( A2 FROM t1 ) OVERLAPS a2 ) AND
( bx )
Step 2: Let tuple t1 of r1 be as follows:
TUPLE { A a, B b, A1 i1, A2 i2 }
Let r2 be the set of all tuples t2 of the form
TUPLE { A a , B b, A1 ( i1 INTERSECT a1 ) , A2 ( i2 INTERSECT a2 ) }
Step 3: Let r3 be the result of
USING ( A1 , A2 ) : r1 MINUS r2
Step 4: Let r2' be that relation that results from applying the specified attribute assignments to r2.
Step 5: Delete all tuples of r1 from R.
Step 6: Use the algorithm for U_INSERT to insert the tuples of r3 into R.
Step 7: Use the algorithm for U_INSERT to insert the tuples of r2' into R.
Note: The remark concerning PORTION DELETE at the end of the previous subsection applies to PORTION UPDATE also, mutatis mutandis.
A Final Remark
The UNPACK operator is a crucial conceptual component of our approach to the management of interval data in general and temporal data in particular. But UNPACK has been criticized in the literature on the grounds that it necessarily entails poor performance. We hope the discussions in this appendix will help to lay such criticisms to rest. To say it again, UNPACK is a crucial conceptual component of our approach—but it’s only a conceptual component. We don’t want unpackings per se ever to be physically performed if we can possibly avoid them; and in this appendix we’ve shown how they can usually be avoided.