Cyclic Point Types
Point types are usually assumed to have a first (minimum) and last (maximum) value. This appendix concerns itself with point types such as days of the week for which that assumption isn’t necessarily valid. For example, in the case of days of the week, an interval such as “Friday to Tuesday” does make sense, at least intuitively. Allen’s operators are reexamined in this light and are found still to be applicable, though their definitions need to be refined somewhat. The same goes for the interval UNION, INTERSECT, and MINUS operators, also for the PACK and UNPACK operators.
Keywords: cyclic type; periodic type; wraparound interval; Allen’s operators
What goes around comes around.
—late 20th century catchphrase
All of the intervals [b:e] discussed in the body of this book were required—in fact, defined—to satisfy the condition b ≤ e. And yet intervals that appear to violate this condition are quite common in everyday life. For example, someone doing shiftwork might be required to work from 11:00 pm to 7:00 am, or a restaurant might be open each week from Thursday to Tuesday. The intervals in these two examples are based on what might be called wraparound or cyclic point types—to be specific, “time of day” and “day of week,” respectively, with the obvious semantics in each case. Such types share with modular arithmetic the property that the available values can be thought of as points arranged around the circumference of a circle, such that every value has both a successor and a predecessor, and there’s no first or last value. So the question is: To what extent can the ideas discussed in the body of the book for regular—or what might be called linear—point types be made to work for cyclic types? Indeed, can they be made to work at all? Investigating this issue is the purpose of this appendix.
The Weekday Example
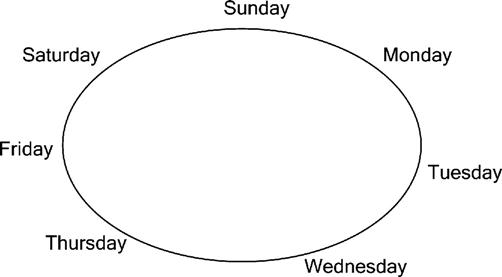
For definiteness, let’s focus on the weekday example (see Fig. A.1).
Here then is a possible type definition, or at least the beginnings of such a definition, for type WEEKDAY:
TYPE WEEKDAY
POSSREP WDPRI { WDI INTEGER CONSTRAINT WDI ≥ 0 AND WDI ≤ 6 } POSSREP WDPRC { WDC CHAR CONSTRAINT WDC = 'Sun' OR WDC = 'Mon' OR WDC = 'Tue' OR WDC = 'Wed' OR WDC = 'Thu' OR WDC = 'Fri' OR WDC = 'Sat' } ;As you can see, we’ve defined two possible representations (“possreps”) for this type—one, WDPRI, as an integer WDI in the range [0:6], and the other, WDPRC, as a character string WDC with values ‘Sun’, ‘Mon’, etc. Note: For the rest of this appendix we’ll refer to individual days, much of the time, by those shorthand names Sun, Mon, etc. Also, we’ll take Sunday to be day 0, Monday to be day 1, and so on.
Here now are the selector definition and associated THE_ operator definition for possrep WDPRI (in outline only—coding details are omitted, since they presumably reference whatever the physical representation for weekdays might be, and such matters are irrelevant to our main purpose in this appendix):
OPERATOR WDPRI ( WDI INTEGER ) RETURNS WEEKDAY ;
/* code to return the WEEKDAY value corresponding */
/* to the given integer WDI */
END OPERATOR ;
OPERATOR THE_WDI ( WD WEEKDAY ) RETURNS INTEGER ;
/* code to return the integer corresponding */
/* to the given WEEKDAY value WD */
END OPERATOR ;
By definition, the WDPRI selector takes an integer as input and returns a weekday. However, it turns out to be convenient, for reasons we’ll see later, not to require the input integer WDI to fall in the range [0:6] but to allow it to be any integer, negative or nonnegative. Thus, we assume the first thing the implementation code for WDPRI does is compute NNR = the nonnegative remainder after dividing WDI by 7;1 then it returns the weekday corresponding to NNR. The value NNR here can be regarded as a canonical representation for the input integer WDI. Note: By contrast, we assume, reasonably enough, that the integer result returned by THE_WDI is always in the range [0:6].
Turning to possrep WDPRC, here now are definitions for the selector and THE_ operator associated with that possrep. Observe that the selector (WDPRC) is defined in terms of WDPRI and the THE_operator (THE_WDC) is defined in terms of THE_WDI.
OPERATOR WDPRC ( WDC CHAR ) RETURNS WEEKDAY ;
RETURN CASE
WHEN WDC = ‘Sun’ THEN WDPRI ( 0 )
WHEN WDC = ‘Mon’ THEN WDPRI ( 1 )
WHEN WDC = ‘Tue’ THEN WDPRI ( 2 )
WHEN WDC = ‘Wed’ THEN WDPRI ( 3 )
WHEN WDC = ‘Thu’ THEN WDPRI ( 4 )
WHEN WDC = ‘Fri’ THEN WDPRI ( 5 )
WHEN WDC = ‘Sat’ THEN WDPRI ( 6 )
END CASE ;
END OPERATOR ;
OPERATOR THE_WDC ( WD WEEKDAY ) RETURNS CHAR ;
RETURN CASE
WHEN THE_WDI (WD ) = 0 THEN 'Sun'
WHEN THE_WDI (WD ) = 1 THEN 'Mon'
WHEN THE_WDI (WD ) = 2 THEN 'Tue'
WHEN THE_WDI (WD ) = 3 THEN 'Wed'
WHEN THE_WDI (WD ) = 4 THEN 'Thu'
WHEN THE_WDI (WD ) = 5 THEN 'Fri'
WHEN THE_WDI (WD ) = 6 THEN 'Sat'
END CASE ;
END OPERATOR ;
Of course, we also need the “=” operator:
OPERATOR “=” ( WD1 WEEKDAY , WD2 WEEKDAY ) RETURNS BOOLEAN ;
RETURN ( THE_WDI ( WD1 ) = THE_WDI ( WD2 ) ) ;
END OPERATOR ;
Note: This last definition could and probably should be provided automatically by the system. We show it explicitly for pedagogic reasons.
Weekday as a Point Type
So is WEEKDAY a valid point type? Well, intervals of the form “Wednesday to Friday” or “Friday to Monday” certainly make good intuitive sense. But in Chapter 18 we said point types were supposed to be ordinal types, and WEEKDAY doesn’t fit the definition of an ordinal type, because there’s no first value of the type and no last. On the other hand, values of the type are certainly ordered; we all know that, e.g., Friday comes after Thursday. So there’s an ordering all right, but that ordering isn’t linear but cyclic,2 meaning that when we’ve cycled through all the values we start again (Sunday follows immediately after Saturday).
How do such considerations affect our usual notions of point types and interval types? Well, here’s a definition, paraphrased from Chapter 18, of what it means to be an ordinal type:
Definition: An ordinal type is a type T such that (a) the expression v1 > v2 is defined for all pairs of values v1 and v2 of type T, returning TRUE if and only if v1 follows v2 with respect to the pertinent ordering, and (b) certain additional operators are required: first, last, next, prior, and possibly others.
First of all, then, does “>” apply to values of type WEEKDAY? Well, there seem to be two ways we might define such an operator:
■ We could define v1 > v2 to be true if and only if THE_WDI (v1) > THE_WDI (v2) is true, so that Sat > Fri > … > Mon > Sun. This definition doesn’t seem very useful, since (among other things) it would apparently outlaw intervals like [Fri:Mon].
■ We could define v1 > v2 to be true if and only if v1 follows v2 according to the cyclic ordering. This definition seems even more useless than the previous one, since it implies that “>” would be indistinguishable from ‘≠’ (v1 > v2 would be true if and only if v1 ≠ v2 was also true).
So if WEEKDAY is going to be usable as a point type, it seems we’re going to have to find a way to make it be so without relying on a “>” operator as such.
Second, as already noted, type WEEKDAY has no “first” and “last” operators. But it does have successor and predecessor functions. Here are the definitions:3
OPERATOR NEXT_WEEKDAY ( WD WEEKDAY ) RETURNS WEEKDAY ;
RETURN WDPRI ( THE_WDI ( WD ) + 1 ) ) ;
END OPERATOR ;
OPERATOR PRIOR_WEEKDAY ( WD WEEKDAY ) RETURNS WEEKDAY ;
RETURN WDPRI ( THE_WDI ( WD ) − 1 ) ) ;
END OPERATOR ;
What’s more, these functions, unlike their counterparts for ordinal types, never fail.
So let’s invent some syntax for indicating that a given type is a cyclic type—perhaps as indicated here (note the highlighted text):
TYPE WEEKDAY CYCLIC … ;
We interpret the CYCLIC specification as implying that:
■ A niladic cardinality operator must be defined, which returns the number N of values in the type (N is 7, of course, in the case of type WEEKDAY). A real language might require the name of that operator—COUNT_WEEKDAY, say—to be stated as part of the CYCLIC specification.4
■ Monadic “next” and “prior” operators must also be defined, and they must be isomorphic to “add one” and “subtract one,” respectively, in arithmetic modulo N. A real language might require the names of those operators—NEXT_WEEKDAY and PRIOR_WEEKDAY, in our running example—to be stated as part of the CYCLIC specification.
The Corresponding Interval Type
Now let’s see if we can make sense of an interval type of the form INTERVAL_WEEKDAY. Values of this type, if they do make sense, will be intervals of the form [b:e], where b and e are both values of type WEEKDAY. What happens to the associated operators?
First we define the necessary interval selector operator, as follows: The selector invocation INTERVAL_WEEKDAY ([b:e]), where b and e are values of type WEEKDAY, returns the interval consisting of the sequence b, b+1, …, e, such that no weekday appears more than once in that sequence.5 That is, starting at day b, we trace our steps around the cyclic ordering until we meet day e for the first time, and then we stop (so no interval is ever more than seven days in length). Here are some examples:
INTERVAL_WEEKDAY ( [ WDPRC('Mon') : WDPRC('Fri') ] )INTERVAL_WEEKDAY ( [ WDPRC('Fri') : WDPRC('Mon') ] )INTERVAL_WEEKDAY ( [ WDPRC('Wed') : WDPRC('Wed') ] )INTERVAL_WEEKDAY ( [ WDPRC('Wed') : WDPRC('Tue') ] )The first three of these examples are straightforward: They denote the five-day interval from Monday to Friday, the four-day interval from Friday to Monday, and the unit (one-day) interval consisting of just Wednesday, respectively. The fourth example deserves a closer look, however. On the face of it, of course, it simply denotes the seven-day interval from Wednesday to Tuesday—but that interval is slightly special, in that it contains all possible values of the underlying point type; in other words, it’s what we might call (for the purposes of this appendix, at any rate) a universal interval. The obvious question arises: If, e.g., [Sun:Sat] and [Thu:Wed]—to adopt an obvious shorthand notation—are two such intervals, but with different begin and end points, are they equal or not?
We answer this question in the negative. Certainly there’s an intuitive distinction, and indeed a pragmatically useful distinction, to be drawn between, e.g., the interval [Sun:Sat] and the interval [Thu:Wed]. Of course, it’s true that these intervals do both contain the same set of points; however, those points appear in a different sequence with respect to the intervals in which they appear. (All universal intervals of type INTERVAL_WEEKDAY consist of some cyclic permutation of the sequence Sun, Mon, Tue, Wed, Thu, Fri, Sat, of course.)6
Further Operators
The BEGIN, END, PRE, POST, POINT FROM, “∈”, “∋”, and COUNT operators are all straightforward and require no further discussion here.
Allen’s Operators
Allen’s operators do apply to intervals where the underlying point type is cyclic, but some of the definitions need revision. Let i1 = [b1:e1] and i2 = [b2:e2] be two such intervals (both defined, of course, over the same point type). Then:
Equals: This operator is unaffected: that is, i1 = i2 is true if and only if b1 = b2 and e1 = e2 are both true. Observe that this definition is consistent with our earlier statement to the effect that universal intervals such as, e.g., [Sun:Sat] and [Thu:Wed] are different intervals.
Inclusion: The “⊆”, “⊂”, “⊇”, and “⊃” operators do apply, but their definitions need to be stated somewhat differently, as follows. Consider, e.g., the intervals i1 = [Fri:Mon] and i2 = [Sun:Sat]. Clearly, every point in i1 is also a point in i2. Equally clearly, it seems unreasonable to say i1 is included in i2, because even though the set of points in i1 is a subset of the set of points in i2, the sequence of points in i1 isn’t a subsequence of the sequence of points in i2. The following definition is motivated by such considerations. Consider the process of examining the set of points b2, b2+l, b2+2, …, e2—i.e., the set of points in i2—in sequence according to the cyclic ordering. Then i1 ⊆ i2 is true if and only if, as we perform this process, we encounter both b1 and e1 and we do not encounter e1 before b1. (So if i1 ⊆ i2, then every point p that appears in i1 also appears in i2. However, the converse isn’t necessarily true. That is, the fact that every point p that appears in i1 also appears in i2 does not imply that i1 ⊆ i2.)
The operators “⊂”, “⊇”, and “⊃” are then defined in terms of “⊆” in the usual way: i1 ⊂ i2 is true if and only if i1 ⊆ i2 and i1 ≠ i2 are both true; i2 ⊇ i1 is true if and only if i1 ⊆ i2 is true; i2 ⊃ i1 is true if and only if i1 ⊂ i2 is true.
Examples:
[Tue:Thu] ⊂ [Mon:Fri] : TRUE
[Sat:Wed] ⊃ [Sun:Mon] : TRUE
[Mon:Fri] ⊇ [Thu:Sat] : FALSE
[Thu:Tue] ⊆ [Mon:Fri] : FALSE
Note the last of these in particular; as we examine the set of points Mon, Tue, Wed, Thu, Fri, we do encounter both Thu and Tue, but we do so “the wrong way round,” as it were (we get to the end point Tue before the begin point Thu). For similar reasons, neither of the universal intervals [Mon:Sun] and [Tue:Mon] is considered to be included in the other.
BEFORE and AFTER: These operators also apply, but the definitions need to be stated a little differently, as follows: i1 BEFORE i2 is true if and only if, in the cyclic ordering starting from b1, (a) e1 is encountered before b2 and (b) e2 is encountered before b1 is encountered a second time. Note that it follows from this definition that i2 BEFORE i1 is true if and only if i1 BEFORE i2 is true (!). It also follows that i1 BEFORE i2 is true if and only if i1 and i2 are disjoint—i.e., there’s no point p that appears in both i1 and i2. Also, i2 AFTER i1 is true if and only if i1 BEFORE i2 is true (so in fact the operators BEFORE and AFTER are one and the same, both reducing to simply NOT OVERLAPS, or DISJOINT).
Examples:
[Tue:Wed] BEFORE [Fri:Sat] : TRUE
[Fri:Sat] BEFORE [Tue:Wed] : TRUE
[Tue:Wed] AFTER [Fri:Sat] : TRUE
[Fri:Sat] AFTER [Tue:Wed] : TRUE
[Tue:Fri] BEFORE [Wed:Sat] : FALSE
OVERLAPS: The simplest way to define this operator is simply to say that i1 OVERLAPS i2 is true if and only if i1 and i2 aren’t disjoint—i.e., if and only if there exists at least one point p that appears in both i1 and i2. Equivalently, i1 OVERLAPS i2 is true if and only if i1 BEFORE i2 is false. Note, however, that i1 can overlap i2 at both ends, as it were (see, e.g., the fifth example below), something that can’t happen with ordinal point types.
Examples: The following pairs of intervals overlap:
[Tue:Thu] and [Wed:Fri]
[Tue:Thu] and [Mon:Wed]
[Tue:Thu] and [Mon:Tue]
[Tue:Thu] and [Fri:Wed]
[Thu:Tue] and [Mon:Fri]
The following, by contrast, don’t—i.e., they’re disjoint:
[Tue:Thu] and [Sat:Sun]
[Tue:Thu] and [Fri:Sun]
[Tue:Thu] and [Sun:Mon]
MEETS: The original definition from Chapter 7 remains unchanged: i1 MEETS i2 is true if and only if b2 = e1+1 is true or b1 = e2+1 is true (and i2 MEETS i1 is true if and only if i1 MEETS i2 is true). Note, however, that i1 can meet i2 at both ends, as it were, something that can’t happen with ordinal point types; note also that i1 can meet i2 at one end and overlap it at the other, again something that can’t happen with ordinal point types.
Examples: The following pairs of intervals meet:
[Tue:Thu] and [Fri:Sat]
[Tue:Thu] and [Sun:Mon]
[Tue:Thu] and [Fri:Wed]
(The last pair don’t just meet, they also overlap.) By contrast, the following don’t meet:
[Tue:Thu] and [Sat:Sat]
[Tue:Thu] and [Sat:Sun]
MERGES: The original definition from Chapter 7 remains unchanged: i1 MERGES i2 is true if and only if i1 OVERLAPS i2 is true or i1 MEETS i2 is true. Here’s an example of a pair of intervals that don’t “merge” in this sense:
[Mon:Wed] and [Fri:Sat]
BEGINS and ENDS: The original definitions from Chapter 7 remain unchanged: (a) i1 BEGINS i2 is true if and only if b1 = b2 and e1 ∈ i2 are both true; (b) i1 ENDS i2 is true if and only if e1 = e2 and b1 ∈ i2 are both true.
Examples:
[Tue:Wed] BEGINS [Tue:Sat] : TRUE
[Tue:Fri] BEGINS [Tue:Thu] : FALSE
[Tue:Wed] ENDS [Sun:Wed] : TRUE
[Fri:Mon] ENDS [Sat:Mon] : FALSE
Union, Intersect, and Minus
Again let i1 and i2 be intervals defined over the same point type. Now, we saw in Chapter 7 that:
■ i1 UNION i2 is defined if and only if i1 MERGES i2 is true.
■ i1 INTERSECT i2 is defined if and only if i1 OVERLAPS i2 is true.
■ i1 MINUS i2 is defined if and only if (a) i1 and i2 are disjoint, or (b) i1 contains either b2 or e2 but not both, or (c) exactly one of i2 BEGINS i1 and i2 ENDS i1 is true.
But in that chapter, of course, the underlying point type was an ordinal type. As a consequence, we were able to define the foregoing operators in terms of the auxiliary operators MAX and MIN, and these latter operators in turn were defined in terms of “>”. If UNION, INTERSECT, and MINUS are to apply to intervals over cyclic point types, therefore, we need to come up with some different definitions, since “>” is no longer available to us. We propose the following. First, let PT be the cyclic point type in question, and let i1 = [b1:e1] and i2 = [b2:e2], where b1, e1, b2, and e2 are values of type PT. Then we can define UNION, INTERSECT, and MINUS as follows.
UNION: Consider the expression i1 UNION i2, where, as before, i1 MERGES i2 is true (the expression is undefined otherwise). The easiest way to define the semantics of this expression seems to be by means of a short pseudocode algorithm, as follows.7
Aside: It would be nice to come up with an alternative, nonalgorithmic (i.e., nonprocedural) definition; unfortunately, it seems to be quite difficult to do so. Perhaps there’s a way to generalize MAX and MIN so that the original definition from Chapter 7 still works. Of course, it’s true that when it’s defined, i = i1 UNION i2 contains exactly the points that appear in i1 or i2 or both, but it seems to be quite difficult to distinguish nonalgorithmically between the case where BEGIN(i) = BEGIN(i1) and the case where BEGIN(i) = BEGIN(i2), and similarly for END(i) = END(i1) vs. END(i) = END(i2). Analogous remarks apply to INTERSECT and MINUS also (see later). End of aside.
■ Starting at the point b1, trace around the cyclic ordering until one of the points {b2, e1, e2} is reached.
■ Let “p 
q” mean either that p and q coincide or that q is encountered before p when tracing around the cyclic ordering starting at some specified point.
■ Let “first p such that p q” mean whichever of the points {b1,b2,e1,e2} is encountered first when tracing around the cyclic ordering starting at q.8
Then we have:
IF i1 NOT MERGES i2 THEN error (undefined) END IF ;
CASE ;
WHEN first p such that p
CASE ;
WHEN first p such that p
WHEN first p such that p
END CASE ;
WHEN first p such that p
CASE /* i1 MEETS i2 must be true */ ;
WHEN b2 = e1+1 THEN RETURN [b1:e2] ;
WHEN b1 = e2+1 THEN RETURN [b2:e1] ;
END CASE ;
WHEN first p such that p
CASE ;
WHEN first p such that p
WHEN first p such that p
END CASE ;
END CASE ;
Here are some examples:
[Mon:Wed] UNION [Fri:Sat] : undefined
[Mon:Thu] UNION [Tue: Fri] = [Mon:Fri]
[Tue:Fri] UNION [Mon:Thu] = [Mon:Fri]
[Mon:Thu] UNION [Sat:Tue] = [Sat:Thu]
[Thu:Sat] UNION [Mon:Thu] = [Mon:Sat]
[Sat:Sat] UNION [Sat:Sat] = [Sat:Sat]
[Tue:Fri] UNION [Sat:Tue] = [Sat:Fri]
[Tue:Fri] UNION [Sat:Mon] = [Tue:Mon]
[Sat:Mon] UNION [Tue:Fri] = [Sat:Fri]
Note: As the last two examples demonstrate, the algorithm isn’t guaranteed to produce the same result for i1 UNION i2 and i2 UNION i1 in the special case where i1 and i2 between them contain all of the available values. (Both results are universal intervals, of course—i.e., they both contain all of the available values—but in general they begin at different points.) Clearly it would be preferable not to lose the commutativity of union, and so the algorithm needs a small adjustment to fix this problem.9
INTERSECT: Now consider the expression i1 INTERSECT i2. As before, i1 OVERLAPS i2 must be true; note, however, that this requirement, though necessary, isn’t sufficient for the expression to be defined. To be specific, we mustn’t have the intervals overlapping each other at both ends, as it were (unless at least one of the intervals in question is a universal interval). Thus, with the same notation and initial conditions as for UNION above, we have:
IF i1 NOT OVERLAPS i2 THEN error (undefined) END IF ;
IF i1 overlaps i2 at both ends10
AND COUNT(i1) ≠ COUNT_WEEKDAY ( )
AND COUNT(i2) ≠ COUNT_WEEKDAY ( )
THEN error (undefined) END IF ;
CASE ;
WHEN first p such that p
CASE ;
WHEN first p such that p
WHEN first p such that p
END CASE ;
WHEN first p such that p
/* i1 ⊂ i2 must be true */ RETURN [b1:e1] ;
WHEN first p such that p
CASE ;
WHEN first p such that p
/* e1 = b1−1 must be true */ RETURN [b2:e2] ;
WHEN first p such that p
END CASE ;
END CASE ;
Here are some examples (all of which use the same input intervals as their union example counterpart shown earlier, except for the last two, which had no such counterparts):
[Mon:Wed] INTERSECT [Fri:Sat] : undefined
[Mon:Thu] INTERSECT [Tue: Fri] = [Tue:Thu]
[Tue:Fri] INTERSECT [Mon:Thu] = [Tue:Thu]
[Mon:Thu] INTERSECT [Sat:Tue] = [Mon:Tue]
[Thu:Sat] INTERSECT [Mon:Thu] = [Thu:Thu]
[Sat:Sat] INTERSECT [Sat:Sat] = [Sat:Sat]
[Tue:Fri] INTERSECT [Sat:Tue] = [Tue:Tue]
[Tue:Fri] INTERSECT [Sat:Mon] = undefined
[Sat:Mon] INTERSECT [Tue:Fri] = undefined
[Tue:Wed] INTERSECT [Sat:Fri] = [Sat:Fri]
[Sat:Fri] INTERSECT [Thu:Wed] = [Thu:Wed]
Note: As the last two examples demonstrate, the algorithm isn’t guaranteed to produce the same result for i1 INTERSECT i2 and i2 INTERSECT i1 in the special case where i1 and i2 are both universal intervals.11 As in the case of UNION, therefore, the algorithm needs a small adjustment to fix this problem.
MINUS: Now consider the expression i1 MINUS i2. This expression is certainly defined if any of the following is the case (as before):
b. i1 contains either b2 or e2 but not both.
c. Exactly one of i2 BEGINS i1 and i2 ENDS i1 is true.
But there’s another possibility too—the operator is also defined if:
d. i1 and i2 overlap at both ends (so long as i2 isn’t a universal interval, of course).
Thus, with the same notation and initial conditions as for UNION and INTERSECT above, we have:
IF COUNT ( i2 ) = COUNT_WEEKDAY ( ) THEN error (undefined) END IF ;
IF i1 OVERLAPS i2
AND NOT ( b2 ∈ i1 XOR e2 ∈ i1 ) /* XOR = exclusive OR */
AND NOT ( i2 BEGINS i1 XOR i2 ENDS i1 )
AND NOT ( i1 overlaps i2 at both ends )
THEN error (undefined) END IF ;
CASE ;
WHEN first p such that p
WHEN first p such that p
CASE ;
WHEN first p such that p
WHEN first p such that p
END CASE ;
WHEN first p such that p
CASE ;
WHEN first p such that p
WHEN first p such that p
END CASE ;
END CASE ;
Here are some examples, most of which use the same input intervals as their intersection example counterpart shown earlier:12
[Mon:Wed] MINUS [Fri:Sat] = [Mon:Wed]
[Mon:Thu] MINUS [Tue:Fri] = [Mon:Mon]
[Tue:Fri] MINUS [Mon:Thu] = [Fri:Fri]
[Mon:Thu] MINUS [Sat:Tue] = [Wed:Thu]
[Thu:Sat] MINUS [Mon:Thu] = [Fri:Sat]
[Sat:Sat] MINUS [Sat:Sat] : undefined
[Tue:Fri] MINUS [Sat:Tue] = [Wed:Fri]
[Tue:Fri] MINUS [Sat:Mon] = [Tue:Fri]
[Sat:Mon] MINUS [Tue:Fri] = [Sat:Mon]
[Tue:Sun] MINUS [Sat:Wed] : [Thu:Fri]
[Sat:Fri] MINUS [Thu:Wed] : undefined
[Tue:Thu] MINUS [Thu:Fri] = [Tue:Wed]
PACK and UNPACK
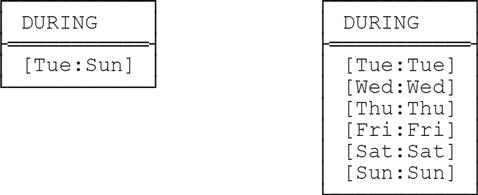
Given that union and intersection can both be defined for intervals over cyclic point types, so too can the PACK and UNPACK operators. For example, suppose we’re given a relation r that looks like this:
Then the packed and unpacked forms of r look like this (packed on the left, unpacked on the right):
Overall, therefore, we conclude that:
a. Cyclic types such as WEEKDAY are indeed valid as point types.
b. Such types behave normally, except that FIRST_T and LAST_T don’t apply and NEXT_T and PRIOR T never fail.
c. The corresponding interval types also behave more or less normally, except that we don’t—actually we can’t—require the begin point to be less than or equal to the end point, and certain operators need somewhat revised definitions.
d. The conditions stated previously in Chapters 6 and 18 for a type to be usable as a point type are sufficient but not all necessary.
Exercises
A.1 Define “time of day,” with a scale of one hour, as a cyclic point type. Include all necessary associated operator definitions.
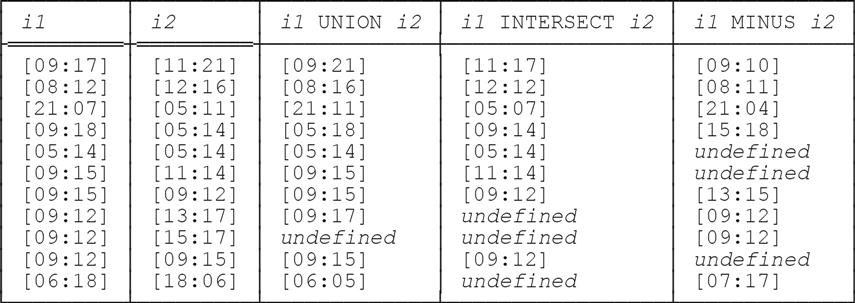
A.2 Given that i1 and i2 denote intervals over the “time of day” point type, fill in the blanks in the following table:
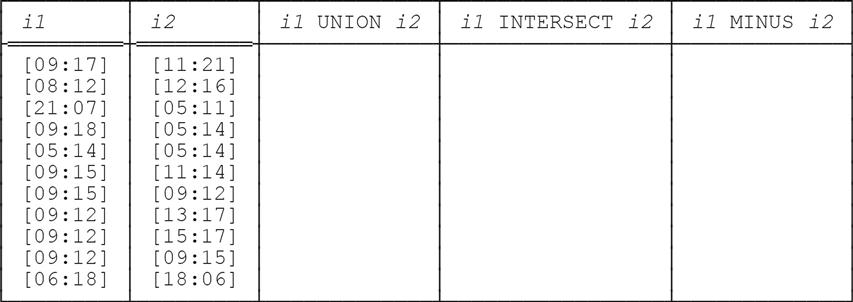
Note: We assume for simplicity here that intervals over the “time of day” point type are expressed in the form [xx:yy], where xx and yy are two-digit integers in the range [00:23] and denote time points accurate to the hour on the 24-hour clock.
A.3 Certain commercial enterprises (e.g., shops, restaurants) are open for business only at certain times on certain days (e.g., Monday to Friday, 9:00 am to 5:00 pm). Design a database to represent such information. What are some of the considerations that might influence your design?
Answers
A.1 TYPE TOD CYCLIC POSSREP HOUR { H INTEGER CONSTRAINT 0 ≤ H AND H ≤ 23 } ;
OPERATOR HOUR ( H INTEGER ) RETURNS TOD ;
/* code to return the TOD value corresponding */
/* to the given integer H */
END OPERATOR ;
By definition, the HOUR selector takes an integer and returns a time of day accurate to the hour. We assume the argument corresponding to the parameter H is any integer. Thus, we assume the implementation code for HOUR computes NNR = the nonnegative remainder after dividing H by 24 and then returns the time of day corresponding to NNR.
OPERATOR THE_H ( T WEEKDAY ) RETURNS INTEGER ;
/* code to return the integer corresponding */
/* to the given TOD value T */
END OPERATOR ;
The integer value returned by THE_H is always in the range [00:23].
OPERATOR “=” ( T1 TOD,T2 TOD ) RETURNS BOOLEAN ;
RETURN ( THE_H ( T1 ) = THE_H ( T2 ) ) ;
END OPERATOR ;
OPERATOR NEXT_TOD ( T TOD ) RETURNS TOD ;
RETURN HOUR ( THE_H ( T ) + 1 ) ) ;
END OPERATOR ;
OPERATOR PRIOR_TOD ( T TOD ) RETURNS TOD ;
RETURN HOUR ( THE_H ( T ) − 1 ) ) ;
END OPERATOR ;
A.3 The exercise is open ended, so this answer is necessarily only partial. Consider a relvar R with attributes CE (commercial enterprise), D (interval of days), and H (interval of hours). The general case is: CE is open for business only on selected days (e.g., weekdays), and during different hours on different days (e.g., Thursday is early closing day), and during two or more disjoint intervals on at least some days (e.g., Mondays 9:00 am to 12:30 pm, 2:00 pm to 5:00 pm, closed for lunch 12:30 pm to 2:00 pm). In this general case, relvar R is all key. If CE is open for business during different hours on different days but not during two or more disjoint intervals on any given day, then relvar R has key {CE,D}. If CE is open for business for the same hours every day it’s open, then again relvar R has key {CE,D}, but now the functional dependency {CE} → {H} holds, and R isn’t in 6NF (in fact, it isn’t even in 2NF). And so on … E.g., what if CE is open for business every day of the year except for certain national holidays?
As a subsidiary exercise, try writing the predicates for the various aforementioned cases.