Interval Operators
This chapter introduces a convenient informal notation for points and intervals and for some of the most fundamental operators on such points and intervals: first, last, next, prior, BEGIN, END, PRE, POST, and so on. Using that notation, it then defines and illustrates a collection of generic comparison operators for intervals, known generically as Allen’s operators: interval equality, interval inclusion and proper inclusion, BEFORE and AFTER, OVERLAPS, MEETS, MERGES, and BEGINS and ENDS. Using these operators, the chapter then goes on to define interval analogs of the well known set theory operators UNION, INTERSECT, and MINUS. Finally, it shows how all of these operators can be used to help with the practical problem of formulating queries.
Keywords
interval comparisons; Allen’s operators; OVERLAPS, MEETS and MERGES; interval UNION, INTERSECT, and MINUS
What Nature provides is the intervals.
—Paul Hindemith:
The Craft of Musical Composition (1937)
In this chapter we discuss a number of useful operators that apply to intervals. Most if not all of the operators in question are described in the literature, under a variety of different names. The names we use ourselves are the ones that seem most satisfactory to us, of course, but you should at least be aware that other names do appear in the literature, and we’ll mention some of those alternative names from time to time in the pages ahead.
Notation
We adopt and extend the notation from Chapter 6, as follows:
■ Let T be a point type and let p be a value of type T. Then we use the expressions p+1, p+2, etc., to denote the value that’s the successor of p, the value that’s the successor of p+1, and so on. Of course, this notation is only informal; a real language would have to provide some kind of explicit next operator. When we need to refer to that formal operator explicitly, we’ll call it NEXT_T—thus, NEXT_T (p) returns p+1, NEXT_T (NEXT_T (p)) returns p+2, and so on. Observe, therefore, that the formal next operator has an explicit “_T” qualifier (and the same is true for the formal prior, first, last, and interval selector operators, as we’ll see in a moment). We’ll explain why that qualifier is necessary in Chapter 18.
■ We also use, again informally, the expressions p-1, p-2, etc., to denote the value whose successor is p, the value whose successor is p-1, etc. A real language would have to provide an explicit prior operator, which we’ll call PRIOR_T; PRIOR_T (p) returns p-1, PRIOR_T (PRIOR_T (p)) returns p-2, and so on.
■ We also need niladic FIRST_T and LAST_T operators; FIRST_T ( ) and LAST_T ( ) return the “first” and “last” value, respectively, of type T.
■ The interval type corresponding to point type T is INTERVAL_T. Informally, we use the expression [p1:pn] to denote the interval whose contained points are exactly p1, p1+1, p1+2, …, pn (1 ≤ n). In fact, of course, an expression such as [p1:pn] can be regarded as informal syntax for an interval selector invocation (indeed, we already said as much in Chapter 6). A real language would have to provide some kind of explicit syntax for such invocations, as in, e.g., INTERVAL_T ([p1:pn]), and we’ll use this latter, more formal, notation in examples later in the book.1
■ We also refer occasionally to the other styles for intervals (closed:open, open:closed, and open:open) discussed briefly in Chapter 6. Here’s an example, just to remind you. Let the point type be INTEGER (so the corresponding interval type is INTERVAL_INTEGER). Then the (informal) expressions [3:5], [3:6), (2:5], and (2:6) all denote the exact same interval: namely, the interval whose contained points are exactly 3, 4, and 5. The respective formal analogs of these expressions are as follows:
INTERVAL_INTEGER ( [ 3 : 5 ] )
INTERVAL_INTEGER ( [ 3 : 6 ) )
INTERVAL_INTEGER ( ( 2 : 5 ] )
INTERVAL_INTEGER ( ( 2 : 6 ) )
We remind you also of the operators BEGIN, END, and “∈” from Chapter 6. For convenience, we repeat the definitions here (slightly reworded in each case). Let i be the interval [b:e] of type INTERVAL_T and let p be a value of type T. Then BEGIN (i) returns b; END (i) returns e; and p ∈ i returns TRUE if and only if b ≤ p and p ≤ e both return TRUE. We also define:
Observe that PRE (i) is undefined if b is the first value of type T, and POST (i) is undefined if e is the last value of type T. Of course, PRE (i) and POST (i) are effectively just shorthand for PRIOR_T (BEGIN (i)) and NEXT_T (END (i)), respectively. Note: POST has been called STOP in the literature [62]. PRE might thus analogously be called START, but doesn’t usually seem to be defined at all. We prefer the names PRE and POST because they’re more obviously distinct from BEGIN and END and because we find them intuitively clearer as well.
Interval Comparisons
A variety of operators can be defined for comparing intervals to see whether two intervals are equal, whether they overlap, and so on. In this section, we describe several such operators, giving in each case a formal definition together with an intuitive picture to illustrate the functionality. Note: The operators in question are often referred to collectively as Allen’s operators, most of them having first been proposed (in effect) by Allen in reference [2]—though in fact the definitions we give below, which are of course the ones we find the most useful, tend to differ somewhat from Allen’s original definitions, at least at the detailed level.
Here and throughout the remainder of this chapter, we take i1 and i2 to be the intervals [b1:e1] and [b2:e2], respectively, both of the same type INTERVAL_T. Note that, in order for the various operators to be defined in the first place, the two intervals must indeed be of the same interval type and so must be defined over the same point type.
Equals (“=”): As we already know from Chapter 6, i1 = i2 is true if and only if b1 = b2 and e1 = e2 are both true.

Includes (“⊇”) and included in (“⊆”): i1 ⊇ i2 is true if and only if b1 ≤ b2 and e1 ≥ e2 are both true; i2 ⊆ i1 is true if and only if i1 ⊇ i2 is true. Note: Reference [2] refers to “⊇” and “⊆” as contains and during, respectively.

Properly includes (“⊃”) and properly included in (“⊂”): i1 ⊃ i2 is true if and only if i1 ⊇ i2 is true and i1 = i2 is false; i2 ⊂ i1 is true if and only if i1 ⊃ i2 is true. Note: The picture just used to illustrate “⊇” and “⊆” in fact illustrates the “proper” versions of these operators (“⊃” and “⊂”, respectively). Here it is again:
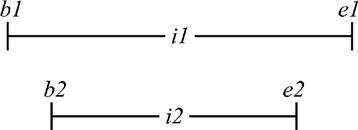
BEFORE and AFTER: i1 BEFORE i2 is true if and only if e1 < b2 is true; i2 AFTER i1 is true if and only if i1 BEFORE i2 is true.

OVERLAPS: i1 OVERLAPS i2 is true if and only if b1 ≤ e2 and b2 ≤ e1 are both true (it follows that i2 OVERLAPS i1 is true if and only if i1 OVERLAPS i2 is true).2

MEETS: i1 MEETS i2 is true if and only if b2 = e1+1 is true or b1 = e2+1 is true (it follows that i2 MEETS i1 is true if and only if i1 MEETS i2 is true).3
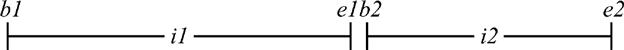
MERGES: i1 MERGES i2 is true if and only if i1 OVERLAPS i2 is true or i1 MEETS i2 is true (it follows that i2 MERGES i1 is true if and only if i1 MERGES i2 is true). Note: This operator was first defined in reference [70], not reference [2]. The keyword MERGES is perhaps not very good from the standpoint of intuition, but it’s hard to find one that catches the sense better and yet is equally succinct. That sense is, of course, “overlaps or meets.”

BEGINS: i1 BEGINS i2 is true if and only if b1 = b2 and e1 ∈ i2 are both true. Note: Reference [2] uses the keyword starts in place of BEGINS.
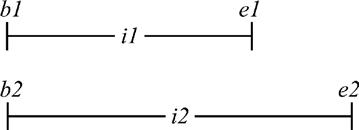
ENDS: i1 ENDS i2 is true if and only if e1 = e2 and b1 ∈ i2 are both true. Note: Reference [2] uses the keyword finishes in place of ENDS.

Negated forms of the foregoing operators can usefully be defined as well; for example, i1 NOT OVERLAPS i2 is true if and only if i1 OVERLAPS i2 is false. (Of course, “NOT =” is just “≠”; likewise, “NOT ⊇”, “NOT ⊆”, “NOT ⊃”, and “NOT ⊂” are just “⊂”, “⊃”, “⊆”, and “⊇”, respectively. Also, NOT OVERLAPS might reasonably be spelled DISJOINT.)4
We observe that the operator “⊃” in particular allows us to give a precise definition for the term maximal interval, which we used several times in Chapter 5:
Definition: Let P be a predicate whose sole parameter is of some interval type. Then interval i is maximal with respect to P if and only if i satisfies P and no j such that j ⊃ i satisfies P. Note: The qualifier “with respect to P” can be omitted if P is understood.
By way of a simple but typical example, consider relvar S_DURING once again. Here’s the predicate we gave for that relvar in Chapter 6:
Supplier SNO was under contract throughout the interval from the day that’s the begin point of DURING to the day that’s the end point of DURING, inclusive, and not throughout any interval that properly includes that interval.
Using the concept of maximal intervals as just defined, we can now simplify this predicate considerably, thus:
DURING denotes a maximal interval of days throughout which supplier SNO was under contract.
“Set Operators”
Clearly, an interval, if we ignore the ordering, can be regarded as a set of points, and the set operators UNION, INTERSECT, and MINUS are thus directly applicable. However, those operators, although they’ll certainly always return a set, won’t always return an interval (after all, an interval isn’t just a set of points—rather, it’s a set of contiguous points). As an extreme example, if intervals i1 and i2 are disjoint, then their intersection i1 INTERSECT i2 will be empty, and intervals as such are never empty. Thus, it makes sense to impose certain limitations on the operands to the interval versions of those set operators, in order to guarantee that the result isn’t just some set of points but is, rather, an interval specifically.
We begin by defining a couple of auxiliary operators, MAX and MIN (essentially just variants on the aggregate operators of the same name). Let p1 and p2 be values of the same type T and let “<” be defined for that type. Then:
■ MAX {p1,p2} returns p2 if p1 < p2 is true and p1 otherwise.
■ MIN {p1,p2} returns p1 if p1 < p2 is true and p2 otherwise.
Now let i1 and i2 be values of the same interval type. Then we have:
UNION: i1 UNION i2 returns [MIN{b1,b2}:MAX{e1,e2}] if i1 MERGES i2 is true and is otherwise undefined.
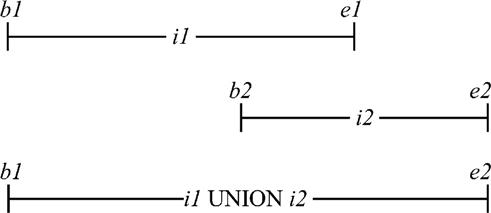
Incidentally, note that interval union, unlike set theory union (unlike the union operator of the relational algebra also) has no corresponding identity value. (If it had one, it would be the empty interval of the applicable type, and intervals are never empty.)
Aside: In case you’re not familiar with the concept of an identity value, here’s a definition. Let Op be a commutative dyadic operator, and assume for definiteness that Op is expressed in infix style. If there exists a value i such that i Op v and v Op i are both equal to v for all possible values v, then i is the identity, or identity value, with respect to Op. End of aside.
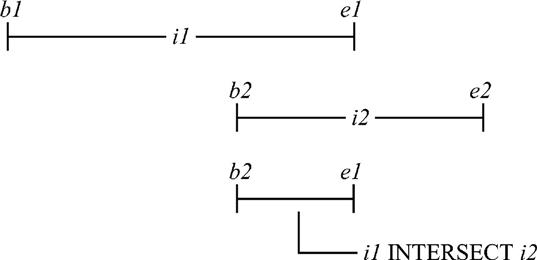
INTERSECT: i1 INTERSECT i2 returns [MAX{b1,b2}:MIN{e1,e2}] if i1 OVERLAPS i2 is true and is otherwise undefined.
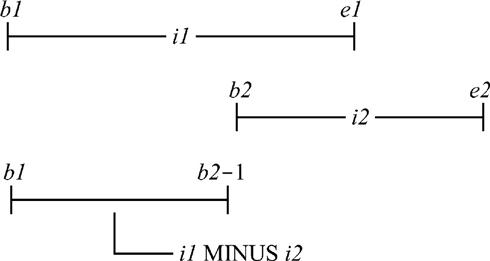
MINUS: i1 MINUS i2 returns [b1:MIN{b2−1,e1}] if b1 < b2 and e1 ≤ e2 are both true, [MAX{e2+1,b1}:e1] if b1 ≥ b2 and e1 > e2 are both true, and is otherwise undefined. Note, therefore, that i1 MINUS i2 is defined if and only if (a) i1 and i2 are disjoint (in which case i1 MINUS i2 reduces to simply i1), or (b) i1 contains either b2 or e2 but not both, or (c) exactly one of i2 BEGINS i1 and i2 ENDS i1 is true. (The following picture illustrates case (b) only; development of pictures to illustrate the other cases—and perhaps the cases where MINUS isn’t defined, too—is left as an exercise. Also, what happens exactly if b2 > b1 and e2 < e1 are both true or b1 > b2 and e1 < e2 are both true?)
Note: Reference [70] calls the interval UNION and INTERSECT operators MERGE and INTERVSECT, respectively (it doesn’t discuss an interval MINUS operator). Observe that if i1 INTERSECT i2 is defined, then i1 UNION i2 is certainly defined, but the converse is false (i.e., some pairs of intervals—which ones, exactly?—have a union but no intersection). Observe also that i1 MINUS i2 is sometimes defined when i1 UNION i2 and i1 INTERSECT i2 aren’t, and vice versa. (It follows, incidentally, that certain identities that hold for the set operators in general—for example, s1 INTERSECT s2 ≡ s1 MINUS (s1 MINUS s2)—don’t necessarily hold for the interval analogs of those operators.)5
Finally, we define the operator COUNT (i), which returns a count of the number of points in interval i (in other words, it returns the cardinality—sometimes called the length or duration—of that interval). For example, if i is the interval [d03:d07], of type INTERVAL_DATE, then COUNT (i) is 5.
Queries
The operators discussed in previous sections are of course available for use in all of the usual contexts, including queries in particular. Let’s look at some examples. Consider the database of Fig. 6.1 (the fully temporal version with intervals, where the relvars are S_DURING and SP_DURING). Consider also this query: “Get supplier numbers for suppliers who were able to supply part P2 on day 8.” Here’s a possible formulation:
( SP_DURING WHERE PNO = PNO ( 'P2' ) AND d08 ∈ DURING ) { SNO }This expression should be pretty much self-explanatory; we note, however, that in a real language the reference to day 8 (“d08”) in the WHERE condition would have to be replaced by an appropriate DATE selector invocation. For example, if “day 8” is actually April 30th, 2013, that date selector invocation might look like this: DATE ('2013/4/30').6
By way of another example, here’s a possible formulation of the query “Get pairs of suppliers who were able to supply the same part at the same time”:
WITH ( t1 := SP_DURING RENAME { SNO AS XNO , DURING AS XD } , t2 := SP_DURING RENAME { SNO AS YNO , DURING AS YD } ,t3 := t1 JOIN t2 ,
t4 := t3 WHERE XD OVERLAPS YD ,
t5 := t4 WHERE XNO < YNO ) :
t5 { XNO , YNO }Explanation: Recall from Chapter 2 that WITH isn’t an operator as such, it’s just a syntactic device that lets us introduce names for subexpressions, thereby enabling us to formulate what might otherwise be rather complicated expressions one step at a time.7 Thus:
■ t1 is just the current value of SP_DURING, except that attributes SNO and DURING are renamed XNO and XD, respectively.
■ t2 is the same except that the new attribute names are YNO and YD.
■ t3 is the join of t1 and t2 (over part numbers, because PNO is the only attribute common to t1 and t2, thanks to the renaming steps).
■ t4 is the restriction of t3 to just those tuples where the XD and YD intervals overlap (meaning the suppliers in question weren’t just able to supply the same part but in fact were able to supply the same part at the same time, as required).
■ t5 is the restriction of t4 to just those tuples where supplier number XNO is less than supplier number YNO. The purpose of this step is twofold: It eliminates pairs of supplier numbers of the form (x,x), and it guarantees that the pairs (x,y) and (y,x) don’t both appear. Of course, as noted in Chapter 2, the operator “<” must be defined for type SNO in order for this step to be legitimate.
■ The final projection of t5 on XNO and YNO produces the desired result.
As a third example, suppose we want to get, not just pairs of suppliers who were able to supply the same part at the same time, but the parts and times in question as well. Here then is a possible formulation:
WITH ( t1 := SP_DURING RENAME { SNO AS XNO , DURING AS XD } , t2 := SP_DURING RENAME { SNO AS YNO , DURING AS YD } ,t3 := t1 JOIN t2 ,
t4 := t3 WHERE XD OVERLAPS YD ,
t5 := t4 WHERE XNO < YNO ,
t6 := EXTEND t5 : { DURING := XD INTERSECT YD } ) :t6 { XNO , YNO , PNO , DURING }Explanation: Relations t1-t5 are exactly as they were in the previous example. The EXTEND step then computes the relevant intervals, and the final projection produces the desired result.
Concluding Remarks
We close this chapter by stressing the fact that all of the operators on intervals we’ve been discussing—BEGIN, END, PRE, POST, POINT FROM, “∈” and “∋”, Allen’s operators, and interval UNION, INTERSECT, MINUS, and COUNT—are generic, in the sense that they apply to all possible intervals. Of course, the operators are generic precisely because they’re associated with the INTERVAL type generator (just as the operators of the relational algebra are generic because they’re associated with the RELATION type generator, as pointed out in Chapter 6). In other words, these operators are polymorphic—see the remarks on this topic in the section “Types” in Chapter 1—and the kind of polymorphism they exhibit is generic polymorphism.
Aside: In fact, the UNION, INTERSECT, and MINUS operators in particular exhibit another kind of polymorphism also. By defining these operators—or operators with these names, rather—to apply to both intervals and relations, we’ve overloaded those operator names. What this means is as follows (let’s concentrate on UNION, just to be definite): In reality, there are two distinct operators here, one for intervals and the other for relations. However, we’ve chosen to give those two operators the same name. And such a state of affairs is described in the literature (by some writers, at any rate) as an example of overloading polymorphism.
We note also that there’s at least one further kind of polymorphism, called inclusion polymorphism, which we’ll be discussing in Chapter 18. End of aside.
Exercises
7.1 We pointed out in the body of the chapter that the interval version of UNION has no identity value. But what about INTERSECT and MINUS?
7.2 We pointed out in the body of the chapter that the set theory identity s1 INTERSECT s2 = s1 MINUS (s1 MINUS s2) ceases to hold, in general, if s1 and s2 aren’t sets but intervals. Why so?
7.3 Let i be a value of type INTERVAL_INTEGER. Write an expression denoting the interval resulting from extending i by its own length in both directions (e.g., [5:7] becomes [2:10]). In what circumstances will evaluation of your expression fail at run time?
7.4 Again let i be a value of type INTERVAL_INTEGER. Write an expression denoting the interval representing the middle third of i. You can assume COUNT (i) is a multiple of three.
7.5 Let i1, i2, and i3 be intervals such that there’s a single interval i4 consisting of every point p such that p ∈ i1 or p ∈ i2 or p ∈ i3. Write an expression defining i4 in terms of i1, i2, and i3. Warning: There’s a trap here.
7.6 Given the relvar STUDIED from Exercise 6.10b in Chapter 6, write an expression that, when evaluated, shows for every grade the average length of study for all students who achieved that grade. Note: We assume for the sake of this exercise that students complete courses at their own pace.
7.7 Given relvars as follows (the semantics are meant to be self-explanatory)—
FEDERAL_GOVT { PRESIDENT , PARTY , DURING }
STATE_GOVT { GOVERNOR , STATE, PARTY , DURING }
—write an expression to produce a result with attributes PRESIDENT, GOVERNOR, STATE, PARTY, and DURING, such that a tuple appears in this result if and only if the specified president and specified state governor both belong to the specified party and have overlapping periods of administration (and DURING specifies exactly the overlap in question).
Answers
7.1 The identity value for INTERSECT is what might be called the universal interval of the applicable type (i.e., the interval [FIRST_T ( ):LAST_T ( )], where T is the applicable point type. MINUS has no identity value (nor does it in set theory, of course).
7.2 Let i1 and i2 be intervals of the same type, and let i2 be properly included in i1. Then i1 INTERSECT i2 returns i2, but i1 MINUS i2 is undefined—and so therefore is i1 MINUS (i1 MINUS i2) a fortiori. Note, however, that the identity does hold so long as i1 MINUS (i1 MINUS i2) is defined.
7.3 INTERVAL_INTEGER ( [ BEGIN ( i ) − COUNT ( i ) : END ( i ) + COUNT ( i ) ] )
Evaluation of this expression will fail at run time if either of the following expressions evaluates to TRUE:
BEGIN ( i ) < FIRST_INTEGER ( ) + COUNT ( i )
END ( i ) > LAST_INTEGER ( ) − COUNT ( i )
7.4 INTERVAL_INTEGER ( [ BEGIN ( i ) + ( COUNT ( i ) / 3 ) : END ( i ) − ( COUNT ( i ) / 3 ) ] )
7.5 INTERVAL_INTEGER
( [ MIN { MIN { BEGIN ( i1 ), BEGIN ( i2 ) }, BEGIN ( i3 ) } :
MAX { MAX { END ( i1 ), END ( i2 ) }, END ( i3 ) } ] )
We’ve assumed for definiteness here that INTEGER is the underlying point type. The trap is this: Under the stated conditions, it can’t be guaranteed that, e.g., i1 UNION i2 is defined, and so an expression of the form (i1 UNION i2) UNION i3 isn’t guaranteed to work.
7.6 ( EXTEND STUDIED { GRADE } :
{ ALS := AVG ( !!STUDIED , COUNT ( DURING ) ) } { GRADE , ALS }
7.7 WITH ( fg := FEDERAL_GOVT RENAME { DURING AS FD } ,
sg := STATE_GOVT RENAME { DURING AS SD } ,
t1 := fg JOIN sg,
t2 := t1 WHERE FD OVERLAPS SD ,
t3 := EXTEND t2 : { DURING := FD INTERSECT SD } ) :
t3 { ALL BUT FD , SD }
