The EXPAND and COLLAPSE Operators
Temporal databases involve not just intervals as such but, more generally, sets of such intervals. For example, projecting a relation on an interval attribute yields a set of tuples whose component values taken together constitute such a set of intervals. In order to reason about (and systematically deal with) such sets of intervals, it’s convenient to introduce two canonical forms, called expanded form and collapsed form, respectively. This chapter explains these canonical forms in detail and introduces the associated operators EXPAND and COLLAPSE. Each of these operators takes a set of intervals all of the same interval type as input and returns the corresponding canonical form of that set as output.
Keywords
EXPAND; COLLAPSE; expanded form; collapsed form
Then all collapsed, and the great shroud of the sea rolled on as it rolled five thousand years ago.
—Herman Melville:
Moby-Dick (1851)
In Chapters 6 and 7, we encountered a variety of generic operators—BEGIN, PRE, OVERLAPS, MERGES, UNION, and so on—that applied to intervals (or pairs of intervals, rather, in most cases). In this chapter, we meet two more generic operators, which we call EXPAND and COLLAPSE, respectively.1 Unlike BEGIN, PRE, and the rest, however, these two operators apply not to intervals as such but rather to sets of intervals. More specifically, each of those operators (a) takes a set of intervals all of the same type as its input and (b) returns another set of intervals of that same type as its result.
Preliminary Remarks
The result sets produced by EXPAND and COLLAPSE can each be regarded as a particular canonical form for the corresponding input set—and the canonical forms in question both have an important role to play in the solutions we’re at last beginning to approach to the problems we identified in Chapters 4 and 5. Note: It might help to state up front that each of those two canonical forms has the property that every point represented in some interval in the input set is represented exactly once—i.e., as part of exactly one interval—in the corresponding result set.
Aside: The notion of canonical form is central to many branches of mathematics and related disciplines. In case you’re unfamiliar with it, we digress for a moment to explain it briefly. The basic idea is this: Given a set s1, together with a stated notion of equivalence among the elements of that set, subset s2 of s1 is a set of canonical forms for s1 if and only if every element a1 of s1 is equivalent, under that notion of equivalence, to just one element a2 of s2 (and that element a2 is a canonical form for the element a1). We can also say, a trifle loosely, that the set s2 taken as a whole is a canonical form for the set s1 as such. Various ‘interesting’ properties that apply to s1 also apply to s2, mutatis mutandis; thus, we can study just the ‘small’ set s2, not the ‘large’ set s1, in order to prove a variety of interesting theorems or results. Here’s a simple example:
■ Let s1 be the set of nonnegative integers {0,1,2,…}.
■ Define equivalence among elements of s1 as follows: Elements a and b are equivalent if and only if they leave the same remainder on division by five. Thus, e.g., the integers 8, 13, 18, 23, etc., are all equivalent to 3 (as is 3 itself, of course).
■ Under this definition of equivalence, then, s2 is the set {0,1,2,3,4}—every element of s1 is equivalent to just one of these five integers, and each of these five is in fact the canonical form for an infinite number of elements of s1. Note in particular that s2 here is finite, whereas s1 is infinite.
■ As for an ‘interesting’ property that applies in this example, let a1, b1, and c1 be any three elements of s1, and let their canonical forms in s2 be a2, b2, and c2, respectively. Then the product b1 * c1 is equivalent to a1 if and only if the product b2 * c2 is equivalent to a2.
End of aside.
The applicability of the foregoing ideas to sets of intervals in particular is explained in the next two sections.
Expanded Form
As already indicated, the objects we wish to study are sets of intervals,2 where the intervals in question are all of the same interval type and are thus necessarily defined over the same point type. Let X1 and X2 be two such sets. Then we define the necessary notion of equivalence thus:
Definition: Sets X1 and X2 are equivalent if and only if the set of all points contained in intervals in X1 is equal to the set of all points contained in intervals in X2.
By way of example, let X1 and X2 be as follows:
{ [d01:d01] , [d03:d05] , [d04:d06] } /* X1 */{ [d01:d01] , [d03:d04] , [d05:d05] , [d05:d06] } /* X2 */Clearly, X1 and X2 aren’t equal—they’re not the same set. However, it’s easy to see they’re equivalent under the foregoing definition, because the set of all points p such that p is contained in some interval in X1 is equal to the set of all points p such that p is contained in some interval in X2. The set of points in question is, obviously enough, this set:
{ d01 , d03 , d04 , d05 , d06 }For reasons that’ll quickly become apparent, however, we’re interested not so much in this set of points as such, but rather in the corresponding set of unit intervals (let’s call it X3):
{ [d01:d01] , [d03:d03] , [d04:d04] , [d05:d05] , [d06:d06] }X3 here is clearly equivalent to each of X1 and X2; in fact, it’s the expanded form of each of those sets. Here’s the definition:
Definition: Let X be a set of intervals all of the same type. Then the expanded form of X is the set of all intervals—more precisely, the set of all unit intervals—of the form [p:p] such that p is a point in some interval in X.
From this definition, it should be clear that if X is a set of intervals all of the same type, then:
Observe in particular that if X is empty, then the expanded form of X is empty too.
The expanded form of X is one possible canonical form for X. To be specific, it’s that unique equivalent set whose contained intervals are all of the minimum possible length (i.e., one). Intuitively, the expanded form of X allows us to focus on the information content of X at an atomic level, without having to worry about the many different ways that information might be bundled together into ‘clumps.’
Note: The concept of expanded form allows us to restate our original definition of equivalence more succinctly, thus:
Definition: Two sets of intervals are equivalent if and only if they have the same expanded form.
As an exercise, consider the projections on DURING of the relations shown as values of relvars S_DURING and SP_DURING in Fig. 6.1 in Chapter 6. Are the sets of intervals in those two projections equivalent? What are the corresponding expanded forms?
Collapsed Form
The sets X1, X2, and X3 discussed in the previous section all have different cardinalities. In fact, it so happens in that particular example that X3, the expanded form, is the one whose cardinality is the greatest. However, it’s easy to find another set X4 that has the same expanded form—i.e., that’s equivalent to X1 and X2—but has cardinality greater than that of X3. One such set X4 (not the only one possible) is:
{ [d01:d01] , [d03:d03] , [d03:d04] , [d03:d05] , [d03:d06] , [d04:d04] , [d04:d05] , [d04:d06] }It’s also easy to find the much more interesting set X5 that has the same expanded form and the minimum possible cardinality:
{ [d01:d01] , [d03:d06] }X5 is the collapsed form of X1 (also of X2, X3, and X4). Here’s the definition:
Definition: Let X be a set of intervals all of the same type. Then the collapsed form of X is the set Y of intervals of the same type such that:
■ X and Y have the same expanded form.
■ No two distinct intervals i1 and i2 in Y are such that i1 MERGES i2 is true (recall that MERGES means ‘overlaps or meets’). Equivalently, no two distinct intervals i1 and i2 in Y are such that i1 UNION i2 is defined.
Note: It follows from this latter point that Y can be computed from X by successively replacing pairs of intervals in X by their union (assuming their union is defined, of course) until no further such replacements are possible. It also follows that no two distinct intervals i1 and i2 in Y are such that i1 INTERSECT i2 is defined, either.
Aside: The intersection i1 INTERSECT i2 is likewise not defined for any pair of intervals i1 and i2 in the expanded form of X; however, the union i1 UNION i2 might be. To be specific, i1 UNION i2 will be defined for such a pair of intervals if and only if the (necessarily unique) points p1 and p2 in i1 and i2, respectively, are such that one is the immediate successor of the other. End of aside.
The collapsed form of X is another possible canonical form for X. To be specific, it’s that unique equivalent set that has the minimum possible cardinality. Intuitively, the collapsed form of X allows us to focus on the information content of X in a compressed (‘clumped’) form, without having to worry about the possibility that distinct ‘clumps’ might meet or overlap.
Note that—as indeed we’ve already seen—many distinct sets can have the same collapsed form. Also, it should be clear from the foregoing definition that if X is a set of intervals all of the same type, then:
Observe in particular that if X is empty, then the collapsed form of X is empty too.
Note: The concept of collapsed form also allows us to restate our original definition of equivalence more succinctly, thus:
Definition: Two sets of intervals are equivalent if and only if they have the same collapsed form.
As an exercise, again consider the projections on DURING of the relations shown as values of relvars S_DURING and SP_DURING in Fig. 6.1 in Chapter 6; more specifically, consider the sets of intervals in those two projections. What are the corresponding expanded forms?
Operator Definitions
We can now define the EXPAND and COLLAPSE operators:
Definition: Let X be a set of intervals all of the same type. Then EXPAND (X) returns the expanded form of X and COLLAPSE (X) returns the collapsed form of X.
■ If X has cardinality zero, the result does so too (for both EXPAND and COLLAPSE).
■ If X has cardinality one, the result is equal to X for COLLAPSE, but not for EXPAND (unless the sole interval in X happens to be a unit interval).
By the way, don’t make the mistake of thinking that EXPAND and COLLAPSE are inverses of each other. For example, let X1 be the set
{ [d01:d01] , [d03:d05] , [d04:d06] }(as previously). If we expand this set and then collapse the result, we necessarily obtain the collapsed form X5:
{ [d01:d01] , [d03:d06] }And if we collapse the original set X1 and then expand the result, we (again necessarily) obtain the expanded form X3:
{ [d01:d01] , [d03:d03] , [d04:d04] , [d05:d05] , [d06:d06] }In other words, neither EXPAND (COLLAPSE (X)) nor COLLAPSE (EXPAND (X)) is identically equal to X, in general (though they’re both equivalent to X, of course). Indeed, it’s easy to see that the following identities hold:
EXPAND ( COLLAPSE ( X ) ) ≡ EXPAND ( X )
COLLAPSE ( EXPAND ( X ) ) ≡ COLLAPSE ( X )
The following identities clearly hold as well:
EXPAND ( EXPAND ( X ) ) ≡ EXPAND ( X )
COLLAPSE ( COLLAPSE ( X ) ) ≡ COLLAPSE ( X )
It follows from all of these identities that the first operation in evaluating any of the expressions shown on the left side of the ‘≡’ symbol can simply be ignored, a fact that could be useful for optimization purposes (especially when that first operation is EXPAND).
Alternative Definitions
Note: This subsection is included primarily for completeness. It requires an elementary understanding of the quantifiers of predicate logic (see, e.g., reference [45]). However, it can safely be skipped without interfering with the overall flow.
We now give alternative definitions of the EXPAND and COLLAPSE operators in order to show that—like so much else discussed in this book—they’re really just shorthand. First EXPAND. Let X be a set of intervals all of the same type, IT say, and let i and j be intervals of type IT. Let i = [b:e]. Then we have:
EXPAND ( X ) ![]() { i : b = e AND EXISTS j ∈ X ( b ∈ j ) }
{ i : b = e AND EXISTS j ∈ X ( b ∈ j ) }
In other words, EXPAND (X) is the set of all intervals i of type IT such that (a) the begin and end points of i are one and the same, and (b) the point in question is contained within at least one interval in X. (The symbol ![]() means ‘is defined as.’) Note that we’ve extended our use of the set membership operator ‘∈’ to apply not just to a point and an interval (‘b ∈ j’), but also to an interval and a set of intervals (‘j ∈ X’); in fact, we’re overloading ‘∈’ here (see the remarks on this notion near the end of Chapter 7).
means ‘is defined as.’) Note that we’ve extended our use of the set membership operator ‘∈’ to apply not just to a point and an interval (‘b ∈ j’), but also to an interval and a set of intervals (‘j ∈ X’); in fact, we’re overloading ‘∈’ here (see the remarks on this notion near the end of Chapter 7).
COLLAPSE is rather more complicated. Again, let X be a set of intervals all of the same type IT; also, let the underlying point type be T. Let i, i1, i2, and j be intervals of type IT; let p be a point of type T; and let i = [b:e], i1 = [b1:e1], and i2 = [b2:e2]. Then we have:
2. { i : FORALL p ∈ i ( EXISTS j ∈ X ( p ∈ j ) )
4. EXISTS i1 ∈ X ( EXISTS i2 ∈ X
5. ( b = b1 AND e = e2 AND b1 ≤ b2 AND e1 ≤ e2
10. ( EXISTS j ∈ X ( p ∈ j ) ) END IF END IF
14. NOT EXISTS j ∈ X ( PRE ( i ) ∈ j ) END IF
■ Line 2 ensures that if interval i appears in COLLAPSE (X), then every point p in i must also appear in at least one interval j in X. Note: Of course, the converse is true as well— every point in some interval j in X must also appear in some i in COLLAPSE (X)—but this requirement is taken care of implicitly by the remaining lines taken together.
■ Lines 4-5 ensure that the begin point of i is the begin point b1 of some interval i1 in X and the end point of i is the end point e2 of some interval i2 in X (i1 and i2 not necessarily distinct). The condition b1 ≤ b2 AND e1 ≤ e2 in line 5 ensures that i1 neither begins nor ends after i2 does, so we can say definitively that BEGIN (i) is b1 and END (i) is e2.
■ Lines 7-10 ensure that every point between intervals i1 and i2 is in fact a point in some interval in X, so that merging i1 and i2 to form i is legitimate. By the way, note the use of open:open notation in line 9, avoiding the rather more complicated expression ‘[POST (i1) : PRE (i2)]’ that use of closed:closed notation would have entailed.
■ Lines 12-14 ensure that there’s no interval in X containing the predecessor b−1 of BEGIN (i)—because if there were, it should have been merged with i.
■ Lines (12 and) 16-17 ensure likewise that there’s no interval in X containing the successor e+1 of END (i), for essentially similar reasons.
Unary Relations
Now, you might have noticed that we’ve been indulging in a tiny sleight of hand in this chapter so far. To be specific, we’ve described two operators, EXPAND and COLLAPSE, that apply to sets—sets of intervals, to be specific3—but the relational model deals with relations, not general sets, and EXPAND and COLLAPSE as described so far are thus not a good fit with that model. So we have a little tidying up to do, and that’s the purpose of this section.
We begin by observing that of course any set of values all of the same type can easily be converted to a unary relation. To be specific, if v1, v2,…, vn are distinct values of the same type T, then the relation selector invocation
RELATION { A T } { TUPLE { A v1 } , TUPLE { A v2 } , ……. TUPLE { A vn } }produces this relation:

Note: Relation selectors were discussed in Chapter 1. Just to remind you, the specification {A T} in the example defines the heading for the relation being selected. Such a specification can always be omitted from a given relation selector invocation unless the given set of values v1, v2, …, vn happens to be empty. If such were the case in the foregoing example, the relation selector invocation shown would degenerate to just RELATION {A T} { }.
In order to stay within the framework of the relational model, therefore, what we need to do—and of course what we can do, without loss of generality—is replace the EXPAND and COLLAPSE operators as previously described by versions in which the argument is specified as a unary relation instead of just a set. Replacing the operators as just suggested is straightforward, of course. To be specific, the unary relation versions of the operators are essentially similar to the set versions as previously described, except that the input and output, instead of just being sets of intervals, are now unary relations whose tuples contain those intervals as such. For example, suppose the input relation (r, say) looks like this:

Then EXPAND (r) and COLLAPSE (r) produce results that look like this (EXPAND on the left, COLLAPSE on the right):
We can also define a notion of equivalence for such unary relations. To be specific, two such relations are equivalent if and only if they have the same expanded form (or the same collapsed form).
Finally, please note that we take all references to EXPAND and COLLAPSE throughout the remainder of this book as references to the versions just defined for unary relations, barring explicit statements to the contrary. However, please note also that certain of those ‘explicit statements to the contrary’ appear in the section immediately following!
Nullary Relations
For reasons that should become clear in Chapters 10 and (especially) 11, it turns out to be highly desirable to define versions of EXPAND and COLLAPSE that work on nullary relations instead of unary ones. Just to remind you, a nullary relation is one that has no attributes, and there are exactly two such:
■ TABLE_DEE, which contains just one tuple (necessarily the 0-tuple, which is the unique tuple with no components)
Of course, a nullary relation can’t possibly contain intervals—more precisely, it can’t contain tuples that contain intervals—but this fact need not deter us. To be specific, we simply define the result of expanding or collapsing a nullary relation, reasonably enough, to be equal to the input in both cases. For example, COLLAPSE (TABLE_DEE) returns TABLE_DEE, and EXPAND (TABLE_DUM) returns TABLE_DUM. Note that it follows from this definition, again reasonably enough, that two nullary relations are equivalent if and only if they’re equal.
We close this section, and this chapter, by observing that EXPAND and COLLAPSE as we’ve defined them are still not quite what we need to deal with temporal data; they’re still just another stepping stone on the way, so to speak. The point is, those operators work on unary (or nullary) relations, and what we’re going to need are operators that work on general n-ary relations instead—in particular, on n-ary relations with interval attributes. We’ll introduce such operators in the next chapter.
Exercises
8.1 (Repeated from the body of the chapter.) Consider the projections on DURING of the relations shown as values of relvars S_DURING and SP_DURING in Fig. 6.1 in Chapter 6; more specifically, consider the sets of intervals in those two projections. Are those two sets equivalent? What are the corresponding expanded and collapsed forms?
8.2 Let MOD3 be the type whose values are the integers 0, 1, and 2. Consider the type RELATION {DURING INTERVAL_MOD3}. How many relations xr of this type satisfy the condition EXPAND (xr) = xr? List every relation cr of this type satisfying the condition COLLAPSE (cr) = cr.
Answers
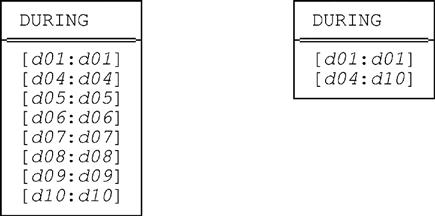
8.1 Here first are the expanded and collapsed forms of the projection of S_DURING on DURING:
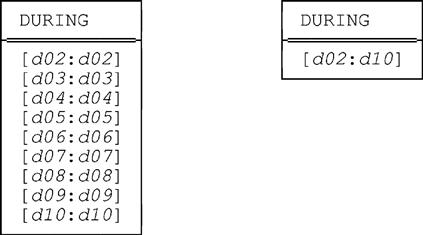
The expanded form is on the left and the collapsed form is on the right, of course. And it’s easy to see that the expanded and collapsed forms of the projection of SP_DURING on DURING are identical to the foregoing, whence it follows that the two projections are indeed equivalent.
8.2 Note first that there are precisely six intervals of type INTERVAL_MOD3, as follows:
[0:0] [0:1] [0:2] [1:1] [1:2] [2:2]
It follows that there are precisely 26 = 64 relations of the specified type. Then:
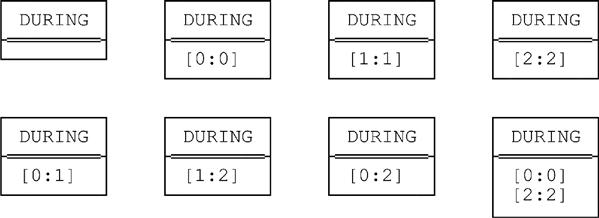
■ A relation of the specified type will be equal to its expanded form if and only if all of the DURING values it contains are unit intervals. There are precisely eight such relations:
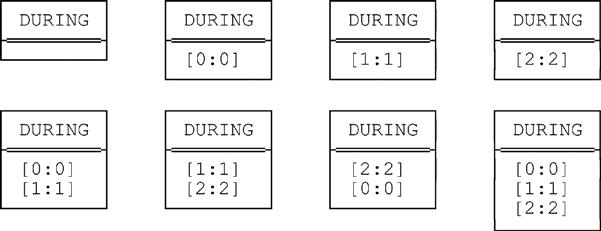
■ A relation of the specified type will be equal to its collapsed form if and only if it contains no overlapping or abutting DURING values. Again there are precisely eight such relations: