Keywords

UNPACK; PACK; unpacked form; packed form; equivalence of relations; redundancy

PACKING and UNPACKING on NO Attributes

As just noted, we wish to extend the PACK and UNPACK operators to operate in terms of any subset of the interval attributes of the relation in question. The first case to consider is the one in which the subset in question is empty (the empty set is a subset of every set, of course).¹ As we’ll see in the next chapter, the ability to pack or unpack a relation on no attributes at all is going to turn out, perhaps surprisingly, to be rather important. The syntax is as follows:

PACK r ON ( )

UNPACK r ON ( )

We define the result of each of these expressions to be simply r, and justify this definition as follows. First, PACK. Consider the expression:

WITH ( r1 := r GROUP { } AS X , r2 := EXTEND r1 : { X := COLLAPSE ( X ) } ) :

r2 UNGROUP X

As you can see, this expression is identical to our usual expansion for PACK r ON (A)—see Chapter 9—except that the first step (the grouping step) specifies “GROUP { }” instead of “GROUP {A}.” Thus, the semantics are as follows:

Turning now to UNPACK, UNPACK r ON ( ) is shorthand for the following:

WITH ( r1 := r GROUP { } AS X, ( r2 := EXTEND r1 : { X := EXPAND ( X ) } ) :

r2 UNGROUP X

By an argument analogous to that for PACK above, this expression is readily seen to evaluate to r as well.

Note: One obvious consequence of the foregoing definitions is that unpacking some relation r on no attributes and then packing the result, also on no attributes, returns r. We’ll be appealing to this seemingly rather trivial observation in the section “Packing on Two or More Attributes” later in the chapter; however, its real significance won’t become apparent until we get to the final section of Chapter 11.

UNPACKING ON Two or More Attributes

Now we turn to the question of packing and unpacking relations on more than one attribute. For reasons that’ll become clear in the next section, it’s convenient to deal with UNPACK first. We begin by considering the case of unpacking on exactly two attributes.

Let r be a relation with two interval attributes A1 and A2 (possibly other attributes as well, interval valued or otherwise). Just to be definite, suppose r looks like this:

This relation is in fact the restriction of the relation shown in Fig. 9.2—a hypothetical sample value for relvar S_PARTS_DURING—to just the tuples for supplier S2, projected over PARTS and DURING, except that we’ve renamed those two attributes A1 and A2, respectively. (Actually, we could have retained the SNO attribute if we’d wanted to—it would have made essentially no difference to the analysis that follows.)

Now consider the following expression:

UNPACK ( UNPACK r ON ( A1 ) ) ON ( A2 )

The inner expression UNPACK r ON (A1) yields:

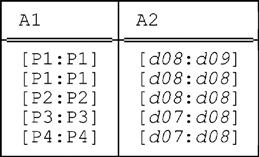
Unpacking this relation on A2 then yields:

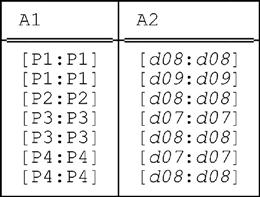
Now let’s see what happens if we do the two unpackings in the reverse order—i.e., consider the following expression:

UNPACK ( UNPACK r ON ( A2 ) ) ON ( A1 )

The inner expression UNPACK r ON (A2) yields:

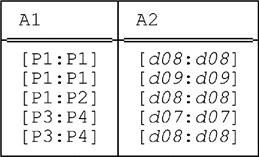
Unpacking this relation on A1 then yields:

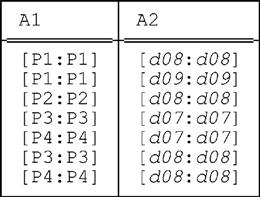
And this overall result is readily seen to be the same as before.² In fact, it’s easy to see that if r is any relation with interval attributes A1 and A2, then the following identity holds:

UNPACK ( UNPACK r ON ( A1 ) ) ON ( A2 ) ≡

UNPACK ( UNPACK r ON ( A2 ) ) ON ( A1 )

(Working through the foregoing example in detail should be sufficient to give you the necessary insight as to why this identity holds.) Indeed, it’s easy to see more generally that if r has interval attributes A1, A2,…, An, then unpacking r on those attributes one at a time in any order whatsoever will always yield the same overall result. We therefore propose the following extended definition:

Note: The commalist A1, A2, …, An in the expression UNPACK r ON (A1, A2, …, An) actually denotes a set, not a sequence, of attribute names (since the sequence as such is irrelevant). In Tutorial D, therefore, we would normally enclose it in braces, not parentheses. As we’ll see in the next section, however, parentheses are required in the case of PACK—that is, the sequence in which the attribute names are specified is significant for PACK—and we thus felt it would be more user friendly to use parentheses instead of braces in the case of UNPACK as well, but then to state explicitly that for UNPACK the sequence is arbitrary.

PACKING ON Two or More Attributes

We turn now to PACK. Here we proceed a little differently. In fact, for reasons we hope will shortly become clear, we begin with a definition instead an example:

Observe, therefore, that we define PACK to operate by first unpacking the specified relation on all of the specified attributes (in some arbitrary order, of course), and then packing it on those same attributes, in the order specified. Thus, for example, the expression

PACK r ON ( A1 , A2 )

is defined to be shorthand for the expression

PACK ( PACK ( UNPACK r ON ( A1 , A2 ) ) ON ( A1 ) ) ON ( A2 )

In other words, the original PACK invocation PACK r ON (A1,A2) is evaluated by first unpacking relation r on A1 and A2, then packing the result on A1, and finally packing that result on A2.

Note: You might be forgiven for thinking the foregoing definition is circular, since it’s apparently defining the PACK operator in terms of itself. But it isn’t. Rather, all of the references to PACK in the formal expansion are, as you can see, references to the single-attribute version of that operator, which was defined in Chapter 9. (As for the implicit reference to UNPACK—this time on several attributes, not just one—that’s a reference to UNPACK as defined in the previous section.) Thus, there’s in fact no circularity involved.

Now, before we consider the question of packing on two or more attributes in detail, we ought really to convince ourselves that the definition given above for packing on n attributes is at least consistent with the definitions previously given for n = 1 (in Chapter 9) and n = 0 (earlier in the present chapter). In other words, let’s see what happens if we drop the requirement that n be greater than one. Consider first the case n = 1, for which the text of the definition given above reduces to:

As we saw in Chapter 9, however, this expression reduces to just PACK r ON (A)—i.e., the initial UNPACK can be ignored—and so we see that PACK as defined in Chapter 9 is indeed a special case of PACK as defined above, at the start of the present section.

What about the case n = 0? Here the text of the definition given above reduces to:

As we saw earlier in this chapter, however, UNPACK r ON ( ) and PACK r ON ( ) both return r, and so PACK on no attributes too is just a special case of PACK as defined at the start of the present section.

Now let’s consider the question of packing on two attributes. Let r be a relation with two interval attributes A1 and A2 (possibly other attributes as well, interval valued or otherwise). Just to be definite, suppose r looks like this:

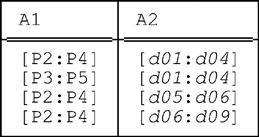
This relation is in fact the restriction of the relation shown in Fig. 9.2—a hypothetical sample value for relvar S_PARTS_DURING—to just those tuples for supplier S3, projected over PARTS and DURING, except that we’ve renamed those two attributes A1 and A2, respectively. (As in the case of the UNPACK discussion in the previous section, we could have retained the SNO attribute if we had wanted to—it would have made essentially no difference to the analysis that follows.)

Now consider the following expression:

PACK r ON ( A1 , A2 )

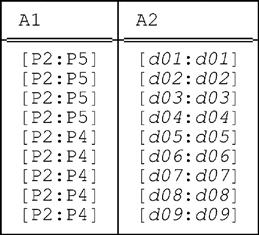
Here first is the result of evaluating the implicit UNPACK r ON (A1,A2) that lies at the heart of the expansion of this expression:

Packing this relation on A1 yields:

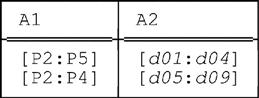
And packing this relation on A2 then yields:

Now we consider what happens if we do the two packings in the reverse order—i.e., we consider the following expression:

PACK r ON ( A2 , A1 )

First of all, the implicit UNPACK yields the same relation as before, of course. Packing that relation on A2 then yields:

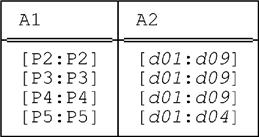
And packing this relation on A1 then yields:

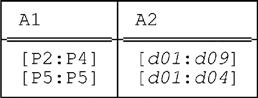
And this final result is clearly not the same as before. Thus we see that if r is a relation with interval attributes A1 and A2, then

PACK r ON ( A1 , A2 ) ≡ PACK r ON ( A2 , A1 )

(in general). Of course, an analogous remark applies to an arbitrary relation r with n interval attributes A1, A2, …, An for arbitrary n > 1. That’s why, in the general syntax proposed earlier—

PACK r ON ( A1 , A2 , … , An )

—the sequence of attribute names matters (and that’s why we enclose it in parentheses instead of braces).

A Graphical Representation

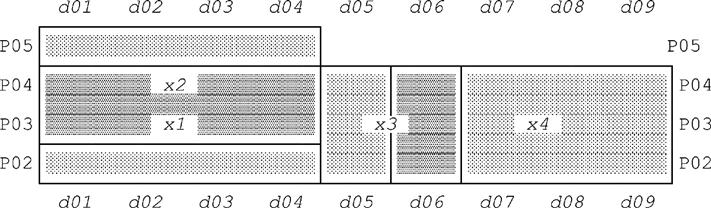
We’ve just seen an example in which we obtained different results from (a) packing a certain relation r on attributes A1 then A2 and (b) packing that same relation r on attributes A2 then A1. Such examples lend themselves to a simple pictorial—i.e., graphical, or geometric—interpretation that some readers might find helpful. We explain the basic idea in terms of that same example. Here again is the original relation r (but now we’ve added some tuple labels):

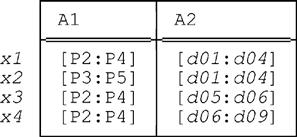
We can represent this relation by means of a two-dimensional graph with A1 values shown vertically and A2 values shown horizontally (see Fig. 10.1, where shaded rectangles correspond to tuples x1-x4 as indicated and heavy shading shows where tuples overlap, as it were):

Packing r on A1 then A2 gives the following relation (again we’ve added some tuple labels):

The corresponding graph is as shown in Fig. 10.2:

By contrast, packing r on A2 then A1 gives—

—for which the corresponding graph is as shown in Fig. 10.3:

As you can see, the two packed forms both cover the same area of the graph by means of two nonoverlapping rectangles (corresponding to nonoverlapping tuples), but they do so in two different ways. In other words, the fact that (a) the problem Cover the shaded area of the graph by two nonoverlapping rectangles has two different solutions offers some good insight into why (b) relation r has two different “fully packed” forms.

Further examples of such graphs can be found in Appendix E.

A Logical Difference

As noted at the beginning of this chapter, the full consequences of generalizing PACK and UNPACK as we’ve been doing—i.e., to allow packing and unpacking to be done on any subset of the interval attributes of the relation in question—aren’t always immediately obvious. One of those consequences is as follows. Consider once again the relation r we used in the previous section to demonstrate that, at least for PACK, the order (i.e., of attribute names) matters:

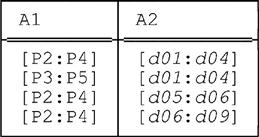
■ As we saw in the previous section, the expression
PACK r ON ( A1 , A2 )
yields this result:

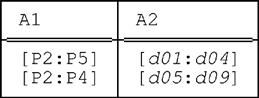
In fact, the expression
PACK ( PACK r ON ( A1 ) ) ON ( A2 )
yields the same result, as you can—and, we strongly suggest, you should—confirm for yourself.

■ By contrast, the expression
PACK r ON ( A2 , A1 )
yields this result (as we also saw in the previous section):

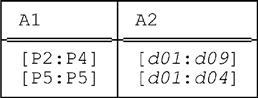
But the expression
PACK ( PACK r ON ( A2 ) ) ON ( A1 )
does not yield this same result. Instead, as you can—and, we again strongly suggest, you should—confirm for yourself, it yields this relation:

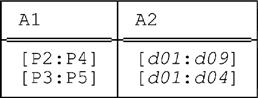
Note: Drawing the graph corresponding to this latter relation might help you appreciate what’s going on here. In fact, in examples from this point forward you might always want to consider drawing such graphs, if you find them helpful.

So the first message from this example is that (to generalize slightly) the expressions

PACK r ON ( A1 , A2 , … , An )

and

PACK (… ( PACK ( PACK r ON ( A1 ) ) ON ( A2 ) ) … ) ON ( An )

aren’t logically equivalent, in general. (Just to remind you, the first expression involves a preliminary “total UNPACK”—i.e., an UNPACK of r on (A1,A2, …,An)—while the second doesn’t.)

To return to the second bullet item above, the difference between the two results is this: Where the relation produced by PACK r ON (A2,A1) has the interval [P5:P5], the relation produced by PACK (PACK r ON (A2)) ON (A1) has the interval [P3:P5] instead. Thus, this latter relation effectively tells us twice that parts P3 and P4 appear in combination with days 1, 2, 3, and 4; in other words, it contains some redundancy. The former relation, by contrast, doesn’t. And this state of affairs explains why we define multiattribute PACK the way we do, with a preliminary total UNPACK, instead of—as might seem on the face of it more “natural”—just as a sequence of single-attribute PACKs: We do so because that definition is guaranteed to eliminate redundancy, which the apparently more natural definition isn’t. See the section “Some Remarks on Redundancy” later in this chapter for further discussion.

Equivalence of Relations

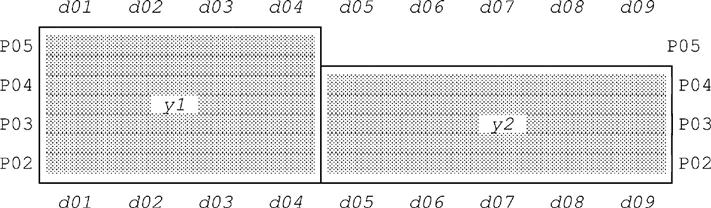
Consider yet again the relation r we used earlier to demonstrate that, for PACK, order matters:

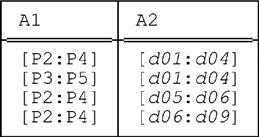
Here again are the relations that result from evaluating the expressions PACK r ON (A1,A2) and PACK r ON (A2,A1), now shown side by side (relation left corresponds to packing on A1 then A2, relation right to packing on A2 then A1):

Now, relations left and right certainly aren’t equal, but they’re at least equivalent, in a sense which we now explain. Loosely, we can say they both represent the same information; however, they do so from two different points of view, as it were. To be more specific, left shows the ranges of parts (A1) corresponding to given intervals of time (A2), while right shows the intervals of time (A2) corresponding to given ranges of parts (A1).⁵ Tightening these remarks up slightly, we obtain the predicates:

Observe in particular, therefore, that:

Thus, both relations are nonredundant—i.e., neither of them displays the kind of redundancy we identified in the previous section (and will be discussing further in the next).

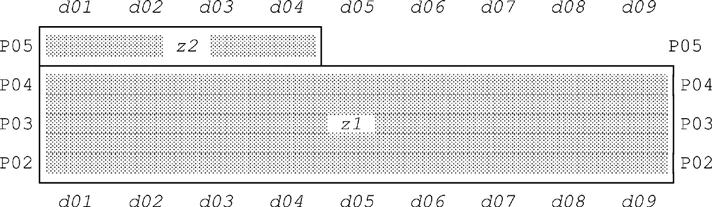
Of course, the foregoing difference in interpretation between left and right is perhaps more significant from a psychological perspective than it is from a logical one. Also, of course, it’s a trivial matter—conceptually speaking, at any rate—to convert either relation into the other. For example, the following expression will effectively convert left into right:

PACK left ON ( A2 , A1 )

With the foregoing discussion by way of motivation, we can now define the notion of equivalence for n-ary relations as follows:

Observe, incidentally, that if r1 and r2 are equal, then they’re certainly equivalent—with respect to every possible subset of their attributes, in fact, just so long as every attribute in the subset in question is interval valued.

Expand and Collapse Revisited

The following example (repeated from the section “Unary Relations” in Chapter 8) shows a relation r containing just one attribute, which is interval valued, together with the corresponding expanded and collapsed forms:

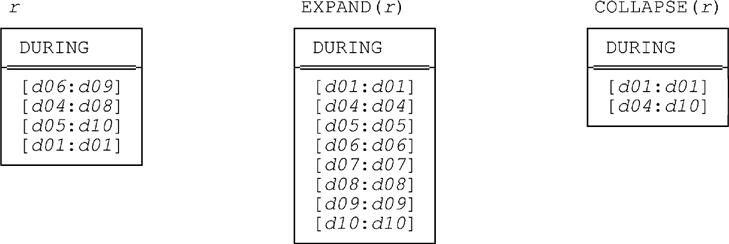
Consider now what happens if we unpack r on DURING. Since there’s just one interval attribute, the definition from Chapter 9 applies, and so we have:

UNPACK r ON ( DURING ) $\underset{¯}{\underset{¯}{\mathrm{def}}}$

  WITH ( r1 := r GROUP { DURING } AS X,

   r2 := EXTEND r1 : { X := EXPAND ( X ) } ) :

  r2 UNGROUP X

Hence:

■ The GROUP step gives an intermediate result r1 that looks like this (observe that it has degree and cardinality both one—attribute X is a relation valued attribute or RVA—and the single value it contains is exactly relation r):

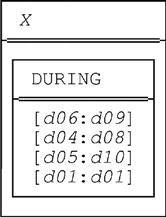
■ The EXTEND step gives an intermediate result r2 that looks like this (observe that it too has degree and cardinality both one, and the single value it contains is exactly the expanded form of relation r):

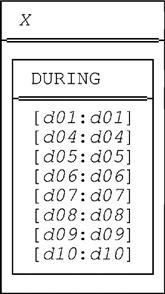
■ The UNGROUP step then produces the final result, which is exactly EXPAND (r).

In other words, EXPAND is just a special case of UNPACK! Thus, there was no logical need to introduce the EXPAND operator at all—we could have called it UNPACK right from the outset, in Chapter 8. Rightly or wrongly, however, we judged that it would have been too confusing to do so, since it would have meant we would have to say something along the lines of “We now introduce an operator called UNPACK that we need as a stepping stone on the way to defining an operator called UNPACK.” Be that as it may, from this point forward we’ll drop our references to EXPAND as such and talk in terms of UNPACK only.

Analogously, it turns out that—as you’ll surely be expecting—COLLAPSE is just a special case of PACK. It’s not worth going through the detailed argument here (though you might like to have a go at producing that argument for yourself); suffice it to say that from this point forward we’ll drop our references to COLLAPSE as such and talk in terms of PACK only.

Some Remarks on Redundancy

Here’s yet another example that bears close examination. Let relation r be as follows:

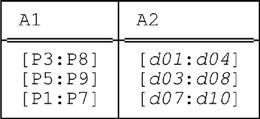
Then the results of PACK r ON (A1,A2) and PACK r ON (A2,A1) are as shown here (and once again we recommend that you verify these results for yourself):

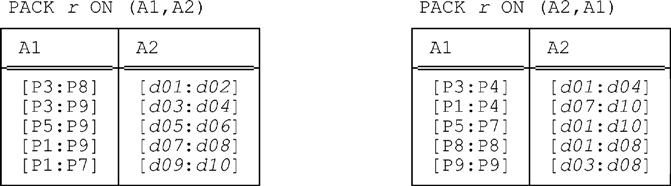
The interesting thing about this example isn’t so much that the two packed forms are different once again (though they are), but rather that—perhaps somewhat counterintuitively—they both have cardinality greater than that of the original relation! Thus, while the original relation certainly involves some redundancy (for example, it tells us twice that part P5 appears in combination with day 3), it’s in a sense more compact than the two packed forms, even though those packed forms don’t display that same kind of redundancy.⁷

So what does it mean for a relation to display, or not to display, redundancy in the foregoing sense? Well, here’s a definition:

For example, the relation r shown at the beginning of this section is redundant with respect to attributes A1 and A2, because if we perform a “total unpack” of that relation—i.e., if we unpack it on A1 and A2—then the result contains the following tuple among many others:

And this tuple derives from both of the following tuples of r:

By contrast, PACK r ON (A1,A2) and PACK r ON (A2,A1)—i.e., both of the fully packed forms of the original relation r—are nonredundant in the foregoing sense. (Exercise: Check this claim.) In general, in fact, any fully packed form of any relation is guaranteed to be free of redundancy in the foregoing sense.

The foregoing example also raises a couple of further points:

■ First, note that the result of PACK r ON (A2,A1) contains two distinct tuples corresponding to part number P3 (also two distinct tuples corresponding to part number P4). Thus, we have here—as promised in the section “Equivalence of Relations” earlier—an example to show that the result of PACK r ON (A1,A2, …,An) is not guaranteed to contain just one tuple for each point p that’s contained in at least one interval that’s an An value somewhere in the original relation r.

■ Second, note that although the two fully packed forms in the example both have cardinality greater than that of the original relation, they do at least both have the same cardinality. Again, however, this state of affairs is a fluke. By way of a counterexample, let relation r be as follows:

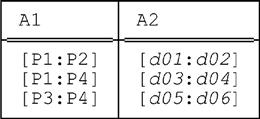
Then packing this relation on (A1,A2) returns the original relation r, with cardinality three. By contrast, packing it on (A2,A1) returns the following relation, with cardinality two:

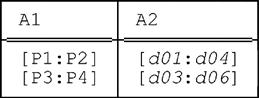
However, returning to the previous example (the one from the beginning of this section), we see that if r is a relation and FP is the set of all fully packed forms of r, then there isn’t in general just one relation fp in FP with minimum cardinality—i.e., with cardinality less than that of all other relations fp' (fp' ≠ fp) in FP. It follows that, if we regard each fp in FP as a canonical form of r, then there’s no canonical form fp in general that’s somehow “more canonical” than all the rest.

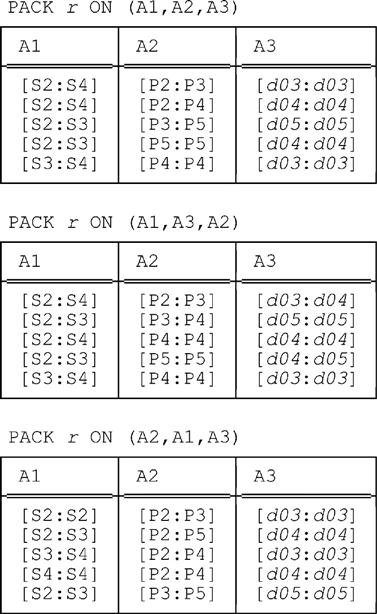
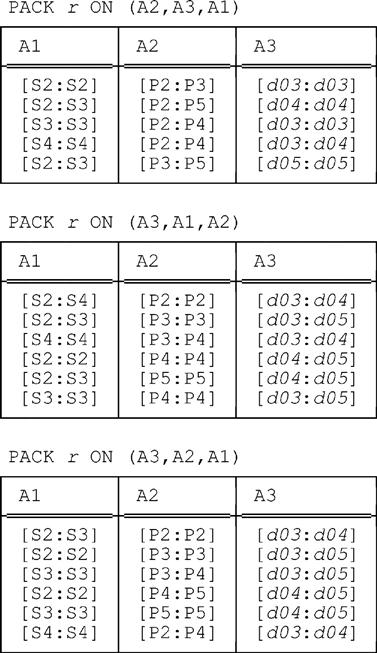
A More Complex Example

We conclude this chapter by briefly examining an example involving three interval attributes. Consider the following relation r (which is identical to the relation shown at the very end of Chapter 6, except that we’ve renamed the attributes A1, A2, and A3 for simplicity):

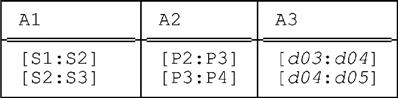
This relation has six fully packed forms, which we now show:

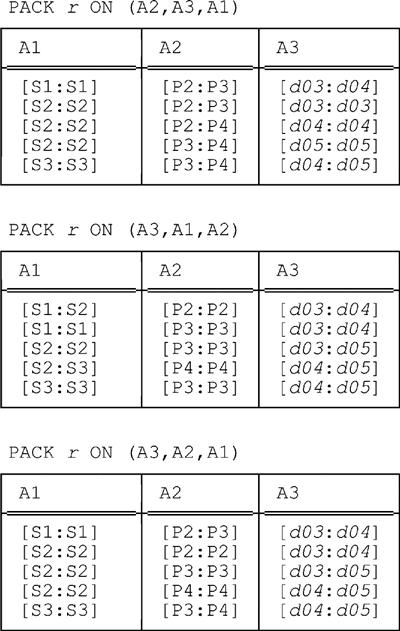
All of these relations have the same cardinality, as it happens, though that cardinality is greater than that of the original relation. Of course, they’re all redundancy free.

Exercises

10.1 If relation r is in packed form (on attributes A1, A2, …, An, say), is it true that every restriction of r is also in that same packed form?

10.2 What exactly does it mean to say some relation r is redundancy free with respect to attributes A1, A2, …, An?

10.3 Let relation r be as follows:

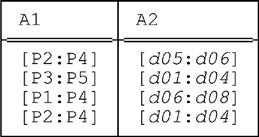
Show the result of PACK r ON (A1,A2) and PACK r ON (A2,A1).

10.4 Let relation r be as follows:

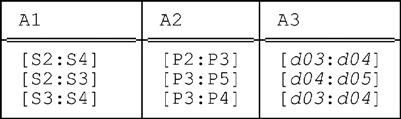
Show all fully packed forms of r (where by fully packed we mean the relation is packed on all of its attributes A1, A2, and A3, in some order).

10.5 Let T be a type consisting of all positive integers in the range [1: n]. Find the smallest value for n such that relations r1 and r2 of type
RELATION { A1 INTERVAL_T , A2 INTERVAL_T }
exist that satisfy all of the following conditions a.-f.:

a. r1 ≠ r2

b. UNPACK r1 ON ( A1 , A2 ) = UNPACK r2 ON ( A1 , A2 )

c. r1 ≠ PACK r1 ON ( A1 , A2 )

d. r2 ≠ PACK r2 ON ( A1 , A2 )

e. COUNT ( r1 ) = COUNT ( r2 )

f. There’s no relation r3 of the same type as r1 and r2 such that the following expression evaluates to TRUE:
UNPACK r3 ON ( A1 , A2 ) = UNPACK r1 ON ( A1 , A2 )
AND COUNT ( r3 ) < COUNT ( r1 )

What do you conclude from this exercise?

Answers

10.1 Yes, it is.

10.2 See the section “Some Remarks on Redundancy” in the body of the chapter.

10.3 

10.4 

10.5 Suppose n = 1. Then:

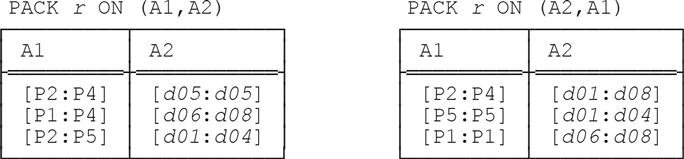
■ Type INTERVAL_T has just one value—the unit interval [1:1].

■ All relations of the specified type are thus in unpacked form (in fact, there are exactly two such relations), and so conditions a. and b. can’t both be satisfied.

■ We remark as an aside that all relations of the specified type are also in packed form, since their cardinality is less than two in every case, and conditions c. and d. can’t be satisfied either. Nor can conditions a. and e.
It follows that n = 1 is impossible. So suppose n = 2. Then:

■ Type INTERVAL_T has exactly three values—[1:1], [1:2], and [2:2].

■ It follows that there are exactly nine distinct tuples that can appear in relations of the specified type, and therefore exactly 2⁹ = 512 relations of that type.

■ Of those 512 relations, we can eliminate all in which the attribute value [1:2] fails to appear, because all such relations are in unpacked form, and conditions a. and b. thus can’t possibly both be satisfied by two such relations.

■ We can also eliminate all relations of cardinality less than two, because all relations of cardinality less than two are in unpacked form; thus (again) conditions a. and b. can’t possibly both be satisfied by two such relations.

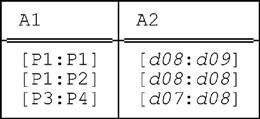
■ Observe now that there are exactly five tuples of the relevant type in which either A1 = [1:2] or A2 = [1:2]:

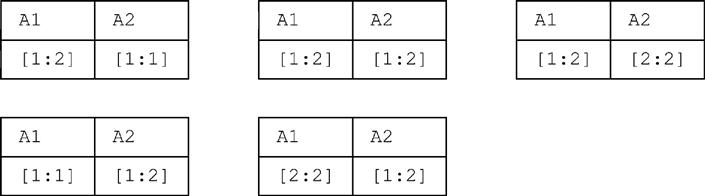
It can be seen by inspection that no relation that contains just one of these five tuples and just one other tuple is in packed form, and moreover that the packed form of each such relation contains just a single tuple. It follows that even if we can find two relations of the type at hand with cardinality greater than one that satisfy conditions a.-e., they would fail to satisfy condition f. because their packed form is of cardinality one.

It follows that n = 2 is also impossible. We now show that there does exist a pair of relations satisfying the given conditions when n = 3. Consider the following relations r1 and r2:

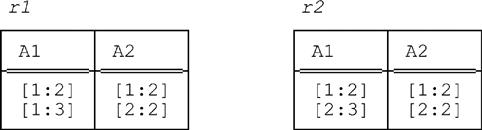
■ Conditions a. and e. are clearly satisfied. Condition b. is also satisfied, because the unpacked form u of both r1 and r2 is as follows:

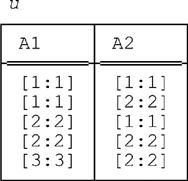
■ Conditions c. and d. are also satisfied, because packing u on (A1,A2) yields:

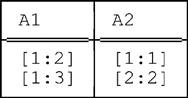
(which is distinct from both r1 and r2). As an aside, we note that packing u on (A2,A1) yields yet another distinct relation:

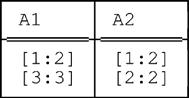
■ Condition f. is satisfied because every relation of cardinality one is in packed form and the packed form of r1 and r2 is of cardinality two. Thus, no relation of cardinality one, when unpacked, can yield the unpacked form of r1.

We conclude from this exercise that, given a certain relation u in unpacked form and the set Ru of relations whose unpacked form is u, in general there’s no unique member of Ru whose cardinality is less than that of all of the other members of Ru, except possibly when some fully packed form of u has that property. In other words (and indeed as noted in the body of the chapter), there’s no third canonical form in addition to packed and unpacked forms that’s based on minimum cardinality alone. (Of course, there’s obviously no canonical form based on maximum cardinality alone, because the unpacked form always has that property.)