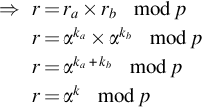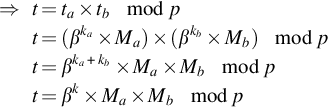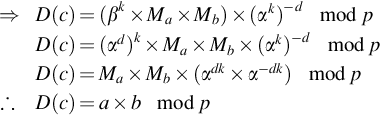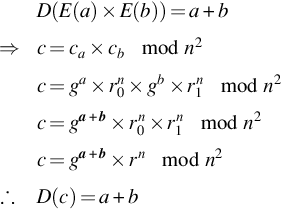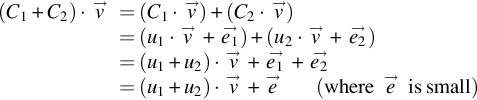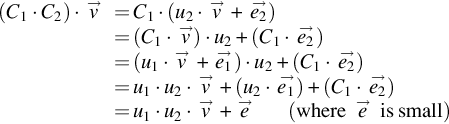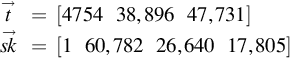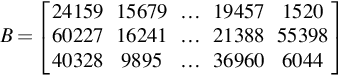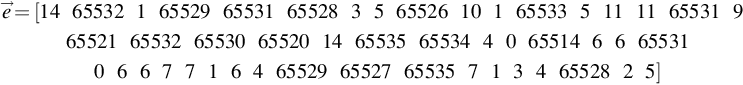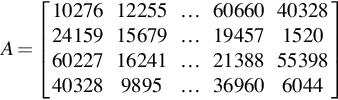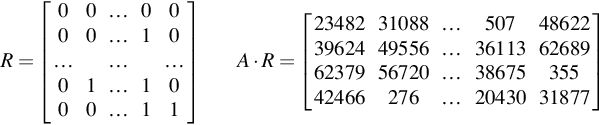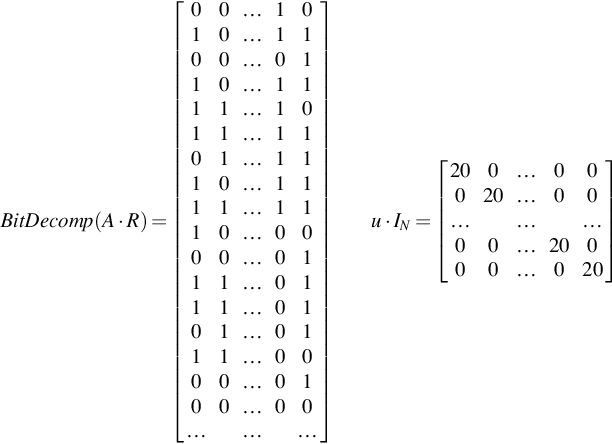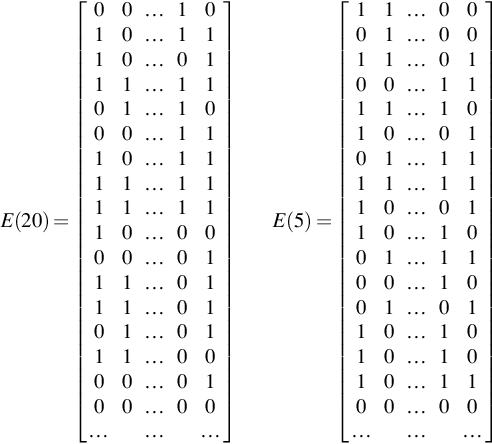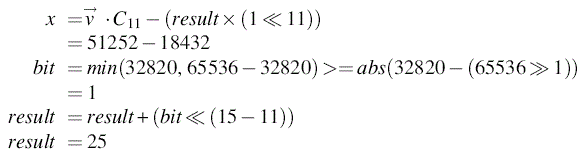Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Chapter 5

A guide to homomorphic encryption

Mark A. Will; Ryan K.L. Ko Cyber Security Lab, Department of Computer Science, University of Waikato, Hamilton, New Zealand

Abstract

Traditional cryptography techniques require our data to be unencrypted to be processed correctly. This means that at some stage on a system we have no control over, our data will be processed in plaintext. Homomorphic encryption or specifically, fully homomorphic encryption is a viable solution to this problem. It allows encrypted data to be processed as if it were in plaintext and will produce the correct value once decrypted. While many know that homomorphic encryption promises to be an ideal solution to trust, security, and privacy issues in cloud computing, few actually knows how it works and why it is not yet a practical solution despite its promises. This chapter serves as a much needed primer on current homomorphic encryption techniques, discusses about several practical challenges, and introduces workarounds proposed by practitioners and researchers to overcome these challenges.

Keywords

Homomorphic Encryption

Cloud Security

Fully Homomorphic Encryption

Partial Homomorphic Encryption

Data Privacy

1 Introduction

In cloud computing, fully homomorphic encryption (FHE) is commonly touted as the “holy grail” (Gentry, 2009a; Micciancio, 2010; Van Dijk and Juels, 2010) of cloud security. While many know this potential, few actually understands how FHE works and why it is not yet a practical solution despite its promises. Homomorphic encryption schemes allow users’ data to be protected anytime it is sent to the cloud, while keeping some of the useful properties of cloud services like searching for strings within files. This is because it can allow operations and functions to be preformed over encrypted data, meaning that the data is never unencrypted outside the users’ environment. It prevents malicious employees of cloud service providers from accessing private data. A report (Chen, 2010) of an employee at Google in 2010 described a former engineer abusing his privileges to view private information. He used this information to stalk teenage girls and spy on their chat sessions. Many employees of cloud services have the required privileges to view our data, and we need to prevent such incidents from happening again.

There are two flavors of homomorphic encryption: partially and fully. Partially Homomorphic Encryption (PHE) is where only a single operation can be performed on cipher text, for example, addition or multiplication. Schemes for PHE exist and are usable today, with two being described in Section 4. However, many cloud services require more functionality than just addition or multiplication. This is where FHE, also known as the “holy grail” of encryption, can start to play a huge role in securing cloud services. FHE can support multipliable operations (currently addition and multiplication), allowing more computation to be performed over encrypted data.

Looking at an example, Alice runs an accounting firm, which stores all of her customers balances on the cloud. By utilizing the cloud, it means that she does not have to manage the underlying infrastructure of the cloud. Instead it is managed by a third-party cloud service provider. The problem Alice faces is that in order to keep her customers accounts secure, she encrypts them when they are in the database/storage. This prevents a malicious outsider gaining direct access to the information, while also stopping the cloud service employees from being able to see the data. But when she needs to make a change to an account balance, she has to either transfer the encrypted account back to the her trusted environment, or decrypt the account data in the cloud, update the account, then encrypt it again before storage. This creates a risk where the data has to be decrypted at a point before it can be used. Because homomorphic encryption can process data while encrypted, Alice can simply apply changes to the encrypted account balance by sending encrypted data to the cloud and have the account updated without it ever being in decrypted form (i.e., plaintext). This allows Alices’ cloud accounting firm to keep its customers secure, while having the added benefits of using the cloud.

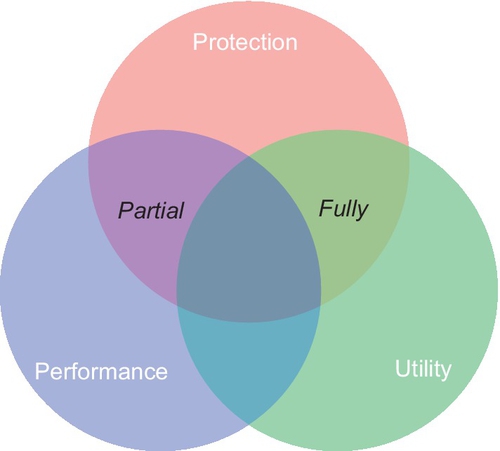
There is however a catch with this example. The performance of FHE is currently quite inefficient, where simple operations can take anywhere from seconds to hours depending on security parameters (Gentry and Halevi, 2011). Therefore, homomorphic encryption is currently a balancing act between utility, protection, and performance. FHE has good protection and utility, but poor performance. Where PHE has good performance and protection, but is very limited in its utility. This is illustrated in Figure 1, where the perfect solution would be in the center of the Venn diagram.

f05-01-9780128015957 — Figure 1 Protection versus utility versus performance for homomorphic encryption

This chapter will give an in-depth overview of homomorphic encryption, and why it is so important for the cloud. We start with why homomorphic encryption is needed in the cloud, and some basic background information on the history of homomorphic encryption. In Section 4, we will describe and provide examples of two PHE schemes, El Gamal and Paillier. This leads into FHE where the Approximate Eigenvector Algorithm will be given, with details of how it works, the mathematical properties, and an example. From Section 6, some examples of homomorphic encryption in use today will be shown, followed by the some thoughts about the future of homomorphic encryption. For businesses requiring the protection of their data, homomorphic encryption is not the only answer available today, and Section 8 will give another methodology for storing encrypted data in the cloud.

2 Current industry work-arounds and their gaps

The cloud is built upon many technologies and ideas, but none more important than trust. As uses of cloud services, we have to trust that the providers will not misuse our data and information, but on top of that, we have to trust that their security defences will prevent malicious users from gaining access it as well.

Dropbox is one of the most widely used cloud storage services today, producing equivalent to one-third of the traffic that YouTube produces (Drago et al., 2012). On a help page titled How secure is Dropbox? (Dropbox Inc, 2014), is some useful information on how Dropbox is trying to protect its users. Analyzing a couple of these points: Dropbox uses modern encryption methods to both transfer and store your data (Secure Sockets Layer and AES-256 bit encryption) and Dropbox employees are prohibited from viewing the content of files you store in your account (Dropbox Inc, 2014). It is clear that even though your data is encrypted when stored, it is still possible for someone other than you to view the data in the unencrypted form. Be it a rogue Dropbox employee or a malicious attacker.

Then there are cloud storage services such as Mega Limited (Mega ltd, 2014), which provide privacy and protection by only having the end users device encrypt and decrypt their data. This ensures that only the user can access the unencrypted data, even if the service is compromised. This does however come with a cost, because only you can view your files. Therefore, it is difficult for Mega to provide advanced features such as searching for strings within files or sharing files with others. These features are still possible to implement, for example, having the client build and use a search index which can be encrypted and stored in the cloud, or for sharing files, encrypt with a different key allowing the user to give it to whomever needs access.

The problem is that Dropbox can perform the same tasks automatically, faster, and more efficiently. So the trade-off between utility, protection, and performance is a key problem for cloud service providers. This is where homomorphic encryption can play such a huge role in the cloud, because it can help combine the features of both Dropbox and Mega. Allowing the creation of more secure and trustworthy cloud services, by bridging the gap between utility and protection. Note that the algorithms for how homomorphic encryption will be able to actually search files is still unknown. However it could be done in a similar manner as encryption gateways described in Section 8 or using another encrypted search technique (Li et al., 2014; Kuzu et al., 2012; Li et al., 2010; Wang et al., 2014). But once FHE becomes more practical, these algorithms will start to be developed.

Even though homomorphic encryption cannot currently easily support searching, it is ideal for computing mathematical functions on encrypted data. For example, computing statistics, such as the mean or average value in a large dataset. Other application groups that can benefit are banking and data mining. So, therefore, homomorphic encryption is very important for the cloud, and once it matures, it will be widely used.

3 History and related work

To the best of our knowledge, the idea of using homomorphic encryption for protecting data has been around for decades, with Rivest et al. proposing special encryption functions called “privacy homomorphisms” in 1978 (Rivest et al., 1978b). The authors discuss the use of hardware to process data securely, with the data only ever decrypted on a physically secure processor. This way, any time the data leaves the processor (i.e. to memory) it is encrypted, similar to the AEGIS chip we see today (Suh et al., 2003, 2005). However, the issue with these types of chips is that because it is custom hardware, costly to implement, and still requires a decryption key for the data. Rivest el al. then mention a solution where the data is not decrypted, but standard hardware can still process the data correctly, and the concept of homomorphic encryption was born. They present some proof-of-concept examples that are not practical for use, but importantly show that this idea of processing encrypted data is possible, finishing off with two open questions:

• Does this approach have enough utility to make it worthwhile in practice? (Rivest et al., 1978b)

• For what algebraic systems U does a useful privacy homomorphism exist? (Rivest et al., 1978b)

In the same year, the RSA encryption scheme was made public by the same two authors of Rivest et al. (1978b), Rivest and Adleman, with the addition of Shamir (Note: RSA actually stands for the initials of the authors) (Rivest et al., 1978a). The original paper has no mention of homomorphic encryption; however, it was later proved that RSA does support multiplication over encrypted data (Denning, 1982). This is due to the mathematical properties of RSA, where by raising a message to e in modulo n, allows the two encrypted messages to be multiplied correctly once the e’s are removed at the decryption stage. Therefore, PHE has been conceptually supported for some time now.

In 1985, Blakley et al. proposed a database encryption scheme which supports computing some statistical operations over encrypted data stored in the database. Even though the paper does not specifically mention homomorphism, this is a step in showing that homomorphic encryption can be worthwhile in practice. In 1987 Ahituv et al. (1987) provides some more example algorithms that can support homomorphic operations, however have very weak security. In the following year Brickell and Yacobi (1988) evaluated the security of the first proposed homomorphic algorithms in Rivest et al. (1978b) and proposed an additive homomorphic algorithm where there was a maximum number of additions that could occur before it would break.

It was not until 1996 that we saw the first homomorphic algorithm to support both addition and multiplication (Ferrer, 1996). Domingo-Ferrer provided a needed breakthrough in the field, and later showed in 2002 that the proposed scheme was secure against known clear-text attacks; however, the scheme was broken a year later by Wagner (2003).

The problem up until this point was developing a scheme that was secure, without losing its homomorphic properties, able to support the repeating of operations many times, or being incredibly inefficient. Armknecht et al. proposed a solution which supported arbitrary number of additions and a fixed number of multiplications (Armknecht and Sadeghi, 2008), while remaining secure under a known decoding problem.

However, the real breakthrough occurred in 2009 when Gentry proposed a scheme that could support an arbitrary number of additions and multiplications and based the security on the hardness of lattice problems (Gentry, 2009a). Since then, Gentry has been involved in many different schemes (Gentry, 2009b; Van Dijk et al., 2010; Gentry et al., 2013) for FHE, gradually improving the schemes, but still to this day are not efficient enough to be used in the real world. The brief history given in this section is summarised in Table 1.

Table 1

Historic Overview of Homomorphic Encryption

2013	Homomorphic encryption from learning with errors: Conceptually simpler, asymptotically faster, attribute-based (Gentry et al., 2013)
2010	Fully homomorphic encryption over the integers (Van Dijk et al., 2010)
2009	A fully homomorphic encryption scheme (Gentry, 2009a)
	Fully homomorphic encryption using ideal lattices (Gentry, 2009b)
2008	A new approach for algebraically homomorphic encryption (Armknecht and Sadeghi, 2008)
2002	A provably secure additive and multiplicative privacy homomorphism (Domingo-Ferrer, 2002)
1996	A new privacy homomorphism and applications (Ferrer, 1996)
1988	On privacy homomorphisms (Brickell and Yacobi, 1988)
1987	Processing encrypted data (Ahituv et al., 1987)
1985	A database encryption scheme that allows the computation of statistics using encrypted data (Blakley and Meadows, 1985)
1982	Signature protocols for RSA and Other Public-Key Cryptosystems (Denning, 1982)
1978	On data banks and privacy homomorphisms (Rivest et al., 1978b)

4 Overview of partial homomorphic encryption schemes

Algorithms supporting the idea of homomorphic encryption have been around for quite some time, as discussed by Section 3. In this section, two PHE schemes, ElGamal (1985) and Paillier (1999), will be covered. These were chosen so that an addition and a multiplication scheme were shown. This section will first introduce the idea of public key encryption, since both of these schemes fall into that category. Before describing El Gamal and Paillier in detail, examples of addition and multiplication are included.

4.1 Public key encryption

Diffie and Hellman (1976) introduced the concept of public key encryption, also known as asymmetric cryptography in 1976. Like FHE today, practical implementations of public key encryption were limited. However they are now widely used, including the El Gamal and Paillier schemes. Both of these schemes use a large prime number for a modulus operation, which is a security parameter. It is important to note however that even though these schemes can provide homomorphic operations, because of the nature of modulus operation, if the input or output values are greater than the modulus, results may not be as expected.

Looking at an example of public key encryption, Alice, Bob and Claire are good friends who send each other online chat messages at night after school. However, Alice and Bob would like to throw Claire a surprise birthday party. The problem is that neither Alice or Bob can figure out how to remove Claire from the chat session. But they do not want Claire to be able to see their conversion because it will ruin the surprise. One solution to this problem is for them both to create a private and public key, known as public key encryption. Then they can send their public key to everyone in the chat session. This allows Bob to encrypt a secret message to Alice using her public key, before broadcasting it in the chat session. Only Alice will be able to decrypt and read the message, meaning Claire is unable to read any messages about her surprise party.

However looking at the bigger picture, it also prevents malicious users from reading the messages as well. For example, the chat services’ administrators can only see the public key and encrypted messages. The same applies for any user sniffing the network, and finally this means that even if the chat service gets compromised, Alice and Bobs chat history is safe. This is not to say that the encrypted chat is 100% guaranteed to be safe and secure, but it adds another layer of protection to their data.

Therefore, public key encryption proves a means to encrypt data that only the holder of the private key can read. Anyone can gain access to the public key, which is used to encrypt the data. But ideally, only one person/system has the private key to decrypt the data. Everyone using the Internet would have experienced public key encryption, but probably without knowledge. For example, Hypertext Transfer Protocol Secure (HTTPS) sets up a secure tunnel using public key encryption within a browser. The client sends data to the server using the servers public key, and the server sends data back to the client using the clients public key. The setup of the keys is a bit more complicated than the example before, but it all happens in the background.

When designing and setting up a cloud service, it is important to consider how public key encryption will play a role in making the service more secure. Providing secure channels for authentication is a must today, and HTTPS is a viable solution. However, there are other ways to make the service more secure, like the use of PHE. Some real-world examples of homomorphic encryption will be covered in Section 6, but now El Gamal and Paillier’s scheme will be described to show how simple it is to implement PHE.

4.2 El Gamal

The security strength of El Gamal is based on the hardness of solving discrete logarithms, which was first proposed in 1985 by ElGamal (1985). Conceptually, El Gamal supports homomorphic multiplication operations on encrypted data. The key generation algorithm is given in Algorithm 1.

Algorithm 1

El gamal key generation algorithm

1: Select a large prime p

2: Select a primitive value α in modulo p

3: Randomly select d so that 2 ≤ d ≤ p −2

4: Calculate β = α^d mod p

5: Public Key = (p,α,β)

6: Private Key = d

Now that the keys are generated, the algorithms to encrypt E(x) and decrypt D(x) are given in Algorithms 2 and 3, respectively.

Algorithm 2

El gamal encryption algorithm

Encrypt an Integer message M where M is less than the large prime p

1: Select a random integer k (which must remain private)

2: Calculate r = α^k mod p

3: Calculate t = β^k × M mod p

4: Discard k

5: Encrypted Message = (r,t)

Line 2 in Algorithm 2 allows us to hide k, so that it can be removed from t when we are decrypting the message. We discard k so that it remains a secret and cannot be leaked. This is necessary because the strength of this algorithm is based upon solving for k is hard. Therefore, if a malicious user gains access to k, they can decrypt the message without the private key.

Algorithm 3

El gamal decryption algorithm

Decrypt a message (r,t) to find M

1: Calculate M = t × r^−d mod p

It is important to understand the proof of encryption and decryption as it shows how the public and private keys cancel each other out, leaving the original message. This allows an appreciation of the mathematics behind El Gamal. Even though to implement an encryption algorithm does not require knowledge of how they work, security holes found are often in the implementation, and not the algorithm itself.

Proof:

1: M = t × r^−d mod p

2: M = β^k × M × (α^k)^−d mod p

3: M = (α^d)^k × M × (α^k)^−d mod p

4: M = M × (α^dk × α^−dk) mod p

5: M = M × 1 mod p

Because the algorithm only uses multiplication operations on the message value, it is quite easy to see how it supports homomorphic multiplication operations. Given a and b, we want to show that encrypting them, multiplying, then decrypting gives a × b.

$\begin{array}{l} D (E (a) \times E (b)) mod p = t_{a} \times t_{b} \times {(r_{a} \times r_{b})}^{- d} mod p \end{array}$

First, when the r values are multiplied, because the k values are random, then adding them still gives a random k.

$\begin{array}{l} \Rightarrow & r = r_{a} \times r_{b} mod p \\ r = α^{k_{a}} \times α^{k_{b}} mod p \\ r = α^{k_{a} + k_{b}} mod p \\ r = α^{k} mod p \end{array}$

si2_e

The multiplication of the t values also involves random ks, which can be combined in the same manner. This leaves the a and b values multiplied together, along with β^k.

$\begin{array}{l} \Rightarrow & t = t_{a} \times t_{b} mod p \\ t = (β^{k_{a}} \times M_{a}) \times (β^{k_{b}} \times M_{b}) mod p \\ t = β^{k_{a} + k_{b}} \times M_{a} \times M_{b} mod p \\ t = β^{k} \times M_{a} \times M_{b} mod p \end{array}$

si3_e

Now by substituting the t and r values into the decryption equation, the αs cancel themselves out, resulting in the decrypted value equaling a × b.

$\begin{array}{l} \Rightarrow & D (c) = (β^{k} \times M_{a} \times M_{b}) \times {(α^{k})}^{- d} mod p \\ D (c) = {(α^{d})}^{k} \times M_{a} \times M_{b} \times {(α^{k})}^{- d} mod p \\ D (c) = M_{a} \times M_{b} \times (α^{d k} \times α^{- d k}) mod p \\ ∴ & D (c) = a \times b mod p \end{array}$

si4_e

To this point, the mathematics show that El Gamal supports homomorphic multiplications. However to conclude, an example of El Gamal in operation will be shown. Given 6 and 5, we want to solve E(6) × E(5) where p = 47, α = 7, d = 35, and β = 7³⁵ mod 47 = 17. Also this example will show that addition is not supported.

Encrypt 6 Encrypt 5

$\begin{array}{l} k & = 41 \\ r & = 7^{41} mod 47 \\ = 42 mod 47 \\ t & = 1 7^{41} \times 6 mod 47 \\ = 14 mod 47 \\ E (6) & = (42, 14) \end{array} \begin{array}{l} k & = 29 \\ r & = 7^{29} mod 47 \\ = 8 mod 47 \\ t & = 1 7^{29} \times 5 mod 47 \\ = 23 mod 47 \\ E (5) & = (8, 23) \end{array}$

si5_e

Calculate E(6) × E(5) Calculate E(6) + E(5)

$\begin{array}{l} = E (6) \times E (5) \\ = (42 \times 8, 14 \times 23) \\ = (7, 40) \end{array} \begin{array}{l} = E (6) + E (5) \\ = (42 + 8, 14 + 23) \\ = (3, 37) \end{array}$

si6_e

Decrypt (7,40) Decrypt (3,37)

$\begin{array}{l} = 7^{- 35} \times 40 mod 47 \\ = 30 mod 47 \end{array} \begin{array}{l} = 3^{- 35} \times 37 mod 47 \\ = 7 mod 47 \end{array}$

4.3 Paillier cryptosystem

Proposed in 1999 by Paillier (1999), the Paillier cryptosystem is based on the problem that computing nth residue classes is computationally intensive. The nature of the algorithm allows for homomorphic addition operations to produce the current answer once decrypted. The key generation for Paillier Cryptosystem given in Algorithm 4, is a bit more complicated than El Gamal.

Algorithm 4

Paillier cryptosystem key generation algorithm

1: Select two large prime numbers p and q where gcd (pq,(p − 1)(q − 1)) = 1

2: Calculate n = pq

3: Calculate λ = lcm(p − 1,q − 1)

4: Select g as a random integer where g ∈ $Z_{n^{2}}^{*}$

5: Define L(x) = $\frac{x - 1}{n}$

6: Ensure n divides the order of g by checking the existence of the following modular multiplicative inverse

7: u = (L(g^λ mod n²))^− 1 mod n

8: Public Key = (n,g)

9: Private Key = (λ,u)

To encrypt a message, the message is used as the exponent for g, then a random value is raised to the other public key value n, as shown in Algorithm 5. This produces a cipher value in modulo n². Decryption is again a simple equation, like El Gamal, and is given in Algorithm 6. Note that the definition for L(x) was given with key generation.

Algorithm 5

Paillier cryptosystem encryption algorithm

Encrypt a message M where M ∈_n

1: Select r as a random integer where r ∈ $Z_{n^{2}}^{*}$

2: Calculate c = g^m × rⁿ mod n²

Algorithm 6

Paillier cryptosystem decryption algorithm

Decrypt a message c where c ∈ $Z_{n^{2}}^{*}$

1: Calculate m = L(c^λ mod n²) × u mod n

The proof of the encryption and decryption will be now given to show how the public and private key values cancel each other out. This is important because it will help to show why the Paillier Cryptosystem can support homomorphic addition operations.

Proof:

1: m = L(c^λ mod n²) × u mod n

2: m = L(c^λ mod n²) × (L(g^λ mod n²))⁻¹ mod n

3: m = $\frac{L (c^{λ} \mod n^{2})}{L (g^{λ} \mod n^{2})}$ mod n

4: m = $\frac{λ [c] 1 + n}{λ [g] 1 + n}$ mod n (By Lemma 10 in Paillier (1999)

5: m = $\frac{[c] 1 + n}{[g] 1 + n}$ mod n

6: m = [c]_g mod n

7: m = m mod n (Because c = $g^{{[c]}_{g}}$ × rⁿ mod n² ((Paillier, 1999))

If an addition operation is desired to be computed on the encrypted data, it is actually a multiplication operation that needs to be used. This is because the message is encrypted as an exponent. Therefore to add exponents, a multiplication operation needs to be computed on two values of the same base, which in this case is g. Note that because the r₀ and r₁ values are random, they can be combined to form another random value r.

$\begin{array}{l} D (E (a) \times E (b)) = a + b \\ \Rightarrow & c = c_{a} \times c_{b} mod n^{2} \\ c = g^{a} \times r_{0}^{n} \times g^{b} \times r_{1}^{n} mod n^{2} \\ c = g^{a + b} \times r_{0}^{n} \times r_{1}^{n} mod n^{2} \\ c = g^{a + b} \times r^{n} mod n^{2} \\ ∴ & D (c) = a + b \end{array}$

si16_e

5 Fully homomorphic encryption

There are many schemes being introduced today that claim to support FHE (Armknecht and Sadeghi, 2008; Gentry, 2009a,b; Van Dijk et al., 2010; Brakerski and Vaikuntanathan, 2011; Gentry et al., 2013; Brakerski and Vaikuntanathan, 2014). In this chapter, we will focus on just one which uses the Learning With Errors (LWE) problem for FHE as described by Gentry et al. (2013). They call their method the approximate eigenvector method, which allows homomorphic addition and multiplication computation. This is achieved by using matrix addition and multiplication operations and without the need for bootstrapping user keys.

This section will cover some of the ideas that the approximate eigenvector algorithm is based upon. Lattices are a key building block and are explained first, before the problems that help make this algorithm hard to break are covered. Finally, the algorithm will be described, including a small example of homomorphic encryption.

5.1 Lattices

In order to understand why lattices are useful for FHE, we must first understand the basic properties of a lattice.

Definition 1

A lattice is made up of a set of points p₀…p_n in d-dimensional space, which forms independent linear vectors v₀…v_n (also known as the basis vectors), forming a geometrical pattern.

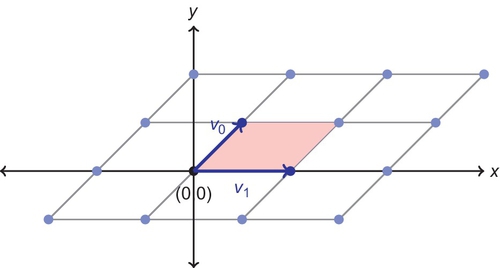
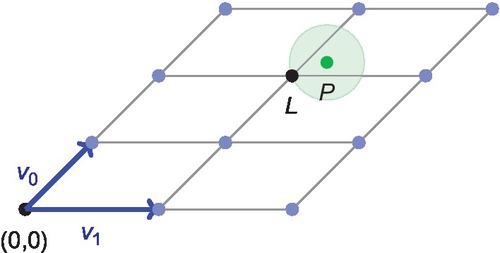
It is important to note that the same lattice can be formed from different basis vectors; therefore, it is said that a lattice is made up of an unique set of vectors which are the closed to the origin.

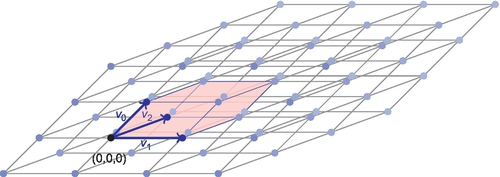
Any point that is the result of combining these vectors is known as a lattice point, and the region that can be translated by a lattice point while repeating the pattern is known as the fundamental region. The fundamental region is used to calculate the determinate of a lattice, which is the volume of the fundamental parallelepiped and represents the reciprocal of the density. Looking at the example in Figure 2, we are given the basis vectors v₀ and v₁, and combining these vectors together in many different ways gives a grid pattern of lattice points. The fundamental region is shown in red (dark gray in the print version), and with this simple 2D example it is easy to see how to repeat the fundamental region to continue the pattern.

f05-02-9780128015957 — Figure 2 Basic 2D lattice.

Now imagine adding a basis vector v₂ which is on the z-axis, making the lattice three dimensions as shown in Figure 3. The square fundamental region is replaced with a cubic one. As humans, lattices beyond three dimensions can be difficult to picture, but larger dimensions are simple for a computer to compute over as the input it receives is a matrix. In August 2010, IBM held a competition (IBM, 2010) for contestants to break FHE keys. The “toy” challenge used for testing had a dimension of 512, and the hardest problem had 32,768 dimensions. This shows that the number of dimensions is directly related to the strength of the key.

f05-03-9780128015957 — Figure 3 Basic 3D lattice using the 2D lattice in Figure 2.

5.2 Lattice problems

A couple of hard lattice problems which cryptography can be built upon is the Closest Vector Problem (CVP) and Shortest Vector Problem (SVP).

Definition 2

Given a point P and the lattice M, the Closest Vector Problem asks us to find the nearest lattice point L in M.

In Figure 4, it is easy to see the closest lattice point in pictorial form. However because a computer is only given a matrix, and the dimensions are much larger, it makes finding the closest lattice point much more computationally intensive.

f05-04-9780128015957 — Figure 4 Finding the nearest lattice point.

Definition 3

Given the lattice M, the Shortest Vector Problem as us to find the smallest non-zero vector V in M.

Non zero is important because every lattice technically has a zero vector. In Figure 4, this is simply v₀ because the example lattice is only showing the basis vectors. However, if larger vectors are given, there may exist a smaller vector which can make up the fundamental region. Note that CVP is actually a generalization of SVP, because if you are given an oracle (function) for CVP, it is possible to find the shortest vector by querying the oracle (Micciancio and Goldwasser, 2002; Goldreich et al., 1999). Therefore because CVP is a NP-Hard problem, so is SVP (van Emde-Boas, 1981; Micciancio, 2001).

5.3 Learning with errors

The LWE problem was introduction by Regev (2010) and is widely used for a range of cryptographic functions, such as public key encryption (Peikert, 2009). This is because it claims to be as hard as worst-case lattice problems (Regev, 2010), implying that any functions built upon LWE are secure. This was briefly discussed in Section 5.2. It is also currently assumed that worst-case lattice problems are even secure against the likes of quantum computers.

Definition 4

The LWE problem asks us to recover a secret $x \in Z_{q}^{n}$ given a sequence of approximate random linear equations on x (Regev, 2010).

Relating this back to lattices, the definition means distinguishing vectors that are created from a set of noisy (contains some error) linear equations between uniformly random vectors. Looking at an example from Regev (2010), we are given the set of linear equations shown in Figure 5 where in this case each equation has an error of approximately ± 1, then all we have to do is solve for x. But by introducing the error it makes solving x more difficult. If you were to try and solve the set of equations using Gaussian elimination (row reduction), for example, the errors would accumulate making the result invalid.

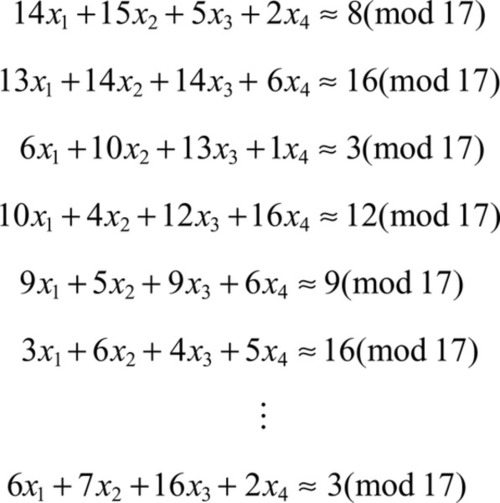
f05-05-9780128015957 — Figure 5 Example set of linear equations (Regev, 2010).

Given $2^{O (n log n)}$ equations we can deduce the secret x in $2^{O (n log n)}$ time but this approach is based more around luck than sense. A simpler technique is the Maximum Likelihood algorithm, which only requires O(n) equations and computes the only value for x that can satisfy the equations. This is achieved with brute force by computing all possible values, resulting in a run time of $2^{O (n log n)}$ (Regev, 2010). Currently, the best, known algorithm for solving LWE is by Blum et al. and requires 2^O(n) equations and time (Blum et al., 2003), which relates to the fact that the best algorithms for solving lattice problems need 2^O(n) time (Ajtai et al., 2001; Micciancio and Voulgaris, 2013).

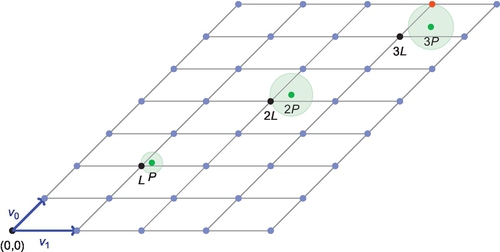
Therefore, homomorphic schemes built on the LWE problem need to keep the errors relatively small otherwise results can become invalid. For example, Figure 6 shows a lattice point L, and the point P which has some error added so that by solving CVP, L will be the result. If P is doubled, 2L is still the closest lattice point, however by adding P again giving 3P, the closest lattice point is not 3L, but instead 3L + v₀; therefore, the result is now invalid. Managing this error is one of the key challenges to homomorphic encryption in general and is a contributing factor to the performance limitations of current FHE schemes, such as the Approximate Eigenvector algorithm.

f05-06-9780128015957 — Figure 6 Combinations of errors or noise can lead to invalid results.

5.4 Approximate eigenvector algorithm

The Approximate Eigenvector scheme for FHE was proposed by Gentry et al. (2013) in 2013, which uses the LWE problem previously described in Section 5.3. This scheme allows for addition and multiplication homomorphic operations to be computed the same as matrix addition and multiplication operations, for most cases. Gentry et al. claim this makes the scheme asymptotically faster and easier to understand (Gentry et al., 2013), which is why we chose it for this chapter. The formal definition of an eigenvector is given below, where T is a square matrix and λ is a scale. Essentially for $\vec{v}$ to be classified as an eigenvector for the matrix T, the result must be equivalent to multiplying $\vec{v}$ by some scale factor. In this scheme, $\vec{v}$ is an approximate eigenvector, not a perfect one.

Definition 5

A vector $\vec{v}$ is an eigenvector (also known as a characteristic vector, proper vector, or latent vector) if $T (\vec{v}) = λ \vec{v}$ for some scale λ (Marcus, 1988).

To make this a leveled scheme (i.e. it will work up to a certain depth), the error must be controlled. As seen in Figure 6, controlling the size of the error is extremely important, so that the decrypted value will be correct. This is achieved by flattening the cipher matrix so that it contains values in {0,1}. Flattening uses bit decomposition operations, which does not affect dot product operations on the matrices. This allows homomorphic operations still be computed correctly, while keeping the errors small.

We will now cover the scheme, starting with the security parameters and function definitions. Before giving the key generation, encryption and decryption algorithms. We will then prove that the scheme does in fact support homomorphic addition and multiplication operations, which will be followed by an example.

Security parameters

q = modulus

n = lattice dimension

χ = error distribution

m = O(n log q)

ℓ = ⌊log₂q⌋ + 1

N = (n + 1) × ℓ

Definitions

Define BitDecomp(a) = Each coefficient of a decomposed into bits = (a_0,bit(0),…,a_0,bit(l−1),…,a_k−1,bit(0),…,a_{k−1,bit(l−1)}) ∈{0,1}^N

Define BitDecomp⁻¹(b ∈ _q^N) = revert b back to a if b = BitDecomp(a) i.e., b ∈{0,1}, else b ∈ _q^k therefore multiple the coefficients by powers of 2. = (∑_j2^jb_0,j mod q,…,∑_j2^jb_k−1,j mod q)

Define Flatten(b ∈ _q^N) = BitDecomp(BitDecomp⁻¹(b)) Define Powersof2(s) = (s₀2⁰,s₀2¹,s₀2²,…,s₀2^l−1,…,s_k−12⁰,s_k−12¹,s_k−12²,…,s_k−12^l−1)I_N denotes the N-dimensional identity matrix.

Key generation

Given the security parameters, the secret key generation is shown in Algorithm 7, where $\vec{s}$ is the secret key. The vector $\vec{t}$ is randomly generated with integer values in modulo q (no values are larger than q) and has the length n. The length is the same as the number of lattice dimensions so that a dot product can be computed over the lattice matrix. The secret key $\vec{s}$ has one more value than $\vec{t}$ (i.e., n + 1), which appends 1 to the front of $\vec{t}$ multiplied by − 1. Vector $\vec{v}$ is the result of the Powersof2 function defined earlier.

Algorithm 7

Approximate eigenvector secret key generation

1: Randomly generate $\vec{t}$ ←_qⁿ

2: Calculate $\vec{s}$ = (1,−t₁,…,−t_n) ∈_qⁿ⁺¹

3: Calculate $\vec{v}$ = Powersof2( $\vec{s}$ )

Once the secret key is generated, we can generate the public key matrix A, as shown in Algorithm 8. We start by randomly generate a matrix B with integer values in modulo q, with the size n × m. Now we must generate an error vector $\vec{e}$ of size m using the error distribution χ. To link together the public and secret key, the vector $\vec{b}$ must be calculated using random vector $\vec{t}$ from the secret key generation step, with some error added. Finally, the public key matrix A can be created by joining together the vector $\vec{b}$ and the matrix B, such that the first column of A is the $\vec{b}$ , with the remaining columns being B. This will be easier to understand in the example given in Section 5.4.1.

Algorithm 8

Approximate eigenvector public key generation

1: Randomly generate matrix B ←_q^m×n

2: Generate $\vec{e}$ ←χ^m

3: Calculate $\vec{b}$ = B ⋅ $\vec{t}$ + $\vec{e}$

4: Generate matrix A to have (n + 1) columns, where the first column is $\vec{b}$ , and the remaining columns are that of matrix B.

5.4.1 Encryption and decryption

Now that the public and secret keys can be generated, we will show how they can be used to encrypt and decrypt data. The algorithm for encrypting an integer u in modulo q is given in Algorithm 9. In order to make cipher values different even if the input message u is the same, first we must generate a random matrix R. The matrix R is then multiplied (dot product) by the public key matrix A before applying the bit decomposition function. This result will vary each time which helps hide the message. The message u is multiplied by an identity matrix I of size N × N (u is diagonally added to a square matrix of zeros), before being added to the result of the bit decomposition function. The message u becomes the scale value λ in the eigenvector definition shown earlier.

Algorithm 9

Approximate eigenvector encryption

To encrypt a message u where u ∈ _q

1: Randomly generate a uniform matrix R ∈{0,1}^N×m

2: Calculate cipher matrix C = Flatten(u ⋅I_N + BitDecomp(R ⋅A)) ∈_q^N×N

Decrypting a cipher matrix can be achieved using a couple of different techniques, depending on the value chosen for q. If q is a power of 2, then the MPDec function can be used for decryption. Otherwise the standard Decrypt function will have to be used. First, we will describe the standard Decrypt function given in Algorithm 10, where C is the encrypted cipher matrix. Once a value for i has been chosen which meets the conditions shown, compute the inner product (scalar product) of the ith row in matrix C, and $\vec{v}$ . Now the message u can be recovered.

Algorithm 10

Approximate eigenvector decryption

1: Set i where i < ℓ and q/4 < 2ⁱ < q/2

2: Compute x_i ←〈C_i, $\vec{v}$ 〉 where C_i is the i −th row

3: Then message u = x_i/2ⁱ

The description of the MPDec function shown in Algorithm 11 is better shown in Section 5.4.1 and in Micciancio and Peikert (2012). However to summarize, we can recover the least significant bit of the message u from the ℓ − 2 column of the cipher matrix C. Then process the columns back to the 0th column, which will contain the most significant bit. Whether the bit should be high or low, given the column C_i, and the current result will now be described. Note that the result should be initialized to 0 when computing C_ℓ−2.

Algorithm 11

Approximate eigenvector mpdec

1: x = C_i ⋅ $\vec{v}$ −(result × (1 i))

2: if x is closer to q/2 than q or 0, then the bit is high, else low

3: result+ = bit (ℓ −2 −i)

Proof for homomorphic addition and multiplication

Now that the algorithm has been described, we will now prove that homomorphic addition and multiplication operations are supported.

Given:

$\begin{array}{l} C_{n} \cdot \vec{v} = u_{n} \cdot \vec{v} + \vec{e_{n}} (where \vec{e} is small) \end{array}$

Addition:

$\begin{array}{l} (C_{1} + C_{2}) \cdot \vec{v} & = (C_{1} \cdot \vec{v}) + (C_{2} \cdot \vec{v}) \\ = (u_{1} \cdot \vec{v} + \vec{e_{1}}) + (u_{2} \cdot \vec{v} + \vec{e_{2}}) \\ = (u_{1} + u_{2}) \cdot \vec{v} + \vec{e_{1}} + \vec{e_{2}} \\ = (u_{1} + u_{2}) \cdot \vec{v} + \vec{e} (where \vec{e} is small) \end{array}$

si50_e

Multiplication:

$\begin{array}{l} (C_{1} \cdot C_{2}) \cdot \vec{v} & = C_{1} \cdot (u_{2} \cdot \vec{v} + \vec{e_{2}}) \\ = (C_{1} \cdot \vec{v}) \cdot u_{2} + (C_{1} \cdot \vec{e_{2}}) \\ = (u_{1} \cdot \vec{v} + \vec{e_{1}}) \cdot u_{2} + (C_{1} \cdot \vec{e_{2}}) \\ = u_{1} \cdot u_{2} \cdot \vec{v} + (u_{2} \cdot \vec{e_{1}}) + (C_{1} \cdot \vec{e_{2}}) \\ = u_{1} \cdot u_{2} \cdot \vec{v} + \vec{e} (where \vec{e} is small) \end{array}$

si51_e

Example

To help make this algorithm easier to understand, a simple example will now be explained for the addition of 5 and 20. Due to the large sizes of the matrices that are generated, they will be shown in a compressed form. The following parameters have been chosen for this example in order to keep the sizes of the vectors and matrices small.

$\begin{array}{l} q = 65, 536 n = 3 χ = 8 m = 48 ℓ = 17 N = 68 \end{array}$

Now we need to generate the secret key. First, $\vec{t}$ is randomly generated with values in modulo q. The secret key vector can then be created, be simpling joining 1 and the negative values of $\vec{t}$ . For example, ${\vec{t}}_{0} = 4754$ , becomes −4754, then find the modulus in q, −4754 + 65,536 which results in 60,782.

$\begin{array}{l} \vec{t} & = [4754 38, 896 47, 731] \\ \vec{s k} & = [1 60, 782 26, 640 17, 805] \end{array}$

si56_e

Calculating $\vec{v}$ involves computing the Powersof2 function on $\vec{s k}$ . The first 17 values are powers of 2 from 2⁰ to 2¹⁶, because they are multiplied by ${\vec{s k}}_{0}$ which is 1. Note that these are the modulus values in q, hence 1 × 2¹⁶ = 0. Now we do the same but instead multiply 2⁰ to 2¹⁶ by ${\vec{s k}}_{1}$ . Therefore, the next value is 2⁰ × 60,782 = 60,782, followed by 2¹ × 60,782 = 121,564 = 56,028 (mod q).

$\vec{v} = [1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 32768 0, 60782 56028 46520 27504 55008 44480 23424 46848 28160 56320 47104 28672 57344 49152 32768 0 0, 26640 53280 41024 16512 33024 512 1024 2048 4096 8192 16384 32768 0 0 0 0 0, 17805 35610 5684 11368 22736 45472 25408 50816 36096 6656 13312 26624 53248 40960 16384 32768 0]$

si61_e

The public key now needs to be generated. We randomly generate the matrix B and vector $\vec{e}$ .

$B = [\begin{matrix} 24159 & 15679 & \dots & 19457 & 1520 \\ 60227 & 16241 & \dots & 21388 & 55398 \\ 40328 & 9895 & \dots & 36960 & 6044 \end{matrix}]$

si63_e

$\vec{e} = [14 65532 1 65529 65531 65528 3 5 65526 10 1 65533 5 11 11 65531 9 65521 65532 65530 65520 14 65535 65534 4 0 65514 6 6 65531 0 6 6 7 7 1 6 4 65529 65527 65535 7 1 3 4 65528 2 5]$

si64_e

Compute the vector $\vec{b}$ .

$\begin{array}{l} \vec{b} & = [4754 38896 47731] \cdot [\begin{matrix} 24159 & 15679 & \dots & 19457 & 1520 \\ 60227 & 16241 & \dots & 21388 & 55398 \\ 40328 & 9895 & \dots & 36960 & 6044 \end{matrix}] + [14 65532 \dots 2 5] \\ = [10276 12255 \dots 60660 40328] \end{array}$

si66_e

Now we can join the vector $\vec{b}$ with the matrix B, to form the matrix A.

$A = [\begin{matrix} 10276 & 12255 & \dots & 60660 & 40328 \\ 24159 & 15679 & \dots & 19457 & 1520 \\ 60227 & 16241 & \dots & 21388 & 55398 \\ 40328 & 9895 & \dots & 36960 & 6044 \end{matrix}]$

si68_e

That concludes the key generation, so we can start encrypting an integer value. The encryption process for 20 will be shown now, and the cipher matrix for 5 will be given. So first we randomly generate the matrix R. It is important to note that the random matrix R will be different for the encryption of 20 and 5. Then we multiple this random matrix by the public key (matrix A).

$R = [\begin{matrix} 0 & 0 & \dots & 0 & 0 \\ 0 & 0 & \dots & 1 & 0 \\ \dots & \dots & \dots \\ 0 & 1 & \dots & 1 & 0 \\ 0 & 0 & \dots & 1 & 1 \end{matrix}] A \cdot R = [\begin{matrix} 23482 & 31088 & \dots & 507 & 48622 \\ 39624 & 49556 & \dots & 36113 & 62689 \\ 62379 & 56720 & \dots & 38675 & 355 \\ 42466 & 276 & \dots & 20430 & 31877 \end{matrix}]$

si69_e

Because we want values in {0,1} to keep errors small, we must now bit decompose A ⋅ R. If we take the first value 23,482, converted to a 17 bit value it becomes 00101101110111010₂. This is then put into a matrix vertically, from the least significant bit. Only the values 23,482, 31,088, 507 and 48,622 are shown. We must also calculate the identity matrix and multiply it by the value u we are encrypting, which is 20.

$B i t D e c o m p (A \cdot R) = [\begin{matrix} 0 & 0 & \dots & 1 & 0 \\ 1 & 0 & \dots & 1 & 1 \\ 0 & 0 & \dots & 0 & 1 \\ 1 & 0 & \dots & 1 & 1 \\ 1 & 1 & \dots & 1 & 0 \\ 1 & 1 & \dots & 1 & 1 \\ 0 & 1 & \dots & 1 & 1 \\ 1 & 0 & \dots & 1 & 1 \\ 1 & 1 & \dots & 1 & 1 \\ 1 & 0 & \dots & 0 & 0 \\ 0 & 0 & \dots & 0 & 1 \\ 1 & 1 & \dots & 0 & 1 \\ 1 & 1 & \dots & 0 & 1 \\ 0 & 1 & \dots & 0 & 1 \\ 1 & 1 & \dots & 0 & 0 \\ 0 & 0 & \dots & 0 & 1 \\ 0 & 0 & \dots & 0 & 0 \\ \dots & \dots & \dots \end{matrix}] u \cdot I_{N} = [\begin{matrix} 20 & 0 & \dots & 0 & 0 \\ 0 & 20 & \dots & 0 & 0 \\ \dots & \dots & \dots \\ 0 & 0 & \dots & 20 & 0 \\ 0 & 0 & \dots & 0 & 20 \end{matrix}]$

si70_e

These two matrices now have to be added together. Note that in the example, only the top 17 rows are shown, hence only two additions of 20 appear.

$u \cdot I_{N} + B i t D e c o m p (A \cdot R) = [\begin{matrix} 20 & 0 & \dots & 1 & 0 \\ 1 & 20 & \dots & 1 & 1 \\ 0 & 0 & \dots & 0 & 1 \\ 1 & 0 & \dots & 1 & 1 \\ 1 & 1 & \dots & 1 & 0 \\ 1 & 1 & \dots & 1 & 1 \\ 0 & 1 & \dots & 1 & 1 \\ 1 & 0 & \dots & 1 & 1 \\ 1 & 1 & \dots & 1 & 1 \\ 1 & 0 & \dots & 0 & 0 \\ 0 & 0 & \dots & 0 & 1 \\ 1 & 1 & \dots & 0 & 1 \\ 1 & 1 & \dots & 0 & 1 \\ 0 & 1 & \dots & 0 & 1 \\ 1 & 1 & \dots & 0 & 0 \\ 0 & 0 & \dots & 0 & 1 \\ 0 & 0 & \dots & 0 & 0 \\ \dots & \dots & \dots \end{matrix}]$

si71_e

After the addition, we must get the values small again. This involves using the Flatten function, which performs an inverse bit decomposition, then a regular bit decomposition. Taking the values in the 0th column [20, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0], performing an inverse bit decomposition becomes the value 00101101110111010₂ + 20, resulting in 23,502. This value is then represented in bits from least to most significant bits 01110011110110100 and stored in the cipher matrix vertically. Note than when undecomposing column 1, the 20 is added as 20 1. The final cipher matrix is given as E(20), and the cipher matrix for 5 is also given.

$E (20) = [\begin{matrix} 0 & 0 & \dots & 1 & 0 \\ 1 & 0 & \dots & 1 & 1 \\ 1 & 0 & \dots & 0 & 1 \\ 1 & 1 & \dots & 1 & 1 \\ 0 & 1 & \dots & 1 & 0 \\ 0 & 0 & \dots & 1 & 1 \\ 1 & 0 & \dots & 1 & 1 \\ 1 & 1 & \dots & 1 & 1 \\ 1 & 1 & \dots & 1 & 1 \\ 1 & 0 & \dots & 0 & 0 \\ 0 & 0 & \dots & 0 & 1 \\ 1 & 1 & \dots & 0 & 1 \\ 1 & 1 & \dots & 0 & 1 \\ 0 & 1 & \dots & 0 & 1 \\ 1 & 1 & \dots & 0 & 0 \\ 0 & 0 & \dots & 0 & 1 \\ 0 & 0 & \dots & 0 & 0 \\ \dots & \dots & \dots \end{matrix}] E (5) = [\begin{matrix} 1 & 1 & \dots & 0 & 0 \\ 0 & 1 & \dots & 0 & 0 \\ 1 & 1 & \dots & 0 & 1 \\ 0 & 0 & \dots & 1 & 1 \\ 1 & 1 & \dots & 1 & 0 \\ 1 & 0 & \dots & 0 & 1 \\ 0 & 1 & \dots & 1 & 1 \\ 1 & 1 & \dots & 1 & 1 \\ 1 & 0 & \dots & 0 & 1 \\ 1 & 0 & \dots & 1 & 0 \\ 0 & 1 & \dots & 1 & 1 \\ 0 & 0 & \dots & 1 & 0 \\ 0 & 1 & \dots & 0 & 1 \\ 1 & 0 & \dots & 1 & 0 \\ 1 & 0 & \dots & 1 & 0 \\ 1 & 0 & \dots & 1 & 1 \\ 0 & 0 & \dots & 0 & 0 \\ \dots & \dots & \dots \end{matrix}]$

si72_e

With the encryption done, we can now perform the addition of the two cipher matrices. This is just a simple matrix addition operation. Note that if many operations are required, the result matrix will need to be flattened. If multiplication is performed on two cipher matrices. The result matrix will also need to be flattened. In this example, we do not require a flatten operation because the values are still small.

$E (20) + E (5) = [\begin{matrix} 1 & 1 & \dots & 1 & 0 \\ 1 & 1 & \dots & 1 & 1 \\ 2 & 1 & \dots & 0 & 2 \\ 1 & 1 & \dots & 2 & 2 \\ 1 & 2 & \dots & 2 & 0 \\ 1 & 0 & \dots & 1 & 2 \\ 1 & 1 & \dots & 2 & 2 \\ 2 & 2 & \dots & 2 & 2 \\ 2 & 1 & \dots & 1 & 2 \\ 2 & 0 & \dots & 1 & 0 \\ 0 & 1 & \dots & 1 & 2 \\ 1 & 1 & \dots & 1 & 1 \\ 1 & 2 & \dots & 0 & 2 \\ 1 & 1 & \dots & 1 & 1 \\ 2 & 1 & \dots & 1 & 0 \\ 1 & 0 & \dots & 1 & 2 \\ 0 & 0 & \dots & 0 & 0 \\ \dots & \dots & \dots \end{matrix}]$

si73_e

Because the q in this example is a power of 2, we can use the MPDec function to decrypt. Using MPDec allows us to start at column 15 and work back to column 0 to give the 16-bit answer. Column 15 contains the value for the 0th bit, and column 0 has the value for the 15th bit.

$\begin{array}{l} r e s u l t & = 0 \\ x & = \vec{v} \cdot C_{15} - (r e s u l t \times (1 ≪ 15)) \\ = 32802 - 0 \\ b i t & = m i n (32802, 65536 - 32802) > = a b s (32802 - (65536 ≫ 1)) \\ = 1 \\ r e s u l t & = r e s u l t + (b i t ≪ (15 - 15)) \\ r e s u l t & = 1 \\ x & = \vec{v} \cdot C_{14} - (r e s u l t \times (1 ≪ 14)) \\ = 16430 - 16384 \\ b i t & = m i n (46, 65536 - 46) > = a b s (46 - (65536 ≫ 1)) \\ = 0 \\ r e s u l t & = r e s u l t + (b i t ≪ (15 - 14)) \\ r e s u l t & = 1 \\ \dots \\ x & = \vec{v} \cdot C_{12} - (r e s u l t \times (1 ≪ 12)) \\ = 36849 - 4096 \\ b i t & = m i n (32753, 65536 - 32753) > = a b s (32753 - (65536 ≫ 1)) \\ = 1 \\ r e s u l t & = r e s u l t + (b i t ≪ (15 - 12)) \\ r e s u l t & = 9 \end{array}$

si74_e

$\begin{matrix} x & = \vec{v} \cdot C_{11} - (r e s u l t \times (1 ≪ 11)) \\ = 51252 - 18432 \\ b i t & = m i n (32820, 65536 - 32820) > = a b s (32820 - (65536 ≫ 1)) \\ = 1 \\ r e s u l t & = r e s u l t + (b i t ≪ (15 - 11)) \\ r e s u l t & = 25 \end{matrix}$

si9800_e

6 Homomorphic encryption in the cloud

Today real-world applications of FHE in the cloud are nigh-on impossible to find, due to the severe performance limitations of currently proposed schemes making them unattractive for cloud services to employ. Research for practical implementations of FHE are currently pursued by organizations such as IBM Research and Microsoft. But also by universities across the global, for example, Stanford and The University of Waikato (CROW, 2014). Until schemes are made practical, we will not see them in services exposed to the public. On the other hand, PHE has enabled some cloud services and systems to reap benefits. Some examples are:

• CryptDB (Popa et al., 2011) is a database privacy layer that explored the use of FHE for performing queries over encrypted data but opted do use a selection of techniques to perform different types of queries. For basic addition operations over integers, the Paillier cryptosystem (Paillier, 1999) was implemented, which offers PHE. When using Paillier, to perform the addition of two values x and y, the encrypted values are multiplied together, which when decrypted, is the equivalent of adding the unencrypted values together.

• Helios (Adida, 2008) is a cloud-based open-audit voting system, which as off version 2.0 uses homomorphic encryption to tally the votes (Adida et al., 2009). This allows all the votes to be submitted and tallied in an encrypted form, then only once the final votes have been cast and added to the tallies, is the result decrypted. The PHE scheme used is a variant of El Gamal, which was described in Section 4.2, Exponential El Gamal.

• Porticor (2014a), which was founded in 2010, is to the best of our knowledge one of the first commercial implementations of homomorphic encryption, which provides a secure cloud key management platform using PHE. The company states that FHE isn’t yet feasible for a real-world system (Porticor, 2014b), and that by only supporting a few computational operations you benefit from fast, reliable performance for your business-critical applications (Porticor, 2014b) while keeping the keys secure.

7 Future of homomorphic encryption and open issues

Homomorphic encryption in the cloud is still relatively young and is only being adopted at a slow rate. Even though FHE is currently not plausible to implement for real-world scenarios, there is no reason why PHE cannot offer cloud providers an extra level of security right now. Then in time migrate to FHE when schemes offer better performance. The cloud requires an increased level of security, and homomorphic encryption is a viable answer. Some cloud solutions have already realized this, like the samples in Section 6, but in the near future this will be more common across a far more diverse group of cloud applications and services.

As discussed throughout this chapter, there are still some problems with homomorphic encryption which will impact its future. For example, FHE can support more than a single operation. However, an open issue is that FHE also has limitations on supporting a wide range of operations/functions, even though this is the very definition of FHE. This is because two operations could be used to cancel each other out and make the security pointless. Supporting subtractions by an unencrypted value and comparing the encrypted value with zero would be one case. Because a malicious user can just subtract 1 until the encrypted value is zero, giving the answer. This leads to another issue, currently FHE is thought of as the perfect solution; however, it needs to be considered on an application by application basis. A one size fits all solution is not going to be as secure as a scheme which is designed for the application in mind. And finally, by having homomorphic encryption protect user information/data, it stops cloud services from learning information about them. This can stop targeted ads, selling anonymous user data and many other ways cloud services make money even though there is no cost to the end user. The issue is that even though users want to be more secure online, will they be willing to pay for the cloud service, or will they prefer the free, unsecured service instead? These are just some of the current issues that homomorphic encryption faces as it tries to become the future of security in the cloud.

8 Alternatives to homomorphic encryption

Cloud adoption by businesses handling sensitive data is slow because they cannot afford their data to be leaked. Be it their private cooperate data, or their customers data. This could be to protect their image, or because they are contractible obliged to keep the data confidential. While homomorphic encryption is a viable answer, there are other solutions which target this problem, and for some businesses could be a perfect fit for their business model or infrastructure.

A model widely adopted for securing cloud data is to provide a gateway between the cooperate network and the cloud (Salehi et al., 2014), which encrypts data before it leaves the network, and decrypts data from the cloud. This is similar to the Mega cloud service (Mega ltd, 2014) described early, however it is designed for enterprise, where Mega is intended more for personal use. That is not to say Mega cannot be used for enterprise, in fact it is perfect for small businesses, but the gateway solution is more powerful and flexible.

The general idea of using an encryption gateway is shown in Figure 7. This shows two computers within the company, used by Alice and Bob, that are connected to the companies internal network. Then any traffic leaving the internal network exists through what is known as the border router. However, there is a gateway that any data heading for the cloud service must go through. For example, Bob creates a files and wants to save it to the cloud. When the file is being saved, before it goes out onto the Internet, it must go through the gateway appliance. This gateway encrypts the file and forwards it to the cloud service via the border router. Then Alice wants to view this file, so she requests it from the cloud service. The encrypted file then goes back through the gateway appliance and is decrypted before reaching Alice. This guarantees that files are always encrypted before leaving the internal network to be stored on the cloud service. It also means that the company manages its own keys, unlike services like Dropbox. Alice and Bob are not affected by the encryption gateway, yet the companies data remains secure.

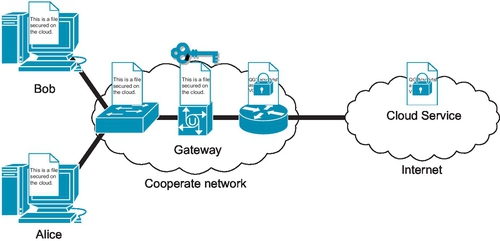
f05-07-9780128015957 — Figure 7 Encryption gateway

Encryption gateways can do more than just encrypting and decrypting data. RESeED (Salehi et al., 2014) allows searching over encrypted files in the cloud using regular expressions, by creating an index from the unencrypted files before they are encrypted and saved to the cloud. This device still has some limitations, such as the keys cannot be recovered off the device. So if the device has a fault and stops working, the encrypted data stored in the cloud is not recoverable. CipherCloud (2014) is another example of an encryption gateway, which supports cloud services such as Amazon Web Services, Gmail, and Office 365. These encryption gateway devices can be implemented into networks now, unlike solutions involving homomorphic encryption which are still years away from full-scale use.

9 Summary

This chapter has given an in-depth overview of homomorphic encryption schemes. It has provided proofs to show that the schemes can support homomorphic operations, while also providing examples to help make the mathematics and algorithms easier to understand. Homomorphic encryption will become more essential for cloud services as the performance of the schemes improves, allowing for more secure and trust worthy applications. Some cloud services are already benefiting from homomorphic encryption, and hopefully many more will follow.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 5: A guide to homomorphic encryption

Create new playlist

Sign In

Sign Up