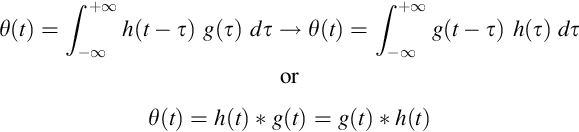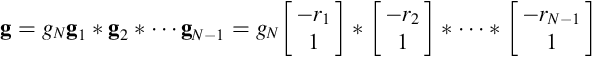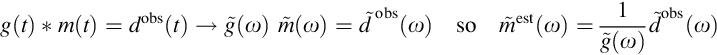7.1 Behavior sensitive to past conditions

Consider a scenario in which a thermometer is placed on the flame emitted by a burner (Figure 7.1A). The gas supplied to the burner varies with time, causing the heat, h(t), of the flame, measured in Watts (W), to fluctuate. An ideal thermometer would respond instantaneously to changes in heat, so the temperature, θ(t), measured in Kelvin (K), would track heat exactly, that is, θ(t) ∝ h(t). In this case, the past history of the heat has no effect on the temperature. The temperature now depends only on the heat at this moment. If, however, a metal plate is inserted into the flame between the burner and the thermometer (Figure 7.1B), the situation changes radically. The plate takes time to warm up or cool down. The thermometer does not immediately detect a change in heat; it now takes time to respond to changes. Even if the flame were turned off, the thermometer would not immediately detect the event. For a while, it would continue to register high temperatures that reflected the heat supplied by the flame in the past. In this case, θ(t) would not be proportional to h(t), although the two would still be related in some fashion.

The relationship between θ(t) and h(t) might be linear. Suppose that the time history of heat, h(t), caused temperature, θ(t). If the heat were doubled to 2h(t), we might find that the temperature also doubled, to 2θ(t). Moreover, if two flames were operated individually, with h₁(t) causing θ₁(t) and h₂(t) causing θ₂(t), we might find that the combined heat of the two flames, h₁(t) + h₂(t), caused temperature, θ₁(t) + θ₂(t).

Another aspect of this scenario is that only relative time matters. If we turn on the burner at 9 AM today, varying its heat, h(t), and recording temperature, θ(t), we might expect that the same experiment, if started at 9 AM tomorrow with the same h(t), would lead to exactly the same θ(t) (as long as we measured time from the start of each experiment). The underlying notion is that the physics of heat transport through the plate does not depend on day of the week.

This linear behavior can be quantified by assuming that both the heat, h(t), and temperature, θ(t), are time series; then writing the temperature, θ_i, at time, t_i, as a linear function of past and present heat, h_j, with j ≤ I,

$\begin{array}{c}\text{the data}=\text{a linear function of past values of another time series}\\ {\theta }_i=g_1{h}_i+g_2{h}_{i-1}+g_3{h}_{i-2}+g_4{h}_{i-3}+···\\ {\theta }_{i+1}=g_1{h}_{i+1}+g_2{h}_i+g_3{h}_{i-1}+g_4{h}_{i-2}+···\\ {\theta }_{i+2}=g_1{h}_{i+2}+g_2{h}_{i+1}+g_3{h}_i+g_4{h}_{i-1}+···\\ \text{or}{\theta }_i=\sum _{j=1}^{\infty }{g}_j{h}_{i-j+1}\text{or}\mathbf{\theta }=\mathbf{g}*\mathbf{h}\end{array}$

Note that each formula involves only current and past values of the heat. This is an expression of causality—the future cannot affect the present. The relationship embodied in Equation (7.1) is called a convolution, and is denoted by the asterisk, * (which does not mean multiplication when used in this context).

The gs in Equation (7.1) are coefficients that express the linear proportionality between heat and temperature. Note that exactly the same coefficients, g₁, g₂, g₃, g₄ … are used in all the formulas in Equation (7.1). This pattern implements the time-shift invariance that we discussed earlier—only the relative time between the application of the heat and the measurement of the temperature matters. Of course, this is only an idealization. If, for instance, the plate were oxidizing during the experiment, then its thermal properties would change with time and the set of coefficients that linked θ(t) to h(t) at one time would be different from that at another.

For Equation (7.1) to be of any practical use, we need to assume that only the recent past affects the present, that is, the coefficients, g₁, g₂, g₃, g₄, …, eventually diminish in magnitude, sufficiently for the sequence to be approximated as having a finite length. This notion implies that the underlying physics has a characteristic time scale over which equilibration occurs. Heat that was supplied prior to this characteristic response time has negligible effect on the current temperature. In the case of the flame in the laboratory, we would not expect that yesterday’s experiment would affect today’s experiment. The temperature of the plate has adequate time to equilibrate overnight.

As Equation (7.1) is linear, it can be arranged into a matrix equation of the form d = Gm:

$\begin{array}{c}\text{temperature}=\text{linear},\text{causal},\text{time}-\text{shift invariant function of heating}\\ \text{or}\\ \left[\begin{array}{c}{\theta }_1\\ {\theta }_2\\ {\theta }_3\\ \dots \\ {\theta }_N\end{array}\right]=\left[\begin{array}{ccccc}{g}_1& 0& 0& \dots & 0\\ g_2& g_1& 0& \dots & 0\\ g_3& g_2& g_1& \dots & 0\\ \dots & \dots & \dots & \dots & 0\\ g_N& g_{N-1}& g_{N-2}& \dots & g_1\end{array}\right]\left[\begin{array}{c}{h}_1\\ h_2\\ h_3\\ \dots \\ h_N\end{array}\right]\\ \text{or}\\ \mathbf{\theta }=\mathbf{Gh}\end{array}$

Note, however, that a problem arises because of the lack of observation before time, t₁. Here, we have simply ignored those values (or equivalently, assumed that they are zero). At time t₁, the best that we can write is θ₁ = g₁h₁, as we have no information about heating at earlier times.

When grouped together in a column vector, g, the coefficients are called a filter. A filter has a simple and important interpretation as the temperature time series that one would observe if a unit impulse (spike) of heat were applied: inserting h = [1, 0, 0, 0, …, 0]^T into Equation (7.2) yields θ = [g₁, g₂, g₃, …, g_N]^T. Thus, the time series, g, is often called the impulse response of the system (Figure 7.2). The equation, θ = g * h, can then be understood to mean that the output—the data, θ—equals the input—the heat, h—convolved with the impulse response of the system.

Each column, c⁽ⁱ⁾, of the matrix, G, in Equation (7.2) is the time series, g, which is shifted so that g₁ aligns with row i; that is, it is the response of an impulse at time t_i. If we read the matrix equation as θ = h₁c⁽¹⁾ + h₂c⁽²⁾ + h₃c⁽³⁾ +, …, then we can see that the temperature, θ, is built up by adding together many time-shifted versions of the impulse response, each with an amplitude governed by the amount of heat. In this view, the time series of heat is composed of a sequence of spikes and the time series for temperature is constructed by mixing together scaled versions of the impulse responses of each of those spikes (Figure 7.3).

So far, we have been examining a scenario in which the data vary with time. The same sort of behavior occurs in spatial contexts as well. Consider a scenario in which a spatially variable mass, h(x), of a pollutant is accidentally spilled on a highway. If, a year later, its concentration, θ(x), on the road surface is measured, it will not obey θ(x) ∝ h(x), because weather and traffic will have spread out the deposit. This type of scenario can also be represented with filters, but in this case they are noncausal, that is, the concentration at position x₀ is affected by deposition at both x ≤ x₀ and x > x₀:

$\begin{array}{c}\text{concentration}=\text{linear},\text{spatial}-\text{shift invariant function of mass at all positions}\\ \text{or}\\ {\theta }_i=···+g_{-2}{h}_{i+3}+g_{-1}{h}_{i+2}+g_0{h}_{i+1}+g_1{h}_i+g_2{h}_{i-1}+g_3{h}_{i-2}+g_4{h}_{i-3}+···\end{array}$

We need to assume that the filter coefficients (the gs) die away at both the left and the right so that the filter can be approximated by one of finite length.

7.2 Filtering as convolution

Equations (7.1) and (7.2) involve the discrete time series θ, h, and g. They can readily be generalized to the corresponding continuous case, for functions θ(t), h(t), and g(t), by viewing Equation (7.1) as the Riemann sum approximation of an integral. Then the heat, h(t), is related to the temperature, θ(t), by the convolution integral introduced in Section 6.11:

$\theta (t)={\int }_{-\infty }^{+\infty }h(t-\tau )g(\tau )d\tau \to \theta (t_i)\approx \Delta t\sum _{j=1}^{\infty }h(t_i-{\tau }_j)g({\tau }_j)\approx \Delta t\sum _{j=1}^{\infty }{h}_{i-j+1}{g}_j$

Note that the function, g(t) (as in Equation 7.3), and the time series, g (as in Equation 7.1) differ by a scaling factor: g_i = Δtg(t_i), which arises from the Δt in the Riemann summation.

The integral formulation is useful because it will allow us to deduce properties of filters that might not be so obvious from the matrix equation (Equation 7.2) that describes the discrete case. As an example, we note that an alternative form of the convolution can be derived from Equation (7.3) by the transformation of variables, t′ = (t−τ):

$\begin{array}{c}\theta (t)={\int }_{-\infty }^{+\infty }h(t-\tau )g(\tau )d\tau \to \theta (t)={\int }_{-\infty }^{+\infty }g(t-\tau )h(\tau )d\tau \\ \text{or}\\ \theta (t)=h(t)*g(t)=g(t)*h(t)\end{array}$

For causal filters, the function, g(t), is zero for times t < 0. In the first integral, g(t) is forward in time and h(t) is backward in time, and in the second integral, it is vice-versa. Just as with the discrete version of the convolution, the integral version is denoted by the asterisk: θ(t) = h(t) * g(t). The integral convolution is symmetric, in the sense that h(t) * g(t) = g(t) * h(t).

In Section 7.1, we interpreted the discrete convolution, θ = g * h, to mean that the output, θ, is the input, h, convolved with the impulse response of the system, g. We interpreted the column vector, g, as the impulse response because θ = g when the input is a spike, h = [1, 0, 0, 0, …, 0]^T. The same rationale carries over to the integral convolution. The equation θ(t) = g(t) * h(t) means that the output, θ(t), is the input, h(t), convolved with the impulse response of the system, g(t). We represent the spike with the Dirac function, δ(t) (see Section 6.6). Then θ(t) = g(t) when h(t) = δ(t) (as can be verified by inserting h(t) = δ(t) into Equation 7.4).

The alternative form of the integral convolution (Equation 7.4), when converted to a Riemann summation, yields the following matrix equation:

$\begin{array}{c}\text{output}=\text{linear function of impulse response}\\ \text{or}\\ \left[\begin{array}{c}{\theta }_1\\ {\theta }_2\\ {\theta }_3\\ \dots \\ {\theta }_N\end{array}\right]=\left[\begin{array}{ccccc}{h}_1& 0& 0& \dots & 0\\ h_2& h_1& 0& \dots & 0\\ h_3& h_2& h_1& \dots & 0\\ \dots & \dots & \dots & \dots & 0\\ h_N& h_{N-1}& h_{N-2}& \dots & h_1\end{array}\right]\left[\begin{array}{c}{g}_1\\ g_2\\ g_3\\ \dots \\ g_N\end{array}\right]\end{array}$

In Equation (7.2), the heat plays the role of the model parameters. If solved by least squares, this equation allows the reconstruction of the heat, using observations of temperature (with the impulse response assumed known, perhaps by deriving it from the fundamental physics). In Equation (7.4), the impulse response plays the role of the model parameters. If solved by least squares, this equation allows the reconstruction of the impulse response, using observations of temperature. In this case, the heat is assumed to be known, perhaps by measuring it, too. (Note, however, that the data kernel would then contain potentially noisy observations, which violates one of the underlying assumptions of least-squares methodology.)

As another example of the utility of the integral formulation of the convolution, note that we had previously derived a relation pertaining to the Fourier transform of a convolution (see Section 6.11). In this context, the Fourier transform of temperature, $\tilde{\theta }(\omega )$, is equal to the product of the transforms of the heat and the impulse response, $\tilde{\theta }(\omega )=\tilde{h}(\omega )\tilde{g}(\omega )$. As we will see later in the chapter, this relationship will prove useful in some computational scenarios.

7.3 Solving problems with filters

Here, we consider a more environmentally relevant temperature scenario, which, however, shares a structural similarity with the burner example. Suppose a thin underground layer generates heat (for example, because of a chemical reaction) and the temperature of the surrounding soil or sediment is measured. As with the burner example, the heat production, h(t), of the layer is unknown and the temperature, θ(t), of the soil at a distance, z = 1 meter, away from the layer is the observation. (Perhaps direct observation of the layer is contraindicated owing to concerns about release of hazardous chemicals). The impulse response, g(t), of such a layer is predicted on the basis of the physics of heat flow (Menke and Abbott, 1990, their Equation 6.3.4):

$g(t)=\frac{1}{\rho c_p}\frac{1}{\sqrt{2\pi }\sqrt{2\kappa t}}exp\left(-\frac{1}{2}\frac{z^2}{2\kappa t}\right)$

Note that the impulse response is proportional to a Normal curve with variance, 2κt, centered about z = 0. The equation involves three material constants, the density, ρ, of the soil, its heat capacity, c_p, and its thermal diffusivity, κ. Typical values for soil are ρ ≈ 1500 kg/m³, c_p ≈ 800 J/kg K, and κ ≈ 1.25 × 10⁻⁶ m²/s. Note that time is divided by the quantity (2κ)⁻¹ ≈ 4 × 10⁵ s, which defines a time scale of about 4.6 days for the heat transport process. Thus, observations made every few hours are sufficient to adequately measure variations of temperature. The quantity, ρc_p ≈ 1.2 × 10⁶ J/kg K, is the amount of heat, 1.2 million Joules in this case, that needs to be supplied to raise the temperature of a cubic meter of rock by 1 K. Thus, for example, a chemical reaction supplying heat at a rate of 1 W/m² will warm up a cubic meter of soil by 0.08 K in 1 day.

The impulse response (Figure 7.4A) is problematical in two respects: (1) Although it rapidly rises to its maximum value, it then decays only slowly, so a large number of samples are needed to describe it accurately. (2) It contains a factor of t^−1/2 that is singular at time, t = 0 although the function itself is zero, as the exponential factor tends to zero faster than the t^−1/2 factor blows up. Thus, the t = 0 value must be coded separately in MatLab:

M=1024;
N=M;
Dtdays = 0.5;
tdays = Dtdays*[0:N−1]’;
Dtseconds = Dtdays*3600*24;
tseconds = Dtseconds*tdays;
–––
g = zeros(M,1);
g(1)=0.0; % manually set first value
g(2:M) = (1/(rho*cp)) * (Dtseconds/sqrt(2*pi)) .* …
 (1./sqrt(2*kappa*tseconds(2:M))) .* …
 exp(−0.5*(zˆ2)./ (2*kappa*tseconds(2:M)));

(MatLab eda07_01)

Note that two column vectors of time are being maintained: tdays, with units of days and sampling of ½ day, which is used for plotting, and tseconds, with units of seconds, which is used in formulas that require SI units. Note also that the formula for the impulse response contains a factor of Δt not present in Equation (7.6), the scaling factor between the continuous and discrete forms of the convolution.

Given a heat production function, h(t) (Figure 7.4B), the temperature can be predicted by performing the convolution θ(t) = g(t) * h(t). In MatLab, one can build the matrix, G (Equation 7.2) and then perform the matrix multiplication:

G = toeplitz([g‘, zeros(N−M,1)’]’, [g(1), zeros(1,M−1)]);
qtrue2 = G*htrue;

(MatLab eda07_01)

Here we use the character, q, instead of θ, as MatLab variables need to have Latin names. An alternative (and preferable) way to perform the convolution is to use MatLab’s conv() (for convolve) function, which performs the convolution summation (Equation 7.1) directly:

tmp = conv(g, htrue);
qtrue=tmp(1:N);

The conv() function returns a column vector that is N + M − 1 samples long, which we truncate here to N samples.

When we attempt to solve this problem with least squares, MatLab reports that the solution,

hest1=(G’*G)(G’*qobs);

is ill-behaved. Apparently, more than one heat production, h^est, predicts the same—or nearly the same—observations. A quick fixup is to use the damped least squares solution, which adds prior information that h^est is small. The damped least squares solution is easy to implement. We merely add a factor of ε²I to G^TG:

GTG=G’*G;
GTGmax = max(max(abs(GTG)));
e2=1e−4*GTGmax;
hest1=(GTG+e2*ye(M,M))(G’*qobs);

(MatLab eda07_01)

The function eye() returns the identity matrix, I. In principle, the size of ε² should be governed by the ratio of the variance of the data to the variance of the prior information. However, we make no pretense here of knowing what this ratio might be. Instead, we take a more pragmatic approach, choosing a value for ε² (e2 in the script) by trial-and-error. In order to expedite the trial-and-error tuning, we write ε² as proportional to the largest element in G^TG, so that a small damping factor (10⁻⁴, in this case) corresponds to the case where ε²I is smaller than G^TG.

The damped least squares solution returns a heat production, h^est, that closely resembles the true heat production, h^true, when run on synthetic data with a low (0.1%) noise level (Figure 7.5). The situation is less favorable as the noise level is increased to 1% (Figure 7.6). Although the two peaks in heat production, h^true, can still be discerned in h^est, they are superimposed on a background of high amplitude, high-frequency fluctuations. The problem is that the impulse response, g(t), is a slowly varying function that tends to smooth out high-frequency variations in heat production. Thus, while the low-frequency components of the heat production are well constrained by the data, θ^obs, the high-frequency components are not. The damped least squares implements the prior information of smallness, but smallness does not discriminate between frequencies and, so, does little to correct this problem. As an alternative, we try prior information of smoothness, implemented with generalized least squares. As a smooth solution is one lacking high-frequency fluctuations, this method does much better (Figure 7.7). The MatLab code that created and solved the generalized least squares equation, Fm = f, is as follows:

e=10*max(max(abs(G)));
F=zeros(N + M,M);
f=zeros(N + M,1);
F(1:N,1:M)=G;
f(1:N)= qobs2;
H=toeplitz(e*[−2, 1, zeros(1,M−2)]′,… e*[−2, 1, zeros(1,M−2)]);
F(N+1:N+M,:)=H;
f(N+1:N+M)=0;
hest3 = (F′*F)(F′*f);

(MatLab eda07_02)

Here the matrix equation, f = Fm, is built up from its two component parts, the data equation, d = Gm and the prior information equation, h = Hm. As before, the quantity ε is in principle controlled by the square-root of the ratio of the variances of the data and the prior information. However, we again take a pragmatic approach and tune it by trial-and-error.

The above code makes rather inefficient use of computer memory. The matrix, G, is constructed from exactly one column-vector, g, so that almost all of the elements of the matrix are redundant. Similarly, the matrix, H, has only three nonzero diagonals, so most of its elements are zero. This wastefulness is not a problem for short filters, but the storage requirements and computation time quickly becomes unmanageable for long ones. The solution can be computed much more efficiently using MatLab’s bicg() function. As was described in Section 5.8, this function requires a user-supplied function that efficiently computes F^T(Fv) = G^T(Gv) + H^T(Hv), where v is an arbitrary vector. This function, which we call filterfun(), is analogous to (but more complicated than) the afun() function discussed in Section 5.8:

function y = filterfun(v,transp_flag)
global g H;
% get dimensions
N = length(g);
M = length(v);
[K, M2] = size(H);
temp1 = conv(g,v); % G v is of length N
a=temp1(1:N);
b=H*v; % H v is of length K
temp2=conv(flipud(g),a); % GT (G v) is of length M
a2 = temp2(N:N+M−1);
b2 = H′*b; % HT (H v) is of length M
% FT F v = GT G v+HT H v
y = a2 + b2;
return

(MatLab filterfun)

The quantities, g and H, are defined as global variables, in both this function and the main script, so MatLab recognizes these variables as referring to the same quantities in both scripts. The required vector, G^T(Gv) + H^T(Hv), is built up in five steps: (1) The quantity a = Gv is just the convolution of g and v, and is computed using the conv() function. (2) The quantity b = Hv is performed with a simple matrix multiplication and presumes that H is a sparse matrix. (3) The quantity a₂ = G^Ta is a convolution, but the matrix G^T differs from the normal convolution matrix G in three respects. First, the ordering of g in the columns of G^T is reversed (‘flipped’) with respect to its ordering in G. Second, G^T is upper-triangular, while G is lower-triangular. Third, G^T is M × N whereas G is N × M. Thus, modifications in procedure are required to compute a₂ = G^Ta using the conv() function. The order of the elements of g must be flipped before computing its convolution with a. Moreover, the results must be extracted from the last M elements of the column vector returned by conv() (not, as with Gv, from the first N elements). (4) The quantity b₂ = H^Tb is computed via normal matrix multiplication, again presuming that H is sparse. (5) The quantity a₂ + b₂ is computed by normal vector addition. In the main script, the quantities H, h, and f are created as follows:

clear g H;
global g H;
–––
e=10*max(abs(g));
K=M;
L=N + K;
H=spalloc(K,M,3*K);
for j = [2:K]
 H(j,j−1)=e;
end
for j = [1:K]
 H(j,j)=−2*e;
end
for j = [1:K−1]
 H(j,j+1)=e;
end
h=zeros(K,1);
f(1:N)=qobs2;
f(N+1:N+K)=h;

(MatLab eda07_03)

The spalloc() function creates a K × M sparse matrix H, capable of holding 3 K nonzero elements. Its three nonzero diagonals are set by the three for loops. The column vector h is zero. The column vector f is built up from θ^est and h. The quantity F^Tf is computed using the same methodology as in filterfun() and then both filterfun() and F^Tf are passed to the biconjugate gradient function, bicg():

temp=conv(flipud(g),qobs2);
FTfa = temp(N:N+M−1);
FTfb = H′*h;
FTf=FTfa+FTfb;
hest3=bicg(@filterfun,FTf,1e−10,3*L);

(MatLab eda07_03)

The solution provided by eda07_03 is the same as that provided by eda07_02, but the memory requirements are much less and the execution speed is much faster.

7.4 An example of an empirically-derived filter

At least during the summer when precipitation occurs as rain, we might expect that the discharge of a river is proportional to the amount of rain that falls on its watershed. However, rain does not instantaneously cause discharge but rather is delayed behind it because the rainwater needs time to work its way through soils and tributaries before it can register on a hydrographic station. This scenario is well suited to being described by a filter. River discharge d(t) is related to precipitation g(t) through the convolution relationship $d\left(t\right)=g\left(t\right)*r\left(t\right)$, where the filter r(t) respresents the response of the river’s drainage network to a pulse of rain.

We apply this idea to the Hudson River, using a dataset with daily measurements of river discharge and precipitation, both measured in the Albany, New York area:

We focus on a 101 day long time period in Summer 2004, which contains four signifcant storms and about a dozen days with more moderate precipitation (Figure 7.8 A). As expected, the observed river discharge (Figure 7.8 B, sold curve) rises after each storm and varies more smoothly than does precipitation.

We use the same Generalized Least Squares procedure described in Section 7.3 to estimate the filter r(t). Note, however, that in Section 7.3 we assumed that the output and filter were known and solved for the input, whereas here we are assuming that the input and output are known and are solving for the filter. The underlying equations are the same but the interpretation is different. In the current case, the data kernel G in the standard equation $\mathbf{Gm}=\mathbf{d}$ is built from the precipitation g(t), the model parameters m represent the unknown response r(t) and the data d respresent the discharge d(t). We expect that the response of the river to precipitation is relatvely short-lived, since a pulse of rain should drain away over the course of a few weeks, so this is a case where $M<N$. We also implement prior information of the form $\mathbf{H}\mathbf{m}=\mathbf{h}$. Motivated by the notion that r(t) decays smoothly with time, we use the prior information that $dr/dt\approx 0$, so H is a first difference matrix and $\mathbf{h}=0$. The results depend on the relative error in the data and prior inforation, $\epsilon ={\sigma }_d/{\sigma }_h$. We tune both M and ε by trial and error until we achieve a filter that is a good compromise between being smooth and fitting the data well.

As expected, the estimated filter r(t) (Figure 7.8 C) declines with time, reaching half of its starting value after about 10 days. The predicted discharge matches the observations, with two exceptions: the prediction misses the peak at day 707; and the prediction overestimates the peak at day 742. These errors may be due to our use of data from a single meteorological station to represent precipitation in the whole Hudson River watershed. A storm may miss the station or dump a disproportionate amount of rain on it. A more complicated model that allows for several stations might have worked better:

$d\left(t\right)=g^{\left(1\right)}\left(t\right)*r^{\left(1\right)}\left(t\right)+g^{\left(2\right)}\left(t\right)*r^{\left(2\right)}\left(t\right)+\dots$

Here g⁽ⁱ⁾(t) is the precipitation observed at the i-th meterological station and r⁽ⁱ⁾(t) is the resonse of the river discharge to a pulse of precipitation that falls near that station. This problem can be solved using Generalized Least Squares, but the bookkeeping needed to construct the equations $\mathbf{Gm}=\mathbf{d}$ and $\mathbf{H}\mathbf{m}=\mathbf{h}$ is challenging.

The river’s estimated response r(t) can be used to predict river discharge for past time periods in which meterterological data, but no hydrographic data, are available. This process, sometimes referred to as retrodiction, is often used to close gaps in the historical record of a river’s dischage.

7.5 Predicting the future

Suppose we approximate the present value of a time series, d, as a linear function of its past values:

$\begin{array}{c}\text{present value}=\text{linear function of past values}\\ \text{or}\\ d_i=p_2{d}_{i-1}+p_3{d}_{i-2}+p_4{d}_{i-3}+···+p_M{d}_{i-M-1}\end{array}$

where the p’s are coefficients. If we knew these coefficients, then we could predict the current value d_i using the past values d_i−1, d_i−2, d_i−3,… Equation (7.8) is just the convolution equation:

$p_1{d}_i+p_2{d}_{i-1}+p_3{d}_{i-2}+p_4{d}_{i-3}+···=0\text{with}{p}_1=-1\text{so}\mathbf{p}*\mathbf{d}=0$

Here, the prediction error filter p is the unknown. The convolution equation, p * d = 0, has the same form as the heat production equation, g * h = θ, that we encountered in the previous section, and the same generalized least squared methodology can be used to solve it. The prior information, p₁ = (−1), is assumed to be extremely certain and given much smaller variance than p * d = 0. In most practical cases, the future, insofar as it can be predicted, is a function primarily of the recent past. Thus, the prediction error filter is short and MatLab’s standard matrix algebra can be used in the computation of p (although the bicongugate gradient method remains a good alternative).

As an example, we compute the prediction error filter of the Neuse River Hydrograph (Figure 7.9) using both methods, obtaining, as expected, identical results in the two cases. We choose M = 100 as the length of p. The filter has most of its high amplitude in the first 3 of 4 days, suggesting that a shorter filter might produce a similar prediction. The small feature at a time of 42 days is surprising, because it indicates some dependence of the present on times more than a month in the past. However, degree to which this feature actually improves the prediction needs to be investigated before its significance can be understood.

The prediction error, e = p * d, is an extremely interesting quantity (Figure 7.10), because it contains the part of the present that cannot be predicted from the past; that is, the new information. In this case, we expect that the unpredictable part of the Neuse hydrograph is the pattern of storms, while the predictable part is response of the river to those storms. The narrow spikes in the error, e, which correlate to peaks in the discharge, seem to bear this out.

7.6 A parallel between filters and polynomials

Being able to perform convolutions of short time series by hand is very useful, so we describe here a simple method of organizing the calculation in the convolution formula (Equation 7.1). Suppose we want to calculate c = a * b, where both a and b are of length 3. We start by writing down a and b as row vectors, with a written backward and time and b written forward in time, with one sample of overlap. We obtain c₁ by multiplying column-wise, treating blanks as zeros:

$\begin{array}{ccccc}{a}_3& a_2& a_1& & \\ & & b_1& b_2& b_3\\ \times & & & & \\ & & a_1{b}_1& & \end{array}\stackrel{\text{yields}}{\to }{c}_1=a_1{b}_1$

To obtain c₂, we shift the top time series one sample to the right, multiply column-wise, and add the results:

$\begin{array}{cccc}{a}_3& a_2& a_1& \\ & b_1& b_2& b_3\\ \times & & & \\ & a_2{b}_1& a_1{b}_2& \end{array}\stackrel{\text{yields}}{\to }{c}_2=a_2{b}_1+a_1{b}_2$

To obtain c₃, we shift, multiply, and add again.

$\begin{array}{cccc}{a}_3& a_2& a_1& \\ b_1& b_2& b_3\\ \times & & & \\ a_3{b}_1& a_2{b}_2& a_1{b}_3& \end{array}\stackrel{\text{yields}}{\to }{c}_3=a_3{b}_1+a_2{b}_2+a_1{b}_3$

And so forth. The last nonzero element is c₅:

$\begin{array}{ccccc}& & a_3& a_2& a_1\\ b_1& b_2& b_3& & \\ \times & & & & \\ & & a_3{b}_3& & \end{array}\stackrel{\text{yields}}{\to }{c}_5=a_3{b}_3$

An astute reader might have noticed that this is exactly the same pattern of coefficients that one would obtain if one multiplied the polynomials:

$\begin{array}{c}a(z)=a_1+a_{2}z+a_3{z}^2\text{and}b(z)=b_1+b_{2}z+b_3{z}^2\\ \text{so}\\ c(z)=a(z)b(z)=a_1{b}_1+(a_2{b}_1+a_1{b}_2)z+\dots +a_3{b}_3{z}^4\end{array}$

We can perform a convolution by converting the time series to polynomials, as above, multiplying the polynomials, and forming a time series from the coefficients of the product. The process of forming the polynomial from a time series is trivial: multiply the first element by z⁰, the second by z¹, the third by z², and so forth, and add. The process of forming a time series from a polynomial is equally trivial: the first element is the coefficient of the z⁰ term, the second of the z¹ term, the third of the z² term, and so forth. Yet, while it is trivial to perform, this process turns out to be extremely important, because it allows us to apply a very large body of knowledge about polynomials to issues associated with filters and convolutions. Because of its importance, the process of forming a polynomial from a time series is given a special name, the z-transform.

7.7 Filter cascades and inverse filters

Consider a polynomial g(z) of order N − 1 that represents a filter, g, of length, N. According to the Fundamental Theorem of Algebra, the polynomial can be written as the product of its N − 1 factors:

$g(z)=g_1+g_{2}z+\dots g_N{z}^{N-1}=g_N(z-r_1)(z-r_2)\dots (z-r_{N-1})$

where the rs are the roots of the polynomial (that is, the zs for which the polynomial is zero) and the factor of g_N acts as an overall normalization. Thus the filter, g, can be written as a cascade of convolutions of N − 1 length-two filters:

$\mathbf{g}=g_N{\mathbf{g}}_1*{\mathbf{g}}_2*\dots {\mathbf{g}}_{N-1}=g_N\left[\begin{array}{c}-r_1\\ 1\end{array}\right]*\left[\begin{array}{c}-r_2\\ 1\end{array}\right]*\dots *\left[\begin{array}{c}-r_{N-1}\\ 1\end{array}\right]$

Thus, any long filtering operation can be broken down into a sequence of many small ones. (Note, however, that some of the length-two time series may be complex, as the roots of a polynomial are, in general, complex).

The goal of the temperature scenario in Section 7.3 was to solve an equation of the form g * m = d^obs for m. In that section, we used generalized least squares to solve the equivalent matrix equation Gm = d. Another way to solve the problem is to construct an inverse filter g^inv such that g^inv * g = [1, 0, 0, …, 0]^T. Then g * m = d^obs can be solved by convolving each side of the equation by the inverse filter: m^est = g^inv * d^obs.

The z-transform of the inverse filter is evidently g^inv(z) = 1/g(z), because then g(z)g^inv(z) = 1. Note, however, that the function 1/g(z) is not a polynomial, so the method of inverting the z-transform and thereby converting the function, 1/g(z), back to the time series, g^inv, is unclear. Suppose, however, that g(z) was written as a product of its factors (z − r_i), as in Equation (7.15). Then, the inverse filter is the product of the reciprocal of each of these binomials:

$g^{\text{inv}}(z)=\frac{1}{g_N}{(z-r_1)}^{-1}{(z-r_2)}^{-1}\dots {(z-r_{N-1})}^{-1}$

Each of these reciprocals can now be expanded using the binomial theorem:

${(z-r_i)}^{-1}=(-r_i^{-1}){\left(1-\frac{z}{r_i}\right)}^{-1}=(-r_i^{-1})(1+r_i^{-1}z+r_i^{-2}{z}^2+r_i^{-3}{z}^3\dots )$

Writing the same result in terms of time series

${\left[\begin{array}{c}-r_i\\ 1\end{array}\right]}^{\text{inv}}=(-r_i^{-1})\left[\begin{array}{c}1\\ r_i^{-1}\\ r_i^{-2}\\ \dots \end{array}\right]$

Thus, the inverse of a length-two filter is infinite in length. This is not a problem, as long as the elements of the inverse filter die away quickly, which happens when $\left|r_i^{-1}\right|<1$ or, equivalently, $\left|r_i\right|>1$.

Each length-two filter in the cascade for g turns into an infinite length filter in the cascade for the inverse filter, g^inv. Therefore, while g is a length-N filter, g^inv is an infinite length filter. Any attempt (as in Section 7.3) to find a finite-length version of g^inv is at best approximate, and can really succeed only when all the roots of g(z) satisfy $\left|r_i\right|>1$. Nevertheless, the approximation is quite good in some cases. In the lingo of filter theory, the roots, r_i, must all lie outside the unit circle, $|r_i{|}^2=1$, for the inverse filter to exist. In this case, the filter, g, is said to be minimum phase.

This method can be used to construct inverse filters of short filters (Figure 7.11). The first step is to find the roots of the polynomial associated with the filter, g:

% find roots of g
r = roots(flipud(g));

(MatLab eda07_07)

Here, the filter, g, is of length N. Note that the order of elements in g are flipped, because MatLab’s root() function expects the highest order coefficient first. Then a length, Ni, approximation of the inverse filter is computed:

% construct inverse filter, gi, of length Ni
Ni = 50;
gi = zeros(Ni,1);
gi(1)=1/gN;
% filter cascade, one filter per loop
for j = [1:N−1]
 % construct inverse filter of a length−2 filter
 tmp = zeros(Ni,1);
 tmp(1) = 1;
 for k = [2:Ni]
 tmp(k) = tmp(k−1)/r(j);
 end
 tmp = −tmp/r(j);
 gi = conv(gi,tmp);
 gi=gi(1:Ni);
end
% delete imaginary part (which should be zero)
gi = real(gi);

(MatLab eda07_07)

First, the inverse filter is initialized to a spike of amplitude 1/gN. Then, each component filter (Equation 7.18) of the cascade (Equation 7.17) is constructed and convolved into gi. After each convolution, the results are truncated to length Ni. Finally, the imaginary part of the inverse filter, which is zero up to round-off error, is deleted.

As an aside, we mention that Fourier transforms can also be used to solve the equation g * m = d and to understand the inverse filter. As the Fourier transform of a convolution is the product of the Fourier transforms, we have

$g(t)*m(t)=d^{\text{obs}}(t)\to \tilde{g}(\omega )\tilde{m}(\omega )={\tilde{d}}^{\text{obs}}(\omega )\text{so}{\tilde{m}}^{\text{est}}(\omega )=\frac{1}{\tilde{g}(\omega )}{\tilde{d}}^{\text{obs}}(\omega )$

This equation elucidates the problem of the nonuniqueness of the solution, m^est(t). If the Fourier transform of the impulse response, $\tilde{g}({\omega }_0)$, is zero for any value of frequency, ω₀, then this spectral hole hides the corresponding value of $\tilde{m}({\omega }_0)$, in the sense that the data, $\tilde{d}({\omega }_0)$, does not depend on it. Thus, ${\tilde{m}}^{\text{est}}(\omega )$ is nonunique; its value at frequency ω₀ is arbitrary. In practice, even nonzero but small values of $\tilde{g}(\omega )$ are problematical, as corresponding large values of ${\tilde{g}}^{\text{inv}}(\omega )$ amplify noise in the data, ${\tilde{d}}^{\text{obs}}(\omega )$, and lead to a noisy solution, m^est(t). We encountered this problem in the heat production scenario of Section 7.3. As the impulse response (Figure 7.4A) is a very smooth function, its Fourier transform has low amplitude at high frequencies. This leads to high-frequency noise present in the data being amplified during the solution process.

Equation (7.20) also implies that the Fourier transform of the inverse filter is ${\tilde{g}}^{\text{inv}}(\omega )=1/\tilde{g}(\omega )$; that is, the Fourier transform of the inverse filter is the reciprocal of the Fourier transform of the filter. A problem arises, however, with spectral holes, as ${\tilde{g}}^{\text{inv}}(\omega )$ is singular at those frequencies. Because of problems associated with spectral holes, the spectral division method defined by Equation (7.20) is not usually a satisfactory method for computing the solution to g * m = d or for constructing the inverse filter. The generalized least squares method, based on solving the matrix form of the equation g * g^inv = [1, 0, 0, …, 0]^T, usually performs much better, as prior information can be used to select a well-behaved solution.

7.8 Making use of what you know

In the standard way of evaluating a convolution equation (e.g., θ = g * h, as in Equation 7.1), we compute the elements of θ in sequence, θ₁, θ₂, θ₃, … but independently of one another, even though we know the value of θ₁ before we start to calculate θ₂, know the values of θ₁ and θ₂ before we start to calculate θ₃, and so forth. The known but unused values of θ are a source of information that can be put to work.

Suppose that the convolution equation (Equation 7.1) is modified by adding a second summation:

${\theta }_i=\sum _{j=1}^{\infty }{g}_j{h}_{i-j+1}=\sum _{j=1}^N{u}_j{h}_{i-j+1}-\sum _{j=2}^M{v}_j{\theta }_{i-j+1}$

Here, u and v are filters of length N and M, respectively, whose relationships to g are yet to be determined. Note that the last summation starts at j = 2, so that only previously calculated elements of θ are employed. The introduction of past values of θ into the convolution equation is called recursion and filters that include recursion (i.e., include the last term in Equation 7.21) are called Infinite Impulse Response (IIR) filters. Filters that omit recursion (i.e., omit the last term in Equation 7.21) are called Finite Impulse Response (FIR) filters. If we define v₁ = 1, then we can rewrite Equation (7.21) as:

$\sum _{j=1}^N{u}_j{h}_{i-j+1}=\sum _{j=1}^M{v}_j{\theta }_{i-j+1}\text{or}\mathbf{u}*\mathbf{h}=\mathbf{v}*\mathbf{\theta }$

Recall that we began this discussion by seeking an efficient way to evaluate θ = g * h. Equation (7.22) implies θ = v^inv * u * h and so, if we could find filters u and v so that g = v^inv * u, then Equation (7.21) would be equivalent to θ = g * h. However, it will only improve efficiency if the two filters, u and v, are shorter than g. What makes this possible is the fact that even a very short filter, v, has an infinitely long inverse filter, v^inv.

In order to illustrate how an IIR filter can be designed, we examine the following simple case:

$\mathbf{g}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\left[1,\frac{1}{2},\frac{1}{4},\frac{1}{8},\dots \right]}^T$

Here, g is a causal smoothing filter. It has only positive coefficients that rapidly decrease with time and the sum of its elements is unity. Each element of θ is dependent on just the current value and recent past of h. The choices

$\mathbf{u}={[\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,0]}^T\text{and}\mathbf{v}={[1,-v_2]}^T\text{with}{v}_2=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$

work in this case, as v^inv = [1, v₂, v₂², …]^T = [1, ½, ¼, …]^T (see Equation 7.19). The generalized convolution equation (Equation 7.21) then reduces to

${\theta }_i=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.h_i+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\theta }_{i-1}$

which involves very little computation, indeed! This filter is implemented in MatLab as follows Figure 7.11):

q1=zeros(N,1);
q1(1)=0.5*h1(1);
for j=[2:N]
 q1(j)=0.5*(h1(j) + q1(j−1));
end

(MatLab eda07_08)

Here, h1 is the original time series and q1 is the smoothed version. Both are of length N. MatLab provides a function, filter(), that implements Equation (7.20) and can be used as an alternative to the for loop (Figure 7.12):

u=[0.5,0]′;
v=[1.0,−0.5];
q1 = filter(u, v, h1);

(MatLab eda07_09)

We will return to the issue of IIT filter design in Chapter 9.

Problems

7.1 Calculate by hand the convolution of a = [1, 1, 1, 1]^T and b = [1, 1, 1, 1]^T. Comment on the shape of the function c = a * b.

7.2 Plot the prediction error, E, of the prediction of the Neuse River hydrograph as a function of the length, N, of the prediction error filter. Is a point of diminishing returns reached?

7.3 What is the z-transform of a filter that delays a time series by one sample?

7.4 Note that any filter, g, with g₁ = 0 is a nonstationary phase, as its z-transform is exactly divisible by z and so has a root at z = 0 that is not outside the unit circle. A simple way to change a stationary phase filter into one that is nonstationary phase filter is to decrease the size of its first element towards zero. Modify script eda07_07 to examine what happens to the inverse filter when you decrease the size of g₁ towards zero in a series of steps. Increasing Ni might make the behavior clearer.

7.5 Generalize the recursive filter developed at the end of Section 7.8 for the case g(t) ∝ exp(−t/τ), that is, a smoothing filter of unit area and arbitrary width, τ. Start by writing g_j ∝ [1, c, c², …]^T with c = exp(−Δt/τ).

7.6 Use your result from the previous problem to smooth the Neuse River hydrograph by with a sequence of filters, g(t) ∝ exp(−t/τ), with τ = 5, 15 and 40 days. Plot your results and comment on the effect of filtering on the appearance of the hydrograph.