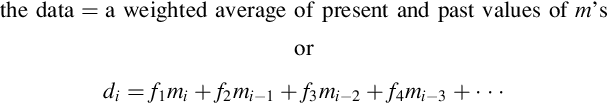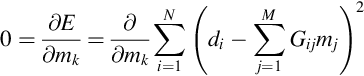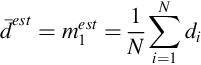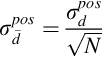4.1 Quantitative models, data, and model parameters

The purpose of any data analysis is to gain knowledge through a systematic examination of the data. While knowledge can take many forms, we assume here that it is primarily numerical in nature. We analyze data to infer, as best we can, the values of numerical quantities—model parameters, in the parlance of this book. The inference process is possible because the data and model parameters are linked through a quantitative model. In the very broadest sense, the model parameters and the data are linked though a functional relationship:

$\begin{array}{c}\text{the data}=\text{a function of the model parameters}\\ \text{or}\\ \begin{array}{l}{d}_1=g_1(m_1,m_2,\mathrm{\dots },m_M)\\ d_2=g_2(m_1,m_2,\mathrm{\dots },m_M)\\ ⋮\\ d_N=g_N(m_1,m_2,\mathrm{\dots },m_M)\end{array}\\ \\ \text{or}\\ d_i=g_i(m_1,m_2,\mathrm{\dots },m_M)\\ \text{or}\\ \mathbf{d}=\mathbf{g}(\mathbf{m})\end{array}$

The data are represented by a length-N vector, d, and the model parameters by a length-M column vector, m. The function, g(m), that relates them is called the quantitative model. We may find, however, that no prediction of the model, regardless of the value of m that is used, matches the observations, d^obs, because of observational noise. Then, Equation (4.1) must be understood in a more abstract sense: if we knew the true values, m^true, of the model parameters, then we could make predictions, d^pre, of data that would match those obtained through noise-free observations, were such observations possible. Alternatively, we could write Equation (4.1) as d = g(m) + n, where the length-N column vector, n, represents measurement noise.

The function, d = g(m), can be arbitrarily complicated. However, in very many important cases it is either linear or can be approximated as linear. In those cases, Equation (4.1) simplifies to

$\begin{array}{c}\text{the data}=\text{a linear function of the model parameters}\\ \text{or}\\ d_i=G_{i1}{m}_1+G_{i2}{m}_2+···+G_{iM}{m}_M\\ \text{or}\\ \begin{array}{l}{d}_1=G_{11}{m}_1+G_{12}{m}_2+···+G_{1M}{m}_M\\ d_2=G_{21}{m}_1+G_{22}{m}_2+···+G_{2M}{m}_M\\ ⋮\\ d_N=G_{N1}{m}_1+G_{N2}{m}_2+···+G_{NM}{m}_M\end{array}\\ \text{or}\\ \left[\begin{array}{c}{d}_1\\ d_2\\ d_3\\ ···\\ d_N\end{array}\right]=\left[\begin{array}{ccccc}{G}_{11}& G_{12}& G_{13}& ···& G_{1M}\\ G_{21}& G_{22}& G_{23}& ···& G_{2M}\\ G_{31}& G_{32}& G_{33}& ···& G_{3M}\\ ···& ···& ···& ···& ···\\ G_{N1}& G_{N2}& G_{N3}& ···& G_{NM}\end{array}\right]\left[\begin{array}{c}{m}_1\\ m_2\\ m_3\\ ···\\ m_M\end{array}\right]\\ \text{or}\\ \mathbf{d}=\mathbf{Gm}\end{array}$

Here, the matrix, G, contains the coefficients of the linear relationship. It relates N data to M model parameters and so is N × M. The matrix, G, is often called the data kernel. In most typical cases, N ≠ M, so G is not a square matrix (and, consequently, has no inverse).

Equation (4.2) can be used in several complementary ways. If the model parameters are known—let us call them m^est—then Equation (4.2) can be evaluated to provide a prediction of the data:

${\mathbf{d}}^{\text{pre}}=\mathbf{G}{\mathbf{m}}^{\text{est}}$

Alternatively, if the data are observed—we call them d^obs—then Equation (4.2) can be solved to determine an estimate of the model parameters:

$\text{find the}{\mathbf{m}}^{\text{est}}\text{so that}{\mathbf{d}}^{\text{obs}}\approx \mathbf{G}{\mathbf{m}}^{\text{est}}$

Note that an estimate of the model parameters will not necessarily equal their true value, that is, m^est ≠ m^true because of observational noise.

4.2 The simplest of quantitative models

The simplest linear model is that in which the data are all equal to the same constant. This is the case of repeated observations, in which we make the same measurement N times. It corresponds to the equation

$\begin{array}{c}\text{the data}=\text{a constant}\\ \text{or}\\ \left[\begin{array}{c}{d}_1\\ d_2\\ d_3\\ ⋮\\ d_N\end{array}\right]=\left[\begin{array}{c}1\\ 1\\ 1\\ ⋮\\ 1\end{array}\right][m_1]\\ \text{or}\\ \mathbf{d}=\mathbf{Gm}\end{array}$

Here, the constant is given by the single model parameter, m₁ so that M = 1. The data kernel is the matrix, G = [1, 1, 1, …, 1]^T. In practice, N observations of the same thing actually would result in N different ds because of observational error. Thus, Equation (4.5) needs to be understood in the abstract sense: if we knew the value of the constant, m₁, and if the observations, d, were noise-free, then they would all satisfy d_i = m₁. Alternatively, we could write Equation (4.5) as d = Gm + n, where the length-N column vector, n, represents measurement noise.

Far from being trivial, this one-parameter model is arguably the most important of all the models in data analysis. It is equivalent to the idea that the data scatter around an average value. As we will see later on in this chapter, when the observational data are Normally distributed, a good estimate of the model parameter, m₁, is the sample mean, $\overline{d}$:

$m_1^{\text{est}}=\overline{d}=\frac{1}{N}\sum _{i=1}^N{d}_i$

4.3 Curve fitting

Another simple but important model is the idea that the data fall on—or scatter around—a straight line. The data are assumed to satisfy the relationship

$\begin{array}{c}\text{the data}=\text{a linear function of}x\\ \text{or}\\ d_i=m_1+m_2{x}_i\\ \text{or}\\ \left[\begin{array}{c}{d}_1\\ d_2\\ d_3\\ ⋮\\ d_N\end{array}\right]=\left[\begin{array}{cc}1& x_1\\ 1& x_2\\ 1& x_3\\ ⋮& ⋮\\ 1& x_N\end{array}\right]\left[\begin{array}{c}{m}_1\\ m_2\end{array}\right]\\ \text{or}\\ \mathbf{d}=\mathbf{Gm}\end{array}$

Here, m₁ is the intercept and m₂ is the slope of the line. In order for this relationship to be linear in form, the data kernel, G, must not contain any data or model parameters. Thus, we must assume that the x's are neither model parameters nor data, but rather auxiliary parameters whose values are exactly known. This may be an accurate, or nearly accurate, assumption in cases where the xs represent distance or time as, compared to most other types of data, time and distance can be determined so accurately as to have negligible error. In other cases, it can be a poor assumption.

A MatLab script that creates this data kernel is

M=2;
G=zeros(N,M);
G(:,1)=1;
G(:,2)=x;

(MatLab eda04_01)

where x is a column vector of length M of x's. Note the call to zeros(N,M), which creates a matrix with N rows and M columns. Strictly speaking, this command is not necessary, but it helps in bug detection.

The formula for a straight line can easily be generalized to any order polynomial, by simply adding additional model parameters that represent the coefficients of higher powers of x's and by adding corresponding columns to the data kernel containing powers of the x's. For example, the quadratic case has M = 3 model parameters, m = [m₁, m₂, m₃]^T, and the equation becomes

$\begin{array}{c}\text{the data}=\text{a quadratic function of}x\text{'}\text{s}\\ \text{or}\\ d_i=m_1+m_2{x}_i+m_3{x_i}^2\\ \text{or}\\ \left[\begin{array}{c}{d}_1\\ d_2\\ d_3\\ ⋮\\ d_N\end{array}\right]=\left[\begin{array}{ccc}1& x_1& {x_1}^2\\ 1& x_2& {x_2}^2\\ 1& x_3& {x_3}^2\\ ⋮& ⋮& ⋮\\ 1& x_N& {x_N}^2\end{array}\right]\left[\begin{array}{c}{m}_1\\ m_2\\ m_3\end{array}\right]\\ \text{or}\\ \mathbf{d}=\mathbf{Gm}\end{array}$

A MatLab script that creates this data kernel is

M=3;
G=zeros(N,M);
G(:,1)=1;
G(:,2)=x;
G(:,3)=x.ˆ2;

(MatLab eda04_02)

where x is a column vector of length M of x's. Note the use of the element-wise multiplication, x.ˆ2, which creates a column vector with elements, x_i². The data kernel for the case of a polynomial of arbitrary degree is computed as

G=zeros(N,M);
G(:,1) = 1; % handle first column individually
for i = [2:M] % loop over remaining columns
 G(:,i) = x .ˆ (i−1);
end

(MatLab eda04_03)

This method is not limited to polynomials; rather, it can be used to represent any curve of the form

$\begin{array}{c}\text{the data}=\text{a sum of functions},f,\text{of known form}\\ \text{or}\\ d_i=m_1{f}_1(x_i)+m_2{f}_2(x_i)+···+m_M{f}_M(x_i)\\ \text{or}\\ \left[\begin{array}{c}{d}_1\\ d_2\\ d_3\\ ⋮\\ d_N\end{array}\right]=\left[\begin{array}{cccc}{f}_1(x_1)& f_2(x_1)& ···& f_M(x_1)\\ f_1(x_2)& f_2(x_2)& ···& f_M(x_2)\\ f_1(x_3)& f_2(x_3)& ···& f_M(x_3)\\ ⋮& ⋮& ⋮& ⋮\\ f_1(x_N)& f_2(x_N)& ···& f_M(x_N)\end{array}\right]\left[\begin{array}{c}{m}_1\\ m_2\\ ⋮\\ m_M\end{array}\right]\end{array}$

Note that the model parameter, m_j, represents the amount of the function, f_j, in the representation of the data.

One important special case—called Fourier analysis—is the modeling of data with a sum of cosines and sines of different wavelength, λ_i:

$\begin{array}{c}\text{the data}=\text{a sum of cosines and sines}\\ \text{or}\\ d_i=m_1\text{cos}\left(\frac{2\pi x_i}{{\lambda }_1}\right)+m_2\text{sin}\left(\frac{2\pi x_i}{{\lambda }_1}\right)+\mathrm{···}+m_{M-1}\text{cos}\left(\frac{2\pi x_i}{{\lambda }_{M/2}}\right)+m_M\text{sin}\left(\frac{2\pi x_i}{{\lambda }_{M/2}}\right)\\ \text{or}\mathbf{d}=\mathbf{Gm}\text{with}\\ \mathbf{G}=\left[\begin{array}{ccccccc}\text{cos}\left(\frac{2\pi x_1}{{\lambda }_1}\right)& \text{sin}\left(\frac{2\pi x_1}{{\lambda }_1}\right)& \text{cos}\left(\frac{2\pi x_1}{{\lambda }_2}\right)& \text{sin}\left(\frac{2\pi x_1}{{\lambda }_2}\right)& \mathrm{···}& \text{cos}\left(\frac{2\pi x_1}{{\lambda }_{M/2}}\right)& \text{sin}\left(\frac{2\pi x_1}{{\lambda }_{M/2}}\right)\\ \text{cos}\left(\frac{2\pi x_2}{{\lambda }_1}\right)& \text{sin}\left(\frac{2\pi x_2}{{\lambda }_1}\right)& \text{cos}\left(\frac{2\pi x_2}{{\lambda }_2}\right)& \text{sin}\left(\frac{2\pi x_2}{{\lambda }_2}\right)& \mathrm{···}& \text{cos}\left(\frac{2\pi x_2}{{\lambda }_{M/2}}\right)& \text{sin}\left(\frac{2\pi x_2}{{\lambda }_{M/2}}\right)\\ \text{cos}\left(\frac{2\pi x_3}{{\lambda }_1}\right)& \text{sin}\left(\frac{2\pi x_3}{{\lambda }_1}\right)& \text{cos}\left(\frac{2\pi x_3}{{\lambda }_2}\right)& \text{sin}\left(\frac{2\pi x_3}{{\lambda }_2}\right)& \mathrm{···}& \text{cos}\left(\frac{2\pi x_3}{{\lambda }_{M/2}}\right)& \text{sin}\left(\frac{2\pi x_3}{{\lambda }_{M/2}}\right)\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ \text{cos}\left(\frac{2\pi x_N}{{\lambda }_1}\right)& \text{sin}\left(\frac{2\pi x_N}{{\lambda }_1}\right)& \text{cos}\left(\frac{2\pi x_N}{{\lambda }_2}\right)& \text{sin}\left(\frac{2\pi x_N}{{\lambda }_2}\right)& \mathrm{···}& \text{cos}\left(\frac{2\pi x_N}{{\lambda }_{M/2}}\right)& \text{sin}\left(\frac{2\pi x_N}{{\lambda }_{M/2}}\right)\end{array}\right]\end{array}$

As we will discuss in more detail in Section 6.1, we normally choose pairs of sines and cosines of the same wavelength, λ_i. The total number of model parameters is M, which represents the amplitude coefficients of the M/2 sines and M/2 cosines.

A MatLab script that creates this data kernel is

G=zeros(N,M);
Mo2=M/2;
for i = [1:Mo2]
 ic = 2*i−1;
 is = 2*i;
 G(:,ic) = cos( 2*pi*x/lambda(i) );
 G(:,is) = sin( 2*pi*x/lambda(i) );
end

(MatLab eda04_04)

This example assumes that the column vector of wavelengths, lambda, omits the lambda=0 case, as it would cause a division-by-zero error. We use the variable wavenumber, k = 2π/λ, instead of wavelength, λ, in subsequent discussions of Fourier sums to avoid this problem.

Gray-shaded versions of the polynomial and Fourier data kernels are shown in Figure 4.1.

4.4 Mixtures

Suppose that we view the data kernel as a concatenation of its columns, say c^(j) (Figure 4.2):

$\begin{array}{c}\text{the data kernel}=\text{a concatenation of column}-\text{vectors}\\ \text{or}\\ G=\left[\begin{array}{ccc}{G}_{11}& G_{12}& G_{13}\\ G_{21}& G_{22}& G_{23}\\ G_{31}& G_{32}& G_{33}\end{array}\right]=\left[\begin{array}{ccc}\left[\begin{array}{c}{G}_{11}\\ G_{21}\\ G_{31}\end{array}\right]& \left[\begin{array}{c}{G}_{12}\\ G_{22}\\ G_{32}\end{array}\right]& \left[\begin{array}{c}{G}_{13}\\ G_{23}\\ G_{33}\end{array}\right]\end{array}\right]=[\begin{array}{ccc}{\mathbf{c}}^{(1)}& {\mathbf{c}}^{(2)}& {\mathbf{c}}^{(3)}\end{array}]\end{array}$

Then the equation d = Gm can be understood to mean that d is constructed by adding together the columns of G in proportions specified by the model parameters, m_j:

$\begin{array}{c}\text{the data}=\text{a linear mixture of column}-\text{vectors}\\ \text{or}\\ \mathbf{d}=m_1{\mathbf{c}}^{(1)}+m_2{\mathbf{c}}^{(2)}+m_3{\mathbf{c}}^{(3)}+\dots +m_M{\mathbf{c}}^{(M)}\\ \text{or}\\ \mathbf{d}=[\begin{array}{ccc}{\mathbf{c}}^{(1)}& {\mathbf{c}}^{(2)}& {\mathbf{c}}^{(3)}\end{array}]\mathbf{m}\end{array}$

This summation can be thought of as a mixing process. The data are a mixture of the columns of the data kernel. Each model parameter represents the amount of the corresponding column-vector in the mixture. Indeed, it can be used to represent literal mixing. For example, suppose that a city has M major sources of pollution, such as power plants, industrial facilities, vehicles (taken as a group), and so on. Each source emits into the atmosphere its unique combination of N different pollutants. An air sample taken from an arbitrary point within the city will then contain a mixture of pollutants from these sources:

$\begin{array}{c}\text{pollutants in air}=\text{mixture of sources}\\ \text{or}\\ \left[\begin{array}{c}\text{pollutant}1\text{in air}\\ \text{pollutant}2\text{in air}\\ \text{pollutant}3\text{in air}\\ ⋮\\ \text{pollutant}N\text{in air}\end{array}\right]=m_1\left[\begin{array}{c}\text{pollutant}1\text{in source}1\\ \text{pollutant}2\text{in source}1\\ \text{pollutant}3\text{in source}1\\ ⋮\\ \text{pollutant}N\text{in source}1\end{array}\right]+···+m_M\left[\begin{array}{c}\text{pollutant}1\text{in source}M\\ \text{pollutant}2\text{in source}M\\ \text{pollutant}3\text{in source}M\\ ⋮\\ \text{pollutant}N\text{in source}M\end{array}\right]\end{array}$

where the model parameters, m_j, represent the contributions of the j-th source to the pollution at that particular site. This equation has the form of Equation (4.12), and so can be put into the form, d = Gm, by concatenating the column vectors associated with the sources into a matrix, G. Note that this quantitative model assumes that the pollutants from each source are conservative, that is, the pollutants are mixed as a group, with no individual pollutant being lost because of degradation, slower transport, and so on.

4.5 Weighted averages

Suppose that we view the data kernel as a column vector of its rows, say r⁽ⁱ⁾:

$\begin{array}{c}\text{the data kernel}=\text{a concatenation of row}-\text{vectors}\\ \text{or}\\ \mathbf{G}=\left[\begin{array}{ccc}{G}_{11}& G_{12}& G_{13}\\ G_{21}& G_{22}& G_{23}\\ G_{31}& G_{32}& G_{33}\end{array}\right]=\left[\begin{array}{c}\left[\begin{array}{ccc}{G}_{11}& G_{12}& G_{13}\end{array}\right]\\ \left[\begin{array}{ccc}{G}_{21}& G_{22}& G_{23}\end{array}\right]\\ \left[\begin{array}{ccc}{G}_{31}& G_{32}& G_{33}\end{array}\right]\end{array}\right]=\left[\begin{array}{c}{\mathbf{r}}^{(1)}\\ {\mathbf{r}}^{(2)}\\ {\mathbf{r}}^{(3)}\end{array}\right]\end{array}$

Then the equation, d = Gm, can be understood to mean that the i-th datum, d_i, is constructed by taking the dot product, r⁽ⁱ⁾m. For example, suppose that M = 9 and

${\mathbf{r}}^{(5)}=\left[0,0,0,¼,½,¼,0,0,0\right]\text{then}{d}_5={\mathbf{r}}^{(5)}\mathbf{m}=¼m_4+½m_5+¼m_6$

Thus, the 5-th datum is a weighted average of the 4-th, 5-th, and 6-th model parameters. This scenario is especially useful when a set of observations are made along one spatial dimension—a profile. Then, the data correspond to a smooth version of the model parameters, with the amount of smoothing being described by the width of averaging. The three-point averaging of Equation (4.15) corresponds to a data kernel, G, of the form

$G=\left[\begin{array}{ccccccccc}½& ¼& 0& 0& 0& 0& 0& 0& 0\\ ¼& ½& ¼& 0& 0& 0& 0& 0& 0\\ 0& ¼& ½& ¼& 0& 0& 0& 0& 0\\ 0& 0& ¼& ½& ¼& 0& 0& 0& 0\\ 0& 0& 0& ¼& ½& ¼& 0& 0& 0\\ 0& 0& 0& 0& ¼& ½& ¼& 0& 0\\ 0& 0& 0& 0& 0& ¼& ½& ¼& 0\\ 0& 0& 0& 0& 0& 0& ¼& ½& ¼\\ 0& 0& 0& 0& 0& 0& 0& ¼& ½\end{array}\right]$

Note that each row must sum to unity for the operation to represent a true weighted average; otherwise, the average of three identical data would be unequal to their common value. Thus, the top and bottom rows of the matrix pose a dilemma. A three-point weighted average is not possible for these rows, because no m₀ or m_M+1 exists. This problem can be solved in two ways: just continue the pattern, in which case these rows do not correspond to true weighted averages (as in Equation 4.16), or use coefficients on those rows that make them true two-point weighted averages (e.g., ¼ and ¾ for the first row and ¾ and ¼ for the last).

In MatLab, a data kernel, G, corresponding to a weighted average can be created with the following script:

w = [2, 1]′;
Lw = length(w);
n = 2*sum(w)−w(1);
w = w/n;
r = zeros(M,1); c = zeros(N,1);
r(1:Lw)=w; c(1:Lw)=w;
G = toeplitz(c,r);

(MatLab eda04_06)

We assume that the weighted average is symmetric around its central point, but allow it to be of any length, Lw. It is specified in the column vector, w, which contains only the central weight and the nonzero weights to the right of it. Only the relative size of the elements of w is important, as the weights are normalized through computation of and division by a normalization factor, n. Thus, w=[2, 1]’ corresponds to the case given in Equation (4.16). The matrix, G, is Toeplitz, meaning that all its diagonals are constant, so it can be specified through its left column, c, and its top row, r, using the toeplitz() function. Grey-scale images of the Gs for weighted averages of different lengths are shown in Figure 4.3.

An important class of weighted averages that are not symmetric around the central value is the causal filter, which appears in many problems that involve time. An instrument, such as an aqueous oxygen sensor (a device that measures the oxygen concentration in water), does not measure the present oxygen concentration, but rather a weighted average of concentrations over the last few instants of time. This behavior arises from a limitation in the sensor's design. Oxygen must diffuse though a membrane within the sensor before it can be measured. Hence, the sensor reading (observation, d_i) made at time t_i is a weighted average of oxygen concentrations (model parameters, m_j), at times t_j ≤ t_i. The weights are called filter coefficients, f, with

$\begin{array}{c}\text{the data}=\text{a weighted average of present and past values of}m\text{'}\text{s}\\ \text{or}\\ d_i=f_1{m}_i+f_2{m}_{\mathrm{i-1}}+f_3{m}_{\mathrm{i-2}}+f_4{m}_{\mathrm{i-3}}+···\end{array}$

The corresponding data kernel, G, has the following form:

$\mathbf{G}=\left[\begin{array}{cccccc}{f}_1& 0& 0& 0& 0& \dots \\ f_2& f_1& 0& 0& 0& \dots \\ f_3& f_2& f_1& 0& 0& \dots \\ f_4& f_3& f_2& f_1& 0& \dots \\ f_5& f_4& f_3& f_2& f_1& \dots \\ \dots & \dots & \dots & \dots & \dots & \dots \end{array}\right]$

The data kernel, G, is both Toeplitz and lower triangular. For filters of length L, the first L − 1 elements of d are inaccurately computed, because they require knowledge of unavailable model parameters, those corresponding to times earlier than t₁. We will discuss filters in more detail in Chapter 7.

4.6 Examining error

Suppose that we have somehow obtained an estimate of the model parameters, m^est—for example, by guessing! One of the most important questions that can then be asked is

$\mathit{How\; do\; the\; predicted\; data},{\mathbf{d}}^{\text{pre}}=\mathbf{G}{\mathbf{m}}^{\text{est}},\mathit{compare\; with\; the\; observed\; data},{\mathbf{d}}^{\text{obs}}?$

This question motivates us to define an error vector, e:

$\mathbf{e}={\mathbf{d}}^{\text{obs}}-{\mathbf{d}}^{\text{pre}}={\mathbf{d}}^{\text{obs}}-\mathbf{G}{\mathbf{m}}^{\text{est}}$

When the error, e_i, is small, the corresponding datum, d_i^obs, is well predicted and, conversely, when the error, e_i, is large, the corresponding datum, d_i^obs, is poorly predicted. A measure of total error, E, is as follows:

$E={\mathbf{e}}^{\text{T}}\mathbf{e}={[{\mathbf{d}}^{\text{obs}}-\mathbf{G}{\mathbf{m}}^{\text{est}}]}^{\text{T}}[{\mathbf{d}}^{\text{obs}}-\mathbf{G}{\mathbf{m}}^{\text{est}}]$

The total error, E, is the length of the error vector, e, which is to say, the sum of squares of the individual errors:

$E=\sum _{i=1}^N{e}_i^2$

The error depends on the particular choice of model parameters, m, so we can write E(m). One possible choice of a best estimate of the model parameters is the choice for which E(m^est) is a minimum. This is known as the principle of least squares.

Plots of error are an extremely important tool for understanding whether a model has the overall ability to fit the data as well as whether the dataset contains anomalous points—outliers—that are unusually poorly fit. An example of the straight-line case is shown in Figure 4.4.

In MatLab, the error is calculated as follows:

dpre = G*mest;
e=dobs−dpre;
E = e′*e;

(MatLab eda04_07)

where mest, dobs, and dpre are the estimated model parameters, m^est, observed data, d^obs, and predicted data, d^pre, respectively.

So far, we have not said anything useful regarding how one might arrive at a reasonable estimate, m^est, of the model parameters. In cases, such as the straight line, where the number of model parameters is small, one might try a grid search. The idea is to systematically evaluate the total error, E(m), for many different m's—a grid of m's—and choose m^est as the m for which E(m) is the smallest (Figure 4.5). Note, however, that the point of minimum error, E^min, is surrounded by a region of almost-minimum error, that is, a region in which the error is only slightly larger than its value at the minimum. Any m chosen from this region is almost as good an estimate as is m^est. As we will see in Section 4.9, this region defines confidence intervals for the model parameters.

For a grid search to be effective, one must have a general idea of the value of the solution, m^est, so as to be able to choose the boundaries of a grid that contains it. We note that a plot of the logarithm of error, ln[E(m)], is often visually more effective than a plot of E(m), because it has less overall range.

In MatLab, a two-dimensional grid search is performed as follows:

% define grid
L1=100; L2=100;
m1min=0; m1max=4;
m2min=0; m2max=4;
m1=m1min+(m1max−m1min)*[0:L1−1]′/(L1−1);
m2=m2min+(m2max−m2min)*[0:L2−1]′/(L2−1);
% evaluate error at each grid point
E=zeros(L1,L2);
for i = [1:L1]
for j = [1:L2]
mest = [ m1(i), m2(j) ]′;
dpre = G*mest;
e = dobs−dpre;
E(i,j) = e′*e;
end
end
% search grid for minimum E
[Etemp, k] = min(E);
[Emin, j] = min(Etemp);
i=k(j);
m1est = m1(i);
m2est = m2(j);

(MatLab eda04_08)

The first section defines the grid of possible values of model parameters, m1 and m2. The second section, with the two nested for loops, computes the total error, E, for every point on the grid, that is, for every combination of m1 and m2. The third section searches the matrix, E, for its minimum value, Emin, and determines the corresponding best estimates of the model parameters, m1est and m2est. This search is a bit tricky. The function min(E) returns a row vector, Etemp, containing the minimum values in each column of E, as well as a row vector, k, of the row index at which the minimum occurs. The function min(Etemp) searches for the minimum of Etemp (which is also the minimum, Emin, of matrix, E) and also returns the column index, j, at which the minimum occurs. The minimum of E is therefore at row, i=k(j), and column, j, and the best-estimates of the model parameters are m1(i) and m2(j).

The overall amplitude of E(m) depends on the amount of error in the observed data, d^obs. The shape of the error surface, however, is mainly dependent on the geometry of observations. For example, merely shifting the xs to the left or right has a major impact on the overall shape of the error, E (Figure 4.6).

4.7 Least squares

In this section, we show that the least squares estimate of the model parameters can be determined directly, without recourse to a grid search. First, however, we return to some of the ideas of probability theory that we put forward in Chapter 3.

Suppose that the measurement error can be described by a Normal probability density function, and that observations, d_i, are uncorrelated and with equal variance, ${{\sigma }_d}^2$. Then, the probability density function, p(d_i), for one observation, d_i, is as follows:

$p(d_i)=\frac{1}{\sqrt{2\pi }{\sigma }_d}\text{exp}\{-{(d_i-{\overline{d}}_i)}^2/(2{{\sigma }_d}^2)\}$

where $\overline{d}$ is the mean. As the observations are uncorrelated, the joint probability density function, p(d), is just the product of the individual probability density functions:

$p(\mathbf{d})=\frac{1}{{(2\pi )}^{\text{N}/2}{\sigma }^N}\text{exp}\left\{-\frac{1}{2{\sigma }_d^2}\sum _{i=1}^N{(d_i-{\overline{d}}_i)}^2\right\}=\frac{1}{{(2\pi )}^{\text{N}/2}{\sigma }^N}\text{exp}\left\{-\frac{1}{2{\sigma }_d^2}{(\mathbf{d}-\overline{\mathbf{d}})}^T(\mathbf{d}-\overline{\mathbf{d}})\right\}$

We now assume that the model predicts the mean of the probability density functions, that is, $\overline{\mathbf{d}}=\mathbf{Gm}$. The resulting probability density function is

$\begin{array}{c}p(\mathbf{d})=\frac{1}{{(2\pi )}^{\text{N}/2}{\sigma }^N}\text{exp}\left\{-\frac{1}{2{\sigma }_d^2}{(\mathbf{d}-\mathbf{G}\mathbf{m})}^{\text{T}}(\mathbf{d}-\mathbf{G}\mathbf{m})\right\}=\frac{1}{{(2\pi )}^{\text{N}/2}{\sigma }^N}\text{exp}\left\{-\frac{1}{2{\sigma }_d^2}E(\mathbf{m})\right\}\\ \text{with}E(\mathbf{m})={(\mathbf{d}-\mathbf{Gm})}^{\text{T}}(\mathbf{d}-\mathbf{Gm})\end{array}$

In Chapter 3, we noted that the mean and mode of a Normal probability density function occur at the same value of m. Thus, the mean of this probability density function occurs at the point at which p(d) is maximum (the mode), which is the same as the point where E(m) is minimum. But this is just the principle of least squares. The m^est that minimizes E(m) is also the m such that Gm^est is the mean of p(d). The two are one and the same.

The actual value of m^est is calculated by minimizing E(m) with respect to a model parameter, m_k. Taking the derivative, $\partial E/\partial m_k$, and setting the result to zero yields

$0=\frac{\partial E}{\partial m_k}=\frac{\partial }{\partial m_k}\sum _{i=1}^N{\left(d_i-\sum _{j=1}^M{G}_{ij}{m}_j\right)}^2$

We then apply the chain rule to obtain

$0=-2\sum _{i=1}^N(\sum _{j=1}^M{G}_{ij}\frac{\partial m_j}{\partial m_k})\left(d_i-\sum _{j=1}^M{G}_{ij}{m}_j\right)$

As m_j and m_k are independent variables, the derivative, $\partial m_j/\partial m_k$, is zero except when j = k, in which case it is unity (this relationship is sometimes written as $\partial m_j/\partial m_k={\delta }_{jk}$, where δ_jk, called the Kronecker delta symbol, is an element of the identity matrix). Thus, we can perform the first summation trivially, that is, by replacing j with k and deleting the derivative and first summation sign:

$0=-2\sum _{j=1}^M{G}_{ik}\left(d_i-\sum _{j=1}^M{G}_{ij}{m}_j\right)\text{or}0=-{\mathbf{G}}^{\text{T}}\mathbf{d}+{\mathbf{G}}^{\text{T}}\mathbf{Gm}\text{or}[{\mathbf{G}}^{\text{T}}\mathbf{G}]\mathbf{m}={\mathbf{G}}^{\text{T}}\mathbf{d}$

As long as the inverse of the M × M matrix, [G^TG], exists, the least-squares solution is

${\mathbf{m}}^{\text{est}}={[{\mathbf{G}}^{\text{T}}\mathbf{G}]}^{-1}{\mathbf{G}}^{\text{T}}{\mathbf{d}}^{\text{obs}}$

Note that the estimated model parameters, m^est, are related to the observed data, d^obs, by multiplication by a matrix, M = [G^TG]⁻¹G^T, that is, m^est= Md^obs. According to the rules of error propagation developed in Chapter 3, the covariance of the estimated model parameters, C_m, is related to the covariance of the observed data, C_d, by C_m = MC_dM^T. In the present case, we have assumed that the data are uncorrelated with equal variance, ${{\sigma }_d}^2$, so C_d = ${{\sigma }_d}^2$I. The covariance of the estimated model parameters is, therefore

${\mathbf{C}}_m=[{[{\mathbf{G}}^{\text{T}}\mathbf{G}]}^{-1}{\mathbf{G}}^{\text{T}}]{\sigma }_d^2\mathbf{I}{[{[{\mathbf{G}}^{\text{T}}\mathbf{G}]}^{-1}{\mathbf{G}}^{\text{T}}]}^{\text{T}}={\sigma }_d^2{[{\mathbf{G}}^{\text{T}}\mathbf{G}]}^{-1}$

Here, we have used the rule (AB)^T= B^TA^T. Note that G^TG is a symmetric matrix, and that the inverse of a symmetric matrix is symmetric.

The derivation above assumes that quantities are purely real, which is the most common case. See Note 4.1 for a discussion of least squares in the case where quantities are complex.

4.8 Examples

In Section 4.2, we put forward the simplest linear problem, where the data are constant, which has M = 1, m = [m₁] and G = [1, 1, …, 1]^T. Then,

${\mathbf{G}}^{\text{T}}\mathbf{G}=\left[\begin{array}{ccccc}1& 1& 1& \dots & 1\end{array}\right]\left[\begin{array}{c}1\\ 1\\ 1\\ ⋮\\ 1\end{array}\right]=N\text{and}{\mathbf{G}}^{\text{T}}\mathbf{d}=\left[\begin{array}{ccccc}1& 1& 1& \dots & 1\end{array}\right]\left[\begin{array}{c}{d}_1\\ d_2\\ d_3\\ \dots \\ d_N\end{array}\right]=\sum _{i=1}^N{d}_i$

Then,

${\mathbf{m}}^{\text{est}}=m_1^{\text{est}}={[{\mathbf{G}}^{\text{T}}\mathbf{G}]}^{-1}{\mathbf{G}}^{\text{T}}\mathbf{d}=\frac{1}{N}\sum _{i=1}^N{d}_i\text{and}{\mathbf{C}}_m=\frac{{\sigma }_d^2}{N}$

As stated in Section 4.2, m^est is the mean of the data—the sample mean. The result for the variance of the sample mean, C_m = ${{\sigma }_d}^2$/N, is a very important one. The variance of the mean is less than the variance of the data by a factor of N⁻¹. Thus, the more the measurements, the greater is the precision of the mean. However, the confidence intervals of the mean, which depend on the square root of the variance, decline slowly with additional measurements: ${\sigma }_m={\sigma }_d/\sqrt{N}$.

Similarly, for the straight line case, we have

$\begin{array}{ll}{\mathbf{G}}^{\text{T}}\mathbf{G}\hfill & =\left[\begin{array}{ccccc}1& 1& 1& 1& 1\\ x_1& x_2& x_3& ···& x_N\end{array}\right]\left[\begin{array}{cc}1& x_1\\ 1& x_2\\ 1& x_3\\ ⋮& ⋮\\ 1& x_N\end{array}\right]=\left[\begin{array}{cc}N& \sum _{i=1}^N{x}_i\\ \sum _{i=1}^N{x}_i& \sum _{i=1}^N{x}_i^2\end{array}\right]\hfill \\ {\mathbf{G}}^{\text{T}}\mathbf{d}\hfill & =\left[\begin{array}{ccccc}1& 1& 1& 1& 1\\ x_1& x_2& x_3& ···& x_N\end{array}\right]\left[\begin{array}{c}{d}_1\\ d_2\\ d_3\\ ⋮\\ d_N\end{array}\right]=\left[\begin{array}{c}\sum _{i=1}^N{d}_i\\ \sum _{i=1}^N{x}_i{d}_i\end{array}\right]\hfill \\ {\mathbf{m}}^{\text{est}}\hfill & ={[{\mathbf{G}}^{\text{T}}\mathbf{G}]}^{-1}{\mathbf{G}}^{\text{T}}\mathbf{d}=\frac{1}{N{\sum }_{i=1}^N{x}_i^2-{\left[{\sum }_{i=1}^N{x}_i\right]}^2}\left[\begin{array}{cc}\sum _{i=1}^N{x}_i^2& -\sum _{i=1}^N{x}_i\\ -\sum _{i=1}^N{x}_i& N\end{array}\right]\left[\begin{array}{c}\sum _{i=1}^N{d}_i\\ \sum _{i=1}^N{x}_i{d}_i\end{array}\right]\hfill \\ \hfill & =\frac{1}{N{\sum }_{i=1}^N{x}_i^2-{\left[{\sum }_{i=1}^N{x}_i\right]}^2}\left[\begin{array}{c}\sum _{i=1}^N{x}_i^2\sum _{i=1}^N{d}_i-\sum _{i=1}^N{x}_i\sum _{i=1}^N{x}_i{d}_i\\ N\sum _{i=1}^N{x}_i{d}_i-\sum _{i=1}^N{x}_i\sum _{i=1}^N{d}_i\end{array}\right]\hfill \\ {\mathbf{C}}_m\hfill & ={\sigma }_d^2{[{\mathbf{G}}^{\text{T}}\mathbf{G}]}^{-1}=\frac{{\sigma }_d^2}{N{\sum }_{i=1}^N{x}_i^2-{\left[{\sum }_{i=1}^N{x}_i\right]}^2}\left[\begin{array}{cc}\sum _{i=1}^N{x}_i^2& -\sum _{i=1}^N{x}_i\\ -\sum _{i=1}^N{x}_i& N\end{array}\right]\hfill \end{array}$

Here, we have used the fact that the inverse of a 2 × 2 matrix is

${\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]}^{-1}=\frac{1}{ad-bc}\left[\begin{array}{cc}d& -b\\ -c& a\end{array}\right]$

In MatLab, all these quantities are computed by first defining the data kernel, G, and then forming all the other quantities using linear algebra:

G=zeros(N,M);
G(:,1)=1;
G(:,2)=x;
mest = (G′*G)(G′*dobs);
dpre = G*mest;
e=dobs−dpre;
E = e′*e;
sigmad2 = E/(N−M);
Cm = sigmad2*inv(G′*G);

(MatLab eda04_10)

Note that we use the backslash operator,, when evaluating the formula, m^est = [G^TG]⁻¹G^Td. An extremely important issue is how the variance of the data, ${{\sigma }_d}^2$, is obtained. In some cases, determining the observational error might be possible in advance, based on some knowledge of the measurement system that is being used. If, for example, a ruler has 1 mm divisions, then one might assume that σ_d is about 1 mm. This is called a prior estimate of the variance. Another possibility is to use the total error, E, to estimate the variance in the data

${\sigma }_d^2=\frac{E}{(N-M)}$

as is done in the eda04_10 script above. This is essentially approximating the variance by the mean squared error E/N = (${e_1}^2+{e_1}^2+\dots +{e_N}^2$)/N. The factor of M is added to account for the ability of an M-parameter model to predict M data exactly (e.g., a straight line fan fits any two points, exactly). The actual variance of the data is larger than E/N. This estimate is called a posterior estimate of the variance. The quantity, N − M, is called the degrees of freedom of the problem.

One problem with posterior estimates is that they are influenced by the quality of the quantitative model. If the model is not a good one, then it will not fit the data well and a posterior estimate of variance will be larger than the true variance of the observations.

We now return to the Black Rock Forest temperature data discussed in Chapter 2. One interesting question is whether we can observe a long-term increase or decrease in temperature over the 12 years of observations. The problem is detecting such a trend, which is likely to be just fractions of a degree against the very large annual cycle. One possibility is to model both:

$d_i=m_1+m_2{t}_i+m_3\text{cos}\frac{2\pi t_i}{T}+m_4\text{sin}\frac{2\pi t_i}{T}$

where T is a period of 1 year or 365.25 days. While we solve for four model parameters, only m₂, which quantifies the rate of increase of temperature with time, is of interest. The other three model parameters are included to provide a better fit of the model to the data.

Before proceeding, we need to have some strategy to deal with the errors that we detect in the dataset. One strategy is to identify bad data points and throw them out. This is a dangerous strategy because the data that are thrown out might not all be bad, because the data that are included might not all be good, and especially because the reason why bad data are present in the data has never been determined. Nevertheless, it is the only viable strategy, in some cases.

The Black Rock Forest dataset has three types of bad data: cold spikes that fall below −40°C, warm spikes that with temperatures above 38°C, and dropouts with a temperature of exactly 0 °C. The following MatLab script eliminates them:

Draw=load(‘brf_temp.txt’);
traw=Draw(:,1);
draw=Draw(:,2);
n = find((draw~=0) & (draw>−40) & (draw<38));
t=traw(n);
d=draw(n);

(MatLab eda04_11)

The find() function returns a column vector, n, of indices that satisfy a logical expression, in this case

(draw~ =0) & (draw>−40) & (draw<38)

(MatLab eda04_11)

which means the elements of d^raw that satisfy d_i^raw≠ 0, d_i^raw > −40, and d_i^raw < 38. Note that, in MatLab, the tilde, ~, means not, so that ~= means not equal. The vector, n, is then used in the statements t=traw(n) and d=draw(n), which form two new versions of data, d, and time, t, containing only good data.

The MatLab code that creates the data kernel, G, is

Ty=365.25;
G=zeros(N,4);
G(:,1)=1;
G(:,2)=t;
G(:,3)=cos(2*pi*t/Ty);
G(:,4)=sin(2*pi*t/Ty);

(MatLab eda04_11)

The results of the fit are shown in Figure 4.7. Note that the model does poorly in fitting the overall amplitude of the seasonal cycle, mainly because the annual oscillations, while having a period of 1 year, do not have a sinusoidal shape. The fit could be substantially improved by adding oscillations of half-year, third-year and quarter-year periods (see Problem 4.5). The estimated long-term slope is m₂= −0.03°C/yr, corresponding to a slight cooling trend. The prior error of the slope, based on an estimate of σ_d = 0.01°C (the resolution of the data, which is recorded to hundredths of a degree), is about σ_m2= 10⁻⁵ °C/yr. The error based on the posterior variance of the data, σ_d = 5.6 °C, is larger, σ_m2= 0.0046 °C/yr. In both cases, the slope is significantly different from zero to better than 95% confidence, in the sense that m₂ + 2σ_m2< 0, so we may be justified in claiming that this site has experienced a slight cooling trend. However, the poor overall fit of the model to the data should give any practitioner of data analysis pause. More effort should be put into improving the model.

4.9 Covariance and the behavior of error

Back in Section 4.6, during our discussion of the grid search, we alluded to a relationship between the shape of the total error, E(m) and the corresponding error in the estimated model parameters, m^est. We defined an elliptical region of near-minimum errors, centered on the point, m^est, of minimum error, and claimed that any m within this region was almost as good as m^est. We asserted that the size of the elliptical region is related to the confidence intervals, and its orientation to correlations between the individual ms. This reasoning suggests that there is a relationship between the covariance matrix, C_m, and the shape of E(m) near its minimum.

This relationship can be understood by noting that, near its minimum, the total error, E(m), can be approximated by the first two nonzero terms of its Taylor series (see Section 11.6) :

$E(\mathbf{m})\approx E({\mathbf{m}}^{\text{est}})+\sum _{i=1}^M\sum _{j=1}^M½[m_i-m_i^{\text{est}}][m_j-m_j^{\text{est}}]{\frac{\partial E}{\partial m_i\partial m_j}|}_{\mathbf{m}={\mathbf{m}}^{\text{est}}}$

Note that the linear term is missing, as $\partial E/\partial m_i$ is zero at the minimum of E(m). The error is related to the data kernel, G, via

$E(\mathbf{m})={[\mathbf{d}-\mathbf{Gm}]}^{\text{T}}\left[\mathbf{d}-\mathbf{Gm}\right]={\mathbf{d}}^{\text{T}}\mathbf{d}-2{\mathbf{d}}^{\text{T}}\mathbf{Gm}+{\mathbf{m}}^{\text{T}}[{\mathbf{G}}^{\text{T}}\mathbf{G}]\mathbf{m}$

This equation, when twice differentiated, yields

${\frac{\partial E}{\partial m_i\partial m_j}|}_{\mathbf{m}={\mathbf{m}}^{\text{est}}}=2{[{\mathbf{G}}^{\text{T}}\mathbf{G}]}_{ij}$

However, we have already shown that C_m = ${{\sigma }_d}^2$[G^TG]⁻¹ (see Equation 4.26). Thus, Equation (4.35) implies

${\mathbf{C}}_m=2{\sigma }_d^2{\mathbf{D}}^{-1}\text{where}{D}_{ij}={\frac{\partial E}{\partial m_i\partial m_j}|}_{\mathbf{m}={\mathbf{m}}^{\text{est}}}$

The matrix, D, of second derivatives of the error describes the curvature of the error surface near its minimum. The covariance matrix, C_m, is inversely proportional to the curvature. A steeply curved error surface has small covariance, and a gently curved surface has large covariance.

Equation (4.36) is of practical use in grid searches, where a finite-difference approximation to the second derivative can be used to estimate the second-derivative matrix, D, which can then be used to estimate the covariance matrix, C_m.

Problems

4.1. Suppose that a person wants to determine the weight, m_j, of M = 40 objects by weighing the first, and then weighing the rest in pairs: the first plus the second, the second plus the third, the third plus the fourth, and so on. (A) What is the corresponding data kernel, G? (B) Write a MatLab script that creates this data kernel and computes the covariance matrix, C_m, assuming that the observations are uncorrelated and have a variance, ${{\sigma }_d}^2$= 1 kg². (C) Make a plot of σ_mj as a function of the object number, j, and comment on the results.

4.2. Consider the equation d_i= m₁exp(−m₂t_i). Why cannot this equation be arranged in the linear form, d = Gm? (A) Show that the equation can be linearized into the form, d′= G′m′, where the primes represent new, transformed variables, by taking the logarithm of the equation. (B) What would have to be true about the measurement error in order to justify solving this linearized problem by least squares? (Notwithstanding your answer, this problem is often solved with least squares in a let's-hope-for-the-best mode).

4.3. (A) What is the relationship between the elements of the matrix, G^TG, and the columns, c^(j), of G? (B) Under what circumstance is G^TG a diagonal matrix? (C) What is the form of the covariance matrix in this case? (D) What is the form least-squares solution in this case? Is it harder or easier to compute than the case where G^TG is not diagonal? (E) Examine the straight line case in this context?

4.4. The dataset shown in Figure 4.4 is in the file, linedata01.txt. Write MatLab scripts to least-squares fit polynomials of degree 2, 3, and 4 to the data. Make plots that show the observed and predicted data. Display the value of each coefficient and its 95% confidence limits. Comment on your results.

4.5. Modify the MatLab script, eda04_11, to try to achieve a better fit to the Black Rock Forest temperature dataset. (A) Add additional periods of T_y/2 and T_y/3, where T_y is the period of 1 year, in an attempt to better capture the shape of the annual variation. (B) In addition to the periods in part A, add additional periods of T_d, T_d/2, and T_d/3, where T_d is the period of 1 day. (C) How much does the total error change in the cases? If it goes up, your code has a bug! (D) How much do the slope, m₂, and its confidence intervals change?