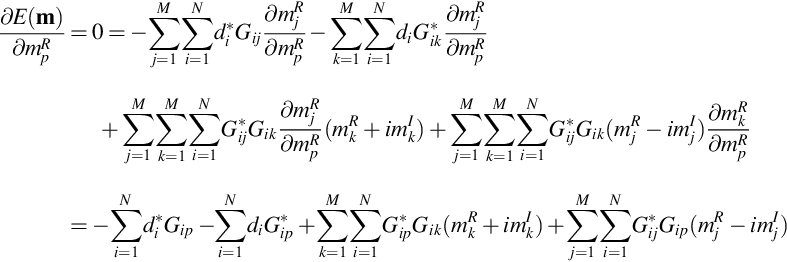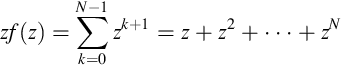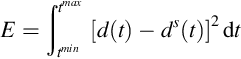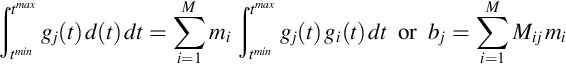Note 1.1 On the persistence of MatLab variables

MatLab variables accumulate in its Workspace and can be accessed not only by the script that created them but also through both the Command Window and the Workspace Window (which has a nice spreadsheet-like matrix viewing tool). This behavior is mostly an asset: You can create a variable in one script and use it in a subsequent script. Further, you can check the values of variables after a script has finished, making sure that they have sensible values. However, this behavior also leads to the following common errors:

(1) you forget to define a variable in one script and the script, instead of reporting an error, uses the value of an identically named variable already in the Workspace;

(2) you accidentally delete a line of code from a script that defines a variable, but the script continues to work because the variable was defined when you ran an earlier version of the script; and

(3) you use a predefined constant such as pi, or a built-in function such as max(), but its value was reset to an unexpected value by a previous script. (Note that nothing prevents you from defining pi=2 and max=4).

Such problems can be detected by deleting all variables from the workspace with a clear all command and then running the script. (You can also delete particular variables with a clear followed by the variable's name, e.g., clear pi). A really common mistake is to overwrite the value of the imaginary unit, i, by using that variable's name for an index counter. Our suggestion is that a clear i be routinely included at the top of any script that expects i to be the imaginary unit.

Note 2.1 On time

Datasets often contain time expressed in calendar (year, month, day) and clock (hour, minute, second) format. This format is not suitable for data analysis and needs to be converted into a format in which time is represented by a single, uniformly increasing variable, say t. The choice of units of the time variable, t, and the definition of the start time, t = 0, will depend on the needs of the data analysis. In the case of the Black Rock Forest, which consisted of 12.6 years of hourly samples, a time variable that expresses days, starting on January 1 of the first year of the dataset, is a reasonable choice, especially because the diurnal cycle is so strong. However, time in years starting on January 1 of the first year of the dataset might be preferred when examining annual periodicities. In this case, having a start time that allows us to easily recognize the season of a particular time is important.

The conversion of calendar/clock time to a single variable, t, is complicated, because of the different lengths of the months and special cases such as leap years. MatLab provides a time arithmetic function, datenum() that expedites this conversion. It takes the calendar date (year, month, day) and time (hour, minute, second) and returns date number; that is, the number of days (including fractions of a day) that have elapsed since midnight on January 1, 0000. The time interval between two date numbers can be computed by subtraction. For example, the number of seconds between Feb 11, 2008 03:04:00 and Feb 11, 2008 03:04:01 is

86400*(datenum(2008,2,11,4,4,1)-datenum(2008,2,11,4,4,0))

which evaluates to 1.0000 s.

Finally, we note a complication, relevant to cases where time accuracy of seconds or better is required, which is related to the existence of leap seconds. Leap seconds are analogous to leap years. They are integral-second clock corrections, applied on June 30 and December 31 of each year, that account for small irregularities in the rotation of the earth. However, unlike leap years, which are completely predictable, leap seconds are determined semiannually by the International Earth Rotation and Reference Systems Service (IERS). Hence, time intervals cannot be calculated accurately without an up-to-date table of leap seconds. To make matters worse, while the most widely used time standard, Coordinated Universal Time (UTC), uses leap seconds, several other standards, including the equally widely used Global Positioning System (GPS), do not. Thus, the determination of long time intervals to second-level accuracy is tricky. The time standard used in the dataset must be known and, if that standard uses leap seconds, then they must be properly accounted for by the time arithmetic software. As of the end of 2010, a total of 34 leap seconds have been declared since they were first implemented in 1972. Thus, very long (decade) time intervals can be in error by tens of seconds, if leap seconds are not properly accounted for. The MatLab function, datenum(), does not account for leap seconds and hence does not provide second-level accuracy for UTC times.

Note 2.2 On reading complicated text files

MatLab's load() function can read only text files containing a table of numerical values. Some publicly accessible databases, including many sponsored by government agencies, provide data as more complicated text files that are a mixture of numeric and alphabetic values. For instance, the Black Rock Forest temperature dataset, which contains time and temperature, contains lines of text such as:

2100−2159 31 Jan 1997 −1.34
2200−2259 31 Jan 1997 −0.958
2300−2400 31 Jan 1997 −0.601
0000−0059 1 Feb 1997 −0.245
0100−0159 1 Feb 1997 −0.217

(file brf_raw.txt)

In the first line above, the date of the observation is 31 Jan 1997, the start and end times are 2100−2159, and the observed temperature is −1.34. This data file is one of the simpler ones, as each line has the same format and most of the fields are delimited by tabs or spaces. We occasionally encounter much more complicated cases, in which the number of fields varies from line to line and where adjacent fields are run together without delimiters.

Some of the simpler cases, including the one above, can be reformatted using the Text Import Wizard module of Microsoft's Excel spreadsheet software. But we know of no universal and easy-to-use software that can reliably handle complicated cases. We resort to writing a custom MatLab script for each file. Such a script sequentially processes each line in the file, according to what we perceive to be the rules under which it was written (which are sometimes difficult to discern). The heart of such a script is a for loop that sequentially reads lines from the file:

fid = fopen(filename);
for i = [1:N]
 tline = fgetl(fid);
 % now process the line
 –––
end
fclose(fid);

(MatLab brf_convert)

Here, the function, fopen(), opens a file so that it can be read. It returns an integer, fid, which is subsequently used to refer to the file. The function, fgetl(), reads one line of characters from the file and puts them into the character string, tline. These characters are then processed in a portion of the script, omitted here, whose purpose is to convert all the data fields into numerical values stored in one of more arrays. Finally, after every line has been read and processed, the file is closed with the fclose() function. The processing section of the script can be quite complicated. One MatLab function that is extremely useful in this section is sscanf(), which can convert a character string into a numerical variable. It is the inverse of the previously discussed sprintf() function, and has similar arguments (see Section 2.4 and the MatLab Help files). Typically, one first determines the portion of the character string, tline, that contains a particular data field (for instance, tline(6:9) for the second field, above) and then converts that portion to a numerical value using sscanf().

Data format conversion scripts are tedious to write. They should always be tested very carefully, including by spot-checking data values against the originals. Spot checks should always include data drawn from near the end of the file.

Note 3.1 On the rule for error propagation

Suppose that we form M_A model parameters, m_A, from N data, d, using the linear rule m_A = M_Ad. We have already shown that when M_A = N, the covariance matrices are related by the rule, C_MA = M_AC_dM_A^T. To verify this rule for the M_A < N case, first devise M_B = N − M_A complementary model parameters, m_B, such that m_B = M_Bd. Now concatenate the two sets of model parameters so that their joint matrix equation is square:

$\left[\begin{array}{c}{\mathbf{m}}_A\\ {\mathbf{m}}_B\end{array}\right]=\left[\begin{array}{c}{\mathbf{M}}_A\\ {\mathbf{M}}_B\end{array}\right]\mathbf{d}$

The normal rule for error propagation now gives

${\mathbf{C}}_m=\left[\begin{array}{c}{\mathbf{M}}_A\\ {\mathbf{M}}_B\end{array}\right]{\mathbf{C}}_{\text{d}}\left[\begin{array}{ccc}{\mathbf{M}}_A^{\mathbf{T}}& & {\mathbf{M}}_B^{\mathbf{T}}\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{M}}_A{\mathbf{C}}_d{\mathbf{M}}_A^{\text{T}}& & {\mathbf{M}}_A{\mathbf{C}}_d{\mathbf{M}}_B^{\text{T}}\\ {\mathbf{M}}_B{\mathbf{C}}_d{\mathbf{M}}_A^{\text{T}}& & {\mathbf{M}}_B{\mathbf{C}}_d{\mathbf{M}}_B^{\text{T}}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{C}}_{m_A}& {\mathbf{C}}_{m_{A,B}}\\ {\mathbf{C}}_{m_{B.A}}& {\mathbf{C}}_{m_B}\end{array}\right]$

The upper left part of ${\mathbf{C}}_m,{\mathbf{C}}_{m_A}={\mathbf{M}}_A{\mathbf{C}}_d{\mathbf{M}}_A^{\text{T}}$, which comprises all the variances and covariances of the m_A model parameters, satisfies the normal rule of error proposition and is independent of the choice of M_B. Hence, the rule can be applied to the M_A < N case in which M_A is rectangular, without concern for the particular choice of complementary model parameters.

Note 3.2 On the eda_draw() function

We provide a simple function, eda_draw(), for plotting a sequence of square matrices and vectors as grey-shaded images. The function can also place a caption beneath the matrices and vectors and plot a symbol between them. For instance, the command

eda_draw(d, ‘caption d’, ‘=’, G, ‘caption G’, m, ‘caption m’);

MatLab eda12_01

creates a graphical representation of the equation, d = Gm (Figure 13.1). The function accepts vectors, square matrices, and character strings, in any order. A character string starting with the word “caption”, as in ‘caption d’, is plotted beneath the previous vector or matrix (but with the word “caption” removed). Other character strings are plotted to the right of the previous matrix or vector.

Note 4.1 On complex least squares

Least-squares problems with complex quantities occasionally arise (e.g., when the model parameters are the Fourier transform of a function). In this case, all the quantities in Gm = d are complex. The correct definition of the total error is

$E(\mathbf{m})={\mathbf{e}}^{*\text{T}}\mathbf{e}={(\mathbf{d}-\mathbf{G}\mathbf{m})}^{*\text{T}}(\mathbf{d}-\mathbf{G}\mathbf{m})$

where * signifies complex conjugation. This combination of complex conjugate and matrix transpose is called the Hermitian transpose and is denoted e^H = e*^T. Note that the total error, E, is a nonnegative real number. The least-squares solution is obtained by minimizing E with respect to the real and imaginary parts of m, treating them as independent variables. Writing m = m^R + im^I, we have

$\begin{array}{c}E(\mathbf{m})=\sum _{i=1}^N\left(d_{\text{i}}^{*}-\sum _{j=1}^M{G}_{ij}^{*}{m}_j^{*}\right)\left(d_i-\sum _{k=1}^M{G}_{ik}{m}_k\right)=\sum _{i=1}^N{d}_i^{*}{d}_i-\sum _{j=1}^M\sum _{i=1}^N{d}_i^{*}{G}_{ij}(m_j^R+i{m}_j^I)\\ -\sum _{k=1}^M\sum _{i=1}^N{d}_i{G}_{ik}^{*}(m_j^R-i{m}_j^I)+\sum _{j=1}^M\sum _{k=1}^M\sum _{i=1}^N{G}_{ij}^{*}{G}_{ik}(m_j^R-{\mathit{im}}_j^I)(m_k^R+i{m}_k^I)\end{array}$

Differentiating with respect to the real part of m yields

$\begin{array}{ll}\frac{\partial E(\mathbf{m})}{\partial m_p^R}& =0=-\sum _{j=1}^M\sum _{i=1}^N{d}_i^{*}{G}_{ij}\frac{\partial m_j^R}{\partial m_p^R}-\sum _{k=1}^M\sum _{i=1}^N{d}_i{G}_{ik}^{*}\frac{\partial m_j^R}{\partial m_p^R}\\ & +\sum _{j=1}^M\sum _{k=1}^M\sum _{i=1}^N{G}_{ij}^{*}{G}_{\mathit{ik}}\frac{\partial m_j^R}{\partial m_p^R}(m_k^R+i{m}_k^I)+\sum _{j=1}^M\sum _{k=1}^M\sum _{i=1}^N{G}_{\mathit{ij}}^{*}{G}_{\mathit{ik}}(m_j^R-{\mathit{im}}_j^I)\frac{\partial m_k^R}{\partial m_p^R}\\ & =-\sum _{i=1}^N{d}_i^{*}{G}_{\mathit{ip}}-\sum _{i=1}^N{d}_i{G}_{\mathit{ip}}^{*}+\sum _{k=1}^M\sum _{i=1}^N{G}_{\mathit{ip}}^{*}{G}_{\mathit{ik}}(m_k^R+i{m}_k^I)+\sum _{j=1}^M\sum _{i=1}^N{G}_{ij}^{*}{G}_{\mathit{ip}}(m_j^R-i{m}_j^I)\end{array}$

Note that ∂m_k^R/∂m_p^R = δ_kp, as m_k^R and m_p^R are independent variables. Differentiating with respect to the imaginary part of m yields

$\begin{array}{ll}\frac{\partial E(\mathbf{m})}{\partial m_p^I}& =0\\ & =-i\sum _{i=1}^N{d}_i^{*}{G}_{ip}+i\sum _{i=1}^N{d}_i{G}_{ip}^{*}-i\sum _{k=1}^M\sum _{i=1}^N{G}_{ip}^{*}{G}_{ik}(m_k^R+i{m}_k^I)+i\sum _{j=1}^M\sum _{i=1}^N{G}_{ij}^{*}{G}_{ip}(m_j^R-i{m}_j^I)\\ & =\sum _{i=1}^N{d}_i^{*}{G}_{ip}-\sum _{i=1}^N{d}_i{G}_{ip}^{*}+\sum _{k=1}^M\sum _{i=1}^N{G}_{ip}^{*}{G}_{ik}(m_k^R+i{m}_k^I)-\sum _{j=1}^M\sum _{i=1}^N{G}_{ij}^{*}{G}_{ip}(m_j^R-i{m}_j^I)\end{array}$

Finally, adding the two derivative equations yields

$\begin{array}{c}-2\sum _{i=1}^N{d}_i{G}_{ip}^{*}+\sum _{k=1}^M\sum _{i=1}^N{G}_{ip}^{*}{G}_{ik}(m_k^R+i{m}_k^I)=0\\ \text{or}\\ -2{\mathbf{G}}^{\text{H}}\mathbf{d}+2[{\mathbf{G}}^{\text{H}}\mathbf{G}]\mathbf{m}=0\end{array}$

The least-squares solution and its covariance are

${\mathbf{m}}^{\text{est}}={[{\mathbf{G}}^{\text{H}}\mathbf{G}]}^{-1}{\mathbf{G}}^{\text{H}}\mathbf{d}\text{and}{\mathbf{C}}_{\mathbf{m}}={\sigma }_d^2{[{\mathbf{G}}^{\text{H}}\mathbf{G}]}^{-1}$

In MatLab, the Hermitian transpose of a complex matrix, G, is denoted with the same symbol as transposition, as in G′, and transposition without complex conjugation is denoted G.′. Thus, no changes need to be made to the MatLab formulas to implement complex least squares.

Note 5.1 On the derivation of generalized least squares

Strictly speaking, in Equation (5.4), the probability density function, p(h), can only be said to be proportional to p(m) when the K × M matrix, H, in the equation, Hm = h, is square so that H⁻¹ exists. In other cases, the Jacobian determinant is undefined. Nonsquare cases arise whenever only a few pieces of prior information are available. The derivation can be patched by imagining that H is made square by adding M − K rows of complementary information and then assigning them negligible certainty so that they have no effect on the generalized least-squares solution. This patch does not affect the results of the derivation; all the formulas for the generalized least-squares solution and its covariance are unchanged. The underlying issue is that the uniform probability density function, which represents a state of no information, does not exist on an unbounded domain. The best that one can do is a very wide normal probability density function.

Note 5.2 On MatLab functions

MatLab provides a way to define functions that perform in exactly the same manner as built-in functions such as sin() and cos(). As an example, let us define a function, areaofcircle(), that computes the area of a circle of radius, r:

function a = areaofcircle(r)
% computes area, a, of circle of radius, r.
a = pi * (r○2);
return

MatLab areaofcircle

We place this script in a separate m-file, areaofcircle.m. The first line declares the name of the function to be areaofcircle, its input to be r, and its output to be a. The last line, return, denotes the end of the function. The interior lines perform the actual calculation. One of them must set the value of the output variable. The function is called in from the main script as follows:

radius=2;
area = areaofcircle(radius);

MatLab eda12_02

Note that the variable names in the main script need not agree with the names in the function; the latter act only as placeholders.

MatLab functions can take several input variables and return several output variables, as is illustrated in the following example that computes the circumference and area of a rectangle:

function [c,a] = CandAofrectangle(l, w)
% computes circumference, c, and area, a, of
% a rectangle of length, l, and width, w.
c = 2*(l+w);
a = l*w;
return

MatLab CandAofrectangle

The function is placed in the m-file, CandAofrectangle.m. It is called in from the main script as follows:

a=2;
b=4;
[circ, area] = CandAofrectangle(a,b);

MatLab eda12_02

Note 5.3 On reorganizing matrices

Owing to the introductory nature of this book, we have intentionally omitted discussion of a group of advanced MatLab functions that allow one to reorganize matrices. Nevertheless, we briefly describe some of the key functions here. In MatLab, a key feature of a matrix is that its elements can be accessed with a single index, instead of the normal two indices. In this case, the matrix, say A, acts a column-vector containing the elements of A arranged column-wise. Thus, for a $\text{3}\times \text{3}$ matrix, A(4) is equivalent to A(1,2). The MatLab functions, sub2ind() and ind2sub(), translate between two “subscripts”, i and j, and a vector “index”, k, such that A(i,j)=A(k). The reshape() function can reorganize any N × M matrix into a K × L matrix, as long as NM = KL. Thus, for example, a 4 × 4 matrix can be easily converted into equivalent 1 × 16, 2 × 8, 8 × 2, and 16 × 1 matrices. These functions often work to eliminate for loops from the matrix-reorganization sections of the scripts. They are demonstrated in MatLab script eda12_03.

Note 6.1 On the MatLab atan2() function

The phase of the Discrete Fourier Transform, $\varphi ={tan}^{-1}(B/A)$, is defined on the interval, (−π, +π). In MatLab, one should use the function, atan2(B,A), and not the function atan(B/A). The latter version is defined on the wrong interval, (−π/2, +π/2), and will also fail when A = 0.

Note 6.2 On the orthonormality of the discrete Fourier data kernel

The rule, [G*^TG] = N I, for the complex version of the Fourier data kernel, G, can be derived as follows. First write down the definition of un-normalized version of the data kernel for the Fourier series:

$G_{kp}=exp(2\pi i(k-1)(p-1)/N)$

Now compute [G*^TG]

${[{\mathbf{G}}^{*\text{T}}\mathbf{G}]}_{pq}=\sum _{k=1}^N{G}_{kp}^{*}{G}_{kq}=\sum _{k=0}^{N-1}exp(2\pi ik(p-q)/N)=\sum _{k=0}^{N-1}{z}^k=f(z)$

with

$z=exp(2\pi i(p-q)/N)$

Now consider the series

$f(z)=\sum _{k=0}^{N-1}{z}^k=1+z+z^2+···+z^{N-1}$

Multiply by z

$zf(z)=\sum _{k=0}^{N-1}{z}^{k+1}=z+z^2+···+z^N$

and subtract, noting that all but the first and last terms cancel:

$f(z)-zf(z)=1-z^N\text{or}f(z)=\frac{1-z^N}{1-z}$

Now substitute in $z=exp(2\pi i(p-q)/N)$:

$f(z)=\frac{1-exp(2\pi i(p-q))}{1-exp(2\pi i(p-q)/N)}$

The numerator is zero, as exp(2πis) = 1 for any integer, s = p − q. In the case, p ≠ q, the denominator is nonzero, so f(z) = 0. Thus, the off-diagonal elements of G*^TG are zero. In the case, p = q, the denominator is also zero, and we must use l'Hopital's rule to take the limit, s → 0. This rule requires us to take the derivative of both numerator and denominator before taking the limit:

$f(z)=\underset{s\to 0}{lim}\frac{2\pi iexp(2\pi is)}{\left(\frac{2\pi i}{N}\right)exp(2\pi is/N)}=N$

The diagonal elements of G*^TG are all equal to N.

Note 6.3 On the expansion of a function in an orthonormal basis

Suppose that we approximate an arbitrary function d(t) on the interval t ^min < t < t ^max as a sum of basis functions g_i(t):

$d\left(t\right)\approx d^s\left(t\right)\mathrm{with}{d}^s\left(t\right)=\sum _{i=1}^M{m}_i{g}_i\left(t\right)$

Here, m_i are unknown coefficients. The Fourier series is one such approximation, with sines and cosines as the basis functions:

$g_i\left(t\right)=\left\{\begin{array}{cc}cos\left({\omega }_{i}t\right)& i\mathrm{odd}\\ sin\left({\omega }_{i}t\right)& i\mathrm{even}\end{array}\right.$

For any given sets of coefficients, the quality of the approximation can be measured by defining an error:

$E={\int }_{t^{\mathit{min}}}^{t^{\mathit{max}}}{\left[d\left(t\right)-d^s\left(t\right)\right]}^2\mathrm{d}t$

This is a generalization of the usual least squares error, and has the properties that $E=0$ when $d\left(t\right)=d^s\left(t\right)$. In general, zero error can be achieved only in the $M\to \infty$ limit. We now take an approach that is very similar to the one used in the derivation of the least squares formula in Section 4.7 and view E as a function of the unknown coefficients and minimize it with respect them by solving $\mathit{\partial }E/\mathit{\partial }{m}_k=0$. This procedure leads to an equation for the unknown coefficients:

${\int }_{t^{\mathit{min}}}^{t^{\mathit{max}}}{g}_j\left(t\right)d\left(t\right)dt=\sum _{i=1}^M{m}_i{\int }_{t^{\mathit{min}}}^{t^{\mathit{max}}}{g}_j\left(t\right)g_i\left(t\right)dt\mathrm{or}{b}_j=\sum _{i=1}^M{M}_{ij}{m}_i$

$\mathrm{with}{b}_j={\int }_{t^{\mathit{min}}}^{t^{\mathit{max}}}{g}_j\left(t\right)d\left(t\right)dt\mathrm{and}{M}_{ij}={\int }_{t^{\mathit{min}}}^{t^{\mathit{max}}}{g}_j\left(t\right)g_i\left(t\right)dt$

Solving for the coefficients, we find that $\mathbf{m}={\mathbf{M}}^{-1}\mathbf{b}$.

In some cases, the basis functions g_i(t) may be orthonormal, meaning that any pair of them obeys:

${\int }_{t^{\mathit{min}}}^{t^{\mathit{max}}}{g}_i\left(t\right)g_j\left(t\right)dt=\left\{\begin{array}{cc}1& i=j\\ 0& i\ne j\end{array}\right.$

In this case, $\mathbf{M}=\mathbf{I}$ and the formula for the coefficients simplifies to $\mathbf{m}=\mathbf{b}$. Each coefficient is determined separately; any given basis function has the same coefficient regardless of the number of terms in the summation, or even on the identity of the other basis functions. The coefficients are even the same in the $M\to \infty$ limit. However, whether $E\to 0$ in this limit depends on whether the set of basis functions is complete, an issue that we do not address further here.

Now suppose that only a discrete version of d(t) is available; that is, we know the time series $d_i=d\left(t_i\right)$ (for $i=1,\dots ,N$). We can approximate the integrals as Riemann sums:

$M_{ij}\approx \Delta t\sum _{k=1}^N{g}_i\left(t_k\right)g_j\left(t_k\right)=\Delta t\sum _{k=1}^N{G}_{kj}{G}_{kj}$

$b_j\approx \Delta t\sum _{k=1}^N{g}_j\left(t_k\right)d\left(t_k\right)\approx \Delta t\sum _{i=1}^N{G}_{kj}{d}_k$

where $G_{ij}=g_j\left(t_i\right)$. We have achieved a result that is identical to least squares: $\mathbf{m}\approx {\left[{\mathbf{G}}^{\mathrm{T}}\mathbf{G}\right]}^{-1}{\mathbf{G}}^{\mathrm{T}}\mathbf{d}$. Furthermore, when the functions are orthonormal, m can be determined without computing a matrix inverse, since $\Delta t\left[{\mathbf{G}}^{\mathrm{T}}\mathbf{G}\right]\approx \mathbf{I}$ and $\mathbf{m}={\mathbf{G}}^{\mathrm{T}}\mathbf{d}$. The estimated coefficients are uncorrelated, since by the usual rules of error propagation, ${\mathbf{C}}_m={\sigma }_d^2{\left[{\mathbf{G}}^{\mathrm{T}}\mathbf{G}\right]}^{-1}={\sigma }_d^2\mathbf{I}$, where σ_d² is the variance of d_i. These results explain the popularity of series of orthogonal functions.

Note 8.1 On singular value decomposition

The derivation of the singular value decomposition is not quite complete, as we need to demonstrate that the eigenvalues, λ_i, of S^TS are all nonnegative so that the singular values of S, which are the square roots of the eigenvalues, are all real. This result can be demonstrated as follows. Consider the minimization problem

$E(\mathbf{m})={(\mathbf{d}-\mathit{S}\mathbf{m})}^{\text{T}}(\mathbf{d}-\mathit{S}\mathbf{m})$

This is just the least-squares problem with G = S. Note that E(m) is a nonnegative quantity, irrespective of the value of m; therefore, a point (or points), m₀, of minimum exists, irrespective of the choice of S. In Section 4.9, we showed that in the neighborhood of m₀ the error behaves as

$E(\mathbf{m})=E({\mathbf{m}}_0)+\mathrm{\Delta }{\mathbf{m}}^{\text{T}}{\mathbf{S}}^{\text{T}}\mathbf{S}\mathrm{\Delta }\mathbf{m}\text{where}\mathrm{\Delta }\mathbf{m}=\mathbf{m}-{\mathbf{m}}_0$

Now let Δm be proportional to an eigenvector, v⁽ⁱ⁾, of S^TS; that is, Δm = cv⁽ⁱ⁾. Then,

$E(\mathbf{m})=E({\mathbf{m}}_0)+c^2{\mathbf{v}}^{(i)\text{T}}{\mathbf{S}}^{\text{T}}\mathbf{S}{\mathbf{v}}^{(i)}=E({\mathbf{m}}_0)+c^2{\lambda }_i$

Here, we have used the relationship, S^TSv⁽ⁱ⁾ = λ_iv⁽ⁱ⁾. As we increase the constant, c, we move away from the point, m₀, in the direction of the eigenvector. By hypothesis, the error must increase, as E(m₀) is the point of minimum error. The eigenvalue, λ_i, must be positive or else the error would decrease and m₀ could not be a point of minimum error.

As an aside, we also mention that this derivation demonstrated that the point, m₀, is nonunique if any of the eigenvalues are zero, as the error is unchanged when one moves in the direction of the corresponding eigenvector.

Note 9.1 On coherence

The coherence can be interpreted as the zero lag cross-correlation of the band-passed versions of the two time series, $u(t)$ and $v(t)$. However, the band-pass filter, $f(t)$, must have a spectrum, $\tilde{f}(\omega )$, that is one-sided; that is, it must be zero for all negative frequencies. This is in contrast to a normal filter, which has a two-sided spectrum. Then, the first of the two integrals in Equation (9.32) is zero and no cancelation of imaginary parts occurs. Such a filter, $f(t)$, is necessarily complex, implying that the band-passed time series, $f(t)*u(t)$ and $f(t)*v(t)$, are complex, too. Thus, the interpretation of coherence in terms of the zero-lag cross-correlation still holds, but becomes rather abstract.

Note that the coherence must be calculated with respect to a finite bandwidth. If we were to omit the frequency averaging, then the coherence is unity for all frequencies, regardless of the shapes of the two time series, $u(t)$ and $v(t)$:

$C_{uv}^2({\omega }_0,\mathrm{\Delta }\omega )=\frac{{\left|\overline{{\stackrel{~}{u}}^{*}({\omega }_0)\stackrel{~}{v}({\omega }_0)}\right|}^2}{\overline{|\stackrel{~}{u}({\omega }_0){|}^2}\overline{|\stackrel{~}{v}({\omega }_0){|}^2}}\to \frac{{\tilde{u}}^{*}({\omega }_0)\tilde{u}({\omega }_0){\tilde{v}}^{*}({\omega }_0)\tilde{v}({\omega }_0)}{{\tilde{u}}^{*}({\omega }_0)\tilde{u}({\omega }_0){\tilde{v}}^{*}({\omega }_0)\tilde{v}({\omega }_0)}=1\text{as}\mathrm{\Delta }\omega \to 0$

This rule implies that $C_{uv}^2({\omega }_0=\omega \text{'})=1$ when the two time series are pure sinusoids, regardless of their relative phase. The coherence of $u(t)=\text{cos}(\omega \text{'}t)$ and $(t)=\text{sin}(\omega \text{'}t)$, where $\omega \text{'}$ is an arbitrary frequency of oscillation, is unity. In contrast, ${\mathcal{C}}_{uv}^2({\omega }_0=\omega \text{'})=0$, as the zero lag cross-correlation of, $u(t)$ and $v(t)$ is

${\int }_{-\infty }^{+\infty }sin(\omega \text{'}t)cos(\omega \text{'}t)\text{d}t=½{\int }_{-\infty }^{+\infty }sin(2\omega \text{'}t)\text{d}t=0$

This is the main difference between the two quantities, $C_{uv}^2({\omega }_0,\mathrm{\Delta }\omega )$ and ${\mathcal{C}}_{uv}^2({\omega }_0,\mathrm{\Delta }\omega )$(Menke 2014).

Note 9.2 On Lagrange multipliers

The method of Lagrange multipliers is used to solve constrained minimization problems of the following form: minimize Φ(x) subject to the constraint C(x) = 0. It can be derived as follows: The constraint equation defines a surface. The solution, say x₀, must lie on this surface. In an unconstrained minimization problem, the gradient vector, ∂Φ/∂x_i, must be zero at x₀, as Φ must not decrease in any direction away from x₀. In contrast, in the constrained minimization, only the components of the gradient tangent to the surface need be zero, as the solution cannot be moved off the surface to further minimize Φ (Figure 13.2). Thus, the gradient is allowed to have a nonzero component parallel to the surface's normal vector, ∂C/∂x_i. As ∂Φ/∂x_i is parallel to ∂C/∂x_i, we can find a linear combination of the two, ∂Φ/∂x_i + λ∂C/∂x_i, where λ is a constant, which is zero at x₀. The constrained inversion satisfies the equation, (∂/∂x_i)(Φ + λC) = 0, at x₀. Thus, the constrained minimization is equivalent to the unconstrained minimization of Φ + λC, except that the constant, λ, is unknown and needs to be determined as part of the solution process.

Note 11.1 On the chain rule for partial derivatives

Consider a variable f(x) that depends upon a variable x. The notion that a small change $\Delta x$ in x causes a small change $\Delta f$ in f is denoted $\Delta f=df/dx\Delta x$, where df/dx is the derivative of f with respect to x. Now suppose that f(x, y) depends upon two variables, x and y. The notion that small changes in x and y causes a small change $\Delta f$ in f is denoted:

$\Delta f=\frac{\mathit{\partial }f}{\mathit{\partial }x}\Delta x+\frac{\mathit{\partial }f}{\mathit{\partial }y}\Delta y$

The quantities $\mathit{\partial }f/\mathit{\partial }x$ and $\mathit{\partial }f/\mathit{\partial }y$ are called partial derivatives. If another variable g(x, y) also depends upon x and y, then by analogy, small changes in x and y also cause a small change in g:

$\Delta g=\frac{\mathit{\partial }g}{\mathit{\partial }x}\Delta x+\frac{\mathit{\partial }g}{\mathit{\partial }y}\Delta y$

These two equations can be written compactly in matrix form:

$\left[\begin{array}{c}\Delta f\\ \Delta g\end{array}\right]=\left[\begin{array}{cc}\frac{\mathit{\partial }f}{\mathit{\partial }x}& \frac{\mathit{\partial }f}{\mathit{\partial }y}\\ \frac{\mathit{\partial }g}{\mathit{\partial }x}& \frac{\mathit{\partial }g}{\mathit{\partial }y}\end{array}\right]\left[\begin{array}{c}\Delta x\\ \Delta y\end{array}\right]$

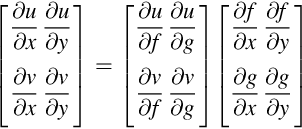
If two variables u(f, g) and v(f, g) depend upon variables f and g, the analogous equation expressing the notion that small changes in f and g cause small changes in u and v is denoted:

$\left[\begin{array}{c}\Delta u\\ \Delta v\end{array}\right]=\left[\begin{array}{cc}\frac{\mathit{\partial }u}{\mathit{\partial }f}& \frac{\mathit{\partial }u}{\mathit{\partial }g}\\ \frac{\mathit{\partial }v}{\mathit{\partial }f}& \frac{\mathit{\partial }v}{\mathit{\partial }g}\end{array}\right]\left[\begin{array}{c}\Delta f\\ \Delta g\end{array}\right]$

The notion that small changes in x and y causes small changes in f and g which in turn causes small changes in u and v is expressed by substituting one matrix equation onto the other:

$\left[\begin{array}{c}\Delta u\\ \Delta v\end{array}\right]=\left[\begin{array}{cc}\frac{\mathit{\partial }u}{\mathit{\partial }f}& \frac{\mathit{\partial }u}{\mathit{\partial }g}\\ \frac{\mathit{\partial }v}{\mathit{\partial }f}& \frac{\mathit{\partial }v}{\mathit{\partial }g}\end{array}\right]\left[\begin{array}{cc}\frac{\mathit{\partial }f}{\mathit{\partial }x}& \frac{\mathit{\partial }f}{\mathit{\partial }y}\\ \frac{\mathit{\partial }g}{\mathit{\partial }x}& \frac{\mathit{\partial }g}{\mathit{\partial }y}\end{array}\right]\left[\begin{array}{c}\Delta x\\ \Delta y\end{array}\right]\mathrm{or}\left[\begin{array}{c}\Delta u\\ \Delta v\end{array}\right]=\left[\begin{array}{cc}\frac{\mathit{\partial }u}{\mathit{\partial }x}& \frac{\mathit{\partial }u}{\mathit{\partial }y}\\ \frac{\mathit{\partial }v}{\mathit{\partial }x}& \frac{\mathit{\partial }v}{\mathit{\partial }y}\end{array}\right]\left[\begin{array}{c}\Delta x\\ \Delta y\end{array}\right]$

Equating the matrices yields the chain rule:

$\left[\begin{array}{cc}\frac{\mathit{\partial }u}{\mathit{\partial }x}& \frac{\mathit{\partial }u}{\mathit{\partial }y}\\ \frac{\mathit{\partial }v}{\mathit{\partial }x}& \frac{\mathit{\partial }v}{\mathit{\partial }y}\end{array}\right]=\left[\begin{array}{cc}\frac{\mathit{\partial }u}{\mathit{\partial }f}& \frac{\mathit{\partial }u}{\mathit{\partial }g}\\ \frac{\mathit{\partial }v}{\mathit{\partial }f}& \frac{\mathit{\partial }v}{\mathit{\partial }g}\end{array}\right]\left[\begin{array}{cc}\frac{\mathit{\partial }f}{\mathit{\partial }x}& \frac{\mathit{\partial }f}{\mathit{\partial }y}\\ \frac{\mathit{\partial }g}{\mathit{\partial }x}& \frac{\mathit{\partial }g}{\mathit{\partial }y}\end{array}\right]$