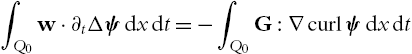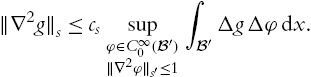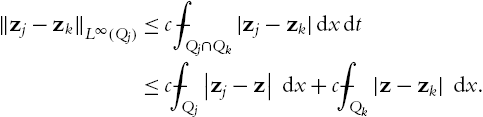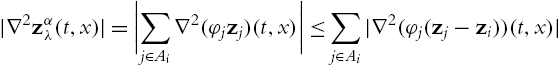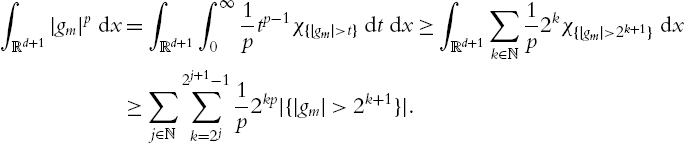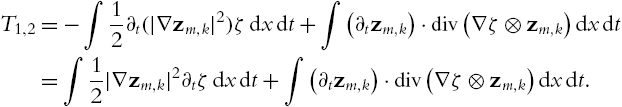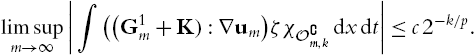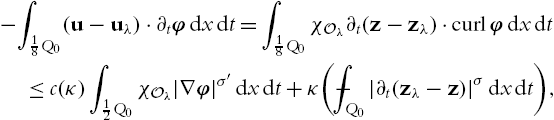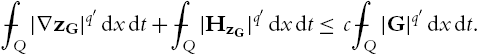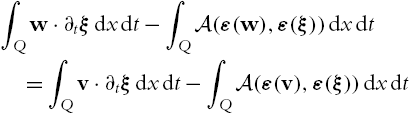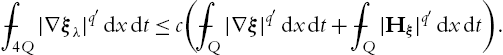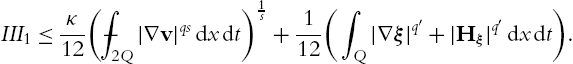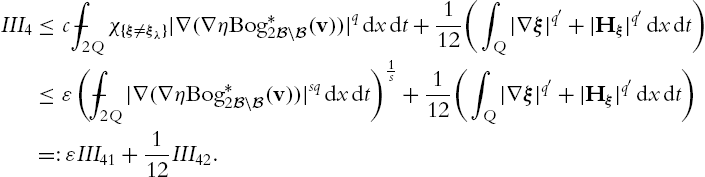Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Chapter 6

Solenoidal Lipschitz truncation

Abstract

In this chapter we present the solenoidal Lipschitz truncation for non-stationary problems: we show how to construct a Lipschitz truncation which preserves the divergence-free character of a given Sobolev function. As a matter of fact, it suffices to have distributional time-derivatives in the sense of divergence-free test-functions. After this, we present the $A$ -Stokes approximation for non-stationary problems. It aims at approximating almost solutions to the non-stationary $A$ -Stokes system by exact solutions. Thanks to the solenoidal Lipschitz truncation this can be done on the level of gradients.

Keywords

Solenoidal Lipschitz truncation; Divergence-free constraint; Parabolic PDEs; Inverse curl-operator; $A$ -Stokes approximation; Almost solutions

In this chapter we develop a non-stationary counterpart of the solenoidal Lipschitz truncation from Chapter 3. Here, the main difficulty is to handle problems connected with the distributional time derivative of the function we aim to truncate. Let us be a little bit more precise. Let $Q_{0} = I_{0} \times B_{0} \subset R \times R^{3}$ be a space time cylinder and $σ \in (1, \infty)$ . Let $u \in L^{σ} (I_{0}, W_{div}^{1, σ} (B_{0}))$ and $G \in L^{σ} (Q_{0})$ satisfy

$\int_{Q_{0}} \partial_{t} u \cdot ξ d x d t = \int_{Q_{0}} G : \nabla ξ d x d t for all ξ \in C_{0, div}^{\infty} (Q_{0}) .$

(6.0.1)

The main purpose of the solenoidal Lipschitz truncation is to avoid the appearance of the pressure function. Hence we start in (6.0.1) with an equation on the level of divergence-free test-functions. Unfortunately, this is not enough information on the time derivative for a Poincaré-type inequality as in (5.2.6). Hence the approach from [65] as explained in Section 5.2 will not give $L^{\infty}$ -estimates for the gradient of the truncation, cf. the proof of Lemma 5.2.3. Our aim is to construct a truncation which preserves the properties from [65] and is, in addition, divergence-free.

We will show that there is a truncation $u_{λ}$ of u with roughly the following properties (see Theorem 6.1.25 for a precise formulation).

(a) $\nabla u_{λ} \in L^{\infty} (Q_{0})$ with ${‖ \nabla u_{λ} ‖}_{\infty} ⩽ c λ$ and $div u_{λ} = 0$ .

(b) $u_{λ} = u$ a.e. outside a suitable set $O_{λ}$ .

$| 〈 \partial_{t} u, u_{λ} - u 〉 | + {‖ χ_{O_{λ}^{α}} \nabla u_{λ} ‖}_{p}^{p} ⩽ c λ^{p} | O_{λ} | ⩽ δ (λ),$

with $δ (λ) \to 0$ if $λ \to \infty$ .

In the following we sketch the construction on a heuristic level. In fact, the rigorous approach which we shall present in the next section requires a series of localization arguments, so it is quite technical. Let us start with a function

$u \in L^{\infty} (I_{0}; L^{2} (B_{0})) \cap L^{p} (I_{0}; W_{0, div}^{1, p} (B_{0}))$

with $\partial_{t} u = div H$ in $D_{div}^{'} (B_{0})$ , where $H \in L^{σ} (B)$ for some $σ > 1$ . We define

$w : = {curl}^{- 1} u \in L^{\infty} (I_{0}; W^{1, 2} (B_{0})) \cap L^{p} (I_{0}; W_{div}^{2, p} (B_{0})) .$

It follows that $\partial_{t} Δ w = curl div H$ in $D^{'} (B_{0})$ . Also we can obtain an information about the time derivative of w as a distribution acting on all test-functions. However, we do not have control about a possible harmonic part of w. Hence we decompose w into a harmonic and anti-harmonic part. To do this we define, pointwise in time,

$w (t) = z (t) + h (t),$

where $z (t) \in Δ W_{0}^{2, p} (B_{0})$ and $Δ h (t) = 0$ . This decomposition is based on a singular integral operator which is continuous on $L^{p}$ -spaces such that

$z, w \in L^{\infty} (I_{0}; W^{1, 2} (B_{0})) \cap L^{p} (I_{0}; W^{2, p} (B_{0})) .$

(6.0.2)

Moreover, we have

$\partial_{t} Δ z = \partial_{t} w = curl div H$

in $D^{'} (B_{0})$ . As z is anti-harmonic by construction this yields

${‖ \partial_{t} z ‖}_{σ} ⩽ c {‖ H ‖}_{σ} .$

In fact, $\partial_{t} z$ is a measurable function. Now, we truncate z to $z_{λ}$ with an approach similar to (5.2.8). This truncation satisfies with ${‖ \nabla^{2} z_{λ} ‖}_{\infty} ⩽ c λ$ as well as $z_{λ} = z$ in $O_{λ}$ , where $O_{λ} = O_{λ} (M (\nabla^{2} z); M (\partial_{t} z))$ . Finally, we set

$u_{λ} : = curl z_{λ} + curl h .$

Obviously, we have $div u_{λ} = 0$ . Due to (6.0.2) and the properties of harmonic functions we have $h \in L^{\infty} (I_{0}; W^{k, 2} (B_{0}))$ for any $k \in N$ (at least locally in space). Hence $u_{λ}$ has the same regularity as $curl z_{λ}$ . In particular, $\nabla u_{λ}$ is bounded.

In Section 6.2 we develop the $A$ -Stokes approximation for non-stationary problems, see [29]. This is, on the one hand, a non-stationary variant of the $A$ -Stokes approximation from Section 3.3. On the other hand it is a fluid-mechanical counterpart of the $A$ -caloric approximation from [68] which is concerned with the $A$ -heat equation.

6.1 Solenoidal truncation – evolutionary case

In this section we examine solenoidal functions, whose time derivative is only a distribution acting on solenoidal test-functions. Let $u \in L^{σ} (I_{0}, W_{div}^{1, σ} (B_{0}))$ be such that (6.0.1) holds for some $G \in L^{σ} (Q_{0})$ . So the time derivative is only well defined via the duality with solenoidal test functions. The goal of this section is to construct a solenoidal truncation $u_{λ}$ of u which preserves the properties of the truncation in [65].

First we extend our function u in a suitable way to the whole space and then apply the inverse curl operator. Let $γ \in C_{0}^{\infty} (B_{0})$ with $χ_{\frac{1}{2} B_{0}} ⩽ γ ⩽ χ_{B_{0}}$ , where $B_{0}$ is a ball. Let $C_{0}$ denote the annulus $B_{0} ∖ \frac{1}{2} B_{0}$ . Then according to Theorem 2.1.6 (with $A (t) = B (t) = t^{q}$ ) there exists a Bogovskiĭ operator ${Bog}_{C_{0}} : C_{0, ⊥}^{\infty} (C_{0}) \to C_{0}^{\infty} (C_{0})$ which is bounded from $L_{⊥}^{q} (C_{0}) \to W_{0}^{1, q} (C_{0})$ for all $q \in (1, \infty)$ , and such that $div {Bog}_{C_{0}} = Id$ . Define

$\tilde{u} : = γ u - {Bog}_{C_{0}} (div (γ u)) = γ u - {Bog}_{C_{0}} (\nabla γ \cdot u) .$

Then $div \tilde{u} = 0$ on $I_{0} \times B_{0}$ and $\tilde{u} (t) \in W_{0}^{1, σ} (B_{0})$ , so we can extend $\tilde{u}$ by zero in space to $\tilde{u} \in L^{σ} (I_{0}, W_{div}^{1, σ} (R^{3}))$ . Since $\tilde{u} = u$ on $I_{0} \times \frac{1}{2} B_{0}$ , we have

$\int_{Q_{0}} \partial_{t} \tilde{u} \cdot ξ d x d t = \int_{Q_{0}} G : \nabla ξ d x d t for all ξ \in C_{0, div}^{\infty} (\frac{1}{2} Q_{0}) .$

(6.1.3)

Now, we define, pointwise in time,

$w : = {curl}^{- 1} (\tilde{u}) = {curl}^{- 1} (γ u - {Bog}_{C_{0}} (\nabla γ \cdot u)) .$

Overall, we get the following lemma.

Lemma 6.1.1

We have

$\begin{matrix} curl w & = \tilde{u} = u & in \frac{1}{2} Q_{0} \\ div w & = 0 & in R^{3} \end{matrix}$

and

$\begin{matrix} {‖ w (t) ‖}_{L^{s} (R^{3})} & ⩽ c_{s} {‖ \tilde{u} (t) ‖}_{L^{a} (B_{0})} \\ {‖ \nabla w (t) ‖}_{L^{s} (R^{3})} & ⩽ c_{s} {‖ \tilde{u} (t) ‖}_{L^{s} (B_{0})} \\ {‖ \nabla^{2} w (t) ‖}_{L^{s} (R^{3})} & ⩽ c_{s} {‖ \nabla \tilde{u} (t) ‖}_{L^{s} (B_{0})}, \end{matrix}$

for $a = \max {1, \frac{3 s}{3 + s}}$ , $t \in I_{0}$ and $s \in (1, \infty)$ .

Let us derive from (6.0.1) the equation for w. For $ψ \in C_{0}^{\infty} (\frac{1}{2} Q_{0})$ we have

$\int_{Q_{0}} \partial_{t} u \cdot curl ψ d x d t = \int_{Q_{0}} G : \nabla curl ψ d x d t .$

We use $u = curl w$ and partial integration to show that

$\int_{Q_{0}} \partial_{t} w \cdot curl curl ψ d x d t = \int_{Q_{0}} G : \nabla curl ψ d x d t .$

Now, because

$\int_{Q_{0}} w \cdot \partial_{t} \nabla div ψ d x d t = \int_{Q_{0}} div w \partial_{t} div ψ d x d t = 0$

and $curl curl ψ = - Δ ψ + \nabla div ψ$ we obtain

$\int_{Q_{0}} w \cdot \partial_{t} Δ ψ d x d t = - \int_{Q_{0}} G : \nabla curl ψ d x d t$

(6.1.4)

for every $ψ \in C_{0}^{\infty} (\frac{1}{2} Q_{0})$ . We can rewrite this as

$\int_{Q_{0}} w \cdot \partial_{t} Δ ψ d x d t = - \int_{Q_{0}} H : \nabla^{2} ψ d x d t,$

(6.1.5)

with $| G | \sim | H |$ pointwise. In particular, in the sense of distributions we have

$\partial_{t} Δ w = - curl div G = - div div H .$

So in passing from u to w we got a system valid for all test functions $ψ \in C_{0}^{\infty} (Q_{0})$ . However, we only have control of $\partial_{t} Δ w$ , so that the time derivative of the harmonic part of w cannot be seen. Hence, a parabolic Poincaré inequality for w still does not hold; i.e. $\partial_{t} w$ is not controlled! In order to remove this harmonic invariance we will replace w by some function z such that $\partial_{t} Δ w = \partial_{t} Δ z$ . This will imply that $\partial_{t} z$ can be controlled by H. To define z conveniently we need some auxiliary results.

For a ball $B^{'} \subset R^{3}$ and a function $f \in L^{s} (B^{'})$ we define $Δ_{B^{'}}^{- 2} Δ f$ as the weak solution $F \in W_{0}^{2, s} (B^{'})$ of

$\int_{B^{'}} Δ F Δ φ d x = \int_{B^{'}} f Δ φ d x for all φ \in C_{0}^{\infty} (B^{'}) .$

(6.1.6)

Then $f - Δ (Δ_{B^{'}}^{- 2} Δ f)$ is harmonic on $B^{'}$ .

According to [117] and Lemma 2.1 of [140] we have the following variational estimate.

Lemma 6.1.2

Let $s \in (1, \infty)$ . Then for all $g \in W_{0}^{2, s} (B^{'})$ we have

${‖ \nabla^{2} g ‖}_{s} ⩽ c_{s} \sup_{\binom{φ \in C_{0}^{\infty} (B^{'})}{{‖ \nabla^{2} φ ‖}_{s^{'}} ⩽ 1}} \int_{B^{'}} Δ g Δ φ d x .$

This implies the following two corollaries.

Corollary 6.1.1

Let $s \in (1, \infty)$ . Then

$\int_{B^{'}} | \nabla^{2} (Δ_{B^{'}}^{- 2} Δ f) |^{s} d x ⩽ c_{s} \sup_{\binom{φ \in C_{0}^{\infty} (B^{'})}{{‖ \nabla^{2} φ ‖}_{s^{'}} ⩽ 1}} \int_{B^{'}} f Δ φ d x ⩽ c_{s} \int_{B^{'}} | f |^{s} d x$

for $f \in L^{s} (B^{'})$ , where $c_{s}$ is independent of the ball $B^{'}$ .

Proof

The claim follows by Lemma 6.1.2,

$\int_{B^{'}} Δ (Δ_{B^{'}}^{- 2} Δ f) Δ φ d x = \int_{B^{'}} f Δ φ d x,$

and Hölder's inequality. □

Corollary 6.1.2

Let $s \in (1, \infty)$ . Then

$\begin{matrix} \int_{\frac{2}{3} B^{'}} | \nabla^{3} (Δ_{B^{'}}^{- 2} Δ f) |^{s} d x & ⩽ c_{s} \int_{B^{'}} | \nabla f |^{s} d x for f \in W^{1, s} (B^{'}), \\ \int_{\frac{2}{3} B^{'}} | \nabla^{4} (Δ_{B^{'}}^{- 2} Δ f) |^{s} d x & ⩽ c_{s} \int_{B^{'}} | \nabla^{2} f |^{s} d x for f \in W^{2, s} (B^{'}), \end{matrix}$

where $c_{s}$ is independent of the ball $B^{'}$ .

Proof

The claim follows from Corollary 6.1.1 by standard interior regularity theory (difference quotients, localization and Poincaré's inequality). □

For $V \in L^{s} (B^{'})$ we define $Δ_{B^{'}}^{- 2} div div V$ as the weak solution $F \in W_{0}^{2, s} (B^{'})$ of

$\int_{B^{'}} Δ F Δ φ d x = \int_{B^{'}} V \nabla^{2} φ d x for all φ \in C_{0}^{\infty} (B^{'}) .$

Similar to Corollary 6.1.1 we get the following result.

Corollary 6.1.3

Let $s \in (1, \infty)$ . Then

$\int_{B^{'}} | \nabla^{2} (Δ_{B^{'}}^{- 2} div div V) |^{s} d x ⩽ c_{s} \int_{B^{'}} | V |^{s} d x$

for $V \in L^{s} (B^{'})$ , where $c_{s}$ is independent of the ball $B^{'}$ .

The next lemma shows the wanted control of the time derivative.

Lemma 6.1.3

For a cube $Q^{'} = I^{'} \times B^{'} \subset Q_{0}$ let $z_{Q^{'}} : = Δ Δ_{B^{'}}^{- 2} Δ w$ . Then for $s \in (1, \infty)$ we have

$\begin{matrix} ⨍_{Q^{'}} | z_{Q^{'}} |^{s} d x & ⩽ c_{s} ⨍_{Q^{'}} | w |^{s} d x \\ ⨍_{Q^{'}} | \frac{z_{Q^{'}}}{r^{'}} |^{s} d x + ⨍_{\frac{2}{3} Q^{'}} | \nabla z_{Q^{'}} |^{s} d x & ⩽ c_{s} ⨍_{Q^{'}} | \nabla w |^{s} d x \\ ⨍_{Q^{'}} | \frac{z_{Q^{'}}}{{(r^{'})}^{2}} |^{s} d x + ⨍_{\frac{2}{3} Q^{'}} | \frac{\nabla z_{Q^{'}}}{r^{'}} |^{s} d x + ⨍_{\frac{2}{3} Q^{'}} | \nabla^{2} z_{Q^{'}} |^{s} d x & ⩽ c_{s} ⨍_{Q^{'}} | \nabla^{2} w |^{s} d x, \\ ⨍_{Q^{'}} | \partial_{t} z_{Q^{'}} |^{s} d x d t & ⩽ c_{s} ⨍_{Q^{'}} | H |^{s} d x d t, \end{matrix}$

where $r^{'} : = r_{B^{'}}$ .

Proof

The estimate of $z_{Q^{'}}$ in terms of w follows directly from Corollary 6.1.1 and integration over time. The estimate of $z_{Q^{'}}$ in terms of $\nabla w$ and $\nabla^{2} w$ follows from this by Poincaré's inequality, using the fact that we can subtract a linear polynomial from w without changing the definition of $z_{Q^{'}}$ . The other estimate for $\nabla z_{Q^{'}}$ and $\nabla^{2} z_{Q^{'}}$ follow analogously from Corollary 6.1.2.

For all $ρ \in C_{0}^{\infty} (I^{'})$ and $φ \in C_{0}^{\infty} (B^{'})$ it follows from (6.1.5) that

$\int_{I^{'}} \int_{B^{'}} w \cdot Δ φ d x \partial_{t} ρ d t = - \int_{I^{'}} \int_{B^{'}} H : \nabla^{2} φ d x ρ d t .$

Let $d_{t}^{h}$ denote the forward difference quotient in time with step size h. We use $ρ (t) : = ⨍_{t}^{t - h} \tilde{ρ} (τ) d τ$ with $\tilde{ρ} \in C_{0}^{\infty} (I^{'})$ and h sufficiently small. Then $\partial_{t} ρ = d_{t}^{- h} \tilde{ρ}$ and

$\int_{I^{'}} \int_{B^{'}} w \cdot Δ φ d x d_{t}^{- h} \tilde{ρ} d t = - \int_{I^{'}} \int_{B^{'}} H : \nabla^{2} φ d x ⨍_{t}^{t - h} \tilde{ρ} (τ) d τ d t .$

This implies that

$\int_{I^{'}} \int_{B^{'}} d_{t}^{h} w \cdot Δ φ d x \tilde{ρ} d t = - \int_{I^{'}} \int_{B^{'}} ⨍_{t}^{t + h} H (τ) d τ : \nabla^{2} φ d x \tilde{ρ} d t .$

Since this is valid for all choices of $\tilde{ρ}$ we have

$\int_{B^{'}} d_{t}^{h} w \cdot Δ φ d x = - \int_{B^{'}} ⨍_{t}^{t + h} H (τ) d τ : \nabla^{2} φ d x .$

Since $d_{t}^{h} z_{Q^{'}} = d_{t}^{h} (Δ Δ_{B^{'}}^{- 2} Δ w) = Δ Δ_{B^{'}}^{- 2} Δ (d_{t}^{h} w)$ , it follows by Corollary 6.1.1 that

$\begin{matrix} {(\int_{B^{'}} | d_{t}^{h} z_{Q^{'}} |^{s} d x)}^{\frac{1}{s}} & ⩽ c \sup_{\binom{φ \in C_{0}^{\infty} (B)}{{‖ \nabla^{2} φ ‖}_{s^{'}} ⩽ 1}} \int_{B^{'}} d_{t}^{h} w Δ φ d x \\ = \sup_{\binom{φ \in C_{0}^{\infty} (B)}{{‖ \nabla^{2} φ ‖}_{s^{'}} ⩽ 1}} (- \int_{B^{'}} ⨍_{t}^{t + h} H (τ) d τ : \nabla^{2} φ d x) \\ ⩽ c {(\int_{B^{'}} ⨍_{t}^{t + h} | H (τ) |^{s} d τ d x)}^{\frac{1}{s}} . \end{matrix}$

Integrating over time and passing to the limit $h \to 0$ yields

${(\int_{Q^{'}} | \partial_{t} z_{Q^{'}} |^{s} d x d t)}^{\frac{1}{s}} ⩽ c {(\int_{Q^{'}} | H |^{s} d x d t)}^{\frac{1}{s}}$

which finishes the proof. □

Defining $z (t) : = z_{\frac{1}{2} Q_{0}} (t) = Δ Δ_{\frac{1}{2} B_{0}}^{- 2} Δ w (t)$ for $t \in \frac{1}{2} I_{0}$ , we then have

$\int_{Q_{0}} z \cdot \partial_{t} Δ ψ d x d t = \int_{Q_{0}} w \cdot \partial_{t} Δ ψ d x d t = - \int_{Q_{0}} H : \nabla^{2} ψ d x d t,$

(6.1.7)

for all $ψ \in C_{0}^{\infty} (\frac{1}{2} Q_{0})$ . Since the function $Δ_{\frac{1}{2} B_{0}}^{- 2} w (t) \in W_{0}^{2, s} (\frac{1}{2} B_{0})$ , we can extend it by zero to a function in $W^{2, s} (R^{3})$ . In this sense it is natural to extend $z (t)$ by zero to a function in $L^{s} (R^{3})$ .

Note that Lemma 6.1.3 enables us to control $\partial_{t} z$ by H in $L^{s} (\frac{1}{2} Q_{0})$ .

Lemma 6.1.4

We have

$\begin{matrix} {‖ z (t) ‖}_{L^{s} (\frac{1}{3} B_{0})} & ⩽ c_{s} {‖ \tilde{u} (t) ‖}_{L^{\frac{3 s}{s + 3}} (B_{0})} \\ {‖ \nabla z (t) ‖}_{L^{s} (\frac{1}{3} B_{0})} & ⩽ c_{s} {‖ \tilde{u} (t) ‖}_{L^{s} (B_{0})} \\ {‖ \nabla^{2} z (t) ‖}_{L^{s} (\frac{1}{3} B_{0})} & ⩽ c_{s} {‖ \nabla \tilde{u} (t) ‖}_{L^{s} (B_{0})}, \end{matrix}$

for $t \in I$ and $s \in (1, \infty)$ .

Proof

This follows from Corollary 6.1.1, Corollary 6.1.2 and Lemma 6.1.1. □

For $λ, α > 0$ and $σ > 1$ we define

$O_{λ}^{α} : = {M_{σ}^{α} (χ_{\frac{1}{3} Q_{0}} | \nabla^{2} z |) > λ} \cup {α M_{σ}^{α} (χ_{\frac{1}{3} Q_{0}} | \partial_{t} z |) > λ} .$

(6.1.8)

Later we will choose $α = λ^{2 - p}$ and σ smaller than the integrability exponent of $\partial_{t} z$ . We want to redefine z on $O_{λ}^{α}$ . The first step is to cover $O_{λ}^{α}$ by well selected cubes. By the lower-semi-continuity property of the maximal functions the set $O_{λ}^{α}$ is open. We assume in the following that $O_{λ}^{α}$ is non-empty. (In the case that $O_{λ}^{α}$ is empty, we do not need to truncate at all.) We cover $O_{λ}^{α}$ by an α-parabolic Whitney covering ${Q_{i}}$ with partition of unity in accordance with Lemmas 5.2.1 and 5.2.2.

Due to property (PW3) we have that $16 Q_{j} \cap (R^{d + 1} ∖ O_{λ}^{α}) \neq \emptyset$ . Thus, the definition of $O_{λ}^{α}$ implies that

${(⨍_{16 Q_{j}} | \nabla^{2} z |^{σ} χ_{\frac{1}{3} Q_{0}} d x d t)}^{\frac{1}{σ}} ⩽ λ,$

(6.1.9)

$α {(⨍_{16 Q_{j}} | \partial_{t} z |^{σ} χ_{\frac{1}{3} Q_{0}} d x d t)}^{\frac{1}{σ}} ⩽ λ .$

(6.1.10)

Lemma 6.1.5

Assume that there exists $c_{0} > 0$ such that $λ^{p} | O_{λ}^{α} | ⩽ c_{0}$ with $p > \frac{2 d}{d + 2}$ . Then the following holds:

if $λ ⩾ λ_{0} = λ_{0} (c_{0})$ , $α = λ^{2 - p}$ and $Q_{i} \cap \frac{1}{4} Q_{0} \neq \emptyset$ , then $Q_{i} \subset \frac{1}{3} Q_{0}$ and $Q_{j} \subset \frac{1}{3} Q_{0}$ for all $j \in A_{i}$ .

Proof

Let $Q_{i} \cap \frac{1}{4} Q_{0} \neq \emptyset$ . We claim that $Q_{i} \subset \frac{7}{24} Q_{0} \subset \frac{1}{3} Q_{0}$ . Let $s_{i} : = α r_{i}^{2}$ . It suffices to show that $r_{i}, s_{i} \to 0$ as $λ \to \infty$ . Because $Q_{i} \subset O_{λ}^{α}$ and by assumption, we find

$λ^{2} r_{i}^{d + 2} = λ^{p} s_{i} r_{i}^{d} ⩽ c λ^{p} | Q_{i} | ⩽ c λ^{p} | O_{λ}^{α} | ⩽ c c_{0} .$

(6.1.11)

This implies that $r_{i} ⩽ {(c c_{0} λ^{- 2})}^{\frac{1}{d + 2}} \to 0$ as $λ \to \infty$ . Moreover, $r_{i} = s_{i}^{\frac{1}{2}} α^{- \frac{1}{2}}$ and (6.1.11) imply

$c c_{0} ⩾ λ^{p} s_{i} r_{i}^{d} = λ^{p} s_{i}^{\frac{d + 2}{2}} α^{- \frac{3}{2}} = λ^{\frac{d + 2}{2} p - d} s_{i}^{\frac{d + 2}{2}} .$

If $p > \frac{2 d}{d + 2}$ , then $λ \to \infty$ implies $s_{i} \to 0$ as desired.

The claim on $j \in A_{i}$ follows from the fact that $Q_{i}$ and $Q_{j}$ have comparable size and that $\frac{7}{24} Q_{0}$ is strictly contained in $\frac{1}{3} Q_{0}$ . □

Let us show that the assumption $λ^{p} | O_{λ}^{α} | ⩽ c_{0}$ from Lemma 6.1.5 is satisfied in our situation. To do this we assume from now on that

$α : = λ^{2 - p}$

(6.1.12)

and that $σ < \min {p, p^{'}}$ .

Lemma 6.1.6

Let $c_{0} : = {‖ \nabla^{2} z ‖}_{L^{p} (\frac{1}{3} Q_{0})}^{p} + {‖ \partial_{t} z ‖}_{L^{p^{'}} (\frac{1}{3} Q_{0})}^{p^{'}}$ . Then

$λ^{p} | O_{λ}^{α} | ⩽ c_{0} .$

Proof

It follows from the weak-type estimate of $M_{σ}^{α}$ in (5.2.5), if $σ < \min {p, p^{'}}$ , then

$\begin{matrix} | O_{λ}^{α} | & ⩽ c λ^{- p} {‖ \nabla^{2} z ‖}_{L^{p} (\frac{1}{3} Q_{0})}^{p} + c {(λ α^{- 1})}^{- p^{'}} {‖ \partial_{t} z ‖}_{L^{p^{'}} (\frac{1}{3} Q_{0})}^{p^{'}} \\ = c λ^{- p} ({‖ \nabla^{2} z ‖}_{L^{p} (\frac{1}{3} Q_{0})}^{p} + {‖ \partial_{t} z ‖}_{L^{p^{'}} (\frac{1}{3} Q_{0})}^{p^{'}}) . \end{matrix}$

□

In the following we choose $λ_{0}$ such that the conclusion of Lemma 6.1.5 is valid and assume $λ ⩾ λ_{0}$ . Without loss of generality we can assume further that

$λ_{0} ⩾ {(⨍_{\frac{1}{3} Q_{0}} | \nabla^{2} z |^{σ} d x d t)}^{\frac{1}{σ}} + r_{0}^{- 2} {(⨍_{\frac{1}{3} Q_{0}} | z |^{σ} d x d t)}^{\frac{1}{σ}} .$

(6.1.13)

We define

$I : = {i : Q_{i} \cap \frac{1}{4} Q_{0} \neq \emptyset} .$

Then Lemma 6.1.5 implies that $Q_{i} \subset \frac{1}{3} Q_{0}$ (and $Q_{j} \subset \frac{1}{3} Q_{0}$ for $j \in A_{i}$ ) for all $i \in I$ . For each $i \in I$ we define local approximation $z_{i}$ for z on $Q_{i}$ by

$z_{i} : = Π_{I_{i}}^{0} Π_{B_{i}}^{1} (z),$

(6.1.14)

where $Π_{B_{i}}^{1} (z)$ is the first order averaged Taylor polynomial [37,63] with respect to space and $Π_{I_{i}}^{0}$ is the zero order averaged Taylor polynomial in time. Note that this definition implies the Poincaré-type inequality.

Lemma 6.1.7

For all $j \in N$ and $1 ⩽ s < \infty$ , if $\nabla^{2} z, \partial_{t} z \in L^{s} (\frac{1}{4} Q_{0})$ , then

$\begin{matrix} ⨍_{Q_{j}} | \frac{z - z_{j}}{r_{j}^{2}} |^{s} d x d t + ⨍_{Q_{j}} | \frac{\nabla (z - z_{j})}{r_{j}} |^{s} d x d t \\ ⩽ c ⨍_{Q_{j}} | \nabla^{2} z |^{s} d x d t + c α^{s} ⨍_{Q_{j}} | \partial_{t} z |^{s} d x d t . \end{matrix}$

Proof

The estimate is a consequence of Fubini's Theorem, Poincaré estimates and the properties of the averaged Taylor polynomials see Lemma 3.1 of [63]. We find

$\begin{matrix} ⨍_{Q_{j}} | \frac{z - z_{j}}{r_{j}^{2}} |^{s} d x d t \\ ⩽ c ⨍_{Q_{j}} | \frac{z - Π_{B_{j}}^{1} (z)}{r_{j}^{2}} |^{s} d x d t + c ⨍_{B_{j}} ⨍_{I_{j}} | \frac{Π_{B_{j}}^{1} (z) - Π_{I_{j}}^{0} Π_{B_{j}}^{1} (z)}{r_{j}^{2}} |^{s} d x d t \\ ⩽ c ⨍_{Q_{j}} | \nabla^{2} z |^{s} d x d t + c α ⨍_{I_{j}} ⨍_{B_{j}} | \partial_{t} Π_{B_{j}}^{1} (z) |^{s} d x d t . \end{matrix}$

Now the continuity of $Π_{B_{j}}^{1}$ on $L^{s}$ gives the estimate. Similarly we find (since all norms for polynomials are equivalent)

$\begin{matrix} ⨍_{Q_{j}} | \frac{\nabla (z - z_{j})}{r_{j}} |^{s} d x d t \\ ⩽ c ⨍_{Q_{j}} | \frac{\nabla (z - Π_{B_{j}}^{1} (z))}{r_{j}} |^{s} d x d t + c ⨍_{Q_{j}} | \frac{\nabla (Π_{B_{j}}^{1} (z) - Π_{I_{j}}^{0} Π_{B_{j}}^{1} (z))}{r_{j}} |^{s} d x d t \\ ⩽ c ⨍_{Q_{j}} | \frac{\nabla (z - Π_{B_{j}}^{1} (z))}{r_{j}} |^{s} d x d t + c ⨍_{Q_{j}} | \frac{Π_{B_{j}}^{1} (z) - Π_{I_{j}}^{0} Π_{B_{j}}^{1} (z)}{r_{j}^{2}} |^{s} d x d t \\ ⩽ c ⨍_{Q_{j}} | \nabla^{2} z |^{s} d x d t + c α ⨍_{Q_{j}} | \partial_{t} z |^{s} d x d t . \end{matrix}$

□

We can now define our truncation $z_{λ}^{α}$ for $λ ⩾ λ_{0}$ on $\frac{1}{4} Q_{0}$ by

$z_{λ}^{α} : = z - \sum_{i \in I} φ_{i} (z - z_{i}) .$

(6.1.15)

It suffices to sum over i with $Q_{i} \cap \frac{1}{4} Q_{0} \neq \emptyset$ .

Since the $φ_{i}$ are locally finite, this sum is pointwise well-defined. We will see later that the sum converges also in other topologies. Using $\sum_{i \in I} φ_{i} = 1$ on $\frac{1}{4} Q_{0}$ , we can also write $z_{λ}^{α}$ in the form

$z_{λ}^{α} = {\begin{matrix} z & in \frac{1}{4} Q_{0} ∖ O_{λ}^{α}, \\ \sum_{i \in I} φ_{i} z_{i} & in \frac{1}{4} Q_{0} \cap O_{λ}^{α} . \end{matrix}$

(6.1.16)

In the following we describe some properties of the truncation (e.g. $\nabla^{2} z_{λ}^{α} \in L^{\infty} (\frac{1}{4} Q_{0})$ ).

Lemma 6.1.8

For all $j \in N$ and all $k \in N$ with $Q_{j} \cap Q_{k} \neq \emptyset$ we have

(a) $⨍_{Q_{j}} | \nabla^{2} z | d x d t + α ⨍_{Q_{j}} | \partial_{t} z | d x d t ⩽ c λ$ .

(b) ${‖ z_{j} - z_{k} ‖}_{L^{\infty} (Q_{j})} ⩽ c ⨍_{Q_{j}} | z - z_{j} | d x d t + c ⨍_{Q_{k}} | z - z_{k} | d x d t$ .

Proof

Part (a) follows from $Q_{j} \subset 16 Q_{j}$ and $16 Q_{j} \cap O_{λ}^{∁} \neq \emptyset$ , so

$⨍_{16 Q_{j}} (| \nabla^{2} z | + α | \partial_{t} z |) χ_{\frac{1}{3} Q_{0}} d x d t ⩽ {(⨍_{16 Q_{j}} {(| \nabla^{2} z | + α | \partial_{t} z |)}^{σ} χ_{\frac{1}{3} Q_{0}} d x d t)}^{\frac{1}{σ}} ⩽ c λ .$

Part (b) follows from the geometric property of the $Q_{j}$ . If $Q_{j} \cap Q_{k} \neq \emptyset$ , then $| Q_{j} \cap Q_{k} | ⩾ c \max {| Q_{j} |, | Q_{k} |}$ . This and the norm equivalence for linear polynomials imply

$\begin{matrix} {‖ z_{j} - z_{k} ‖}_{L^{\infty} (Q_{j})} & ⩽ c ⨍_{Q_{j} \cap Q_{k}} | z_{j} - z_{k} | d x d t \\ ⩽ c ⨍_{Q_{j}} | z_{j} - z | d x + c ⨍_{Q_{k}} | z - z_{k} | d x . \end{matrix}$

Finally, (c) is a consequence of Lemma 6.1.7, (a) and (b). □

Next, we prove the stability of the truncation.

Lemma 6.1.9

Let $1 < s < \infty$ and $z \in L^{s} (R; W^{2, s} (R^{3}))$ . Then

$\begin{matrix} {‖ z_{λ}^{α} ‖}_{L^{s} (\frac{1}{4} Q_{0})} & ⩽ c {‖ z ‖}_{L^{s} (\frac{1}{3} Q_{0})}, \\ {‖ \nabla z_{λ}^{α} ‖}_{L^{s} (\frac{1}{4} Q_{0})} & ⩽ c {‖ \nabla z ‖}_{L^{s} (\frac{1}{3} Q_{0})} + c α r_{0} {‖ \partial_{t} z ‖}_{L^{s} (\frac{1}{3} Q_{0})}, \\ {‖ \nabla^{2} z_{λ}^{α} ‖}_{L^{s} (\frac{1}{4} Q_{0})} + α {‖ \partial_{t} z_{λ}^{α} ‖}_{L^{s} (\frac{1}{3} Q_{0})} & ⩽ c {‖ \nabla^{2} z ‖}_{L^{s} (\frac{1}{3} Q_{0})} + c α {‖ \partial_{t} z ‖}_{L^{s} (\frac{1}{3} Q_{0})} . \end{matrix}$

Moreover, the sum in (6.1.15) converges in $L^{s} (\frac{1}{4} I_{0}, W^{2, s} (\frac{1}{4} B_{0}))$ .

Proof

We first show that the sum in (6.1.15) converges absolutely in $L^{s} (\frac{1}{4} Q_{0})$ :

$\int_{\frac{1}{4} Q_{0}} | z - z_{λ}^{α} |^{s} d x ⩽ \sum_{i \in I} \int_{Q_{i}} | z - z_{i} |^{s} d x d t ⩽ c \sum_{i \in I} \int_{Q_{i}} | z |^{s} d x d t ⩽ c \int_{\frac{1}{3} Q_{0}} | z |^{s} d t,$

where we used continuity of the mapping $z \mapsto z_{i}$ in $L^{s} (Q_{i})$ , (PP1) and the finite intersection property of $Q_{i}$ (PW4). We start by showing the estimate for the second derivatives

$\begin{matrix} \int_{O_{λ}^{α}} | \nabla^{2} (z - z_{λ}^{α}) |^{s} d x d t = | \sum_{i \in I} \int_{Q_{i}} \nabla^{2} (φ_{i} (z - z_{i})) d x d t | \\ ⩽ c \sum_{i \in I} \int_{Q_{i}} | \nabla^{2} z |^{s} + | \frac{\nabla (z - z_{i})}{r_{i}} |^{s} + | \frac{z - z_{i}}{r_{i}^{2}} |^{s} d x d t . \end{matrix}$

For the time derivative we find (since $z_{i}$ is constant in time), that

$\begin{matrix} \int_{O_{λ}^{α}} | \partial_{t} (z - z_{λ}^{α}) |^{s} d x d t = | \sum_{i \in I} \int_{Q_{i}} \partial_{t} (φ_{i} (z - z_{i})) d x d t | \\ ⩽ c \sum_{i \in I} \int_{Q_{i}} | \partial_{t} z |^{s} + | \frac{z - z_{i}}{α r_{i}^{2}} |^{s} d x d t . \end{matrix}$

(6.1.17)

Using Lemma 6.1.7 and the finite intersection of the $Q_{i}$ shows that

$\begin{matrix} \int_{\frac{1}{4} Q_{0}} | \nabla^{2} (z - z_{λ}^{α}) |^{s} + α^{s} | \partial_{t} (z - z_{λ}^{α}) |^{s} d x d t & ⩽ c \sum_{i \in I} \int_{Q_{i}} | \nabla^{2} z |^{s} + α^{s} | \partial_{t} z |^{s} d x d t \\ ⩽ c \int_{\frac{1}{3} Q_{0}} | \nabla^{2} z |^{s} + α^{s} | \partial_{t} z |^{s} d x d t . \end{matrix}$

The estimate of the gradient is analogous, since

$\int_{O_{λ}^{α}} | \nabla (z - z_{λ}^{α}) |^{s} d x d t ⩽ \sum_{i \in I} | \nabla (z - z_{i}) |^{s} + | \frac{z - z_{i}}{r_{i}} |^{s} d x d t .$

□

The truncation $z_{λ}^{α}$ has better regularity properties than z. Indeed, $\nabla z$ is Lipschitz.

Lemma 6.1.10

For $λ > λ_{0}$ we have

${‖ \nabla^{2} z_{λ}^{α} ‖}_{L^{\infty} (\frac{1}{4} Q_{0})} + r_{0}^{- 1} {‖ \nabla z_{λ}^{α} ‖}_{L^{\infty} (\frac{1}{4} Q_{0})} + r_{0}^{- 2} {‖ z_{λ}^{α} ‖}_{L^{\infty} (\frac{1}{4} Q_{0})} + α {‖ \partial_{t} z_{λ}^{α} ‖}_{L^{\infty} (\frac{1}{4} Q_{0})} ⩽ c λ .$

Proof

If $(t, x) \in Q_{i}$ , then

$| \nabla^{2} z_{λ}^{α} (t, x) | = | \sum_{j \in A_{i}} \nabla^{2} (φ_{j} z_{j}) (t, x) | ⩽ \sum_{j \in A_{i}} | \nabla^{2} (φ_{j} (z_{j} - z_{i})) (t, x) |$

because ${φ_{j}}$ is a partition of unity. Now we find (since all norms on polynomials are equivalent, $# A_{j} ⩽ c$ and Lemma 6.1.8) that

$| \nabla^{2} z_{λ}^{α} (t, x) | ⩽ c \sum_{j \in A_{i}} \frac{{‖ z_{i} - z_{j} ‖}_{L^{\infty} (Q_{i})}}{r_{i}^{2}} ⩽ c λ .$

Concerning the time derivative for $(t, x) \in Q_{i}$ since $z_{i}$ is constant in time we find that

$\begin{matrix} | \partial_{t} z_{λ}^{α} (t, x) | & = | \partial_{t} \sum_{j \in A_{i}} (φ_{j} z_{j}) (t, x) | ⩽ \sum_{j \in A_{i}} | \partial_{t} (φ_{j}) (z_{j} - z_{i}) (t, x) | \\ ⩽ \sum_{j \in A_{i}} \frac{{‖ z_{i} - z_{j} ‖}_{L^{\infty} (Q_{i})}}{α r_{i}^{2}} ⩽ \frac{c λ}{α} . \end{matrix}$

The zero order term is estimated by Poincaré's inequality; first in time and then in space

$\begin{matrix} r_{0}^{- 2} {‖ z_{λ}^{α} ‖}_{L^{\infty} (\frac{1}{4} I_{0}; L^{\infty} (\frac{1}{4} B_{0}))} & ⩽ c α {‖ \partial_{t} z_{λ}^{α} ‖}_{L^{\infty} (\frac{1}{4} Q_{0})} + c r_{0}^{- 2} {‖ z_{λ}^{α} ‖}_{L^{1} (\frac{1}{4} I_{0}; L^{\infty} (\frac{1}{4} B_{0}))} \\ ⩽ c λ + c {‖ \nabla^{2} z_{λ}^{α} ‖}_{L^{\infty} (\frac{1}{4} Q_{0})} + c r_{0}^{- 2} {‖ z_{λ}^{α} ‖}_{L^{1} (\frac{1}{4} Q_{0})} . \end{matrix}$

This implies, by the norm equivalence of polynomials, Jensen's inequality, Lemma 6.1.9 and (6.1.13),

$r_{0}^{- 1} {‖ \nabla z_{λ}^{α} ‖}_{L^{\infty} (\frac{1}{4} Q_{0})} + r_{0}^{- 2} {‖ z_{λ}^{α} ‖}_{L^{\infty} (\frac{1}{4} Q_{0})} ⩽ c λ + r_{0}^{- 2} {‖ z ‖}_{L^{σ} (\frac{1}{3} Q_{0})} ⩽ c λ .$

□

The next lemma will control the time error we get when we apply the truncation as a test function.

Lemma 6.1.11

For all $ζ \in C_{0}^{\infty} (\frac{1}{4} Q_{0})$ with ${‖ \nabla^{2} ζ ‖}_{\infty} ⩽ c$ and $λ ⩾ λ_{0}$ ,

$| \int_{\frac{1}{4} Q_{0}} \partial_{t} (z - z_{λ}^{α}) Δ (ζ z_{λ}^{α}) d x d t | ⩽ c α^{- 1} λ^{2} | O_{λ}^{α} |,$

where the constant c is independent of α and λ.

Proof

We use Hölder's inequality and Lemma 6.1.10 to derive

$\begin{matrix} (I) & : = | \int_{\frac{1}{4} Q_{0}} \partial_{t} (z - z_{λ}^{α}) Δ (ζ z_{λ}^{α}) d x d t | \\ ⩽ \sum_{i \in I} {(\int_{Q_{i}} | \partial_{t} (φ_{i} (z - z_{i}) |^{σ} d x d t)}^{\frac{1}{σ}} {(\int_{Q_{i}} | Δ (ζ z_{λ}^{α}) |^{σ^{'}} d x d t)}^{\frac{1}{σ^{'}}} \\ ⩽ c λ \sum_{i \in I} | Q_{i} | {(⨍_{Q_{i}} | \partial_{t} (φ_{i} (z - z_{i}) |^{σ} d x d t)}^{\frac{1}{σ}} . \end{matrix}$

Combining this with (6.1.17), (6.1.9) and (6.1.10) yields

$\begin{matrix} (I) & ⩽ c λ \sum_{i \in I} | Q_{i} | (α^{- 1} {(⨍_{Q_{j}} | \nabla^{2} z |^{σ} d x d t)}^{\frac{1}{σ}} + {(⨍_{Q_{j}} | \partial_{t} z |^{σ} d x d t)}^{\frac{1}{α}}) \\ ⩽ c α^{- 1} λ^{2} \sum_{i \in I} | Q_{i} | ⩽ c α^{- 1} λ^{2} | O_{λ}^{α} |, \end{matrix}$

using the local finiteness of the ${Q_{i}}$ in the final step. □

Theorem 6.1.24

Let $1 < p < \infty$ with $p, p^{'} > σ$ . Let $w_{m}$ and $H_{m}$ satisfy $\partial_{t} Δ w_{m} = - div div H_{m}$ in the sense of distributions $D^{'} (\frac{1}{2} Q_{0})$ , see (6.1.5). Further assume that $w_{m}$ is a weak null sequence in $L^{p} (\frac{1}{2} I_{0}; W^{2, p} (\frac{1}{2} B_{0}))$ and a strong null sequence in $L^{σ} (\frac{1}{2} Q_{0})$ . Further, assume that $H_{m} = H_{m}^{1} + H_{m}^{2}$ such that $H_{m}^{1}$ is a weak null sequence in $L^{p^{'}} (Q_{0})$ and $H_{m}^{2}$ converges strongly to zero in $L^{σ} (Q_{0})$ . Define $z_{m} : = Δ Δ_{\frac{1}{2} B_{0}}^{- 2} Δ w_{m}$ pointwise in time on $\frac{1}{2} I_{0}$ . Then there is a double sequence $(λ_{m, k}) \subset R^{+}$ and $k_{0} \in N$ such that

(a) $2^{2^{k}} ⩽ λ_{m, k} ⩽ 2^{2^{k + 1}}$

such that the double sequence $z_{m, k} : = z_{λ_{m, k}}^{α_{m, k}}$ with $α_{m, k} : = λ_{m, k}^{2 - p}$ satisfies the following properties for all $k ⩾ k_{0}$

(b) ${z_{m, k} \neq z} \subset O_{m, k} : = O_{λ_{m, k}}^{α_{m, k}}$ ,

(d) $z_{m, k} \to 0$ and $\nabla z_{m, k} \to 0$ in $L^{\infty} (\frac{1}{4} Q_{0})$ for $m \to \infty$ and k fixed,

(e) $\nabla^{2} z_{m, k} ⇀^{⁎} 0$ in $L^{\infty} (\frac{1}{4} Q_{0})$ for $m \to \infty$ and k fixed,

(f) We have for all $ζ \in C_{0}^{\infty} (\frac{1}{4} Q_{0})$

$| \int (\partial_{t} (z_{m} - z_{m, k})) \cdot Δ (ζ z_{m, k}) d x d t | ⩽ c λ_{m, k}^{p} | O_{m, k} |,$

(g) $\underset{m \to \infty}{\lim \sup} λ_{m, k}^{p} | O_{m, k} | ⩽ c 2^{- k} \sup_{m} ({‖ \nabla^{2} z_{m} ‖}_{p} + c {‖ H_{m}^{1} ‖}_{p^{'}}^{\frac{1}{p - 1}})$ .

Proof

Let us assume that $λ_{m, k}$ satisfies (a). We will choose the precise values of $λ_{m, k}$ later. Due to Lemma 6.1.3 we have $z_{m} ⇀ 0$ in $L^{p} (\frac{1}{4} I_{0}; W^{2, p} (\frac{1}{4} B_{0}))$ ; this is due to the fact that the operator $w \mapsto Δ Δ_{\frac{1}{2} B_{0}}^{- 2} Δ w = z$ is linear and continuous in $L^{p} (\frac{1}{4} I_{0}; W^{2, p} (\frac{1}{4} B_{0}))$ . Then the properties (b) and (c) follow from Lemma 6.1.10. Moreover, Corollary 6.1.1 ensures that the strong convergence in $L^{σ} (\frac{1}{2} Q_{0})$ transfers from $w_{m}$ to $z_{m}$ . By Lemma 6.1.9 we get the same for $z_{m, k}$ and that the sequence $\nabla^{2} z_{m, k}$ is, for fixed k and s, bounded in $L^{s} (\frac{1}{4} Q_{0})$ . The combination of these convergence properties implies (by interpolation) (d). Moreover, the boundedness of $\nabla^{2} z_{m, k}$ in $L^{s} (\frac{1}{4} Q_{0})$ implies the weak convergence of a subsequence. Since (d) ensures that the limit is zero, we get, by the usual arguments, weak convergence of the whole sequence. This proves (e). Moreover, (f) follows by Lemma 6.1.11 and the choice of $α_{m, k}$ .

It remains to choose $2^{2^{k}} ⩽ λ_{m, k} ⩽ 2^{2^{k + 1}}$ such that (g) holds. We use the decomposition

$\begin{matrix} \partial_{t} z_{m} & = Δ Δ_{\frac{1}{2} B_{0}}^{- 2} div div H_{m} = Δ Δ_{\frac{1}{2} B_{0}}^{- 2} div div H_{m}^{1} + Δ Δ_{\frac{1}{2} B_{0}}^{- 2} div div H_{m}^{2} \\ = : h_{m}^{1} + h_{m}^{2} . \end{matrix}$

We decompose

$\begin{matrix} O_{m, k} & = {M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | \nabla^{2} z_{m, k} |) > λ_{m, k}} \cup {α_{m, k} M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | \partial_{t} z_{m} |) > λ_{m, k}} \\ \subset {M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | \nabla^{2} z_{m, k} |) > λ_{m, k}} \cup {α_{m, k} M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | h_{m}^{1} |) > \frac{1}{2} λ_{m, k}} \\ \cup {α_{m, k} M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | h_{m}^{2} |) > \frac{1}{2} λ_{m, k}} \\ = : I \cup I I \cup I I I . \end{matrix}$

Define

$g_{m} : = 2 M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | \nabla^{2} z_{m} |) + {(2 M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | h_{m}^{1} |))}^{\frac{1}{p - 1}} .$

Then by the boundedness of $M_{σ}$ on $L^{p}$ and $L^{p^{'}}$ (using $p, p^{'} > σ$ ), as well as Corollary 6.1.3, we have

$\begin{matrix} {‖ g_{m} ‖}_{p} & ⩽ {‖ 2 M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | \nabla^{2} z_{m} |) ‖}_{p} + {‖ {(2 M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | h_{m}^{1} |))}^{\frac{1}{p - 1}} ‖}_{p} \\ = {‖ 2 M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | \nabla^{2} z_{m} |) ‖}_{p} + {‖ 2 M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | h_{m}^{1} |) ‖}_{p^{'}}^{\frac{1}{p - 1}} \\ ⩽ c {‖ \nabla^{2} z_{m} ‖}_{L^{p} (\frac{1}{3} Q_{0})} + c {‖ h_{m}^{1} ‖}_{L^{p^{'}} (\frac{1}{2} Q_{0})}^{\frac{1}{p - 1}} \\ ⩽ c {‖ \nabla^{2} z_{m} ‖}_{L^{p} (\frac{1}{3} Q_{0})} + c {‖ H_{m}^{1} ‖}_{L^{p^{'}} (\frac{1}{2} Q_{0})}^{\frac{1}{p - 1}} . \end{matrix}$

Let $K : = \sup_{m} ({‖ \nabla^{2} z_{m} ‖}_{p} + c {‖ h_{m}^{1} ‖}_{p^{'}}^{\frac{1}{p - 1}})$ . In particular, ${‖ g_{m} ‖}_{p} ⩽ K$ uniformly in k. Note that

$\begin{matrix} I \cup I I & = {M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | \nabla^{2} z_{m, k} |) > λ_{m, k}} \cup {{(M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | h_{m}^{1} |))}^{\frac{1}{p - 1}} > λ_{m, k}} \\ \subset {2 M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | \nabla^{2} z_{m, k} |) + {(2 M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | h_{m}^{1} |))}^{\frac{1}{p - 1}} > λ_{m, k}} \\ = {g_{m} > λ_{m, k}} . \end{matrix}$

We estimate

$\begin{matrix} \int_{R^{d + 1}} | g_{m} |^{p} d x & = \int_{R^{d + 1}} \int_{0}^{\infty} \frac{1}{p} t^{p - 1} χ_{{| g_{m} | > t}} d t d x ⩾ \int_{R^{d + 1}} \sum_{k \in N} \frac{1}{p} 2^{k} χ_{{| g_{m} | > 2^{k + 1}}} d x \\ ⩾ \sum_{j \in N} \sum_{k = 2^{j}}^{2^{j + 1} - 1} \frac{1}{p} 2^{k p} | {| g_{m} | > 2^{k + 1}} | . \end{matrix}$

For fixed $m, j$ the sum over k involves $2^{j}$ summands and not all of them can be large. Consequently there exists $λ_{m, k} \in {2^{2^{k} + 1}, \dots, 2^{2^{k + 1}}}$ , such that

$λ_{m, k}^{p} | {| g_{m} | > λ_{m, k}} | ⩽ c 2^{- k} K^{p}$

uniformly in m and k, and hence

$λ_{m, k}^{p} | I \cup I I | ⩽ λ_{m, k}^{p} | {g_{m} > λ_{m, k}} | ⩽ c 2^{- k} K^{p} .$

(6.1.18)

On the other hand, from the weak- $L^{σ}$ estimate for $M_{σ}^{α_{m, k}}$ we see that

$\begin{matrix} \underset{m \to \infty}{\lim \sup} (λ_{m, k}^{p} | I I I |) & = \underset{m \to \infty}{\lim \sup} (λ_{m, k}^{p} | {α_{m, k} M_{σ}^{α_{m, k}} (χ_{\frac{1}{3} Q_{0}} | h_{m}^{2} |) > \frac{1}{2} λ_{m, k}} |) \\ ⩽ \underset{m \to \infty}{\lim \sup} (c λ_{m, k}^{p} {‖ h_{m}^{2} ‖}_{L^{σ} (\frac{1}{3} Q_{0})}^{σ} {(α_{m, k} / λ_{m, k})}^{σ}) . \end{matrix}$

Since $2^{2^{k} + 1} ⩽ λ_{m, k} ⩽ 2^{2^{k + 1}}$ , $α_{m, k} = λ_{m, k}^{2 - p}$ and $h_{m}^{2} \to 0$ in $L^{σ} (\frac{1}{2} Q_{0})$ (which is a consequence of $H_{m}^{2} \to 0$ in $L^{σ} (\frac{1}{2} Q_{0})$ and Corollary 6.1.3), it follows that

$\underset{m \to \infty}{\lim \sup} (λ_{m, k}^{p} | I I I |) = 0 .$

This and (6.1.18) prove (g). □

Theorem 6.1.25

Let $1 < p < \infty$ with $p, p^{'} > σ$ . Let $u_{m}$ and $G_{m}$ satisfy $\partial_{t} u_{m} = - div G_{m}$ in the sense of distributions $D_{div}^{'} (Q_{0})$ . Assume that $u_{m}$ is a weak null sequence in $L^{p} (I_{0}; W^{1, p} (B_{0}))$ and a strong null sequence in $L^{σ} (Q_{0})$ and bounded in $L^{\infty} (I_{0}, T; L^{σ} (B_{0}))$ . Further assume that $G_{m} = G_{m}^{1} + G_{m}^{2}$ such that $G_{m}^{1}$ is a weak null sequence in $L^{p^{'}} (Q_{0})$ and $G_{m}^{2}$ converges strongly to zero in $L^{σ} (Q_{0})$ . Then there is a double sequence $(λ_{m, k}) \subset R^{+}$ and $k_{0} \in N$ with

(a) $2^{2^{k}} ⩽ λ_{m, k} ⩽ 2^{2^{k + 1}}$

such that the double sequences $u_{m, k} : = u_{λ_{m, k}}^{α_{m, k}} \in L^{1} (Q_{0})$ , $α_{m, k} : = λ_{m, k}^{2 - p}$ and $O_{m, k} : = O_{λ_{m, k}}^{α_{m, k}}$ (defined in Theorem 6.1.24) satisfy the following properties for all $k ⩾ k_{0}$ .

(b) $u_{m, k} \in L^{s} (\frac{1}{4} I_{0}; W_{0, div}^{1, s} (\frac{1}{6} B_{0}))$ for all $s < \infty$ and $supp (u_{m, k}) \subset \frac{1}{6} Q_{0}$ .

(d) ${‖ \nabla u_{m, k} ‖}_{L^{\infty} (\frac{1}{4} Q_{0})} ⩽ c λ_{m, k}$ .

(e) $u_{m, k} \to 0$ in $L^{\infty} (\frac{1}{4} Q_{0})$ for $m \to \infty$ and k fixed.

(f) $\nabla u_{m, k} ⇀^{⁎} 0$ in $L^{\infty} (\frac{1}{4} Q_{0})$ for $m \to \infty$ and k fixed.

(g) $\underset{m \to \infty}{\lim \sup} λ_{m, k}^{p} | O_{m, k} | ⩽ c 2^{- k} .$

(h) $\underset{m \to \infty}{\lim \sup} | \int G_{m} : \nabla u_{m, k} d x d t | ⩽ c λ_{m, k}^{p} | O_{m, k} |$ .

Proof

We define, pointwise in time on $I_{0}$ ,

$\begin{matrix} {\tilde{u}}_{m} & : = γ u_{m} - {Bog}_{B_{0} ∖ \frac{1}{2} B_{0}} (\nabla γ \cdot u_{m}), \\ w_{m} & : = {curl}^{- 1} {\tilde{u}}_{m}, \\ z_{m} & : = Δ Δ_{\frac{1}{2} Q_{0}}^{- 2} Δ w_{m}, \end{matrix}$

where $γ \in C_{0}^{\infty} (Q_{0})$ with $χ_{\frac{1}{2} Q_{0}} ⩽ γ ⩽ χ_{Q_{0}}$ . Then we apply Theorem 6.1.24 to the sequence $z_{m}$ . Finally, let

$u_{m, k} : = curl (ζ z_{m, k}) + curl (ζ (w_{m} - z_{m})),$

(6.1.19)

where $ζ \in C_{0}^{\infty} (\frac{1}{6} Q_{0})$ with $χ_{\frac{1}{8} Q_{0}} ⩽ ζ ⩽ χ_{\frac{1}{6} Q_{0}}$ . This means on $\frac{1}{8} Q_{0}$ we have

$u_{m, k} = u_{m} + curl (z_{m, k} - z_{m}) .$

Note that $curl (w_{m} - z_{m})$ is harmonic (in space) on $\frac{1}{2} Q_{0}$ and bounded in time, due to the assumption that $u_{m}$ is bounded uniformly in $L^{\infty} (I_{0}; L^{σ} (B_{0}))$ , which transfers to $w_{m}$ and $z_{m}$ by Lemma 6.1.1 and 6.1.4. This allows us to estimate the higher order spaces derivatives on $\frac{1}{4} Q_{0}$ by lower order ones on $\frac{1}{2} Q_{0}$ . This, (6.1.19) and Theorem 6.1.24 immediately imply all the claimed properties except (h).

The claim of (g) follows exactly as (g) of Theorem 6.1.24.

Let us prove (h). It follows by simple density arguments that $u_{m, k}$ is an admissible test function for the equation $\partial_{t} u_{m} = - div G_{m}$ . We thus obtain

$\begin{matrix} \int G_{m} : \nabla u_{m, k} d x d t \\ = \int \partial_{t} u_{m} \cdot u_{m, k} d x d t \\ = \int (\partial_{t} curl w_{m}) \cdot curl (ζ z_{m, k}) d x d t \\ + \int (\partial_{t} curl w_{m}) \cdot curl (ζ (w_{m} - z_{m})) d x d t \\ = - \int (\partial_{t} z_{m}) \cdot Δ (ζ z_{m, k}) d x d t - \int (\partial_{t} z_{m}) \cdot Δ (ζ (w_{m} - z_{m})) d x d t \\ = : T_{1} + T_{2} . \end{matrix}$

Here we took into account $curl curl w_{m} = - Δ w_{m}$ (due to $div w_{m} = 0$ ) and $Δ w_{m} = Δ z_{m}$ . By assumption $G_{m}$ is bounded in $L^{σ} (Q_{0})$ . Using regularity properties of harmonic functions (for $w_{m} - z_{m}$ ) as well as Lemma 6.1.3 and Lemma 6.1.1 we gain (after choosing a subsequence)

$\begin{matrix} {(⨍_{Q_{0}} | Δ (ζ (w_{m} - z_{m})) |^{σ^{'}} d x d t)}^{\frac{1}{σ^{'}}} \\ ⩽ c r_{0}^{- 2} {(⨍_{\frac{1}{4} Q_{0}} | w_{m} - z_{m} |^{\frac{3 σ}{3 + σ}} d x d t)}^{\frac{3 + σ}{3 σ}} \\ ⩽ c r_{0}^{- 2} {(⨍_{\frac{1}{2} Q_{0}} | w_{m} |^{\frac{3 σ}{3 + σ}} d x d t)}^{\frac{3 + σ}{3 σ}} \\ ⩽ c r_{0}^{- 3} {(⨍_{Q_{0}} | {\tilde{u}}_{m} |^{σ} d x d t)}^{\frac{1}{σ}} ⟶ 0 as m \to \infty . \end{matrix}$

Since, additionally, $\partial_{t} z_{m}$ is uniformly bounded in $L^{σ} (\frac{1}{2} Q_{0})$ by Lemma 6.1.3, we have $T_{2} \to 0$ as $m \to \infty$ . Furthermore, there holds

$\begin{matrix} T_{1} & = \int (\partial_{t} (z_{m} - z_{m, k})) \cdot Δ (ζ z_{m, k}) d x d t + \int (\partial_{t} z_{m, k}) \cdot Δ (ζ z_{m, k}) d x d t \\ = : T_{1, 1} + T_{1, 2}, \end{matrix}$

where the first term can be bounded using Theorem 6.1.24 (f). So it remains to show that

$T_{1, 2} : = \int (\partial_{t} z_{m, k}) \cdot Δ (ζ z_{m, k}) d x d t ⟶ 0 as m \to \infty .$

We have

$\begin{matrix} T_{1, 2} & = - \int \frac{1}{2} \partial_{t} (| \nabla z_{m, k} |^{2}) ζ d x d t + \int (\partial_{t} z_{m, k}) \cdot div (\nabla ζ \otimes z_{m, k}) d x d t \\ = \int \frac{1}{2} | \nabla z_{m, k} |^{2} \partial_{t} ζ d x d t + \int (\partial_{t} z_{m, k}) \cdot div (\nabla ζ \otimes z_{m, k}) d x d t . \end{matrix}$

The first term is estimated by Theorem 6.1.24 (d). For the second we use Lemma 6.1.9 and Lemma 6.1.3 ( $s = σ$ ) to find

$\begin{matrix} \int | \partial_{t} z_{m, k} | | div (\nabla ζ \otimes z_{m, k}) | d x d t \\ ⩽ c {(\int_{\frac{1}{3} Q_{0}} | G_{m} |^{σ} + | \nabla^{2} z_{m} |^{σ} d x d t)}^{\frac{1}{σ}} {(\int_{\frac{1}{3} Q_{0}} | \nabla z_{m, k} |^{σ^{'}} + | z_{m, k} |^{σ^{'}} d x d t)}^{\frac{1}{σ^{'}}} . \end{matrix}$

Now because $G_{m}$ and $\nabla^{2} z_{m}$ are uniformly bounded in $L^{σ} (\frac{1}{2} Q_{0})$ we find by Theorem 6.1.24 (d), that

$\lim_{m \to \infty} T_{1, 2} = 0,$

which proves the claim of (h). □

The following corollary is useful in the application of the solenoidal Lipschitz truncation.

Corollary 6.1.4

Let all assumptions of Theorem 6.1.25 be satisfied with $ζ \in C_{0}^{\infty} (\frac{1}{6} Q_{0})$ with $χ_{\frac{1}{8} Q_{0}} ⩽ ζ ⩽ χ_{\frac{1}{6} Q_{0}}$ as in the proof of Theorem 6.1.25. If additionally $u_{m}$ is uniformly bounded in $L^{\infty} (I_{0}, L^{σ} (B_{0}))$ , then for every $K \in L^{p^{'}} (\frac{1}{6} Q_{0})$

$\underset{m \to \infty}{\lim \sup} | \int ((G_{m}^{1} + K) : \nabla u_{m}) ζ χ_{O_{m, k}^{∁}} d x d t | ⩽ c 2^{- k / p} .$

Proof

It follows from (f), (g) and (h) of Theorem 6.1.25 that

$\underset{m \to \infty}{\lim \sup} | \int (G_{m} + K) : \nabla u_{m, k} d x d t | ⩽ c λ_{m, k}^{p} | O_{m, k} | ⩽ c 2^{- k} .$

(6.1.20)

Recall that $u_{m, k} = curl (ζ z_{m, k}) + curl (ζ (w_{m} - z_{m}))$ . So, by Theorem 6.1.24, we have $z_{m, k}, \nabla z_{m, k} \to 0$ in $L^{\infty} (\frac{1}{4} Q_{0})$ as $m \to \infty$ with k fixed. Since $u_{m}$ is a strong null sequence in $L^{σ} (Q_{0})$ and is bounded in $L^{\infty} (I_{0}, L^{σ} (B_{0}))$ we see that $u_{m} \to 0$ strongly in $L^{s} (I_{0}, L^{σ} (B_{0}))$ for any $s \in (1, \infty)$ . By continuity of the Bogovskiĭ operator (see Theorem 2.1.6 with $A (t) = B (t) = t^{σ}$ ) we have the same convergence for ${\tilde{u}}_{m}$ . Now, Lemma 6.1.1 implies $w_{m} = {curl}^{- 1} {\tilde{u}}_{m} \to 0$ in $L^{s} (I_{0}, W^{1, σ} (R^{3}))$ . Using $z_{m} : = Δ Δ_{\frac{1}{2} Q_{0}}^{- 2} Δ w_{m}$ and Corollary 6.1.1 we also have $z_{m} \to 0$ in $L^{s} (I_{0}, W^{1, σ} (R^{3}))$ . Since $z_{m} - w_{m}$ is harmonic on $\frac{1}{4} Q_{0}$ , we have $z_{m} - w_{m} \to 0$ in $L^{s} (I_{0}, W^{2, s} (\frac{1}{6} B_{0}))$ . These convergences imply that

$\nabla u_{m, k} = ζ \nabla curl z_{m, k} + a_{m, k},$

with $a_{m, k} \to 0$ in $L^{s} (\frac{1}{6} Q_{0})$ as $m \to \infty$ with k fixed. This, the boundedness of $G_{m}$ in $L^{σ} (\frac{1}{6} Q_{0})$ , $K \in L^{p^{'}} (\frac{1}{6} Q_{0})$ and (6.1.20) imply (using $s > σ^{'}$ )

$\underset{m \to \infty}{\lim \sup} | \int ((G_{m} + K) : \nabla curl z_{m, k}) ζ d x d t | ⩽ c 2^{- k} .$

Since $G_{m} = G_{m}^{1} + G_{m}^{2}$ , $G_{m}^{2} \to 0$ in $L^{σ} (\frac{1}{6} Q_{0})$ and $z_{m, k} ⇀ 0$ in $L^{σ^{'}} (\frac{1}{6} Q z)$ for $m \to \infty$ and k fixed, we have

$\underset{m \to \infty}{\lim \sup} | \int ((G_{m}^{1} + K) : \nabla curl z_{m, k}) ζ d x d t | ⩽ c 2^{- k} .$

(6.1.21)

The boundedness of $G_{m}^{1}$ and K in $L^{p^{'}} (\frac{1}{6} Q_{0})$ and Theorem 6.1.24 and (g) prove

$\underset{m \to \infty}{\lim \sup} | \int ((G_{m}^{1} + K) : \nabla curl z_{m, k}) ζ χ_{O_{m, k}} d x d t | ⩽ c 2^{- k / p} .$

This, together with (6.1.21) and $z_{m, k} = z_{m}$ in $O_{m, k}^{∁}$ yield

$\underset{m \to \infty}{\lim \sup} | \int ((G_{m}^{1} + K) : \nabla curl z_{m}) ζ χ_{O_{m, k}^{∁}} d x d t | ⩽ c 2^{- k / p} .$

Recall that $z_{m} - w_{m} \to 0$ in $L^{s} (I_{0}, W^{2, s} (\frac{1}{6} B_{0}))$ for any $s \in (1, \infty)$ . This and the boundedness of $G_{m}^{1}$ in $L^{p^{'}} (Q_{0})$ allows us to replace $z_{m}$ in the previous integral by $w_{m}$ . Now $curl w_{m} = u_{m}$ proves the claim. □

The next corollary follows by combining Lemma 6.1.9, Lemma 6.1.10, Theorem 6.1.24 (g) (with $α = 1$ ) and the continuity of ${curl}^{- 1}$ with a scaling procedure.

Corollary 6.1.5

For some $σ > 0$ let $u \in L^{σ} (I_{0}; W_{div}^{1, σ} (B_{0})) \cap L^{\infty} (I; L^{σ} (B_{0}))$ with $\partial_{t} u = div H$ in $D_{div}^{'} (Q_{0})$ for some $H \in L^{σ} (Q_{0})$ . Then for every $m_{0} ≫ 1$ and $γ > 0$ there exist $λ \in [2^{m_{0}} γ, 2^{2 m_{0}} γ]$ and a function $u_{λ}$ with the following properties.

(a) It holds $u_{λ} \in L^{\infty} (I_{0}, W_{0, div}^{1, \infty} (B_{0}))$ with ${‖ \nabla u_{λ} ‖}_{\infty} ⩽ c λ$ .

(b) We have

$\begin{matrix} λ^{σ} \frac{L^{d + 1} (\frac{1}{2} Q_{0} \cap {u_{λ} \neq u})}{| Q_{0} |} \\ ⩽ \frac{c}{m_{0}} (⨍_{Q_{0}} r_{0}^{- σ} | u |^{σ} + | \nabla u |^{σ} d x d t + ⨍_{Q_{0}} | H |^{σ} d x d t) . \end{matrix}$

$\begin{matrix} ⨍_{Q_{0}} | u_{λ} |^{σ} d x d t & ⩽ c (⨍_{Q_{0}} | u |^{σ} + ⨍_{Q_{0}} r_{0}^{σ} | H |^{σ} d x d t), \\ ⨍_{Q_{0}} | \nabla u_{λ} |^{σ} d x d t & ⩽ c (⨍_{Q_{0}} r_{0}^{- σ} | u |^{σ} + | \nabla u |^{σ} d x d t + ⨍_{Q_{0}} | H |^{σ} d x d t) . \end{matrix}$

(d) We have $\partial_{t} (u - u_{λ}) \in L^{σ^{'}} (\frac{1}{2} I_{0}, W^{- 1, σ^{'}} (\frac{1}{2} B_{0}))$ and

$\begin{matrix} - ⨍_{\frac{1}{2} Q_{0}} (u - u_{λ}) \cdot \partial_{t} φ d x d t \\ ⩽ c (κ) \int_{\frac{1}{2} Q_{0}} χ_{{u_{λ} \neq u}} | \nabla φ |^{σ^{'}} d x d t + κ (⨍_{Q_{0}} r_{0}^{- σ} | u |^{σ} + | \nabla u |^{σ} + | H |^{σ} d x d t) \end{matrix}$

for all $φ \in C_{0}^{\infty} (\frac{1}{2} Q_{0})$ and all $κ > 0$ .

Proof

We apply the arguments used in the proof of Theorem 6.1.25 to the constant sequence u with the choice $α = 1$ . So we set

$u_{λ} : = curl (ζ z_{λ}) + curl (ζ (w - z)),$

(6.1.22)

where $ζ \in C_{0}^{\infty} (\frac{1}{6} Q_{0})$ with $χ_{\frac{1}{8} Q_{0}} ⩽ ζ ⩽ χ_{\frac{1}{6} Q_{0}}$ . Hence, in $\frac{1}{8} Q_{0}$ we have

$u_{λ} = u + curl (z_{λ} - z) .$

We immediately obtain the claim of (a). As a consequence of the Lemmas 6.1.1, 6.1.4 and 6.1.9 we obtain the inequalities

$\begin{matrix} ⨍_{Q} | u_{λ} |^{σ} d x d t & ⩽ c (⨍_{Q_{0}} | u |^{σ} + ⨍_{Q} r_{0}^{σ} | \partial_{t} z |^{σ} d x d t), \\ ⨍_{Q_{0}} | \nabla u_{λ} |^{σ} d x d t & ⩽ c (⨍_{Q_{0}} r_{0}^{- σ} | u |^{σ} + | \nabla u |^{σ} d x d t + ⨍_{Q} | \partial_{t} z |^{σ} d x d t), \end{matrix}$

claimed in c). Finally we can replace $\partial_{t} z$ by H on account of Lemma 6.1.3.

It remains to find good levels. We define for some $s \in (1, \max {σ, σ^{'}})$

$\begin{matrix} O_{λ} & : = {M_{s} (χ_{\frac{1}{3} Q_{0}} | \nabla^{2} z |) > λ} \cup {M_{s} (χ_{\frac{1}{3} Q_{0}} | H |) > λ}, \\ g & : = M_{s} (χ_{\frac{1}{3} Q_{0}} | \nabla^{2} z |) + M_{s} (χ_{\frac{1}{3} Q_{0}} | H |) . \end{matrix}$

It now follows from the continuity of $M_{s}$ in (5.2.4), together with Lemmas 6.1.1 and 6.1.4

$\int_{R^{d + 1}} | g |^{σ} d x ⩽ c (\int_{Q_{0}} r_{0}^{- σ} | u |^{σ} + | \nabla u |^{σ} d x d t + \int_{Q_{0}} | H |^{σ} d x d t) .$

(6.1.23)

Furthermore, the following holds for every $m_{0} \in N$ and every $γ > 0$

$\begin{matrix} \int_{R^{d + 1}} | g |^{σ} d x & = \int_{R^{d + 1}} \int_{0}^{\infty} \frac{1}{σ} t^{σ - 1} χ_{{| g | > t}} d t d x \\ ⩾ \int_{R^{d + 1}} \sum_{m = m_{0}}^{2 m_{0} - 1} \frac{1}{σ} {(2^{m} γ)}^{σ} χ_{{| g | > γ 2^{m + 1}}} d x . \end{matrix}$

So, there is $m_{1} \in {m_{0}, . . ., 2 m_{0} - 1}$ such that

$\int_{R^{d + 1}} {(2^{m_{1}} γ)}^{σ} χ_{{| g | > γ 2^{m_{1} + 1}}} d x ⩽ \frac{c}{m_{0}} \int_{R^{d + 1}} | g |^{σ} d x .$

Setting $λ = γ 2^{m_{1} + 1}$ yields

$λ^{σ} | \frac{1}{3} Q_{0} \cap {| g | > λ} | ⩽ \frac{c}{m_{0}} \int_{R^{d + 1}} | g |^{σ} d x .$

Combining this with (6.1.23) gives the estimate in b) due to the definition of $O_{λ}$ .

Finally, we prove d). We have $u_{λ} - u = curl (z_{λ} - z)$ in $\frac{1}{8} Q_{0}$ such that Lemma 6.1.3 and 6.1.9 imply $\partial_{t} (u_{λ} - u) \in L^{σ^{'}} (\frac{1}{8} I_{0}, W^{- 1, σ^{'}} (\frac{1}{8} B_{0}))$ . Moreover, we have for $φ \in C_{0}^{\infty} (\frac{1}{8} Q_{0})$

$\begin{matrix} - \int_{\frac{1}{8} Q_{0}} (u - u_{λ}) \cdot \partial_{t} φ d x d t = \int_{\frac{1}{8} Q_{0}} χ_{O_{λ}} \partial_{t} (z - z_{λ}) \cdot curl φ d x d t \\ ⩽ c (κ) \int_{\frac{1}{2} Q_{0}} χ_{O_{λ}} | \nabla φ |^{σ^{'}} d x d t + κ (⨍_{Q_{0}} | \partial_{t} (z_{λ} - z) |^{σ} d x d t), \end{matrix}$

as a consequence of Young's inequality. Applying Lemmas 6.1.3, 6.1.4 and 6.1.9 yields

$⨍_{Q_{0}} | \partial_{t} (z_{λ} - z) |^{σ} d x d t ⩽ c (⨍_{Q_{0}} r_{0}^{- σ} | u |^{σ} + | \nabla u |^{σ} d x d t + ⨍_{Q_{0}} | H |^{σ} d x d t) .$

So we have shown the estimate claimed in (d) on $\frac{1}{8} Q_{0}$ .

A simple scaling argument allows us the obtain all the estimates on $\frac{1}{2} Q_{0}$ . □

Remark 6.1.10

The higher dimensional case

For general dimensions, the solenoidal Lipschitz truncation is best understood in terms of differential forms. We start with $\tilde{u}$ as given in (6.1.3). Now, we have to find w such that $curl w = \tilde{u}$ and $div w = 0$ . Let us define the 1-form α in $R^{d}$ associated to the vector field $\tilde{u}$ by $α : = \sum_{i} {\tilde{u}}_{i} d x^{i}$ . Then we need to find a 2-form G such that $d^{⁎} G = α$ and $d G = 0$ , where d is the outer derivative and $d^{⁎}$ its adjoint by the scalar product for k-forms. Similar to $w = {curl}^{- 1} \tilde{u} = curl Δ^{- 1} \tilde{u}$ we get G by $G : = d Δ^{- 1} α$ . Since we are on the whole space, $Δ^{- 1}$ can be constructed by mollification with $c | x |^{2 - d}$ . Thus, we have

$G (x) = (d Δ^{- 1} α) (x) = d \sum_{i} (\int_{R^{d}} \frac{u_{i} (y)}{| x - y |^{d - 2}} d y) d x^{i} .$

Let us explain how to substitute the equation $\partial_{t} Δ w = - curl div G$ , see (6.1.4). Instead of test functions ψ with $div ψ = 0$ we use the associated 1-forms $β = \sum_{i} ψ_{i} d x^{i}$ with $d^{⁎} β = 0$ . Thus there exists a 2-form γ with $d^{⁎} γ = 0$ . Then

$〈 \partial_{t} \tilde{u}, ψ 〉 = 〈 \partial_{t} α, β 〉 = 〈 \partial_{t} d^{⁎} G, d^{⁎} γ 〉 = 〈 \partial_{t} d d^{⁎} G, γ 〉 = 〈 - \partial_{t} Δ G, γ 〉,$

where we used $- Δ = d d^{⁎} + d^{⁎} d$ and $d α = 0$ in the last step. Note that −Δ applied to the form G is the same as −Δ applied to the vector field of all components of G. Now we define w as the associated vector field (with $(\begin{matrix} d \\ 2 \end{matrix})$ components) of G and we arrive again at an equation for $\partial_{t} Δ w$ . This concludes the construction; the rest can be done exactly as for dimension three. The restriction $p > \frac{6}{5}$ used in this section will change to $\frac{2 d}{d + 2}$ .

6.2 $A$ -Stokes approximation – evolutionary case

By $A$ we denote a symmetric, elliptic tensor, i.e.

$c_{0} | τ |^{2} ⩽ A (τ, τ) ⩽ c_{1} | τ |^{2} for all τ \in R^{d \times d} .$

(6.2.24)

We set $| A | : = c_{1} / c_{0}$ . Let $B \subset R^{d}$ be a ball and $J = (t_{0}, t_{1})$ a bounded interval. We set $Q = J \times B$ . For a function $w \in L^{1} (Q)$ with $\partial_{t} w \in L^{q^{'}} (J; W^{- 1, q^{'}} (B))$ we introduce the unique function $H_{w} \in L_{0}^{q^{'}} (Q)$ with

$\int_{Q} w \cdot \partial_{t} φ d x d t = \int_{Q} H_{w} : \nabla φ d x d t$

for all $φ \in C_{0, div}^{\infty} (Q)$ . We begin with a variational inequality for the non-stationary $A$ -Stokes system.

Lemma 6.2.1

Suppose that (6.2.24) holds and that $q > 1$ . There holds for every $u \in C_{w} ([t_{0}, t_{1}]; L^{1} (B)) \cap L^{q} (J; W^{1, q} (B))$ with $u (t_{0}, \cdot) = 0$ a.e.

$\begin{matrix} ⨍_{Q} | \nabla u |^{q} d x d t & ⩽ c \sup_{ξ \in C_{0, div}^{\infty} (Q)} [⨍_{Q} (A (ε (u), ε (ξ)) - u \cdot \partial_{t} ξ) d x d t \\ - ⨍_{Q} (| \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}}) d x d t], \end{matrix}$

where c only depends on $A$ , q and d.

Proof

Duality arguments show that

$\frac{1}{q} ⨍_{Q} | \nabla u |^{q} d x d t = \sup_{G \in L^{q^{'}} (Q)} [⨍_{Q} \nabla u : G d x d t - \frac{1}{q^{'}} ⨍_{Q} | G |^{q^{'}} d x d t] .$

For a given $G \in L^{q^{'}} (Q)$ let $z_{G}$ be the unique $L^{q^{'}} (J; W_{0, div}^{1, q^{'}} (B))$ -solution to

$⨍_{Q} z \cdot \partial_{t} ξ d x d t + \int_{Q} A (ε (z), ε (ξ)) d x d t = \int_{Q} G : \nabla ξ d x d t$

(6.2.25)

for all $ξ \in C_{0, div}^{\infty} ((t_{0}, t_{1}] \times B)$ . This is a backward parabolic equation with end datum zero. We have that $\partial_{t} z_{G} \in L^{q^{'}} (J; W_{div}^{- 1, q^{'}} (B))$ , so test-functions can be chosen from the space $L^{q} (J; W_{0, div}^{1, q} (B))$ . Due to Theorem B.3.50 (which can be applied to ${\tilde{z}}_{\tilde{G}} (t, \cdot) = z_{G} (t_{1} - t, \cdot)$ , where $\tilde{G} (t, \cdot) = G (t_{1} - t, \cdot)$ ) this solution satisfies

$⨍_{Q} | \nabla z_{G} |^{q^{'}} d x d t + ⨍_{Q} | H_{z_{G}} |^{q^{'}} d x d t ⩽ c ⨍_{Q} | G |^{q^{'}} d x d t .$

In other words, the mapping $L^{q^{'}} (B) ∋ G \mapsto z_{G} \in L^{q^{'}} (J; W_{0, div}^{1, q^{'}} (B))$ is continuous. This and $u (t_{0}, \cdot) = 0$ yield (using u as a test-function in (6.2.25))

$\begin{matrix} ⨍_{Q} | \nabla u |^{q} d x d t \\ ⩽ c \sup_{G \in L^{q^{'}} (Q)} [⨍_{Q} A (ε (u), ε (z_{G})) d x d t - ⨍_{Q} \partial_{t} z_{G} \cdot u d x d t \\ - ⨍_{Q} (| \nabla z_{H} |^{q^{'}} + | H_{z_{G}} |^{q^{'}}) d x d t] \\ ⩽ c \sup_{ξ \in C_{0, div}^{\infty} (Q)} [⨍_{Q} A (ε (u), ε (ξ)) d x d t - ⨍_{Q} u \cdot \partial_{t} ξ d x d t \\ - ⨍_{Q} (| \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}}) d x d t], \end{matrix}$

which yields the claim. □

Let us now state the $A$ -Stokes approximation. In the following let $B$ be a ball with radius r and J an interval with length $2 r^{2}$ . Let $\tilde{Q}$ denote either $Q = J \times B$ or 2Q. We use similar notations for $\tilde{J}$ and $\tilde{B}$ .

Theorem 6.2.26

Suppose that (6.2.24) holds. Let $v \in L^{q s} (2 \tilde{J}; W_{div}^{1, q s} (2 \tilde{B}))$ , $q, s > 1$ , be an almost $A$ -Stokes solution in the sense that

$\begin{matrix} | ⨍_{2 Q} v \cdot \partial_{t} ξ d x d t - ⨍_{2 Q} A (ε (v), ε (ξ)) d x d t | ⩽ δ ⨍_{2 \tilde{Q}} | ε (v) | d x d t {‖ \nabla ξ ‖}_{\infty} \end{matrix}$

(6.2.26)

for all $ξ \in C_{0, div}^{\infty} (2 Q)$ and some small $δ > 0$ . Then the unique solution $w \in L^{q} (J; W_{0, div}^{1, q} (B))$ to

$\begin{matrix} \int_{Q} w \cdot \partial_{t} ξ d x d t - \int_{Q} A (ε (w), ε (ξ)) d x d t \\ = \int_{Q} v \cdot \partial_{t} ξ d x d t - \int_{Q} A (ε (v), ε (ξ)) d x d t \end{matrix}$

(6.2.27)

for all $ξ \in C_{0, div}^{\infty} ([t_{0}, t_{1}) \times B)$ satisfies

$⨍_{Q} | \frac{w}{r} |^{q} d x d t + ⨍_{Q} | \nabla w |^{q} d x d t ⩽ κ {(⨍_{2 \tilde{Q}} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} .$

It holds $κ = κ (q, s, δ)$ and $\lim_{δ \to 0} κ (q, s, δ) = 0$ . The function $h : = v - w$ is called the $A$ -Stokes approximation of v.

Remark 6.2.11

From the proof of Theorem 6.2.26 we have the following stability result, choosing $p = q s = q$ .

$⨍_{Q} | \frac{w}{r} |^{p} d x d t + ⨍_{Q} | \nabla w |^{p} d x d t ⩽ c ⨍_{2 \tilde{Q}} | \nabla v |^{p} d x d t .$

Indeed κ stays bounded if $s \to 1$ .

Proof

Let w be defined as in (6.2.27). Combining Poincaré's inequality with Lemma 6.2.1 and (6.2.27) shows that

$\begin{matrix} ⨍_{Q} | \frac{w}{r} |^{q} d x d t + ⨍_{Q} | \nabla w |^{q} d x d t \\ ⩽ c \sup_{ξ \in C_{0, div}^{\infty} (Q)} [⨍_{Q} A (ε (v), ε (ξ)) d x d t - ⨍_{Q} v \cdot \partial_{t} ξ d x d t \\ - ⨍_{Q} (| \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}}) d x d t] . \end{matrix}$

(6.2.28)

In the following let us fix $ξ \in C_{0, div}^{\infty} (Q)$ . Let

$γ : = {(⨍_{Q} | \nabla ξ |^{q^{'}} d x d t + ⨍_{Q} | H_{ξ} |^{q^{'}} d x d t)}^{\frac{1}{q^{'}}},$

and $m_{0} \in N$ , $m_{0} ≫ 1$ . Due to Corollary 6.1.5, applied with $σ = q^{'}$ , we find $λ \in [2^{m_{0}} γ, 2^{2 m_{0}} γ]$ and $ξ_{λ} \in L^{\infty} (4 J; W_{0, div}^{1, \infty} (4 B))$ such that

${‖ \nabla ξ_{λ} ‖}_{L^{\infty} (4 Q)} ⩽ c λ,$

(6.2.29)

$λ^{q^{'}} \frac{L^{d + 1} (2 Q \cap {ξ_{λ} \neq ξ})}{| Q |} ⩽ \frac{c}{m_{0}} (⨍_{Q} | \nabla ξ |^{q^{'}} d x d t + ⨍_{Q} | H_{ξ} |^{q^{'}} d x d t),$

(6.2.30)

$⨍_{4 Q} | ξ_{λ} |^{q^{'}} d x d t ⩽ c (⨍_{Q} | ξ |^{q^{'}} d x d t + ⨍_{Q} r^{q^{'}} | H_{ξ} |^{q^{'}} d x d t),$

(6.2.31)

$⨍_{4 Q} | \nabla ξ_{λ} |^{q^{'}} d x d t ⩽ c (⨍_{Q} | \nabla ξ |^{q^{'}} d x d t + ⨍_{Q} | H_{ξ} |^{q^{'}} d x d t) .$

(6.2.32)

Note that ξ can be extended by 0 to 4Q thus the equation

$\partial_{t} ξ = div {Bog}_{B} (\partial_{t} ξ) = : div H_{ξ}$

holds on 4Q by the properties of ${Bog}_{B}$ (since $H_{ξ}$ can be extended as well). For the properties of the Bogovskiĭoperator we refer to Section 2.1, in particular Theorem 2.1.6. Corollary 6.1.5 (d) implies that $\partial_{t} (ξ - ξ_{λ}) \in L^{q^{'}} (2 J, W^{- 1, q^{'}} (2 B))$ and

$\begin{matrix} \int_{2 J} 〈 \partial_{t} (ξ - ξ_{λ}), φ 〉 d t \\ ⩽ c (κ) \int_{2 Q} χ_{{ξ \neq ξ_{λ}}} | \nabla φ |^{q} d x d t + κ (\int_{Q} | \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}} d x d t), \end{matrix}$

(6.2.33)

for all $φ \in W_{0}^{1, q} (2 Q)$ . For $η \in C_{0}^{\infty} (2 Q)$ with $η \equiv 1$ on Q, $| \nabla^{k} η | ⩽ c r^{- k}$ and $| \partial_{t} \nabla^{k - 1} η | ⩽ c r^{- (k + 1)}$ ( $k = 1, 2$ ) we see that

$\begin{matrix} ⨍_{Q} A (ε (v), ε (ξ)) d x d t - ⨍_{Q} v \cdot \partial_{t} ξ d x d t \\ = 2^{d + 2} ⨍_{2 Q} A (ε (v), ε (η ξ - {Bog}_{2 B ∖ B} (\nabla η ξ))) d x d t \\ - ⨍_{2 Q} v \cdot \partial_{t} (η ξ - . . .) d x d t \\ = 2^{d + 2} (⨍_{2 Q} A (ε (v), ε (η ξ_{λ} - {Bog}_{2 B ∖ B} (\nabla η ξ_{λ}))) d x d t \\ + ⨍_{2 Q} \partial_{t} v \cdot (η ξ_{λ} - . . .) d x d t) \\ + 2^{d + 2} ⨍_{2 Q} A (ε (v), ε (η (ξ - ξ_{λ}) - {Bog}_{2 B ∖ B} (\nabla η (ξ - ξ_{λ})))) d x d t \\ + 2^{d + 2} ⨍_{2 Q} \partial_{t} v \cdot (η (ξ - ξ_{λ}) - {Bog}_{2 B ∖ B} (\nabla η (ξ - ξ_{λ}))) d x d t \\ = : 2^{d + 2} (I + I I + I I I) . \end{matrix}$

Note that the time-derivative of v exists in the $W_{div}^{- 1, \infty}$ -sense as a consequence of (6.2.26), so all terms are well-defined by the properties of $ξ_{λ}$ . We have the following inequality on account of the continuity properties of ∇Bog on $L^{p}$ -spaces, (6.2.31), (6.2.32) and Poincaré's inequality (we set $\tilde{ξ_{λ}} : = ξ - ξ_{λ}$ ):

$\begin{matrix} ⨍_{2 Q} | \nabla Ψ_{λ} |^{q^{'}} d x d t & : = ⨍_{2 Q} | \nabla (η {\tilde{ξ}}_{λ}) - \nabla {Bog}_{2 B ∖ B} (\nabla η {\tilde{ξ}}_{λ}) |^{q^{'}} d x d t \\ ⩽ c ⨍_{2 Q} | \nabla {\tilde{ξ}}_{λ} |^{q^{'}} d x d t + c ⨍_{2 Q} | \frac{{\tilde{ξ}}_{λ}}{r} |^{q^{'}} d x d t \\ ⩽ c ⨍_{Q} | \nabla ξ |^{q^{'}} d x d t + c ⨍_{Q} | \frac{ξ}{r} |^{q^{'}} d x d t + c ⨍_{Q} | H_{ξ} |^{q^{'}} d x d t \\ ⩽ c ⨍_{Q} | \nabla ξ |^{q^{'}} d x d t + c ⨍_{Q} | H_{ξ} |^{q^{'}} d x d t . \end{matrix}$

(6.2.34)

Young's inequality, with an appropriate choice of $ε > 0$ , together with (6.2.31) and (6.2.32), implies that

$\begin{matrix} I I & ⩽ c (ε) ⨍_{2 Q} | ε (v) |^{q} χ_{{ξ \neq ξ_{λ}}} d x d t + ε ⨍_{2 Q} | \nabla Ψ_{λ} |^{q^{'}} d x d t \\ ⩽ c ⨍_{2 Q} | ε (v) |^{q} χ_{{ξ \neq ξ_{λ}}} d x d t + \frac{1}{3} ⨍_{Q} | \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}} d x d t \\ = : I I_{1} + I I_{2}, \end{matrix}$

where c depends on $A$ , q and $q^{'}$ . Hölder's inequality now yields

$I I_{1} ⩽ c {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} {(\frac{L^{d + 1} (2 Q \cap {ξ_{λ} \neq ξ})}{| Q |})}^{1 - \frac{1}{s}} .$

If follows from (6.2.30), by the choice of γ and $λ ⩾ γ$ that

$\frac{L^{d + 1} (2 Q \cap {ξ_{λ} \neq ξ})}{| Q |} ⩽ \frac{c γ^{q^{'}}}{m_{0} λ^{q^{'}}} ⩽ \frac{c}{m_{0}} .$

(6.2.35)

Thus

$I I_{1} ⩽ c {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} {(\frac{c}{m_{0}})}^{1 - \frac{1}{s}} .$

We choose $m_{0}$ sufficiently large that

$I I_{1} ⩽ \frac{κ}{3} {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} .$

Since $\partial_{t} (ξ - ξ_{λ}) \in L^{q^{'}} (2 J, W^{- 1, q^{'}} (2 B))$ we can write III as

$\begin{matrix} I I I & = ⨍_{2 Q} v \cdot \partial_{t} η (ξ - ξ_{λ}) d x d t + ⨍_{2 Q} η v \cdot \partial_{t} (ξ - ξ_{λ}) d x d t \\ - ⨍_{2 Q} v \cdot {Bog}_{2 B ∖ B} (\partial_{t} \nabla η (ξ - ξ_{λ})) d x d t \\ - ⨍_{2 Q} {Bog}_{2 B ∖ B}^{⁎} (v) \nabla η \cdot \partial_{t} (ξ - ξ_{λ}) d x d t \\ = : I I I_{1} + I I I_{2} + I I I_{3} + I I I_{4} . \end{matrix}$

The Bogovskiĭ operator is continuous from $L_{⊥}^{2} \to L^{2}$ . Hence its dual (in the sense of $L^{2}$ -duality) is continuous from $L^{2} \to L_{⊥}^{2}$ . Therefore ${Bog}_{2 B ∖ B}^{⁎} (v)$ is well-defined. We consider the four terms separately. For the first one we have

$\begin{matrix} I I I_{1} & ⩽ c ⨍_{2 I} ⨍_{2 B ∖ B} χ_{{ξ_{λ} \neq ξ}} | \frac{v}{r} | | \frac{ξ - ξ_{λ}}{r} | d x d t \\ ⩽ c (ε) ⨍_{2 I} ⨍_{2 B ∖ B} | \frac{v}{r} |^{q} χ_{{ξ_{λ} \neq ξ}} d x d t + ε ⨍_{2 Q} | \frac{ξ - ξ_{λ}}{r} |^{q^{'}} d x d t \\ = : c (ε) I I I_{11} + ε I I I_{12} . \end{matrix}$

Poincaré's inequality and Young's inequality yield

$\begin{matrix} I I I_{11} & ⩽ c {(⨍_{2 I} ⨍_{2 B ∖ B} | \frac{v}{r} |^{q s} d x d t)}^{\frac{1}{s}} {(\frac{L^{d + 1} (2 Q \cap {ξ_{λ} \neq ξ})}{| Q |})}^{1 - \frac{1}{s}} \\ ⩽ c {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} {(\frac{L^{d + 1} (2 Q \cap {ξ_{λ} \neq ξ})}{| Q |})}^{1 - \frac{1}{s}} . \end{matrix}$

Arguing as for the term $I I_{1}$ implies that

$I I I_{11} ⩽ \frac{κ}{12} {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} .$

Moreover, we gain from (6.2.31) and Poincaré's inequality

$\begin{matrix} I I I_{12} & ⩽ c ⨍_{Q} | \frac{ξ}{r} |^{q^{'}} d x d t + c ⨍_{Q} | H_{ξ} |^{q^{'}} d x d t \\ ⩽ c ⨍_{Q} | \nabla ξ |^{q^{'}} d x d t + c ⨍_{Q} | H_{ξ} |^{q^{'}} d x d t, \end{matrix}$

and finally

$I I I_{1} ⩽ \frac{κ}{12} {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} + \frac{1}{12} (\int_{Q} | \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}} d x d t) .$

The formulation in (6.2.26) does not change if we subtract terms which are constant in space from v (note that $(\partial_{t} ξ) = 0$ for every t due to $\partial_{t} ξ (t, \cdot) \in C_{0, div}^{\infty} (B)$ ). So we can assume that

$⨍_{2 B ∖ B} v (t) d x = 0 for a.e. t \in 2 J .$

(6.2.36)

As a consequence of (6.2.33), (6.2.36) and Poincaré's inequality we obtain similarly as for $I I I_{1}$

$\begin{matrix} I I I_{2} & ⩽ c (ε) \int_{2 Q} χ_{{ξ \neq ξ_{λ}}} | \nabla (η v) |^{q} d x d t + ε (\int_{Q} | \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}} d x d t) \\ ⩽ \frac{κ}{12} {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} + \frac{1}{12} (\int_{Q} | \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}} d x d t) . \end{matrix}$

Taking into account continuity properties of the Bogovskiĭ operator from $L_{⊥}^{q} \to W_{0}^{1, q}$ we can estimate $I I I_{3}$ via (we use again (6.2.36) and Poincaré's inequality)

$\begin{matrix} I I I_{3} & ⩽ {(⨍_{2 Q} ⨍_{2 B ∖ B} | \frac{v}{r} |^{q s} d x d t)}^{\frac{1}{q s}} \\ \times {(⨍_{2 Q} r^{{(q s)}^{'}} | {Bog}_{2 B ∖ B} (\partial_{t} \nabla η (ξ - ξ_{λ}))) |^{{(q s)}^{'}} d x d t)}^{\frac{1}{{(q s)}^{'}}} \\ ⩽ c {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{q s}} {(⨍_{2 Q} r^{2 {(q s)}^{'}} | \partial_{t} \nabla η (ξ - ξ_{λ}) |^{{(q s)}^{'}} d x d t)}^{\frac{1}{{(q s)}^{'}}} \\ ⩽ c {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{q s}} {(⨍_{2 Q} χ_{{ξ \neq ξ_{λ}}} | \frac{ξ - ξ_{λ}}{r} |^{{(q s)}^{'}} d x d t)}^{\frac{1}{{(q s)}^{'}}} . \end{matrix}$

Hence, from Young's inequality for every $ε > 0$ , we deduce that

$\begin{matrix} I I I_{3} & ⩽ \frac{ε^{q}}{12} {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} + c ε^{- q^{'}} {(⨍_{2 Q} χ_{{ξ \neq ξ_{λ}}} | \frac{ξ - ξ_{λ}}{r} |^{{(q s)}^{'}} d x d t)}^{\frac{q^{'}}{{(q s)}^{'}}} \\ = : \frac{ε^{q}}{12} I I I_{31} + c ε^{- q^{'}} I I I_{32} . \end{matrix}$

It follows due to Hölder's inequality, Poincaré's inequality, (6.2.30), (6.2.32) and (6.2.35) for $m_{0}$ large enough

$\begin{matrix} I I I_{32} & ⩽ {(\frac{L^{d + 1} (2 Q \cap {ξ_{λ} \neq ξ})}{| Q |})}^{1 - \frac{1}{s}} (⨍_{2 Q} | \frac{ξ - ξ_{λ}}{r} |^{q^{'}} d x d t) \\ ⩽ c {(\frac{L^{d + 1} (2 Q \cap {ξ_{λ} \neq ξ})}{| Q |})}^{1 - \frac{1}{s}} (⨍_{4 Q} | \frac{ξ - ξ_{λ}}{4 r} |^{q^{'}} d x d t) \\ ⩽ c {(\frac{L^{d + 1} (2 Q \cap {ξ_{λ} \neq ξ})}{| Q |})}^{1 - \frac{1}{s}} (⨍_{4 Q} (| \nabla ξ |^{q^{'}} + | \nabla ξ_{λ} |^{q}) d x d t) \\ ⩽ \frac{κ}{12 c} (\int_{Q} | \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}} d x d t) . \end{matrix}$

Choosing $ε : = κ^{1 / q^{'}}$ implies

$I I I_{3} ⩽ \frac{κ}{12} {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} + \frac{1}{12} (\int_{Q} | \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}} d x d t) .$

By (6.2.33) and (6.2.35) we have for $m_{0}$ large enough

$\begin{matrix} I I I_{4} & ⩽ c ⨍_{2 Q} χ_{{ξ \neq ξ_{λ}}} | \nabla (\nabla η {Bog}_{2 B ∖ B}^{⁎} (v)) |^{q} d x d t + \frac{1}{12} (\int_{Q} | \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}} d x d t) \\ ⩽ ε {(⨍_{2 Q} | \nabla (\nabla η {Bog}_{2 B ∖ B}^{⁎} (v)) |^{s q} d x d t)}^{\frac{1}{s}} + \frac{1}{12} (\int_{Q} | \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}} d x d t) \\ = : ε I I I_{41} + \frac{1}{12} I I I_{42} . \end{matrix}$

Due to the continuity of $Bog (div (\cdot))$ on $L^{p}$ for any $1 < p < \infty$ (see [85, III.3, Theorem 3.3] and Theorem 2.1.7 for the Bogovskiĭ operator and negative norms) we have continuity of $\nabla {Bog}^{⁎}$ as well. This, Poincaré's inequality (note that ${Bog}_{2 B ∖ B}^{⁎} (v) \in L_{0}^{p} (2 B ∖ B)$ ) and (6.2.36) yield

$\begin{matrix} I I I_{41} & ⩽ c {(⨍_{2 Q} | \frac{{Bog}_{2 B ∖ B}^{⁎} (v)}{r^{2}} |^{s q} d x d t + ⨍_{2 Q} | \frac{\nabla {Bog}_{2 B ∖ B}^{⁎} (v)}{r} |^{s q} d x d t)}^{\frac{1}{s}} \\ ⩽ c {(⨍_{2 Q} | \frac{\nabla {Bog}_{2 B ∖ B}^{⁎} (v)}{r} |^{s q} d x d t)}^{\frac{1}{s}} ⩽ c {(⨍_{2 I} ⨍_{2 B ∖ B} | \frac{v}{r} |^{s q} d x d t)}^{\frac{1}{s}} \\ ⩽ c {(⨍_{2 Q} | \nabla v |^{s q} d x d t)}^{\frac{1}{s}}, \end{matrix}$

and hence for $ε : = κ / 12 c$ ,

$I I I_{4} ⩽ \frac{κ}{12} {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} + \frac{1}{12} (\int_{Q} | \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}} d x d t) .$

Combining the estimates for $I I I_{1}$ – $I I I_{4}$ , we see that

$I I I ⩽ \frac{κ}{3} {(⨍_{2 Q} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} + \frac{1}{3} (\int_{Q} | \nabla ξ |^{q^{'}} + | H_{ξ} |^{q^{'}} d x d t) .$

Since v is an almost $A$ -Stokes solution and ${‖ \nabla ξ_{λ} ‖}_{\infty} ⩽ c λ ⩽ c 2^{m_{0}} γ$ we have

$\begin{matrix} | I | & ⩽ δ ⨍_{2 \tilde{Q}} | \nabla v | d x d t {‖ \nabla ξ_{λ} ‖}_{\infty, 2 Q} \\ ⩽ δ {(⨍_{2 \tilde{Q}} | \nabla v |^{q s} d x d t)}^{\frac{1}{q s}} c 2^{m_{0}} γ . \end{matrix}$

We apply Young's inequality and Jensen's inequality to give

$\begin{matrix} | I | & ⩽ δ 2^{m_{0}} c {(⨍_{2 \tilde{Q}} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} + δ 2^{m_{0}} c γ^{q^{'}} \\ ⩽ δ 2^{m_{0}} c {(⨍_{2 \tilde{Q}} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} + δ 2^{m_{0}} c (⨍_{Q} | \nabla ξ |^{q^{'}} d x d t + ⨍_{Q} | H_{ξ} |^{q^{'}} d x d t) . \end{matrix}$

Now, we choose $δ > 0$ so small such that $δ 2^{m_{0}} c ⩽ κ / 3$ . Thus

$| I | ⩽ \frac{κ}{3} {(⨍_{2 \tilde{Q}} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} + \frac{1}{3} (⨍_{Q} | \nabla ξ |^{q^{'}} d x d t + ⨍_{Q} | H_{ξ} |^{q^{'}} d x d t) .$

Combining the estimates for I, II and III we have established

$\begin{matrix} ⨍_{2 Q} A (ε (v), ε (ξ)) d x d t - ⨍_{Q} v \cdot \partial_{t} ξ d x d t \\ ⩽ κ {(⨍_{2 \tilde{Q}} | \nabla v |^{q s} d x d t)}^{\frac{1}{s}} + ⨍_{Q} | \nabla ξ |^{q^{'}} d x d t + ⨍_{Q} | H_{ξ} |^{q^{'}} d x d t . \end{matrix}$

Inserting this in (6.2.28) shows the claim. □

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 6: Solenoidal Lipschitz truncation

Create new playlist

Sign In

Sign Up

6.1 Solenoidal truncation – evolutionary case

6.2 A<math><mi mathvariant="script">A</mi></math>-Stokes approximation – evolutionary case

Table of Contents for
Chapter 6: Solenoidal Lipschitz truncation

6.2 $A$ -Stokes approximation – evolutionary case