Financial futures and forward rate agreements (FRAs)
Forward rate agreements (FRAs)
INTRODUCTION
Futures and FRAs are derivative instruments based on a short-term forward interest rate. They enable investors and borrowers to fix the interest rate today for a period that starts in the future. There is no exchange of principal amount, only the difference between the futures/FRA rate and the underlying cash (spot) market rate is settled. Futures are exchange-traded securities and implicitly offer liquidity, credit default protection and price transparency. The contract range and specification is fixed, hence the clients who need more flexibility would trade FRAs in the OTC market. The main purpose of both instruments is the same, with some differences that will be highlighted in the following sections where they are discussed in more detail.
FINANCIAL FUTURES
Futures market
Futures are instruments that have existed in various forms for over 100 years. They became exchange-traded instruments in 1970s and since then their popularity has grown. There are many international exchanges offering variety of futures contracts, the oldest ones being:
- CBOT (Chicago Board of Trade)
- CME (Chicago Mercantile Exchange).
These, together with
- LIFFE (London International Financial Futures and Options Exchange)
trade the largest volumes of futures contracts.
Some futures contracts are available globally, whilst some exchanges cater for their own domestic market. The main users of futures are investment banks and large corporations; smaller investors may find trading them expensive, as they have to transact through an exchange member, incurring additional, often prohibitive, costs.
Futures contract specification and trading
Futures contracts are clearly specified by the exchange. For example, a LIFFE three-month sterling contract is specified as shown in Table 6.1.
Table 6.1 LIFFE three-month interest rate future contract specification
| LIFFE three-month-interest rate future contract specification | |
|---|---|
| Unit of trading | £500,000 |
| Delivery months | March, June, September, December |
| Delivery day | First business day after the last trading day |
| Last trading day | 11:00 a.m., 3rd Wednesday of the delivery month |
| Quotation | 100 minus interest rate |
| Minimum price movement | 0.01% (or ‘tick’) |
| Tick value | £12.50 |
| Trading hours | 8:00 a.m.–9:00 p.m. |
Each futures contract will have a similar specification. Based on the contract specification, a trader can buy or sell a whole number of futures contracts, each based on a notional amount of £500,000, as no actual borrowing/lending takes place. The contract is the obligation between the counterparties to settle on delivery day the difference between the futures price and Libor (fixed at 11:00 a.m., third Wednesday of the delivery month). The delivery months, and thus available futures contracts, run in the cycle March–June–September–December for several years in the future. As one contract expires, a new one is added, keeping the number of available contracts constant. The futures price is quoted as 100 – rate, which can be counterintuitive, as to protect himself against the interest rate increase the client needs to sell the future. The ‘tick’ value of £12.50 is derived from the fact that futures contracts are three months long, whilst the implied rate is annual; hence only a quarter applies to the futures period.
Most exchanges worldwide require margin payment. This enables the exchange to take the role of counterparty to each side of transaction, thus accepting the credit risk. There are two types of margin:
Initial margin is payable at the inception of a contract. The amount required for each contract is based on the estimate of potential daily loss for that type of security. At contract expiry the initial margin is paid back to the client with interest.
Variation margin is calculated and paid daily, based on the profit/loss on the contract compared to the official settlement price. This is called ‘marking to market’. If the variation margin is not settled by the close of the business day, the exchange closes out the position, minimising the exposure. Hence the futures contract at expiry already has all but the last day’s profit/loss incorporated into the margin.
Futures valuation
Valuation refers to the pricing of futures contracts available for trading. Futures prices depend on several factors including the cash market (spot market) values, market expectations of interest rate movements, supply and demand, the economic and political situation and many others. The relationship between cash and futures prices is called simple basis:
Simple basis = Cash price – Futures price
Typically, futures prices are expected to be higher than spot prices, due to the risk associated with uncertainty. Such market is said to be in contango (premium). The term for the opposite situation is backwardation (discount).
Another measure of the futures price is theoretical basis:
Theoretical basis = Cash price – Fair value
and value basis:
Value basis = Fair value – Futures price
The fair value is the futures price that would make the investor indifferent to whether they buy an underlying now or in the future. As in the case of interest rate futures the underlying is the three-month interest rate, this means that the futures buyer should achieve the same rate if he borrows money in the cash market now for the entire period and deposits it until the start of the futures contract as if he simply buys the future now and then borrows the funds at the prevailing market rates when needed.
For example, it is 21 March and a client requires funds for the period covered by June futures (three months). He can either:
- Borrow money now for six months at six-month Libor and immediately invest it in a three-month Libid until 21 June (start of the June futures period), or
- Buy June futures now.
The two transactions should achieve the same net result. In practice any discrepancies in the futures prices would soon be eliminated from the market, due to supply and demand, hence it can be assumed that the futures price and fair value are one and the same. However, such price would only be theoretical, as the traders will build in the spread to allow for their profit. Naturally they would sell (offer) contracts at a higher price than buy (bid), creating a bid/offer spread around the theoretical price.
Futures settlement price
Calculating the futures settlement price is relatively simple. Whether the contract is held until expiry, or closed out by entering into an opposite transaction (if we bought a future, we would need to sell it), the settlement price can be calculated as:
Calculation Summary: Futures settlement price

Or, Expressed in terms of ‘ticks’:
Profit/Loss = Tick movement × Tick size × Number of contracts
Buying a futures contract for a single delivery month will only provide an interest rate guarantee for a period of three months. If a longer period needs to be covered, there are two possible strategies:
Futures strips consist of trading the appropriate number of futures contracts that span the entire period of exposure, whilst
Futures stacks require purchase of the required number of contracts in the nearest month and then rolling over to the next delivery month and so on.
Whilst the first option is clearly more desirable, as it provides certainty in the cost of funds, it may not be practical due to the lack of liquidity in the far-dated contracts. The second option overcomes this problem, but leaves the client exposed to uncertainty in the interest rate movements.
The futures strip rate can be calculated from the individual futures implied rates as follows:
Calculation Summary: Futures strip rate
where:
fi are individual futures implied rates
ti are time periods (fractions of a year) covered by the respective contracts (three months)
fs is the achieved strip rate
ts is the total time period covered.
FORWARD RATE AGREEMENTS (FRAs)
Introduction
Forward rate agreements (FRAs) are an OTC alternative to futures contracts. They are based on the same underlying instruments (short-term forward interest rates), but the contract specifications are tailored to individual customer needs. In contrast to forward–forward borrowing/lending, where a cash borrowing or deposit starts on one forward date and ends in another, there is no principal exchange involved. The FRA contract only pays the difference between the agreed rate and the prevailing spot interest rate (Libor) at settlement. It is assumed that the principal (if needed) is transacted elsewhere. Unlike futures, FRAs can have flexible start and end dates, as long they are both in the future. Hence the futures stack and strip strategies can be simplified by entering into longer-period FRAs. Another FRA characteristic is that FRAs are settled at the start of the contract period, whilst futures are margined (marked to market) daily during the lifetime of the contract. Hence their pricing methods vary slightly. The FRA market is very liquid with contracts available in different currencies, for many periods, start dates and underlying forward interest rates (typically three-month and one-month Libor).
FRA valuation
FRA valuation is based on the forward–forward borrowing of a notional amount. Just as in the example of futures fair price, if a principal amount is borrowed for six months and immediately deposited for the first three, the net result in the initial period is zero, thus creating a forward–forward three-month borrowing that starts in three months from now. The forward–forward three-month rate should reflect this, i.e.:
Calculation Summary
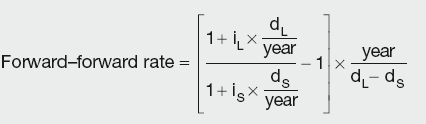
where:
iL and iS are the interest rates for the longer and shorter periods
dL and dS are the number of days in the longer/shorter periods
year is the number of days in the year.
In forward–forward borrowing two rates would come into play, the longer period Libor and the shorter period Libid. As FRAs always settle against Libor, their valuation would be exactly as above, but with either Libor used for both long- and short-term rates or with a spread added to the theoretical price.
FRA settlement price
The settlement price for FRAs is the difference between the rate under FRA and the Libor prevailing at the start of the FRA period, discounted at Libor. Discounting is done because the FRA contract is settled at the beginning of the period and the borrowing interest rate (which the FRA contract fixes) is repaid at the end of the FRA period. If there was no discounting, the investor would simply deposit the excess amount to realise risk-free profit. Thus:
Calculation Summary

where:
f is the FRA interest rate
df is the number of days in the FRA period
year is the number of days in the year.
Just as with futures contracts, FRA strips and stacks can be purchased to create a fixed rate for a desired period. FRAs are particularly useful for covering periods outside the futures delivery cycle, e.g. 2v5 month FRA, or 7v10 month FRA.
FUTURES VS. FRAs
An important practical difference between futures and FRAs is their settlement. FRAs are settled at the beginning of the period they cover (and discounted at the prevailing market rate), whilst futures are margined daily. This creates price discrepancy between otherwise identical contracts. A FRA is sensitive to two rates (the forward rate underlying the contract and the spot rate used for discounting), whilst the future is only sensitive to the forward rate due to daily marking-to-market. Thus, the relationship between future payoff and forward rate is linear, whereas it is convex for FRAs.
Another important point is that futures prices are quoted as 100 – interest rate, whilst FRAs are quoted as interest rate. Hence they move in opposite directions: if the borrower believes that the interest rates will rise, he/she will buy a FRA but sell futures and vice versa. Similarly, for hedging purposes one should either buy FRA and future or sell both contracts.
It can be shown that a short futures position is more profitable than purchase of a FRA, as it will respond quicker to the interest rate increase. The futures profits are marked to market daily and can be reinvested at the higher rate, increasing the profit even further. In contrast, FRAs settle up-front and cannot further benefit from the increase in interest rates. Hence, the implied futures rate is higher than the equivalent FRA rate. This difference is often called convexity. It will be referred to later in Chapter 14 on yield curve construction.

