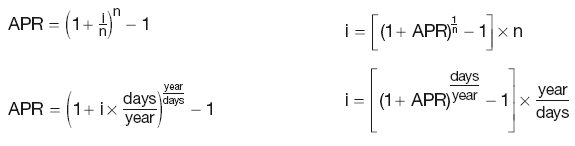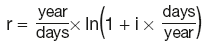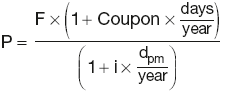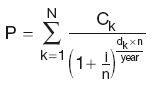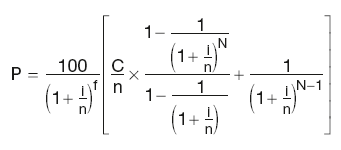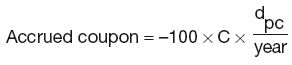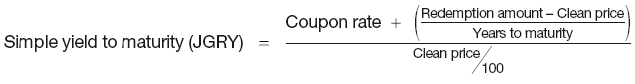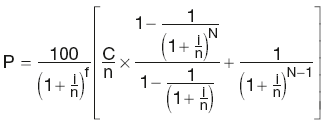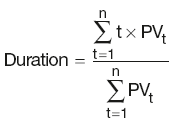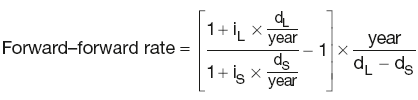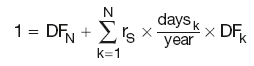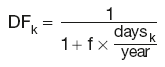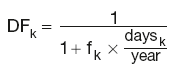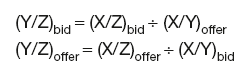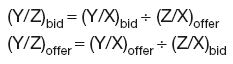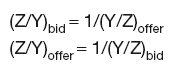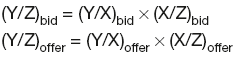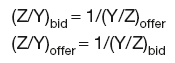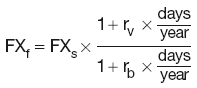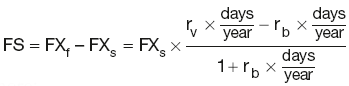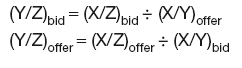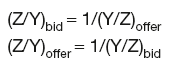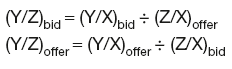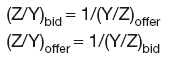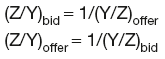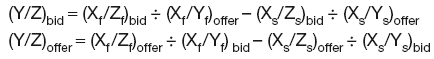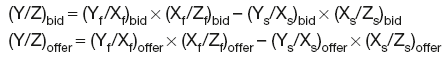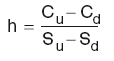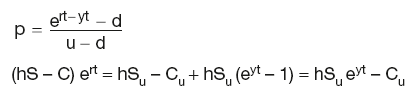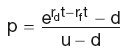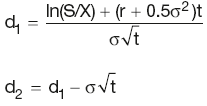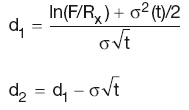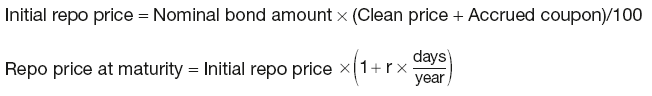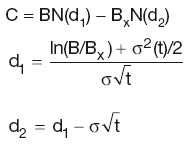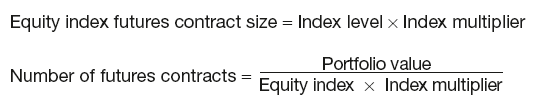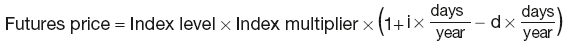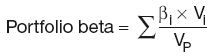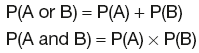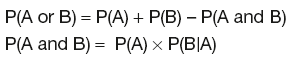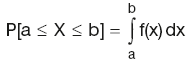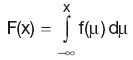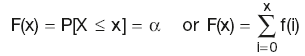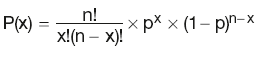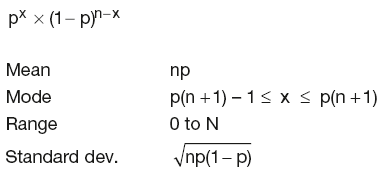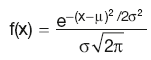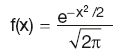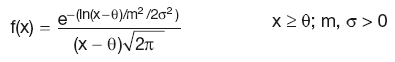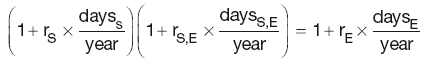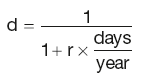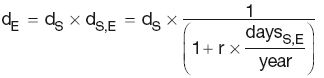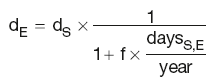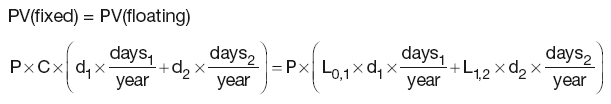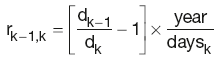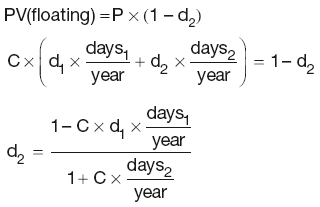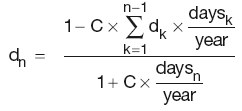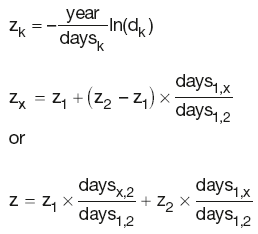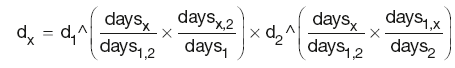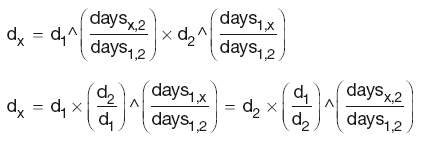16
Forward rate agreements (FRAs)
NOTATION
| i | annual interest rate |
| n | number of payments per year |
| days | number of days in the investment/coupon period |
| year | number of days in a year |
| N | number of years or coupon periods |
| P | price |
| APR | annual percentage rate, effective rate or equivalent annual rate |
| PV | present value |
| FV | future value |
| DF | discount factor |
TIME VALUE OF MONEY
Effective and nominal rates
Relationship between the interest rate i with n payments per year and the APR:
Continuously compounded rate
where i is the nominal interest rate.
For annual effective rate APR:
r = ln(1 + APR)
Reinvestment rates
For unequal rates applying to different investment periods:
![]()
Short-term investments
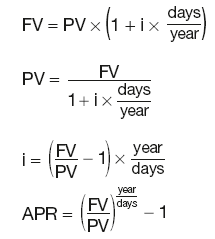
Long-term investments
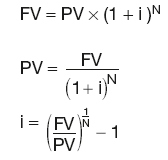
Discount factors

NPV and IRR
Internal rate of return (IRR) is the rate that discounts all the cashflows, including any cashflow now, to zero.
IRR discounts all the future cashflows to a given NPV.
MONEY MARKETS CALCULATIONS
Certificate of deposit (CD)
Proceeds at maturity:
Secondary market yield:
Discount instruments
Proceeds at maturity:
Maturity proceeds P = F(face value)
Secondary market price:
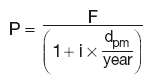
CAPITAL MARKETS INSTRUMENTS
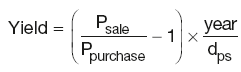
Simple bond dirty price formula
where:
Ck is the kth cashflow (including the final redemption amount)
i is the bond yield, based on the payment frequency
n is the number of coupons per year
dk is the number of days until the kth cashflow.
Accrued coupon
where dcs is the time period between the last coupon date and the sale of the bond.
Clean bond price
where:
C is the annual coupon rate
N is the number of outstanding coupons
i is the annual bond yield, based on the payment frequency
n is the number of coupons per year
f is the ratio between the number of days until the next coupon and the full coupon period.
Ex-dividend
where:
dpc is the time period between the bond purchase and the next coupon.
Bond yield
Flat yield:
Flat yield = (Coupon rate/Clean price) × 100
Simple yield to maturity:
Yield accounting for coupon payments and irregular first coupon period (derived from the pricing formula):
where:
C is the annual coupon rate
N is the number of outstanding coupons
i is the annual bond yield, based on the payment frequency
n is the number of coupons per year
f is the ratio between the number of days until the next coupon and the full coupon period.
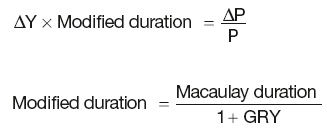
Portfolio duration
Macaulay duration:
Modified duration:
FINANCIAL FUTURES
Futures price
Price = 100 – Implied forward interest rate × 100
Futures settlement price
Expressed in terms of ‘ticks’:
Profit/Loss = Tick movement × Tick size × Number of contracts
Futures strip rate
FORWARD RATE AGREEMENTS (FRAs)
FRA rate
where:
iL is the interest rate for the longer period
iS is the interest rate for the shorter period
dL is the number of days in the longer period
dS is the number of days in the shorter period
year is the number of days in the year.
FRA settlement price
where:
f is the FRA interest rate
df is the number of days in the FRA period
year is the number of days in the year.
INTEREST RATE SWAPS
Short-term swap valuation at inception
where:
rS is the swap rate
daysk is the number of days covered by the kth FRA contract
DFk is the discount factor derived from the kth FRA rate f using:
Later valuation of short-term swap fixed leg

where:
P is the value of the fixed leg at a later date
rS is the swap rate, fixed at inception
daysk is the number of days covered by the kth FRA contract
DFk is the discount factor derived from the kth FRA rate fk using:
FOREIGN EXCHANGE
Spot rates
Given exchange rates X/Y and X/Z, the cross-rates are:
and
Given exchange rates Y/X and Z/X, the cross-rates are:
and
Given exchange rates Y/X and X/Z, the cross-rates are:
and
Forward outrights
where:
FXf is the forward exchange rate
FXs is the spot exchange rate
rv is the interest rate applicable to variable currency
rb is the interest rate applicable to base currency.
Forward swaps
Forward swap = Forward outright – Spot
where:
FS is the forward swap price
FXf is the forward exchange rate
FXs is the spot exchange rate
rv is the interest rate applicable to variable currency
rb is the interest rate applicable to base currency.
Cross-rate forwards
Given forward exchange rates X/Y and X/Z, the forward cross-rates are:
and
Given forward exchange rates Y/X and Z/X, the forward cross-rates are:
and
Given forward exchange rates Y/X and X/Z, the forward cross-rates are:
and
Cross-rate forward swaps
Given spot exchange rates Xs/Ys and Xs/Zs and forward exchange rates Xf/Yf and Xf/Zf, the forward cross-rate swap prices are:
Given exchange rates Y/X and Z/X, the forward cross-rates are:
Given exchange rates Y/X and X/Z, the forward cross-rates are:
OPTION CHARACTERISTICS
Put-call parity
C − P = S − K
where:
C is the call premium, P is the put premium
S is the futures price, K is the exercise price/option strike.
Physically settled options
C − P = S − Ke–rt
where:
r is the continuously compounded interest rate
t is time to expiry expressed as
.
Options on dividend-paying stocks
C − P = S − Ke–rt − D
where:
D is the present value of the expected dividend.
Options on stock index (dividend yield continuous)
C − P = Se–dt − Ke–rt
where:
d is the continuously compounded dividend yield.
Cross-currency options
C − P = Se–ft − Ke–rt
where:
f is the continuously compounded foreign currency interest rate
S is the spot exchange rate.
Options on futures with up-front premiums
C − P = S − K
Options on futures with margined premiums
C − P = Se–rt − Ke–rt
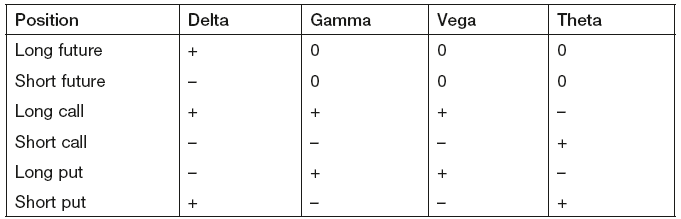
Option value sensitivities – ‘option Greeks’
| Options sensitivity to | Named as |
|---|---|
| Underlying | Delta |
| Changes in delta | Gamma |
| Volatility | Vega or kappa |
| Time decay | Theta |
| Interest rates | Rho |
OPTION PRICING
Risk-neutral pricing using binomial trees
Call option premium boundaries:
Probability-weighted stock price
Pricing options using hedge ratio
where:
Dividend paying stock options
Cross-currency options
Option pricing using Black–Scholes
Black–Scholes model:
where:
and
S is the underlying stock/share price
X is the exercise price
r is the annual continuously compounded risk-free rate
t is the time (in years)
σ is the annual stock price volatility
N(d) is the cumulative probability that deviations less than d will occur in a normal distribution with a mean of 0 and a standard deviation of 1
N(d1) is the probability of the stock price rising to a certain level
N(d2) is the probability of the stock price rising above the strike (but it is irrelevant by how much).
Options on futures (premiums paid up front)
Options on futures (premiums margined)
Currency options
Black model
Black model for interest rate derivatives:
where:
where F is the current market forward swap rate, and Rx is the underlying swap rate (option strike). All other variables have the same meaning as before.
BOND DERIVATIVES
Bond futures
Deliverable bond valuation:
Bond futures price:
Forward bond price:
Bond repos
where r is the repo rate and days refers to number of days until maturity.
Bond options
Black model for bond options:
Put–call parity for bond options:
F is the futures price
K is the exercise price/option strike
r is the continuously compounded interest rate.
EQUITY DERIVATIVES
Equity index futures
The futures settlement price:
where:
i is the annual funding rate
d is the dividend yield on underlying equity.
Stock beta
Portfolio beta:
where:
βi is the individual equity beta
Vi is the individual equity share value
VP is the total value of the portfolio.
Equity index options
Black–Scholes for equity index options:
where dividend yield d is assumed to be paid continuously.
Put-call parity for equity index options:
Single stock options
Black–Scholes for single stock options:
where dividend payments until expiry are captured by reducing the stock price by the present value of dividends.
Put–call parity for dividend-paying single stocks:
C − P = S − D − Ke−rt
where D is the present value of expected dividend.
Equity index swap valuation
PV(swap) = PV(equity index leg) − PV(floating leg) = 0
PROBABILITY AND STATISTICS
Main concepts of probability
Probability of an event E when there are several equally likely outcomes:
P(E) = Number of ways E can occur/Total number of possible outcomes
Sample-based probability:
P(E) = Number of observed occurrences of E/Total number of observed occurrences
Joint probability
Independent events:
Dependent events:
Probability distribution
Probability that the continuous variable x has a value between a and b inclusive:
Probability that the discrete variable x has a value X or lies between a and b inclusive:
Probability that the continuous variable x has a value less than or equal to X:
Probability that the discrete variable x has a value less than or equal to X:
Binomial distribution
Binomial probability function:
where the number of possible combinations of x successes in n trials is given by:
and the probability of x successes and n – x failures in a trial is given by:
Normal distribution
Normal distribution function:
Standard normal distribution function:
| Mean | location parameter μ |
| Median | location parameter μ |
| Mode | location parameter μ |
| Standard dev. | scale parameter σ |
Log-normal distribution
Log-normal distribution function:
Standard log-normal distribution function:
YIELD CURVES
Choice of instruments
- Cash deposits.
- Interest rate futures.
- Interest rate swaps.
Deposit discount factors
The forward–forward rate is given by:
and the relationship between the rate and the DF is:
where:
year is the number of days in the year
daysS, daysE and daysS,E are the relevant time periods
dS and dE are the discount factors for the period start and end date
dS,E is the discount factor for the period daysS,E
rS and rE are the spot rates for the period start and end dates
rS,E is the interest rate for the period daysS,E.
Futures discount factors
Given the futures rate:
the DF for the end of the forward period is given by:
Swap discount factors
where:
P is the notional principal
dk is the discount factor for the end of period k, implying d0 = 1
daysk is the number of days in the coupon period k
Lk-1,k is the Libor for that period
C is the fixed coupon rate for the duration of the swap.
As the interest rate r implied by the DFs for adjacent periods can be calculated as:
It follows:
In general:
Interpolation methods
Zero rate linear interpolation:
which, when rearranged, gives:
DF for the unknown point can be calculated as:
where the symbol ^ denotes ‘power of ’.