CHAPTER 3
A GENERAL APPROACH FOR MODELING AND INFERENCE

3.1 PREVIEW

This chapter is concerned with a general discussion that is relevant for much of the book. First, we provide an introduction to linear mixed-effects models. This includes a discussion of prediction, model fitting, and model diagnostics. Next, we present the large-sample methodology for statistical inference based on ML estimators. Special attention is paid to construction of confidence intervals and bounds using both the standard large-sample theory and bootstrap. Finally, we present a general framework for modeling method comparison data using mixed-effects models and doing inference on measures of similarity and agreement. This framework is followed in subsequent chapters in the analysis of various types of data. Readers familiar with mixed-effects modeling and large-sample inference may just skim through this chapter. Those not interested in technical details may skip it entirely.

3.2 MIXED-EFFECTS MODELS

Suppose there are n subjects in the study. Let Y_i be an M_i × 1 vector of observations on the ith subject, i = 1,...,n. The M_i need not be equal for all i. The total number of observations in the data is . The observations from different subjects are independent, whereas those from the same subject are assumed to be dependent.

3.2.1 The Model

A general mixed-effects model for the data Y₁,..., Y_n can be written as

(3.1)

where

• β is a p × 1 vector of fixed effects,
• X_i is an M_i × p design (or regression) matrix associated with the fixed effects,
• u_i is a q × 1 vector of random effects of subject i,
• Z_i is an M_i × q design matrix associated with the random effects, and
• e_i is an M_i × 1 vector of within-subject random errors.

Both X_i and Z_i are assumed to have full rank. It is further assumed that

• u_i ∼ independent N_q(0, G) distributions,
• e_i ∼ independent N_Mi (0, R_i) distributions, and
• u_i and e_i are mutually independent.

The q × q matrix G and the M_i × M_i matrix R_i are unknown positive definite covariance matrices. This formulation allows the random effects of a subject as well as the within-subject errors to be correlated and to have nonconstant variances. These matrices are usually assumed to have some structure among their elements and are parameterized in terms of a small number of unknown parameters. For example, the matrices may have a diagonal structure with unequal diagonal elements, or a compound symmetric structure wherein all diagonal elements are equal and all off-diagonal elements are equal.

The model assumptions imply that the conditional distribution of the observation vector given the random effects is

Thus, the marginal distribution of the observation vector is (Exercise 3.1)

(3.2)

Notice that the covariance structure of the observations is induced by the covariance structures of the random effects and errors and the design matrix of the random effects. One can also deduce that (Exercise 3.2)

(3.3)

from which it follows that

(3.4)

3.2.2 Prediction

In classical statistics, estimation of random quantities is called “prediction” to distinguish it from estimation of parameters that are fixed quantities. To discuss prediction of the random u_i based on the data Y₁,..., Y_n, we begin by ignoring the model (3.1), but retaining the independence assumptions and further assuming that the joint distribution of u_i and the data is known. This, in particular, implies that the first-and second-order moments of the distribution are known.

Suppose ũ_i is a predictor of u_i. Obviously, the difference ũ_i – u_i represents the error in prediction. A predictor ũ_i of u_i is unbiased if its prediction error is zero on average, that is,

(3.5)

The notion of an unbiased predictor is similar to that of an unbiased estimator. An overall measure of error of a predictor ũ_i is given by the mean squared prediction error,

(3.6)

It represents the sum of mean squares of errors in predicting each element of u_i. See Exercise 3.6 for a generalization of this measure.

Our interest is in finding a predictor that is the best in that it minimizes (3.6) over certain classes of predictors. First we consider the class of all predictors. It is well known that the best member of this class—the best predictor of u_i—based on the data Y₁,..., Y_n is the conditional mean E(u_i|Y₁,..., Y_n) (Exercise 3.6). The mean actually equals E(u_i|Y_i) because the random effects and data from different subjects are independent. This predictor is unbiased since E(E(u_i|Y_i)) = E(u_i), implying that (3.5) holds.

In practice, however, an explicit expression for the best predictor is generally not available. Besides, it is not necessarily linear in Y_i, that is, of the form

(3.7)

for some matrix A and vector b that may both depend on i. To simplify the prediction problem, one alternative is to reduce the class of predictors to only the predictors that are linear in Y_i and find the best member in the smaller class. This leads to the best linear predictor of u_i, which can be explicitly obtained as (Exercise 3.7)

This predictor requires knowing only the first-and second-order moments of (u_i, Y_i). It is also unbiased as its expectation equals that of u_i.

We now return to the mixed-effects model (3.1) but without the normality assumption. However, we still assume that all the model parameters are known. Using the moments in (3.3), the best linear predictor of u_i under this model can be written as

(3.8)

Next, we allow β in (3.1) to be unknown, while still assuming that the matrices G and R_i are known. The task now is to jointly estimate β and u₁,..., u_n from the data. For this, it is common to take the approach of best linear unbiased predictor (BLUP), see Exercise 3.8 for the details. It shows that the BLUP of u_i has the same form as (3.8) but with β replaced by its best linear unbiased estimator (BLUE).

Finally, we consider the mixed-effects model (3.1) that already incorporates the normality assumption. If all parameters are known, we have from (3.4) that the best predictor of u_i is

(3.9)

The right-hand side of (3.9) is nothing but the expression in (3.8), implying that the best linear predictor of u_i under normality is also its best predictor. In case β is unknown but G and R_i are known, this predictor is also the BLUP provided β is replaced by its BLUE. To further compare the three predictors of u_i—the best predictor, the best linear predictor, and the BLUP—assume now that all parameters in (3.1) are unknown. In this case, one can replace the unknown parameters appearing in the expressions of these predictors by the corresponding ML estimators to get the estimated versions of the predictors. It can be seen that the BLUE of β appearing in the BLUP of u_i is actually its ML estimator under (3.1). It then follows that the estimated BLUP of u_i is identical to the estimated versions of the other two predictors. Thus, we have the remarkable conclusion that the estimated versions of all three predictors of u_i are identical under model (3.1).

3.2.3 Model Fitting

Let θ be a K ×1 vector denoting the unknown parameters in the mixed-effects model (3.1). Letting μ_i = X_iβ in (3.2), the joint pdf of the observations Y₁,..., Y_n can be written as

Considering this pdf as a function of θ while keeping the observed data fixed gives the likelihood function L(θ). Taking its log yields the log-likelihood function as

The value of θ that maximizes this function is the ML estimator of θ. In principle, the function in its present form can be given to an optimization routine for numerical maximization. However, this computation is often quite involved as one has to resolve a number of issues before employing the optimization routine to make the computations feasible, reliable, and fast. This is best left to a good statistical software package for fitting mixed-effects models. A reference is provided in Section 3.6 for the reader interested in the computational details.

Replacing θ by in β, G, R_i, and V_i gives their ML estimators , Ĝ, i, and _i, respectively. Similar substitution in (3.9) gives û_i—the estimated BLUP of u_i—as

(3.10)

These can be used to get the fitted values and the residuals, respectively, as

We can also get the standardized residuals

(3.11)

where is a matrix inverse square root of . These residuals play a key role in checking model adequacy. The predicted random effects, the fitted values, and the residuals are automatically computed by a model fitting software.

When the within-subject errors are independent, R_i is a diagonal matrix, and the standardized residuals in (3.11) are simply the residuals divided by the corresponding estimated error standard deviations. Such residuals are often called studentized residuals. If, however, there is dependence in the within-subject errors, the residuals standardized as (3.11) are often called normalized residuals to distinguish them from their studentized counterparts.

The REML method is a popular alternative to the ML method for fitting mixed-effects models. However, as explained in Section 1.12.2, we do not use REML in this book because it does not provide a joint covariance matrix of the parameter estimates, which is needed for analysis of method comparison data.

3.2.4 Model Diagnostics

The mixed-effects model (3.1) involves a number of assumptions. After fitting a model, it is a good idea to verify that the assumptions are adequate before proceeding with the inference. Of particular importance is the assumption about the within-subject errors e_i that they follow independent N_Mi (0, R_i) distributions. This assumption is equivalent to assuming that the elements of the standardized errors are distributed as independent draws from a standard normal distribution. Essentially, there are four assumptions here for the standardized errors: (a) they have mean zero, (b) they are homoscedastic, (c) they are normally distributed, and (d) they are independent. These assumptions are assessed using standardized residuals, defined in (3.11). The model also assumes that the random effects u_i follow independent N_q(0, G) distributions. It is assessed using estimated BLUPs of the random effects, given by (3.10). The errors and residuals do not have identical distributions, and the same holds for the random effects and their predicted values. Notwithstanding this fact, as far as model checking is concerned, the residuals and the predicted random effects serve as adequate proxies for the errors and the random effects, respectively. We will rely on diagnostic plots to examine compliance with the model assumptions.

Consider first the assumptions of zero mean and homoscedasticity for the standardized errors. The residual plot—the plot of standardized residuals against the fitted values—is the key diagnostic for checking these assumptions. If the assumptions hold, the points in the plot would be scattered around zero in a random manner. In particular, the presence in the plot of a trend or a nonconstant vertical scatter casts doubt on the respective assumptions of zero mean and homoscedasticity. In the specific context of method comparison studies, these violations are critical as they affect validity of the overall conclusions. Sometimes the violations can be corrected by a log transformation of the data. But if this transformation fails, then instead of looking for other more sophisticated transformations, we prefer explicit modeling of the heteroscedasticity or the trend. These topics are covered in Chapters 6 and 8, respectively.

It is often helpful to examine some variations of the basic residual plot. For example, the plot of absolute values of residuals against the fitted values makes it easier to check for heteroscedasticity because now one has to look for a trend rather than a nonconstant vertical scatter. In addition, this plot would suggest a model for the trend, essentially providing a model for the heteroscedasticity. Also, separate residual plots for different levels of important categorical covariates, for example, measurement method or gender of the subject, may reveal hidden patterns of dependence that may be missed in the basic plot. Moreover, if the error variances are suspected to depend on a continuous covariate such as age, then the residuals or their absolute values should also be plotted against that covariate.

Next, we take up the normality assumption. For errors, this can be checked by examining the normal quantile-quantile (Q-Q) plot of the standardized residuals. If the assumption holds, the points in the plot should fall on a straight line. In the same manner, the normality of each random effect can be examined using the Q-Q plot of its predicted values. However, this assessment of normality of marginals may not be enough if the random effects are jointly multivariate normal. In this case, we can examine a Q-Q plot of using a χ² distribution with q degrees of freedom as the reference distribution. This diagnostic is based on the fact if then has a χ² distribution with q degrees of freedom. Using the proxy in place of is an approximation that is adequate for the assessment of normality. The evaluation of joint normality is typically not needed for errors. It may be noted that mild to moderate departures from normality of either residuals or random effects are not of much concern in method comparison studies because generally they do not result in seriously incorrect estimates of parameters of interest and their standard errors.

The residual plot and the Q-Q plots may also reveal outliers. If these are seen and they cannot be attributed to data coding errors, a sensitivity analysis should be performed. At the minimum, this involves comparing the conclusions of interest with and without the outliers. If outliers exert substantial effect on the conclusions, then alternative modeling strategies, for example, using a nonparametric approach or an approach that replaces the normality of errors by a heavy-tailed distribution may be employed. A nonparametric approach is presented in Chapter 10. References are provided in the Bibliographic Note (Section 3.6) for mixed-effects models for skewed and heavy-tailed data.

Finally, there is the assumption of independence of standardized errors from the same subject. This may be an issue when a subject’s measurements are collected over a period of time, for example, as in longitudinal data. The independence can be checked by examining the plot of autocorrelation of standardized residuals. We consider such plots in Chapter 9.

3.3 A LARGE-SAMPLE APPROACH TO INFERENCE

We now describe the standard asymptotic or large-sample methodology for statistical inference that is used throughout the book. This methodology assumes that the number of subjects n is large. It applies to any parametric model fit by the ML method, including the mixed-effects model (3.1) and the bivariate normal model of Chapter 4. We assume that the model is parameterized in terms of a K × 1 unknown parameter vector θ. Its ML estimator is .

3.3.1 Approximate Distributions

When n is large, under some regularity conditions, the sampling distribution of can be approximated as

(3.12)

where

(3.13)

is the K × K Hessian matrix of second-order partial derivatives of the negative log-likelihood function evaluated at the ML estimate. It is also known as the observed information matrix. While this matrix may be available in closed-form for some simple models, it is often computed using numerical differentiation techniques. Its inverse serves as the approximate covariance matrix of . The regularity conditions needed for the normal approximation to hold are usually satisfied in practice. It follows from (3.12) that _k—the kth element of is approximately normal with mean θ_k, and its approximate standard error is

(3.14)

We are often interested in inference on one or more functions of θ. Let there be Q (≥ 1) such functions denoted as ϕ₁ = ϕ₁(θ),...,ϕ_Q = ϕ_Q(θ). Their ML estimators are obtained by simply replacing θ by to get . Let us collectively denote the vectors of these functions and their ML estimators by the Q × 1 vectors ϕ and , respectively. These are defined as

Assuming that ϕ is a differentiable function of θ, the sampling distribution of can be approximated by the multivariate delta method as

(3.15)

where is the K × K observed information matrix defined in (3.13) and

(3.16)

is the K × Q Jacobian matrix of derivatives of ϕ with respect to θ, evaluated at its ML estimate. The derivatives involved in this matrix are sometimes available in a closed-form but they are usually computed numerically. The Q × Q matrix serves as the approximate covariance matrix for . As before, it follows from (3.15) that _q—the qth element of —is approximately normal with mean ϕ_q, and its standard error can be approximated as

(3.17)

3.3.2 Confidence Intervals

To construct a confidence interval, we need a pivot—a function of both estimator and parameter whose distribution is completely known. Pivots determine the form of the interval and their percentiles are used as critical points in the interval. For θ_k, the approximate normality of _k calls for using

as a pivot. Recalling that z_α is the 100αth percentile of a N₁(0, 1) distribution and also that it is a symmetric distribution, we have

Here we presume that 1 – α is large enough so that z_1–α/2 is positive. Rearranging terms in the event on the left, we can write

from which we can deduce that

is an approximate two-sided 100(1–α)% confidence interval for θ_k. The actual confidence level approaches the nominal level .

We also need two-sided confidence intervals as well as one-sided confidence bounds for the parametric functions ϕ_q. For the confidence intervals, we proceed as in the case of θ_k to see that

(3.18)

is an obvious pivot for ϕ_q. As before, this allows us to write

implying that

This readily gives

(3.19)

as an approximate two-sided 100(1 – α)% confidence interval for ϕ_q. To get the one-sided bounds, we can analogously write

obtaining

(3.20)

as an approximate 100(1 – α)% upper confidence bound for ϕ_q. We can also write

leading to

(3.21)

as an approximate 100(1 – α)% lower confidence bound for ϕ_q.

The confidence intervals given thus far are individual ones in that each interval separately covers a single parameter with probability approximately equal to 1 – α. Sometimes we are also interested in simultaneous confidence intervals for multiple parameters, say, ϕ₁,...,ϕ_Q. To get the pivots for them, consider the Z_q defined in (3.18). We know that, marginally, each Z_q has an approximately N₁(0, 1) distribution. Their joint distribution is approximately multivariate normal with mean vector 0, and the covariance matrix is obtained from a pre-and post-multiplication of , given in (3.15), by a diagonal matrix whose elements are reciprocals of the standard errors SE(₁),..., SE(_Q) (see Exercise 3.11). Now, define

(3.22)

These three functions serve as the pivots for the simultaneous confidence intervals—Z_min for the upper bounds, Z_max for the lower bounds, and |Z|_max for the two-sided intervals. They have known, albeit complicated skewed distributions.

Next, define the percentiles of these pivots as

Since

and the associated multivariate normal pdf is symmetric around its mean vector 0, we get b_α = – c_1–α. The percentiles are computed numerically assuming that the normal approximation for (Z₁,..., Z_Q) is exact. They also depend on the number of functions Q and the covariance matrix of (Z₁,..., Z_Q), but this dependence is suppressed from their notation for convenience. Thus,

(3.23)

from which we can, respectively, deduce that (Exercise 3.12)

(3.24)

These probability statements imply that for ϕ₁,...,ϕ_Q we can take

(3.25)

as simultaneous approximate 100(1 – α)% two-sided intervals;

(3.26)

as simultaneous approximate 100(1 – α)% upper confidence bounds; and

(3.27)

as simultaneous approximate 100(1 – α)% lower confidence bounds. When Q = 1, the critical points used in the simultaneous intervals and bounds in (3.25), (3.26), and (3.27), respectively, reduce to the standard normal percentiles used in their individual counterparts in (3.19), (3.20), and (3.21).

For convenience, we often collectively refer to the confidence intervals and bounds considered in this section as having the form

with the understanding that the appropriate confidence limit and the critical point, including its sign, will be clear from the context.

3.3.3 Parameter Transformation

The accuracy of the estimated standard errors and the corresponding confidence intervals considered so far crucially depend on the accuracy of the normal approximation of the ML estimators. If, however, a parameter (or a parametric function ϕ) is such that the range of its possible values does not constitute (–∞, ∞), the range of a normal random variable, the normal approximation to the distribution of its ML estimator may be poor. Take, for example, a variance whose range is (0, ∞) and a correlation whose range is (–1, 1). Transforming such parameters by applying a normalizing transformation often improves the normal approximation for the estimators. These transformations are one-to-one functions that make the real line as the range on the transformed scale. The inference on the transformed parameters proceeds exactly as described in preceding sections. Once the confidence limits are available on the transformed scale, the inverse transformation is applied to them to get the limits on the original scale (Exercise 3.10). The normalizing transformations are not unique and sometimes they are not helpful.

We now consider three specific situations where a parameter transformation is commonly employed. The first is a ϕ with range (0, ∞), for example, a variance component or the TDI, defined by (2.29). In this case, a log transformation is applied as log(ϕ) has range (–∞, ∞). If l is a confidence limit for log(ϕ), then exp(l) is the corresponding confidence limit on the original scale.

The second is when ϕ represents a correlation-type parameter with range (–1, 1), for example, Pearson correlation or the CCC, defined by (2.6). In this case, the Fisher's z-transformation , defined in (1.32), is applied as its range is (–∞, ∞). If l is a confidence limit on the transformed scale, then

is the corresponding limit on the original scale.

(3.28)

with range (–∞, ∞), is applied. If l is a confidence limit on the transformed scale, then

is the corresponding limit on the original scale.

Although by definition the correlation-type measures such as CCC may be negative, their expressions based on a mixed-effects model are often constrained to be positive, see, for example, (4.11). The Fisher’s z-transformation is used in this case as well, even though the range of the transformed scale is not (–∞, ∞) (see Bibliographic Note for references).

3.3.4 Bootstrap Confidence Intervals

In the preceding section, we described the standard large-sample approach for constructing confidence intervals. This methodology requires the number of subjects n to be large to justify the normal approximation (3.12) for the sampling distribution of . If n is not large enough, the accuracy of this approximation and hence that of the confidence intervals based upon it are in doubt. Possible reasons for the inaccuracy include a bias in the estimator, underestimation of its standard error, and lack of symmetry in its sampling distribution. Although we do not know exactly how large n should be for this methodology to produce reasonably accurate conclusions, we believe that for n of less than 30, the accuracy may be short of being acceptable.

Therefore, we seek an alternative that works when n is not large enough for the application of the standard large-sample approach. This is where the resampling-based methodology of bootstrap is helpful. We may think of bootstrap as a generally more accurate alternative to the standard approach for small to moderate n. Of course, it can be used for a large n as well, but in this case bootstrap loses its accuracy advantage as its results tend to be similar to the standard approach while its computational costs increase.

In essence, the bootstrap methodology consists of employing a resampling strategy to obtain a large number of draws from the bootstrap distribution of the estimator. This distribution commonly provides a better approximation to the sampling distribution of the estimator than the usual normal approximation. The bootstrap draws are then used to approximate features of the sampling distribution such as percentiles. There are a variety of techniques that fall under the umbrella of bootstrap. Here we restrict attention to the technique of parametric studentized bootstrap as we have found it to work well in method comparison applications. The interval produced by this method has the same form as the ordinary large-sample interval, but the critical points are percentiles of the bootstrap distribution of the pivot employed.

To describe the studentized bootstrap methodology, we focus on the confidence intervals, both individual and simultaneous, for the components of the vector ϕ of Q functions of the model parameter vector θ. The confidence intervals for θ become a special case. The ordinary large-sample intervals of ϕ were constructed in Section 3.3.2. The underlying setup there can be summarized as follows: we have independent observations Y₁,..., Y_n following a model that depends on an unknown parameter vector θ. Fitting this model by the ML method yields the ML estimator . From (3.12), its approximate covariance matrix is var . The ML estimator of the parametric function vector ϕ is . From (3.15), its approximate covariance matrix is var . The estimates of elements of ϕ and their standard errors are used to compute the pivots Z₁,...,Z_Q defined in (3.18), for the individual intervals; and also the pivots Z_min, Z_max, and |Z|_max defined in (3.22), for the simultaneous intervals.

We now provide the steps needed for computing the percentiles of these pivots. The percentiles will be used as critical points in studentized bootstrap intervals. In what follows, a quantity associated with resampled data is marked by an asterisk (*) to distinguish it from its counterpart based on the original data.

• Step 1. Simulate n observations independently from the assumed model by taking θ = 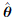. These simulated data constitute a parametric resample of the original data.

• Step 2. Fit the assumed model to the resampled data by the ML method. Let 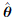^* be the resulting ML estimator of θ. Compute the bootstrap counterparts of

  

  by replacing , obtaining

  

• Step 3. Repeat Steps 1 and 2 a large number of times, say B. Only the draws of the pivots need to be saved. Denote the draws of the pivots in the bth repetition as

  

  Order the B draws of each pivot from smallest to largest. Denote the ordered draws of the pivot , whose actual draws are as . Use a similar notation to denote the ordered draws of the other pivots.

• Step 4. Compute appropriate sample percentiles of the bootstrap draws obtained in Step 3 for each pivot. Assuming that B is chosen so that (B + 1)α is a positive integer, the (B + 1)αth ordered draw of a pivot can be taken as its 100αth sample percentile. Thus, the 100αth percentiles of the pivots , can be, respectively, approximated as:

(3.29)

Replacing the normality-based percentiles in the intervals for ϕ₁,...,ϕ_Q in Section 3.3.2 by their counterparts from (3.29) gives the corresponding studentized bootstrap 100(1–α)% intervals. Upon doing so in (3.19), (3.20) and (3.21) we, respectively, get the individual two-sided intervals and one-sided upper and lower bounds for ϕ_Q as

(3.30)

However, unlike normal distributions, the bootstrap distributions are discrete and nonsymmetric. Consequently, , implying that one has to compute upper and lower percentiles from separate calculations. Proceeding in a similar manner, we, respectively, get simultaneous two-sided intervals and one-sided upper and lower bounds for ϕ₁,...,ϕ_Q from (3.25), (3.26), and (3.27) as

(3.31)

The bootstrap process can get computationally intensive, especially if the model is complex, because almost all the computations involved in model fitting and estimating standard errors must be repeated B times. The B should be a relatively large number for accurate estimation of the percentiles. Moreover, just like the ordinary large-sample intervals, the studentized bootstrap intervals also benefit from parameter transformation (Section 3.3.3). Finally, we must emphasize that bootstrap is a not a panacea for data with small n. It may not work satisfactorily if n is too small, say, less than 15 or so.

3.3.5 Confidence Bands

Sometimes we are interested in inference on a scalar parametric function ϕ that also depends on a covariate x ∈ χ. The covariate may be categorical or continuous. If it is categorical, let it have Q levels x₁,..., x_Q. If it is continuous, we discretize its domain χ into a moderately large grid of Q points x₁,...,x_Q. Often, 20 to 30 points on the grid are good enough in practice. The points may be equally spaced in the domain, or they may be the observed values of the covariate or the percentiles thereof. In any case, define

Now, the methodology for constructing one-and two-sided confidence intervals developed in Section 3.3.2 or 3.3.4 can be applied to get individual and simultaneous intervals for ϕ₁,...,ϕ_Q. If x is continuous, the individual intervals form a pointwise band and the simultaneous intervals form a band with approximate simultaneous coverage probability 1 – α. The latter, an approximate simultaneous band, is usually more useful in practice because it allows inference for the function ϕ(x) simultaneously over its entire domain χ.

3.3.6 Test of Homogeneity

Let ϕ₁,...,ϕ_Q denote values of a scalar parametric function ϕ under Q different settings. Sometimes we want to test the hypotheses

The test of this null hypothesis of equality is often called a test of homogeneity. Using the matrix notation, the hypotheses can be reformulated as

where C is the (Q – 1) × Q matrix

These hypotheses can be tested using a Wald test. Its test statistic is

with the matrix given by (3.15). When n is large, under certain regularity conditions, the null distribution of the statistic can be approximated by a χ² distribution with Q – 1 degrees of freedom. Therefore, the p-value for the test can be approximated by the probability under this distribution to the right of the observed value of the statistic. This p-value can be used to decide whether to accept or reject the null hypothesis at a given significance level.

3.3.7 Model Comparison

Often we are interested in comparing fits of two models to the same data where one model is a special case of the other. Such models are called nested. Suppose the larger model has K₂ and the smaller model has K₁ (K₁ < K₂) unknown parameters. Because of nesting, we can assume without loss of generality that the smaller model is obtained by fixing K₂ – K₁ parameters in the larger model at known values, usually zeros. This means the problem of comparing two nested models can be formulated as the problem of testing a null hypothesis that assigns known values to these K₂ – K₁ parameters, against the alternative hypothesis that represents the complement of the null. If the null hypothesis is accepted, the smaller is adequate. But if it is rejected, the larger model is taken to provide a better fit than the smaller model.

These hypotheses can be tested using the likelihood ratio test. Suppose L₂ is the maximum likelihood for the larger model, that is, its likelihood function evaluated at the ML estimate, and L₁ is the maximum likelihood for the smaller model. The test statistic for the likelihood ratio test is

(3.32)

This statistic is non-negative because by construction we have L₂ ≥ L₁, implying log(L₂) ≥ log(L₁). Under certain regularity conditions, when n is large, the null distribution of the test statistic can be approximated by a χ² distribution with K₂ – K₁ degrees of freedom. Thus, the p-value for the test can be approximated by the probability under this distribution to the right of the observed value of the statistic. The p-value can be used to decide whether to accept the null hypothesis and select the smaller model, or reject the null hypothesis and select the larger model.

In the context of mixed-effects models, the smaller model is often obtained by setting the variance of a random effect in the larger model equal to zero. This results in violation of one of the regularity conditions for the likelihood ratio test, which requires the parameters under the null hypothesis to be in the interior of the parameter space. Although the test can still be used to compare the two models, it becomes conservative in that its p-value is greater than what it should be (see Bibliographic Note).

An alternative to comparing models using likelihood ratio tests is to use information theoretic criteria such as Akaike information criterion (AIC) and Bayesian information criterion (BIC). For a given model with θ as the K × 1 vector of unknown parameters that is fit by the ML method to a dataset consisting of N observations, these are defined as

(3.33)

where is the ML estimator of θ. One can think of these criteria as representing a compromise between the goodness-of-fit of the model, as measured by the first term in the sum on the right, and the complexity of the model, as measured by the second term. We would like the model to provide a good fit without being overly complex. The principle of “smaller is better” is used for comparing two or more models using these criteria. In other words, the model with the smallest value of a criterion is preferred on the basis of that criterion. As is obvious from (3.33), the two criteria differ in the penalty for model complexity—2K in the case of AIC versus K log(N) in the case of BIC. If N > 8, we have log(N) > 2, implying that BIC > AIC for the same data. The converse is true for N ≤ 7. Unlike the likelihood ratio test, these model comparison criteria do not require the models to be nested and provide a less formal approach for model selection.

3.4 MODELING AND ANALYSIS OF METHOD COMPARISON DATA

In a method comparison study, we have measurements from two or more methods on each subject in the study. The data on the same subject are dependent while those from different subjects are independent. This particular feature of the data makes it particularly attractive for modeling by a mixed-effects model of the form (3.1). Our task now is to develop a general framework for mixed-effects modeling and analysis of method comparison data.

To fix ideas, consider a method comparison study involving J (≥ 2) methods and n subjects. The subjects are indexed as i = 1,...,n, and the methods as j = 1,...,J. Let there be m_ij measurements from method j on subject i. The m_ij × 1 vector of these measurements is Y_ij. Let denote the total number of measurements on subject i and in the study, respectively.

We would like the modeling framework to be flexible enough to allow for more than two methods, multiple measurements from each method on every subject, balanced or unbalanced designs, covariates, and heteroscedasticity. Besides these basic requirements, some additional considerations regarding multilevel fixed effects, random effects, and within-subject errors arise while developing a general framework. These include the following:

• There may be two types of fixed effects. One at the level of subjects that do not depend on the methods, for example, the effects of gender or age of the subject, and the other at the level of methods that may or may not depend on the subjects. For example, the main effect of the methods themselves and the method × gender interaction effects are both method-level fixed effects, but the main effect of the methods does not depend on the subjects, whereas the interaction does.
• There may be two types of random effects as well. One at the level of subjects that do not depend on the method, for example, the effects of the subjects themselves, and the other at the level of methods that are nested within the subjects, for example, subject × method interactions.
• The within-subject errors necessarily depend on the methods, but the parameters of their distributions may also be of two types. One that changes with the method, for example, the error variances, and the other that is common across all the methods, for example, an autocorrelation parameter.

Further, the nature of the method comparison problem itself suggests that the data from each method should be modeled in a similar way so as to allow differences in marginal characteristics of the methods to be reflected in the measures of similarity. In particular, this means that the models for data from different methods should be identical except for possible differences in values of the model parameters and aspects of models that are tied to the study design, for example, the number of measurements on a subject.

These considerations suggest a mixed-effects model of the following form for the data vectors

(3.34)

where

• β₀ is the vector of fixed effects common to all methods,
• β_j is the vector of fixed effects of method j,
• u_i0 is the vector of random effects of subject i common to all methods,
• u_ij is the vector of random effects of subject i specific to method j,
• are full rank design matrices associated with β₀, β_j, u_i0, and u_ij, respectively, and
• e_ij is the vector of within-subject random errors of method j.

It is also assumed that, with appropriate dimensions,

• u_i0 follow independent N (0, G₀) distributions,
• u_ij follow independent N (0, G_j) distributions,
• e_ij follow independent N (0, R_ij) distributions, and
• u_i0, u_ij, and e_ij are mutually independent.

The covariance matrices are positive definite. They are generally represented in terms of a relatively small number of parameters. We have deliberately avoided specifying dimensions of the vectors and matrices involved in this model to avoid introducing much new notation. They should be clear from the context.

The marginal models for the J methods are of the same form in that their mean vectors and covariance matrices of random effects as well as errors are parameterized identically. The models may differ in values of the parameters but the parameters hold the same interpretation across the J models. This, in particular, implies that the columns of the design matrices correspond to identical effects. This way the differences

for j ≠ l are well defined even though Y_ij and Y_il may have different dimensions. The model (3.34) can be written in the form of the general mixed-effects model (3.1) by defining the various vectors and matrices as (Exercise 3.14)

(3.35)

It follows from the assumptions for the model (3.34) that (Y_i1,..., Y_iJ)—the vector of all observations on subject i—jointly follows independent multivariate normal distributions for i = 1,...,n with (Exercise 3.13)

(3.36)

The mixed-effects model (3.34) offers a general framework for handling method comparison. It allows modeling of the mean functions through both common and method-specific fixed effects. It also allows for dependence in a subject’s multiple measurements from the same method through both common and method-specific random effects of the subject. Dependence in a subject’s measurements from different methods is modeled through common random effects. It lets the covariance matrices of the within-subject errors vary with subject and method, allowing one to account for correlation and certain forms of heteroscedasticity in the errors as well. Special cases of (3.34) are used throughout the book to model various types of continuous data. The model assumes that the method-specific random effects of a subject are independent and so are the within-subject errors of the methods. These assumptions are informed by what we have seen in practice. They may need to be relaxed in some applications.

While employing this model in practice, one has to ensure that the model is identifiable. A model is called identifiable if no two different combinations of its parameter values lead to the same data distribution. It becomes non-identifiable if it is overparameterized and in this case there is not enough information in the data to estimate all the model parameters (see Section 1.6.1 for an example). To make matters worse, a model fitting software generally does not check for identifiability and may happily provide estimates without any warning. However, at least some of the estimates will be meaningless. The remedy for this includes simplifying the model by reducing the number of parameters, changing the model, or collecting more data, though not by simply increasing the number of subjects.

Even if the model is identifiable, it may happen that estimates of some of its parameters are not reliable in that they have unrealistically large standard errors. This often happens when the data do not have enough information to reliably estimate all parameters of the model. A prime example of this is the mixed-effects model (1.19) for paired measurements data (see Chapter 4). This model is identifiable, but the estimate of at least one within-subject variance is frequently unreliable. The remedies for this problem are the same as those for a non-identifiable model.

The principle of model parsimony calls for not having more parameters in the model than what is really necessary. However, a key goal in the analysis of method comparison data is evaluation of similarity and agreement of the methods. On one extreme, if all method-specific parameters are equal across the methods, then the methods are as similar as they possibly can be and they may seem to agree well. But this is just an artifact of the model assumptions. On the other extreme, if all method-specific parameters are assumed unequal, then this may result in a non-identifiable model. In practice, we need to be somewhere between these extremes. Therefore, the guiding principle for us is to let the method-specific parameters that are crucial for evaluating similarity and agreement differ across the methods without worrying about model parsimony. At the minimum, we let the methods have their own fixed intercepts and error variances and include a random subject-specific intercept in the model, provided that the model remains identifiable and the parameters are estimated reliably.

After building an adequate model, the attention shifts to the evaluation of similarity and agreement of the measurement methods. This requires two-sided confidence intervals for measures of similarity and one-sided confidence bounds for measures of agreement. To construct these intervals and bounds, usually we first define Y =(Y₁,...,Y_J)^T as the vector of a single measurement from each of the methods on a randomly selected subject from population. One may think of this Y as representing typical measurements from the methods. Next, we determine the joint distribution of Y that is induced by the assumed model. The mechanics of how this is done is illustrated in later chapters. The distribution of Y depends on the vector θ of model parameters. Then we use this distribution to derive expressions for measures of similarity and agreement as functions ϕ of θ. In the next step, we use the methodology outlined in Section 3.3 to estimate these measures and construct appropriate confidence bounds and intervals for them (see Chapters 4, 5, and 7). If the distribution of Y depends on a covariate, this computation is repeated over the range of values of the covariate that may be of interest (see Chapters 6, 8, and 9).

3.5 CHAPTER SUMMARY

1. A mixed-effects model offers a flexible framework for modeling data where the observations on the same subject are dependent and those on different subjects are independent.
2. The method comparison data are naturally modeled by a mixed-effects model.
3. Standard large-sample inference based on a mixed-effects model assumes that the number of subjects is large and uses normal sampling distributions.
4. If the number of subjects is not large, bootstrap confidence intervals tend to be more accurate and are recommended.

3.6 BIBLIOGRAPHIC NOTE

Pinheiro and Bates (2000) provide a good introduction to linear mixed-effects models. These authors provide a succinct but lucid account of estimation theory as well as computational details. They use a large number of examples to illustrate how their nlme package for fitting mixed-effects model can be used to analyze real data. These examples deal with the whole gamut of issues involved in data analysis—from plots and exploratory analysis to model diagnostics and inference. They also discuss testing for zero variance of a random effect. Searle et al. (1992) and McCulloch et al. (2008) discuss prediction in mixed-effects models in detail.

For data with outliers and skewness, a number of authors propose replacing the normality assumption for random effects or errors with generalizations of the normal distribution. In particular, Verbeke and Lesaffre (1996) consider a finite mixture of normals as the distribution of the random effects. Zhang and Davidian (2001) use a semi-nonparametric representation of random effects. Pinheiro et al. (2001) use a joint t distribution for random effects and errors. Independent multivariate skew-normal distributions for random effects and errors are assumed in Arellano-Valle et al. (2005). Ho and Lin (2010) assume a joint skew-t distribution for random effects and errors. Choudhary et al. (2014) and Sengupta et al. (2015) use a skew-t distribution for random effects and an independent t distribution for errors.

Lehmann (1998) gives an excellent introduction to large-sample theory of inference, including that of the ML estimators. The regularity conditions needed for the asymptotic normality of ML estimators to hold can also be found in Chapter 7 of this book. Efron and Tibshirani (1993) and Davison and Hinkley (1997) provide clear comprehensive accounts of bootstrap, including its applications.

To compute simultaneous confidence intervals and bounds, one needs percentiles of appropriate functions of multivariate normally distributed pivots (Section 3.3.2). These can be computed, for example, using the multcomp package of Hothorn et al. (2008) in R. It uses an algorithm of Genz (1992) for efficient computation of multivariate normal probabilities.

Specific mixed-effects models for method comparison data have been considered by a number of authors, including Carrasco and Jover (2003), Quiroz (2005), Lai and Shiao (2005), Carstensen et al. (2008), and Choudhary (2008). These authors also consider likelihood-based inference on specific agreement measures. For example, Carstensen et al. (2008) and Lai and Shiao (2007) focus on limits of agreement; Choudhary (2008) considers TDI; and Carrasco and Jover (2003) and Quiroz (2005) focus on CCC. Lin et al. (2007) also consider a mixed-effects model and discuss inference on several agreement measures, including TDI and CCC. But they use a generalized estimating equations approach (GEE; Hardin and Hilbe, 2012) to fit the model instead of the ML approach. Carrasco and Jover (2003) and Lin et al. (2007) use Fisher’s z-transformation for inference on CCC even though the range on the transformed scale does not constitute the real line.

EXERCISES

1. Verify that the marginal distribution of Y₁,..., Y_n following the mixed-effects model (3.1) is given by (3.2).

2. Consider the mixed-effects model (3.1).

   1. Verify that the joint distribution of (u_i, Y_i) is given by (3.3).
   2. Deduce that the conditional distribution of u_i|Y_i is given by (3.4).

3. Suppose Y and u are continuous univariate random variables. We want to predict u using a function ũ of Y. The predictor’s error is measured using its mean absolute prediction error, E(|ũ– u|).

   1. Show that the constant c that minimizes E(|u – c|) is the median of u.
   2. Deduce that the predictor ũ that minimizes E{(|ũ– u|)|Y } is the conditional median of u given Y.
   3. Show that the conditional median in (b) is also the best predictor in the sense of minimizing the mean absolute prediction error.
   4. Assume now that Y and u are independent and the median u₀ of u is known. Deduce that u₀ is the best predictor ũ.
4. (Brockwell and Davis, 2001) Suppose Y and u are random variables with μ = E(u) and σ² = var(u). We want to predict u using a function ũ of Y. The predictor’s error is measured using its mean squared prediction error, E(ũ – u)² .
   1. Show that the constant c that minimizes E(u – c)² is c = μ. What is the minimum value?
   2. Deduce that the predictor ũ that minimizes E{(ũ– u)²|Y } is ũ = E(u|Y).
   3. Show that ũ = E(u|Y) is also the best predictor in the sense of minimizing the mean squared prediction error.
   4. Assume now that Y and u are independent and μ is known. Deduce that the best predictor is ũ = μ.

5. (A generalization of Exercise 3.4; Brockwell and Davis, 2001) Suppose Y₁,...,Y_n and u are random variables with μ = E(u) and σ² = var(u). We would like to predict u using a function ũ of Y₁,...,Y_n, with error measured by the predictor’s mean squared prediction error.

   1. Show that the predictor ũ that minimizes E{(ũ – u)²|Y₁,...,Y_n} is ũ = E(u|Y₁,...,Y_n).
   2. Deduce that ũ = E(u|Y₁,...,Y_n) is also the best predictor.
   3. Assume now that Y₁,...,Y_n and u are i.i.d. and μ is known. Deduce that the best predictor is ũ = μ.
   4. Assume that the conditions of part (c) hold except that μ is now unknown. Consider estimating μ in terms of Y₁,..., Y_n using a linear unbiased estimator. Show that the sample mean 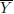= (Y₁ + ... + Y_n)/n is the best linear unbiased estimator of μ in that it minimizes the variance of the estimator.
   5. Assume that the conditions of part (d) hold. Returning to prediction of u using Y₁,...,Y_n, deduce that 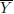is the best linear unbiased predictor of u.

6. (Another generalization of Exercise 3.4) Suppose we want to predict a q × 1 random vector u using an m × 1 random vector Y. The two vectors have a joint distribution. Suppose the error of a predictor ũ—a q × 1 function of Y—is measured using

   

   where B is a q × q positive definite symmetric matrix. The mean squared prediction error defined in (3.6) is obtained by taking B to be an identity matrix.

   1. Show that the best predictor that minimizes the above criterion is ũ= E(u|Y).

   2. For the best predictor ũ, establish the following claims:

      1. It is unbiased for u.
      2. The covariance matrix of its prediction error is var(ũ–u)= E{var(u|Y)}.
      3. cov(ũ, u)= var(ũ).
      4. cov(ũ, Y)= cov(u, Y).

7. Consider the same setup as in Exercise 3.6 but restricted to predictors ũ that are linear in Y, that is, are of the form

   

   where A is a q ×m matrix and b is a q ×1 vector. This exercise follows McCulloch et al. (2008, Chapter 13) to find the best linear predictor ũ by minimizing the generalized mean squared prediction error C given in Exercise 3.6 with respect to A and b. (For an excellent introduction to vector calculus, see Graybill (2001).)

   1. Show that the criterion to be minimized can be written as

      

   2. Solve for b and verify that the solution is

      

   3. Show that with b found in part (b) the criterion C can be expressed as

      

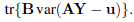
      Deduce that minimizing this expression with respect to A is equivalent to minimizing tr(BE), where E is a q × q matrix given by

      

      Denoting the ith row of A as and the jth column of cov(Y, u) as c_j, the (i, j)th element of E can be written as

      

   4. Solve for a_i and verify that the solution is

      

      The solutions can be written in the matrix form as

      

   5. Deduce from parts (b) and (d) that the desired best linear predictor is

      

   6. Argue that solving in part (b) to get b and solving in (d) to get A defined there are equivalent to solving

      

      The equations (i) and (ii) above, respectively, imply that the best linear predictor is unbiased and its error is uncorrelated with Y.

   7. Show that covariance matrix of the prediction error ũ – u of the best linear predictor is

      

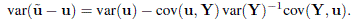
8. Suppose that Y follows the mixed-effects model

   

   where

   

   The dimensions of these vectors and matrices can be taken from (3.3) applied to a single subject i. Also, as before, V = ZGZ^T +R is var(Y) and cov(u, Y)= GZ^T . Assume that β is unknown but G and R are known. We would like to jointly estimate β and u. This exercise follows McCulloch et al. (2008, Chapter 13) to find the BLUP of the scalar quantity

   

   where s and t are arbitrary known vectors. This involves finding a predictor of the form a^T Y that minimizes the mean squared prediction error

   

   with respect to the vector a, subject to the unbiasedness condition

   

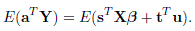
   1. Show that the unbiasedness condition is equivalent to X^T a = X^T s. Deduce that, under this condition, the mean squared prediction error is the variance of the prediction error, given as

      

   2. Let 2λ be a vector of Lagrange multipliers. Then, the expression to be minimized with respect to a and λ is

      

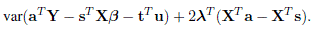
      Show that a and λ that minimize this expression are solutions of

      

   3. Show that solving for a leads to the desired BLUP of s^T Xβ + t^T u as

      

      where

      

      is the BLUE of β. It is also the generalized least squares estimator of β.

   4. Deduce that is the BLUP of u.
   5. Compare the BLUP with the best linear predictor found in Exercise 3.7, part (e).

9. Consider the setup of Exercises 3.6 and 3.7. Assume in addition that (u, Y) jointly follow a multivariate normal distribution. Show that the best predictor and the best linear predictor of u are identical.

10. Suppose the interval (L, U) is a 100(1–α)% confidence interval for a monotonically increasing function g of parameter θ. Let g^–1 be the inverse function of g.

    1. Show that confidence interval for θ.

    2. Suppose . Determine g^-1.

    3. What will be the confidence interval for θ if g is a monotonically decreasing function of θ?

11. Consider the pivots Z₁,...,Z_Q defined in (3.18). Use (3.15) to show that the joint distribution of the Z_q can be approximated by a Q-variate normal distribution with mean vector 0 and covariance matrix obtained by pre-and post-multiplying by a diagonal matrix whose elements are reciprocals of the standard errors SE(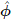₁),..., SE(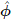Q), given by (3.17).

12. Show that the probability statements in (3.24) follow from (3.23).

13. Show that the joint distribution of (Y_i1,..., Y_iJ) under the mixed-effects model (3.34) is multivariate normal with parameters given by (3.36).

14. Verify that the model (3.34) can be written in the form (3.1) by using the vectors and matrices defined in (3.35).