Chapter 11. Difference Views
I’ll teach you differences: away, away!
—
In this chapter I’ll consider the question of updating through the relational difference operator (MINUS, in Tutorial D). Now, I’m sure you won’t be surprised to learn the chapter is fairly similar in structure to its immediate predecessors, on intersection and union. However, it also differs—how appropriate!—in certain important respects, as you’ll quickly see. To elaborate briefly: Suppose we’re given two relvars A and B. Clearly, if A = B, the difference A MINUS B and the difference B MINUS A are both empty, so that case isn’t very interesting. Also, if A and B are disjoint, then A MINUS B is equal to A and B MINUS A is equal to B, so that case isn’t very interesting either. So the interesting case is the one in which A and B aren’t equal but do overlap. As in Chapter 9, therefore (on intersection), I’ll consider two examples, one in which the overlap is explicit and one in which it’s merely implicit. For reasons that will become clear later, however, this time I want to consider the implicit case first.
Example 1: Implicit Overlap
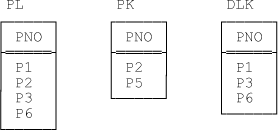
My first example is based once again on the “parts on sale” vs. “parts in stock” example from Chapters Chapter 9 and Chapter 10. Once again, then, we have two relvars PL and PK, each with just a single attribute PNO—relvar PL gives part numbers for parts on sale, and relvar PK gives part numbers for parts in stock. Now, there are obviously two possible differences we might consider; for definiteness, let’s focus on the difference PL MINUS PK (DLK, say), which gives part numbers for parts that are on sale but not in stock. Thus, the predicates are as follows:
| PL: Part PNO is on sale. |
| PK: Part PNO is in stock. |
| DLK: Part PNO is on sale and not in stock. |
Sample values are shown in Figure 11-1.
As for constraints, {PNO} is obviously the sole key for each of the three relvars, and of course DLK is equal to the difference—or, rather, one of the two possible differences—between the other two:
CONSTRAINT ... DLK = PL MINUS PK ;
Turning now to compensatory actions,[111] here first is the rule for deletes on relvar PL:
ON DELETEdFROM PL : DELETEdFROM DLK ;
Imagine deleting tuple t from PL. Now, t will appear in DLK only if it appears in PL and not in PK. And this state of affairs certainly won’t exist after the delete on PL, regardless of whether it did so before; hence the specified rule.
Next, here’s the rule for inserts on relvar PL:
ON INSERTiINTO PL : INSERT (iMINUS PK ) INTO DLK ;
Imagine inserting tuple t into PL. Again, t will appear in DLK only if it appears in PL and not in PK. And this state of affairs will exist after the insert on PL only if t didn’t appear in PK before the delete, and still doesn’t do so afterward; hence the specified rule.
What about relvar PK? Well, first let me point out that PL and PK play asymmetric roles in the definition of DLK, and it’s therefore only to be expected that the corresponding compensatory actions will be asymmetric too—and so indeed they turn out to be. Let’s think about inserts first. Again imagine inserting tuple t (into PK this time). Now, either t already existed in PK or it did not. If it did,[112] then it certainly didn’t appear in DLK before the insert, and it’ll continue not to do so afterward. Conversely, if it didn’t already exist in PK, then after the insert it certainly won’t appear in DLK, even if it did so before. All of which leads to the following rule:
ON INSERTiINTO PK : DELETEiFROM DLK ;
Finally, imagine deleting tuple t from PK. Now, either t already existed in PL—the other relvar, observe—or it did not. If it did, then it will certainly appear in DLK after the delete, regardless of whether it did so before. Conversely, if it didn’t already exist in PL, then it certainly didn’t appear in DLK before the delete, and it’ll continue not to do so afterward. Which leads to the following rule:
ON DELETEdFROM PK : INSERT (dINTERSECT PL ) INTO DLK ;
I remark before continuing that the two compensatory actions just discussed are the first examples we’ve seen in this book so far in which an insert can cause a delete or vice versa (in other words, they’re the first examples in which the compensatory action isn’t basically just a simple cascade of some kind).
I turn now to updates on DLK. Here first is the insert rule:
ON INSERTiINTO DLK : INSERTiINTO PL , DELETEiFROM PK ;
Imagine inserting a tuple into DLK for part number p. What we mean by that update is that part p is on sale and not in stock. Thus, we must insert the tuple into PL if it isn’t already there, and delete it from PK if it is already there. Note that neither of these two updates is sufficient in itself, in general—if we did the insert and not the delete, we might wind up effectively asserting that part p is both on sale and in stock; likewise, if we did the delete and not the insert, we might wind up effectively asserting that part p is neither on sale nor in stock. Both of these possibilities would cause the tuple for part p not to appear in DLK, thereby giving rise to an Assignment Principle violation.
Aside: Actually there’s another way to think about the foregoing (and this alternative perspective might help you understand the delete rule too, which is discussed next). As you can easily confirm by means of a Venn diagram, any given difference A MINUS B can be regarded as the intersection A INTERSECT C, where C is the (absolute) complement of B. In accordance with the discussions in Chapter 9, therefore, an insert on A MINUS B should cause an insert on A and an insert on C. But an insert on C is a delete on B—in effect, it causes tuples to be removed from B and added to C. End of aside.
So what about deletes on DLK? Well, symmetry suggests the following rule:
ON DELETEdFROM DLK : DELETEdFROM PL , INSERTdINTO PK ;
Does this rule make sense? Imagine deleting the tuple from DLK for part number p. What we mean by that update is that part p is either in stock or not on sale, and possibly both. Clearly, then, it would be sufficient to perform just one of the specified actions—insert the tuple into PK (so the part is in stock) or delete it from PL (so the part is not on sale)—in order to achieve the desired effect; in fact, to do both as the foregoing rule requires is effectively to treat logical OR as logical AND once again. The trouble is, of course, there doesn’t seem to be any good reason to choose either of these two actions over the other. For that reason, I propose to adopt the rule as I’ve stated it above, at least until further notice.[113]
Of course, we’re dealing here with another situation in which information equivalence is lost. To be specific, any information that can be represented by relvar DLK alone can certainly be represented by relvars PL and PK taken in combination, but the converse is false. (Here’s an example of a query on the latter that has no exact counterpart on the former: “Get part numbers for parts that are in stock and not on sale.”) As a consequence, it should be obvious that there’ll be certain updates that can be done on PL and/or PK that have no exact counterpart on DLK. An example of such an update is “Insert some new tuple into both PL and PK” (i.e., update the database to say some part is both on sale and in stock).
I’ll leave it as an exercise to determine the implications of all of the foregoing for a user who sees just relvar DLK. However, let me now point out that, as in the case of the intersection and union analogs of this example in the previous two chapters, there’s unfortunately another issue here. Suppose we start off with just relvars PL and PK, without the difference view. Suppose too, just to be definite, that part P1 is represented in PL but not PK. Then each of the following updates is clearly legitimate:
DELETE ( P1 ) FROM PL ; INSERT ( P1 ) INTO PK ;
Observe in particular that there’s no question of the foregoing delete causing an insert on relvar PK or the foregoing insert causing a delete on relvar PL. But now suppose we introduce the difference view DLK. Given the rules defined above, then, the delete on PL will now cause an insert on PK, and the insert on PK will now cause a delete on PL!—and they’ll do so, moreover, even if view DLK isn’t visible to the user issuing the delete on PL or the insert on PK. Or to put the point another way: Introducing that view apparently requires the simultaneous introduction of a rule that makes deletes on PL cause inserts on PK and vice versa.[114]
Now, one possible fix for this problem, in the particular case at hand, is to execute another delete or another insert immediately following the original one, as shown here:
DELETE ( P1 ) FROM PL ; DELETE ( P1 ) FROM PK ; INSERT ( P1 ) INTO PK ; INSERT ( P1 ) INTO PL ;
However, the solution to be discussed in the subsection immediately following is in my opinion greatly to be preferred. Of course, it’s essentially the same as the solution to the corresponding problem in the intersection and union cases as discussed in the previous two chapters.
A Better Design
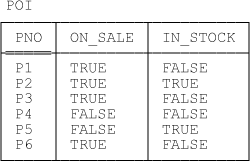
As you’ll recall from those previous chapters, the solution I have in mind involves replacing relvars PL and PK in their entirety by a single relvar, POI, with attributes PNO, ON_SALE, and IN_STOCK (where attributes ON_SALE and IN_STOCK are of type BOOLEAN and have the obvious interpretations, and {PNO} is the sole key). A possible value for such a relvar is shown in Figure 11-2 (a repeat of Figure 9-3 from Chapter 9, also Figure 10-4 from Chapter 10).
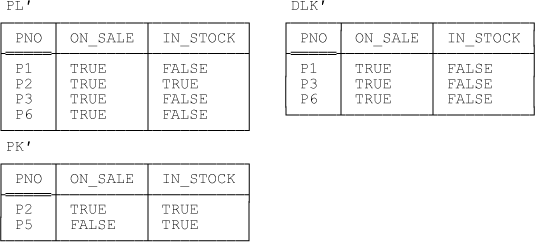
Now we define restriction views PL’ and PK’ and difference view DLK’ as indicated by the following constraints:
CONSTRAINT ... PL' = POI WHERE ON_SALE ; CONSTRAINT ... PK' = POI WHERE IN_STOCK ; CONSTRAINT ... DLK' = PL' MINUS PK' ;
Figure 11-3 shows sample values corresponding to those in Figure 11-2.
Each of these relvars has {PNO} as sole key, and {PNO} is also a foreign key, referencing PL’, in DLK’. The following constraints also obviously hold:[115]
CONSTRAINT ... IS_EMPTY ( PL' WHERE NOT ( ON_SALE ) ) ; CONSTRAINT ... IS_EMPTY ( PK' WHERE NOT ( IN_STOCK ) ) ; CONSTRAINT ... IS_EMPTY ( DLK' WHERE NOT ( ON_SALE ) OR IN_STOCK ) ) ;
As in Chapter 9 (though not Chapter 10), we need an additional constraint to the effect that if some part is represented in both PL’ and PK’, then the two tuples representing that part are in fact one and the same:
CONSTRAINT ... UNION { PL' , PK' } KEY { PNO } ;Of course, this constraint will be enforced automatically if relvars PL’ and PK’ are indeed, as stated, views of POI.
Here now repeated from Chapters Chapter 9 and Chapter 10 are the update rules involving relvar POI and relvars PL’ and PK’:
ON INSERTiINTO POI : INSERT (iWHERE ON_SALE ) INTO PL' , INSERT (iWHERE IN_STOCK ) INTO PK' ; ON DELETEdFROM POI : DELETE (dWHERE ON SALE ) FROM PL' , DELETE (dWHERE IN_STOCK ) FROM PK' ; ON INSERTiINTO PL' : INSERTiINTO POI ; ON INSERTiINTO PK' : INSERTiINTO POI ; ON DELETEdFROM PL' : DELETEdFROM POI ; ON DELETEdFROM PK' : DELETEdFROM POI ;
And here are the rules involving relvars PL’ and PK’ and relvar DLK’:
ON INSERTiINTO PL' : INSERT (iWHERE NOT ( IN_STOCK ) ) INTO DLK' ; ON INSERTiINTO PK' : DELETEiFROM DLK' ; ON DELETEdFROM PL' : DELETEdFROM DLK' ; ON DELETEdFROM PK' : INSERT (dWHERE ON_SALE ) INTO DLK' ; ON INSERTiINTO DLK' : INSERTiINTO PL' ; ON DELETEdFROM DLK' : DELETEdFROM PL' ;
And these rules are all, as I hope you’ll agree, completely noncontroversial (though as in Chapters Chapter 9 and Chapter 10 I think it’s instructive to compare them with the rules I gave in connection with the previous version of the example). So, to repeat from those previous chapters: In effect, what I’ve done here is redesign the database in such a way that information that was previously represented only implicitly, by the relvar names PL and PK, is now represented explicitly by values of the attributes ON_SALE and IN_STOCK instead. And the effect of that redesign is to convert the previous version of the example—viz., the version with at least arguably unacceptable update behavior—into a version that behaves much more acceptably.
I’ll leave it as an exercise to determine the implications of all of the foregoing for a user who sees just relvar DLK’. As for defining DLK’ directly as a restriction of POI—which we clearly could have done if we’d wanted to—I’ll leave it as another exercise to show that the behavior of such a restriction with respect to updates would be essentially identical to that of the difference version as described above. Finally, I’ll also leave it as an exercise to show that (assuming it’s supposed to be capable of supporting update operations properly) a “double prime” version of the example—analogous to the “double prime” version of the counterpart example, Example 2, in Chapter 9—is effectively a nonstarter.
A Remark on Included Difference
I’d like to consider, briefly, a slightly different example. Suppose we’re given two relvars, PL (giving, as above, part numbers for parts on sale) and PD (giving part numbers for parts manufactured domestically), and there’s a business rule in effect that says that only parts manufactured domestically can be on sale—implying that, at all times, the relation that’s the current value of PL is included in the relation that’s the current value of PD. Of course, the difference DDL = PD MINUS PL gives part numbers for parts that are manufactured domestically and aren’t on sale. (Note that DDL is an example of an “included difference,” because the second operand, relvar PL, is included in the first—meaning, more precisely, that the body of PL at any given time is a subset of the body of PD at the time in question.) The predicates are as follows:
| PL: Part PNO is on sale. |
| PD: Part PNO is manufactured domestically. |
| DDL: Part PNO is manufactured domestically and isn’t on sale. |
Now, the significant point about this example, compared to the example involving relvars PL and PK discussed earlier in this section (where the difference wasn’t an included difference), is that the following constraint clearly holds:
CONSTRAINT ... PL ⊆ PD ;
As a consequence of this constraint, given compensatory actions along the lines of those defined in the first part of this section, deletes on DDL will always fail on a Golden Rule violation.
Example 2: Explicit Overlap
Note: I include this section for completeness. It doesn’t really add very much, and you can skip it if you like.
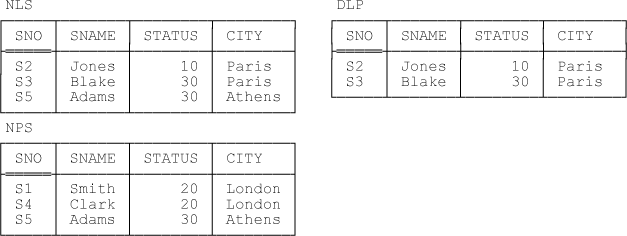
Now let’s take a look at another example, based on the by now very familiar relvars NLS (“non London suppliers”) and NPS (“non Paris suppliers”):
NLS { SNO , SNAME , STATUS , CITY } KEY { SNO }
NPS { SNO , SNAME , STATUS , CITY } KEY { SNO }Here once again are the predicates:
| NLS: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY isn’t London). |
| NPS: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY isn’t Paris). |
Now let’s define the difference NLS MINUS NPS as a view DLP:
DLP { SNO , SNAME , STATUS , CITY } KEY { SNO }The predicate for this relvar is:
| DLP: Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY is Paris).[116] |
Sample values are shown in Figure 11-4.
The following constraints clearly apply:
CONSTRAINT ... DLP = NLS MINUS NPS ;
CONSTRAINT ... IS_EMPTY ( NLS WHERE CITY = 'London' ) ;
CONSTRAINT ... IS_EMPTY ( NPS WHERE CITY = 'Paris' ) ;
CONSTRAINT ... IS_EMPTY ( DLP WHERE CITY ≠ 'Paris' ) ;
CONSTRAINT ... ( NLS WHERE CITY ≠ 'Paris' ) =
( NPS WHERE CITY ≠ 'London' ) ;Also, each of the three relvars has {SNO} as its sole key, as already indicated, and {SNO} in DLP is a foreign key referencing NLS. Note: As usual, we additionally need a constraint to the effect that {SNO} is a key for the union of NLS and NPS, in order to guarantee that if some supplier is represented in both of those relvars, then the two tuples representing that supplier are in fact one and the same:
CONSTRAINT ... UNION { NLS , NPS } KEY { SNO } ;Of course, this constraint will be enforced automatically if relvars NLS and NPS are in fact views of the suppliers relvar S.
Here now are the compensatory actions—first, the usual rules for cascading updates from NLS to NPS and vice versa:
ON INSERTiINTO NLS : INSERT (iWHERE CITY ≠ 'Paris' ) INTO NPS ; ON INSERTiINTO NPS : INSERT (iWHERE CITY ≠ 'London' ) INTO NLS ; ON DELETEdFROM NLS : DELETE (dWHERE CITY ≠ 'Paris' ) FROM NPS ; ON DELETEdFROM NPS : DELETE (dWHERE CITY ≠ 'London' ) FROM NLS ;
Next, here’s the rule for cascading inserts on NLS to DLP:
ON INSERTiINTO NLS : INSERT (iWHERE CITY = 'Paris' ) INTO DLP ;
And the rule for cascading deletes on NLS to DLP:
ON DELETEdFROM NLS : DELETE (dWHERE CITY = 'Paris' ) FROM DLP ;
(We could drop the restriction condition here without loss.)
As for inserts on NPS, the analysis in previous sections should lead you to expect something like the following:
ON INSERTiINTO NPS : DELETEiFROM DLP ;
But if tuple t is to be inserted into NPS, then tuple t must have CITY value something other than Paris—and since tuples in DLP all have CITY value Paris, the compensatory action here becomes a “no op.”
Finally, what about deletes on NPS? Again, the analysis in previous sections should lead you to expect something like the following:
ON DELETEdFROM NPS : INSERT (dINTERSECT NLS ) INTO DLP ;
But tuples in NPS all have CITY value something other than Paris; hence, so do all tuples in d, and so do all tuples in d INTERSECT NLS a fortiori.[117] And since tuples in DLP all have CITY value Paris, the compensatory action here becomes a “no op” again. Note: Actually, taking these two “no op” rules together, it should be intuitively obvious that—speaking pretty loosely, of course—inserts and deletes on NPS (= non Paris suppliers) can’t possibly have any effect on DLP (= Paris suppliers).
As for updates on the difference relvar as such, it’s easy to see by an analysis very similar to the foregoing that the rules reduce to the following simple form:
ON INSERTiINTO DLP : INSERTiINTO NLS ; ON DELETEdFROM DLP : DELETEdFROM NLS ;
This brings me to the end of Example 2. But perhaps you can now see why I wanted to discuss Example 1, the “parts on sale” vs. “parts in stock” example, first—Example 2, the NLS vs. NPS example, although in a sense better behaved than Example 1, isn’t so good as an illustration of the underlying concepts, precisely because of the existence of certain constraints that cause the update rules to take a particularly simple form (a state of affairs that makes it hard to see the trees for the forest, one might say).
Concluding Remarks
Let me abstract from the examples discussed in previous sections and summarize the update rules when there’s a difference involved. Let V be defined as A MINUS B. Further, assume for simplicity that tuples to be inserted into A and B are required to satisfy boolean expressions ax and bx, respectively, where ax and bx denote restriction conditions (default simply TRUE). Then we have:
ON INSERTiINTOA: INSERT (iWHERE NOT (bx) ) INTOV; ON INSERTiINTOB: DELETEiFROMV; ON DELETEdFROMA: DELETEdFROMV; ON DELETEdFROMB: INSERT (dWHEREax) INTOV; ON INSERTiINTOV: INSERTiINTOA, DELETEiFROMB; ON DELETEdFROMV: DELETEdFROMA, INSERTdINTOB;
Once again I’ll leave it as an exercise to show that the specific rules given in connection with the examples earlier in the chapter are all special cases—sometimes slightly “optimized” special cases—of the foregoing general rules.
Now, we saw, in connection with Example 1 (the implicit overlap example), that the rule for deleting through a difference can sometimes lead to results that in practice might be unacceptable, or at least undesirable. Let me elaborate on this point for a moment. Let the predicates for A and B be PA and PB, respectively; then the predicate for V = A MINUS B is PA AND NOT (PB). Thus, if we delete t from V, we mean the proposition PA(t) AND NOT (PB(t)) is false, which is logically equivalent to saying NOT(PA(t)) OR PB(t) is true. By contrast, deleting t from A and inserting it into B means NOT(PA(t)) AND PB(t) is true. So if deleting t from V causes t be deleted from A and inserted into B, we’re effectively treating logical OR as logical AND once again.[118]
To repeat, the foregoing criticism applied to the first version of the “parts on sale” vs. “parts in stock” example. However, the real problem with that example was that, given a particular tuple to be deleted from the difference DLK, the DBMS was unable to tell whether that tuple logically belonged in relvar PK or not. In effect, the pertinent restriction condition for relvar PK in that example was simply TRUE. And my proposed solution to this problem was, in effect, to redesign the database in such a way that the DBMS could tell which relvar(s) a given tuple logically belonged in after all—a solution that I venture to suggest will often work in practice, and indeed is likely to offer benefits in other areas as well, in addition to view updating as such.
[111] I suggest using Venn diagrams to help in following the ensuing discussion.
[112] Actually we could ignore this possibility, since we saw in Chapter 4 that no rule ever requests insertion of a tuple that’s already present, even if its formulation in concrete syntax appears to do so.
[113] Once again I remind you that David McGoveran has a proposal for resolving such ambiguities, which I’ll be discussing in Chapter 15.
[114] You might recall from the previous two chapters that there was a related issue that arose at this point: Under the update rules defined in those chapters, inserting a tuple into an intersection view and then deleting it again, or deleting a tuple from a union view and then inserting it again, might not preserve the status quo (the status quo, that is, with respect to the relvars in terms of which the view in question is defined—the status quo is always preserved with respect to the view as such). I’ll leave it as another exercise to determine whether any analogous issues arise with difference views.
[115] As in Chapters Chapter 9 and Chapter 10, there’s also a constraint to the effect that the restrictions PL’ WHERE IN_STOCK and PK’ WHERE ON_SALE must be equal, as a consequence of which relvars PL’ and PK’ violate The Principle of Orthogonal Design.
[116] Strictly speaking, the portion of this predicate in parentheses should read “and CITY is not London and is not (not Paris).” But it’s easy to see that this latter simplifies to just “and CITY is Paris.” It follows that the update behavior of DLP and NPS with respect to each other should be identical to that of LS and NLS with respect to each other (see Chapter 4), except of course for the fact that references to London must all be replaced by references to Paris. Note: By contrast, the predicate for NPS MINUS NLS is Supplier SNO is under contract, is named SNAME, has status STATUS, and is located in city CITY (and CITY is London).
[117] Again recall our assumption from Chapter 4, according to which every tuple in d also appears in NPS.
[118] I remind you yet again that David McGoveran has a proposal for resolving such ambiguities, which I’ll be discussing in Chapter 15.