The secant method uses secant lines to find the root. A secant line is a straight line that intersects two points of a curve. In the secant method, a line is drawn between two points on the continuous function such that it extends and intersects the axis. This method can be thought of as a Quasi-Newton method. By successively drawing such secant lines, the root of the function can be approximated.

The secant method is graphically represented in the following screenshot. An initial guess of the two axis values and is required to find and . A secant line y is drawn from to and intersects at point on the axis such that:

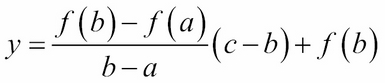
The solution to is therefore:

On the next iteration, and will take on the values of and respectively. The method repeats itself, drawing secant lines for the axis values of and , and , and , and so on. The solution terminates when the maximum number of iterations has been reached or the difference between and has reached a prespecified tolerance level, as shown in the following graph:

The rate of convergence of the secant method is considered to be superlinear. Its secant method converges much faster than the bisection method and slower than Newton's method. In Newton's method, the number of floating-point operations takes up twice as much time as the secant method in the computation of both its function and its derivative on every iteration. Since the secant method requires only computation of its function at every step, it can be considered faster in absolute time.

It is required that the initial guess values of the secant method be close to the root, otherwise it has no guarantee of converging to the solution.

The Python code for the secant method is given as follows:

""" The secant root-finding method """


def secant(f, a, b, tol=0.001, maxiter=100):
    """
    :param f: The function to solve
    :param a: Initial x-axis guess value
    :param b: Initial x-axis guess value, where b>a
    :param tol: The precision of the solution
    :param maxiter: Maximum number of iterations
    :return: The x-axis value of the root,
                number of iterations used
    """
    n = 1
    while n <= maxiter:
        c = b - f(b)*((b-a)/(f(b)-f(a)))
        if abs(c-b) < tol:
            return c, n

        a = b
        b = c
        n += 1

    return None, n

Again, we will reuse the same nonlinear function and return the results from the secant method:

>>> y = lambda x: x**3 + 2*x**2 - 5
>>> root, iterations = secant(y, -5.0, 5.0, 0.00001, 100)
>>> print "Root is:", root
>>> print "Iterations:", iterations
Root is: 1.24189656226 
Iterations: 14

Though all of the preceding root-finding methods gave very close solutions, the secant method performs with fewer iterations compared to the bisection method, but with more than Newton's method.