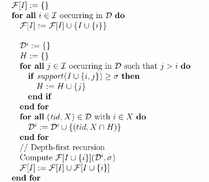Market basket analysis is the methodology used to mine a shopping cart of items bought or just those kept in the cart by customers. The concept is applicable to a variety of applications, especially for store operations. The source dataset is a massive data record. The aim of market basket analysis is to find the association rules between the items within the source dataset.
The market basket model is a model that illustrates the relation between a basket and its associated items. Many tasks from different areas of research have this relation in common. To summarize them all, the market basket model is suggested as the most typical example to be researched.
The basket is also known as the transaction set; this contains the itemsets that are sets of items belonging to same itemset.
The A-Priori algorithm is a level wise, itemset mining algorithm. The Eclat algorithm is a tidset intersection itemset mining algorithm based on tidset intersection in contrast to A-Priori. FP-growth is a frequent pattern tree algorithm. The tidset denotes a collection of zeros or IDs of transaction records.
As a common strategy to design algorithms, the problem is divided into two subproblems:
- The frequent itemset generation
- Rule generation
The strategy dramatically decreases the search space for association mining algorithms.
As the input of the A-Priori algorithm, the original input itemset is binarized, that is, 1 represents the presence of a certain item in the itemset; otherwise, it is 0. As a default assumption, the average size of the itemset is small. The popular preprocessing method is to map each unique available item in the input dataset to a unique integer ID.
The itemsets are usually stored within databases or files and will go through several passes. To control the efficiency of the algorithm, we need to control the count of passes. During the process when itemsets pass through other itemsets, the representation format for each itemset you are interested in is required to count and store for further usage of the algorithm.
There is a monotonicity feature in the itemsets under research; this implies that every subset of a frequent itemset is frequent. This characteristic is used to prune the search space for the frequent itemset in the process of the A-Priori algorithm. It also helps compact the information related to the frequent itemset. This feature gives us an intrinsic view that focuses on smaller-sized frequent itemsets. For example, there are three frequent 2-itemsets contained by one certain frequent 3-itemset.
The basket is in a format called the horizontal format and contains a basket or transaction ID and a number of items; it is used as the basic input format for the A-Priori algorithm. In contrast, there is another format known as the vertical format; this uses an item ID and a series of the transaction IDs. The algorithm that works on vertical data format is left as an exercise for you.
Two actions are performed in the generation process of the A-Priori frequent itemset: one is join, and the other is prune.
- Join action: Given that
 is the set of frequent k-itemsets, a set of candidates to find
is the set of frequent k-itemsets, a set of candidates to find  is generated. Let's call it
is generated. Let's call it  .
.

- Prune action:
 , the size of
, the size of  , the candidate itemset, is usually much bigger than
, the candidate itemset, is usually much bigger than  , to save computation cost; monotonicity characteristic of frequent itemset is used here to prune the size of
, to save computation cost; monotonicity characteristic of frequent itemset is used here to prune the size of  .
.

Here is the pseudocode to find all the frequent itemsets:



R code of the A-Priori frequent itemset generation algorithm goes here. D is a transaction dataset. Suppose MIN_SUP is the minimum support count threshold. The output of the algorithm is L, which is a frequent itemsets in D.
The output of the A-Priori function can be verified with the R add-on package, arules, which is a pattern-mining and association-rules-mining package that includes A-Priori and éclat algorithms. Here is the R code:
Apriori <- function (data, I, MIN_SUP, parameter = NULL){
f <- CreateItemsets()
c <- FindFrequentItemset(data,I,1, MIN_SUP)
k <- 2
len4data <- GetDatasetSize(data)
while( !IsEmpty(c[[k-1]]) ){
f[[k]] <- AprioriGen(c[k-1])
for( idx in 1: len4data ){
ft <- GetSubSet(f[[k]],data[[idx]])
len4ft <- GetDatasetSize(ft)
for( jdx in 1:len4ft ){
IncreaseSupportCount(f[[k]],ft[jdx])
}
}
c[[k]] <- FindFrequentItemset(f[[k]],I,k,MIN_SUP)
k <- k+1
}
c
}To verify the R code, the arules package is applied while verifying the output.
Given:
At first, we will sort D into an ordered list in a predefined order algorithm or simply the natural order of characters, which is used here. Then:

Let's assume that the minimum support count is 5; the following table is an input dataset:
|
tid (transaction id) |
List of items in the itemset or transaction |
|---|---|
|
T001 |
|
|
T002 |
|
|
T003 |
|
|
T004 |
|
|
T005 |
|
|
T006 |
|
|
T007 |
|
|
T008 |
|
|
T009 |
|
|
T010 |
|
In the first scan or pass of the dataset D, get the count of each candidate itemset ![]() . The candidate itemset and its related count:
. The candidate itemset and its related count:
|
Itemset |
Support count |
|---|---|
|
|
6 |
|
|
8 |
|
|
2 |
|
|
5 |
|
|
2 |
|
|
3 |
|
|
3 |
We will get the ![]() after comparing the support count with minimum support count.
after comparing the support count with minimum support count.
|
Itemset |
Support count |
|---|---|
|
|
6 |
|
|
8 |
|
|
5 |
We will generate ![]() by
by ![]() ,
, ![]() .
.
|
Itemset |
Support count |
|---|---|
|
|
4 |
|
|
3 |
|
|
4 |
After comparing the support count with the minimum support count, we will get ![]() . The algorithm then terminates.
. The algorithm then terminates.
The A-Priori algorithm loops as many times as the maximum length of the pattern somewhere. This is the motivation for the Equivalence CLASS Transformation (Eclat) algorithm. The Eclat algorithm explores the vertical data format, for example, using <item id, tid set> instead of <tid, item id set> that is, with the input data in the vertical format in the sample market basket file, or to discover frequent itemsets from a transaction dataset. The A-Priori property is also used in this algorithm to get frequent (k+1) itemsets from k itemsets.
The candidate itemset is generated by set intersection. The vertical format structure is called a tidset as defined earlier. If all the transaction IDs related to the item I are stored in a vertical format transaction itemset, then the itemset is the tidset of the specific item.
The support count is computed by the intersection between tidsets. Given two tidsets, X and Y, ![]() is the cardinality of
is the cardinality of ![]() . The pseudocode is
. The pseudocode is ![]() ,
, ![]() .
.

Here is the R code for the Eclat algorithm to find the frequent patterns. Before calling the function, f is set to empty, and p is the set of frequent 1-itemsets:
Eclat <- function (p,f,MIN_SUP){
len4tidsets <- length(p)
for(idx in 1:len4tidsets){
AddFrequentItemset(f,p[[idx]],GetSupport(p[[idx]]))
Pa <- GetFrequentTidSets(NULL,MIN_SUP)
for(jdx in idx:len4tidsets){
if(ItemCompare(p[[jdx]],p[[idx]]) > 0){
xab <- MergeTidSets(p[[idx]],p[[jdx]])
if(GetSupport(xab)>=MIN_SUP){
AddFrequentItemset(pa,xab,
GetSupport(xab))
}
}
}
if(!IsEmptyTidSets(pa)){
Eclat(pa,f,MIN_SUP)
}
}
}Here is the running result of one example, I = {beer, chips, pizza, wine}. The transaction dataset with horizontal and vertical formats, respectively, are shown in the following table:
|
tid |
X |
|---|---|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
x |
tidset |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
The binary format of this information is in the following table.
|
tid |
beer |
chips |
pizza |
wine |
|---|---|---|---|---|
|
1 |
1 |
1 |
0 |
1 |
|
2 |
1 |
1 |
0 |
0 |
|
3 |
0 |
0 |
1 |
1 |
|
4 |
0 |
1 |
1 |
0 |
Before calling the Eclat algorithm, we will set MIN_SUP=2, ![]() ,
,
The running process is illustrated in the following figure. After two iterations, we will get frequent tidsets, {beer, 12 >, < chips, 124>, <pizza, 34>, <wine, 13>, < {beer, chips}, 12>}:

The output of the Eclat function can be verified with the R add-on package, arules.
The FP-growth algorithm is an efficient method targeted at mining frequent itemsets in a large dataset. The main difference between the FP-growth algorithm and the A-Priori algorithm is that the generation of a candidate itemset is not needed here. The pattern-growth strategy is used instead. The FP-tree is the data structure.
The data structure used is a hybrid of vertical and horizontal datasets; all the transaction itemsets are stored within a tree structure. The tree structure used in this algorithm is called a frequent pattern tree. Here is example of the generation of the structure, I = {A, B, C, D, E, F}; the transaction dataset D is in the following table, and the FP-tree building process is shown in the next upcoming image. Each node in the FP-tree represents an item and the path from the root to that item, that is, the node list represents an itemset. The support information of this itemset is included in the node as well as the item too.
|
tid |
X |
|---|---|
|
1 |
{A, B, C, D, E} |
|
2 |
{A, B, C, E} |
|
3 |
{A, D, E} |
|
4 |
{B, E, D} |
|
5 |
{B, E, C} |
|
6 |
{E, C, D} |
|
7 |
{E, D} |
The sorted item order is listed in the following table:
|
item |
E |
D |
C |
B |
A |
|
support_count |
7 |
5 |
4 |
4 |
3 |
Reorder the transaction dataset with this new decreasing order; get the new sorted transaction dataset, as shown in this table:
|
tid |
X |
|---|---|
|
1 |
{E, D, C, B, A} |
|
2 |
{E, C, B, A} |
|
3 |
{E, D, A} |
|
4 |
{E, D, B} |
|
5 |
{E, C, B} |
|
6 |
{E, D, C} |
|
7 |
{E, D} |
The FP-tree building process is illustrated in the following images, along with the addition of each itemset to the FP-tree. The support information is calculated at the same time, that is, the support counts of the items on the path to that specific node are incremented.
The most frequent items are put at the top of the tree; this keeps the tree as compact as possible. To start building the FP-tree, the items should be decreasingly ordered by the support count. Next, get the list of sorted items and remove the infrequent ones. Then, reorder each itemset in the original transaction dataset by this order.
Given MIN_SUP=3, the following itemsets can be processed according to this logic:

The result after performing steps 4 and 7 are listed here, and the process of the algorithm is very simple and straight forward:

A header table is usually bound together with the frequent pattern tree. A link to the specific node, or the item, is stored in each record of the header table.

The FP-tree serves as the input of the FP-growth algorithm and is used to find the frequent pattern or itemset. Here is an example of removing the items from the frequent pattern tree in a reverse order or from the leaf; therefore, the order is A, B, C, D, and E. Using this order, we will then build the projected FP-tree for each item.
Here is the R source code of the main FP-growth algorithm:
FPGrowth <- function (r,p,f,MIN_SUP){
RemoveInfrequentItems(r)
if(IsPath(r)){
y <- GetSubset(r)
len4y <- GetLength(y)
for(idx in 1:len4y){
x <- MergeSet(p,y[idx])
SetSupportCount(x, GetMinCnt(x))
Add2Set(f,x,support_count(x))
}
}else{
len4r <- GetLength(r)
for(idx in 1:len4r){
x <- MergeSet(p,r[idx])
SetSupportCount(x, GetSupportCount(r[idx]))
rx <- CreateProjectedFPTree()
path4idx <- GetAllSubPath(PathFromRoot(r,idx))
len4path <- GetLength(path4idx)
for( jdx in 1:len4path ){
CountCntOnPath(r, idx, path4idx, jdx)
InsertPath2ProjectedFPTree(rx, idx, path4idx, jdx, GetCnt(idx))
}
if( !IsEmpty(rx) ){
FPGrowth(rx,x,f,MIN_SUP)
}
}
}
}The GenMax algorithm is used to mine maximal frequent itemset (MFI) to which the maximality properties are applied, that is, more steps are added to check the maximal frequent itemsets instead of only frequent itemsets. This is based partially on the tidset intersection from the Eclat algorithm. The diffset, or the differential set as it is also known, is used for fast frequency testing. It is the difference between two tidsets of the corresponding items.
The candidate MFI is determined by its definition: assuming M as the set of MFI, if there is one X that belongs to M and it is the superset of the newly found frequent itemset Y, then Y is discarded; however, if X is the subset of Y, then X should be removed from M.
Here is the pseudocode before calling the GenMax algorithm, ![]() , where D is the input transaction dataset.
, where D is the input transaction dataset.

Here is the R source code of the main GenMax algorithm:
GenMax <- function (p,m,MIN_SUP){
y <- GetItemsetUnion(p)
if( SuperSetExists(m,y) ){
return
}
len4p <- GetLenght(p)
for(idx in 1:len4p){
q <- GenerateFrequentTidSet()
for(jdx in (idx+1):len4p){
xij <- MergeTidSets(p[[idx]],p[[jdx]])
if(GetSupport(xij)>=MIN_SUP){
AddFrequentItemset(q,xij,GetSupport(xij))
}
}
if( !IsEmpty(q) ){
GenMax(q,m,MIN_SUP)
}else if( !SuperSetExists(m,p[[idx]]) ){
Add2MFI(m,p[[idx]])
}
}
}Closure checks are performed during the mining of closed frequent itemsets. Closed frequent itemsets allow you to get the longest frequent patterns that have the same support. This allows us to prune frequent patterns that are redundant. The Charm algorithm also uses the vertical tidset intersection for efficient closure checks.
Here is the pseudocode before calling the Charm algorithm, ![]() , where D is the input transaction dataset.
, where D is the input transaction dataset.



Here is the R source code of the main algorithm:
Charm <- function (p,c,MIN_SUP){
SortBySupportCount(p)
len4p <- GetLength(p)
for(idx in 1:len4p){
q <- GenerateFrequentTidSet()
for(jdx in (idx+1):len4p){
xij <- MergeTidSets(p[[idx]],p[[jdx]])
if(GetSupport(xij)>=MIN_SUP){
if( IsSameTidSets(p,idx,jdx) ){
ReplaceTidSetBy(p,idx,xij)
ReplaceTidSetBy(q,idx,xij)
RemoveTidSet(p,jdx)
}else{
if( IsSuperSet(p[[idx]],p[[jdx]]) ){
ReplaceTidSetBy(p,idx,xij)
ReplaceTidSetBy(q,idx,xij)
}else{
Add2CFI(q,xij)
}
}
}
}
if( !IsEmpty(q) ){
Charm(q,c,MIN_SUP)
}
if( !IsSuperSetExists(c,p[[idx]]) ){
Add2CFI(m,p[[idx]])
}
}
}During the process of generating an algorithm for A-Priori frequent itemsets, the support count of each frequent itemset is calculated and recorded for further association rules mining processing, that is, for association rules mining.
To generate an association rule ![]() ,
, l is a frequent itemset. Two steps are needed:
- First to get all the nonempty subsets of l.
-
Then, for subset X of l,
 , the rule
, the rule  is a strong association rule only if
is a strong association rule only if  The support count of any rule of a frequent itemset is not less than the minimum support count.
The support count of any rule of a frequent itemset is not less than the minimum support count.

R code of the algorithm to generate A-Priori association is as follows:
Here is the R source code of the main algorithm:AprioriGenerateRules <- function (D,F,MIN_SUP,MIN_CONF){
#create empty rule set
r <- CreateRuleSets()
len4f <- length(F)
for(idx in 1:len4f){
#add rule F[[idx]] => {}
AddRule2RuleSets(r,F[[idx]],NULL)
c <- list()
c[[1]] <- CreateItemSets(F[[idx]])
h <- list()
k <-1
while( !IsEmptyItemSets(c[[k]]) ){
#get heads of confident association rule in c[[k]]
h[[k]] <- getPrefixOfConfidentRules(c[[k]],
F[[idx]],D,MIN_CONF)
c[[k+1]] <- CreateItemSets()
#get candidate heads
len4hk <- length(h[[k]])
for(jdx in 1:(len4hk-1)){
if( Match4Itemsets(h[[k]][jdx],
h[[k]][jdx+1]) ){
tempItemset <- CreateItemset
(h[[k]][jdx],h[[k]][jdx+1][k])
if( IsSubset2Itemsets(h[[k]],
tempItemset) ){
Append2ItemSets(c[[k+1]],
tempItemset)
}
}
}
}
#append all new association rules to rule set
AddRule2RuleSets(r,F[[idx]],h)
}
r
}To verify the R code, Arules and Rattle packages are applied while verifying the output.