Some R machine learning packages present confusion matrices and performance measures during the model building process. The purpose of these statistics is to provide insight about the model's resubstitution error, which occurs when the training data is incorrectly predicted in spite of the model being built directly from this data. This information can be used as a rough diagnostic to identify obviously poor performers.
The resubstitution error is not a very useful marker of future performance. For example, a model that used rote memorization to perfectly classify every training instance with zero resubstitution error would be unable to generalize its predictions to data it has never seen before. For this reason, the error rate on the training data can be extremely optimistic about a model's future performance.
Instead of relying on resubstitution error, a better practice is to evaluate a model's performance on data it has not yet seen. We used this approach in previous chapters when we split the available data into a set for training and a set for testing. In some cases, however, it is not always ideal to create training and test datasets. For instance, in a situation where you have only a small pool of data, you might not want to reduce the sample any further.
Fortunately, there are other ways to estimate a model's performance on unseen data. The caret package we used to calculate performance measures also offers a number of functions to estimate future performance. If you are following the R code examples and haven't already installed the caret package, please do so. You will also need to load the package to the R session, using the library(caret) command.
The procedure of partitioning data into training and test datasets that we used in previous chapters is known as the holdout method. As shown in the following diagram, the training dataset is used to generate the model, which is then applied to the test dataset to generate predictions for evaluation. Typically, about one-third of the data is held out for testing, and two-thirds is used for training, but this proportion can vary depending on the amount of available data. To ensure that the training and test data do not have systematic differences, their examples are randomly divided into the two groups.
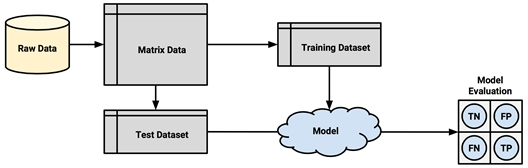
For the holdout method to result in a truly accurate estimate of the future performance, at no time should the performance on the test dataset be allowed to influence the model. It is easy to unknowingly violate this rule by choosing the best model based upon the results of repeated testing. For example, suppose we built several models on the training data, and selected the one with the highest accuracy on the test data. Because we have cherry-picked the best result, the test performance is not an unbiased measure of the performance on unseen data.
To avoid this problem, it is better to divide the original data so that in addition to the training datasets and the test datasets, a validation dataset is available. The validation dataset would be used for iterating and refining the model or models chosen, leaving the test dataset to be used only once as a final step to report an estimated error rate for future predictions. A typical split between training, test, and validation would be 50 percent, 25 percent, and 25 percent, respectively.

Tip
A keen reader will note that holdout test data was used in the previous chapters to both evaluate models and improve model performance. This was done for illustrative purposes, but it would indeed violate the rule as stated previously. Consequently, the model performance statistics shown were not valid estimates of future performance on unseen data and the process could have been more accurately termed validation.
A simple method to create holdout samples uses random number generators to assign records to partitions. This technique was first used in Chapter 5, Divide and Conquer – Classification Using Decision Trees and Rules to create training and test datasets.
Suppose we have a data frame named credit with 1000 rows of data. We can divide it into three partitions as follows. First, we create a vector of randomly ordered row IDs from 1 to 1000 using the runif() function, which by default generates a specified number of random values between 0 and 1. The runif() function gets its name from the random uniform distribution, which was discussed in Chapter 2, Managing and Understanding Data.
> random_ids <- order(runif(1000))
The order() used here returns a vector indicating the rank order of the 1,000 random numbers. For example, order(c(0.5, 0.25, 0.75, 0.1)) returns the sequence 4 2 1 3 because the smallest number (0.1) appears fourth, the second smallest (0.25) appears second, and so on.
We can use the resulting random IDs to divide the credit data frame into 500, 250, and 250 records comprising the training, validation, and test datasets:
> credit_train <- credit[random_ids[1:500], ] > credit_validate <- credit[random_ids[501:750], ] > credit_test <- credit[random_ids[751:1000], ]
One problem with holdout sampling is that each partition may have a larger or smaller proportion of some classes. In certain cases, particularly those in which a class is a very small proportion of the dataset, this can lead a class to be omitted from the training dataset. This is a significant problem, because the model will not be able to learn this class.
In order to reduce the chance of this occurring, a technique called stratified random sampling can be used. Although in the long run a random sample should contain roughly the same proportion of each class value as the full dataset, stratified random sampling guarantees that the random partitions have nearly the same proportion of each class as the full dataset, even when some classes are small.
The caret package provides a createDataPartition() function that will create partitions based on stratified holdout sampling. The code to create a stratified sample of training and test data for the credit dataset is shown in the following commands. To use the function, a vector of the class values must be specified (here, default refers to whether a loan went into default) in addition to a parameter p, which specifies the proportion of instances to be included in the partition. The list = FALSE parameter prevents the result from being stored in the list format:
> in_train <- createDataPartition(credit$default, p = 0.75, list = FALSE) > credit_train <- credit[in_train, ] > credit_test <- credit[-in_train, ]
The in_train vector indicates row numbers included in the training sample. We can use these row numbers to select examples for the credit_train data frame. Similarly, by using a negative symbol, we can use the rows not found in the in_train vector for the credit_test dataset.
Although it distributes the classes evenly, stratified sampling does not guarantee other types of representativeness. Some samples may have too many or few difficult cases, easy-to-predict cases, or outliers. This is especially true for smaller datasets, which may not have a large enough portion of such cases to be divided among training and test sets.
In addition to potentially biased samples, another problem with the holdout method is that substantial portions of data must be reserved to test and validate the model. Since these data cannot be used to train the model until its performance has been measured, the performance estimates are likely to be overly conservative.
A technique called repeated holdout is sometimes used to mitigate the problems of randomly composed training datasets. The repeated holdout method is a special case of the holdout method that uses the average result from several random holdout samples to evaluate a model's performance. As multiple holdout samples are used, it is less likely that the model is trained or tested on nonrepresentative data. We'll expand on this idea in the next section.
The repeated holdout is the basis of a technique known as k-fold cross-validation (or k-fold CV), which has become the industry standard for estimating model performance. Rather than taking repeated random samples that could potentially use the same record more than once, k-fold CV randomly divides the data into k to completely separate random partitions called folds.
Although k can be set to any number, by far, the most common convention is to use 10-fold cross-validation (10-fold CV). Why 10 folds? The reason is that the empirical evidence suggests that there is little added benefit in using a greater number. For each of the 10 folds (each comprising 10 percent of the total data), a machine learning model is built on the remaining 90 percent of data. The fold's matching 10 percent sample is then used for model evaluation. After the process of training and evaluating the model has occurred for 10 times (with 10 different training/testing combinations), the average performance across all the folds is reported.
Tip
An extreme case of k-fold CV is the leave-one-out method, which performs k-fold CV using a fold for each of the data's examples. This ensures that the greatest amount of data is used to train the model. Although this may seem useful, it is so computationally expensive that it is rarely used in practice.
Datasets for cross-validation can be created using the createFolds() function in the caret package. Similar to the stratified random holdout sampling, this function will attempt to maintain the same class balance in each of the folds as in the original dataset. The following is the command to create 10 folds:
> folds <- createFolds(credit$default, k = 10)
The result of the createFolds() function is a list of vectors storing the row numbers for each of the requested k = 10 folds. We can peek at the contents, using str():
> str(folds) List of 10 $ Fold01: int [1:100] 1 5 12 13 19 21 25 32 36 38 ... $ Fold02: int [1:100] 16 49 78 81 84 93 105 108 128 134 ... $ Fold03: int [1:100] 15 48 60 67 76 91 102 109 117 123 ... $ Fold04: int [1:100] 24 28 59 64 75 85 95 97 99 104 ... $ Fold05: int [1:100] 9 10 23 27 29 34 37 39 53 61 ... $ Fold06: int [1:100] 4 8 41 55 58 103 118 121 144 146 ... $ Fold07: int [1:100] 2 3 7 11 14 33 40 45 51 57 ... $ Fold08: int [1:100] 17 30 35 52 70 107 113 129 133 137 ... $ Fold09: int [1:100] 6 20 26 31 42 44 46 63 79 101 ... $ Fold10: int [1:100] 18 22 43 50 68 77 80 88 106 111 ...
Here, we see that the first fold is named Fold01 and stores 100 integers, indicating the 100 rows in the credit data frame for the first fold. To create training and test datasets to build and evaluate a model, an additional step is needed. The following commands show how to create data for the first fold. We'll assign the selected 10 percent to the test dataset, and use the negative symbol to assign the remaining 90 percent to the training dataset:
> credit01_test <- credit[folds$Fold01, ] > credit01_train <- credit[-folds$Fold01, ]
To perform the full 10-fold CV, this step would need to be repeated a total of 10 times; building a model and then calculating the model's performance each time. At the end, the performance measures would be averaged to obtain the overall performance. Thankfully, we can automate this task by applying several of the techniques we've learned earlier.
To demonstrate the process, we'll estimate the kappa statistic for a C5.0 decision tree model of the credit data using 10-fold CV. First, we need to load some R packages: caret (to create the folds), C50 (for the decision tree), and irr (to calculate kappa). The latter two packages were chosen for illustrative purposes; if you desire, you can use a different model or a different performance measure along with the same series of steps.
> library(caret) > library(C50) > library(irr)
Next, we'll create a list of 10 folds as we have done previously. The set.seed() function is used here to ensure that the results are consistent if the same code is run again:
> set.seed(123) > folds <- createFolds(credit$default, k = 10)
Finally, we will apply a series of identical steps to the list of folds using the lapply() function. As shown in the following code, because there is no existing function that does exactly what we need, we must define our own function to pass to lapply(). Our custom function divides the credit data frame into training and test data, builds a decision tree using the C5.0() function on the training data, generates a set of predictions from the test data, and compares the predicted and actual values using the kappa2() function:
> cv_results <- lapply(folds, function(x) { credit_train <- credit[-x, ] credit_test <- credit[x, ] credit_model <- C5.0(default ~ ., data = credit_train) credit_pred <- predict(credit_model, credit_test) credit_actual <- credit_test$default kappa <- kappa2(data.frame(credit_actual, credit_pred))$value return(kappa) })
The resulting kappa statistics are compiled into a list stored in the cv_results object, which we can examine using str():
> str(cv_results) List of 10 $ Fold01: num 0.343 $ Fold02: num 0.255 $ Fold03: num 0.109 $ Fold04: num 0.107 $ Fold05: num 0.338 $ Fold06: num 0.474 $ Fold07: num 0.245 $ Fold08: num 0.0365 $ Fold09: num 0.425 $ Fold10: num 0.505
There's just one more step remaining in the 10-fold CV process: we must calculate the average of these 10 values. Although you will be tempted to type mean(cv_results), because cv_results is not a numeric vector, the result would be an error. Instead, use the unlist() function, which eliminates the list structure, and reduces cv_results to a numeric vector. From here, we can calculate the mean kappa as expected:
> mean(unlist(cv_results)) [1] 0.283796
This kappa statistic is fairly low, corresponding to "fair" on the interpretation scale, which suggests that the credit scoring model performs only marginally better than random chance. In the next chapter, we'll examine automated methods based on 10-fold CV that can assist us in improving the performance of this model.
Tip
Perhaps the current gold standard method to reliably estimate model performance is repeated k-fold CV. As you might guess from the name, this involves repeatedly applying k-fold CV and averaging the results. A common strategy is to perform 10-fold CV ten times. Although it is computationally intensive, it provides a very robust estimate.
A slightly less frequently used alternative to k-fold CV is known as bootstrap sampling, the bootstrap or bootstrapping for short. Generally speaking, these refer to the statistical methods of using random samples of data to estimate the properties of a larger set. When this principle is applied to machine learning model performance, it implies the creation of several randomly selected training and test datasets, which are then used to estimate performance statistics. The results from the various random datasets are then averaged to obtain a final estimate of future performance.
So, what makes this procedure different from k-fold CV? Whereas cross-validation divides the data into separate partitions in which each example can appear only once, the bootstrap allows examples to be selected multiple times through a process of sampling with replacement. This means that from the original dataset of n examples, the bootstrap procedure will create one or more new training datasets that will also contain n examples, some of which are repeated. The corresponding test datasets are then constructed from the set of examples that were not selected for the respective training datasets.
Using sampling with replacement as described previously, the probability that any given instance is included in the training dataset is 63.2 percent. Consequently, the probability of any instance being in the test dataset is 36.8 percent. In other words, the training data represents only 63.2 percent of available examples, some of which are repeated. In contrast to 10-fold CV, which uses 90 percent of the examples for training, the bootstrap sample is less representative of the full dataset.
Because a model trained on only 63.2 percent of the training data is likely to perform worse than a model trained on a larger training set, the bootstrap's performance estimates may be substantially lower than what would be obtained when the model is later trained on the full dataset. A special case of bootstrapping known as the 0.632 bootstrap accounts for this by calculating the final performance measure as a function of performance on both the training data (which is overly optimistic) and the test data (which is overly pessimistic). The final error rate is then estimated as:
One advantage of bootstrap over cross-validation is that it tends to work better with very small datasets. Additionally, bootstrap sampling has applications beyond performance measurement. In particular, in the next chapter we'll learn how the principles of bootstrap sampling can be used to improve model performance.

