While deciding between several job offers with various levels of pay and benefits, many people begin by making lists of pros and cons, and eliminate options based on simple rules. For instance, ''if I have to commute for more than an hour, I will be unhappy.'' Or, ''if I make less than $50k, I won't be able to support my family.'' In this way, the complex and difficult decision of predicting one's future happiness can be reduced to a series of simple decisions.
This chapter covers decision trees and rule learners—two machine learning methods that also make complex decisions from sets of simple choices. These methods then present their knowledge in the form of logical structures that can be understood with no statistical knowledge. This aspect makes these models particularly useful for business strategy and process improvement.
By the end of this chapter, you will learn:
- How trees and rules "greedily" partition data into interesting segments
- The most common decision tree and classification rule learners, including the C5.0, 1R, and RIPPER algorithms
- How to use these algorithms to perform real-world classification tasks, such as identifying risky bank loans and poisonous mushrooms
We will begin by examining decision trees, followed by a look at classification rules. Then, we will summarize what we've learned by previewing later chapters, which discuss methods that use trees and rules as a foundation for more advanced machine learning techniques.
Decision tree learners are powerful classifiers, which utilize a tree structure to model the relationships among the features and the potential outcomes. As illustrated in the following figure, this structure earned its name due to the fact that it mirrors how a literal tree begins at a wide trunk, which if followed upward, splits into narrower and narrower branches. In much the same way, a decision tree classifier uses a structure of branching decisions, which channel examples into a final predicted class value.
To better understand how this works in practice, let's consider the following tree, which predicts whether a job offer should be accepted. A job offer to be considered begins at the root node, where it is then passed through decision nodes that require choices to be made based on the attributes of the job. These choices split the data across branches that indicate potential outcomes of a decision, depicted here as yes or no outcomes, though in some cases there may be more than two possibilities. In the case a final decision can be made, the tree is terminated by leaf nodes (also known as terminal nodes) that denote the action to be taken as the result of the series of decisions. In the case of a predictive model, the leaf nodes provide the expected result given the series of events in the tree.

A great benefit of decision tree algorithms is that the flowchart-like tree structure is not necessarily exclusively for the learner's internal use. After the model is created, many decision tree algorithms output the resulting structure in a human-readable format. This provides tremendous insight into how and why the model works or doesn't work well for a particular task. This also makes decision trees particularly appropriate for applications in which the classification mechanism needs to be transparent for legal reasons, or in case the results need to be shared with others in order to inform future business practices. With this in mind, some potential uses include:
- Credit scoring models in which the criteria that causes an applicant to be rejected need to be clearly documented and free from bias
- Marketing studies of customer behavior such as satisfaction or churn, which will be shared with management or advertising agencies
- Diagnosis of medical conditions based on laboratory measurements, symptoms, or the rate of disease progression
Although the previous applications illustrate the value of trees in informing decision processes, this is not to suggest that their utility ends here. In fact, decision trees are perhaps the single most widely used machine learning technique, and can be applied to model almost any type of data—often with excellent out-of-the-box applications.
This said, in spite of their wide applicability, it is worth noting some scenarios where trees may not be an ideal fit. One such case might be a task where the data has a large number of nominal features with many levels or it has a large number of numeric features. These cases may result in a very large number of decisions and an overly complex tree. They may also contribute to the tendency of decision trees to overfit data, though as we will soon see, even this weakness can be overcome by adjusting some simple parameters.
Decision trees are built using a heuristic called recursive partitioning. This approach is also commonly known as divide and conquer because it splits the data into subsets, which are then split repeatedly into even smaller subsets, and so on and so forth until the process stops when the algorithm determines the data within the subsets are sufficiently homogenous, or another stopping criterion has been met.
To see how splitting a dataset can create a decision tree, imagine a bare root node that will grow into a mature tree. At first, the root node represents the entire dataset, since no splitting has transpired. Next, the decision tree algorithm must choose a feature to split upon; ideally, it chooses the feature most predictive of the target class. The examples are then partitioned into groups according to the distinct values of this feature, and the first set of tree branches are formed.
Working down each branch, the algorithm continues to divide and conquer the data, choosing the best candidate feature each time to create another decision node, until a stopping criterion is reached. Divide and conquer might stop at a node in a case that:
- All (or nearly all) of the examples at the node have the same class
- There are no remaining features to distinguish among the examples
- The tree has grown to a predefined size limit
To illustrate the tree building process, let's consider a simple example. Imagine that you work for a Hollywood studio, where your role is to decide whether the studio should move forward with producing the screenplays pitched by promising new authors. After returning from a vacation, your desk is piled high with proposals. Without the time to read each proposal cover-to-cover, you decide to develop a decision tree algorithm to predict whether a potential movie would fall into one of three categories: Critical Success, Mainstream Hit, or Box Office Bust.
To build the decision tree, you turn to the studio archives to examine the factors leading to the success and failure of the company's 30 most recent releases. You quickly notice a relationship between the film's estimated shooting budget, the number of A-list celebrities lined up for starring roles, and the level of success. Excited about this finding, you produce a scatterplot to illustrate the pattern:

Using the divide and conquer strategy, we can build a simple decision tree from this data. First, to create the tree's root node, we split the feature indicating the number of celebrities, partitioning the movies into groups with and without a significant number of A-list stars:

Next, among the group of movies with a larger number of celebrities, we can make another split between movies with and without a high budget:
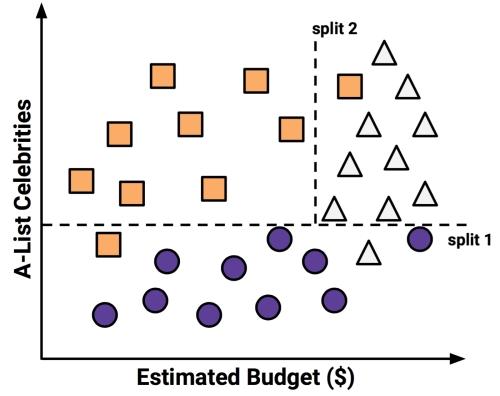
At this point, we have partitioned the data into three groups. The group at the top-left corner of the diagram is composed entirely of critically acclaimed films. This group is distinguished by a high number of celebrities and a relatively low budget. At the top-right corner, majority of movies are box office hits with high budgets and a large number of celebrities. The final group, which has little star power but budgets ranging from small to large, contains the flops.
If we wanted, we could continue to divide and conquer the data by splitting it based on the increasingly specific ranges of budget and celebrity count, until each of the currently misclassified values resides in its own tiny partition, and is correctly classified. However, it is not advisable to overfit a decision tree in this way. Though there is nothing to stop us from splitting the data indefinitely, overly specific decisions do not always generalize more broadly. We'll avoid the problem of overfitting by stopping the algorithm here, since more than 80 percent of the examples in each group are from a single class. This forms the basis of our stopping criterion.
Tip
You might have noticed that diagonal lines might have split the data even more cleanly. This is one limitation of the decision tree's knowledge representation, which uses axis-parallel splits. The fact that each split considers one feature at a time prevents the decision tree from forming more complex decision boundaries. For example, a diagonal line could be created by a decision that asks, "is the number of celebrities is greater than the estimated budget?" If so, then "it will be a critical success."
Our model for predicting the future success of movies can be represented in a simple tree, as shown in the following diagram. To evaluate a script, follow the branches through each decision until the script's success or failure has been predicted. In no time, you will be able to identify the most promising options among the backlog of scripts and get back to more important work, such as writing an Academy Awards acceptance speech.

Since real-world data contains more than two features, decision trees quickly become far more complex than this, with many more nodes, branches, and leaves. In the next section, you will learn about a popular algorithm to build decision tree models automatically.
There are numerous implementations of decision trees, but one of the most well-known implementations is the C5.0 algorithm. This algorithm was developed by computer scientist J. Ross Quinlan as an improved version of his prior algorithm, C4.5, which itself is an improvement over his Iterative Dichotomiser 3 (ID3) algorithm. Although Quinlan markets C5.0 to commercial clients (see http://www.rulequest.com/ for details), the source code for a single-threaded version of the algorithm was made publically available, and it has therefore been incorporated into programs such as R.
Note
To further confuse matters, a popular Java-based open source alternative to C4.5, titled J48, is included in R's RWeka package. Because the differences among C5.0, C4.5, and J48 are minor, the principles in this chapter will apply to any of these three methods, and the algorithms should be considered synonymous.
The C5.0 algorithm has become the industry standard to produce decision trees, because it does well for most types of problems directly out of the box. Compared to other advanced machine learning models, such as those described in Chapter 7, Black Box Methods – Neural Networks and Support Vector Machines, the decision trees built by C5.0 generally perform nearly as well, but are much easier to understand and deploy. Additionally, as shown in the following table, the algorithm's weaknesses are relatively minor and can be largely avoided:
|
Strengths |
Weaknesses |
|---|---|
|
|
To keep things simple, our earlier decision tree example ignored the mathematics involved in how a machine would employ a divide and conquer strategy. Let's explore this in more detail to examine how this heuristic works in practice.
The first challenge that a decision tree will face is to identify which feature to split upon. In the previous example, we looked for a way to split the data such that the resulting partitions contained examples primarily of a single class. The degree to which a subset of examples contains only a single class is known as purity, and any subset composed of only a single class is called pure.
There are various measurements of purity that can be used to identify the best decision tree splitting candidate. C5.0 uses entropy, a concept borrowed from information theory that quantifies the randomness, or disorder, within a set of class values. Sets with high entropy are very diverse and provide little information about other items that may also belong in the set, as there is no apparent commonality. The decision tree hopes to find splits that reduce entropy, ultimately increasing homogeneity within the groups.
Typically, entropy is measured in bits. If there are only two possible classes, entropy values can range from 0 to 1. For n classes, entropy ranges from 0 to log2(n). In each case, the minimum value indicates that the sample is completely homogenous, while the maximum value indicates that the data are as diverse as possible, and no group has even a small plurality.
In the mathematical notion, entropy is specified as follows:

In this formula, for a given segment of data (S), the term c refers to the number of class levels and pi refers to the proportion of values falling into class level i. For example, suppose we have a partition of data with two classes: red (60 percent) and white (40 percent). We can calculate the entropy as follows:
> -0.60 * log2(0.60) - 0.40 * log2(0.40) [1] 0.9709506
We can examine the entropy for all the possible two-class arrangements. If we know that the proportion of examples in one class is x, then the proportion in the other class is (1 – x). Using the curve() function, we can then plot the entropy for all the possible values of x:
> curve(-x * log2(x) - (1 - x) * log2(1 - x), col = "red", xlab = "x", ylab = "Entropy", lwd = 4)
This results in the following figure:
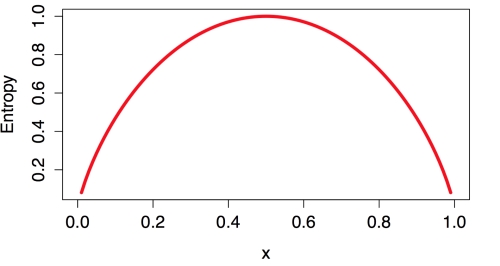
As illustrated by the peak in entropy at x = 0.50, a 50-50 split results in maximum entropy. As one class increasingly dominates the other, the entropy reduces to zero.
To use entropy to determine the optimal feature to split upon, the algorithm calculates the change in homogeneity that would result from a split on each possible feature, which is a measure known as information gain. The information gain for a feature F is calculated as the difference between the entropy in the segment before the split (S1) and the partitions resulting from the split (S2):
One complication is that after a split, the data is divided into more than one partition. Therefore, the function to calculate Entropy(S2) needs to consider the total entropy across all of the partitions. It does this by weighing each partition's entropy by the proportion of records falling into the partition. This can be stated in a formula as:

In simple terms, the total entropy resulting from a split is the sum of the entropy of each of the n partitions weighted by the proportion of examples falling in the partition (wi).
The higher the information gain, the better a feature is at creating homogeneous groups after a split on this feature. If the information gain is zero, there is no reduction in entropy for splitting on this feature. On the other hand, the maximum information gain is equal to the entropy prior to the split. This would imply that the entropy after the split is zero, which means that the split results in completely homogeneous groups.
The previous formulae assume nominal features, but decision trees use information gain for splitting on numeric features as well. To do so, a common practice is to test various splits that divide the values into groups greater than or less than a numeric threshold. This reduces the numeric feature into a two-level categorical feature that allows information gain to be calculated as usual. The numeric cut point yielding the largest information gain is chosen for the split.
Note
Though it is used by C5.0, information gain is not the only splitting criterion that can be used to build decision trees. Other commonly used criteria are Gini index, Chi-Squared statistic, and gain ratio. For a review of these (and many more) criteria, refer to Mingers J. An Empirical Comparison of Selection Measures for Decision-Tree Induction. Machine Learning. 1989; 3:319-342.
A decision tree can continue to grow indefinitely, choosing splitting features and dividing the data into smaller and smaller partitions until each example is perfectly classified or the algorithm runs out of features to split on. However, if the tree grows overly large, many of the decisions it makes will be overly specific and the model will be overfitted to the training data. The process of pruning a decision tree involves reducing its size such that it generalizes better to unseen data.
One solution to this problem is to stop the tree from growing once it reaches a certain number of decisions or when the decision nodes contain only a small number of examples. This is called early stopping or pre-pruning the decision tree. As the tree avoids doing needless work, this is an appealing strategy. However, one downside to this approach is that there is no way to know whether the tree will miss subtle, but important patterns that it would have learned had it grown to a larger size.
An alternative, called post-pruning, involves growing a tree that is intentionally too large and pruning leaf nodes to reduce the size of the tree to a more appropriate level. This is often a more effective approach than pre-pruning, because it is quite difficult to determine the optimal depth of a decision tree without growing it first. Pruning the tree later on allows the algorithm to be certain that all the important data structures were discovered.
Note
The implementation details of pruning operations are very technical and beyond the scope of this book. For a comparison of some of the available methods, see Esposito F, Malerba D, Semeraro G. A Comparative Analysis of Methods for Pruning Decision Trees. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1997;19: 476-491.
One of the benefits of the C5.0 algorithm is that it is opinionated about pruning—it takes care of many decisions automatically using fairly reasonable defaults. Its overall strategy is to post-prune the tree. It first grows a large tree that overfits the training data. Later, the nodes and branches that have little effect on the classification errors are removed. In some cases, entire branches are moved further up the tree or replaced by simpler decisions. These processes of grafting branches are known as subtree raising and subtree replacement, respectively.
Balancing overfitting and underfitting a decision tree is a bit of an art, but if model accuracy is vital, it may be worth investing some time with various pruning options to see if it improves the performance on test data. As you will soon see, one of the strengths of the C5.0 algorithm is that it is very easy to adjust the training options.
